Application of Finite Element Method to Create a Digital Elevation Model
Abstract
1. Introduction
- Obtaining a large number of points (using LiDAR, as already stated).
- Filtering the points; there are many published articles around this effort [6].
- Creating the three-dimensional surface to be used in CAD software. This is normally done with associated proprietary software from the scanning apparatus or company.
2. Methodology
- Locate the set of known points within the domain (horizontal coordinates).
- Mesh the domain.
- Apply boundary conditions.
- Solve the finite element model.
2.1. Thin Plate Formulation
2.2. Domain Definition
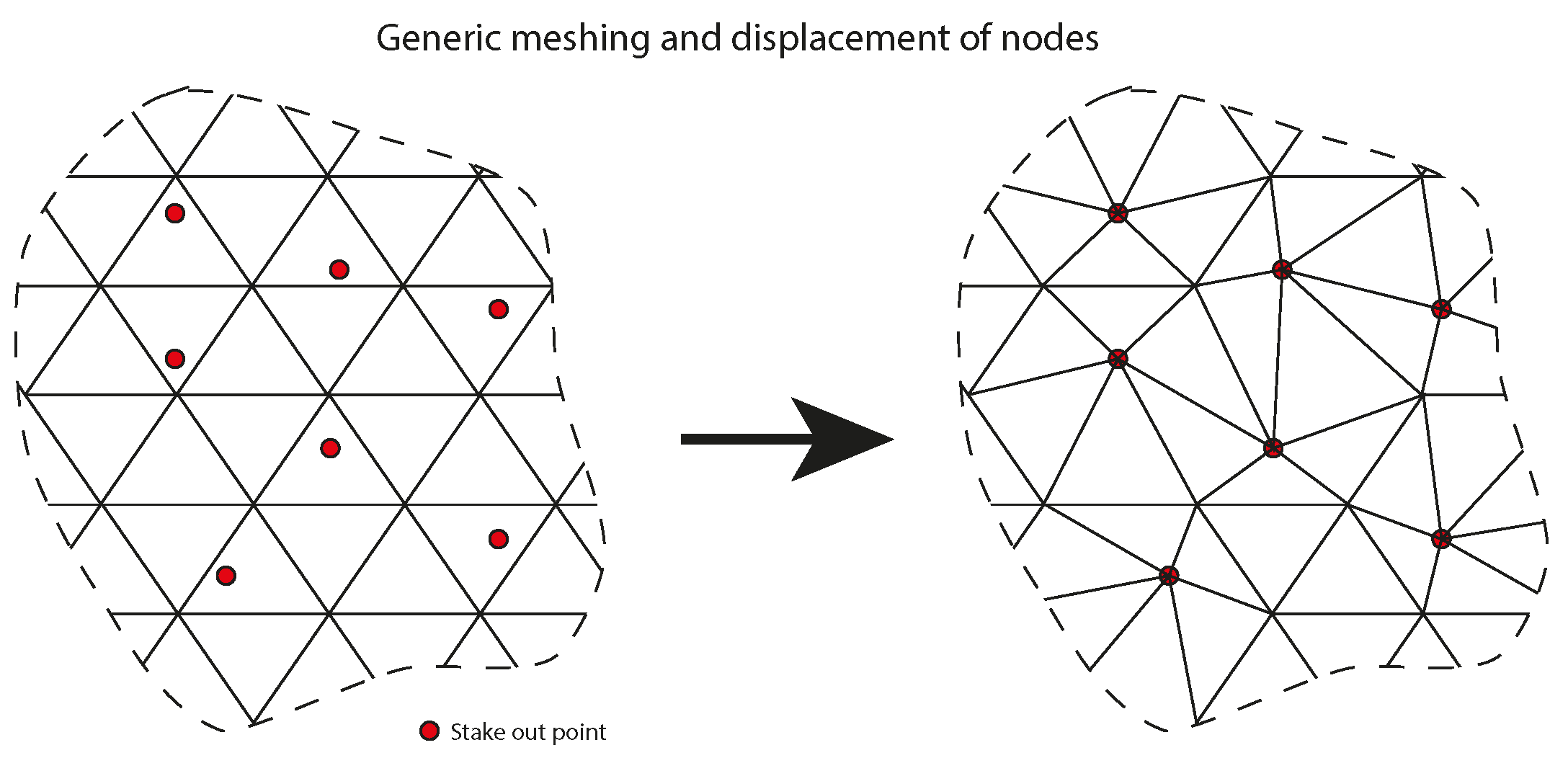
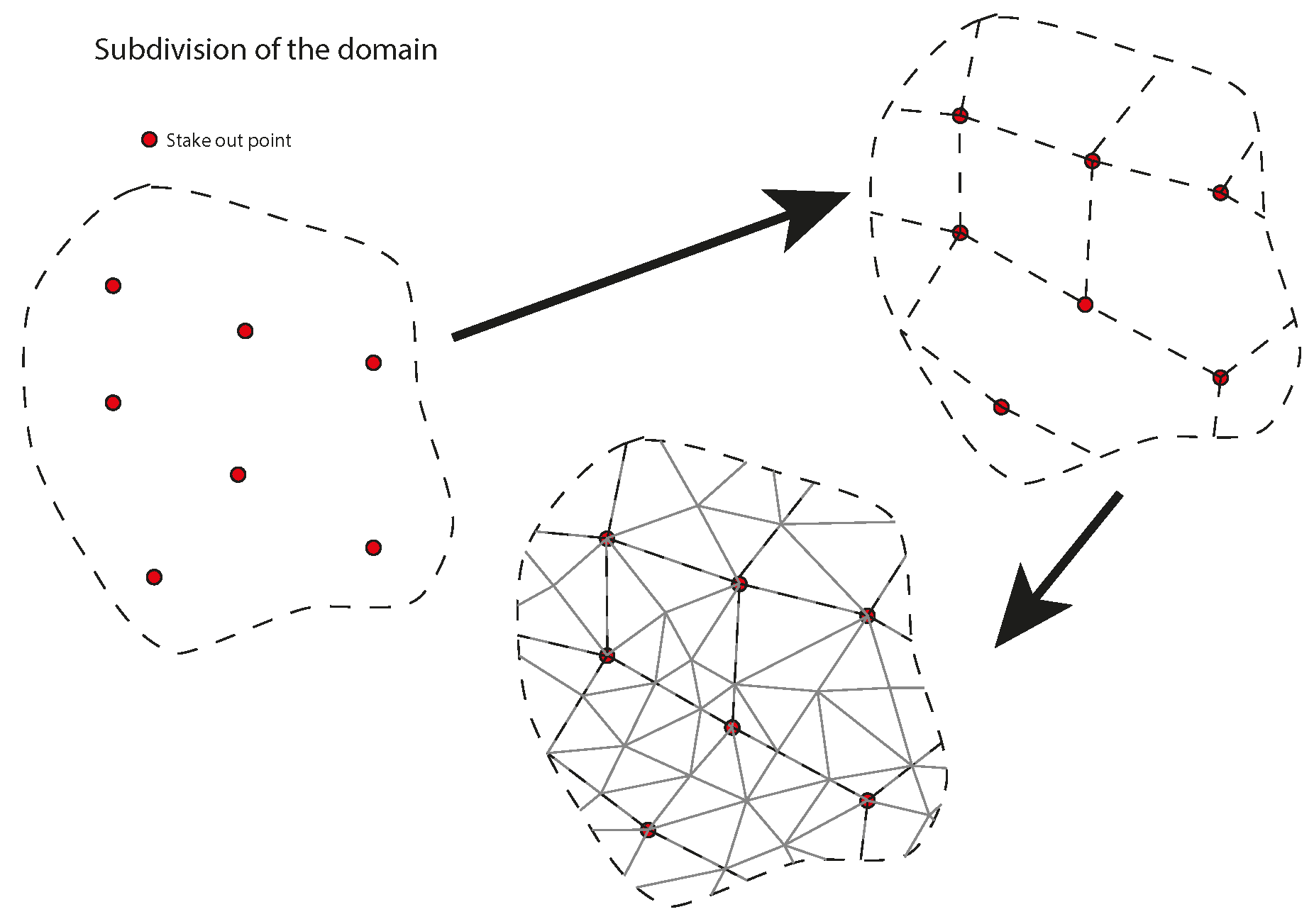
2.3. Meshing of the Domain
- Displacement of nodes on a generic mesh,
- Subdivision of the domain,
- Remeshing.
2.3.1. Generic Meshing and Displacement of Nodes
2.3.2. Subdivision of the Domain
2.3.3. Remeshing
2.4. Boundary Conditions
3. Influence of Material Parameters
4. Verification Examples
- As a regular mesh (equidistant) and
- Randomly distributed.
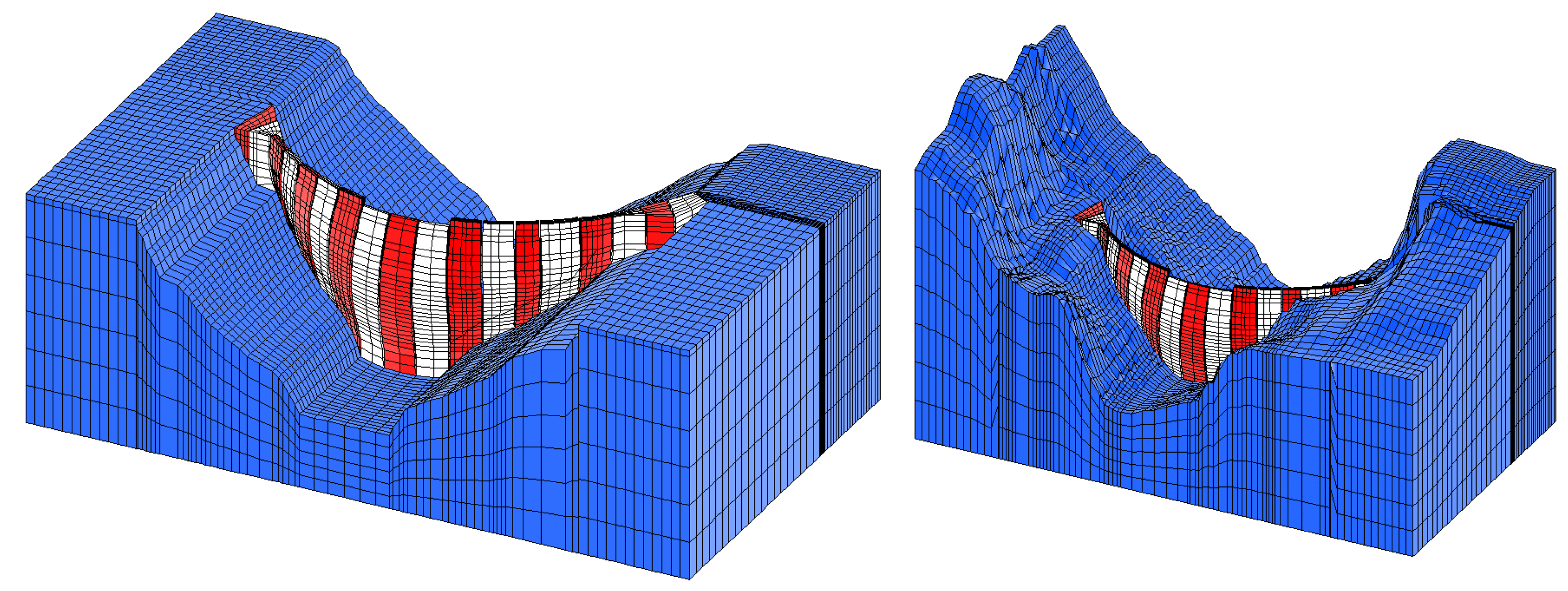
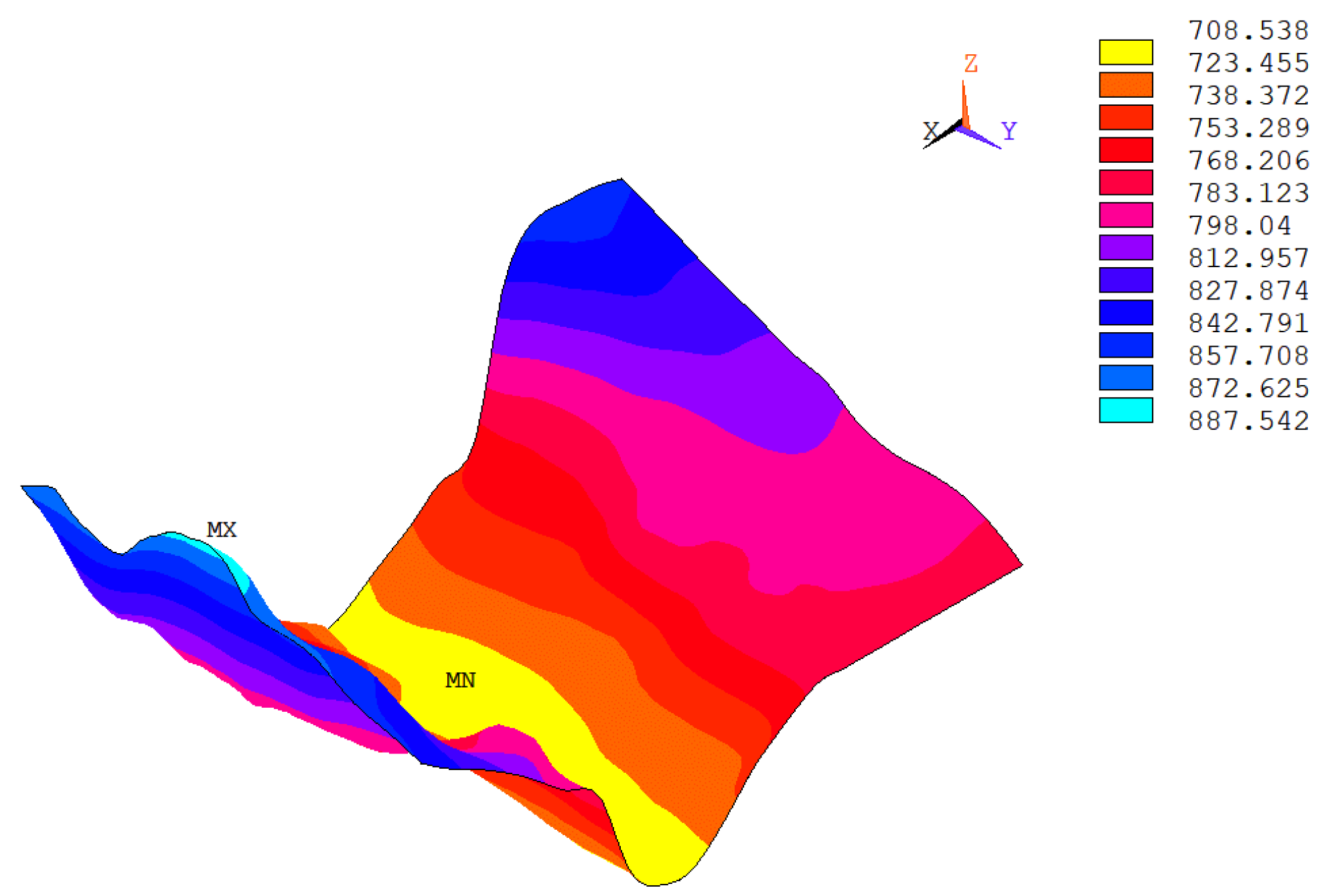
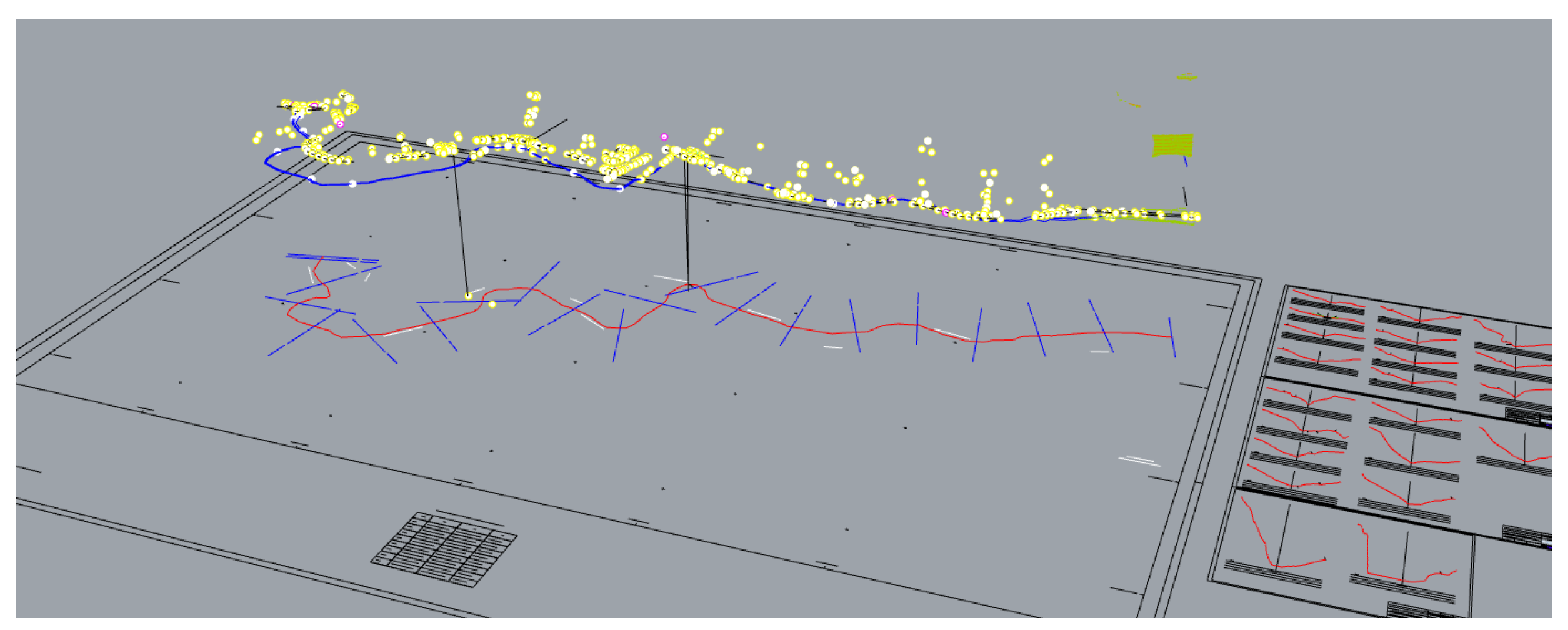
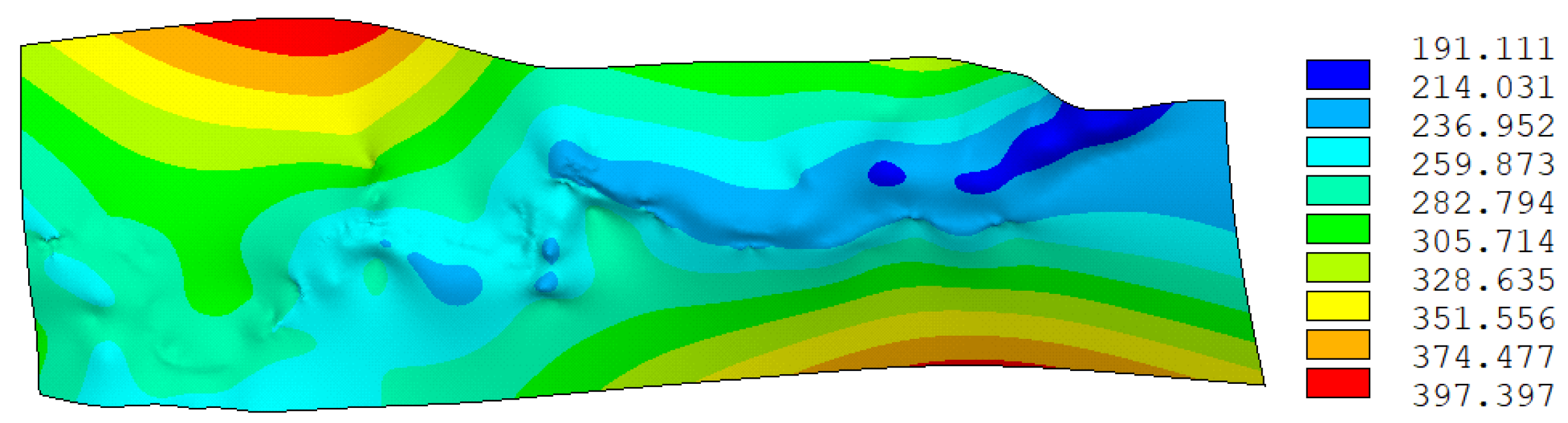
5. Real Case Example
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FEM | Finite element model |
| DEM | Digital elevation model |
| DTM | Digital terrain model |
| LiDAR | Laser Imaging Detection and Ranging |
| CAD | Computer aided design |
Appendix A. Sample Code
References
- Southard, D. Piecewise Planar Surface Models from Sampled Data. In Scientific Visualization of Physical Phenomena; ch. 11.5; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Feciskanin, R.; Minár, J. Polygonal Simplification and Its Use in DEM Generalization for Land Surface Segmentation. Trans. Gis 2021, 25, 2361–2375. [Google Scholar] [CrossRef]
- Sun, W.; Wang, H.; Zhao, X. A simplification method for grid-based DEM using topological hierarchies. Surv. Rev. 2018, 50, 454–467. [Google Scholar] [CrossRef]
- Zhu, D.; Cheng, X.; Zhang, F.; Yao, X.; Gao, Y.; Liu, Y. Spatial interpolation using conditional generative adversarial neural networks. Int. J. Geogr. Inf. Sci. 2020, 34, 735–758. [Google Scholar] [CrossRef]
- Alzaghoul, E.; Al-Zoubi, M.B.; Obiedat, R.; Alzaghoul, F. Applying Machine Learning to DEM Raster Images. Technologies 2021, 9, 87. [Google Scholar] [CrossRef]
- Podobnikar, T.; Vrečko, A. High Quality DEM from LiDAR Data. Trans. Gis 2012, 16, 603–617. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures; Klaus-Jurgen Bathe: USA, 2006; ISBN 097900490X. [Google Scholar]
- Benito, J.J.; Álvarez, R.; Ureña, F.; Salete, E.; Aranda, E. Introduction to Finite Element Method; Editorial UNED: Madrid, Spain, 2014; ISBN 978-84-362-6752-5. [Google Scholar]
- Ahmad, S.; Irons, B.M.; Zienkiewicz, O.C. Analysis of Thick and Thin Shell Structures by Curved Finite Elements. Int. J. Numer. Methods Eng. 1970, 2, 419–451. [Google Scholar] [CrossRef]
- Sharma, D.; Jiwari, R.; Kumar, S. Numerical Solution of Two Point Boundary Value Problems Using Galerkin-Finite Element Method. Int. J. Nonlinear Sci. 2012, 13, 204–210. [Google Scholar]
- Ankur; Jiwari, R.; Kuma, N. Analysis and simulation of Korteweg-de Vries-Rosenau-regularised long-wave model via Galerkin finite element method. Comput. Math. Appl. 2023, 135, 134–148. [Google Scholar] [CrossRef]
- Mitchell, A.R.; Griffiths, D.F. The Finite Difference Method in Partial Differential Equations; John Wiley & Sons: Hoboken, NJ, USA, 1980; ISBN 041727641. [Google Scholar]
- Liszka, T.; Orkisz, J. The finite difference method at arbitrary irregular grids and its application in applied mechanics. Comput. Struct. 1980, 11, 83–95. [Google Scholar] [CrossRef]
- Benito, J.J.; Ureña, L.F. Gavete, Influence of several factors in the generalized finite difference method. Appl. Math. Model. 2001, 25, 1039–1053. [Google Scholar] [CrossRef]
- Peng, Z.; Doroodchi, E.; Moghtaderi, B. Heat transfer modelling in Discrete Element Method (DEM)-based simulations of thermal processes: Theory and model development. Prog. Energy Combust. Sci. 2020, 79, 100847. [Google Scholar] [CrossRef]
- Ansys®Academic Research Mechanical APDL. Release 2022 R1, Help System, Theory Reference; ANSYS, Inc.: USA, 2022. [Google Scholar]
- Ansys®Academic Research Mechanical APDL. Release 2022 R1, Structural Analysis Guide, Theory Reference; ANSYS, Inc.: USA, 2022. [Google Scholar]
- Ansys®Academic Research Mechanical APDL. Release 2022 R1, Modeling and Meshing Guide, Theory Reference; ANSYS, Inc.: USA, 2022. [Google Scholar]



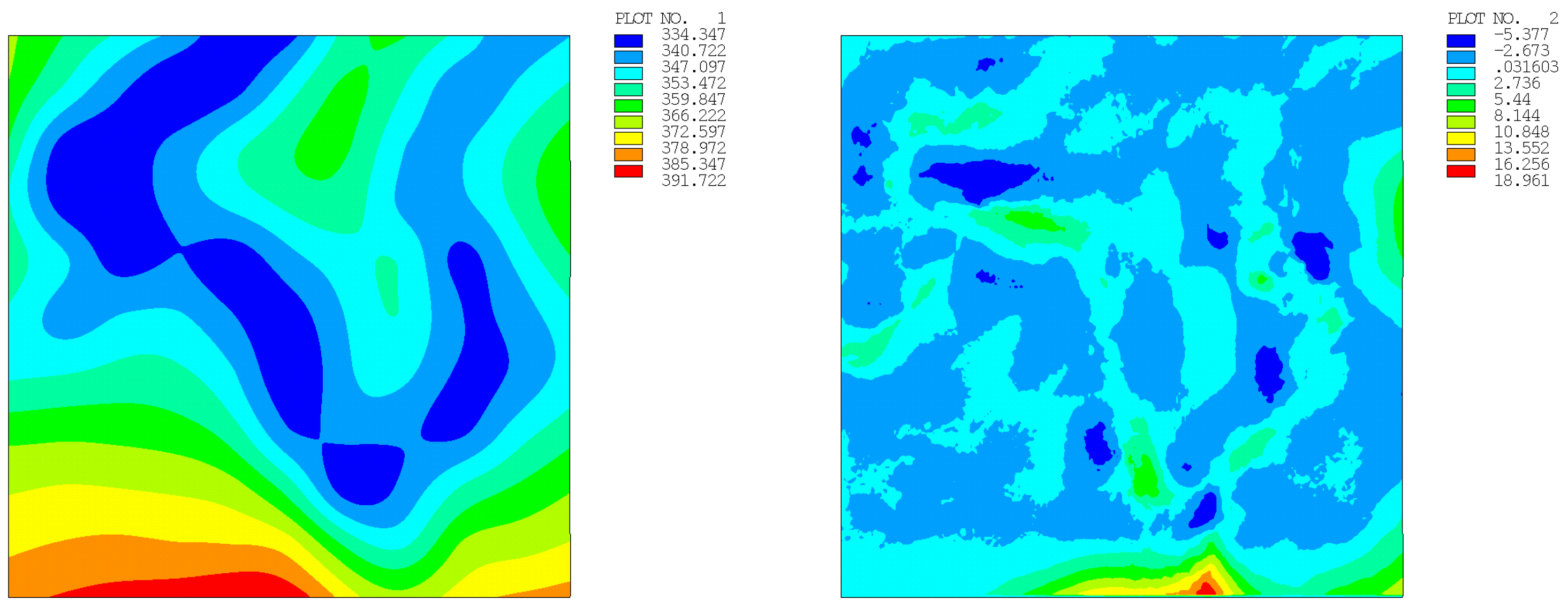


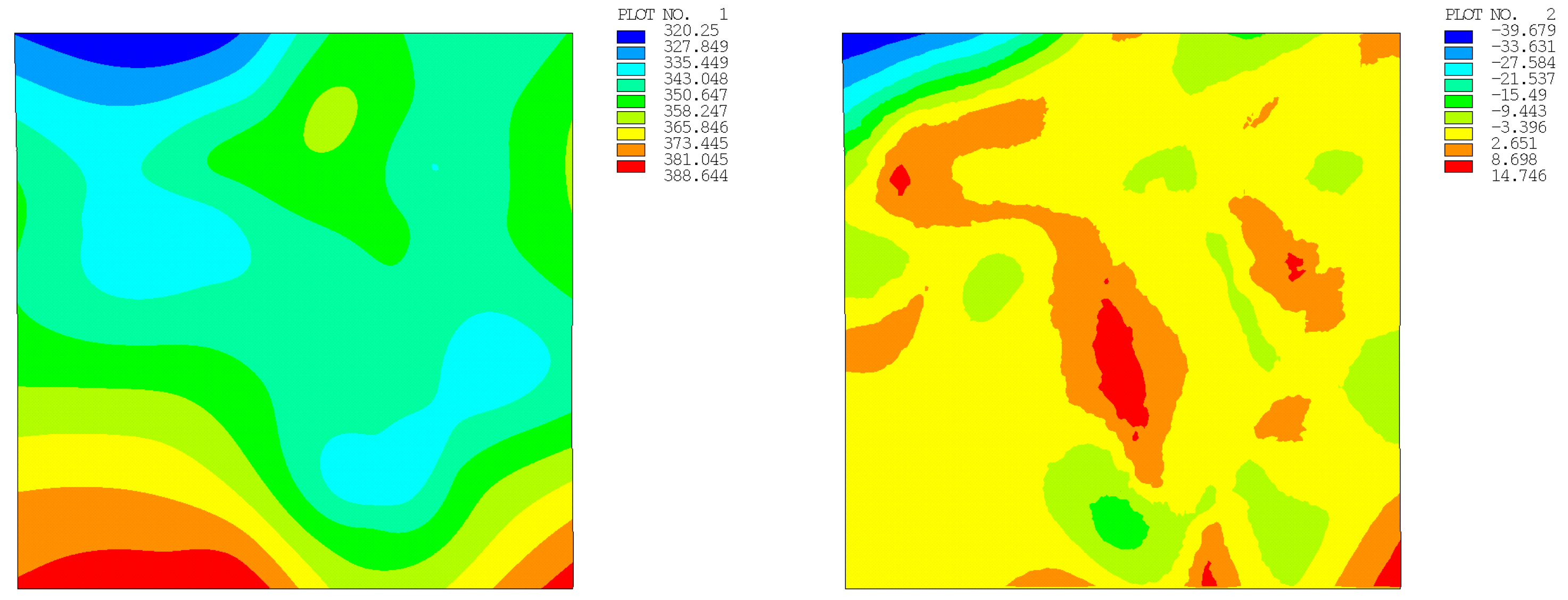
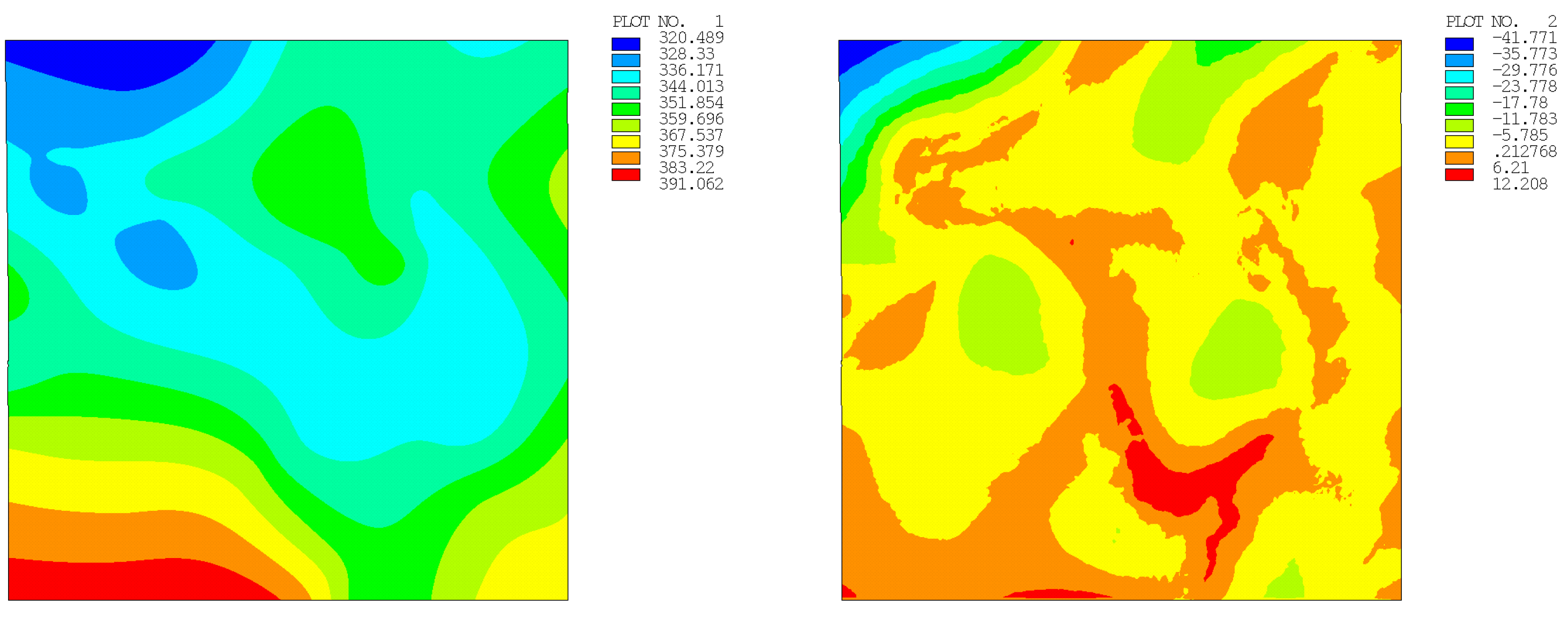

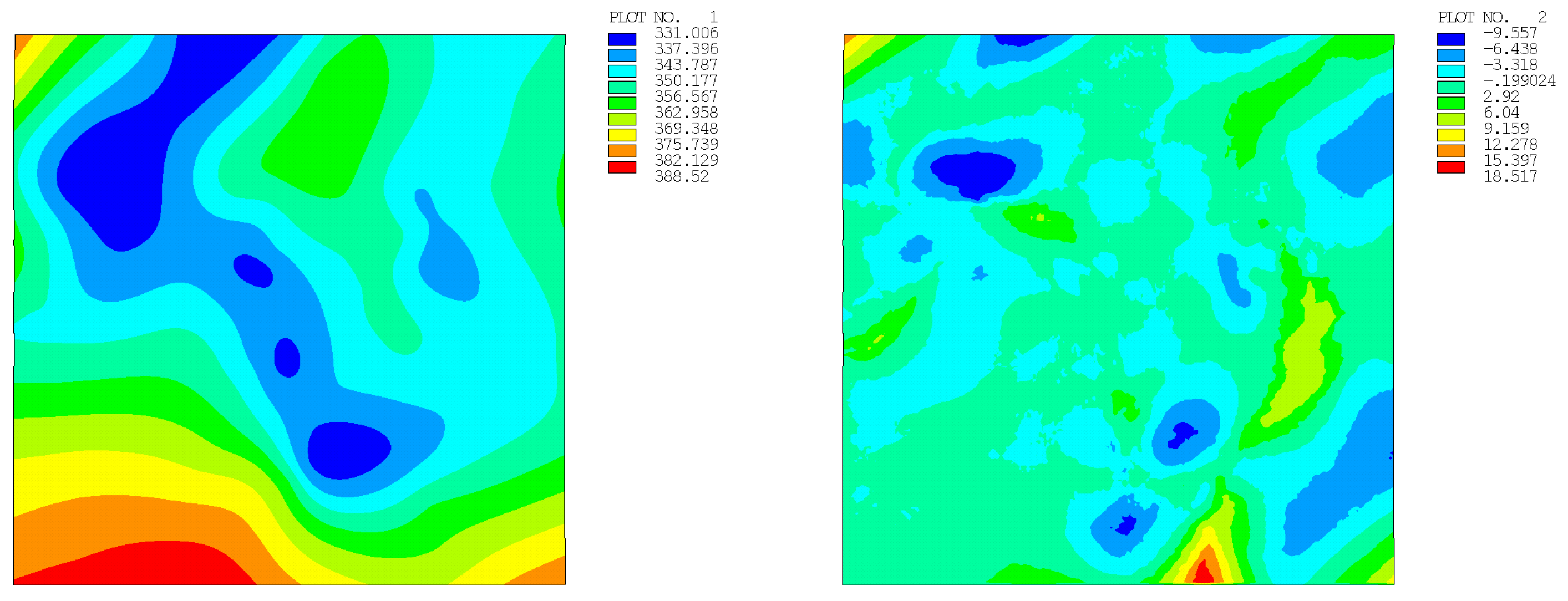

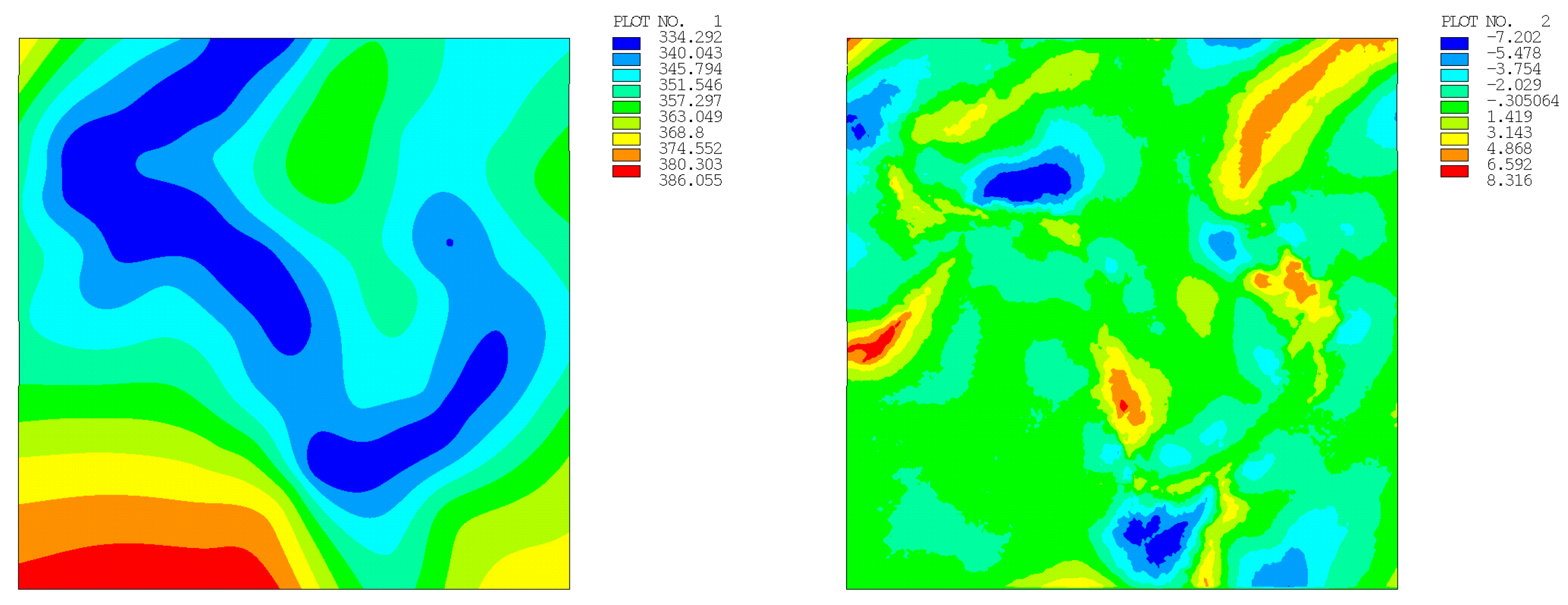

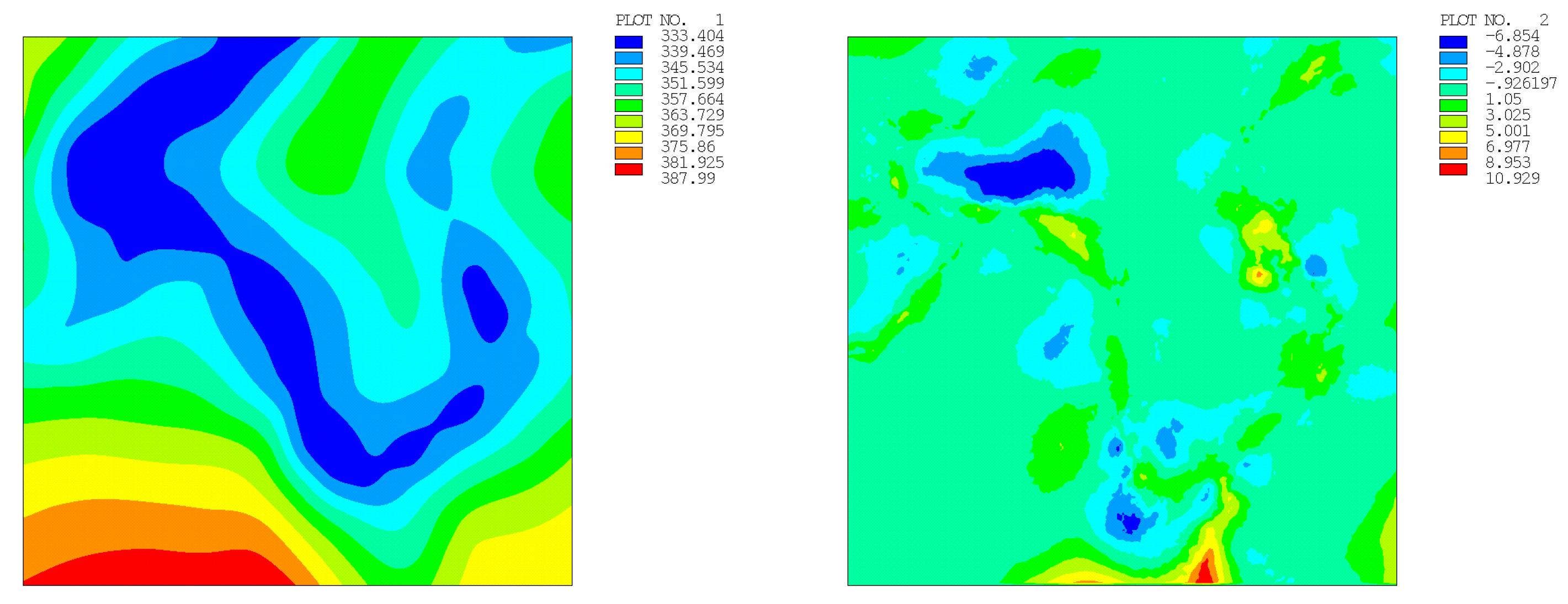
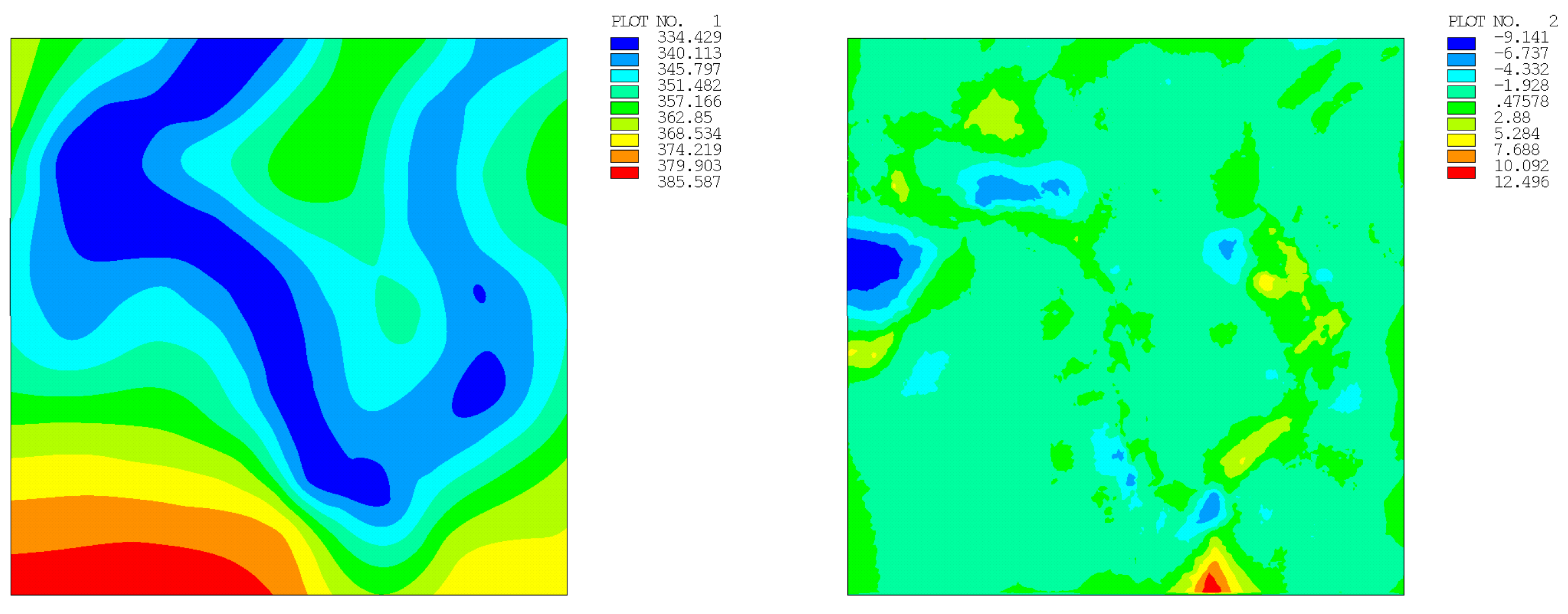
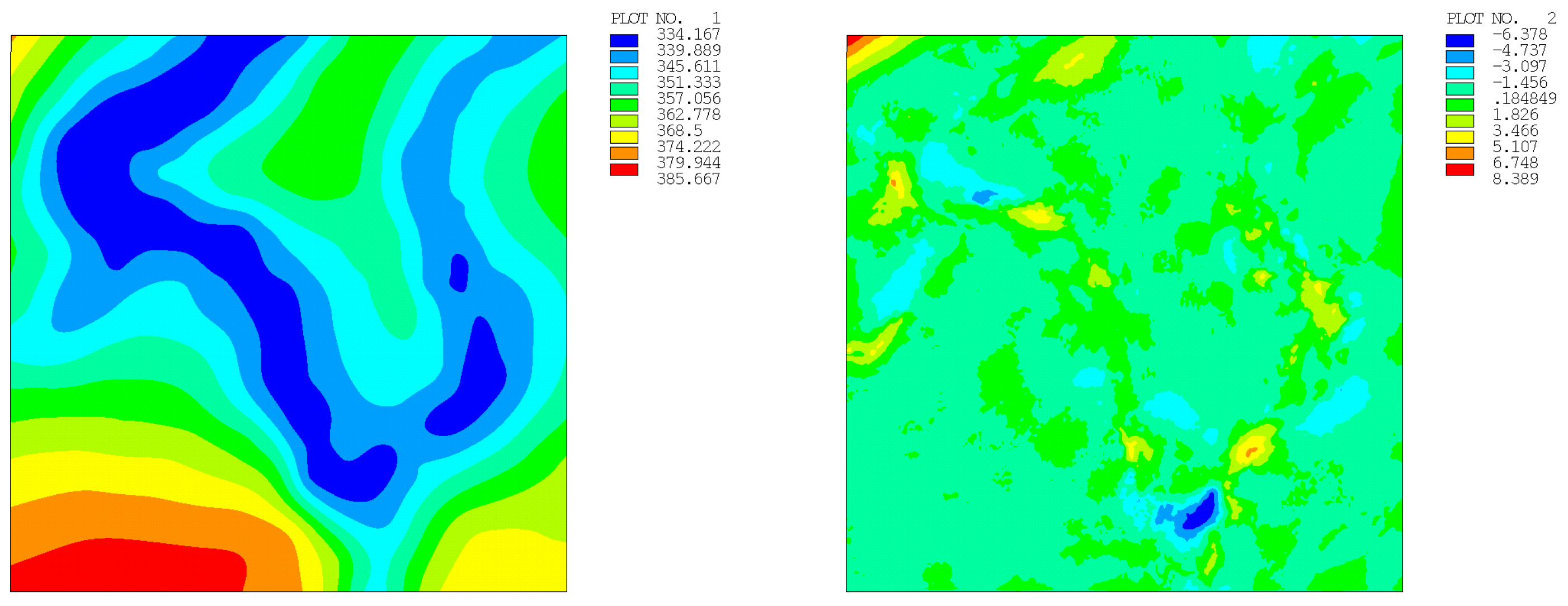
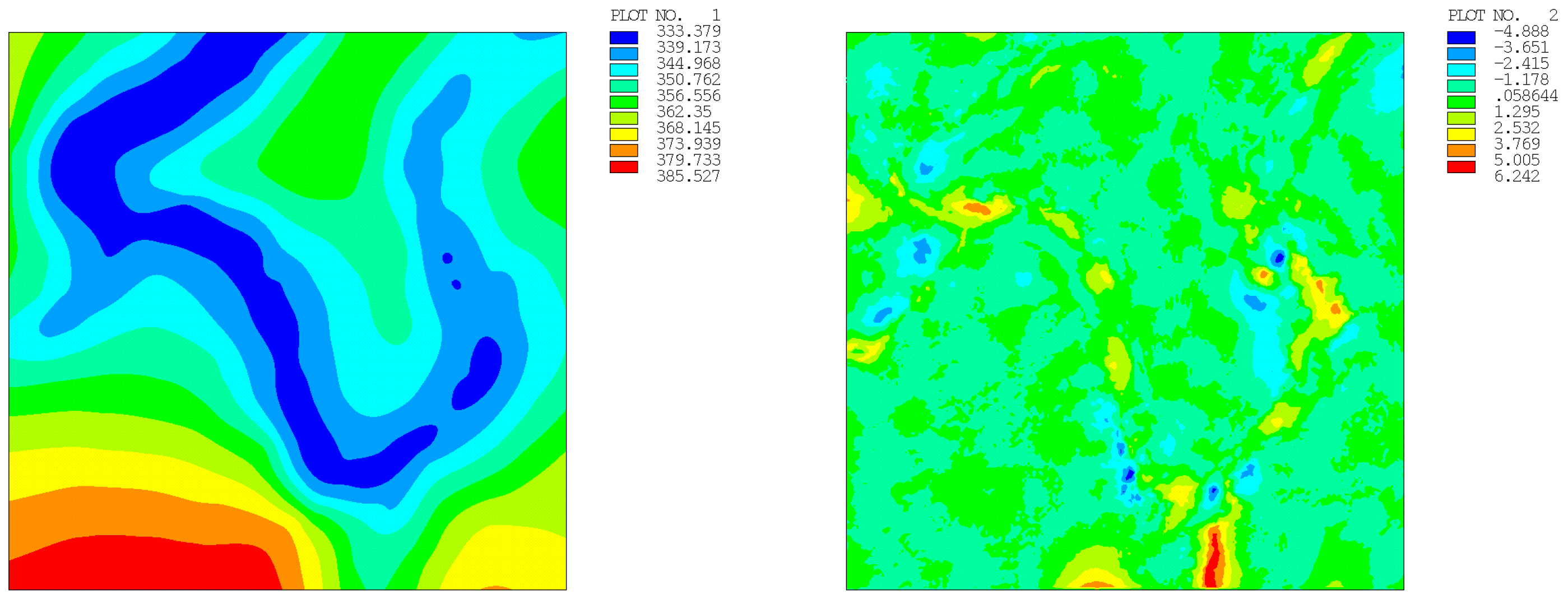
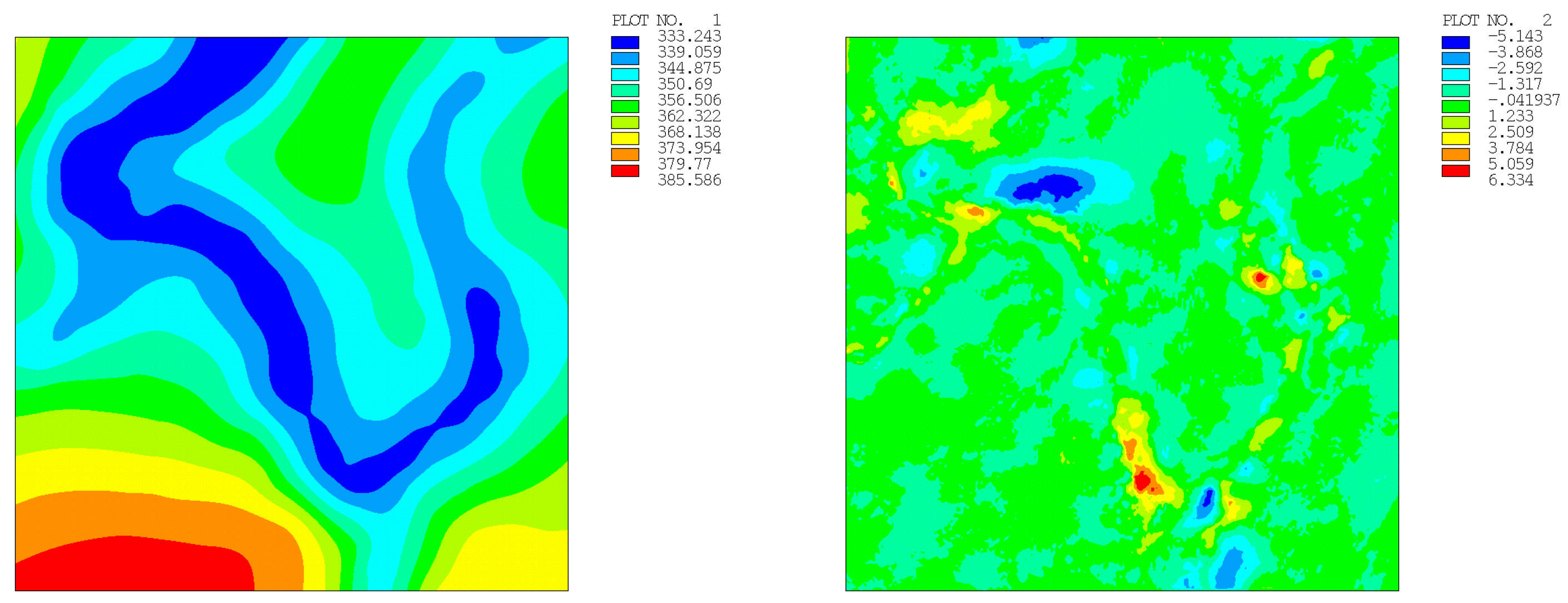


| Number of Points | Regular Distribution | Random Distribution | ||
|---|---|---|---|---|
| Seed 1 | Seed 2 | Seed 3 | ||
| 49 | 25.365 (2.790) | 39.838 (3.573) | 41.930 (3.785) | 17.980 (2.816) |
| 100 | 18.961 (1.279) | 18.517 (1.885) | 18.114 (1.768) | 8.316 (1.397) |
| 196 | 14.162 (0.762) | 11.058 (1.011) | 10.929 (0.984) | 12.496 (0.938) |
| 400 | 4.857 (0.344) | 8.389 (0.582) | 6.242 (0.512) | 6.334 (0.537) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Conde López, E.; Salete Casino, E.; Flores Escribano, J.; Vargas Ureña, A. Application of Finite Element Method to Create a Digital Elevation Model. Mathematics 2023, 11, 1522. https://doi.org/10.3390/math11061522
Conde López E, Salete Casino E, Flores Escribano J, Vargas Ureña A. Application of Finite Element Method to Create a Digital Elevation Model. Mathematics. 2023; 11(6):1522. https://doi.org/10.3390/math11061522
Chicago/Turabian StyleConde López, Eduardo, Eduardo Salete Casino, Jesús Flores Escribano, and Antonio Vargas Ureña. 2023. "Application of Finite Element Method to Create a Digital Elevation Model" Mathematics 11, no. 6: 1522. https://doi.org/10.3390/math11061522
APA StyleConde López, E., Salete Casino, E., Flores Escribano, J., & Vargas Ureña, A. (2023). Application of Finite Element Method to Create a Digital Elevation Model. Mathematics, 11(6), 1522. https://doi.org/10.3390/math11061522







