Abstract
The ranked set sampling (RSS) is an efficient and flexible sampling method. Based on a modified RSS named minimum ranked set sampling samples (MinRSSU), inference of a dependent competing risks model is proposed in this paper. Then, Marshall–Olkin bivariate distribution model is used to describe the dependence of competing risks. When the competing risks data follow the proportional hazard rate distribution, a dependent competing risks model based on MinRSSU sampling is constructed. In addition, the model parameters and reliability indices were estimated by the classical and Bayesian method. Maximum likelihood estimators and corresponding asymptotic confidence intervals are constructed by using asymptotic theory. In addition, the Bayesian estimator and highest posterior density credible intervals are established under the general prior. Furthermore, according to E-Bayesian theory, the point and interval estimators of model parameters and reliability indices are obtained by a sampling algorithm. Finally, extensive simulation studies and a real-life example are presented for illustrations.
Keywords:
dependent competing risks; bivariate distribution family; maximum likelihood estimation; bayesian estimation; E-Bayesian estimation MSC:
62F10; 62F15
1. Introduction
In order to enhance the efficiency of simple random sampling (SRS) scheme, the ranked set sampling (RSS) method was proposed by McIntyre [1] as an alternative scenario for making inferences about the target population using less sample resource. Since the RSS scheme could improve the inference accuracy by using informal ranking information, the RSS could be viewed as a more suitable sampling scheme to improve testing efficient and inferential accuracy when experiment is time and cost consuming. The traditional RSS scenario proposed by McIntyre [1] can be implemented as follows. Suppose that identical units are randomly selected from a population and are divided into n groups with n units in each testing group. The n units are conducted in each testing group simultaneously, the i-th failure times in group j is denoted as . Then, the i-th smallest ranked data is recorded in the i-th group. Under this scheme, the sketch of the RSS can be described as follows:
Therefore, observation is collected as the RSS sample. Inference with using RSS scheme has been investigated by many authors under various perspectives. Takahasi and Wakimoto [2] and Takahasi [3] have developed the mathematical background of the method (and its efficiency) based on RSS samples. Dell and Clutter [4] showed that mean estimation based on RSS samples gives better results than using SRS samples in terms of the mean square error and cost efficiency. For some recent contributions, one could also refer to the works of Basikhasteh et al. [5], Esemen and Gürler [6], Samawi et al. [7], and Zamanzade et al. [8] among others.
In practice, the ranking steps of traditional RSS are tedious, and ranking errors are easy to occur in the process. Moreover, units are needed to obtain the associated ranking failure times in this complete sampling process. From the perspective of time and cost, this sampling scheme is still less efficient for traditional RSS. Therefore, Muttlak [9] proposed the median RSS, and Samawi et al. [10] proposed the extreme RSS to reduce the influence of ranking errors on RSS. Further, many other modified RSS schemes have been proposed, such as Double-RSS (Al-Saleh and Al-Kadiri [11]), Multi-stage RSS (Al-Saleh and Al-Omari [12]), and quartile RSS (Muttlak [13]). In particular, Al-Odat and Al-Saleh [14] proposed an effective modified RSS scheme called minimum ranked set sampling with unequal samples (MinRSSU), which has attracted much attention in recent years. The MinRSSU sample is conducted with only units in its testing. Under MinRSSU scenario, n groups are conducted where i-th group contains i units in experiment. The smallest observation in each group is selected in the ranking process, and the MinRSSU data can be described as follows:
From the sketch of the MinRSSU sampling, it is noted that the size of MinRSSU sampling is smaller than that of the traditional RSS, and such a scenario also reduces the ranking error in consequence. Similarly, if the maximum lifetimes are selected from each testing group, one could obtain the maximum ranked set sampling with unequal samples (MaxRSSU) (Biradar and Santosha [15]). In the literature, MinRSSU and MaxRSSU samples sometimes are called together as the moving extreme ranking set sampling (MERSS). As another efficient sampling scenario, both MinRSSU and MaxRSSU have been extensively discussed by many authors. For instance, Yao et al. [16] verified that MERSS can provide more information than SRS by comparing Fisher information matrix. Qiu and Eftekharian [17] considered the information measurements of MinRSSU and MaxRSSU from the perspective of entropy. Rahmani and Razmkhah [18] also showed that the parameter estimation has higher accuracy in MinRSSU and MaxRSSU scenarios, even though there are ordering errors in the sampling process.
In reliability and survival analysis, the failure of an individual unit is often yielded by multiple failure causes that compete with each other throughout the life cycle of the unit. In the literature, this problem is referred to as the competitive risk model. In general, competing risk data includes the failure times and corresponding indicators showing the cause of failure. In theoretical and practical studies, inference of competing risks model has been analyzed under the assumption that there are independent failure causes. In this regard, various inferential works have been done under different perspectives. See, for example, the works of Ren and Gui [19], Wang et al. [20], Sarhan et al. [21], Mahto et al. [22], among others. However, due to the complexity of internal structure and external environment of units, such independence assumption sometimes inappropriate. For example, there are two main failure causes namely cancer recurrence and death in colon cancer, and these two causes are dependent and competing with each other in clinical analysis. In reliability application for a two-engine aeroplane, the breakdown of one aeroplane engine could cause additional pressure on the remaining functional engine and increase the risk of engine failure. In this regard, inference for competing risks model with dependent failure causes seems more reasonable. In particular, competing risks models involving two dependent causes of failure are frequently studied in theoretical and practical analysis, and different approaches are proposed for modelling dependent characteristic including multivariate lifetime distribution, copula model, and frailty model among others (e.g., Wang et al. [23], Gorfine and Hsu [24], Lo and Wilke [25], Fan et al. [26]). Among different approaches, Marshall and Olkin [27] proposed a popular bivariate distribution based on exponential and Weibull baseline model in reliability studies, which provided successful applications for competing risk analysis with dependent causes. Since then, the Marshall–Olkin lifetime model has been used extensively to analyze two dependent failure causes because of its simple structure and attractive statistical properties. For example, Guan et al. [28] considered the objective Bayesian analysis of dependent competing risks model using MOBE distribution. Feizjavadian and Hashemi [29] used Marshall–Olkin bivariate Weibull (MOBW) distribution to study diabetic retinopathy data. Paul et al. [30] considers a Bayesian analysis of a dependent competing risk model using Marshall–Olkin bivariate Pareto (MOBP) distribution. See also Kundu and Gupta [31], Mulinacci [32], Shen and Xu [33] for more discussions.
Let U be a random variable from a family of continuous distribution with a resilience parameter , the associated probability density function (PDF) and the cumulative distribution function (CDF) of U are, respectively, given by
where is an arbitrary continuous function with and , and . In addition, the survival function (SF) can be expressed as
The model (1) is a subclass of a regular one parameter exponential family of distributions and refers as proportional hazard rate (PHR) model (e.g., Lawless [34]). By different choices of the baseline function , many well-known distributions are the specific cases of PHR model like exponential, Rayleigh, Pareto, among others (e.g., Contreras-Reyes et al. [35]). Inference for the PHR model has been studied by several authors. For example, some recent contributions of Chaturvedi et al. [36], Bai et al. [37], Kizilaslan [38], Popović et al. [39], among others. In this paper, it is assumed that the marginal distribution of the failure causes follows the PHR distribution, and then an Marshall–Olkin type bivariate PHR distribution (MOBPHR) is proposed for modelling the dependent competing risks.
Motivated by the former, this paper proposes inference for dependent competing risks model when the failure time is MOBPHR distributed under the MinRSSU scenario. The model parameters and reliability indices were estimated by the classical and Bayesian method. In addition, the expected-Bayesian (E-Bayesian) approach is also proposed for comparison. To the best of our knowledge, estimation for the dependent MinRSSU competing risks data has been not discussed in the literature.
The rest of the article is organized as follows. In Section 2, the MOBPHR model and the MinRSSU competing risks data are described, respectively. Section 3 presents the maximum likelihood estimators (MLEs) of the model parameters, and the associated approximate confidence intervals (ACIs) are also established in consequence. Bayesian and E-Bayesian estimations are presented in Section 4. Extensive simulation studies and a real-life example are conducted in Section 5 for illustration. Finally, some brief concluding remarks are given in Section 6.
2. Model and Data Description
2.1. Marshall–Olkin Bivariate Proportional Hazard Rate Distribution
Let U1, U3 and U3 be independent random variables following the PHR distributions (1) with parameters and , respectively. Define T1 = min(U1,U3) and T2 = min(U2,U3), then random vector follow the MOBPHR distribution with parameters , denoted by . For the sake of completeness, some basic properties of the MOBPHR are provided in following theorems.
Theorem 1.
Suppose random vector follows MOBPHR. The joint SF of is given by
Proof.
See Appendix A. □
A direct calculation based on the relationship between SF and PDF yields the following results, with details omitted for simplicity.
Corollary 1.
Suppose random vector follows MOBPHR. The joint PDF of can be expressed as
For the sake of simplicity, denote , and in rest of the paper. According to the above definition, one further has the following results.
Corollary 2.
Let MOBPHR, then
- follows the PHR distribution with parameter ;
- The SF and the hazard rate function (HRF) of T at mission time are given by
From (3) with , it is noted that variables and are statistical independent implying that parameter can be regarded as the dependence structure between and . Furthermore, one can observe from (4) that the probability for events and are and , respectively. In addition, it is also seen from Corollary 2 that the failure time of units can be described by variable following MOBPHR model.
2.2. Data Description and Notation
Without loss of generality, suppose n identical units are tested under the MinRSSU scenario, and their lifetimes are described by independent and identically distributed (i.i.d.) random variables . For sake of simplicity, the following notations are used in this paper when the dependent MinRSSU competing risk data is available:
- :
- failure time of ith unit under cause
- :
- observed lifetime of the i-th unit, i.e., .
- :
- indicator variable for the failure cause of ith unit with
- :
- set of indices of case and 3
- :
- cardinality of . It is assumed that
In this paper, the dependent lifetime variables of the competing risks are denoted by from population MOBPHR. Therefore, the dependent competing risks sample is under MinRSSU scenario with failure cause and the associated observations are given by
Theorem 2.
Suppose the observation (5) comes from MOBPHR model with parameters and . The likelihood function of parameters , and can be expressed as
where .
Proof.
See Appendix B. □
3. Classical Inference
In this section, the MLEs of model parameters and reliability indices are presented, and the correspondingly ACIs are also constructed based on asymptotic theory.
3.1. Maximum Likelihood Estimation
From (6), the log-likelihood function is given by
where .
Theorem 3.
Suppose the observation (5) follow the MOBPHR distribution with parameters . For , the MLE of can be written as
Proof.
See Appendix C. □
Further, using invariance principle of maximum likelihood estimation, the MLEs of the SF and HRF can be constructed as
with .
Remark 1.
It is noted that the condition guarantees the existence of MLE . If (without loss of generality) , sample (5) provides no information about and the MLE of does not exist in this manner.
3.2. Approximate Confidence Intervals
The expected Fisher information matrix and asymptotic theory in this subsection to obtain the ACIs of . Let , the expected Fisher information matrix can be constructed by
where for and if . Under mild regularity conditions, the asymptotic distribution of the MLE is
where is the inverse of the expected Fisher information matrix given by
For arbitrary , a ACI of is given by
where is the upper -th quantile of the standard normal distribution.
Sometimes, the previous obtained ACIs may have a negative lower bound which further yields worse performance for interval estimation of positive parameter. In order to avoid such drawback, one can use logarithmic transformation method and delta technique to construct the ACI in consequence. The asymptotic normality distribution of can be obtained as
where notation . Therefore, a alternative ACI of can be expressed as
Let be arbitrary function of parameter , the asymptotic distribution of can be constructed by using delta method as
where notations is the MLE of and
Therefore, the confidence interval of can be further constructed following similar approach as previous. Under this manner, the ACIs of the SF and the HRF can be obtained directly and detailed expressions are omitted for saving space.
4. Bayesian Inference
In inferential approach, Bayesian estimation has received much attention as an alternative to classical likelihood approach where the capability of incorporating prior information makes it very valuable in analysis. In this section, estimation problems based on traditional Bayesian and E-Bayesian approaches are discussed under different loss functions, respectively, and corresponding algorithms are given to solve Bayesian point estimation and credible interval.
4.1. Prior Information and Posterior Analysis
Assume that parameters and are statistically independent, and the gamma conjugate prior for is implemented with hyper-parameters and as
Therefore, the joint prior of can be written as
Based on (6) and (9), the joint posterior density of can be expressed as
and the marginal posterior density of is also gamma distribution given by
4.2. Bayesian Estimation under Symmetry and Asymmetry Losses
Loss function plays an important role in Bayesian analysis and decision theory. The symmetric loss gives equal weighted to overestimation and underestimation, whereas asymmetric loss may be appropriate for estimation when overestimation and underestimation have different consequences. Suppose is an estimator of parameter , the following symmetric squared error loss and asymmetric linear-exponential (Linex) loss are used in this paper:
- (squared error loss): ,
- (Linex loss): ,
In addition, Bayesian estimator with squared error and Linex losses are the posterior expectation and , respectively. Through straightforward computation, the Bayes estimators of model parameters and reliability indices can be obtained as follows and the detailed proofs are omitted for simplicity and saving space.
Theorem 4.
Under squared error loss , one has
- The Bayes estimator of is given by
- The Bayes estimators of the SF and HRF can be expressed, respectively, aswith .
Theorem 5.
Under Linex loss , one has
- The Bayes estimator of is given by
- The Bayes estimators of the SF and HRF can be expressed, respectively, asand
For arbitrary , a Bayesian highest posterior density interval (HPDI) of can be also constructed. A simple constrained optimization approach is provided as follows. Let denote the credibility interval of for under the posterior (11) satisfying
Thus, the HPDI of denoted by can be obtained by solving following constrained optimization problem as
which is equivalent to minimize the Lagrangian function defined by
where is the Lagrangian multiplier and solutions and can be further obtained numerically from following nonlinear equations as
4.3. E-Bayesian Estimation
The E-Bayesian estimation was firstly proposed by Han [40], which is a special hierarchical Bayesian estimation scenario, and then was further discussed by Han [41,42]. Recently, the E-Bayesian approach has attracted wide attention and has been discussed by many authors. See, for example, some recent works of Basheer et al. [43], Wu et al. [44], Okasha and Wang [45] for comprehensive discussions.
Following the idea of Han [40], the hyper-parameters and should be selected to guarantee the prior density function decreases in under E-Bayesian scenario, which implies that and when . Under such requirements, it is assumed that the hyper-parameters and are statistically independent and have the following three priors as
Theorem 6.
Under squared error loss , it is seen that
- For prior , the E-Bayesian estimator of are given by
- For prior , the E-Bayesian estimator of can be written as
- For prior , the E-Bayesian estimator of can be expressed as
Proof.
See Appendix D. □
Theorem 7.
Under squared error loss , one has that
- For prior , the E-Bayesian estimators of and are given byand
- For prior , the E-Bayesian estimators of and can be written asand
- For prior , the E-Bayesian estimators of and can be expressed asand
Proof.
See Appendix E. □
Analogously to Theorems 6 and 7, the E-Bayesian estimators of parameters and reliability indices can be obtained under Linex loss, and the proofs are omitted for concision.
Theorem 8.
Under Linex loss , it is seen that
- For prior , the E-Bayesian estimator of are given by
- For prior , the E-Bayesian estimator of can be written as
- For prior , the E-Bayesian estimator of can be expressed as
Theorem 9.
Let D be the range of , it is noted under Linex loss that
- For prior , the E-Bayesian estimators of and are given byand
- For prior , the E-Bayesian estimators of and can be written asand
- For prior , the E-Bayesian estimators of and can be expressed asand
In order to construct HPDI estimates under E-Bayesian scenario, a sampling based approach is proposed as follows. Based on (6), (9) and (12), the posterior density function of with respect to hyper-prior can be expressed, respectively, as
Further, the conditional marginal posterior distribution of can be obtained from the posterior distribution (13), respectively, as follows:
and
It can be seen from (15) and (16) that the full conditional posterior distribution of and cannot be analyzed by using some well-known models. Therefore, the Markov-Chain Monte Carlo (MCMC) method is used here for complex computation. To be specific, the Metropolis-Hastings (M-H) algorithm via Gibbs sampling is implemented for posterior sampling under the E-Bayesian scenario. Then, a MCMC approach called Algorithm 1 is provided to obtain the E-Batesian estimates of , SF and HRF .
4.4. Some Results of Bayesian and E-Bayesian Estimation
In this section, the posterior risk (PR) of Bayesian estimators and the E-posterior risk (EPR) of E-Bayesian estimators are further presented for complementary which generally can be used to measure the associated estimated risk.
Theorem 10.
For Bayes estimators
- under squared error loss , the PR of can be expressed as
- under Linex loss , the PR of can be expressed as
Proof.
See Appendix F. □
Following Han [46], the EPR of various E-Bayesian estimators are also obtained.
Theorem 11.
For E-Bayesian estimators,
- under SE loss, the EPR of with respect to priors can be expressed, respectively, as
- under Linex loss, the EPR of with respect to priors can be expressed, respectively, as
Proof.
See Appendix G. □
In addition, some order results among E-Bayesian estimators are also presented as follows.
Theorem 12.
Let , the E-Bayesian estimators under squared error loss feature following results
- ,
- .
Proof.
See Appendix H. □
Theorem 13.
Let , the E-Bayesian estimators from Linex loss have following results
- for , .
- .
Proof.
See Appendix I. □
| Algorithm 1: E-Bayesian interval estimation based M-H algorithm via Gibbs sampling |
|
5. Numerical Illustration
5.1. Simulation Studies
Extensive simulation studies are conducted for investigating the performance of the proposed methods when dependent MinRSSU competing risks samples are available, the associated point estimates are evaluated in terms of absolute bias (AB) and mean squared error (MSE), and the interval estimates are investigated by average length (AL) and coverage probability (CP). In this illustration, the following approach entitled Algorithm 2 is provided to generate dependent MinRSSU competing risks samples.
| Algorithm 2: Generation dependent MinRSSU competing risks samples |
|
Since the proposed MOBPHR model is a general family, the following three distributions are selected as its special cases in the study:
In the simulation study, two sets of random chosen values of the parameters and , correspondingly the associated hyper-parameters are taken to be and satisfying the prior means are the same as the original means. Therefore, the criteria quantities ABs, MSEs, CPs and ALs are carried out based on 10,000 repetitions. All simulation results are tabulated in Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9 and Table 10, where the significance level is for interval estimates, and the results of model parameters are just presented for and for concision. In addition, it is worth mentioning that the Bayesian interval estimates of reliability indices and are obtained by using sampling approach like Algorithm 1 based on the posterior function (11).

Table 1.
The AB and MSEs (within bracket) of point estimates with .

Table 2.
The ALs and CPs (within bracket) of interval estimates with .

Table 3.
The AB and MSEs (within bracket) of point estimates with .

Table 4.
The ALs and CPs (within bracket) of interval estimates with .

Table 5.
The PR and EPR of Bayes estimates for with .

Table 6.
The AB and MSEs (within bracket) of point estimates with .

Table 7.
The ALs and CPs (within bracket) of interval estimates with .

Table 8.
The AB and MSEs (within bracket) of point estimates with .

Table 9.
The ALs and CPs (within bracket) of interval estimates with .

Table 10.
The PR and EPR of Bayes estimators for parameters with .
From the simulated results in Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9 and Table 10, one can observe the following conclusions for point and interval estimates:
- For point estimation, AB and MSEs of point estimates from E-Bayesian methods under and , as well as Bayesian and maximum likelihood methods, decrease with increase of the sample size n.
- For a given n, AB and MSEs of Bayes and E-Bayesian estimates under and are smaller than those of MLEs. In addition, three E-Bayesian estimates are superior to the Bayesian results, where estimates under prior perform best among all E-Bayesian estimates.
- For interval estimation, when sample size n increases, ALs of ACIs, HPDI and intervals from E-Bayesian scenario decrease in all cases.
- Under fixed sample size n, ALs of Bayesian HPDIs are smaller than those of ACIs, but slightly larger than those of credible intervals obtained from E-Bayesian approaches in general.
- The CPs of different interval estimates are all close to nominal significance level.
- The PRs of E-Bayesian are all smaller than those of Bayesian estimates, where the PRs under the prior seems to perform best among all estimates.
5.2. Real Data Illustrations
A real data example is presented for showing the applications of the proposed methods. In this data set, the time (in years) from human immunodeficiency virus (HIV) infection to the development of acquired immune deficiency syndrome (AIDS) or switch to syncytium inducing (SI) phenotype in 329 homosexual men was discussed. The data set was also original reported by Putter et al. [47] and Geskus [48], where events AIDS and SI can be regarded as competing risks denoted as and , respectively. In order to obtain dependent competing risks data, we randomly select some data from the overall data and treated these data as failure times due to causes 1 and 2 simultaneous, which is denoted as . Before further proceeding, the MOBPHR model is implemented with exponential, Pareto and Rayleigh baseline distributions for fitting the data set. Since there is no general goodness-of-fit approach for bivariate model, here we provide the Kolmogorov–Smirnov (KS) distance and associated p-value for three baseline models by ignoring the failure causes and the results are presented in Table 11. In addition, empirical cumulative distributions via theoretical distribution plot, Probability-Probability (P-P) and Quantile-Quantile (Q-Q) plots under three baseline distributions are presented in Figure 1. It is conducted that the Rayleigh distribution can be used as a proper model to fit the real data set, and then we use the MOBPHR model with Rayleigh baseline marginal distribution for further illustration.

Table 11.
Goodness-of-fit results for real data.
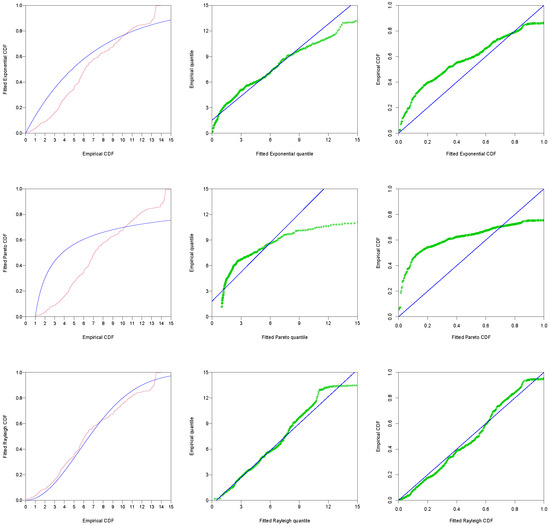
Figure 1.
Empirical cumulative distribution plot, Q-Q and P-P plots for the exponential, Pareto and Rayleigh distribution under AIDSSI data.
Furthermore, a group of MinRSSU competing risk samples with a sample size of were obtained by sampling AIDSSI data through MinRSSU sampling strategy. The sample data set is shown in Table 12. Since there is no historical information for model parameters, the hyper-parameters are set to be in this illustration indicating that the priors are proper but almost non-informative. The point and interval estimates are presented in Table 13 and Table 14 with significance level for interval estimation and in Linex loss, where the associated interval lengths are also provided in squared brackets.

Table 12.
MinRSSU samples of HIV infection competing risks data.

Table 13.
Point estimates for unknown parameters under HIV infection competing risk data.

Table 14.
Interval estimates for unknown parameters under HIV infection competing risk data.
Based on the listed results shown in Table 13 and Table 14, it is observed that the classical and Bayes estimates appear close to each other, whereas the E-Bayesian HPDIs and ACIs have shortest and longest interval length, respectively. For further illustration, CDF and PDF of Rayleigh distribution for the minimum of the failure causes are plotted in Figure 2 by using different parameter estimates, where the notations E-Bayes-1, E-Bayes-2 and E-Bayes-3 represent the E-Bayesian estimates obtained under priors , and , respectively. From Figure 2, it is shown that the plots of Rayleigh PDF and CDF via classical and Bayes estimates also appear similar performance. In addition, Figure 3 shows the trend diagram of the M-H sampling algorithm for the parameters , and , it is also noted that the E-Bayesian sampling has good mixing performance.
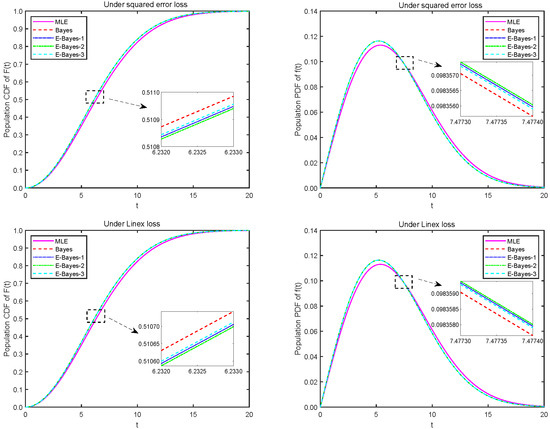
Figure 2.
The CDF and PDF plots of Rayleigh distribution for real data.
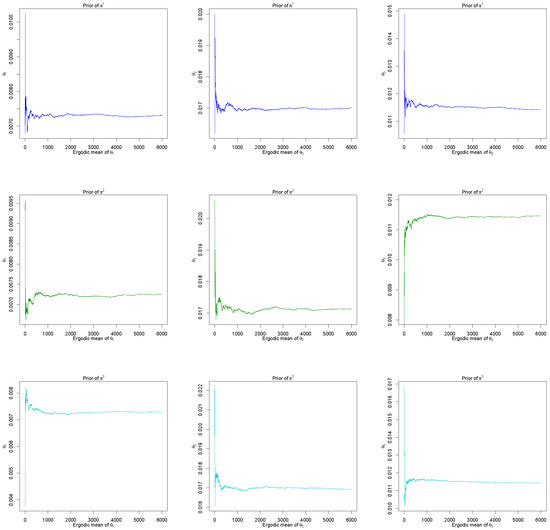
Figure 3.
Plots of , and under different prior distributions.
Finally, Figure 4 also shows the plots of HRF via different point estimates in mission time , and the plots of interval lengths of HRF are presented as well. It can be seen that there are certain differences between classical and Bayesian point estimates of HRF, and the associated Bayesian and E-Bayesian point estimates are similar. In addition, it is also seen that the ACI of HRF at different mission time features longest interval length, whereas the E-Bayesian HPDI of HRF features shortest interval length.

Figure 4.
Point estimate and interval length of HRF at different mission time under real data.
6. Conclusions
This paper studies estimation of dependent competing risk model under the MinRSSU scenario. When the MOBPHR distribution is proposed for modeling failure causes, point and interval estimation of the unknown parameters as well as the reliability indices are estimated by classical, Bayesian and E-Bayesian methods, respectively. Simulation studies and a real-life example are carried out to investigate the performance of different methods, the results indicate that all classical and Bayesian estimates work satisfactory, and the proposed E-Bayesian method performs better than other results in general. Although the MOBPHR distribution is constructed in this paper to model the lifetime of dependent failure causes, this work can be extended to other bivariate models when the MinRSSU competing risks samples are available. In addition, there are many types of modified RSS sampling strategies. In this study, MinRSSU sampling method is selected according to the characteristics of life-time data. In future studies, RSS or modified RSS sampling method should be selected according to different characteristics of life-time data for corresponding statistical analysis. Secondly, the PHR model considered in this paper is a single-parameter distribution model. Due to the complexity of failure causes, the competing risks data may come from more complex distribution models. Therefore, the multi-parameter distribution models, such as generalized gamma, beta prime and generalized inverse Gaussian, will be considered in future studies.
Author Contributions
Funding acquisition, L.W.; Methodology, Y.Z. and L.W.; Writing-original draft, T.-R.T. and Y.M.T. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by Yunnan Fundamental Research Projects (No. 202101AT070103).
Data Availability Statement
The numerical data used to support the findings of this study are included within the article.
Acknowledgments
Authors would like to thank the Editor and reviewers for their valuable comments and suggestions which improve this paper significantly.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. The Proof of Theorem 1
Using the independent property of and , one has
Then the assertion is proved.
Appendix B. The Proof of Theorem 2
For MinRSSU competing risks data , a brief explanation of the probability contribution of is shown here. For , it means that the first failure of unit in i-th group is yielded due to cause one, then one equivalently has and . Using distribution property of order statistic, the likelihood contribution of data can be established as
Similarly, the likelihood contribution of can be obtained as well.
For , failure is yielded by causes one and two simultaneously implying that . Then the likelihood contribution is given by
Therefore, the assertion is completed.
Appendix C. The Proof of Theorem 3
By taking derivatives of with respect to and , one can obtain MLE directly. Using the inequality , let , then one has
Using the above inequality, it can be obtained that
Since , and . Then it is observed that
where equality holds if and only if . Therefore, the assertion is completed.
Appendix D. The Proof of Theorem 6
Under squared error loss, the E-Bayesian estimator of can be obtained by using priors and as follows
and
Therefore, the assertion is completed.
Appendix E. The Proof of Theorem 7
Under squared error loss, the E-Bayesian estimator of reliability indices and with respect to prior can be expressed, respectively, as
and
When the priors and are available, the associated E-Bayesian estimator of and could be also obtained similarly. The details are omitted for simplicity. Therefore, the assertion is completed.
Appendix F. The Proof of Theorem 10
Under squared error and Linex loss functions, the PR of the Bayes estimator can be obtained with respect to posterior density (11) as
and
for . Therefore, the assertion is completed.
Appendix G. The Proof of Theorem 11
Following Han [46], the EPR of and under squared error and Linex loss functions can be expressed, respectively, as
and
In addition, the EPR of and can be obtained under both loss functions similarly, and the details are omitted for saving space. Therefore, the assertion is completed.
Appendix H. The Proof of Theorem 12
Using expressions of , and , it is seen that
For and using Taylor expansion , one has
Thus, the order relation among , and is proved. Whereas the second result can be shown by taking direct limitation. Therefore, the assertion is completed.
Appendix I. The Proof of Theorem 13
Using expressions of , and , it is seen that
Following similar line as Theorem 12 and denoting and for , then using Taylor expansion , one has
implying , the first result is proved. The second result is established by taking direct limitation. Therefore, the assertion is completed.
References
- McIntyre, G.A. A method for unbiased selective sampling using ranked sets. Aust. J. Agric. Res. 1952, 3, 385–390. [Google Scholar] [CrossRef]
- Takahasi, K.; Wakimoto, K. On unbiased estimates of the population mean based on the sample stratified by means of ordering. Ann. Inst. Stat. Math. 1968, 20, 1–31. [Google Scholar] [CrossRef]
- Takahasi, K. Practical note on estimation of population means based on samples stratified by means of ordering. Ann. Inst. Stat. Math. 1970, 22, 421–428. [Google Scholar] [CrossRef]
- Dell, T.R.; Clutter, J.L. Ranked set sampling theory with order statistics background. Biometrics 1972, 28, 545–555. [Google Scholar] [CrossRef]
- Basikhasteh, M.; Lak, F.; Afshari, M. Bayesian estimation of stress-strength reliability for two-parameter bathtub-shaped lifetime distribution based on maximum ranked set sampling with unequal samples. J. Stat. Comput. Simul. 2020, 90, 1–16. [Google Scholar] [CrossRef]
- Esemen, M.; Gürler, S. Parameter estimation of generalized Rayleigh distribution based on ranked set sample. J. Stat. Comput. Simul. 2018, 88, 615–628. [Google Scholar] [CrossRef]
- Samawi, H.M.; Rochani, H.; Linder, D.; Chatterjee, A. More efficient logistic analysis using moving extreme ranked set sampling. J. Appl. Stat. 2015, 44, 753–766. [Google Scholar] [CrossRef]
- Zamanzade, E.; Mahdizadeh, M.; Samawi, H.M. Efficient estimation of cumulative distribution function using moving extreme ranked set sampling with application to reliability. AStA-Adv. Stat. Anal. 2020, 104, 485–502. [Google Scholar] [CrossRef]
- Muttlak, H.A. Median ranked set sampling. J. Appl. Stat. Sci. 1997, 6, 577–586. [Google Scholar]
- Samawi, H.M.; Ahmed, M.S.; Abu-Dayyeh, W. Estimating the population mean using extreme ranked set sampling. Biom. J. 1996, 38, 577–586. [Google Scholar] [CrossRef]
- Al-Saleh, M.F.; Al-Kadiri, M.A. Double-ranked set sampling. Stat. Probab. Lett. 2000, 48, 205–212. [Google Scholar] [CrossRef]
- Al-Saleh, M.F.; Al-Omari, A.I. Multistage ranked set sampling. J. Stat. Plan. Inference 2002, 102, 273–286. [Google Scholar] [CrossRef]
- Muttlak, H.A. Investigating the use of quartile ranked set samples for estimating the population mean. Appl. Math. Comput. 2003, 146, 437–443. [Google Scholar] [CrossRef]
- Al-Odat, M.; Al-Saleh, M.F. A variation of ranked set sampling. J. Appl. Stat. Sci. 2001, 10, 137–146. [Google Scholar]
- Biradar, B.S.; Santosha, C.D. Estimation of the mean of the exponential distribution using maximum ranked set sampling with unequal samples. Open J. Stat. 2014, 4, 641–649. [Google Scholar] [CrossRef]
- Yao, D.; Chen, W.; Yang, R.; Long, C. Fisher information in moving extreme ranked set sampling with application to parameter estimation. J. Syst. Sci. Complex. 2022, 35, 361–372. [Google Scholar] [CrossRef]
- Qiu, G.; Eftekharian, A. Extropy information of maximum and minimum ranked set sampling with unequal samples. Commun. Stat.-Theory Methods 2021, 50, 2979–2995. [Google Scholar] [CrossRef]
- Rahmani, H.; Razmkhah, M. Perfect ranking test in moving extreme ranked set sampling. Stat. Pap. 2017, 58, 855–875. [Google Scholar] [CrossRef]
- Ren, J.; Gui, W. Statistical analysis of adaptive type-II progressively censored competing risks for Weibull models. Appl. Math. Model. 2021, 98, 323–342. [Google Scholar] [CrossRef]
- Wang, L.; Tripathi, Y.M.; Lodhi, C. Inference for Weibull competing risks model with partially observed failure causes under generalized progressive hybrid censoring. J. Comput. Appl. Math. 2020, 368, 112537. [Google Scholar] [CrossRef]
- Sarhan, A.M.; Hamilton, D.C.; Smith, B. Statistical analysis of competing risks models. Reliab. Eng. Syst. Saf. 2010, 95, 953–962. [Google Scholar] [CrossRef]
- Mahto, A.K.; Lodhi, C.; Tripathi, Y.M.; Wang, L. Inference for partially observed competing risks model for Kumaraswamy distribution under generalized progressive hybrid censoring. J. Appl. Stat. 2021, 49, 2064–2092. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.C.; Emura, T.; Fan, T.H.; Lo, S.M.S.; Wilke, R.A. Likelihood-based inference for a frailty-copula model based on competing risks failure time data. Qual. Reliab. Eng. Int. 2020, 36, 1622–1638. [Google Scholar] [CrossRef]
- Gorfine, M.; Hsu, L. Frailty-based competing risks model for multivariate survival data. Biometrics 2011, 67, 415–426. [Google Scholar] [CrossRef]
- Lo, S.M.S.; Wilke, R.A. A copula model for dependent competing risks. J. R. Stat. Soc. C-Appl. 2010, 59, 359–376. [Google Scholar] [CrossRef]
- Fan, T.H.; Wang, Y.F.; Ju, S.K. A competing risks model with multiply censored reliability data under multivariate Weibull distributions. IEEE. Trans. Reliab. 2019, 68, 462–475. [Google Scholar] [CrossRef]
- Marshall, A.W.; Olkin, I. A multivariate exponential distribution. J. Am. Stat. Assoc. 1967, 62, 30–44. [Google Scholar] [CrossRef]
- Guan, Q.; Tang, Y.C.; Xu, A.C. Objective Bayesian analysis for bivariate Marshall-Olkin exponential distribution. Comput. Stat. Data Anal. 2013, 64, 299–313. [Google Scholar] [CrossRef]
- Feizjavadian, S.H.; Hashemi, R. Analysis of dependent competing risks in the presence of progressive hybrid censoring using Marshall-Olkin bivariate Weibull distribution. Comput. Stat. Data Anal. 2015, 82, 19–34. [Google Scholar] [CrossRef]
- Paul, B.; Dey, A.K.; Kundu, D. Bayesian analysis of three parameter absolute continuous Marshall-Olkin bivariate Pareto distribution. Commun. Stat. Case Stud. Data Anal. Appl. 2018, 4, 57–68. [Google Scholar] [CrossRef]
- Kundu, D.; Gupta, A.K. Bayes estimation for the Marshall-Olkin bivariate Weibull distribution. Comput. Stat. Data Anal. 2013, 57, 271–281. [Google Scholar] [CrossRef]
- Mulinacci, S. Archimedean-based Marshall-Olkin distributions and related dependence structures. Methodol. Comput. Appl. Probab. 2018, 20, 205–236. [Google Scholar] [CrossRef]
- Shen, Y.; Xu, A. On the dependent competing risks using Marshall-Olkin bivariate Weibull model: Parameter estimation with different methods. Commun. Stat.-Theory Methods 2018, 47, 5558–5572. [Google Scholar] [CrossRef]
- Lawless, J.F. Statistical Models and Methods for Lifetime Data; Wiley: New York, NY, USA, 2003. [Google Scholar]
- Contreras-Reyes, J.E.; Gallardo, D.I.; Kharazmi, O. Time-dependent residual Fisher information and distance for some special continuous distributions. Commun. Stat.-Simul. Comput. 2022, 1–21. [Google Scholar] [CrossRef]
- Chaturvedi, A.; Pathak, A.; Kumar, N. Statistical inferences for the reliability functions in the proportional hazard rate models based on progressive type-II right censoring. J. Stat. Comput. Simul. 2019, 89, 2187–2217. [Google Scholar] [CrossRef]
- Bai, X.; Shi, Y.; Liu, Y.; Liu, B. Reliability inference of stress-strength model for the truncated proportional hazard rate distribution under progressively type-II censored samples. Appl. Math. Model. 2018, 65, 377–389. [Google Scholar] [CrossRef]
- Kizilaslan, F. E-Bayesian estimation for the proportional hazard rate model based on record values. Commun. Stat.-Simul. Comput. 2019, 48, 350–371. [Google Scholar] [CrossRef]
- Popovicć, B.V.; Ristić, M.M.; Genc, A.I. Dependence properties of multivariate distributions with proportional hazard rate marginals. Appl. Math. Model. 2020, 77, 182–198. [Google Scholar] [CrossRef]
- Han, M. The structure of hierarchical prior distribution and its applications. Oper. Res. Manag. Sci. 1997, 63, 31–40. [Google Scholar]
- Han, M. E-Bayesian estimation of the reliability derived from Binomial distribution. Appl. Math. Model. 2011, 35, 2419–2424. [Google Scholar] [CrossRef]
- Han, M. The E-Bayesian and hierarchical Bayesian estimations of Pareto distribution parameter under different loss functions. J. Stat. Comput. Simul. 2017, 87, 577–593. [Google Scholar] [CrossRef]
- Basheer, A.M.; Okasha, H.M.; EI-Baz, A.H.; Tarabia, A.M.K. E-Bayesian and hierarchical Bayesian estimations for the inverse Weibull distribution. Ann. Data Sci. 2021, 1–13. [Google Scholar] [CrossRef]
- Wu, M.; Shi, Y.; Wang, Y. E-Bayesian estimation for competing risk model under progressively hybrid censoring. J. Syst. Eng. Elect. 2016, 27, 936–944. [Google Scholar]
- Okasha, H.M.; Wang, J. E-Bayesian estimation for the geometric model based on record statistics. Appl. Math. Model. 2016, 40, 658–670. [Google Scholar] [CrossRef]
- Han, M. E-Bayesian estimation and its E-posterior risk of the exponential distribution parameter based on complete and type-I censored samples. Commun. Stat.-Theory Methods 2020, 49, 1858–1872. [Google Scholar] [CrossRef]
- Putter, H.; Fiocco, M.; Geskus, R.B. Tutorial in biostatistics: Competing risks and multistate models. Stat. Med. 2007, 26, 2389–2430. [Google Scholar] [CrossRef] [PubMed]
- Geskus, R.B. Data Analysis with Competing Risks and Intermediate States; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).