Numerical Analysis of a Swelling Poro-Thermoelastic Problem with Second Sound
Abstract
1. Introduction
2. Thermomechanical Model
3. Numerical Analysis: A Priori Error Estimates
4. Numerical Results
4.1. Numerical Convergence in a Problem with an Exact Solution
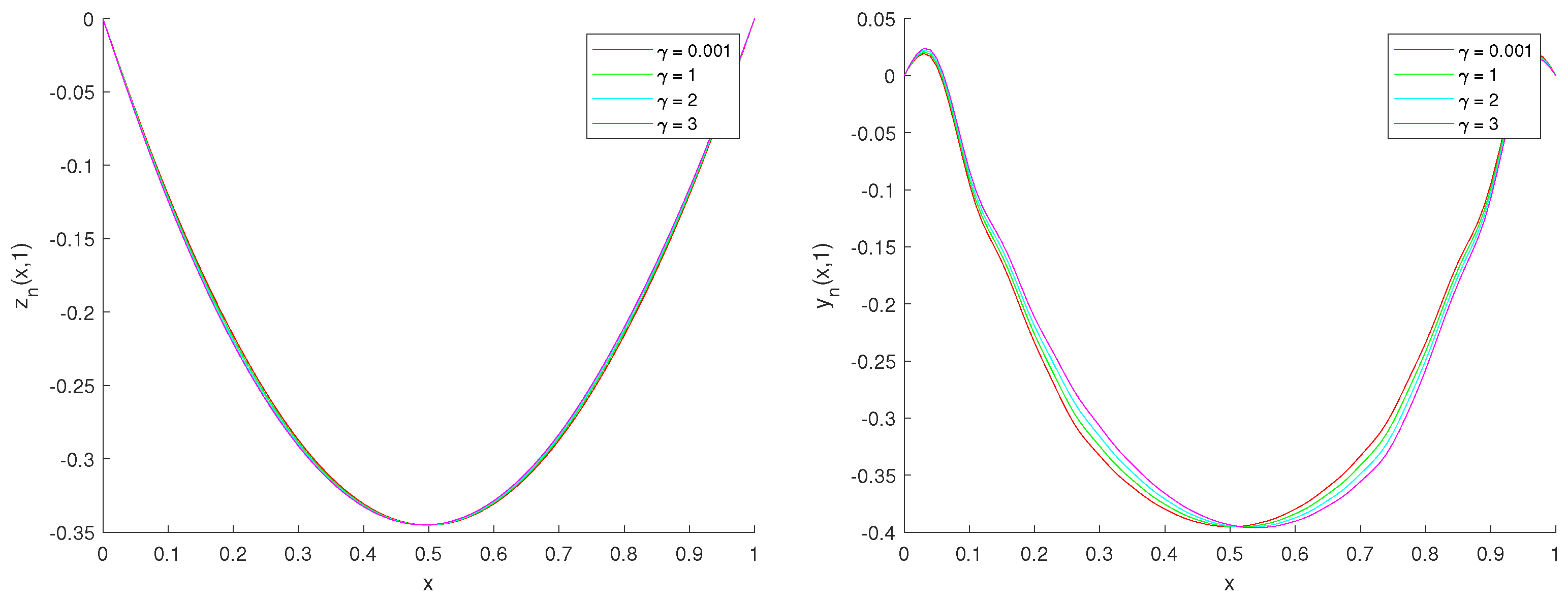
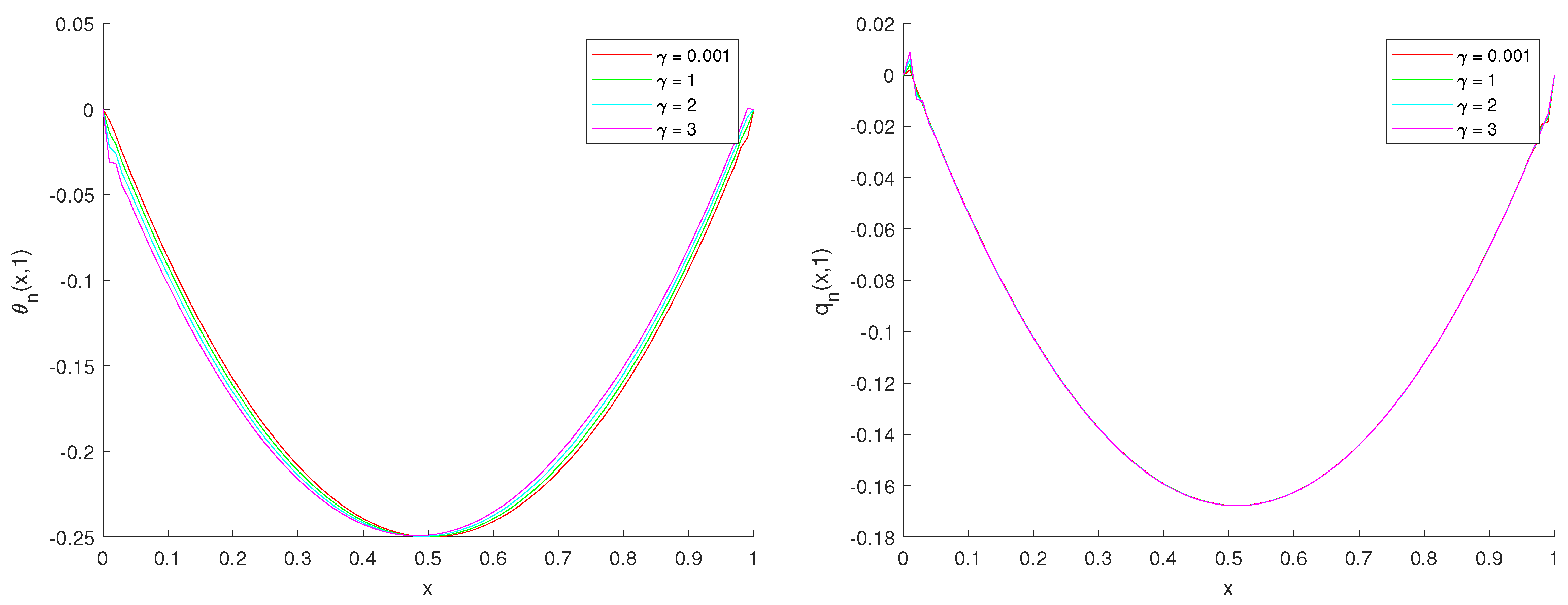
4.2. Dependence of the Solution on the Coupling Parameter
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Karalis, T.K. On the elastic deformation of non-saturated swelling soils. Acta Mech. 1990, 84, 19–45. [Google Scholar] [CrossRef]
- Philip, J.R. Hydrostatics and hydrodynamics in swelling soils. Water Resour. Res. 1969, 5, 1070–1077. [Google Scholar] [CrossRef]
- Sposito, G. Thermodynamics of swelling clay-water systems. Soil Sci. 1972, 114, 243–249. [Google Scholar] [CrossRef]
- Bowen, R.M.; Wiese, J.C. Diffusion in mixtures of elastic materials. Int. J. Eng. Sci. 1969, 7, 689–722. [Google Scholar] [CrossRef]
- Bowen, R.M. Theory of Mixtures in Continuum Physics. In Continuum Physics, Mixtures and EM Field Theories; Academic Press: New York, NY, USA, 1976; Volume III, pp. 1–127. [Google Scholar]
- Ieşan, D.; Quintanilla, R. Existence and continuous dependence results in the theory of interacting continua. J. Elasticity 1994, 36, 85–98. [Google Scholar] [CrossRef]
- Quintanilla, R. Exponential stability for one-dimensional problem of swelling porous elastic soils with fluid saturation. J. Comput. Appl. Math. 2002, 145, 525–533. [Google Scholar] [CrossRef]
- Eringen, A.C. A continuum theory of swelling porous elastic solids. Int. J. Eng. Sci. 1994, 332, 1337–1349. [Google Scholar] [CrossRef]
- Al-Mahdi, A.M.; Al-Gharabli, M.M.; Alahyane, M. Theoretical and numerical stability results for a viscoelastic swelling porous-elastic system with past history. AIMS Math. 2021, 6, 11921–11949. [Google Scholar] [CrossRef]
- Apalara, T.A.; Almutairi, O.B. Well-Posedness and Exponential Stability of Swelling Porous with Gurtin–Pipkin Thermoelasticity. Mathematics 2022, 10, 4498. [Google Scholar] [CrossRef]
- Almeida Júnior, D.S.; Ramos, A.J.A.; Noé, A.S.; Freitas, M.M.; Aum, P.T.P. Stabilization and numerical treatment for swelling porous elastic soils with fluid saturation. Z. Angew. Math. Phys. 2021, 101, e202000366. [Google Scholar]
- Apalara, T.A.; Yusuf, M.O.; Salami, B.A. On the control of viscoelastic damped swelling porous elastic soils with internal delay feedbacks. J. Math. Anal. Appl. 2021, 504, 125429. [Google Scholar] [CrossRef]
- Apalara, T.A. General stability result of swelling porous elastic soils with a viscoelastic damping. Z. Angew. Math. Phys. 2020, 71, 200. [Google Scholar] [CrossRef]
- Chiriţă, S. On the spatial decay of solutions in the theory of swelling porous thermoelastic soils. Internat. J. Engrg. Sci. 2004, 42, 1995–2010. [Google Scholar] [CrossRef]
- Freitas, M.M.; Ramos, A.J.A.; Santos, M.L. Existence and upper-semicontinuity of global attractors for binary mixtures solids with fractional damping. Appl. Math. Optim. 2021, 83, 1353–1383. [Google Scholar] [CrossRef]
- Freitas, M.M.; Ramos, A.J.A.; Almeida Júnior, D.S.; Miranda, L.G.R.; Noé, A.S. Asymptotic dynamics for fractionally damped swelling porous elastic soils with memory. Boll. Unione Mat. Ital. 2023, 16, 1–23. [Google Scholar] [CrossRef]
- Galeş, C. Potential method in the linear theory of swelling porous elastic soils. Eur. J. Mech. A Solids 2004, 23, 957–973. [Google Scholar] [CrossRef]
- Kalantari, B. Engineering significant of swelling soils. Res. J. Appl. Sci. Eng. Technol. 2012, 4, 2874–2878. [Google Scholar]
- Kumar, R.; Batra, D. Fundamental solution of steady oscillation in swelling porous thermoelastic medium. Acta Mech. 2020, 231, 3247–3263. [Google Scholar] [CrossRef]
- Nonato, C.A.S.; Ramos, A.J.A.; Raposo, C.A.; Dos Santos, M.J.; Freitas, M.M. Stabilization of swelling porous elastic soils with fluid saturation, time varying-delay and time-varying weights. Z. Angew. Math. Phys. 2022, 73, 20. [Google Scholar] [CrossRef]
- Ramos, A.J.A.; Apalara, T.A.; Freitas, M.M.; Araújo, M.L. Equivalence between exponential stabilization and boundary observability for swelling problem. J. Math. Phys. 2022, 63, 011511. [Google Scholar] [CrossRef]
- Tomar, S.K.; Goyal, S. Elastic waves in swelling porous media. Transp. Porous Media 2013, 100, 39–68. [Google Scholar] [CrossRef]
- Wang, J.M.; Guo, B.Z. On the stability of swelling porous elastic soils with fluid saturation by one internal damping. IMA J. Appl. Math. 2006, 71, 565–582. [Google Scholar] [CrossRef]
- Youkana, A.; Al-Mahdi, A.M.; Messaoudi, S.A. General energy decay result for a viscoelastic swelling porous-elastic system. Z. Angew. Math. Phys. 2022, 73, 88. [Google Scholar] [CrossRef]
- Apalara, T.A.; Soufyane, A.; Mounir, A. On well-posedness and exponential decay of swelling porous thermoelastic media with second sound. J. Math. Anal. Appl. 2022, 510, 126006. [Google Scholar] [CrossRef]
- Ciarlet, P.G. Basic error estimates for elliptic problems. In Handbook of Numerical Analysis. Vol. II; Elsevier Science Publishers B.V.: North-Holland, The Netherlands, 1991; pp. 17–352. [Google Scholar]
- Campo, M.; Fernández, J.; Kuttler, K.; Shillor, M.; Viaño, J. Numerical analysis and simulations of a dynamic frictionless contact problem with damagen. Comput. Methods Appl. Mech. Eng. 2006, 196, 476–488. [Google Scholar] [CrossRef]
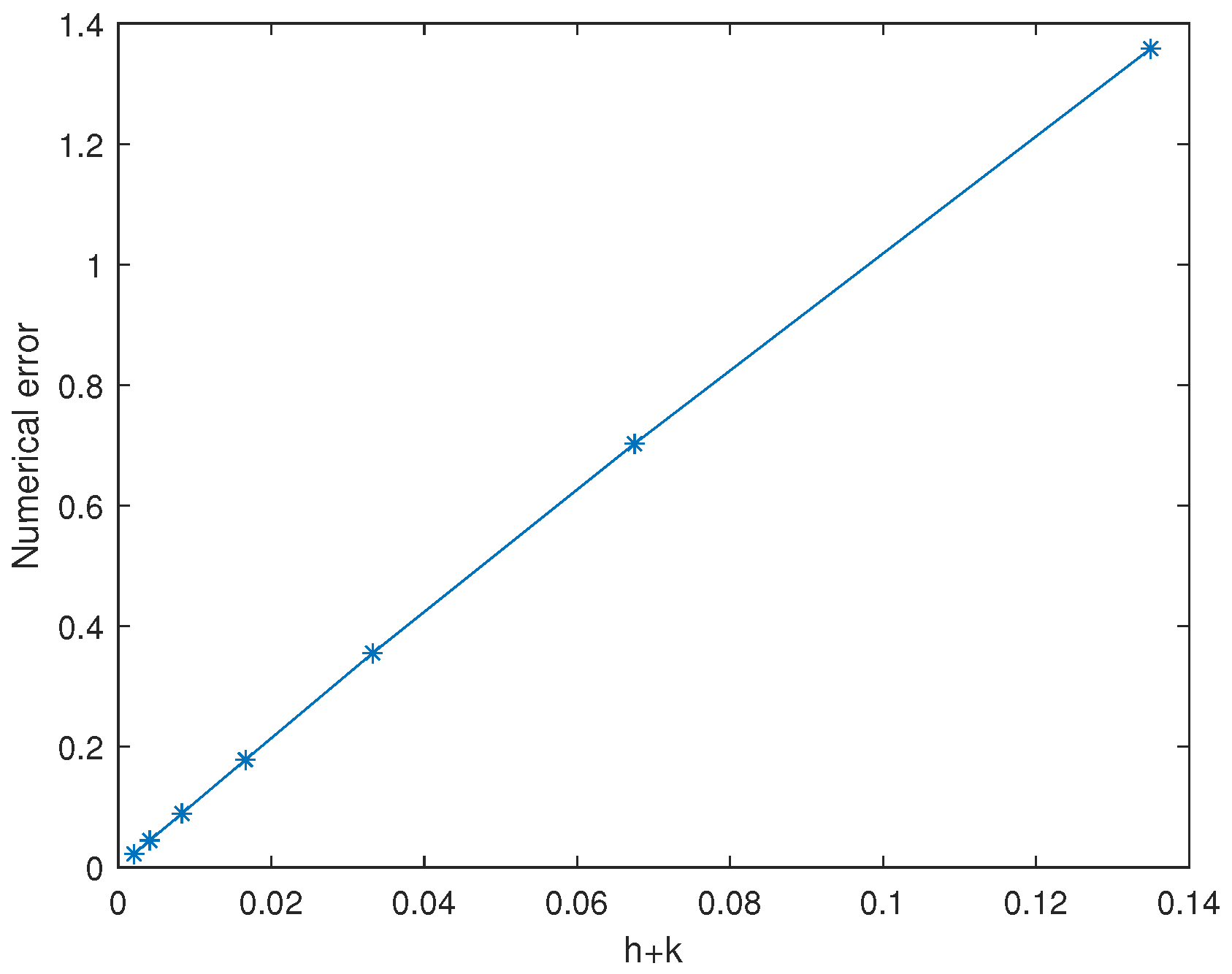


| 0.01 | 0.005 | 0.002 | 0.001 | 0.0005 | 0.0002 | 0.0001 | |
| 1.358170 | 1.358029 | 1.358880 | 1.359455 | 1.359885 | 1.360240 | 1.360385 | |
| 0.706274 | 0.702784 | 0.701989 | 0.702097 | 0.702394 | 0.702808 | 0.703040 | |
| 0.367338 | 0.358107 | 0.355322 | 0.354928 | 0.354879 | 0.354958 | 0.355038 | |
| 0.200097 | 0.185225 | 0.179347 | 0.178370 | 0.178115 | 0.178052 | 0.178060 | |
| 0.119477 | 0.100566 | 0.091755 | 0.089831 | 0.089275 | 0.089112 | 0.089091 | |
| 0.082600 | 0.059873 | 0.048773 | 0.045952 | 0.044941 | 0.044601 | 0.044551 | |
| 0.067673 | 0.041316 | 0.027972 | 0.024416 | 0.022994 | 0.022399 | 0.022294 | |
| 0.062607 | 0.033819 | 0.018282 | 0.013994 | 0.012215 | 0.011385 | 0.011199 | |
| 0.061113 | 0.031276 | 0.014183 | 0.009142 | 0.006999 | 0.005956 | 0.005693 | |
| 0.060690 | 0.030527 | 0.012711 | 0.007091 | 0.004571 | 0.003312 | 0.002978 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bazarra, N.; Fernández, J.R.; Rodríguez-Damián, M. Numerical Analysis of a Swelling Poro-Thermoelastic Problem with Second Sound. Mathematics 2023, 11, 1456. https://doi.org/10.3390/math11061456
Bazarra N, Fernández JR, Rodríguez-Damián M. Numerical Analysis of a Swelling Poro-Thermoelastic Problem with Second Sound. Mathematics. 2023; 11(6):1456. https://doi.org/10.3390/math11061456
Chicago/Turabian StyleBazarra, Noelia, José R. Fernández, and María Rodríguez-Damián. 2023. "Numerical Analysis of a Swelling Poro-Thermoelastic Problem with Second Sound" Mathematics 11, no. 6: 1456. https://doi.org/10.3390/math11061456
APA StyleBazarra, N., Fernández, J. R., & Rodríguez-Damián, M. (2023). Numerical Analysis of a Swelling Poro-Thermoelastic Problem with Second Sound. Mathematics, 11(6), 1456. https://doi.org/10.3390/math11061456








