Abstract
The problem of state estimation of a linear, dynamical state-space system where the output is subject to quantization is challenging and important in different areas of research, such as control systems, communications, and power systems. There are a number of methods and algorithms to deal with this state estimation problem. However, there is no consensus in the control and estimation community on (1) which methods are more suitable for a particular application and why, and (2) how these methods compare in terms of accuracy, computational cost, and user friendliness. In this paper, we provide a comprehensive overview of the state-of-the-art algorithms to deal with state estimation subject to quantized measurements, and an exhaustive comparison among them. The comparison analysis is performed in terms of the accuracy of the state estimation, dimensionality issues, hyperparameter selection, user friendliness, and computational cost. We consider classical approaches and a new development in the literature to obtain the filtering and smoothing distributions of the state conditioned to quantized data. The classical approaches include the extended Kalman filter/smoother, the quantized Kalman filter/smoother, the unscented Kalman filter/smoother, and the sequential Monte Carlo sampling method, also called particle filter/smoother, with its most relevant variants. We also consider a new approach based on the Gaussian sum filter/smoother. Extensive numerical simulations—including a practical application—are presented in order to analyze the accuracy of the state estimation and the computational cost.
Keywords:
extended Kalman filter/smoother; unscented Kalman filter/smoother; Gaussian sum filter/smoother; particle filter/smoother; state estimation; quantized data MSC:
93E11
1. Introduction
In the last two decades, there has been a growing number of applications for sensors, networks, and sensor networks, where common problems include dealing with the loss of information in signals measured with low-resolution sensors, or storing and/or transmitting a reduced representation of such signals—in order to minimize the resource consumption in a communication channel []. This kind of problem encompasses a nonlinear process called quantization, which divides the input signal space into a finite (or infinite but countable) number of intervals and each of them being represented by a single output value []. Applications using quantized data include networked control [,], fault detection [,,,], cyber-physical systems [,], multi-target tracking [], and system identification [,,,], just to mention a few. In these applications, a key element is the state estimation of a dynamical system conditioned upon the available quantized observations. For instance, ref [] deals with the problem of state estimation and control of a microgrid incorporating multiple distributed energy resources, where the state estimation and control are based on uniform quantized observations that are transmitted through a wireless channel.
For linear systems subject to additive Gaussian noise, expressions for the filtering and smoothing probability density functions (filtering and smoothing PDFs) that give estimators with optimal mean-square-error properties can be obtained from the Kalman Filter and the Rauch–Tung–Striebel smoother (KS), respectively, []. However, for general nonlinear systems subject to non-Gaussian additive noise, it is difficult (or even impossible in most cases) to obtain closed-form expressions for these PDFs and, therefore, expressions for a state estimator, given input/output data. Many sub-optimal methods have been developed in order to obtain an approximation of the desired PDFs and an estimate of the state vector; see, e.g., [,,]. For example, the extended Kalman filter (EKF) was studied in [] to deal with quantized data. This approach is difficult to implement since the quantizer is a non-differentiable nonlinear function and requires the computation of a Jacobian matrix. The authors in [] proposed to approximate the quantizer by a smooth function to compute an approximation of the Jacobian matrix. However, since the quantization function is highly nonlinear, the EKF/EKS approach typically produces inaccurate estimates of the system state. The Kalman filter was modified to include the quantization effect in the computation of the filtering state, which has been referred to as the quantized Kalman filter (QKF) [,]. The unscented Kalman filter (UKF) was applied by [] to deal with quantized innovation systems in a wireless sensor network environment. The UKF is based on the Unscented transformation [] that represents the mean and covariance of a Gaussian random variable through a reduced number of points. Then, these points are propagated through the nonlinear function to accurately capture the mean and covariance of the propagated Gaussian random variable. An advantage of the UKF lies in its high estimation accuracy and convergence rate, together with its simplicity of implementation compared with EKF, since it avoids the computation of the Jacobian matrix required in the EKF method.
One of the most used methods in nonlinear filtering is the Sequential Monte Carlo sampling approach called particle filtering (PF) []. The PF uses a set of weights and samples to create an approximation of the filtering and smoothing PDFs. The main advantages of the combined PF and particle smoothing (PS) are the implementation and ability to deal with nonlinear and non-Gaussian systems. Nevertheless, the PF also has drawbacks. One of them is the degeneracy problem, where most weights—calculated at one iteration of the PF approach—go to zero []. To get around this issue, [] proposed an approach called resampling. Here, the heavily weighted particles are replicated sometimes, and the rest of the particles are discarded. A number of resampling techniques have been developed in the literature, such as systematic (SYS), multinomial (ML), Metropolis (MT), and local selection (LS) resampling methods []. These resampling techniques have advantages such as unbiasedness and parallelism capacity. Naturally, the performance of the particle filter depends upon the implemented resampling method []. Unfortunately, the resampling process produces a loss of diversity in the particle set since the particles with high weights are replicated. This problem is called sample impoverishment [], and to mitigate it, a Markov chain Monte Carlo (MCMC) move is usually introduced after the resampling step to provide diversity to the samples so that the new particle set is still distributed according to the posterior PDF []. There are mainly two MCMC methods that we can use to deal with the impoverishment problem: the Gibbs and the Metropolis–Hasting (MH) sampling. Here, we discuss the MH algorithm and a special MH algorithm called random walk Metropolis (RWM [,]) in conjunction with the aforementioned resampling methods.
In addition to the methods detailed above, a new algorithm to deal with quantized output data is proposed in [,]. In these works, the authors defined the probability mass function of the quantized data conditioned upon the system state as an integral whose limits depend on the quantizer regions. This integral is approximated by using Gauss–Legendre quadrature [], yielding a model with a Gaussian sum structure. Such a model is later used to develop a Gaussian sum—filter GSF and smoother GSS—to obtain closed-form filtering and smoothing distributions for systems with quantized output data.
Despite the wide availability of the commonly used and also novel state-estimation methods described above, there is no consensus among the control and estimation community on (1) which methods are more suitable for a particular application and why, and (2) how these methods compare in terms of accuracy, computational cost, and user friendliness. This paper provides a comprehensive overview of the state-of-the-art algorithms to deal with the problem of state estimation of linear dynamical systems using quantized observations. This work aims to serve both as an introduction to the EKF/EKS, QKF/QKS, UKF/UKS, GSF/GSS, and PF/PS algorithms for estimation using quantized output data, and to provide clear guidelines on the advantages and shortcomings of each algorithm based on the accuracy of the state estimation, dimensionality issues, hyperparameter selection, user friendliness, and computational cost.
The organization of this paper is as follows: In Section 2, we define the problem of state estimation with quantized output data. In Section 3, we present a comprehensive review of the most effective filtering and smoothing methods that are available in the literature. In Section 4, a numerical example to show the traits of each method is presented, and in Section 5 a practical application is used for testing the algorithms. In Section 6, general user guidelines are provided. Finally, concluding remarks are given in Section 7.
2. Statement of the Problem
This paper considers the filtering and smoothing problem for the following discrete-time, LTI state-space system with quantized output (see Figure 1):
where is the state vector, is the input of the system, is the non-quantized output, and is the quantized output. The matrix , , , and . The nonlinear map is the quantizer. The state noise and the output noise are zero-mean white Gaussian noises with covariance matrix and R, respectively. Due to the random components (i.e., the noises and ) in (1) and (2), the state-space model can be described using the state transition PDF and the non-quantized output PDF with , where represents a PDF corresponding to a Gaussian distribution with mean and covariance matrix of the random variable . The initial condition , the model noise , and the measurement noise are statistically independent random variables.

Figure 1.
State-space model with quantized output.
On the other hand, the nonlinear map is the quantizer, where is the output set. More precisely, is given by []:
where is the kth output value in the output set , is the kth interval mapped to the value , and the indices set defines the number of quantization levels of the output set . Here we consider two types of quantizers: (i) an infinite-level quantizer (ILQ), in which its output has infinite (but countable) levels of quantization with
Here, are disjoint intervals, and each is the value that the quantizer takes in the region , and (ii) a finite-level quantizer (FLQ), in which the output of the quantizer is limited to minimum and maximum values (saturated quantizer) similar to (4) with
Notice that the FLQ quantizer is comprised of finite and semi-infinite intervals, given by , , and , with . Usually, the sets and the output values are defined in terms of the quantization step , for instance, see, e.g., [,].
Thus, the problem of interest can be defined as follows: given the available data and , where N is the data length, we can obtain the filtering and smoothing PDFs of the state given the quantized measurements, and , respectively, the state estimators
and the corresponding covariance matrices of the estimation error:
where and denotes the conditional expectation of given y.
2.1. Practical Application: Liquid-Level System
To give context to the problem stated above, we included a practical application. Consider the liquid-level system shown in Figure 2; see, e.g., []. The goal is to estimate the liquid level in a tank using the measurements obtained by a low-cost sensor based on a variable resistor that is attached to an arm with a floater. This sensor varies its resistance in discrete steps providing the quantized measurements . and are the total inflow and outflow rates, respectively, and with are small deviations of the inflow and outflow rate from the steady-state value . Additionally, h is a small deviation of the liquid level of the tank from the steady-state value . The total liquid level is .
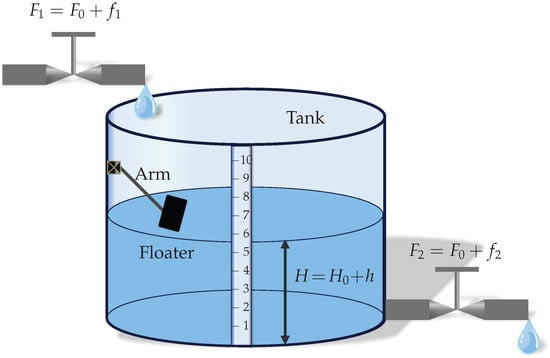
Figure 2.
Liquid-level system.
The linearized model (around the operating points and ) that relates the input to the output h is given by the differential equation . Setting , , and a sampling period leads to the following state-space model:
where is the level of the liquid present in the tank and is a nonavailable signal which is transformed into quantized measurements by the sensor with the following model:
Using only input data and the quantized sensor measurements, the goal is to estimate the liquid level at every time instant , where .
3. Recursive Filtering and Smoothing Methods for Quantized Output Data
3.1. Bayesian Filtering and Smoothing
Under a Bayesian framework, the filtering distributions admit the following recursions; see, e.g., []:
where (14) and (15) are the measurement- and time-update equations. The PDF is directly obtained from the model in (1), and is a normalization constant. On the other hand, the Bayesian smoothing equation, see, e.g., [], is defined by the following:
Notice that to obtain in (15), we need the probability density function (PDF) . Since is a discrete random variable, the probabilistic model of is a probability mass function (PMF). Then, the measurement-update equation in (15) combines both PDFs and a PMF. Here, we use generalized probability density functions; see, e.g., []. They combine both discrete and absolutely continuous distributions. In [], an integral equation for is defined in order to solve the filtering recursion as follows
Here, and are functions of the boundary values of each region of the quantizers defined in Table 1.

Table 1.
Integral limits of Equation (17).
Notice that in (17) is a non-Gaussian random variable. This leads to obtaining non-Gaussian measurement- and time-update distributions. However, the EKF, QKF, and UKF filters are developed under the assumption that the measurement- and time-update distributions are Gaussian, which yields a loss of accuracy in the estimation. On the other hand, (17) is used in GSF/GSS and PF/PS, where the Gaussian assumption is not needed.
3.2. Extended State-Space System
To implement filtering and smoothing algorithms such as the EKF/EKS and the UKF/UKS, the state-space model in (1)–(3) is rewritten in an extended form as follows
The extended system matrices are given by
where is the extended state, is the extended input with . Notice that the extended system transforms the algebraic equation of the linear output into a recursive equation. It is then necessary to define an initial condition for at . Considering , the initial condition of the extended vector become where and . The noise satisfies with
The noise is added in order to obtain the adequate structure of the system to implement the EKF/EKS and the UKF/UKS. However, this does not imply that the measurements are corrupted by the noise . The idea of including an extra noise in the model is proposed to ensure a full-rank covariance matrix in the EM algorithm; see, e.g., []. We assume that , where the variance is small.
3.3. Extended Kalman Filtering and Smoothing
The idea of EKF [,] is to have a linear approximation around a state estimate, using a Taylor series expansion. The EKF is not directly applied to the problem of interest in this paper because the quantizer is a non-differentiable nonlinear function. In [], it was suggested that it is possible to compute the Kalman gain using a smooth arctan-based approximation of the quantizer. Thus, following the idea in [] and the representation of the arctan function found in [], the following approximation for the quantizer is proposed:
Here, is a user parameter that defines how well the approximation fits the quantizer function in the switch point, as shown in Figure 3.
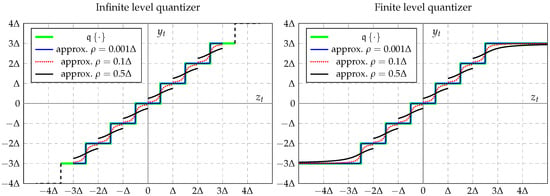
Figure 3.
Quantizer approximation by using the arctan function.
On the other hand, by using the smooth approximation of the quantizer, it is possible to approximate the nonlinear system as a linear time-varying system as follows:
where is the Jacobian matrix of with respect to , and evaluated at and . Then, the equations of the EKF and EKS are summarized in Algorithms 1 and 2, respectively. One of the difficulties in applying the EKF to deal with quantized data is the computation of the Jacobian matrix . Despite the approximation of the quantizer, the Jacobian is nearly zero for all values of , except for the exact switch points, as shown in Figure 4 (left), where . Additionally, Figure 4 (center and right) shows that the quantizer and Jacobian approximations worsen as increases, which reduces the accuracy of the estimation.
| Algorithm 1: Extended Kalman filter algorithm for quantized output data |
 |

Figure 4.
Jacobian matrix of the quantizer approximation.
| Algorithm 2: Extended Kalman smoother algorithm for quantized output data |
 |
3.4. Unscented Kalman Filtering and Smoothing
The unscented Kalman Filter [] is a deterministic sampling-based approach that uses samples called sigma points to propagate the mean and covariance of the system state (assumed to be a Gaussian random variable) through the nonlinear functions of the system. These propagated points accurately capture the mean and covariance of the posterior state to the 3rd-order Taylor series expansion for any nonlinear function []. The key idea of UKF is to directly approximate the mean and covariance of the posterior distribution instead of approximating nonlinear functions []. The unscented Kalman Filter is based on the unscented transformation of the random variable into the random variable , where is a nonlinear function, , and . Thus, the sigma points are defined by
Here, , the scaling parameter , the parameters and determine the propagation of the sigma points around the mean, and the notation refers to the th column of the matrix . The weights associated with the unscented transformation are the sets
where and . In this set of equations, is an additional parameter that can be used to incorporate prior information on the distribution. Then, the statistics of the transformed random variable are the mean and the covariance matrix . Additionally, the cross-covariance matrix between and is given by . The steps to implement the UKF are summarized in Algorithm 3. Notice that for the problem of interest in this paper, the process equation is a linear function. Thus, the UKS algorithm is similar to EKS but uses the filtering and predictive distributions obtained from the UKF algorithm.
| Algorithm 3: Unscented Kalman filter algorithm for quantized output data |
 |
3.5. Quantized Kalman Filtering and Smoothing
The quantized Kalman filter is an alternative version of the Kalman filter that modifies the measurement update equation to include the quantization effect in the computation of the filtering distributions. This modification can be performed in different ways [,]. In this work, we use the following modification of the KF:
where is the Kalman gain. Notice that, with the modification in (30), the QKS algorithm is similar to the standard Kalman smoother (KS).
3.6. Gaussian Sum Filtering and Smoothing
The Gaussian Sum Filter [,] is a novel approach to deal with quantized output data. The key idea of GSF is to approximate the integral of given in (17) using the Gauss–Legendre quadrature rule. This approximation produces a model with a Gaussian sum structure as follows:
Here, K is the number of points from the Gauss–Legendre quadrature rule, , , and are defined in Table 2, and and are weights and points defined by the quadrature rule, given in, e.g., [].

Table 2.
Parameters of the approximation using the Gauss–Legendre quadrature.
Using the approximation of given in (31), the Gaussian sum filter iterates between the following two steps:
All quantities in this recursion can be computed following the algorithm in Algorithm 4. On the other hand, to compute the smoothing distribution, (16) is separated into two formulas, to avoid the division by a non-Gaussian distribution []. The first formula is the backward recursion that is defined as follows (obtained by using the approximation of given in (31)):
All quantities in this recursion can be computed following the algorithm in Algorithm 5. The second formula computes the smoothing distribution as follows:
In this equation, all quantities can be computed following Algorithm 6.
| Algorithm 4: Gaussian sum filter algorithm for quantized output data. | |||||||
| 1 | Input: The PDF of the initial state , e.g., , , , . The points of the Gauss–Legendre quadrature . | ||||||
| 2 | fortoNdo | ||||||
| 3 | Compute and store , , and according to Table 2. | ||||||
| 4 | Measurement Update: | ||||||
| 5 | Set . | ||||||
| 6 | for todo | ||||||
| 7 | for toKdo | ||||||
| 8 | Set the index . | ||||||
| 9 | Compute the weights, means, and covariances matrices as follows:
| ||||||
| 10 | end | ||||||
| 11 | end | ||||||
| 12 | Perform the Gaussian-sum-reduction algorithm according to [] to obtain the reduced GMM of . | ||||||
| 13 | Time Update | ||||||
| 14 | Set . | ||||||
| 15 | fortodo | ||||||
| 16 | Compute and store the weights, means, and covariance matrices as follows:
| ||||||
| 17 | end | ||||||
| 18 | end | ||||||
| 19 | Output: The filtering PDFs , the predictive PDFs , and the set , for . | ||||||
| Algorithm 5: Backward-filtering algorithm for quantized output data. | |||||||
| 1 | Input: The initial backward measurement at with parameters: and | ||||||
| 2 | for to1do | ||||||
| 3 | Backward Prediction | ||||||
| 4 | Set . | ||||||
| 5 | for todo | ||||||
| 6 | Compute and store the backward prediction update quantities as follows
| ||||||
| 7 | end | ||||||
| 8 | Backward Measurement Update: | ||||||
| 9 | Set . | ||||||
| 10 | for todo | ||||||
| 11 | for toKdo | ||||||
| 12 | Set the index . | ||||||
| 13 | Compute the backward measurement update quantities as follows
| ||||||
| 14 | end | ||||||
| 15 | end | ||||||
| 16 | Compute the GMM structure of using Lemma A.3 in []. | ||||||
| 17 | Perform the Gaussian sum reduction algorithm according to [] to obtain the reduced GMM structure of , see Equation (54) in []:
| ||||||
| 18 | Compute and store the backward filter form of the reduced version of using Lemma A.3 in []. | ||||||
| 19 | end | ||||||
| 20 | Output: The backward prediction and the backward measurement update for . | ||||||
| Algorithm 6: Gaussian sum smoothing algorithm for quantized output data. | |||||||
| 1 | Input: The PDFs and obtained from Algorithm 4 and the reduced version of obtained from Algorithm 5, see (54) in []. | ||||||
| 2 | Save the PDF . | ||||||
| 3 | for to 1do | ||||||
| 4 | Set . | ||||||
| 5 | for todo | ||||||
| 6 | for todo | ||||||
| 7 | Set the index . | ||||||
| 8 | Compute the weights, means, and covariance matrices as follows:
| ||||||
| 9 | end | ||||||
| 10 | end | ||||||
| 11 | end | ||||||
| 12 | Output: The smoothing PDFs , for . | ||||||
3.7. Particle Filtering and Smoothing
Particle filtering [,] is a Monte Carlo method that approximately represents the filtering distributions of the state variables conditioned to the observations by using a set of weighted random samples, called particles, so that
where is the Dirac delta function, denotes the ith weight, denotes the ith particle sampled from the filtering distribution , and M is the number of particles. Since the filtering distribution is unknown in the current iteration, it is difficult or impossible to sample directly from it. In this case, the particles are usually generated from a known density that is chosen (by the user) to facilitate the sampling process. This is called importance sampling, and the PDF is called importance density. Then, the importance weight computation can be carried out in a recursive fashion (sequential importance sampling, SIS) as follows:
where is the importance density and are the importance weights of the previous iteration. On the other hand, the choice of importance distribution is critical for performing particle filtering and smoothing. The particle filter literature shows that the importance density is optimal in the sense that it minimizes the variance in the importance weights [,]. However, in most cases, it is difficult or impossible to draw samples for this optimal importance density, except for particular cases such as a state-space model with a nonlinear process and linear output Equation []. Many sub-optimal methods have been developed to approximate the importance density, such as Markov chain Monte Carlo [], ensemble Kalman filter [], local linearization of the state-space model, and local linearization of the optimal importance distribution [], among others. One of the most commonly used importance densities in the literature is the state transition prior ; see, e.g., [,,]. This choice yields an intuitive and simple-to-implement algorithm with . This algorithm is called a bootstrap filter [].
The particle filter suffers from a problem called the degeneracy phenomenon. As shown in [], the variance in the importance weights can only increase over time. This implies that after a few iterations, most particles have negligible weights; see also []. A consequence of the degeneracy problem is that a large computational effort is devoted to updating particles whose contribution to the final estimate is nearly zero. To solve the degeneracy problem, the resampling approach was proposed in []. The resampling method eliminates the particles that have small weights, and the particles with large weights are replicated, generating a new set (with replacement) of equally weighted particles.
Additionally, the resampling method used to reduce the degeneracy effect on the particles produces another unwanted issue called particle impoverishment. This effect implies a loss of diversity in the sample set since the resampled particles will contain many repeated points that were generated from heavily weighted particles. In the worst-case scenario, all particles can be produced by a single particle with a large weight []. To solve the impoverishment problem, methods such as roughening and regularization have been suggested in the literature []. Markov chain Monte Carlo (MCMC) is another method used after the resampling step to add variability to the resampled particles []. The basic idea is to apply the MCMC algorithm to each resampled particle with as the target distribution. That is, we need to build a Markov chain by sampling a proposal particle from the proposal density. Then, is accepted only if , with , where corresponds to the uniform distribution over the real numbers in the interval , and is the acceptance ratio given by
With this process, the diversity of the new particles is greater than the resampled ones, reducing the risk of particle impoverishment. Additionally, the new particles are distributed according to . In this paper, we use the MH and RWM algorithms to build on the MCMC step. In Algorithm 7, we summarize the steps to implement the particle filter with the MCMC step.
| Algorithm 7: MCMC-based particle filter algorithm for quantized output data | ||||||
| 1 | Input: , the number of particles M. | |||||
| 2 | Draw the samples and set for . | |||||
| 3 | for to N do | |||||
| 4 | From the importance distribution draw the samples for . | |||||
| 5 | Calculate the weights using given in (17) according to (38) for . | |||||
| 6 | Normalize the weights to sum one. | |||||
| 7 | Perform resampling and generates a new set of weights and particles for . Notice that in the resampling algorithms MR, SR, and MTR for . The LS algorithm produces a new set of weights; see, e.g., []. | |||||
| 8 | Implement the MCMC move: for . | |||||
| 9 | Pick the sample from the set of the resampled particles. | |||||
| 10 | MH: Sample a proposal particle from the proposal PDF. | |||||
| 11 | RWM: Generate from ( is defined by the user) and compute . | |||||
| 12 | Evaluate given in (39). If , then accept the move () else reject the move (). | |||||
| 13 | end | |||||
| 14 | Output: , and , . | |||||
Similar to particle filtering, particle smoothing is a Monte Carlo method that approximately represents the smoothing distributions of the state variables conditioned upon the observations , using random samples as follows:
where denotes the ith weight, denotes the ith particle sampled from the smoothing distribution , and M is the number of particles. Some smoothing algorithms are based on the particles provided by the particle filtering, i.e., , such as the backward-simulation particle smoother [] and marginal particle smoother []. Particularly in the marginal particle smoother, the weights are updated in reverse time as follows:
where for and the approximation of (40) is performed using for . In this paper, we use the smoothing method developed in []. The problem of interest in this work admits further simplifications; see also []. This smoothing method [] requires the evaluation of the function given by
where . In Algorithm 8, we summarize the steps to implement the particle smoother.
| Algorithm 8: Rejection-based particle smoother algorithm for quantized output data |
 |
On the other hand, provided the weights and particles (from particle filter or smoother), the state estimators in (7) and (8) and the covariance matrices of the estimation error in (9) and (10) can be computed from
where represents a function of . For example, the mean and covariance matrix of the filtering and smoothing distributions can be computed with and , respectively. The variable s represents the observation set that is used, which is for filtering and for smoothing.
4. Numerical Experiment
In this section, we present a numerical example to analyze the performance of KF/KS, EKF/EKS, QKF/QKS, UKF/UKS, GSF/GSS, and MCMC-based PF/PS having quantized observations. We use the discrete-time system in the state-space form given in (1) and (2) with
In (44), is a quantization step, and round is the Matlab function that computes the nearest decimal or integer. The sets are computed using and . We compare the performance of all filtering and smoothing algorithms considering eight variations of the PF, where we use the Markov chain Monte Carlo method MH and RWM with the following resampling methods: SYS, ML, MT, and LS. For clarity of presentation, we use the bootstrap filter, and we solve the integral in (17) using the cumulative distribution function computed with the Matlab function mvncdf. We consider the state-space system given by (1) and (2) with , , , and . We also consider that , , the input signal is drawn from , and , and the quantization step . To implement EKF/EKS , to implement UKF/UKS , , and . To implement the GSF/GSS , and to implement PF/PS we consider , and .
In Figure 5 and Figure 6, we show the filtering and smoothing distributions, i.e., and , for a time instant. We freeze the results of KF, QKF, EKF, UKF, and GSF to observe the behavior of the PF when varying the number of used samples, and when different MCMC methods are used with different resampling algorithms. These figures show that the PDFs obtained using GSF/GSS are the ones that best fit the ground truth, followed by PF/PS. Furthermore, in Figure 7 and Figure 8, we show the boxplot of the mean square error (MSE) between the estimated and the true state after running 1000 Monte Carlo experiments. These figures show the loss of accuracy of the state estimates obtained with KF/KS, EKF/EKS, QKF/QKS, and UKF/UKS, and better performance for GSF/GSS and PF/PS (except for the PF version that uses LS resampling). Additionally, we can observe that in terms of accuracy, the PF/PS implementation that gives the lower MSE is the one that uses the MCMC move RWM with SYS, ML, and MT resampling methods. On the other hand, in terms of the computational load, PS in almost all its versions exhibits the highest execution time, followed by the GSS, EKS, UKS, and KS (see Figure 9). In Table 3, we ranked all the algorithms studied in the present manuscript in terms of the mean of the MSE and the execution time. This table suggests that there is a trade-off between the accuracy of the estimates and the execution time in the case of PF/PS. The GSF/GSS, on the other hand, exhibits high accuracy in the estimation compared with all its analogs and exhibits a relatively short execution time compared with (i) the PF/PS using 500 and 1000 particles, (ii) the PF/PS using the MT resampling method with 100 particles and (iii) the EKF/EKS algorithms.
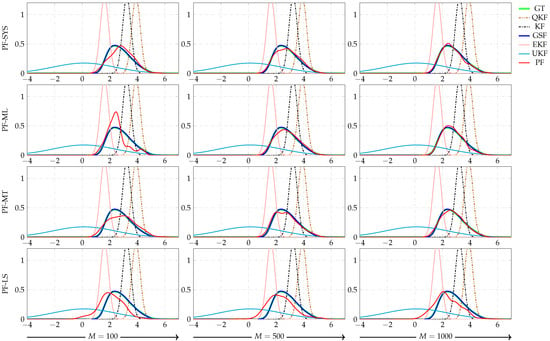
Figure 5.
Filtering PDFs for a time instant. GT stands for the ground truth. KF, EKF, QKF, UKF, GSF, and PF stand for Kalman filter, extended Kalman filter, quantized Kalman filter, unscented Kalman filter, Gaussian sum filter, and particle filter, respectively. The PDFs given by the KF, EKF, QKF, UKF were frozen in all plots to observe the behavior of the PF (with RWM moves) when the number of particles increased. SYS, ML, MT, LS stand for systematic, multinomial, metropolis, and local selection resampling algorithms, respectively.
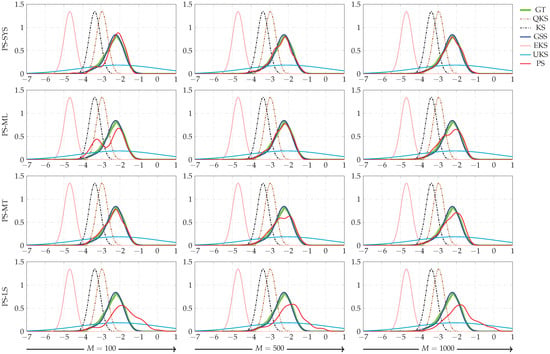
Figure 6.
Smoothing PDFs for a time instant. GT stands for the ground truth. KS, EKS, QKS, UKS, GSS, and PS stand for Kalman smoother, extended Kalman smoother, quantized Kalman smoother, unscented Kalman smoother, Gaussian sum smoother, and particle smoother, respectively. The PDFs given by the KS, EKS, QKS, and UKS were frozen in all plots to observe the behavior of the PS (with RWM moves) when the number of particles increased. SYS, ML, MT, LS stand for systematic, multinomial, metropolis, and local selection resampling algorithms, respectively.
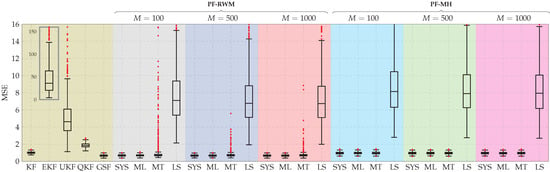
Figure 7.
Boxplot of the MSE between the estimated and true state for 1000 Monte Carlo experiments. KF, EKF, QKF, UKF, GSF, and PF stand for Kalman filter, extended Kalman filter, quantized Kalman filter, unscented Kalman filter, Gaussian sum filter, and particle filter, respectively. Additionally, SYS, ML, MT, LS stand for systematic, multinomial, metropolis, and local selection resampling algorithms, respectively. RWM and MH denote random walk Metropolis and Metropolis–Hasting moves.
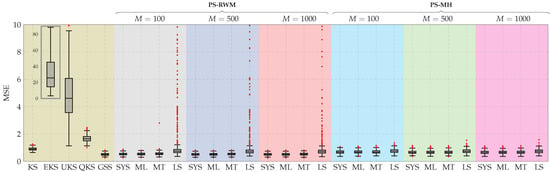
Figure 8.
Boxplot of the MSE between the estimated and true state for 1000 Monte Carlo experiments. KS, EKS, QKS, UKS, GSS, and PS stand for Kalman smoother, extended Kalman smoother, quantized Kalman smoother, unscented Kalman smoother, Gaussian sum smoother, and particle smoother, respectively. Additionally, SYS, ML, MT, and LS stand for systematic, multinomial, metropolis, and local selection resampling algorithms, respectively. RWM and MH denote random walk Metropolis and Metropolis–Hasting moves.
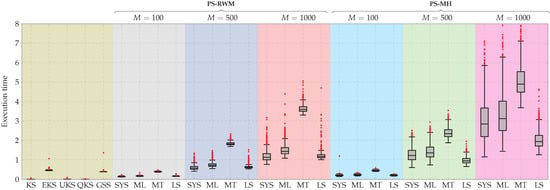
Figure 9.
Boxplot of the execution time for 1000 Monte Carlo experiments. KS, EKS, QKS, UKS, GSS, and PS stand for Kalman smoother, extended Kalman smoother, quantized Kalman smoother, unscented Kalman smoother, Gaussian sum smoother, and particle smoother, respectively. Additionally, SYS, ML, MT, and LS stand for systematic, multinomial, metropolis, and local selection resampling algorithms, respectively. RWM and MH denote random walk Metropolis and Metropolis–Hasting moves.

Table 3.
Rank of the filtering and smoothing recursive algorithms for quantized data. References: KF/KS, EKF/EKS [], QKF/QKS [,], PF/PS [], UKF/UKS [,], GSF/GSS [,]. The notation XX-YY-ZZ(M) denotes the following: XX stands for the filtering or smoothing algorithm (PF or PS), YY stands for the MCMC algorithm (RWM or MH), ZZ stands for the resampling method (SYS, ML, MT or LS), and (M) stands for the number of particles used (100, 500, or 1000).
5. Practical Application Revisited: Liquid-Level System
We now consider the liquid-level system detailed in Section 2.1. To simulate the system in (11) and (12), we consider and . The input is drawn from , and the initial condition satisfies . In this example, we implement the following filtering and smoothing algorithms: EKF/EKS, UKF/UKS, QKF/QKS, GSF/GSS, and PF/PS. The latter filtering algorithm was implemented using the systematic resampling and MH methods with 500 particles. Additionally, to implement the Gaussian Sum algorithms, we consider points from the Gauss–Legendre quadrature rule. We simulate 100 Monte Carlo experiments for both the filtering and smoothing algorithms with .
Figure 10a shows one realization of the non-quantized signal and the quantized output . Figure 10b shows the execution time of all smoothing algorithms, where we see that PS has the highest computational cost by a considerable margin, followed by the GSS. In terms of estimation accuracy, the MSE between the real and estimated tank liquid level corresponding to the filtered and smoothed states is documented in Figure 10c,d, respectively. These boxplots show that GSF and GSS exhibit the lowest MSE, followed by the UKF/UKS, QKF/QKS, PF/PS, and EKF/EKS. Taking into consideration these results, this practical setup also illustrates that the Gaussian sum filter and smoother provides the best trade-off between estimation accuracy and computational cost.
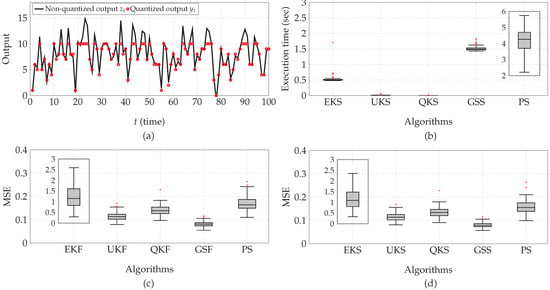
Figure 10.
Practical application: (a) A realization of the non-quantized signal and the quantized output . (b) Boxplot of the execution time of the smoothing algorithms. (c) Boxplot of the MSE between the real and estimated (filtered) tank liquid level. (d) Boxplot of the MSE between the real and estimated (smoothed) tank liquid level. EKF/EKS, QKF/QKS, UKF/UKS, GSF/GSS, and PF/PS stand for extended Kalman filter/smoother, quantized Kalman filter/smoother, unscented Kalman filter/smoother, Gaussian sum filter/smoother, and particle filter/smoother, respectively.
6. User Guidelines and Comments
All the filtering and smoothing algorithms studied in this paper have a number of hyperparameters that need to be chosen based on their purpose. Hence, some guidelines are provided based on both the numerical analysis and also on the authors’ practical experience.
- To implement the EKF/EKS, the user parameter defines the arctan-approximation accuracy of the quantizer, which impacts the accuracy of the approximation for in (24). Choose a small value of to obtain a high accuracy for the quantizer. The disadvantage of these algorithms is that despite an accurate approximation of the quantizer, the estimation of the state of the system is not accurate for a coarse quantization scheme;
- To implement UKF/UKS, the parameter is usually set to a small positive value, for instance, . The parameter is typically set to zero or a very small positive value, for instance, . For the extra parameter , if the random variable to transform is Gaussian distributed, it is known that is optimal []. In the problem of interest in this work, the random variables—after the unscented transformation—are non-Gaussian, and the parameter can be chosen heuristically so that the estimation error is acceptable;
- Based on the authors’ practical experience, the QKF/QKS produces an accurate estimation of the system states (under the assumption that filtering and smoothing distributions are Gaussian) if the quantization step is small compared to the amplitude of the output signal. However, the accuracy of the estimates decreases as the quantization step increases. The advantage of this algorithm is that it is easy to implement, and it is faster compared to more sophisticated implementations such as the PF/PS and the GSF/GSS;
- To implement the GSF/GSS, choose the number of Gauss–Legendre quadrature points as . These values of K produce highly accurate estimates for the system states and the filtering/smoothing PDFs with a low computational cost. Additionally, these algorithms produce directly an explicit model for the filtering and smoothing PDFs without extra algorithms. The disadvantage of the GSF/GSS algorithms is that they are difficult to implement since they require the backward filter recursion and the Gaussian sum reduction algorithms;
- The PF/PS produces accurate estimations of the system state with a relatively low amount of particles. For instance, are good choices for low-order models. These algorithms are easy to implement, and there are many resampling methods that can be replicated. The disadvantage of the PF/PS algorithms is that the computational cost increases rapidly as the number of particles and the system order increases. Additionally, the PF/PS does not directly produce the filtering and smoothing PDFs unless a PDF-fitting algorithm is implemented. This introduces an extra computational cost if filtering and smoothing PDFs are required;
- In some situations, as is the case shown in Figure 7 and Figure 8, the QKF/QKS performs worse than the standard KF/KS in terms of estimation accuracy. This suggests that there are cases with fine quantization, where if the accuracy of the estimation is not critical, but the execution time is, then the user can choose to neglect the quantization block and pick the standard KF/KS algorithms for state estimation.
7. Conclusions
In this paper, we investigated the performance of the extended Kalman filter/smoother, quantized Kalman filter/smoother, unscented Kalman filter/smoother, Gaussian sum filter/smoother, and particle filter/smoother for state-space models with quantized observations. The analysis was carried out in terms of the accuracy of the estimation, using the MSE and the computational cost as performance indexes. Simulations show that the PDFs of Gaussian sum filter/smoother and particle filter/smoother with a high number of particles are the ones best fitting the ground-truth PDFs. However, contrary to the particle filter/smoother, the Gaussian sum filter/smoother does not require a high computational load to achieve accurate results. The extended Kalman filter/smoother, quantized Kalman filter/smoother, and unscented Kalman filter/smoother produce results with low accuracy, although their execution time is minor. From simulations, we observed that the performance of the particle filter is closely related to the number of samples, the choice of the resampling method, and the MCMC algorithms, which address the degeneracy problem and mitigate the sample impoverishment. We used four different resampling schemes combined with two MCMC algorithms. We found out that the implementation of the MCMC-based particle filter and smoothing that produces the lower MSE is the one using random walk Metropolis combined with the systematic resampling technique.
Author Contributions
Conceptualization, A.L.C., R.A.G. and J.C.A.; methodology, A.L.C. and J.C.A.; software, A.L.C.; validation, R.C. and B.I.G.; formal analysis, A.L.C., R.A.G., R.C., B.I.G. and J.C.A.; investigation, A.L.C., R.A.G. and J.C.A.; resources, J.C.A.; writing—original draft preparation, A.L.C., R.A.G., R.C., B.I.G. and J.C.A.; writing—review and editing, A.L.C., R.C., B.I.G. and J.C.A.; visualization, R.C. and B.I.G.; supervision, J.C.A. All authors have read and agreed to the published version of the manuscript.
Funding
Grants ANID-Fondecyt 1211630 and 11201187, and ANID-Basal Project FB0008 (AC3E). Chilean National Agency for Research and Development (ANID) Scholarship Program/Doctorado Nacional/2020-21202410. VIDI Grant 15698, which is (partly) financed by the Netherlands Organization for Scientific Research (NWO). Excellence Center at Linköping, Lund, in Information Technology, ELLIIT.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| KF/KS | Kalman Filter/Rauch–Tung–Striebel smoother |
| EKF/EFS | Extended Kalman filter/smoother |
| UKF/UKS | Unscented Kalman filter/smoother |
| QKF/QKS | Quantized Kalman filter/smoother |
| PF/PS | Particle filter/smoother |
| GSF/GSS | Gaussian sum filter/smoother |
| MCMC | Markov chain Monte Carlo |
| MH | Metropolis–Hasting |
| RWM | Random walk Metropolis |
| Probability density function | |
| PMF | Probability mass function |
| FLQ | Finite level quantizer |
| ILQ | Infinite level quantizer |
| SYS | Systematic (resampling) |
| ML | Multinomial (resampling) |
| MT | Metropolis (resampling) |
| LS | Local selection (resampling) |
| GT | Ground truth |
| MSE | Mean square error |
References
- Gersho, A.; Gray, R.M. Vector Quantization and Signal Compression; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 159. [Google Scholar]
- Widrow, B.; Kollár, I. Quantization Noise: Roundoff Error in Digital Computation, Signal Processing, Control, and Communications; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Li, S.; Sauter, D.; Xu, B. Fault isolation filter for networked control system with event-triggered sampling scheme. Sensors 2011, 11, 557–572. [Google Scholar] [CrossRef]
- Zhang, X.; Han, Q.; Ge, X.; Ding, D.; Ding, L.; Yue, D.; Peng, C. Networked control systems: A survey of trends and techniques. IEEE CAA J. Autom. Sin. 2020, 7, 1–17. [Google Scholar] [CrossRef]
- Zhang, L.; Liang, H.; Sun, Y.; Ahn, C.K. Adaptive Event-Triggered Fault Detection Scheme for Semi-Markovian Jump Systems with Output Quantization. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 2370–2381. [Google Scholar] [CrossRef]
- Noshad, Z.; Javaid, N.; Saba, T.; Wadud, Z.; Saleem, M.Q.; Alzahrani, M.E.; Sheta, O.E. Fault Detection in Wireless Sensor Networks through the Random Forest Classifier. Sensors 2019, 19, 1568. [Google Scholar]
- Huang, C.; Shen, B.; Zou, L.; Shen, Y. Event-Triggering State and Fault Estimation for a Class of Nonlinear Systems Subject to Sensor Saturations. Sensors 2021, 21, 1242. [Google Scholar] [CrossRef]
- Liu, S.; Wang, Z.; Hu, J.; Wei, G. Protocol-based extended Kalman filtering with quantization effects: The Round-Robin case. Int. J. Robust Nonlinear Control 2020, 30, 7927–7946. [Google Scholar] [CrossRef]
- Ding, D.; Han, Q.L.; Ge, X.; Wang, J. Secure State Estimation and Control of Cyber-Physical Systems: A Survey. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 176–190. [Google Scholar] [CrossRef]
- Wang, X.; Li, T.; Sun, S.; Corchado, J.M. A Survey of Recent Advances in Particle Filters and Remaining Challenges for Multitarget Tracking. Sensors 2017, 17, 2707. [Google Scholar] [CrossRef]
- Curry, R.E. Estimation and Control with Quantized Measurements; MIT Press: Cambridge, MA, USA, 1970. [Google Scholar]
- Gustafsson, F.; Karlsson, R. Statistical results for system identification based on quantized observations. Automatica 2009, 45, 2794–2801. [Google Scholar] [CrossRef]
- Wang, L.Y.; Yin, G.G.; Zhang, J.; Zhao, Y. System Identification with Quantized Observations; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Marelli, D.E.; Godoy, B.I.; Goodwin, G.C. A scenario-based approach to parameter estimation in state-space models having quantized output data. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GE, USA, 15–17 December 2010; pp. 2011–2016. [Google Scholar]
- Rana, M.M.; Li, L. An Overview of Distributed Microgrid State Estimation and Control for Smart Grids. Sensors 2015, 15, 4302–4325. [Google Scholar] [CrossRef]
- Särkkä, S. Bayesian Filtering and Smoothing; Cambridge University Press: Cambridge, UK, 2013; Volume 3. [Google Scholar]
- Anderson, B.D.O.; Moore, J.B. Optimal Control: Linear Quadratic Methods; Courier Corporation: Mineola, NY, USA, 2007. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K. New extension of the Kalman filter to nonlinear systems. In Proceedings of the Signal Processing, Sensor Fusion, and Target Recognition VI, Orlando, FL, USA, 21–24 April 1997; International Society for Optics and Photonics: Bellingham, WA, USA, 1997; Volume 3068, pp. 182–193. [Google Scholar]
- Arasaratnam, I.; Haykin, S.; Elliott, R.J. Discrete-time nonlinear filtering algorithms using Gauss–Hermite quadrature. Proc. IEEE 2007, 95, 953–977. [Google Scholar] [CrossRef]
- Sviestins, E.; Wigren, T. Nonlinear techniques for Mode C climb/descent rate estimation in ATC systems. IEEE Trans. Control. Syst. Technol. 2001, 9, 163–174. [Google Scholar] [CrossRef]
- Gómez, J.C.; Sad, G.D. A State Observer from Multilevel Quantized Outputs. In Proceedings of the 2020 Argentine Conference on Automatic Control (AADECA), Buenos Aires, Argentina, 28–30 October 2020; pp. 1–6. [Google Scholar]
- Leong, A.S.; Dey, S.; Nair, G.N. Quantized Filtering Schemes for Multi-Sensor Linear State Estimation: Stability and Performance under High Rate Quantization. IEEE Trans. Signal Process. 2013, 61, 3852–3865. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, J.; Wang, D. Unscented Kalman Filtering based quantized innovation fusion for target tracking in WSN with feedback. In Proceedings of the 2009 International Conference on Machine Learning and Cybernetics, Baoding, China, 12–15 July 2009; Volume 3, pp. 1457–1463. [Google Scholar]
- Gordon, N.J.; Salmond, D.J.; Smith, A.F.M. Novel approach to nonlinear/non-Gaussian Bayesian state estimation. In Proceedings of the IEE Proceedings F (Radar and Signal Processing); IET: London, UK, 1993; Volume 140, pp. 107–113. [Google Scholar]
- Doucet, A.; Godsill, S.; Andrieu, C. On sequential Monte Carlo sampling methods for Bayesian filtering. Stat. Comput. 2000, 10, 197–208. [Google Scholar] [CrossRef]
- Li, T.; Bolic, M.; Djuric, P.M. Resampling Methods for Particle Filtering: Classification, implementation, and strategies. IEEE Signal Process. Mag. 2015, 32, 70–86. [Google Scholar] [CrossRef]
- Douc, R.; Cappe, O. Comparison of resampling schemes for particle filtering. In Proceedings of the ISPA 2005, Proceedings of the 4th International Symposium on Image and Signal Processing and Analysis, Zagreb, Croatia, 15–17 September 2005; pp. 64–69. [Google Scholar]
- Bi, H.; Ma, J.; Wang, F. An Improved Particle Filter Algorithm Based on Ensemble Kalman Filter and Markov Chain Monte Carlo Method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 447–459. [Google Scholar] [CrossRef]
- Zhai, Y.; Yeary, M. Implementing particle filters with Metropolis-Hastings algorithms. In Proceedings of the Region 5 Conference: Annual Technical and Leadership Workshop, Norman, OK, USA, 24 May 2004; pp. 149–152. [Google Scholar]
- Sherlock, C.; Thiery, A.H.; Roberts, G.O.; Rosenthal, J.S. On the efficiency of pseudo-marginal random walk Metropolis algorithms. Ann. Stat. 2015, 43, 238–275. [Google Scholar] [CrossRef]
- Cedeño, A.L.; Albornoz, R.; Carvajal, R.; Godoy, B.I.; Agüero, J.C. On Filtering Methods for State-Space Systems having Binary Output Measurements. IFAC PapersOnLine 2021, 54, 815–820. [Google Scholar] [CrossRef]
- Cedeño, A.L.; Albornoz, R.; Carvajal, R.; Godoy, B.I.; Agüero, J.C. A Two-Filter Approach for State Estimation Utilizing Quantized Output Data. Sensors 2021, 21, 7675. [Google Scholar] [CrossRef]
- Cohen, H. Numerical Approximation Methods; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Agüero, J.C.; González, K.; Carvajal, R. EM-based identification of ARX systems having quantized output data. IFAC PapersOnLine 2017, 50, 8367–8372. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 2010; Volume 5. [Google Scholar]
- DeGroot, M.H. Optimal Statistical Decisions; Wiley Classics Library, Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Solo, V. An EM algorithm for singular state space models. In Proceedings of the 42nd IEEE International Conference on Decision and Control (IEEE Cat. No.03CH37475), Maui, HI, USA, 9–12 December 2003; Volume 4, pp. 3457–3460. [Google Scholar]
- Gelb, A.; Kasper, J.; Nash, R.; Price, C.; Sutherland, A. Applied Optimal Estimation; MIT Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Grewal, M.S.; Andrews, A.P. Kalman Filtering: Theory and Practice with MATLAB; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Traoré, N.; Le Pourhiet, L.; Frelat, J.; Rolandone, F.; Meyer, B. Does interseismic strain localization near strike-slip faults result from boundary conditions or rheological structure? Geophys. J. Int. 2014, 197, 50–62. [Google Scholar] [CrossRef]
- Wan, E.A.; Merwe, R.V.D. The unscented Kalman filter for nonlinear estimation. In Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium (Cat. No.00EX373), Lake Louise, AB, Canada, 4 October 2000; pp. 153–158. [Google Scholar]
- Kitagawa, G. The two-filter formula for smoothing and an implementation of the Gaussian-sum smoother. Ann. Inst. Stat. Math. 1994, 46, 605–623. [Google Scholar] [CrossRef]
- Balenzuela, M.P.; Dahlin, J.; Bartlett, N.; Wills, A.G.; Renton, C.; Ninness, B. Accurate Gaussian Mixture Model Smoothing using a Two-Filter Approach. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami Beach, FL, USA, 17–19 December 2018; pp. 694–699. [Google Scholar]
- Liu, J.S.; Chen, R. Sequential Monte Carlo Methods for Dynamic Systems. J. Am. Stat. Assoc. 1998, 93, 1032–1044. [Google Scholar] [CrossRef]
- Hostettler, R. A two filter particle smoother for Wiener state-space systems. In Proceedings of the 2015 IEEE Conference on Control and Applications, CCA 2015—Proceedings, Dubrovnik, Croatia, 3–5 October 2012; pp. 412–417. [Google Scholar]
- Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Process. 2002, 50, 174–188. [Google Scholar] [CrossRef]
- Doucet, A.; de Freitas, N.; Gordon, N. Sequential Monte Carlo Methods in Practice; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Godsill, S.J.; Doucet, A.; West, M. Monte Carlo Smoothing for Nonlinear Time Series. J. Am. Stat. Assoc. 2004, 99, 156–168. [Google Scholar] [CrossRef]
- Douc, R.; Garivier, A.; Moulines, E.; Olsson, J. Sequential Monte Carlo smoothing for general state space hidden Markov models. Ann. Appl. Probab. 2011, 21, 2109–2145. [Google Scholar] [CrossRef]
- Wills, A.; Schön, T.B.; Ljung, L.; Ninness, B. Identification of Hammerstein–Wiener models. Automatica 2013, 49, 70–81. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).