1. Introduction
We will be considering two species, one of which (say, predator) is sensitive to the concentration gradient of the other one (say, prey). Prey spread in a purely diffusive way. For the predators, we employ the Cattaneo model [
1]. The resulting system of equations belongs to the family of hyperbolic models [
2]. The last reference alludes to a review that delivers much helpful information on the subject.
The present article considers the slow evolution of short-wave packages for the outlined PDE system. In many respects, it continues article [
3] that regards the effect of small-scale fluctuations of the environment on the stability of the homogeneous equilibria for one parabolic model of the Patlak–Keller–Segel family. Currently, we address a similar problem for a hyperbolic model. There are at least two reasons for doing so. The first one is the completeness of the study. Indeed, the hyperbolic and parabolic models, such as the Cattaneo and the Patlak–Keller–Segel formulations, arise from the same kinetic model under different hypotheses. Both models are natural but very different. For instance, the parabolic model must perceive a short wavelength external signal constantly to produce a short wave pattern in response [
3]. In great contrast, the short waves can propagate due to an instantaneous perturbation in the hyperbolic case. The second reason regards the so-called aggregation that review [
2] distinguishes as an important application of the hyperbolic models. Since the aggregation means the spontaneous forming of large-scale patterns from small-scale ones, there should be an intrinsic mechanism of destabilization and destruction of the latter. At the same time, there should be some exclusions as real-life populations sometimes display the small-scale mosaic patterns of spatial distributions [
4].
Of course, such topics as the relevance of the short-wavelength limit to a real life population or the wave solutions of the hyperbolic models (which have got much less attentions than their parabolic counterparts as yet) are worth continuing discussion. However, we skip it for the sake of brevity and allude to freely accessible papers [
3,
5] for these matters and for more references to the subject.
In contrast with the Patlak–Keller–Segel parabolic model, which we addressed in article [
3], the short-wave limit for the Cattaneo model, due to its hyperbolicity, leads to the elementary wave equation, the solutions to which form a kind of short-wave ether. We apply the homogenization over this ether to derive equations for the slow modulation of the short-wave packages. To some extent, this procedure follows that proposed in article [
6]. The main result in the present article is the pumping of the slow amplitudes by the non-linear interactions of the short waves. This feature manifests itself in the excitement of wind, by which we mean some terms that enter the flux equation due to the homogenization. It turns out that this wind is capable of destabilizing the equilibria of the averaged amplitude equation and supporting the growth of their finite perturbations.
The article is organized as follows. In
Section 2, we formulate the governing equation. In
Section 3, we present several motivating examples. In
Section 4, we derive the system that governs the slow evolution of the amplitudes of the short-wave parcels by the homogenization over the short waves. In
Section 5, we consider the simplest model that invokes identically constant transport coefficients of the predator and the Lotka–Volterra kinetics. In
Section 6, we unfold the destabilizing effect of wind through linear stability analysis. In
Section 7, we present numerical solutions of the homogenized system that support our outcomes regarding the crucial part of the wind in supporting the instability and perturbation growth. In
Section 8, we list several conclusions from the research presented.
2. The Governing Equations and Scaling
As we have mentioned above, we invoke the Cattaneo model [
1] for the predators’ transport and the common reaction–diffusion equation for the prey. The former involves the equations for the balance of the predators and the equation for their flux that, in contrast with the Patlak–Keller–Segel law, takes into account the inertia of their responding. The dimensionless form of the governing equations reads as
In article [
5], there are more details on scaling the dimensional governing equations for bringing them into the above dimensionless form.
In system (
1)–(
3), the independent variables,
x and
t, stand for the spatial and temporal coordinates, correspondingly,
,
. The dependent variables are
,
and
. The first and the last ones play the parts of the densities of the species. The first two equations constitute the Cattaneo model for the prey-sensitive movement of the predators, where the remaining dependent variable,
q, stands for predator’s flux. Coefficient
stands as the sensitivity factor. Moreover, Equation (
2) involves term
with constant factor
, which resembles the resistance force in mechanics. We will be calling the corresponding coefficient,
, resistivity. The notation of
stands for the prey diffusivity factor that is constant by assumption.
By default, the predator diffusivity,
, the sensitivity,
, and the reactions terms,
F and
G, are smooth functions in variables
; at that
3. Motivating Examples
Throughout this section, we will be discussing three numerical solutions to the Cauchy problem for Equations (
1)–(
3) with small diffusivity of prey and identically constant coefficients
and
. The initial data and other settings are as follows
Quantities
and
are the equilibrium species densities in the sense that
i.e., the system (
1)–(
3) allows the homogeneous equilibrium in which
,
and
. The value assigned to the parameter
is a threshold for the linear instability of such an equilibrium in the case of
(see
Section 6).
Figure 1 illustrates the numerical solutions, which cover the spatial range of
. For more details of the implementation, see
Section 7. Each row of snapshots shows the instantaneous graphs of the deviation of the species densities from their equilibrium values for one concrete set of initial data (
5). The top row shows those patterns that arise from a short-wave modulation of the homogeneous equilibrium. The middle row demonstrates an interplay of the same modulation with a small smooth localized perturbation. The bottom row corresponds to the same perturbation but with no underlying short wave.
Table 1 states the correspondence between the rows and the versions of initial data (
5).
Overall, the top snapshots row displays a short-wave profile of the predator density amid almost homogeneous prey distribution. The former resembles a linear travelling wave subject to slow amplitude damping. It is not entirely unexpected since the short-wave limit of the governing equations leads to the linear acoustic system with the sound speed equal to
, namely,
The amplitude damping is due to the resistance term, , which is not entirely negligible for the wavelengths adopted for computing.
The middle row shows that the small smooth localized initial perturbation persists and even gets amplified despite the existing resistance. Notice the asymmetry too. It cannot be explained using the above acoustic approximation only. These features sharply contrast with the bottom row, which displays a symmetrical picture of decaying perturbation. This symmetry is due to the mirror invariance of Equations (
1)–(
3) and initial data (
5) (the latter takes place for
only).
The listed observations suggest that short waves are capable of pumping the perturbations. In the rest of the article, we will be addressing this conjecture with the use of homogenization.
4. Homogenization and Wind
Let
in Equation (
3). We seek the short wavelength solutions that read as
For calculating such a solution we employ the formal power expansions as follows
We assume that for every coefficient in these series there exists an averaged value defined as follows
Hence, for every
there is a decomposition
so that the tilde terms vanish on average. To simplify the notation, we will be omitting the zero-valued indices here and there below—that is, the following agreement is valid from here on:
We write the governing equations with the use of the slow variables,
, and the fast variables,
. For this purpose, we substitute
and
with
and
. Then replacing the dependent variables,
, with the above expansions gives a chain of equations for the approximations of successive orders. Specifically, collecting the terms of order
yields equations:
This system is quasi-linear and hyperbolic with respect to unknowns
since function
is positive by assumption. The value of
stands as a constant parameter. Let
Given this, the second equation in system (
9) takes the form of a conservation law that reads as
Eliminating of variable
q reduces system (
9) to a single quasi-linear wave equation that reads as
The next step after resolving Equation (
10) is recovering the other unknown,
, from system (
9). Some compatibility conditions can arise at that. One of them is Equation (
10) itself and it can seem that one more results from system (
9) upon averaging. However, the latter holds identically due to the aforementioned conservatism.
Collecting the terms of order 1 yields equations:
Regarding Equation (
12), it is worth noting that the collection of the terms of order 1 resulting from the term
reads as
and this, by definition of function
M, is equal to
Again, there are several compatibility conditions to hold for isolating unknown
from Equations (
11) and (
12). These are
Equation (
16) is a linear wave equation in fast variables with respect to function
provided that we have determined
,
,
and
. More accurately, this is a two-parametric family of the linear wave equations where the values of
and
stand as parameters.
Assume there exists a two-parametric family of solutions
,
to system (
9). Equation (
13) entails the following compatibility condition
This equation is nothing else than Equation (
13) on average. Assume that it holds. Then Equation (
13) defines a two-parametric family of operators
where
is the inverse to the heat operator on a suitable space of functions vanishing on average.
Further, let us write conditions (
14) and (
15) as equations for
and
:
where
and
, and
Equations (
17)–(
19) constitute a closed system regarding the averaged unknowns,
, which we will call a
homogenized or averaged system.
The homogenized system is similar to the original governing equations but not the same. In the generic case, the effect of the short waves is threefold. First, the averaged reaction terms,
and
, can differ from those specified originally. Second, the same is true regarding the averaged diffusivity,
, and sensitivity,
. Third, last but not least, the
wind term,
W, can enter the flux Equation (
19). The usage of the name “wind” relies on an analogy to some features in the dynamics of compressible fluid [
6].
Now let the following conditions hold
In analogy with fluid mechanics, we will call this function
pressure (if any). Indeed, given an existing pressure, Equation (
2) represents a conservation law:
Note in passing that the occurrence of shock waves is natural in such a case, see [
5].
When the pressure exists, Equation (
12) is written as
Averaging the last equation again leads to the conservation law as follows
Comparing Equation (
23) to Equations (
19)–(
21) (where one can put
now) brings the wind into a simpler form
and formulae (
20) define the averaged transport coefficients,
and
, again. Generally, they satisfy condition (
22) neither with pressure
nor with any others even if it has held originally.
The most tractable averaged system arises from the signal-dependent transport coefficients—that is, for
At the same time, there are examples of considering this assumption for some real-life species in the biological literature. We allude to articles by Tytyunov et al. [
4,
7], and Menolascina et al. [
8] for examples and references. In such a case system (
9) reduces to two uncoupled linear wave equations where the sound speed is
—that is, it is a constant relative to the fast variables. Then the solution reads as
for every pair of function
(as the sound speed is a constant relative to the fast variables). To make the solution positive, choose functions
that are
periodic and positive, and set
Then the solution defined by equality (
25) vanishes on average, while the leading term,
, is positive for every positive function
. The corresponding flux,
, reads as
The envelope of this shortwave parcel,
, the averaged flux,
, and the prey density,
, are a solution to the homogenized system. The last gets simplified substantially, namely,
This is the particular form of integrability condition (
22) so that expression (
24) has to determine the wind too and it is equal to zero as well.
Let us proceed with simplifying the model. Assume the reaction terms to be linear in the predator density (as in the Lotka–Volterra case)—that is, set
Then the reaction terms in Equations (
17) and (
18) remain the same as we have defined by formulae (
29). Equation (
13) now reads as
Hence,
where numbers
are the Fourier coefficients of functions
. Finally,
Thus, in the case under consideration, the homogenized system takes the form as follows
where the wind term,
W, is determined by formula (
30).
Let us consider the maximization of factor
in the absolute value for a fixed
. There are restrictions for functions
to obey; namely, they must be positive and their sum (normalized by
) must be a probabilistic density on the unit circumference. Hence,
and the maximizing (minimizing) pair of sequences is
(
). So, the supremum and infimum of factor
read as
It is worth noting that functional (31) probably does not attain these extremal values at some smooth densities . On the other hand, it tends to one of these values when one concentrates density or near some singular point on the unit circumference. The similar limiting object on the whole real axis is known as the Dirac measure, or , or the atomic measure. To build the same on the circumference, we construct the -periodic grid of the Dirac atoms while setting one atom on the period.
5. The Case of Constant Diffusivity and Sensitivity
For reducing the wind term (
30) into its simplest form, let us set
where
,
and
are positive constants. Then the homogenized system reads as
where
,
, while formula (
31) determines the magnitude of factor
for every
. Since it depends on functions
as well, we will be considering this factor as an additional parameter, which varies within bounds (
35). Actually, we can restrict our considerations within positive values of parameter
due to the system invariance with respect to the following transform
For
, system (
37)–(
39) is nothing else than a version of the original system (
1)–(
3), which possesses the mirror symmetry
. Note in passing that solutions (
25) and (
26), over which we do the homogenization, cannot possess the above invariance unless
. The last, however, entails
and, hence,
by (
31), so that the homogenized system gets the mirror invariance.
Recall now that we aim at studying the slow evolution of the amplitudes of the short-wavelength parcels. In this respect, understanding the effect of the wind seems to be the keynote as the wind is the only difference between the homogenized system (
37)–(
39) and the original system. Fortunately, it is particularly easy under hypotheses (
36), as the wind term,
, is proportional to only one scalar parameter,
. Hence, estimating the effect of wind reduces to estimating the effect of the magnitude of parameter
, which is moreover confined within the known finite interval. It is worth noting that the same is true when the transport coefficients depends on the prey density only, and the reaction terms are linear in the predator density.
6. Linear Stability
The homogenized system (
37)–(
39) allows an equilibrium
For
, this is the equilibrium of the original system. Here by the original system we mean the formulation of system (
1)–(
3) arising from assumptions (
36) in the case of non-diffusive (sedentary) prey (i.e., for
).
In general, from formula (
21), it follows that
provided that
,
and system (
9) has a two-parametric family of solutions
. Hence, the equilibria of the general homogenized system (if any) are to read as
where the equilibrium densities are to set to zero the averaged reaction terms—that is, the following equations are to hold
Every equilibrium of the homogenized system generates the unmodulated short-wave pattern by formula
. In a simpler situation, for
,
, such a quasi-equilibrium pattern results from formulae (
25) and (
26) where
,
.
Applying the rationales above to the case of the linear reactions in the predator density leads to the conclusion that the equilibrium densities of species are the same for both the homogenized and original systems, i.e.,
(where by original we mean the version of the governing system dealt with). This observation opens a relatively easy way towards unfolding the effect of the wind, at least partly. It consists of comparing the stability of the equilibrium with the wind or without it and deciding whether the wind exerts a stabilizing or destabilizing effect. Regarding system (
37)–(
39), the problem simplifies to estimating the effect of the parameter
on the stability of the above equilibria.
Let us consider the linearization of system (
37)–(
39) near the equilibrium (
40) and look for a special solution that reads as
It is common to name solutions (
41) as the normal modes (of the corresponding equilibrium) and say that such a mode is
stable (unstable, neutral) if the real part of decrement
is negative (positive, equal to zero). At that, the so-called spectral stability problem arises for which
is the eigenvalue and the corresponding normal mode is the eigenmode. It is also common to say that an equilibrium (or more general steady regime) is stable (unstable, neutral) provided its normal mode is stable (there exists an unstable (neutral) mode). Note that genuine stability in the Lyapunov sense often needs a much more accurate definition and does not always relate to this spectral test straightforwardly. This notice concerns the instability too.
Typically, the regimes we examine for stability depend on several parameters as, for example, equilibrium (
40) does. Note that the wavelength of the eigenmode,
k, stands as a parameter too. In the parametric space, every point belongs to either
the area of instability or the area of stability or
the critical submanifold that separates them. In the former (latter) area, there exist unstable normal modes (every normal mode is stable).
A smooth path in the parametric space that parameterizes a family of equilibria parameterizes the corresponding family of stability problems. We call a submanifold in the parametric space neutral if the transversal intersection of it by such a path generically entails the transversal intersection of the imaginary axis by a branch of eigenvalues of the corresponding stability problems. The unstable eigenmodes disappearing or arising upon crossing the neutral submanifold is what we call an occurrence of instability. We say that the instability is oscillatory (monotonic) if the corresponding branch of the eigenvalues is not real (is real).
In the case dealt with here, the stability test for an individual normal mode reduces to counting the eigenvalues of some complex matrix
that belong to the right semi-plane. We allude to widely recognized textbook [
9] for more details, though the procedure is routine. Nevertheless, it is worth noting that the characteristic polynomials of the mentioned matrices depend not on the parameter
itself but on
only—that is, the direction of the wind is nothing to do with the stability. This feature also agrees with the invariance of the homogenized system.
Here is the summary of our outcomes concerning the linear stability of equilibrium (
40) for
—that is, for the original system.
The neutral submanifold is the graph of function
, where
For a specific equilibrium and a specific wave number k, the normal mode is stable for and becomes unstable otherwise.
The critical submanifold is the graph of function . A specific equilibrium is stable provided that and becomes unstable otherwise. This instability is always oscillatory and occurs to shorter waves; namely, for every there exists such that every eigenmode is unstable (stable) provided that ().
The above conclusions mainly withstand allowing the prey diffusion, except for the shortwave instability; namely, the neutral submanifold is the graph of function
where
is function (
42) while factors
do not depend on the parameters that enter the right-hand side explicitly.
At that, the critical submanifold is the graph of function
Again, for every a specific equilibrium is stable provided that and becomes unstable otherwise. This instability is always oscillatory and there exist real numbers such that every eigenmode’s mode is unstable provided that its wavenumber obeys the inequality . Interestingly, function is linear in and in too.
Let us pass to the homogenized system (
37)–(
39) and test the linear stability for
and
equal to its maximal absolute value (
35). It turns out that the equilibrium (
40) is unstable while it is stable for
in accordance with what we have been saying above. Hence, the wind can make the equilibria unstable. In more detail, let
and
be set as above. Then for every admissible setting of the other parameters there exist numbers
such that there are unstable normal modes for every wavelength
and all the normal modes are stable for every
.
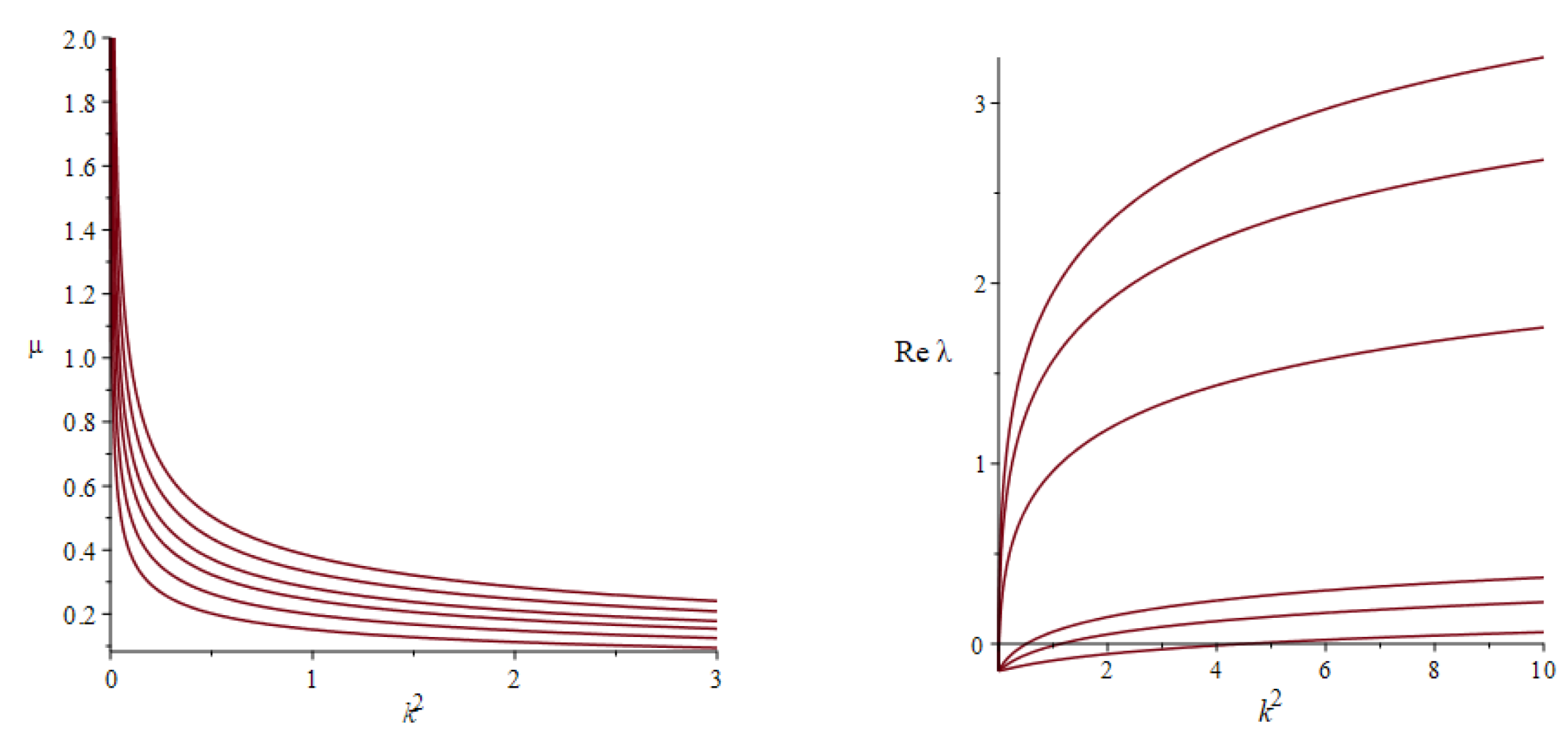
Figure 2 (the right frame) is to illustrate this conclusion. Note that generically there are three different eigenvalues
for every
k. Their expressions in the problem parameters are commonly called the eigenvalues branches. These branches remains smooth unless the eigenvalues collide, while their collisions lead to singularities. The right frame in
Figure 2 shows the real part of the eigenvalue branch that turns positive when the squared wavenumber increases over some threshold. This threshold tends to zero rapidly upon increasing the diffusivity coefficient. Two more branch do not appear there since they always remain in the left complex semi-plane. It is worth mentioning that the increment,
, tends to a limit for
(which depends on other parameters), while
,
.
7. Numerical Results for the Homogenized System
Figure 3 shows typical patterns of the wind-induced pumping of a perturbation (upper row) or decaying it without the wind (lower row),
cf. Figure 1. They both result from the numerical solutions of the Cauchy problems for system (
37)–(
39). Their settings are the same, except for the value of parameter
, which is equal either to zero (lower row) or to its negative absolutely maximal value (upper row). It is the negative quantity given by formula (
35) where
. The initial conditions and the values of the other parameters are as follows
From the numerical experiments, it follows that the behaviour of small finite perturbation qualitatively agrees with the linear theory of
Section 6. Namely, the linear theory states the stability provided that
while the other parameters take the values specified in (
44), and we have observed the decay of the small finite perturbations. At the same time, we see amplifying them once the magnitude of
has attained its maximal value with no changes in the other parameters. This observation also agrees with the linear theory, which predicts the onset of instability upon following such a path in the parametric space.
We emphasize the typicality of the outlined picture. We have tried not a few parameter combinations with stronger or weaker resistance, faster growth of prey (), weaker prey diffusivity, a moderate overabundance of prey (), a greater predation efficiency () and smaller values of parameter (e.g., produced by a single harmonic). Nevertheless, we have not observed any patterns of behaviour, linear or nonlinear, which differ qualitatively from those discussed above.
For numerical solving of the Cauchy problems for system (
37)–(
39) with data (
43) and (
44), we have eliminated the unknown
q from Equations (
37) and (
38) and then have arrived at a system that consists of the reaction–diffusion Equation (
39) and a nonlinear wave equation for the predator density,
p. For completing the reduction, it is necessary to set up an ad hoc initial condition of form
when
, where function
is given. By Equation (
37),
, where
F is the predators’ sources density, and functions
p,
q,
s are specified by the initial condition set up for the first-order system (
37)–(39). Given the initial data (
43) and (
44) and Equation (
37), we set
This is not the case for the Cauchy problem of
Section 3, where we have addressed in fact Equations (
37) and (
38) for
and initial data (
5). Given this, we arrive at
In fact, instead of the Cauchy problem, we had been solving an initial-boundary value problem with Neumann boundary conditions on a sufficiently wide spatial interval with the built-in solver of
Maple. We set the interval of
for computing the results, which we have been discussing in this section, and
for those of
Section 3.