Solving Optimal Power Flow Problem via Improved Constrained Adaptive Differential Evolution
Abstract
1. Introduction
2. Adaptive Differential Evolution Based on Improved pbest Selection
2.1. Initialization
2.2. Mutation
2.3. Crossover
2.4. Improved Method
| Algorithm 1 Improved |
|
3. Problem Formulation
3.1. Problem Formulation
3.1.1. Decision Variables
3.1.2. Objective Functions
3.1.3. Constraints
- (1)
- Generator constraints:where the i-th bus generator active power , reactive power output and voltage magnitude at the i-th generator bus are generated within their lower and upper bounds.
- (2)
- Shunt compensator constraints:where the shunt compensator at the j-th bus should lie in its lower and upper limits.
- (3)
- Transformer constraints:where the k-th branch transformer tap is within its lower and upper limits.
- (4)
- Security constraints:where the voltage magnitude at the m-th load bus and n-th line loading should follow its lower and upper bounds.
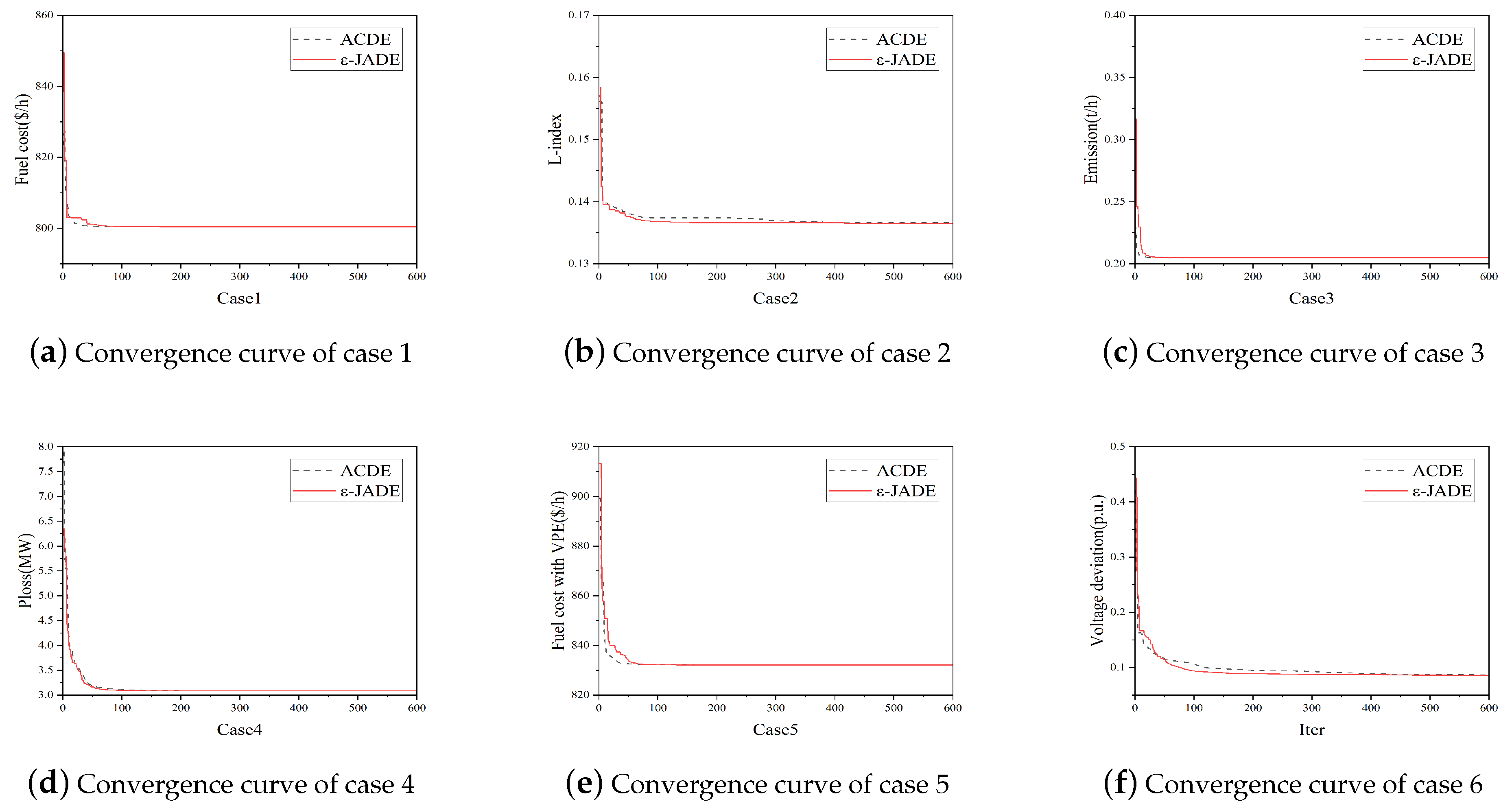
Experimental Results
3.2. Results of the OPF Problems
- For case 1, the simulation results show that ACDE has a better Min values, Max values and Std values than the improved JADE. Improved -JADE presents better mean values in this case, which indicates that the effectiveness of the proposed algorithm.
- For case 2, case 3, case 5, case 6 and case 10, the proposed improved -JADE algorithm exhibits a competitive performance on the Min, Max and Mean values when compared with the other four state-of-the-art DE algorithms;
- For case 4, all compared DE algorithms provide the same competitive results.
- For case 8, ACDE and SP-DE achieve the best Mean value, while the improved JADE demonstrates a remarkable performance in terms of the Min value;
- With regard to case 7 and case 9, the proposed improved JADE demonstrates better results in terms of the Mean and Min values.
Comparison between Improved JADE and ACDE
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, S.; Gong, W.; Hu, C.; Yan, X.; Wang, L.; Gu, Q. Adaptive constraint differential evolution for optimal power flow. Energy 2021, 235, 121362. [Google Scholar] [CrossRef]
- Ida Evangeline, S.; Rathika, P. Wind farm incorporated optimal power flow solutions through multi-objective horse herd optimization with a novel constraint handling technique. Expert Syst. Appl. 2022, 194, 116544. [Google Scholar] [CrossRef]
- Bouchekara, H. Solution of the optimal power flow problem considering security constraints using an improved chaotic electromagnetic field optimization algorithm. Neural Comput. Appl. 2020, 32, 2683–2703. [Google Scholar] [CrossRef]
- Mugemanyi, S.; Qu, Z.; Rugema, F.X.; Dong, Y.; Bananeza, C.; Wang, L. Optimal Reactive Power Dispatch Using Chaotic Bat Algorithm. IEEE Access 2020, 8, 65830–65867. [Google Scholar] [CrossRef]
- Saha, A.; Bhattacharya, A.; Das, P.; Chakraborty, A.K. HSOS: A novel hybrid algorithm for solving the transient-stability-constrained OPF problem. Soft Comput. 2020, 24, 7481–7510. [Google Scholar] [CrossRef]
- Farhat, M.; Kamel, S.; Atallah, A.M.; Hassan, M.H.; Agwa, A.M. ESMA-OPF: Enhanced Slime Mould Algorithm for Solving Optimal Power Flow Problem. Sustainability 2022, 14, 2305. [Google Scholar] [CrossRef]
- Abd el sattar, S.; Kamel, S.; Ebeed, M.; Jurado, F. An improved version of salp swarm algorithm for solving optimal power flow problem. Soft Comput. 2021, 25, 4027–4052. [Google Scholar] [CrossRef]
- Akdag, O. A Improved Archimedes Optimization Algorithm for multi/single-objective Optimal Power Flow. Electr. Power Syst. Res. 2022, 206, 107796. [Google Scholar] [CrossRef]
- Abbasi, M.; Abbasi, E.; Mohammadi-Ivatloo, B. Single and multi-objective optimal power flow using a new differential-based harmony search algorithm. J. Ambient Intell. Humaniz. Comput. 2021, 12, 851–871. [Google Scholar] [CrossRef]
- Teeparthi, K.; Vinod Kumar, D.M. Security-constrained optimal power flow with wind and thermal power generators using fuzzy adaptive artificial physics optimization algorithm. Neural Comput. Appl. 2018, 29, 855–871. [Google Scholar] [CrossRef]
- El-Fergany, A.A.; Hasanien, H.M. Salp swarm optimizer to solve optimal power flow comprising voltage stability analysis. Neural Comput. Appl. 2020, 32, 5267–5283. [Google Scholar] [CrossRef]
- Naderi, E.; Pourakbari-Kasmaei, M.; Cerna, F.V.; Lehtonen, M. A novel hybrid self-adaptive heuristic algorithm to handle single- and multi-objective optimal power flow problems. Int. J. Electr. Power Energy Syst. 2021, 125, 106492. [Google Scholar] [CrossRef]
- Elattar, E.E.; Shaheen, A.M.; Elsayed, A.M.; El-Sehiemy, R.A. Optimal Power Flow With Emerged Technologies of Voltage Source Converter Stations in Meshed Power Systems. IEEE Access 2020, 8, 166963–166979. [Google Scholar] [CrossRef]
- Kahraman, H.T.; Akbel, M.; Duman, S. Optimization of Optimal Power Flow Problem Using Multi-Objective Manta Ray Foraging Optimizer. Appl. Soft Comput. 2022, 116, 108334. [Google Scholar] [CrossRef]
- Attia, A.F.; El Sehiemy, R.A.; Hasanien, H.M. Optimal power flow solution in power systems using a novel Sine-Cosine algorithm. Int. J. Electr. Power Energy Syst. 2018, 99, 331–343. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Mohammadi, F. Optimal Placement of TCSC for Congestion Management and Power Loss Reduction Using Multi-Objective Genetic Algorithm. Sustainability 2020, 12, 2813. [Google Scholar] [CrossRef]
- Mohamed, A.A.; Kamel, S.; Hassan, M.H.; Mosaad, M.I.; Aljohani, M. Optimal Power Flow Analysis Based on Hybrid Gradient-Based Optimizer with Moth–Flame Optimization Algorithm Considering Optimal Placement and Sizing of FACTS/Wind Power. Mathematics 2022, 10, 361. [Google Scholar] [CrossRef]
- Gong, W.; Cai, Z. Differential evolution with ranking-based mutation operators. IEEE Trans. Cybern. 2013, 43, 2066–2081. [Google Scholar] [CrossRef]
- Takahama, T.; Sakai, S. Constrained optimization by the ε constrained differential evolution with gradient-based mutation and feasible elites. In Proceedings of the 2006 IEEE International Conference on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006; pp. 1–8. [Google Scholar]
- Zitzler, E. Evolutionary Algorithms for Multiobjective Optimization: Methods and Applications; Ithaca: Shaker, OH, USA, 1999; Volume 63. [Google Scholar]
- Mohamed, A.A.A.; Mohamed, Y.S.; El-Gaafary, A.A.; Hemeida, A.M. Optimal power flow using moth swarm algorithm. Electr. Power Syst. Res. 2017, 142, 190–206. [Google Scholar] [CrossRef]
- Biswas, P.P.; Suganthan, P.N.; Mallipeddi, R.; Amaratunga, G.A. Optimal power flow solutions using differential evolution algorithm integrated with effective constraint handling techniques. Eng. Appl. Artif. Intell. 2018, 68, 81–100. [Google Scholar] [CrossRef]
- Yi, W.; Gao, L.; Pei, Z.; Lu, J.; Chen, Y. ε Constrained differential evolution using halfspace partition for optimization problems. J. Intell. Manuf. 2021, 32, 157–178. [Google Scholar] [CrossRef]


| Generator | Bus | a | b | c | d | e | alpha | beta | gamma | w | mu |
|---|---|---|---|---|---|---|---|---|---|---|---|
| G1 | 1 | 0 | 2 | 0.00375 | 18 | 0.037 | 4.091 | −5.554 | 6.49 | 0.0002 | 2.857 |
| G2 | 2 | 0 | 1.75 | 0.0175 | 16 | 0.038 | 2.543 | −6.047 | 5.638 | 0.0005 | 3.333 |
| G3 | 5 | 0 | 1 | 0.0625 | 14 | 0.04 | 4.258 | −5.094 | 4.586 | 0.000001 | 8 |
| G4 | 8 | 0 | 3.25 | 0.00834 | 12 | 0.045 | 5.326 | −3.55 | 3.38 | 0.002 | 2 |
| G5 | 11 | 0 | 3 | 0.025 | 13 | 0.042 | 4.258 | −5.094 | 4.586 | 0.000001 | 8 |
| G6 | 13 | 0 | 3 | 0.025 | 13.5 | 0.041 | 6.131 | −5.555 | 5.151 | 0.00001 | 6.667 |
| Case | Algorithm | Min | Max | Mean | Std |
|---|---|---|---|---|---|
| Case1 | ECHT-DE | 800.4148 | 800.4258 | 800.4206 | 0.0026 |
| SF-DE | 800.4131 | 800.4192 | 800.4151 | 0.0015 | |
| SP-DE | 800.4293 | 800.4684 | 800.4413 | 0.0100 | |
| ACDE | 800.4113 | 800.4176 | 800.4133 | 0.0015 | |
| I-JADE | 800.4115 | 800.4229 | 800.4135 | 0.0021 | |
| Case2 | ECHT-DE | 832.1356 | 832.2239 | 832.1811 | 0.0222 |
| SF-DE | 832.0882 | 832.1291 | 832.1056 | 0.0105 | |
| SP-DE | 832.4813 | 832.8760 | 832.6550 | 0.0963 | |
| ACDE | 832.0722 | 832.3941 | 832.0957 | 0.0581 | |
| IJADE | 832.0698 | 832.1225 | 832.0809 | 0.0109 | |
| Case3 | ECHT-DE | 0.1363 | 0.1372 | 0.1369 | 0.0002 |
| SF-DE | 0.1367 | 0.1370 | 0.1369 | 0.0001 | |
| SP-DE | 0.1374 | 0.1386 | 0.1378 | 0.0002 | |
| ACDE | 0.1364 | 0.1368 | 0.1366 | 0.0001 | |
| IJADE | 0.1364 | 0.1367 | 0.1365 | 0.0001 | |
| Case4 | ECHT-DE | 0.2048 | 0.2048 | 0.2048 | 0.0000 |
| SF-DE | 0.2048 | 0.2048 | 0.2048 | 0.0000 | |
| SP-DE | 0.2048 | 0.2048 | 0.2048 | 0.0000 | |
| ACDE | 0.2048 | 0.2048 | 0.2048 | 0.0000 | |
| IJADE | 0.2048 | 0.2048 | 0.2048 | 0.0000 | |
| Case5 | ECHT-DE | 3.0850 | 3.0871 | 3.0858 | 0.0005 |
| SF-DE | 3.0845 | 3.0857 | 3.0849 | 0.0003 | |
| SP-DE | 3.0844 | 3.0854 | 3.0848 | 0.0003 | |
| ACDE | 3.0840 | 3.0862 | 3.0845 | 0.0005 | |
| IJADE | 3.0840 | 3.0851 | 3.0844 | 0.0003 | |
| Case6 | ECHT-DE | 0.0878 | 0.0916 | 0.0893 | 0.0009 |
| SF-DE | 0.0867 | 0.0890 | 0.0880 | 0.0007 | |
| SP-DE | 0.0867 | 0.0892 | 0.0877 | 0.0007 | |
| ACDE | 0.0856 | 0.0878 | 0.0865 | 0.0007 | |
| IJADE | 0.0856 | 0.0884 | 0.0863 | 0.0007 | |
| Case7 | ECHT-DE | 1040.1510 | 1040.2330 | 1040.1810 | 0.0213 |
| SF-DE | 1040.1250 | 1040.1620 | 1040.1400 | 0.0096 | |
| SP-DE | 1040.1340 | 1040.3370 | 1040.2390 | 0.0444 | |
| ACDE | 1040.1133 | 1040.1891 | 1040.1268 | 0.0177 | |
| IJADE | 1040.1127 | 1040.1642 | 1040.1245 | 0.0115 | |
| Case8 | ECHT-DE | 813.1742 | 813.4095 | 814.2470 | 0.0490 |
| SF-DE | 813.1956 | 813.3376 | 813.2585 | 0.0444 | |
| SP-DE | 813.1959 | 813.2643 | 813.2306 | 0.0181 | |
| ACDE | 813.1100 | 813.5334 | 813.1379 | 0.0805 | |
| IJADE | 813.1099 | 813.5583 | 813.1462 | 0.0846 | |
| Case9 | ECHT-DE | 814.1708 | 814.2001 | 814.1843 | 0.0075 |
| SF-DE | 814.1649 | 814.1956 | 814.1767 | 0.0063 | |
| SP-DE | 814.1841 | 814.2273 | 814.2017 | 0.0121 | |
| ACDE | 814.1588 | 814.2957 | 814.1897 | 0.0305 | |
| IJADE | 814.1588 | 814.2162 | 814.1746 | 0.0118 | |
| Case10 | ECHT-DE | 964.1331 | 964.1564 | 964.1437 | 0.0061 |
| SF-DE | 964.1254 | 964.1418 | 964.1307 | 0.0038 | |
| SP-DE | 964.1234 | 964.1399 | 964.1276 | 0.0034 | |
| ACDE | 964.1179 | 964.1493 | 964.1252 | 0.0083 | |
| IJADE | 964.1176 | 964.1380 | 964.1227 | 0.0050 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, W.; Lin, Z.; Lin, Y.; Xiong, S.; Yu, Z.; Chen, Y. Solving Optimal Power Flow Problem via Improved Constrained Adaptive Differential Evolution. Mathematics 2023, 11, 1250. https://doi.org/10.3390/math11051250
Yi W, Lin Z, Lin Y, Xiong S, Yu Z, Chen Y. Solving Optimal Power Flow Problem via Improved Constrained Adaptive Differential Evolution. Mathematics. 2023; 11(5):1250. https://doi.org/10.3390/math11051250
Chicago/Turabian StyleYi, Wenchao, Zhilei Lin, Youbin Lin, Shusheng Xiong, Zitao Yu, and Yong Chen. 2023. "Solving Optimal Power Flow Problem via Improved Constrained Adaptive Differential Evolution" Mathematics 11, no. 5: 1250. https://doi.org/10.3390/math11051250
APA StyleYi, W., Lin, Z., Lin, Y., Xiong, S., Yu, Z., & Chen, Y. (2023). Solving Optimal Power Flow Problem via Improved Constrained Adaptive Differential Evolution. Mathematics, 11(5), 1250. https://doi.org/10.3390/math11051250






