A High Throughput BFV-Encryption-Based Secure Comparison Protocol
Abstract
1. Introduction
1.1. Homomorphic Encryption-Based Secure Comparison
1.2. Secure Decryption
2. The BFV Encryption Scheme
2.1. Security Assumption
2.2. Ciphertext and Algebra
2.3. Encryption and Decryption
2.3.1. Encryption and Decryption on Polynomial Algebra
| Algorithm 1 | |
| Input: | |
| Output: | |
| Ensure: | |
| 1: | |
| 2: | |
| 3: | for do |
| 4: | |
| 5: | end for |
| 6: | |
| 7: | |
| Algorithm 2 | |
| Input: | |
| Output: | |
| 1: | for do |
| 2: | |
| 3: | end for |
| 4: | |
| Algorithm 3 | |
| Input: | |
| Output: | |
| Require: | |
| Ensure: |
|
| 1: | for do |
| 2: | |
| 3: | end for |
| 4: | |
| 5: | for do |
| 6: | |
| 7: | end for |
| 8: | |
| 9: | |
| 10: | |
| Algorithm 4 | |
| Input: | |
| Output: | |
| 1: | |
| 2: | |
| Algorithm 5 | ||
| Input: | ||
| Output: | ||
| Require: |
| |
| 1: | ||
| 2: | for do | |
| 3: | ▻ | |
| 4: | end for | |
| 5: | ||
2.3.2. The Correctness of Homomorphic Operations
| Algorithm 6 | |
| Input: | |
| Output: | |
| Require: | |
| Ensure: | |
| 1: | |
| 2: | |
| Algorithm 7 Mul | |
| Input: | |
| Output: | |
| Require: | Let Require |
| Ensure: | |
| 1: | |
| 2: | |
| Algorithm 8 | |
| Input: | |
| Output: | |
| Require: | Let , Require |
| Ensure: | |
| 1: | |
| 2: | |
2.4. Public Key Generation and Encryption
| Algorithm 9 | |
| Input: | |
| Output: | |
| 1: | |
| Algorithm 10 | |
| Input: | |
| Output: | |
| 1: | for do |
| 2: | |
| 3: | |
| 4: | |
| 5: | end for |
| 6: | |
| 7: | |
| 8: | |
2.5. Time Complexity
2.6. Batching
3. Two-Party Computation and BFV Encryption
3.1. The Secure Decryption Protocol
| Protocol 3.1: | ||
| Party: | A | B |
| Input: | s | |
| Output: | ||
| Round 1 (B’s turn) | ||
| 1: | ||
| 2: | ||
| 3: | ||
| 4: | ||
| 5: | B sends to A | |
| Round 2 (A’s turn) | ||
| 6: | ||
| 7: | Establish m | |
3.2. Separate Decryption
3.3. Two Party Computation via BFV Scheme
4. A High Throughput, Semi-Honest, Secure Comparison Protocol
4.1. Improving DGK Secure Comparison Protocol via the BFV Scheme
4.2. High Throughput Comparison Protocol
4.2.1. The Single Pair Integer Comparison Protocol
4.2.2. The Protocol for Comparing Pairs of Integers Simultaneously
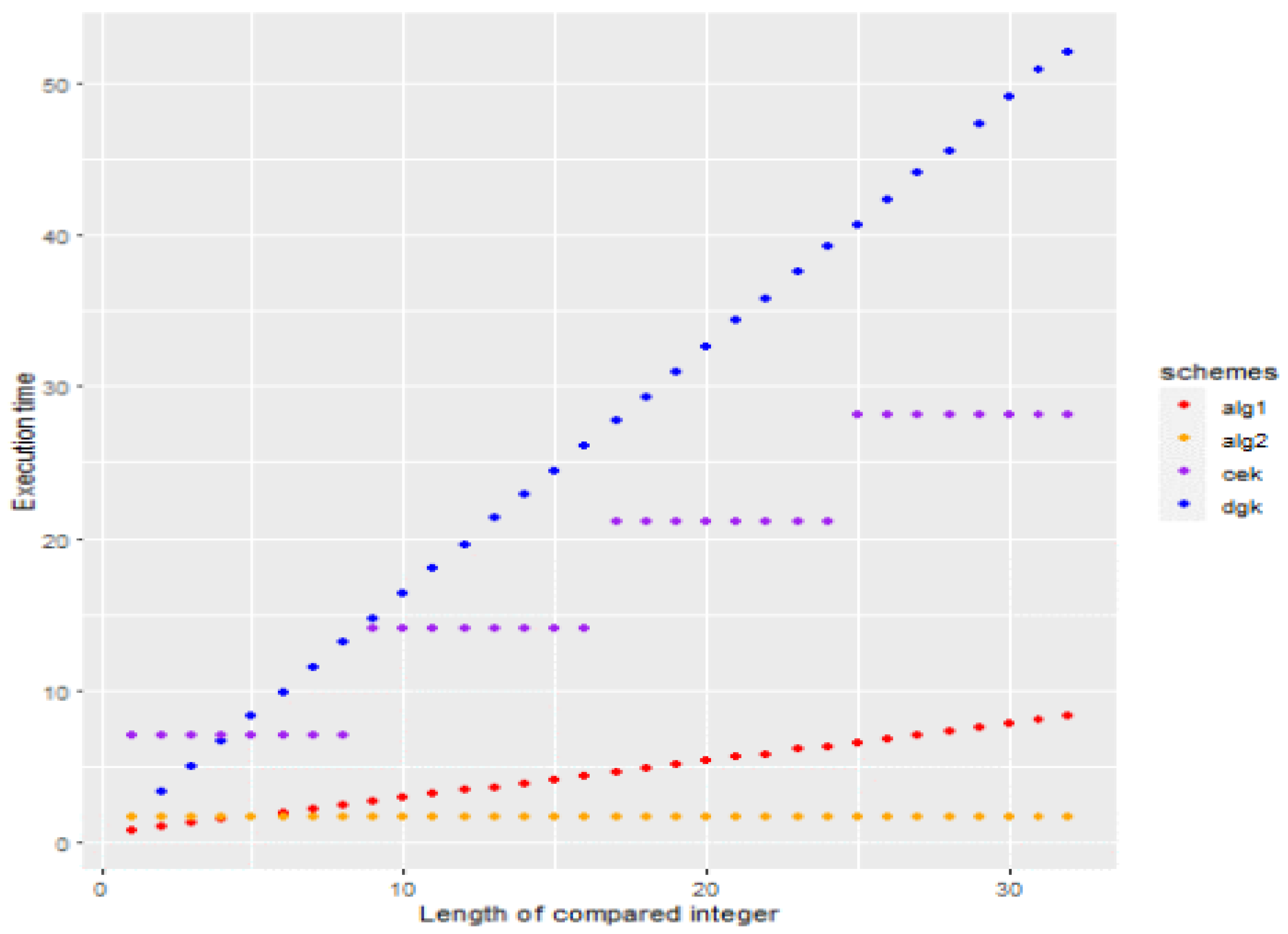
5. Experiment Results
5.1. Encryption Schemes
5.2. Performance Analyses
5.2.1. Computational Cost
5.2.2. Communication Cost
5.3. Remarks on Recently Published Related Works [22,23,24,25]
5.4. Summary
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Algebraic Structures and Notations of the BFV Scheme
Appendix A.1. Quotient Ring
| defined by sending an integer to its residual class, say | ||
| defined by sending to the unique element in . | ||
| defined by sending to | ||
| defined by sending to | ||
| is the infinity norm |
Appendix A.2. Distribution and Sampling
Appendix B. Detailed Proofs Associated with Section 2
Appendix B.1. Proof of Lemma 1 (Sufficient Condition for Correct Decryption)
Appendix B.2. Proofs of Claims 1 to 3
- a.
- Poof of Claim 1 (Correctness of Additions)
- b.
- Proof of Claim 2 (Correctness of Addition between a Plaintext and a Ciphertext).
- c.
- Proof of Claim 3 (Correctness of Multiplication of between a Plaintext and a Ciphertext)
Appendix C. Detailed Proofs Associated with Section 3
Appendix C.1. Proof of Lemma 2 (Distinguishability of a uniform sample with little bias)
Appendix C.2. Proof of Claim 4 (The Security of Bob in Protocol 3.1)
References
- Veugen, T.; Blom, F.; de Hoogh, S.J.A.; Erkin, Z. Secure comparison protocols in the semi-honest model. IEEE J. Sel. Top. Signal Process. 2015, 9, 1217–1228. [Google Scholar] [CrossRef]
- Damga, I.; Geisler, M.; Krøigaard, M. Homomorphic encryption and secure comparison. IJACT 2008, 1, 22–31. [Google Scholar] [CrossRef]
- Paillier, P. Public-key cryptosystems based on composite degree residuosity classes. In Advances in Cryptology—EUROCRYPT ’99, Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Prague, Czech Republic, 2–6 May 1999; Springer: Berlin/Heidelberg, Germany, 1999; pp. 223–238. [Google Scholar]
- Damga, I.; Geisler, M.; Krøigaard, M. A correction to ’efficient and secure comparison for on-line auctions. IJACT 2009, 1, 323–324. [Google Scholar] [CrossRef]
- Groth, J. Cryptography in subgroups of Z∗n. In Theory of Cryptography, Proceedings of the Second Theory of Cryptography Conference, TCC 2005, Cambridge, MA, USA, 10–12 February 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 50–65. [Google Scholar]
- Carlton, R.A. Secure Integer Comparisons using the Homomorphic Properties of Prime Power Subgroups. Ph.D. Dissertation, The University of Western Ontario, London, ON, Canada, 2017. [Google Scholar]
- Carlton, R.; Essex, A.; Kapulkin, K. Threshold properties of prime power subgroups with application to secure integer comparisons. In Topics in Cryptology—CT-RSA 2018, Proceedings of the Cryptographers’ Track at the RSA Conference, San Francisco, CA, USA, 16–20 April 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 137–156. [Google Scholar]
- Damga, I.; Geisler, M.; Krøigaard, M. Efficient and secure comparison for on-line auctions. In Information Security and Privacy, Proceedings of the 12th Australasian Conference, ACISP 2007, Townsville, Australia, 2–4 July 2007, Lecture Notes in Computer Science; Pieprzyk, J., Ghodosi, H., Dawson, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4586, pp. 416–430. [Google Scholar] [CrossRef]
- Veugen, T. Improving the DGK comparison protocol. In Proceedings of the 2012 IEEE International Workshop on Information Forensics and Security (WIFS), Costa Adeje, Spain, 2–5 December 2012; pp. 49–54. [Google Scholar]
- Veugen, T. Correction to” improving the DGK comparison protocol. IACR Cryptol. Eprint Arch. 2018, 2018, 1100. [Google Scholar]
- Gentry, C.; Boneh, D. A Fully Homomorphic Encryption Scheme; Stanford University: Stanford, CA, USA, 2009; Volume 20. [Google Scholar]
- Gentry, C. Fully homomorphic encryption using ideal lattices. In Proceedings of the Forty-First Annual ACM Symposium on Theory of Computing, Bethesda, MD, USA, 31 May 2009–2 June 2009; pp. 169–178. [Google Scholar]
- Van Dijk, M.; Gentry, C.; Halevi, S.; Vaikuntanathan, V. Fully homomorphic encryption over the integers. In Advances in Cryptology—EUROCRYPT 2010, Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, French Riviera, France, 30 May–3 June 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 24–43. [Google Scholar]
- Brakerski, Z.; Vaikuntanathan, V. Efficient fully homomorphic encryption from (standard) LWE. In Proceedings of the 2011 IEEE 52nd Annual Symposium on Foundations of Computer Science, Palm Springs, CA, USA, 22–25 October 2011; FOCS ’11. IEEE Computer Society: Washington, DC, USA, 2011; pp. 97–106. [Google Scholar] [CrossRef]
- Brakerski, Z.; Gentry, C.; Vaikuntanathan, V. (leveled) fully homomorphic encryption without bootstrapping. In Proceedings of the 3rd Innovations in Theoretical Computer Science Conference, ITCS ’12, Cambridge, MA, USA, 8–10 January 2012; Association for Computing Machinery: New York, NY, USA, 2012; pp. 309–325. [Google Scholar] [CrossRef]
- Brakerski, Z. Fully homomorphic encryption without modulus switching from classical GAPSVP. In Advances in Cryptology—CRYPTO 2011, Proceedings of the Annual Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2011; Springer: Berlin/Heidelberg, Germany, 2012; pp. 868–886. [Google Scholar]
- Fan, J.; Vercauteren, F. Somewhat practical fully homomorphic encryption. IACR Cryptol. Eprint Arch. 2012, 2012, 144. [Google Scholar]
- Gentry, C.; Sahai, A.; Waters, B. Homomorphic encryption from learning with errors: Conceptually-simpler, asymptotically-faster, attribute-based. In Advances in Cryptology—CRYPTO 2013, Proceedings of the Annual Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 75–92. [Google Scholar]
- Cheon, J.H.; Kim, A.; Kim, M.; Song, Y. Homomorphic encryption for arithmetic of approximate numbers. In Advances in Cryptology—ASIACRYPT 2017, Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Hong Kong, China, 3–7 December 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 409–437. [Google Scholar]
- Brakerski, Z.; Vaikuntanathan, V. Fully homomorphic encryption from ring-LWE and security for key dependent messages. In Advances in Cryptology—CRYPTO 2011, Proceedings of the Annual Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 505–524. [Google Scholar]
- Albrecht, M.; Chase, M.; Chen, H.; Ding, J.; Goldwasser, S.; Gorbunov, S.; Halevi, S.; Hoffstein, J.; Laine, K.; Lauter, K.; et al. Homomorphic Encryption Security Standard. HomomorphicEncryption.org: Toronto, ON, Canada. 2018. Available online: http://homomorphicencryption.org/wp-content/uploads/2018/11/HomomorphicEncryptionStandardv1.1.pdf (accessed on 15 February 2023).
- Al Badawi, A.; Veeravalli, B.; Lin, J.; Xiao, N.; Kazuaki, M.; Mi, A.K.M. Multi-gpu design and performance evaluation of homomorphic encryption on gpu clusters. IEEE Trans. Parallel. Distrib. Syst. 2021, 32, 379–391. [Google Scholar] [CrossRef]
- Özerk, Ö.; Elgezen, C.; Mert, A.C.; Öztürk, E.; Savaş, E. Efficient number theoretic transform implementation on GPU for homomorphic encryption. J. Supercomput. 2022, 78, 2840–2872. [Google Scholar] [CrossRef]
- Tan, B.H.M.; Lee, H.T.; Wang, H.; Ren, S.Q.; Khin, A.M.M. Efficient private comparison queries over encrypted databases using fully homomorphic encryption with finite fields. In IEEE Transactions on Dependable and Secure Computing; IEEE: Piscataway, NJ, USA, 2020; pp. 2861–2874. [Google Scholar]
- Iliashenko, I.; Zucca, V. Faster homomorphic comparison operations for BGV and BFV. Proc. Priv. Enhancing Technol. 2021, 2021, 246–264. [Google Scholar] [CrossRef]
- Driver, M. Emerging technologies: Homomorphic encryption for data sharing with privacy. Gartner Inc. Tech. Rep. Published: 23 April 2020. Available online: https://www.gartner.com/en/documents/3983970 (accessed on 12 February 2023).
- Huo, M.; Wu, K.; Ye, Q. A note on lower digits extraction polynomial for bootstrapping. arXiv 2019, arXiv:1906.02867. [Google Scholar]
- Lyubashevsky, V.; Peikert, C.; Regev, O. On ideal lattices and learning with errors over rings. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, French Riviera, France, 30 May–3 June 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1–23. [Google Scholar]
- Microsoft SEAL (Release 3.4). Oct. 2019, Microsoft Research, Redmond, WA. Available online: https://github.com/Microsoft/SEAL (accessed on 11 January 2023).



| Operation | Time Complexity |
|---|---|
| PolyMul | |
| KeyGen | |
| EncSym | |
| PubKeyGen | |
| EncAsym | |
| Dec | |
| AddPlain | |
| MulPlain | |
| Add |
| Party | A | B |
|---|---|---|
| Input | ||
| Output |
| Protocol 3.2: | ||
| Party: | A | B |
| Input: | s | |
| Output: | ||
| Round 1 (A’s turn) | ||
| 1: | ||
| 2: | ||
| 3: | B sends to A | |
| Round 2 (A’s turn) | ||
| 4: | ||
| 5: | for do | |
| 6: | ||
| 7: | ||
| 8: | ▻ | |
| 9: | if and then | |
| 10: | ||
| 11: | end if | |
| 12: | if and then | |
| 13: | ||
| 14: | end if | |
| 15: | ▻ | |
| 16: | if then | |
| 17: | ||
| 18: | end if | |
| 19: | if then | |
| 20: | ||
| 21: | end if | |
| 22: | ||
| 23: | end for | |
| 24: | ||
| 25: | A send to B. | |
| Round 2 (B’s turn) | ||
| 26: | ||
| 27: | for do | |
| 28: | ||
| 29: | ||
| 30: | ▻ | |
| 31: | if and then | |
| 32: | ||
| 33: | end if | |
| 34: | if and then | |
| 35: | ||
| 36: | end if | |
| 37: | ▻ | |
| 38: | if then | |
| 39: | ||
| 40: | end if | |
| 41: | if then | |
| 42: | ||
| 43: | end if | |
| 44: | ||
| 45: | if then | |
| 46: | ||
| 47: | end if | |
| 48: | ||
| 49: | end for | |
| 50: | ||
| 52: | B sends to A | |
| Round 3 (A’s turn) | ||
| 53: | ▻ | |
| Protocol 3.3 2PC Protocol | ||
| Party: | A | B |
| Input: | ||
| Output: | ||
| Round 1 (A’s turn) | ||
| 1: | for do | |
| 2: | ||
| 3: | end for | |
| 4: | A sends to B | |
| 5: | Round 2 (B’s turn) | |
| 6: | ||
| Round 3 | ||
| 7: | A and B perform secure decryption to decrypt , and A derived | |
| Protocol 4.1 Basic Secure Comparison Protocol | ||
| Party: | A | B |
| Input: | ||
| Output: | ||
| Round 1 (A’s turn) | ||
| 1: | for do | |
| 2: | ||
| 3: | end for | |
| 4: | A sends to B | |
| Round 2 (B’s turn) | ||
| 5: | ||
| 6: | ||
| 7: | ||
| 8: | for do | |
| 9: | ||
| 10: | ||
| 11: | ||
| 12: | ||
| 13: | ▻ | |
| 14: | ▻ | |
| 15: | ||
| 16: | ||
| 17: | end for | |
| Round 3 Secure Decrypt to A, where the associated message would be | ||
| Round 4 (A’s Turn) | ||
| 18: | ||
| 19: | ||
| 20: | for do | |
| 21: | if then | |
| 22: | ||
| 23: | Establish | |
| Protocol 4.2: | ||
| Party: | A | B |
| Input: | ||
| Output: | ||
| Round 1 (A’s turn) | ||
| 1: | ||
| 2: | ||
| 3: | Sends to B. | |
| Round 2 (B’s turn, computes xor) | ||
| 4: | ||
| 5: | ▻ | |
| 6: | ▻ | |
| 7: | ▻ | |
| 8: | for do | |
| 9: | ||
| 10: | end for | |
| 11: | ||
| 12: | ||
| 13: | Secure Decrypt for A | |
| 14: | Round 3 (A’s turn, computes | |
| 15: | Derived from secure decryption | |
| 16: | ||
| 17: | for do | |
| 18: | ||
| 19: | ||
| 20: | end for | |
| 21: | ||
| 22: | ||
| 23: | Sends to B. | |
| Round 4 (B’s turn, compute | ||
| 24: | ||
| 25: | for do | |
| 26: | ||
| 27: | ||
| 28: | end for | |
| 29: | ||
| 30: | ▻ remove the mask | |
| 31: | ||
| 32: | for do | |
| 33: | ||
| 34: | ||
| 35: | end for | |
| 36: | ||
| 37: | ||
| 38: | ||
| 39: | ▻ | |
| 40: | ||
| Secure Decrypt for A | ||
| 41: | Round 5. (A’s turn, convert message to polynomial mod for rotation) | |
| 42: | Derived from secure decryption | |
| 43: | ||
| 44: | ▻ non-batch format, 1 message followed by d-1 zeros | |
| Sends to B. | ||
| 45: | Round 6 (B’s turn, randomly rotate) | |
| 46: | ||
| 47: | ▻ put as the -th coefficient | |
| 48: | ▻ remove the mask | |
| 49: | ||
| 50: | ||
| 51: | Secure Decrypt for A | |
| 52: | Round Final. (A’s turn, establish result), suppose | |
| 53: | ||
| 54: | ||
| 55: | for do | |
| 56: | if then | |
| 57: | ||
| 58: | end if | |
| 59: | end for | |
| 60: | Establish | |
| Protocol 4.3: k-pairs | ||
| Party: | A | B |
| Input: | ||
| Output: | ||
| Round 1 (A’s turn) | ||
| 1: | ||
| 2: | ||
| 3: | Sends to B. | |
| Round 2 (B’s turn, computes XoR) | ||
| 4: | ||
| 5: | ▻ | |
| 6: | ▻ | |
| 7: | ▻ | |
| 8: | for do | |
| 9: | for do | |
| 10: | ||
| 11: | end for | |
| 12: | end for | |
| 13: | ||
| 14: | ||
| 15: | Secure Decrypt for A | |
| Round 3 (A’s turn, computes | ||
| 16: | Derived from secure decryption | |
| 17: | for do | |
| 18: | ||
| 19: | for do | |
| 20: | ||
| 21: | ||
| 22: | end for | |
| 23: | end for | |
| 24: | ||
| 25: | ||
| 26: | Sends to B. | |
| 27: | Round 4 (B’s turn, compute | |
| 28: | ||
| 29: | for do | |
| 30: | ||
| 31: | for do | |
| 32: | ||
| 33: | ||
| 34: | end for | |
| 35: | end for | |
| 36: | ||
| 37: | ▻ remove the mask | |
| 38: | ||
| 39: | for do | |
| 40: | for do | |
| 41: | ||
| 42: | ||
| 43: | end for | |
| 44: | end for | |
| 45: | ||
| 46: | ||
| 47: | ||
| 48: | ▻ | |
| 49: | ||
| 50: | Secure Decrypt for A | |
| 51: | Round 5. (A’s turn, convert message to polynomial mod for rotation) | |
| 52: | Derived from secure decryption | |
| 53: | ||
| 54: | ▻ -batch of degree polynomials | |
| 55: | ||
| Sends to B. | ||
| Round 6 (B’s turn, randomly rotate) | ||
| 57: | ||
| 58: | ▻ remove the mask | |
| 59: | for do | |
| 60: | ||
| 61: | ||
| 62: | ▻ length is , only -th entry is 1 | |
| 63: | end for | |
| 64: | ||
| 65: | ||
| 66: | Secure Decrypt for A | |
| Round Final. (A’s turn, establish result), suppose | ||
| 67: | ||
| 68: | for do | |
| 69: | ||
| 70: | for do | |
| 71: | if then | |
| 72: | ||
| 73: | end if | |
| 74: | end for | |
| 75: | end for | |
| 76: | Establish | |
| Schemes | Plaintext Space | Enc | Dec | KeyGen | Add | MulPlain |
|---|---|---|---|---|---|---|
| Paillier | 22.98 | 7.756 | 1871 | 0.021 | - | |
| RSA | 0.079 | 2.216 | 1792 | - | 0.008 | |
| RSA [5] | 0.692 | 0.209 | 1038 | 0.002 | - | |
| RSA [7] | 0.685 | 55.49 | 1325 | 0.002 | - | |
| BFV | 0.459 | 0.055 | 0.360 | 0.002 | 0.065 | |
| BFV-opt | 0.251 | 0.060 | 0.198 | 0.002 | 0.058 |
| Schemes | Secure Decryption | Round | Complexity | 32-Bit | 2048-Bit | 4096-Bit |
|---|---|---|---|---|---|---|
| Protocol 4.1 | Protocol 3.2 | 4 | 7.496 | 479.7 | 966.6 | |
| Protocol 4.1 | Protocol 3.1 | 2 | 15.45 | 1000 | 1996.6 | |
| Protocol 4.3 | Protocol 3.2 | 8 | 1.686 | 4.246 | - | |
| Protocol 4.3 | Protocol 3.1 | 6 | - | - | 12.06 | |
| DGK [10] | Add Encryption Zero | 2 | 55.71 | 3488 | 6766 | |
| CEK [7] | Add Encryption Zero | 3~5 | 28.16 | 1696 | 3471 |
| Schemes | Parameters | Ciphertext Size (KB) | Communication Cost (KB) |
|---|---|---|---|
| Protocol 4.1 | n = 1024, log2 q = 27 | 6.75 | 6.75·(l+1) |
| Protocol 4.2 | n = 1024, log2 q = 27 | 6.75 | 40.5 |
| DGK [10] | log2 N = 3072 | 0.375 | 0.65 · l |
| CEK [7] | log2 N = 3072 | 0.375 | 0.08125 · l |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuo, T.-H.; Wu, J.-L. A High Throughput BFV-Encryption-Based Secure Comparison Protocol. Mathematics 2023, 11, 1227. https://doi.org/10.3390/math11051227
Kuo T-H, Wu J-L. A High Throughput BFV-Encryption-Based Secure Comparison Protocol. Mathematics. 2023; 11(5):1227. https://doi.org/10.3390/math11051227
Chicago/Turabian StyleKuo, Tzu-Hsiang, and Ja-Ling Wu. 2023. "A High Throughput BFV-Encryption-Based Secure Comparison Protocol" Mathematics 11, no. 5: 1227. https://doi.org/10.3390/math11051227
APA StyleKuo, T.-H., & Wu, J.-L. (2023). A High Throughput BFV-Encryption-Based Secure Comparison Protocol. Mathematics, 11(5), 1227. https://doi.org/10.3390/math11051227







