Abstract
Secure comparison is a fundamental problem in multiparty computation. There are two different parties, each holding an -bit integer, denoted by and , respectively. The goal of secure comparison is to compute the order relationship between and , say , without revealing their inputs to any others. Since previous solutions based on homomorphic encryption need at least encryptions for each -bit comparison, the total encryption time leads to a computational bottleneck for these protocols. This work presents a fast, semi-honest, secure comparison protocol based on the BFV encryption scheme. With its vector-like plaintext space, the number of required encryptions can be significantly reduced; actually, only six encryptions are needed for each comparison in our protocol. In other words, the proposed protocol can achieve the time complexity ) for a given security parameter λ. As a result, 4096-bit integers can be securely compared within 12.08 ms, which is 280 times faster than the state-of-the-art homomorphic encryption-based secure comparison protocol. Furthermore, we can compare k pairs of -bit integers with almost the same execution time as comparing -bit integers and achieve higher throughput regardless of the compared integer size.
Keywords:
secure comparison; multi-party computation; fully homomorphic encryption; Secure Auction; ring learning with error MSC:
94A60
1. Introduction
1.1. Homomorphic Encryption-Based Secure Comparison
The goal of multi-party computation (MPC) is to create an algorithm that enables different parties to compute a function jointly without revealing their inputs. In areas such as secret voting or e-commerce, MPC provides a solution for protecting each party’s privacy without the involvement of a trusted third party (TTP). However, the high computational costs of MPC make these solutions practically infeasible. Secure comparison is one of the fundamental problems in MPC, with the goal of computing securely for two different parties with private inputs and . Since special-purpose secure comparison protocols (SP-SCPs) often outperform those protocols based on general-purpose MPC constructions, SP-SCPs can improve the performance of most privacy-preserved applications. This fact motivates us to develop high-speed, secure comparison protocols.
Homomorphic Encryption (HE) and Garbled Circuits (GC) are two of the most famous cryptographic techniques for constructing secure comparison protocols. Based on the study presented in [1], HE-based protocols can achieve faster speed and lower round complexity, whereas GC-based protocols provide a lower communication rate and higher flexibility. In this work, we focus on the computational cost and compete for the speed of our protocol to state-of-the-art HE-based comparison protocols. In general, the performance of an HE-based protocol is strongly related to which HE scheme is used. For example, the protocol proposed in [2] needs only two encryptions for each bit, but the final performance is 60.4 milliseconds per bit (ms/bit) (Runs on i5-9400f@4.0 GHz, single core, and set security parameter λ = 128.) since each Paillier encryption [3] needs 23 ms. The authors in [4] replaced Paillier with subgroup-RSA [5], which needs only 0.692 ms/bit for each encryption and provides a much better performance of 1.74 ms/bit. Noticeably, the protocols proposed in [6,7] compare 8 bits simultaneously by the threshold property in the plaintext space, which needs only two encryptions and one private-equality-test (Private-equality-test is to compute (a == b) ∈ {0, 1} securely for two different parties. Notice. two encryptions are needed in the protocol.) for every 8-bit. In their works, the performance reaches 0.8 ms/bit. To the best of our knowledge, these two are the fastest 2-round secure comparison protocol [2,4,8,9,10] and the fastest secure comparison protocol [6,7]. We will refer to them as DGK protocol and CEK protocol, respectively. The Paillier and the subgroup-RSA mentioned above are HE schemes that can execute additions in the encryption domain. We refer to them as additive homomorphic encryption (AHE) schemes.
Fully homomorphic encryption (FHE) specifically addresses those HE schemes that can realize arbitrary arithmetic circuits in the encryption domain. The first construction of FHE was proposed by Gentry [11,12] in 2009. In his construction, Gentry first proposed a somewhat homomorphic encryption (SWE) scheme, which can implement a limited number of additions and multiplications in the encryption domain, and then used bootstrapping mechanism (Bootstrapping technique is to implement a decryption circuit in the encryption domain to create a new ciphertext associated with the same message but with fewer evaluations in the encryption domain.) “refresh” the ciphertexts. Inspired by Gentry’s blueprint, different FHE schemes [13,14,15,16,17,18,19] have been proposed in the following years.
Our work was inspired by the HE scheme proposed by Fan and Vercauteren [17], inherited from [14,15,16,20,21,22,23,24,25,26], and is one of the widely used FHE schemes up to now. To avoid confusion, we always use the “BFV scheme” to represent SHE schemes proposed in [17]. Since the BFV is one of the SHE schemes, the corresponding ciphertext size is determined by the number of evaluations in the encryption domain. While the execution speed of each operation in the BFV scheme would decrease as the ciphertext-size increase; therefore, it is hard to realize complicated functions in a practical use case. On the other hand, if the target function is simple enough, then the ciphertexts can be small, and the performance of the BFV scheme can outperform subgroup-RSA. We observed this fact in our experiments; that is, the encryption of the BFV scheme can be realized within 0.21 ms in our protocol, whereas the encryption of subgroup-RSA needs 0.7 ms. The remarks about and comparisons with recently published related work will be presented in Section 5.3.
1.2. Secure Decryption
Let p be the public key and s be the secret key. We say an encryption scheme can implement an operation ⋆: × → in the encryption domain if there exists a computable function T such that
for arbitrary ciphertexts c1, c2 ∈ . Those encryption schemes that satisfy the property mentioned in Equation (1) are the HE schemes. Since HE enables us to compute over the ciphertexts, we may let the party that does not have a secret key compute the function in the encryption domain; and the other party decrypts the ciphertext(s) associated with the result. The problem is, if the latter party may learn other information while decrypting, then the security of the former party could be compromised. On the other hand, if the two parties can securely decrypt the result, we can achieve the security requirement of two-party computation (2PC), as shown in Figure 1.
Dec (T (c1, c2, p), s) = Dec(c1, s) ⋆ Dec(c2, s)
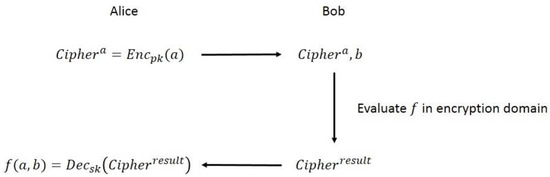
Figure 1.
The Information Flow of Realizing 2PC via the BFV Scheme and the Secure Decryption Process. Party 1(say Alice) holds the secret key sk and public key pk; Party 2 (say Bob) holds the ciphertext Cipher and the public key pk. The goal of secure decryption is to securely compute Dec (Cipher, sk) for Party 1.
2. The BFV Encryption Scheme
BFV scheme is an attractive encryption scheme that is equipped with fast encryption and decryption operations, vector-like plaintext space (optional), and robust computations in the encryption domain. We review some functionalities of the BFV scheme in this section. Other BFV-related operations, such as bootstrapping, can be found in [11,15,17,27]. Moreover, for self-completeness, the algebraic structure and commonly used notations of the BFV scheme are presented in Appendix A.
This section addresses the assumptions and some characteristics related to the BFV scheme. As anonymous reviewers suggest, all the corresponding proof will be presented in Appendix B.
2.1. Security Assumption
Definition 1.
(Ring Learning with Error Distribution) Let be the -th cyclotomic ring with coefficients in . Let and be a small distribution with . Then, the ring learning with error distribution is the distribution of , where is a uniform distribution in and is the degree of .
Assumption 1.
(Infeasibility of decision-RLWE) The decision problem of Ring Learning with Error (RLWE), denoted by decision-, is to distinguish uniform distribution and . The decision-RLWE assumption is to assume decision- is infeasible.
The decision-RLWE assumption establishes the security assumption of the BFV encryption scheme. Moreover, we can reduce it to the well-known shortest vector problem (SVP) if is a discrete Gaussian distribution with sufficient large standard error (e.g., ) and the secret key is sampled from [28]. However, we sometimes use small standard error (e.g., in [29]) for better performance.
2.2. Ciphertext and Algebra
Given , and let be the -th cyclotomic polynomial. where . Let be the cyclotomic ring with degree . Plaintexts are in , and ciphertexts are in , where and the ratio can be treated as the “tolerance” of error.
Let be a small distribution, say .
2.3. Encryption and Decryption
2.3.1. Encryption and Decryption on Polynomial Algebra
Multiplication in (denoted as , cf. Algorithm 1 for detailed definition) can be implemented in operations in by Fast Fourier Transformation (FFT), and the time complexity would be . For convenience, we use a bolder case to denote a polynomial, which can be stored as coefficients in in a computer, and it would be the requirement of all of the following algorithms. Similarly, each plaintext could be stored as coefficients in
| Algorithm 1 | |
| Input: | |
| Output: | |
| Ensure: | |
| 1: | |
| 2: | |
| 3: | for do |
| 4: | |
| 5: | end for |
| 6: | |
| 7: | |
Once again, we assume the secret key, s, is generated from a small distribution (cf. Algorithm 2 for details).
| Algorithm 2 | |
| Input: | |
| Output: | |
| 1: | for do |
| 2: | |
| 3: | end for |
| 4: | |
| Algorithm 3 | |
| Input: | |
| Output: | |
| Require: | |
| Ensure: |
|
| 1: | for do |
| 2: | |
| 3: | end for |
| 4: | |
| 5: | for do |
| 6: | |
| 7: | end for |
| 8: | |
| 9: | |
| 10: | |
EncSym (Algorithm 3) is to encrypt a message m with secret key s. That is,
We may use Algorithm 4 to define the error with the corresponding message and ciphertext. Moreover, the ciphertext can be correctly decrypted if and only if the error is less than (see Algorithm 5). We can summarize this subsection’s discussions into the following Lemma.
Lemma 1.
(Sufficient Condition for Correct Decryption). Given ciphertext , and message , and is the corresponding error, then implies Thus, we can decrypt correctly if the error is small enough.
Proof.
Please refer to Appendix B.1 for detailed proof. □
| Algorithm 4 | |
| Input: | |
| Output: | |
| 1: | |
| 2: | |
| Algorithm 5 | ||
| Input: | ||
| Output: | ||
| Require: |
| |
| 1: | ||
| 2: | for do | |
| 3: | ▻ | |
| 4: | end for | |
| 5: | ||
2.3.2. The Correctness of Homomorphic Operations
In this subsection, we introduce the addition between two ciphertexts (denoted as Add), the addition between a ciphertext and a plaintext (denoted as AddPlain, cf. Algorithm 6), and the multiplication between a ciphertext and a plaintext (denoted as MulPlain, cf. Algorithm 7).
Given , suppose the corresponding messages are , and the corresponding errors are . The above-mentioned operations can be defined as follows:
Add (c, c′): Return (c0 + c′0, c1 + c′1)
AddPlain (c, m′): Return (c0 +[m′]p · ρ , c1)
MulPlain (c, m′): Return (c0 · [m′]p, c1 · [m′]p)
Claim 1.
(Correctness of Addition). Suppose ,then
We illustrate the definition and the operation process of the homomorphic addition (denoted as Add, cf. Algorithm 8 for details).
Proof.
Please refer to Appendix B.2.a for details. □
Claim 2.
(Correctness of Addition between a Plaintext and a Ciphertext). Suppose , then
Dec (AddPlain (c, m’), s) = m + m’.
Proof.
Please refer to Appendix B.2.b for details. □
Claim 3.
(Correctness of Multiplication between a Plaintext and a Ciphertext).
Suppose , then
Dec (MulPlain (c, m’), s) = m · m′.
Proof.
Please refer to Appendix B.2.c for details. □
Notice that all the correctness mentioned above is associated with the magnitude of the norm of errors. Claims 1, 2, and 3 are essential for estimating how large should be.
| Algorithm 6 | |
| Input: | |
| Output: | |
| Require: | |
| Ensure: | |
| 1: | |
| 2: | |
| Algorithm 7 Mul | |
| Input: | |
| Output: | |
| Require: | Let Require |
| Ensure: | |
| 1: | |
| 2: | |
| Algorithm 8 | |
| Input: | |
| Output: | |
| Require: | Let , Require |
| Ensure: | |
| 1: | |
| 2: | |
2.4. Public Key Generation and Encryption
The public key generation (denoted as PubKeyGen) involved in our protocol can be illustrated in Algorithm 9. Moreover, the asymmetric encryption function (denoted as EncAsym) concerning our protocol can be depicted in Algorithm 10.
| Algorithm 9 | |
| Input: | |
| Output: | |
| 1: | |
| Algorithm 10 | |
| Input: | |
| Output: | |
| 1: | for do |
| 2: | |
| 3: | |
| 4: | |
| 5: | end for |
| 6: | |
| 7: | |
| 8: | |
To claim the correctness of EncAsym, we should evaluate the norm of the error:
Notice r, e, e’, and s are sampling from and bounded by ; thus, we have
Recall Algorithm 5—the correctness of decryption is ensured if bounds the error. Therefore, we can choose large enough, so the correctness follows. That is,
2.5. Time Complexity
Additions in needs additions in , and the time complexity would be . Multiplications can be implemented in by FFT implementation of the polynomial ring. Let be the security parameter, suppose the -bit pseudo-random number can be generated in , then the time complexity associated with each operation can be listed in Table 1.

Table 1.
Time Complexity of BFV Operations.
Since can be regarded as the affordability of error, should be large enough for the evaluations. However, the security level is inversely proportional to log , so should increase proportional to preserve the same security level. Therefore, we should use the number of evaluations to represent the time complexity.
As seen in Table 1, the performance is dominated by . Recall that the error should be less than . Each multiplication would increase the upper bound of the error by a factor of and the error of fresh ciphertext is less than , so the error after multiplications is at most , and we choose large enough to keep the correctness:
Let be the security level, then . We conclude that the computational cost has a quadratic growth with respect to .
2.6. Batching
Batching is a commonly used technique to speed up cryptographic operations; however, its relation to mathematical derivations has seldom been presented and discussed. Since batching plays a crucial role in our proposed protocol, we detail its definition and derivation in this subsection. Readers who are familiar with batching can jump to the next section directly.
Suppose where are co-prime, then we can apply Chinese Remainder Theorem to derive the following isomorphic relation:
If we further assume is irreducible, and for each , then
Generally, the isomorphic relation given in (Equation (9)) always holds. In the following paragraphs, we will introduce how to choose p for some given d and n.
For convenience, we always choose , so and . We claim that if is a prime with :
We can find a generator , has order , and is a root of . Similarly, let , then has order and is also a root of . Since are different roots of , we may write
and
Notice that is an isomorphism from to , and can be determined by . We may apply the Number Theoretic Transform (NTT) to send to with operations in . We may also let , so
where , and . We derive another isomorphic relation
We may write with , then the isomorphism (cf. Equation (13)) can be defined as
Similarly, can be determined by and the values of can be calculated by -dimension NTT, which needs O ((nd−1) · log (nd−1)) operations in p or the time complexity is O ((nd−1) · log (nd−1)) · O (log q). Consequently, the time complexity of the whole map becomes the summation of d different NTTs plus the time needed for combining them, which equals
O (d·(nd−1) ·log (nd−1) ·log q) + O (n · log q) = O (n · log q · (log n − log d)).
As illustrated in Figure 2, the function that maps (Zp [X ]/(Φd (X)))n/d to Rm,p can be regarded as an “encoder”, and its inverse is the “decoder”. Notice we always suppose 2 · (n/d) divides (p—1), and n is a power of 2. In the following, we will use to denote the function from to , and will be the inverse of Encode.
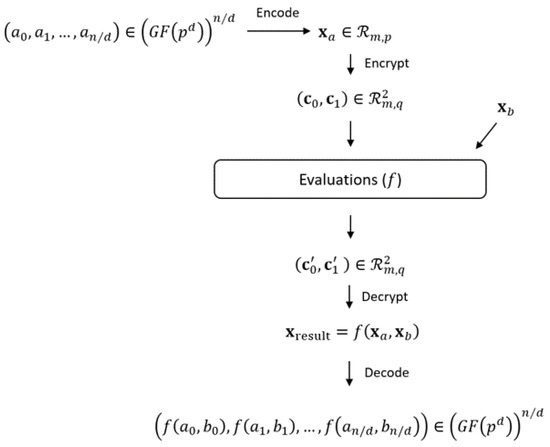
Figure 2.
The Information Flow and the Implementation of the Proposed HE-Domain’s Encoding and Decoding Functions.
3. Two-Party Computation and BFV Encryption
In the following contexts, we name the two players (or parties) Alice and Bob. With the BFV scheme, Alice can delegate the computation to Bob without revealing her private input. Let cresult denote the ciphertext computed by Bob. Suppose there is a protocol that can derive the message in cresult without leaking any information which may infringe the privacy of Bob. In that case, we say the protocol satisfies the security requirement of two-party computation via the BFV scheme, or the protocol can derive the message securely through “secure decryption”.
3.1. The Secure Decryption Protocol
Suppose Bob holds some ciphertext cresult, Alice holds the secure key s, and the goal of secure decryption is to compute Dec (cresult, s) securely, which can be formulated as in Table 2 notice if the secure decryption exists, and Bob can compute the function f in the encryption domain, then they can securely compute f by

Table 2.
Formulas Associated with the Secure Decryption.
(i) Alice encrypting her private input(s) and sending the results to Bob.
(ii) Bob computing the function f in the encryption domain and obtaining the ciphertext cresult associated with the desired result, called mresult.
(iii) Performing the above “secure decryption” protocol; then, Alice learns the mresult without knowing any other information.
Notice that the first term of the public key, say p1, is sampled from a uniform distribution. If Bob randomly sampled , then the pair “looks like” a pair of uniformly sampled samples in the view of Alice, by the RLWE assumption. Based on this idea, we will construct our first secure decryption protocol in the remaining context of this section.
Suppose the error of is , the error of is . Let , then the error in is . By Lemma 2, implies Dec (c′, s) = Dec (cresult, s). Before proving the security of Protocol 3.1, we first analyze the distinguishability between eresult + ezero + e and a uniform sample from .
Lemma 2.
(Distinguishability of a uniform sample with little bias). For some e ∈ , distinguishing two samples, one is sampled uniformly from , the other is from , the advantage of the adversary is no more than .
Proof.
Please refer to Appendix C.1 for details. □
Corollary 1.
(Distinguishability of a uniform vector with little bias). For some e ∈ , distinguishing two samples, one is sampled from , the other is from , the advantage of the adversary is no more than .
Proof.
Since each entry of the vector is independent to each other, the adversary of -th entry is no more than by Lemma 2. Adversary of the whole vector is no more than summing up the adversary of each entry, which is . □
Notice that her security of Alice is guaranteed based on the security of the BFV scheme, so we need only to deal with the security of Bob. We will prove this by simulating the view of Alice from Dec (cresult, s) and s.
Claim 4.
(The Security of Bob in Protocol 3.1). Suppose ‖eresult + ezero‖1 < Esum, T > Esum · (2ε)−1, and RLWE assumption holds, then the view of Alice, which is cresult ∈ (Rm,q)2, can be simulated by Dec (cb, s) and s.
Proof.
Please refer to Appendix C.2 for details. □
Protocol 3.1. The Proposed Secure Decryption Protocol.
| Protocol 3.1: | ||
| Party: | A | B |
| Input: | s | |
| Output: | ||
| Round 1 (B’s turn) | ||
| 1: | ||
| 2: | ||
| 3: | ||
| 4: | ||
| 5: | B sends to A | |
| Round 2 (A’s turn) | ||
| 6: | ||
| 7: | Establish m | |
In a real case, we do not know the exact value of Esum, but we can estimate an upper bound of ‖eb + ezero‖∞, say E > ‖eb + ezero‖∞, by Claims 1, 2, 3. Therefore, Esum < n · E (we sometimes estimate Esum as n1/2 · E since EV[Esum] ≈ n1/2 · E) (notice ε < n· E · q−1 can be smaller than p(n)−1 for any polynomial p and sufficient large n since q is exponential to n for some fixed security parameter and n · E = O (n2) for a fixed task in the encryption domain). In the next section, we will introduce “separate decryption” to improve performance.
3.2. Separate Decryption
Let ; the result of decryption can be computed from c0 and (c1 · s). The idea of separate decryption is: Bob holds c0, Alice holds (c1 · s), and they compute the decryption result jointly.
Let m be the message, be the correspond error. Further suppose
where the coefficients of are in . By the definition of error, we also have , so mod . By discussing the magnitude of , there exists
where , and the message can be computed by.
For convenience, we will write , , , and . Let t ∈ {0,1}, we have
(i) If , then , so is either 0 or 1.
(ii) If, then , so .
Suppose , and define
So can be evaluated from , :
(i) If , then .
(ii) If , then .
(iii) Else,
The procedures of separate decryption can now be listed as in Table 3. From Equation (17), we have . So, if , further suppose sampled uniformly from . Then, Prob 1 − |1 + ei| · ρ−1.

Table 3.
Procedures of the Separable Secure Decryption (also known as Protocol 3.2 in this write-up).
Suppose < ε for some sufficient small ε > 0, then m = m0 + m1 with probability greater than 1 − ε. Therefore, the view of Alice, which is (c′, m0), is equal to (c′, m − m1) with a probability Prob {u = 0} > 1 − ε. Since m1 = F (c′, s) for some computable function F, (c′, m − m1) = (c′, m − F (c′, s)) is not distinguishable from (r, m − F (r)) (to Alice) by RLWE assumption.
An advantage of separate decryption is that we do not need to sample e from a large uniform distribution. Its other advantage is the lower communication rate because the size of is smaller than that of . However, we still need to choose a relatively large q for the indistinguishability in Lemma 2.
3.3. Two Party Computation via BFV Scheme
Since BFV encryption can implement arbitrary computable function in the encryption domain, we can construct the two-party computation (2PC) protocol based on the BFV encryption scheme. That is, a 2PC protocol can be constructed in the following steps (more details are depicted in Table 4):

Table 4.
The 2PC Computations via the BFV Scheme.
Step 1. Alice encrypts her input and sends the encrypted result to Bob.
Step 2. Bob directly computes the ciphertext(s) corresponding to the result in the encryption domain and performs the secure decryption protocol to send the message to Alice.
4. A High Throughput, Semi-Honest, Secure Comparison Protocol
4.1. Improving DGK Secure Comparison Protocol via the BFV Scheme
As mentioned in Section I, the BFV scheme performs well if the target function has shallow multiplication depth. Since the multiplication depth of the function in DGK protocol is 1, we can accelerate DGK protocol via BFV encryption. We briefly describe the DGK protocol in the following:
DGK Protocol (Setup, KeyGen, Enc (Round 1, Round2), Dec)
Setup. Suppose both a and b are -bit integers; say , further assume with . Our goal is to compute whether securely. We use the plaintext space where is a prime number. Choose large enough for evaluation andlarge enough for desired security level. Before the protocol starts, Alice generates the secret key and the public key , and sends the public key to Bob.
Enc. (Encryption)
Round 1. Alice computes , sends to Bob.
Round 2. Bob generates the samples and computes
in the encryption domain and permutes the ciphertexts randomly, so the corresponding message of is.
Let .
Dec. (Decryption)
Alice and Bob perform secure decryption, so Alice derives , and establishes “” if, and only if, for some .
Correctness of DGK.
Notice that if and only if , and for all .
Security of DGK. Since is uniformly sampled from , is uniform in whenever . Therefore, the vector if . In the case , there is exactly one i such that . Since the permutation is random, the distribution is uniform in
Each secure decryption protocol needs one encryption operation, so the Basic Secure Comparison Protocol (we named it Protocol 4.1 in this write-up) presented in Table 5 needs l + 1 encryptions for each l-bit comparison. We will present and analyze various proposed high-speed comparison protocols in the following section.

Table 5.
The Basic Secure Comparison Protocol (or Protocol 4.1).
4.2. High Throughput Comparison Protocol
To enhance the performance, we will use the batching technique presented in Section 2.6 to improve the utility of the plaintext space. Recall that
.
Given , the arithmetic operations of can be defined as (cf. see the following Elementwise Mul-Add Protocol for details):
That is, we can implement the vector-like operation in .
Further, the function evaluated in the encryption domain should be as simple as possible. So, the only function computed in the encryption domain would be
Any other operation should be evaluated in the plaintext domain by the one who holds the secret key.
4.2.1. The Single Pair Integer Comparison Protocol
Parameters. Choose a prime such that and for some integers k and d. Notice the plaintext space is isomorphic to , and Encoden/d and Decoden/d are the isomorphisms between them. The following protocol can compare a pair of -bit integers securely, and we named it Protocol 4.2 in this write-up for ease of discussion.
Protocol 4.2. (The Single Pair Integer Comparison Protocol)
Setup. Alice generates the secret key s and the public key pk with the parameters above. Bob generates the samples u ← {0, 1,..., n/d − 1}, r1, r2 ← and
. We can describe the protocol as three simple 2PC sub-protocols.
2PC-1st. Alice computes xa1 = Encoden/d ((ai)0≤i<n/d). Bob computes xb1 = Encoden/d ((bi)0≤i<n/d) and xr1 = Encoden/d ((r1)i)0≤i<n/d).
They securely compute xmask =xa1 + xb1 − 2·xa1 ·xb1 + xr1 for Alice. (Notice that ai = bi = 0 when i ≥ l).
2PC-2nd. Alice computes Decoden/d (xmask) and derives ((ai − bi)2 + (r1)i)0≤i<n/d. Let xa2 = Encoden/d (( + (r1)i)0≤i<n/d). Bob computes xb2 = Encoden/d (()0≤i<n/d), xr2 = Encoden/d ((r2)i)0≤i<n/d), and x′ = Encoden/d ((r′)i)0≤i<n/d). They securely compute dmask = (xa1 + xa2 − xb1 − xb2 + Encoden/d ((1)0≤i<n/d)) · x′ + xr2 for Alice (notice that (ai − bi)2 = ai bi).
2PC-3rd. Similarly, Alice decodes dmask and derives (ai −bi + 1 + )· (r′)i + (r2)i for each 0 ≤ i < n/d. Let xa3 = ) · Xi·d. They securely compute d′ = (xa3 − r2) · Xu·d for Alice.
Finally, Alice outputs 1 if the number of i such that (d′)i is exactly n/d; Alice outputs 0 in other cases.
Correctness of Protocol 4.2. Notice that Decoden/d (dmask − r2) = ((ai − bi + 1 + ) · (r′)i)0≤i<n/d which shares the same value with the di in Table 5, so the correctness holds for the same reason discussed in the last section.
Security of Protocol 4.2. We first notice that there are three 2PCs in our protocol; Alice derives xmask, dmask, and d′ from them, respectively. Since xmask and dmask are masked by r1 and r2, they behave like samples taken from a uniform distribution in the view of Alice. d′ can be simulated by examining whether (a ≥ b) ∈ {0, 1} {False, Truth} and s by the same arguments presented in Section 4.1, which proves the security of Bob. On the other hand, Bob’s view consists of ciphertexts, so Alice would be secure as long as the BFV scheme is secure. We depict the details of Protocol 4.2 in Table 6.

Table 6.
Secure Comparison Protocol for a Pair of Integers (also known as Protocol 4.2).
4.2.2. The Protocol for Comparing Pairs of Integers Simultaneously
The plaintext space has the best utilization when , while in most practical use cases; however, we rarely need to compare such a large integer. We now modify Protocol 4.2 to compare pairs of -bit integers simultaneously. For making a differentiation, we called this modified version Protocol 4.3 in this write-up.
Assume Alice’s inputs are and Bob’s inputs are where —our goal is to find the order relationships between and , denoted by . We can complete this task by following almost the same steps in Table 6.
Protocol 4.3. (The Protocol for Comparing Pairs of Integers Simultaneously)
Setup. The same as Protocol 4.2.
2PC-1st. Alice computes xa1 = Encoden ((aij)0≤i<k, 0≤j<n/k). Bob computes xb1 = Encoden((bij)0≤i<k,0≤j<n/k) and xr1 = Encoden(r1). They securely compute
xmask =xa1 +xb1 − 2·xa1 ·xb1 +xr1 for Alice.
2PC-2nd. Alice computes Decoden(xmask) to derive ((aij − bij)2 + (r1)ij)0≤i<k,0≤j<n/k.
Let xa2 = Encoden (( + (r1)it)0≤i<k,0≤j<n/k). Bob computes
xb2 = Encoden (()0≤i<k,0≤j<n/k), xr2 = Encoden(r2), and
x′ = Encoden(r′). They securely compute
dmask = (xa1 + xa2 − xb1 − xb2 + Encoden((1)0≤i<k,0≤j<n/k)) · x′ + xr2 for Alice.
(Notice that (ai − bi)2 = ai bi)
2PC-3rd. Similarly, Alice decodes dmask and derives (aij −bij + 1 + )· (r′)ij + (r2)ij, for each 0 ≤ i < n/d. Let xa3 = Encodek ((· Xj)0≤i<k).
Bob computes xb3 = Encodek ((· Xj)0≤i<k), xu = Encodek ((Xui)0≤i<k) They securely compute d′ = (xa3 − xb3) · xu for Alice.
Finally, Alice derives d′ij from the 2PC-3rd. Let δi = 0 if there is some j, such that d′ij = 0, and δi = 1 in other cases. Output (δi)0≤i<k.
Notice that the major difference between Protocols 4.2 and 4.3 is in the 2PC-3rd step. We need to rotate (dij)0≤j<n/k by ui for each 0 ≤ i < k simultaneously, so we compute the encoded version of (·Xj)0≤i<k, and rotate it by multiplying the encoded version of (Xui)0≤i<k. We summarize the detailed processing steps of Protocol 4.3 in Table 7.

Table 7.
The Information Flow and Processing Steps of Protocol 4.3.
5. Experiment Results
5.1. Encryption Schemes
Since the performance of an HE-based secure comparison protocol is strongly related to which homomorphic encryption scheme it used, we examine the performances of Paillier, standard-RSA, subgroup-RSA in [5], and subgroup-RSA in [7] in Table 8. Notice that Paillier is used in the earlier version of DGK protocol [2], subgroup-RSA is used in the DGK [4] and the CEK protocols. BFV scheme is used to build our comparison protocols. Notice that the decryption of subgroup-RSA needs to implement a discrete logarithm on the plaintext space, so the plaintext space needs to be very small (for a ciphertext c in subgroup-RSA, we may decrypt c by computing m = (logg cS) · S−1 for some secret key S and public key g, namely, cS = gmS. Since DGK protocol needs only to determine whether the message is zero, Alice does not need to perform discrete logarithms to derive the direct value of m).

Table 8.
Execution Time of Each One of the Benchmarked Encryption Schemes. (Runs ib i5-9400f@4.0gHz with security level 128, unit ms).
In [7], the authors claimed that if the plaintext space is bd for some small prime b, then they can implement discrete logarithms effectively. However, the speed of decryption is still much slower than that of the encryption without the aid of a sizeable pre-computed table. In the experiment of CEK protocol, we exclude the decryption time since the discrete logarithm is not necessary in their protocol.
We use the GMP library to implement the operations of big numbers. Although the codes run on Golang (Reference code: https://github.com/howard-kuo/cek_protocol/blob/master/rsaCek.go accessed on 18 February 2023), the performance would not be very different from the codes written on C directly. Our claim comes from the fact that the major computation cost lies in operations for evaluating big numbers. Furthermore, those operations are implemented by GMP, which is an efficient c-base library. Moreover, we use the Microsoft SEAL library in C++ to implement the BFV encryption scheme. Since the main computational bottleneck of our protocols is it to draw the samples from a discrete Gaussian distribution χ, we do some optimization on the sampler, as follows:
Since Prob {|χ| > 19} = 0 in the implementation of SEAL, we can store the commutative density function at each point (i.e., CDF(x) = Prob {χ > x} for −19 ≤ x ≤ 19). We may draw a sample from χ by the following function:
DiscreteGaussianSampler():
u ← {0, 1, ..., 232 −1}·2−32
x = arg max{y ∈ {−19, ..., 19} | CDF(y) > u}
Return x
We denote the optimized BFV implementation as “BFV-opt” in Table 8.
5.2. Performance Analyses
5.2.1. Computational Cost
The execution time of the DGK protocol, CEK protocol, and our protocols are shown in Table 9. Recall that DGK protocol uses RSA proposed in [5], CEK protocol uses RSA proposed in [7], and our protocols use an optimized BFV scheme. We use 3072-bit ciphertexts in DGK and CEK protocols (we use the same parameters and algorithms described in [6], and the parameters of our protocol depend on the size of compared integers and the secure decryption protocol we used. As discussed in Chapter 3, Alice may learn other information from the ciphertext generated by Bob. We suggest the reader uses two times the bit length for the security level they claimed (i.e., log2 n = 6144)). As discussed in Section 3.2, in the Secure Decryption portion, Protocol 3.1 needs to use a larger q to achieve indistinguishability; nevertheless, Protocol 3.2 needs to assume further that Bob cannot break the encryption system with some hint of the errors. As a result, Protocol 4.1 uses n = 1024, log2q = 27 and n = 2048, log2q = 55, respectively. Protocol 4.3 uses n = 1024, log2 q = 27 for 32-bit comparison; n = 2048, log2 q = 55 for 2048-bit comparison; n = 4096, log2 q = 109 for 4096-bit comparison, respectively.

Table 9.
The Execution Time of Each One of the Benchmarked Secure Comparison Protocols. (Runs ib i5-9400f@4.0gHz with security level 128, unit ms, notice is the time complexity of subgroup-RSA).
It might sound weird when the ciphertext size, which is n · log2 q, grows quadratic to n in the specific case in Table 9, but the execution time is not (cf. Figure 3). This is because the main computational cost is spent on sampling pseudo-random numbers, and the number of random numbers is linear to n.
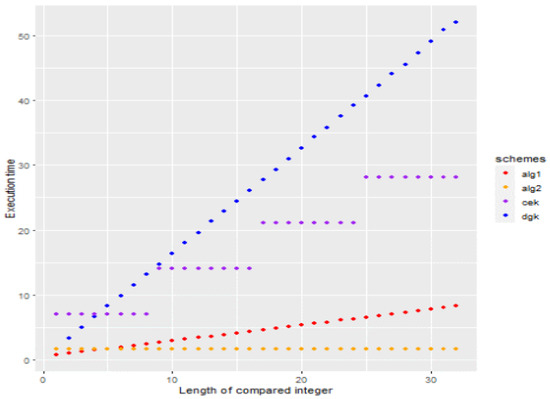
Figure 3.
The Tendencies in Execution Time of the Two Proposed Protocols (Alg-1 in the Figure is the Secure Comparison Protocol 4.1 with Secure Decryption Protocol 3.4, and Alg-2 is Secure Comparison Protocol 4.2 with Secure Decryption Protocol 3.4).
5.2.2. Communication Cost
Ciphertexts in the BFV scheme have size 2 · n · log2 q. In Protocol 4.1, we need to send l + 1 ciphertext in total, and in Protocol 4.2, we need to send 6 ciphertexts. The DGK protocol needs to send 2 · l ciphertexts, and CEK protocols need to send about 2 · l · 8−1 ciphertexts (2 · l · 8−1 RSA ciphertexts and 2 ECC ciphertexts).
We examine their required communication costs and report the results in Table 10 and Table 11, respectively. Since the ciphertext size of the BFV scheme is much larger than that of the RSA, RSA’s communication rate is more extensive than the CEK or DGK protocol when l is small. On the other hand, Protocol 4.2 needs only constant-size ciphertexts, and it would have a better communication rate than the others when l is large. For ease of comparison, we also show the tendency in required communication rates of the two proposed protocols in Figure 4.

Table 10.
Communication Rate of Each One of the Secure Comparison Protocols with Security Level 128 (for short l, i.e., 0 ≤ l < 32).

Table 11.
Communication Rates for Larger l (i.e., for l = 32, 2048, and 4096).
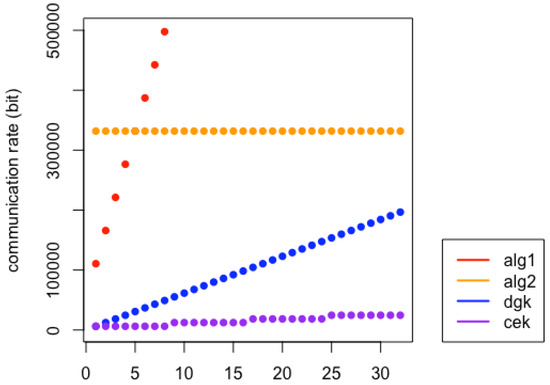
Figure 4.
The Tendencies in Communication Rates of the Two Proposed Protocols (Alg-1 in the Figure is the Secure Comparison Protocol 4.1 with Secure Decryption Protocol 3.4, and Alg-2 is the Secure Comparison Protocol 4.2 with Secure Decryption Protocol 3.4).
5.3. Remarks on Recently Published Related Works [22,23,24,25]
Badawi et al. [22] applied their vector operation-based multi-GPU Levelled-FHE to implement the inference circuit of two CNNs to perform homomorphically image classification on encrypted images from the MNIST and CIFAR 10 datasets. Their implementation gained 1 to 3 orders of magnitude speed-up compared with the CPU implementation on ordinary vector/polynomial operations. Further, Ref. [22] presented data parallelism approaches and applied workload partitioning methods to implement a variant of the BFV scheme on the NVIDIA K80 and P100 GPU clusters. Likewise, Ref. [23] worked toward speeding up the NTT, INTT, and NTT-based polynomial multiplication operations on various GPU platforms and reported that the encryption and the decryption operations of the BFV scheme on Microsoft’s SEAL library could be more than 100 times faster than on its Intel i9-7900X CPU counterpart. More positively, a single NTT operation for polynomials of degree 32768 with 61-bit coefficients can reach the ten-microsecond range on Nvidia GTX and Tesla series GPUs. These encouraging results give us confidence that with the aid of GPU’s computing power, the applicability of our protocol will be primarily enhanced (notice that our computing platform is Intel i5 CPU families only).
In our experiment, the execution time of a single BFV encryption of degree 32,768 is longer than that of our secure comparison protocol (with degree 1024, security level 128). Reducing the complexity of the target function and the ciphertext size is the core idea of our protocol. In more detail, if n = 8192, q has 109 bits, experimentally, a single encryption time cost of SEAL exceeds 10ms in our experimental settings. Under this circumstance, it would be hard to construct a comparison protocol that needs less than 12 ms execution time. On the other hand, 12 ms is the whole time needed for our 4096-bit protocol. This result comes from the fact that, for the same given degree n, a matrix-based LWE encryption would be slower than its polynomial counterpart because the respective time complexities are n2 and n log n.
Specific to the encryption domain comparison, Ref. [24] designed an integer-and-FHE-based private database query (PDQ) protocol supporting compound conditions with equality and order comparisons, which scales efficiently for the length of input integers by applying techniques from the finite field theory. According to [24], the comparison algorithm needs about 25.259 s to compare 697 pairs of 64-bit integers using the BGV-level FHE scheme with SIMD techniques at more than 138 bits of security. This yields an amortized rate of just 36 ms per comparison. In contrast, Ref. [25] showed that FHE schemes suitable for arithmetic circuits (e.g., BGV or BFV) have a similar performance as FHE schemes for non-arithmetic circuits (such as the TFHE) in basic comparison tasks such as less-than, maximum, and minimum operations. Ref. [25] reported that the execution of the less-than function in the HElib library is up to 3 times faster than the prior work [24] based on BGV/BFV schemes. In [21], comparing a pair of 64-bit integers, sorting 64 32-bit integers, and finding the minimum of 64 32-bit integers can be completed in 11 milliseconds, in 19 s, and in 9.5 s, respectively, on an average laptop without multi-threading. In contrast, our comparison protocol can compare 64 pairs of 64-bit integers in 12.06 ms, which yields an amortized cost of 0.188ms. An intuitive reason for better performance is that the degree of our ciphertext is much smaller (n = 4096). On the other hand, we can only implement an elementary target function in the encryption domain since the ciphertext is tiny, forcing our protocol into a higher round of complexity (say, six rounds).
5.4. Summary
The computational cost of the proposed algorithms can be lower than that of the other protocols in most cases, while the communicational cost is much higher. With the rapid growth of internet speed, our protocol can be more practical than the others. Suppose the users attempt to compare many pairs of integers securely. In that case, the method introduced in Section 3.1 provides a solution to compare them securely with almost the same execution time examined in Section 5.2, which has lower communication costs and a faster execution speed than DGK and CEK protocols. Concrete execution times and speed-up ratios of various FHE operators have been reported above; however, those values depend on specific parameters, target functions, hardware configurations, and software implementation techniques adopted at the experiments.
Moreover, working with FHE also introduces significant engineering challenges in practice. Different schemes offer varying performance tradeoffs, and optimal choices are heavily application-dependent. In other words, judging the competing approaches’ superiority is only possible and fair with a standard testing environment and a common target task.
6. Conclusions
Homomorphic encryption enables end-to-end data security by performing computations directly on ciphertexts without needing in-advance decryption. However, due to the unavoidable ciphertext expansion and complicated error-controlling mechanisms, richness in computational and storage resources play dominating roles in the success of applying a homomorphic cryptosystem in real-world applications.
Comparison is a standard function required in many applications concerning orders of involved items; consequently, its homomorphic evaluation has been the object of many FHE-related works. Since inputs are encrypted, an HE-based comparison algorithm cannot terminate, like its plaintext domain counterpart, whenever it finds the first difference between the most significant bits. Comparison is a standard function required in many applications concerning orders of involved items; consequently, its homomorphic evaluation has been the object of many FHE-related works. Since inputs are encrypted, an HE-based comparison algorithm cannot terminate, like its plaintext domain counterpart, whenever it finds the first difference between the most significant bits. As a result, HE-based comparisons correspond to the worst-case complexity in the plain domain.
This work presents a fast, semi-honest, secure comparison protocol based on the BFV encryption scheme. With its vector-like plaintext space and the aid of batching technique, the number of required encryptions can be significantly reduced; each comparison needs only six encryptions in our protocol. In other words, the proposed protocol can achieve the time complexity for a given security parameter λ. As a result, 4096-bit integers can be securely compared within 12.08 ms, which is much faster than the state-of-the-art homomorphic encryption-based secure comparison protocol. Furthermore, we can compare k pairs of bit integers with almost the same execution time as comparing bit integers and achieve higher throughput regardless of the compared integer size.
As for our future work, shortly, we will conduct and examine the following research topics to better the overall BFV scheme’s performance:
(i). For every 2PC protocol with some task f, we may decompose f into simple subtasks, as we have addressed in Section IV, implying that those protocols can be sped up further via BFV encryption.
(ii). The computational bottleneck of our protocols comes mainly from the execution of random number sampling because the cryptographic hash function is much slower than generating RLWE samples in the implementation of SEAL. We can generate pseudo-random numbers by generating RLWE samples, accelerating the proposed protocol furthermore.
Notably, in machine learning, FHE has been used for tasks ranging from linear and logistic regression to Encrypted Neural Network inference. For example, FHE may be critical in running privacy-preserving ML-as-a-Service (MLasS) applications. Consequently, there has been increasing interest in FHE-based secure computation solutions. This tendency explains why Gartner [29] projected that “by 2025, at least 20% of companies will have a budget for projects that include FHE.” Therefore, how to embed our fast, secure comparison protocol to enhance appropriate MLasS applications will undoubtedly be one of our future research topics.
Author Contributions
Formal analysis, T.-H.K.; Funding acquisition, J.-L.W.; Investigation, T.-H.K. and J.-L.W.; Methodology, T.-H.K.; Project administration, J.-L.W.; Resources, J.-L.W.; Software, T.-H.K.; Supervision, J.-L.W.; Writing—original draft, T.-H.K.; Writing—review & editing, T.-H.K. and J.-L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Minister of Science and Technology, Taiwan MOST 109-2218-E-002-015 and MOST 111-2221-E-002-134-MY3.
Data Availability Statement
https://github.com/howard-kuo/bfv_dgk (accessed on 18 February 2023).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Algebraic Structures and Notations of the BFV Scheme
Appendix A.1. Quotient Ring
Basic objects in the BFV scheme are elements in the polynomial ring , where is the -th cyclotomic polynomial, and denotes for and “/” as the ring quotient operator. We always treat an element in or as an integer polynomial with a degree less than . For example, given or we can assume
and we will say the “-th coefficient” of .
The definitions in Table A1 can be extended to elements in m or m, t by operating on each coefficient of them. For example, if a ∈ m, then

Table A1.
Notations and Definitions of Mappings between Different Algebraic Structures.
Table A1.
Notations and Definitions of Mappings between Different Algebraic Structures.
| defined by sending an integer to its residual class, say | ||
| defined by sending to the unique element in . | ||
| defined by sending to | ||
| defined by sending to | ||
| is the infinity norm |
Appendix A.2. Distribution and Sampling
For a distribution , we will use to denote that “ is sampled from a distribution ”. For a finite set , we will use to denote that “ is sampled uniformly from a finite set ”. Notice that the symbol ← is also used as an assignment operator, which can be regarded as sampled from some degenerate distributions.
Appendix B. Detailed Proofs Associated with Section 2
Appendix B.1. Proof of Lemma 1 (Sufficient Condition for Correct Decryption)
Given ciphertext , message , and as the corresponding error, then implies
Proof.
By the definition of error, we may write
for some . Multiply both side with , we obtain
Since , elements of are less than , so
and the result follows:
□
Appendix B.2. Proofs of Claims 1 to 3
- a.
- Poof of Claim 1 (Correctness of Additions)
By the definition of error, we assume and , so
Thus, the error of is mod q, and implies.
Dec (Add (c, c′), s) = m + m′ by Lemma 1
- b.
- Proof of Claim 2 (Correctness of Addition between a Plaintext and a Ciphertext).
Since , the error of new ciphertext would be , which can be correctly decrypted since original ciphertext c can.
- c.
- Proof of Claim 3 (Correctness of Multiplication of between a Plaintext and a Ciphertext)
Since , multiply both side with and derive
The error of new ciphertext is, so can ensure the correctness.
Appendix C. Detailed Proofs Associated with Section 3
Appendix C.1. Proof of Lemma 2 (Distinguishability of a uniform sample with little bias)
Suppose . Any algorithm can be defined by with
We can compute
and
Prob {A(X) = 1} = Prob {X ∊ S} = (2T)−1·|S ⋂ {−T,...,T}|,
Prob {A (X + e) = 1} = (2T) − 1 · |S ⋂ {−T + e,..., T + e}|.
Since |S ∩ {−T,..., T}| − |S ∩ {−T +e,..., T +e}| ≤ |e|, we have
|Prob{A(X) = 1} − Prob{A(X + e) = 1}| ≤ (2T) − 1 ·|e|.
Therefore, the advantage of the adversary is no more than (2T)−1 · |e|.
Appendix C.2. Proof of Claim 4 (The Security of Bob in Protocol 3.1)
We define our simulator by:
(i) Sample from proper distributions: r ← and u ← {−T,...,T}n.
(ii) Output: (r · s + u + πq ([Dec (cresult, s)]p · ρ, −r).
Notice the ciphertext c′ in Protocol 3.1 can be computed by c′1, e′, and Dec (c′, s), so it is sufficient to say that (c′1, e′, Dec (c′, s)) is indistinguishable to (r, u, Dec (cresult, s)). By Corollary 1 and the correctness of Protocol 3.1, (c′b,1, e′b, Dec (c′b, s)) is indistinguishable to (c′b,1, u, Dec (cb, s)) with an adversary less than ε. By the RLWE assumption, r is indistinguishable from c′b,1, and we complete our proof.
References
- Veugen, T.; Blom, F.; de Hoogh, S.J.A.; Erkin, Z. Secure comparison protocols in the semi-honest model. IEEE J. Sel. Top. Signal Process. 2015, 9, 1217–1228. [Google Scholar] [CrossRef]
- Damga, I.; Geisler, M.; Krøigaard, M. Homomorphic encryption and secure comparison. IJACT 2008, 1, 22–31. [Google Scholar] [CrossRef]
- Paillier, P. Public-key cryptosystems based on composite degree residuosity classes. In Advances in Cryptology—EUROCRYPT ’99, Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Prague, Czech Republic, 2–6 May 1999; Springer: Berlin/Heidelberg, Germany, 1999; pp. 223–238. [Google Scholar]
- Damga, I.; Geisler, M.; Krøigaard, M. A correction to ’efficient and secure comparison for on-line auctions. IJACT 2009, 1, 323–324. [Google Scholar] [CrossRef]
- Groth, J. Cryptography in subgroups of Z∗n. In Theory of Cryptography, Proceedings of the Second Theory of Cryptography Conference, TCC 2005, Cambridge, MA, USA, 10–12 February 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 50–65. [Google Scholar]
- Carlton, R.A. Secure Integer Comparisons using the Homomorphic Properties of Prime Power Subgroups. Ph.D. Dissertation, The University of Western Ontario, London, ON, Canada, 2017. [Google Scholar]
- Carlton, R.; Essex, A.; Kapulkin, K. Threshold properties of prime power subgroups with application to secure integer comparisons. In Topics in Cryptology—CT-RSA 2018, Proceedings of the Cryptographers’ Track at the RSA Conference, San Francisco, CA, USA, 16–20 April 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 137–156. [Google Scholar]
- Damga, I.; Geisler, M.; Krøigaard, M. Efficient and secure comparison for on-line auctions. In Information Security and Privacy, Proceedings of the 12th Australasian Conference, ACISP 2007, Townsville, Australia, 2–4 July 2007, Lecture Notes in Computer Science; Pieprzyk, J., Ghodosi, H., Dawson, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4586, pp. 416–430. [Google Scholar] [CrossRef]
- Veugen, T. Improving the DGK comparison protocol. In Proceedings of the 2012 IEEE International Workshop on Information Forensics and Security (WIFS), Costa Adeje, Spain, 2–5 December 2012; pp. 49–54. [Google Scholar]
- Veugen, T. Correction to” improving the DGK comparison protocol. IACR Cryptol. Eprint Arch. 2018, 2018, 1100. [Google Scholar]
- Gentry, C.; Boneh, D. A Fully Homomorphic Encryption Scheme; Stanford University: Stanford, CA, USA, 2009; Volume 20. [Google Scholar]
- Gentry, C. Fully homomorphic encryption using ideal lattices. In Proceedings of the Forty-First Annual ACM Symposium on Theory of Computing, Bethesda, MD, USA, 31 May 2009–2 June 2009; pp. 169–178. [Google Scholar]
- Van Dijk, M.; Gentry, C.; Halevi, S.; Vaikuntanathan, V. Fully homomorphic encryption over the integers. In Advances in Cryptology—EUROCRYPT 2010, Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, French Riviera, France, 30 May–3 June 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 24–43. [Google Scholar]
- Brakerski, Z.; Vaikuntanathan, V. Efficient fully homomorphic encryption from (standard) LWE. In Proceedings of the 2011 IEEE 52nd Annual Symposium on Foundations of Computer Science, Palm Springs, CA, USA, 22–25 October 2011; FOCS ’11. IEEE Computer Society: Washington, DC, USA, 2011; pp. 97–106. [Google Scholar] [CrossRef]
- Brakerski, Z.; Gentry, C.; Vaikuntanathan, V. (leveled) fully homomorphic encryption without bootstrapping. In Proceedings of the 3rd Innovations in Theoretical Computer Science Conference, ITCS ’12, Cambridge, MA, USA, 8–10 January 2012; Association for Computing Machinery: New York, NY, USA, 2012; pp. 309–325. [Google Scholar] [CrossRef]
- Brakerski, Z. Fully homomorphic encryption without modulus switching from classical GAPSVP. In Advances in Cryptology—CRYPTO 2011, Proceedings of the Annual Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2011; Springer: Berlin/Heidelberg, Germany, 2012; pp. 868–886. [Google Scholar]
- Fan, J.; Vercauteren, F. Somewhat practical fully homomorphic encryption. IACR Cryptol. Eprint Arch. 2012, 2012, 144. [Google Scholar]
- Gentry, C.; Sahai, A.; Waters, B. Homomorphic encryption from learning with errors: Conceptually-simpler, asymptotically-faster, attribute-based. In Advances in Cryptology—CRYPTO 2013, Proceedings of the Annual Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 75–92. [Google Scholar]
- Cheon, J.H.; Kim, A.; Kim, M.; Song, Y. Homomorphic encryption for arithmetic of approximate numbers. In Advances in Cryptology—ASIACRYPT 2017, Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Hong Kong, China, 3–7 December 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 409–437. [Google Scholar]
- Brakerski, Z.; Vaikuntanathan, V. Fully homomorphic encryption from ring-LWE and security for key dependent messages. In Advances in Cryptology—CRYPTO 2011, Proceedings of the Annual Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 505–524. [Google Scholar]
- Albrecht, M.; Chase, M.; Chen, H.; Ding, J.; Goldwasser, S.; Gorbunov, S.; Halevi, S.; Hoffstein, J.; Laine, K.; Lauter, K.; et al. Homomorphic Encryption Security Standard. HomomorphicEncryption.org: Toronto, ON, Canada. 2018. Available online: http://homomorphicencryption.org/wp-content/uploads/2018/11/HomomorphicEncryptionStandardv1.1.pdf (accessed on 15 February 2023).
- Al Badawi, A.; Veeravalli, B.; Lin, J.; Xiao, N.; Kazuaki, M.; Mi, A.K.M. Multi-gpu design and performance evaluation of homomorphic encryption on gpu clusters. IEEE Trans. Parallel. Distrib. Syst. 2021, 32, 379–391. [Google Scholar] [CrossRef]
- Özerk, Ö.; Elgezen, C.; Mert, A.C.; Öztürk, E.; Savaş, E. Efficient number theoretic transform implementation on GPU for homomorphic encryption. J. Supercomput. 2022, 78, 2840–2872. [Google Scholar] [CrossRef]
- Tan, B.H.M.; Lee, H.T.; Wang, H.; Ren, S.Q.; Khin, A.M.M. Efficient private comparison queries over encrypted databases using fully homomorphic encryption with finite fields. In IEEE Transactions on Dependable and Secure Computing; IEEE: Piscataway, NJ, USA, 2020; pp. 2861–2874. [Google Scholar]
- Iliashenko, I.; Zucca, V. Faster homomorphic comparison operations for BGV and BFV. Proc. Priv. Enhancing Technol. 2021, 2021, 246–264. [Google Scholar] [CrossRef]
- Driver, M. Emerging technologies: Homomorphic encryption for data sharing with privacy. Gartner Inc. Tech. Rep. Published: 23 April 2020. Available online: https://www.gartner.com/en/documents/3983970 (accessed on 12 February 2023).
- Huo, M.; Wu, K.; Ye, Q. A note on lower digits extraction polynomial for bootstrapping. arXiv 2019, arXiv:1906.02867. [Google Scholar]
- Lyubashevsky, V.; Peikert, C.; Regev, O. On ideal lattices and learning with errors over rings. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, French Riviera, France, 30 May–3 June 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1–23. [Google Scholar]
- Microsoft SEAL (Release 3.4). Oct. 2019, Microsoft Research, Redmond, WA. Available online: https://github.com/Microsoft/SEAL (accessed on 11 January 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).