Retrieval of Optical Solitons with Anti-Cubic Nonlinearity
Abstract
1. Introduction
2. The NLODE Form of NLSE-AC and the Method
3. Implementation of Method to NLSE-AC Equation
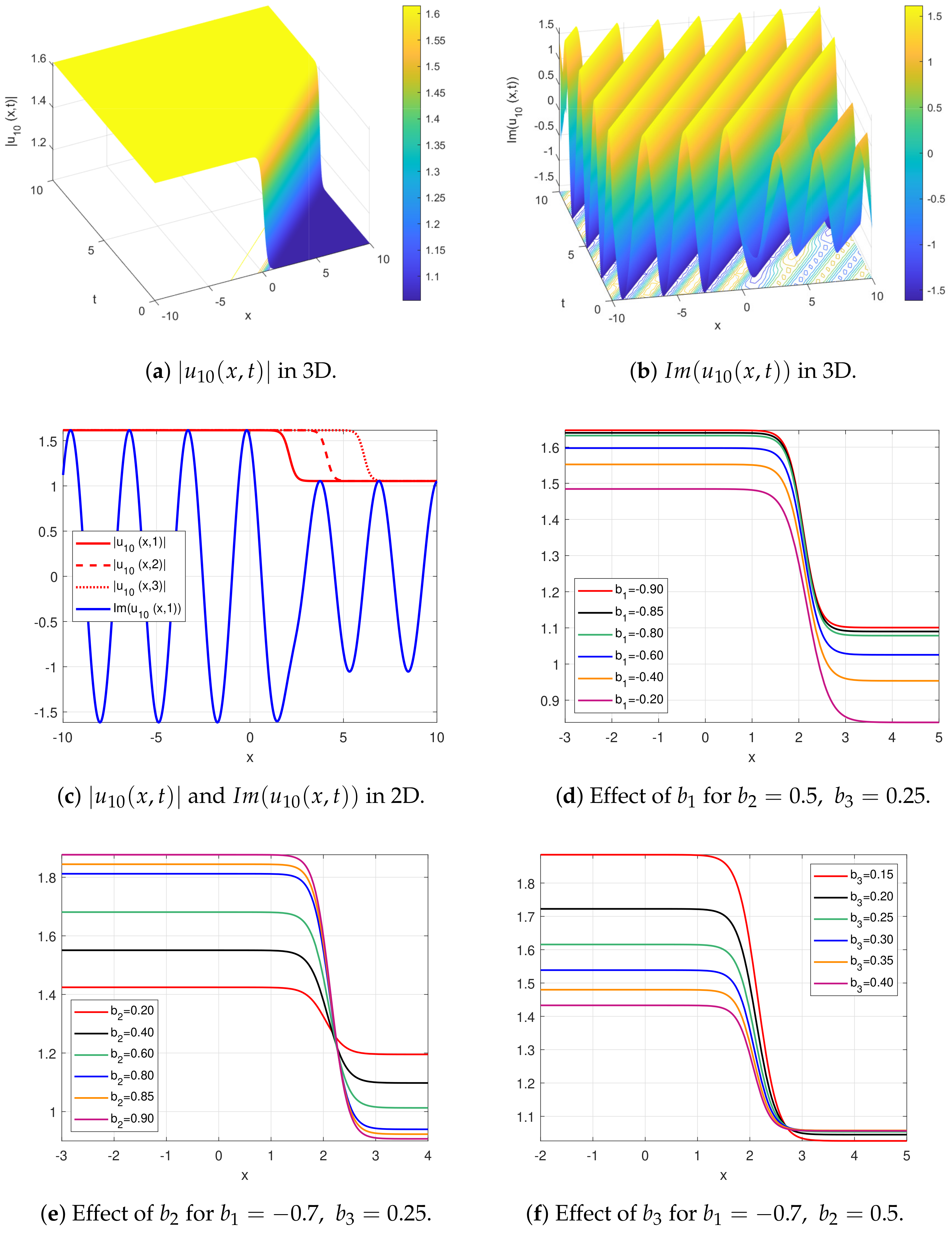
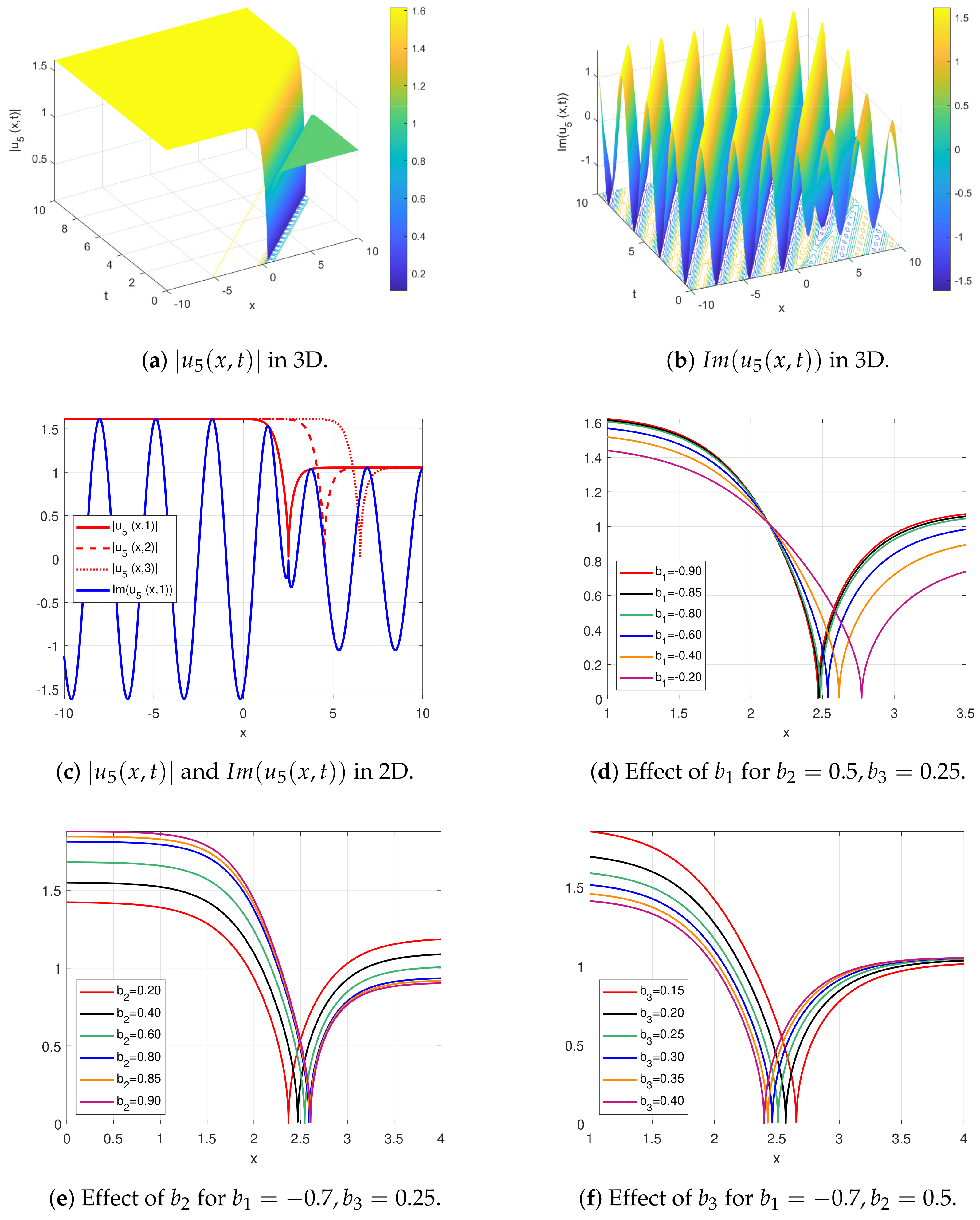
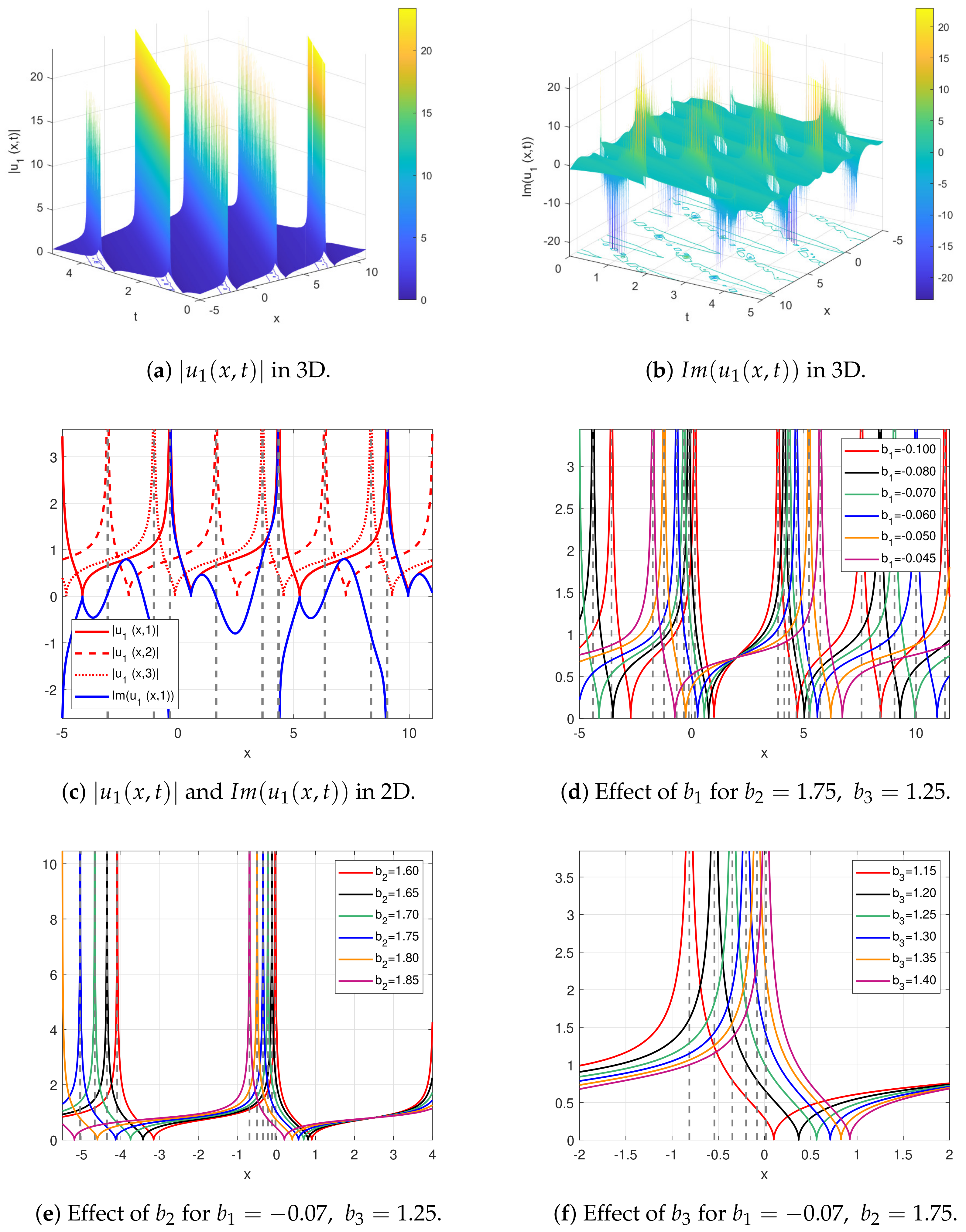
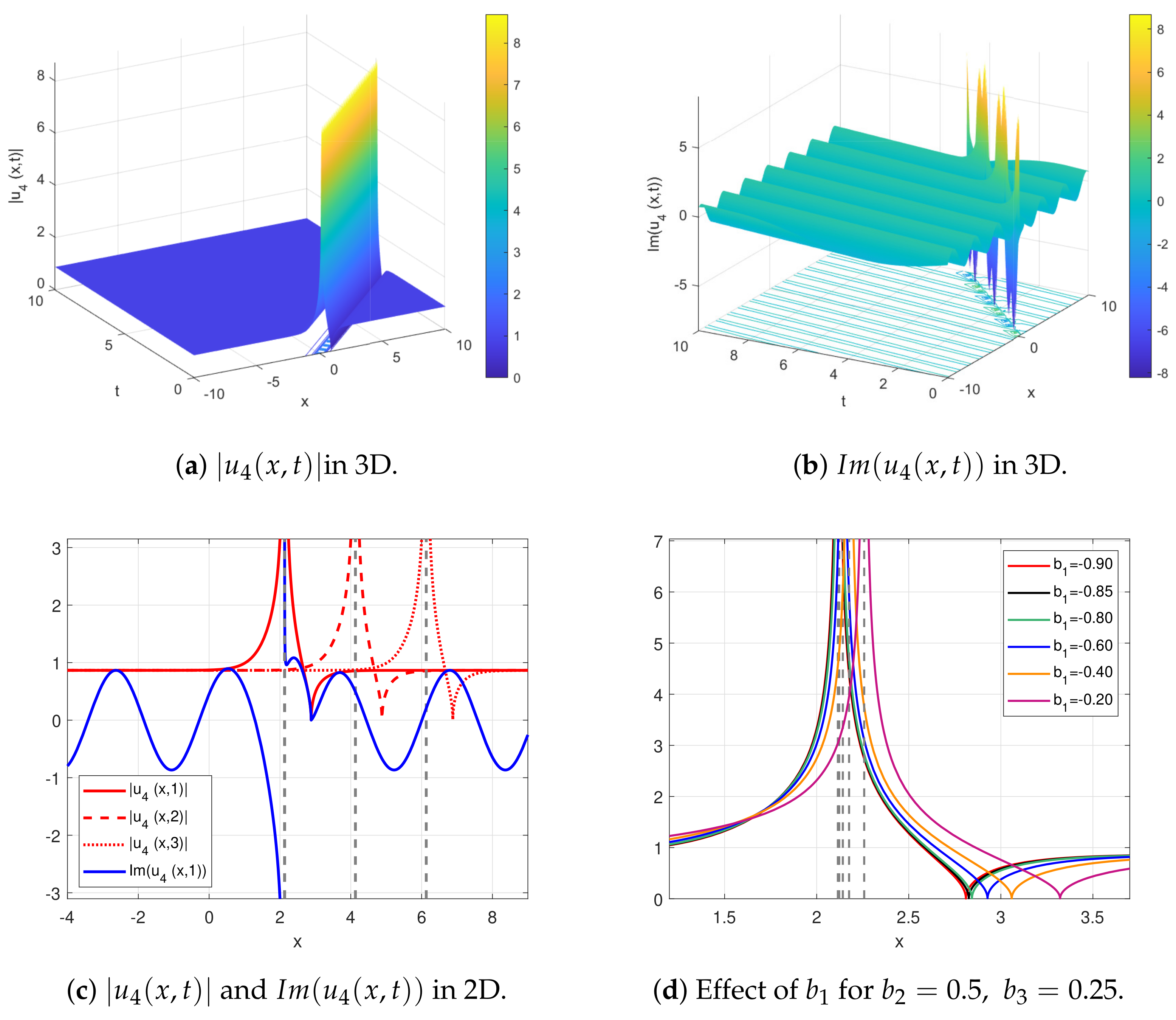
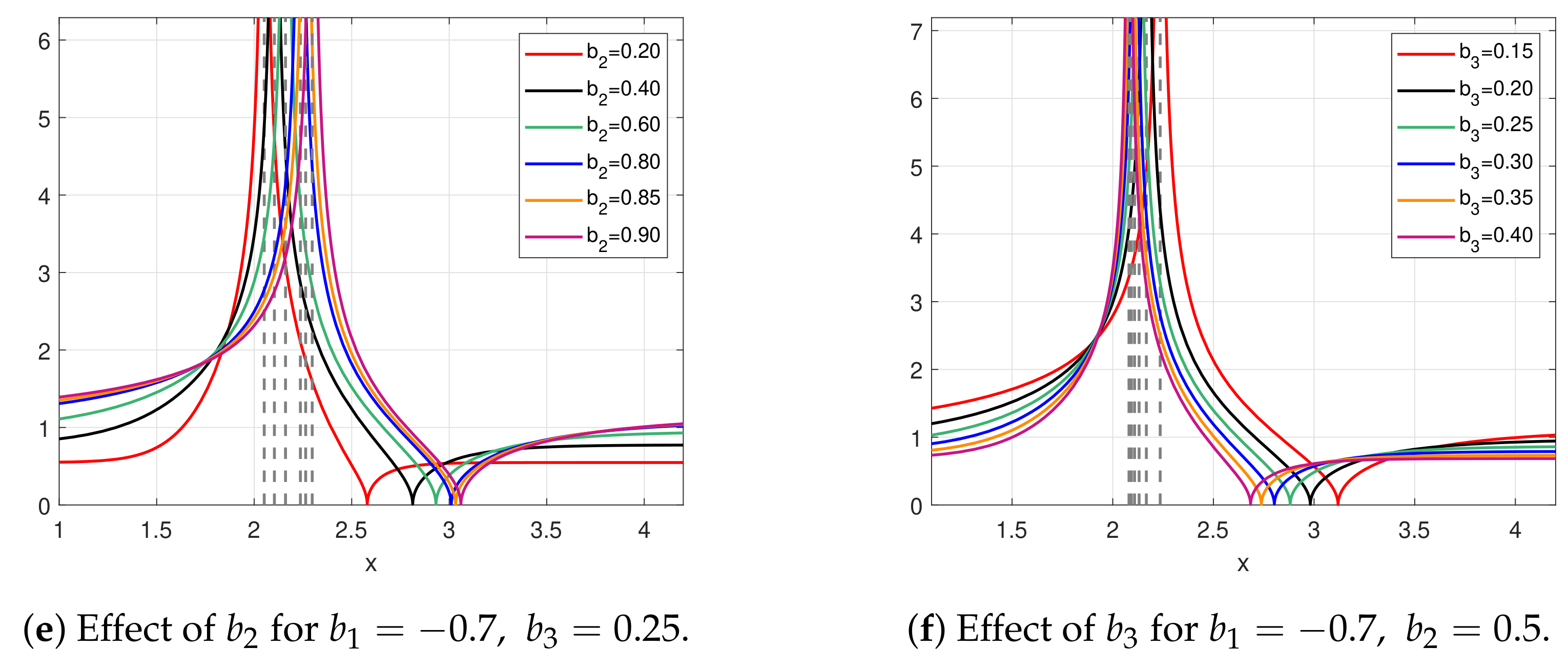
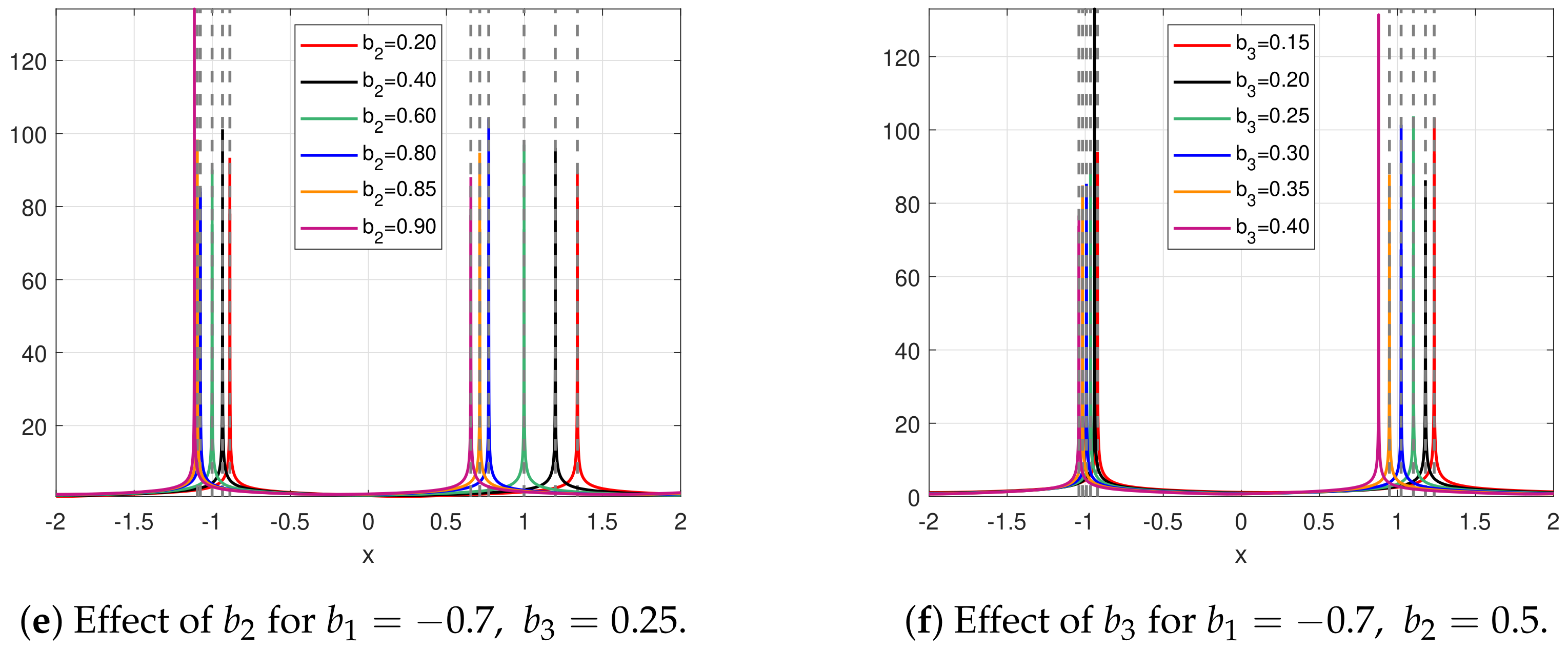
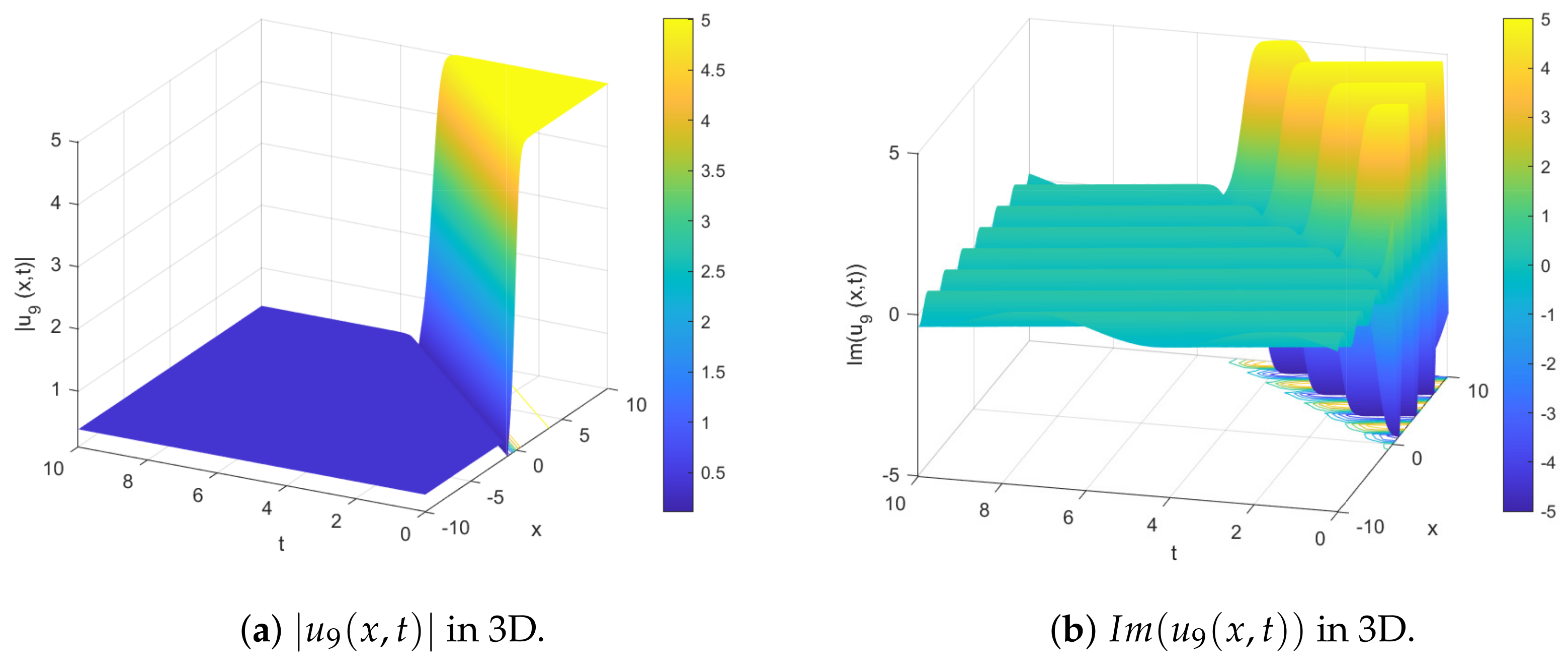
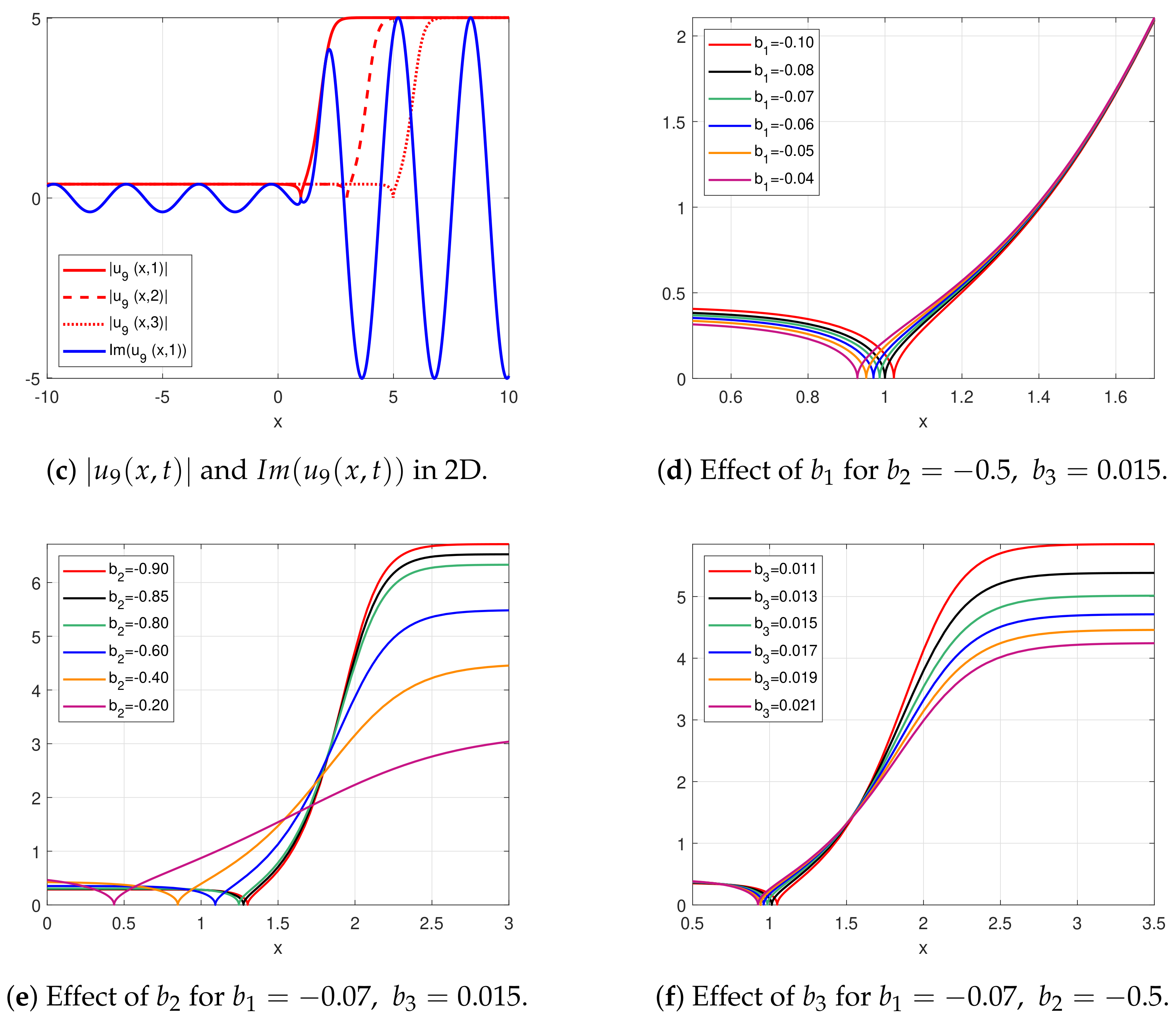
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arshad, M.; Seadawy, A.R.; Lu, D. Study of soliton solutions of higher-order nonlinear Schrödinger dynamical model with derivative non-Kerr nonlinear terms and modulation instability analysis. Results Phys. 2019, 13, 102305. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Stationary solitons of the model with nonlinear chromatic dispersion and arbitrary refractive index. Optik 2022, 259, 168888. [Google Scholar] [CrossRef]
- Eldidamony, H.A.; Ahmed, H.M.; Zaghrout, A.S.; Ali, Y.S.; Arnous, A.H. Highly dispersive optical solitons and other solutions in birefringent fibers by using improved modified extended tanh-function method. Optik 2022, 256, 168722. [Google Scholar] [CrossRef]
- Biswas, A.; Ekici, M.; Sonmezoglu, A.; Belic, M.R. Highly dispersive optical solitons with Kerr law nonlinearity by F-expansion. Optik 2019, 181, 1028–1038. [Google Scholar] [CrossRef]
- Mirzazadeh, M.; Akinyemi, L.; Şenol, M.; Hosseini, K. A variety of solitons to the sixth-order dispersive (3+1)-dimensional nonlinear time-fractional Schrödinger equation with cubic-quintic-septic nonlinearities. Optik 2021, 241, 166318. [Google Scholar] [CrossRef]
- Ozisik, M.; Cinar, M.; Secer, A.; Bayram, M. Optical solitons with Kudryashov’s sextic power-law nonlinearity. Optik 2022, 261, 169202. [Google Scholar] [CrossRef]
- Kohl, R.W.; Biswas, A.; Ekici, M.; Zhou, Q.; Khan, S.; Alshomrani, A.S.; Belic, M.R. Highly dispersive optical soliton perturbation with cubic–quintic–septic refractive index by semi-inverse variational principle. Optik 2019, 199, 163322. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Alngar, M.E.M.; Biswas, A.; Kara, A.H.; Ekici, M.; Alzahrani, A.K.; Belic, M.R. Cubic-quartic optical solitons and conservation laws with Kudryashov’s sextic power-law of refractive index. Optik 2021, 227, 166059. [Google Scholar] [CrossRef]
- Biswas, A.; Ekici, M.; Sonmezoglu, A. Stationary optical solitons with Kudryashov’s quintuple power–law of refractive index having nonlinear chromatic dispersion. Phys. Lett. A 2022, 426, 127885. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Highly dispersive optical solitons of the equation with various polynomial nonlinearity law. Chaos Solitons Fractals 2020, 140, 110202. [Google Scholar] [CrossRef]
- Triki, H.; Wazwaz, A.M. Soliton solutions of the cubic-quintic nonlinear Schrödinger equation with variable coefficients. Rom. J. Phys. 2016, 61, 360–366. [Google Scholar]
- Al-Kalbani, K.K.; Al-Ghafri, K.S.; Krishnan, E.V.; Biswas, A. Pure-cubic optical solitons by Jacobi’s elliptic function approach. Optik 2021, 243, 167404. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Ullah, N.; Akinyemi, L.; Shah, A.; Mirhosseini-Alizamin, S.M.; Chu, Y.-M.; Ahmad, H. Optical soliton solutions of the generalized non-autonomous nonlinear Schrödinger equations by the new Kudryashov’s method. Results Phys. 2021, 24, 104179. [Google Scholar] [CrossRef]
- Mirzazadeh, M.; Eslami, M.; Milovic, D.; Biswas, A. Topological solitons of resonant nonlinear Schrödinger equation with dual-power law nonlinearity by G′/G-expansion technique. Optik 2014, 125, 5480–5489. [Google Scholar] [CrossRef]
- Biswas, A.; Zhou, Q.; Moshokoa, S.P.; Triki, H.; Belic, M.; Alqahtani, R.T. Resonant 1-soliton solution in anti-cubic nonlinear medium with perturbations. Optik 2017, 145, 14–17. [Google Scholar] [CrossRef]
- Asma, M.; Othman, W.A.M.; Wong, B.R.; Biswas, A. Optical soliton perturbation with quadratic-cubic nonlinearity by a semi-inverse variational principle. Proc. Rom. Acad. Ser. A Math. Phys. Tech. Sci. Inf. Sci. 2017, 18, 331–336. [Google Scholar]
- Fedele, R.; Schamel, H.; Karpman, V.I.; Shukla, P.K. Envelope solitons of nonlinear Schrödinger equation with an anti-cubic nonlinearity. J. Phys. A Math. Gen. 2003, 36, 1169. [Google Scholar] [CrossRef]
- Biswas, A.; Ekici, M.; Sonmezoglu, A.; Belic, M. Chirped and chirp-free optical solitons with generalized anti-cubic nonlinearity by extended trial function scheme. Optik 2019, 178, 636–644. [Google Scholar] [CrossRef]
- Krishnan, E.V.; Biswas, A.; Zhou, Q.; Babatin, M.M. Optical solitons with anti-cubic nonlinearity by mapping methods. Optik 2018, 170, 520–526. [Google Scholar] [CrossRef]
- Jawad, A.J.M.; Mirzazadeh, M.; Zhou, Q.; Biswas, A. Optical solitons with anti-cubic nonlinearity using three integration schemes. Superlattices Microstruct. 2017, 105, 1–10. [Google Scholar] [CrossRef]
- Wafaa, R.B.; Ahmed, H.M.; Seadawy, A.R.; Althobaiti, A. The higher-order nonlinear Schrödinger’s dynamical equation with fourth-order dispersion and cubic-quintic nonlinearity via dispersive analytical soliton wave solutions. Opt. Quantum Electron. 2021, 53, 668. [Google Scholar]
- Triki, H.; Kara, A.H.; Biswas, A.; Moshokoa, S.P.; Belic, M. Optical solitons and conservation laws with anti-cubic nonlinearity. Optik 2016, 127, 12056–12062. [Google Scholar] [CrossRef]
- Muniyappan, A.; Hemamalini, D.; Akila, E.; Elakkiya, V.; Anitha, S.; Devadharshini, S.; Biswas, A.; Yıldırım, Y.; Alshehri, H.M. Bright solitons with anti-cubic and generalized anti-cubic nonlinearities in an optical fiber. Optik 2022, 254, 168612. [Google Scholar] [CrossRef]
- Ekici, M.; Mirzazadeh, M.; Sonmezoglu, A.; Ullah, M.Z.; Zhou, Q.; Triki, H.; Moshokoa, S.P.; Biswas, A. Optical solitons with anti-cubic nonlinearity by extended trial equation method. Optik 2017, 136, 368–373. [Google Scholar] [CrossRef]
- Biswas, A. Conservation laws for optical solitons with anti-cubic and generalized anti-cubic nonlinearities. Optik 2019, 176, 198–201. [Google Scholar] [CrossRef]
- Foroutan, M.; Manafian, J.; Ranjbaran, A. Solitons in optical metamaterials with anti-cubic law of nonlinearity by generalized G′/G-expansion method. Optik 2018, 162, 86–94. [Google Scholar] [CrossRef]
- Foroutan, M.; Manafian, J.; Ranjbaran, A. Solitons in optical metamaterials with anti-cubic law of nonlinearity by ETEM and IGEM. J. Eur. Opt.-Soc.-Rapid Publ. 2018, 14, 16. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Exact solutions of equation for description of embedded solitons. Optik 2022, 268, 169801. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Solitary waves of model with triple arbitrary power and non-local nonlinearity. Optik 2022, 262, 169334. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Optical solitons of the model with generalized anti-cubic nonlinearity. Optik 2022, 257, 168746. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Bright and dark solitons in a nonlinear saturable medium. Phys. Lett. A 2022, 427, 127913. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Lavrova, S.F. Dynamical properties of the generalized model for description of propagation pulses in optical fiber with arbitrary refractive index. Optik 2021, 245, 167679. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Safonova, D.V. Painleve analysis and traveling wave solutions of the sixth order differential equation with non-local nonlinearity. Optik 2021, 244, 167586. [Google Scholar] [CrossRef]
- Kudryashov, N.A. The Lakshmanan-Porsezian-Daniel model with arbitrary refractive index and its solution. Optik 2021, 241, 167043. [Google Scholar] [CrossRef]
- Yildirim, Y. Optical solitons to Kundu-Mukherjee-Naskar model with trial equation approach. Optik 2019, 183, 1061–1065. [Google Scholar] [CrossRef]
- Yildirim, Y. Optical solitons to Biswas-Arshed model in birefringent fibers using modified simple equation architecture. Optik 2019, 182, 1149–1162. [Google Scholar] [CrossRef]
- Yildirim, Y. Optical solitons to Chen-Lee-Liu model in birefringent fibers with trial equation approach. Optik 2019, 183, 881–886. [Google Scholar] [CrossRef]
- Yildirim, Y. Sub pico-second pulses in mono-mode optical fibers with Triki- Biswas model using trial equation architecture. Optik 2019, 183, 463–466. [Google Scholar] [CrossRef]
- Yildirim, Y. Optical solitons to Sasa-Satsuma model in birefringent fibers with modified simple equation approach. Optik 2019, 184, 197–204. [Google Scholar] [CrossRef]
- Yildirim, Y. Optical solitons to Sasa-Satsuma model with trial equation approach. Optik 2019, 184, 70–74. [Google Scholar] [CrossRef]
- Yildirim, Y. Optical solitons to Kundu-Mukherjee-Naskar model in birefringent fibers with trial equation approach. Optik 2019, 183, 1026–1031. [Google Scholar] [CrossRef]
- Yildirim, Y. Optical solitons to Schrödinger-Hirota equation in DWDM system with trial equation integration architecture. Optik 2019, 182, 275–281. [Google Scholar] [CrossRef]
- Yildirim, Y. Optical solitons of Biswas-Arshed equation by trial equation technique. Optik 2019, 182, 876–883. [Google Scholar] [CrossRef]
- Yildirim, Y. Optical solitons to Gerdjikov-Ivanov equation in birefringent fibers with trial equation integration architecture. Optik 2019, 182, 349–355. [Google Scholar] [CrossRef]
- Yildirim, Y. Optical solitons of Gerdjikov-Ivanov equation with four-wave mixing terms in birefringent fibers by modified simple equation methodology. Optik 2019, 182, 745–754. [Google Scholar] [CrossRef]
- Yildirim, Y. Optical solitons of Gerdjikov-Ivanov equation in birefringent fibers with modified simple equation scheme. Optik 2019, 182, 424–432. [Google Scholar] [CrossRef]
- Yildirim, Y. Optical solitons of Biswas-Arshed equation in birefringent fibers by trial equation technique. Optik 2019, 182, 810–820. [Google Scholar] [CrossRef]
- Yildirim, Y. Optical solitons in DWDM technology with four-wave mixing by trial equation integration architecture. Optik 2019, 182, 625–632. [Google Scholar] [CrossRef]
- Yildirim, Y. Bright, dark and singular optical solitons to Kundu-Eckhaus equation having four-wave mixing in the context of birefringent fibers by using of trial equation methodology. Optik 2019, 182, 393–399. [Google Scholar] [CrossRef]
- Yildirim, Y. Optical solitons of Biswas-Arshed equation by modified simple equation technique. Optik 2019, 182, 986–994. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ozisik, M.; Secer, A.; Bayram, M.; Biswas, A.; González-Gaxiola, O.; Moraru, L.; Moldovanu, S.; Iticescu, C.; Bibicu, D.; Alghamdi, A.A. Retrieval of Optical Solitons with Anti-Cubic Nonlinearity. Mathematics 2023, 11, 1215. https://doi.org/10.3390/math11051215
Ozisik M, Secer A, Bayram M, Biswas A, González-Gaxiola O, Moraru L, Moldovanu S, Iticescu C, Bibicu D, Alghamdi AA. Retrieval of Optical Solitons with Anti-Cubic Nonlinearity. Mathematics. 2023; 11(5):1215. https://doi.org/10.3390/math11051215
Chicago/Turabian StyleOzisik, Muslum, Aydin Secer, Mustafa Bayram, Anjan Biswas, Oswaldo González-Gaxiola, Luminita Moraru, Simona Moldovanu, Catalina Iticescu, Dorin Bibicu, and Abdulah A. Alghamdi. 2023. "Retrieval of Optical Solitons with Anti-Cubic Nonlinearity" Mathematics 11, no. 5: 1215. https://doi.org/10.3390/math11051215
APA StyleOzisik, M., Secer, A., Bayram, M., Biswas, A., González-Gaxiola, O., Moraru, L., Moldovanu, S., Iticescu, C., Bibicu, D., & Alghamdi, A. A. (2023). Retrieval of Optical Solitons with Anti-Cubic Nonlinearity. Mathematics, 11(5), 1215. https://doi.org/10.3390/math11051215