Urban Heat Island Dynamics in an Urban–Rural Domain with Variable Porosity: Numerical Methodology and Simulation
Abstract
1. Introduction
2. Materials and Methods
2.1. The Computer Fluid Dynamics and Heat Transfer Models on Porous Media
2.2. A Non-Stationary Darcy–Brinkman–Forchheimer Model for an Urban–Rural Porous Media
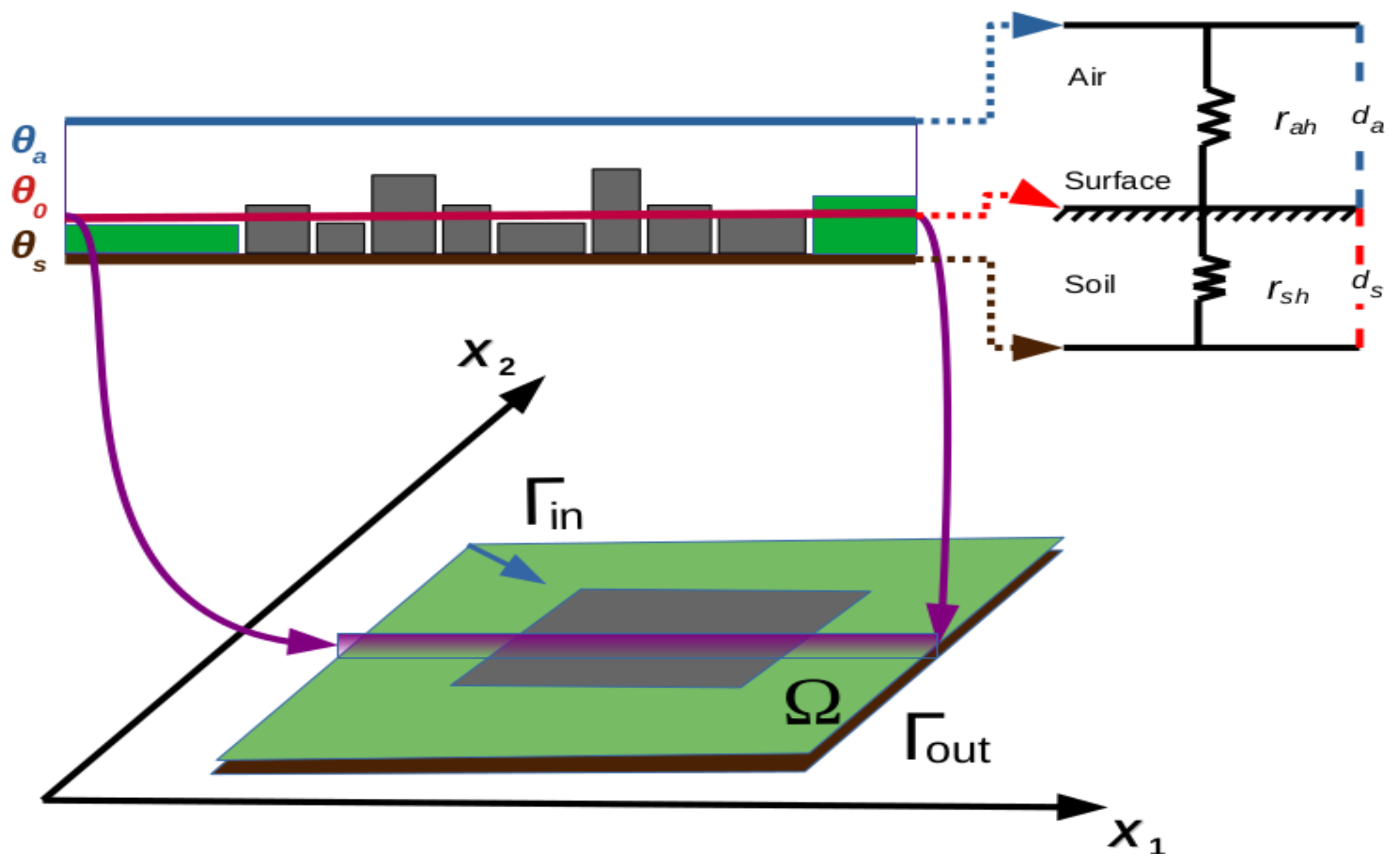
2.3. Model for Heat Transfer in Urban–Rural Domain
2.4. Numerical Solution
2.4.1. An Explicit Scheme for the Darcy–Forchheimer–Brinkman Equation: The Chorin Method
2.4.2. A Finite Element Approach and Implicit Time Schemes to Solve the Heat-Transfer Model
3. Numerical Results
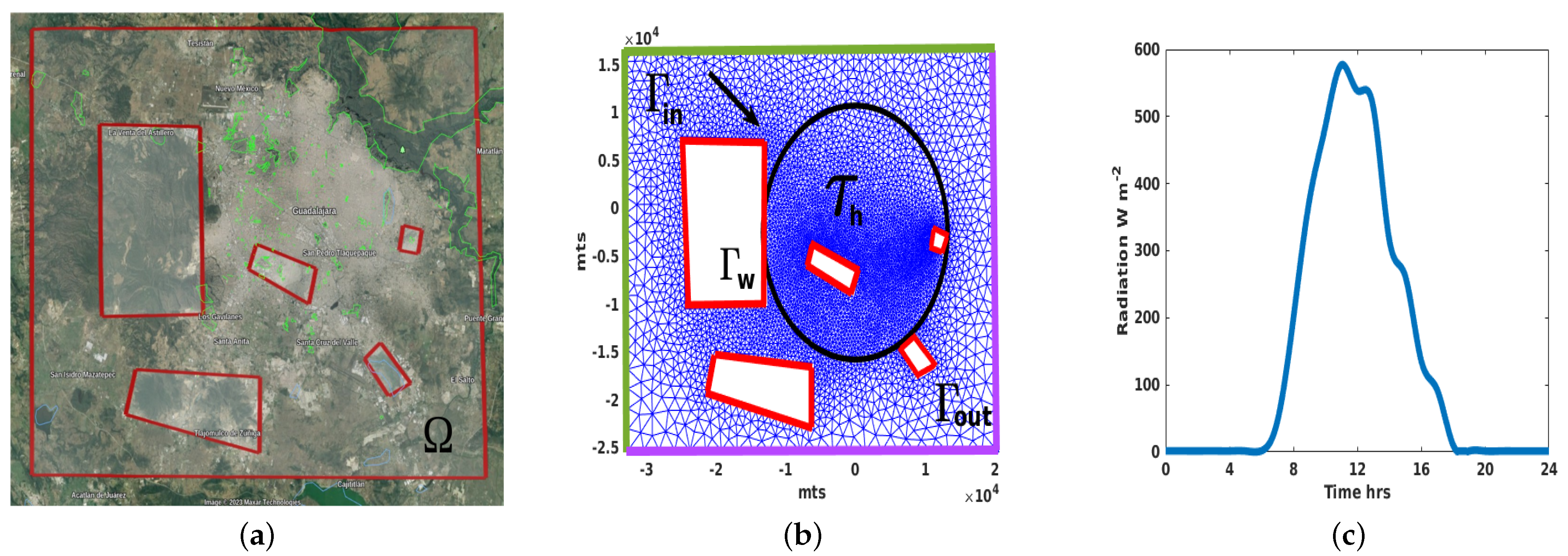
3.1. Parameters Values and the Urban–Rural Domain Based on the Metropolitan Region of Guadalajara
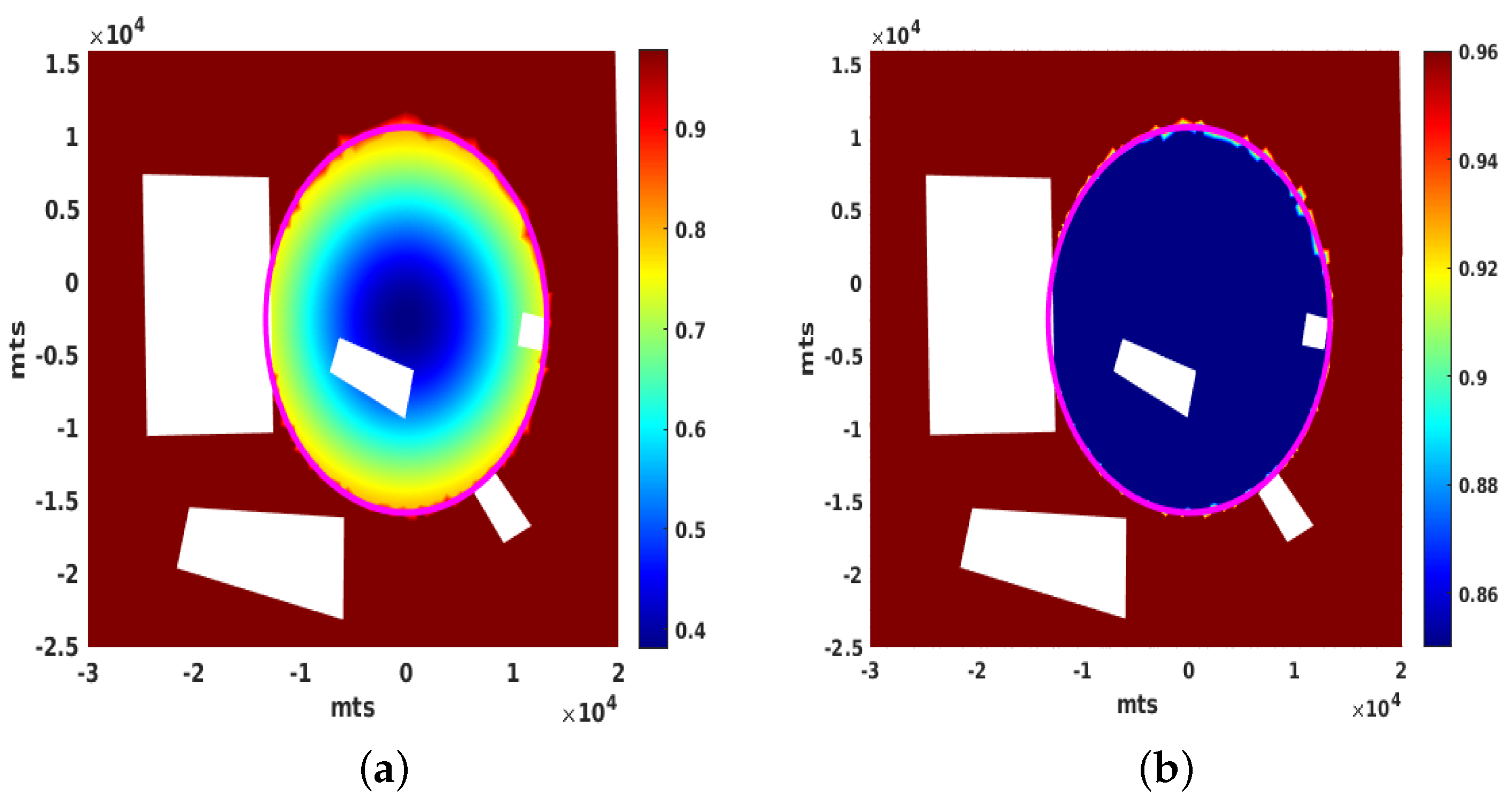
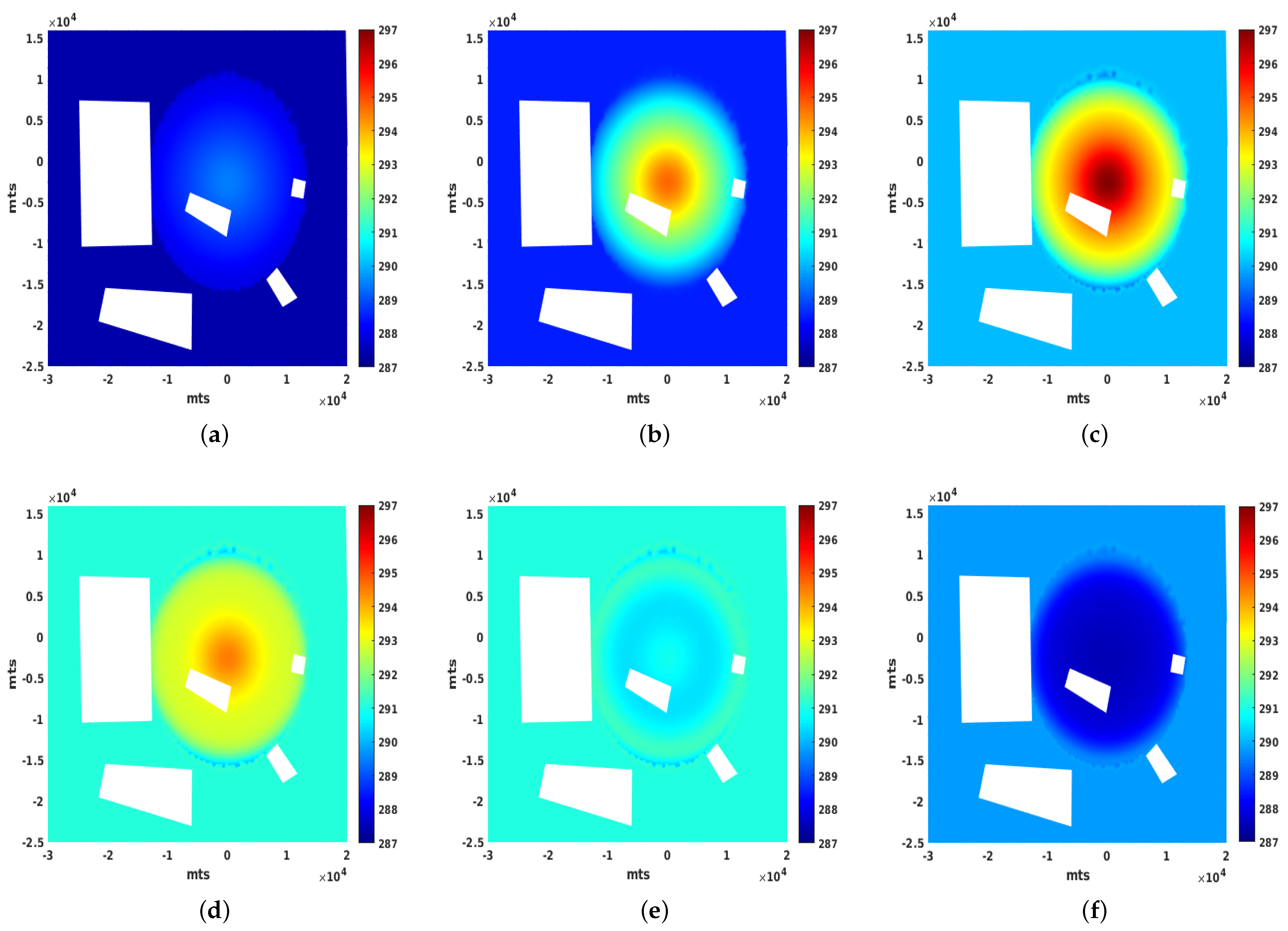
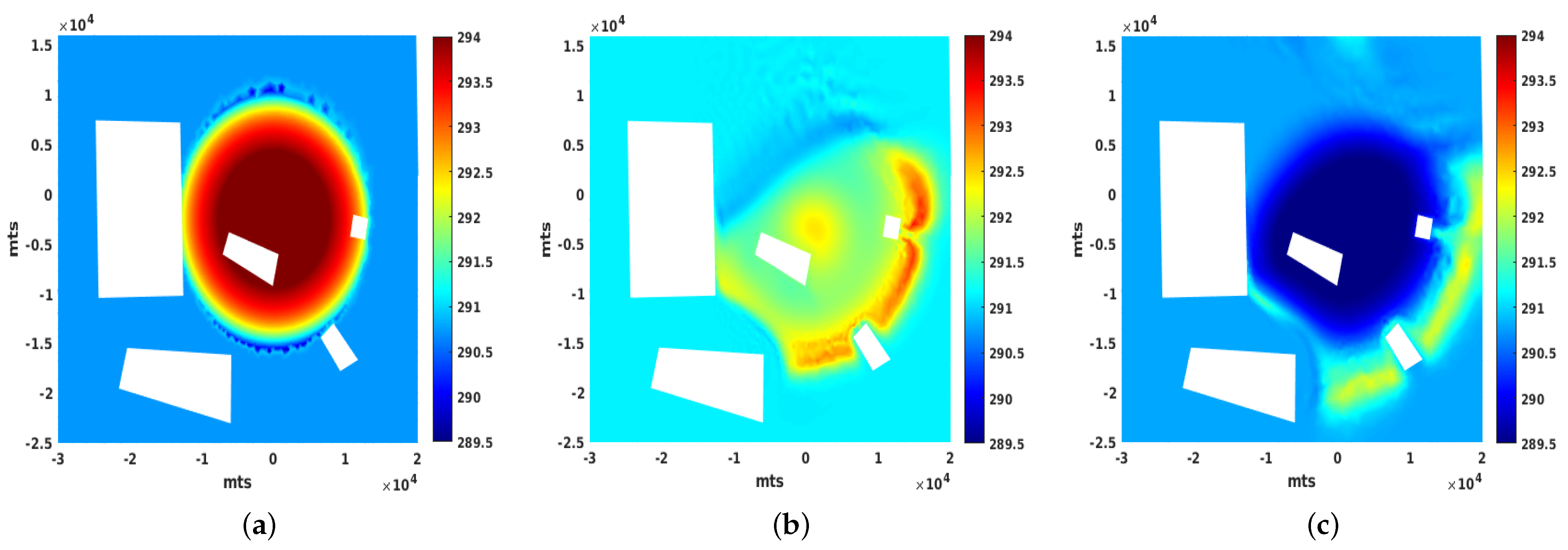
3.2. A 24 h Simulation of the UHI under Ideal Conditions
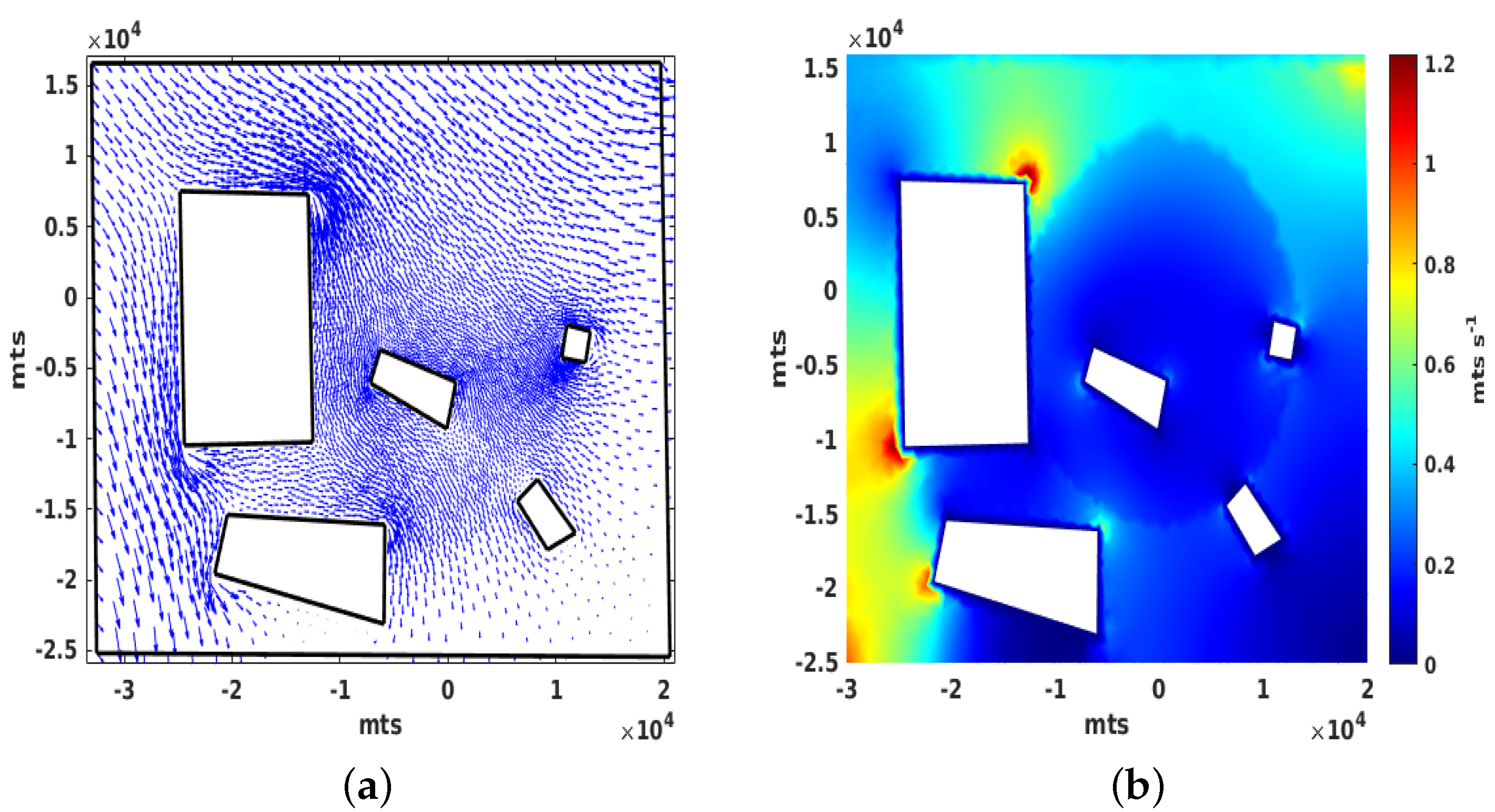
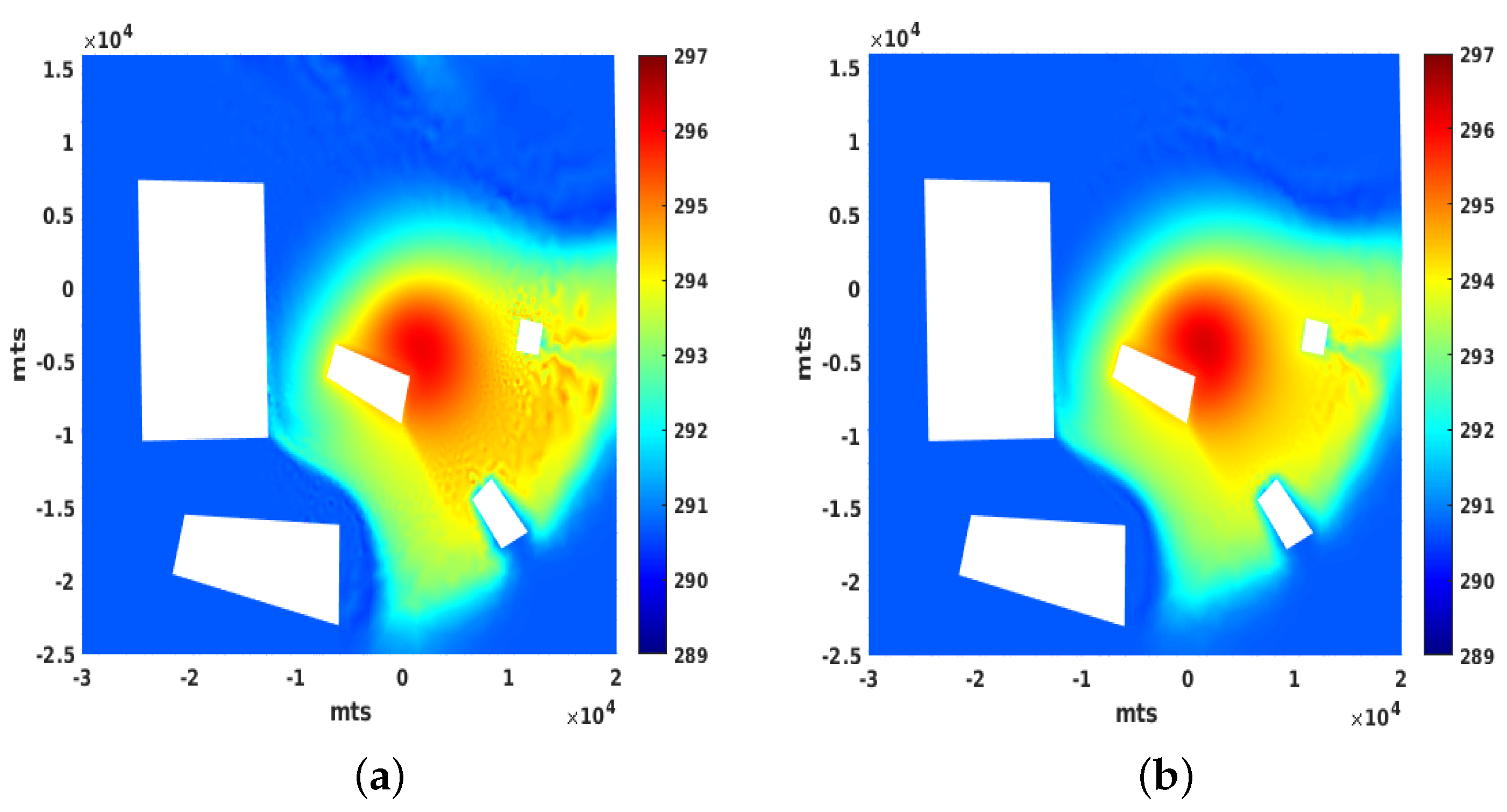
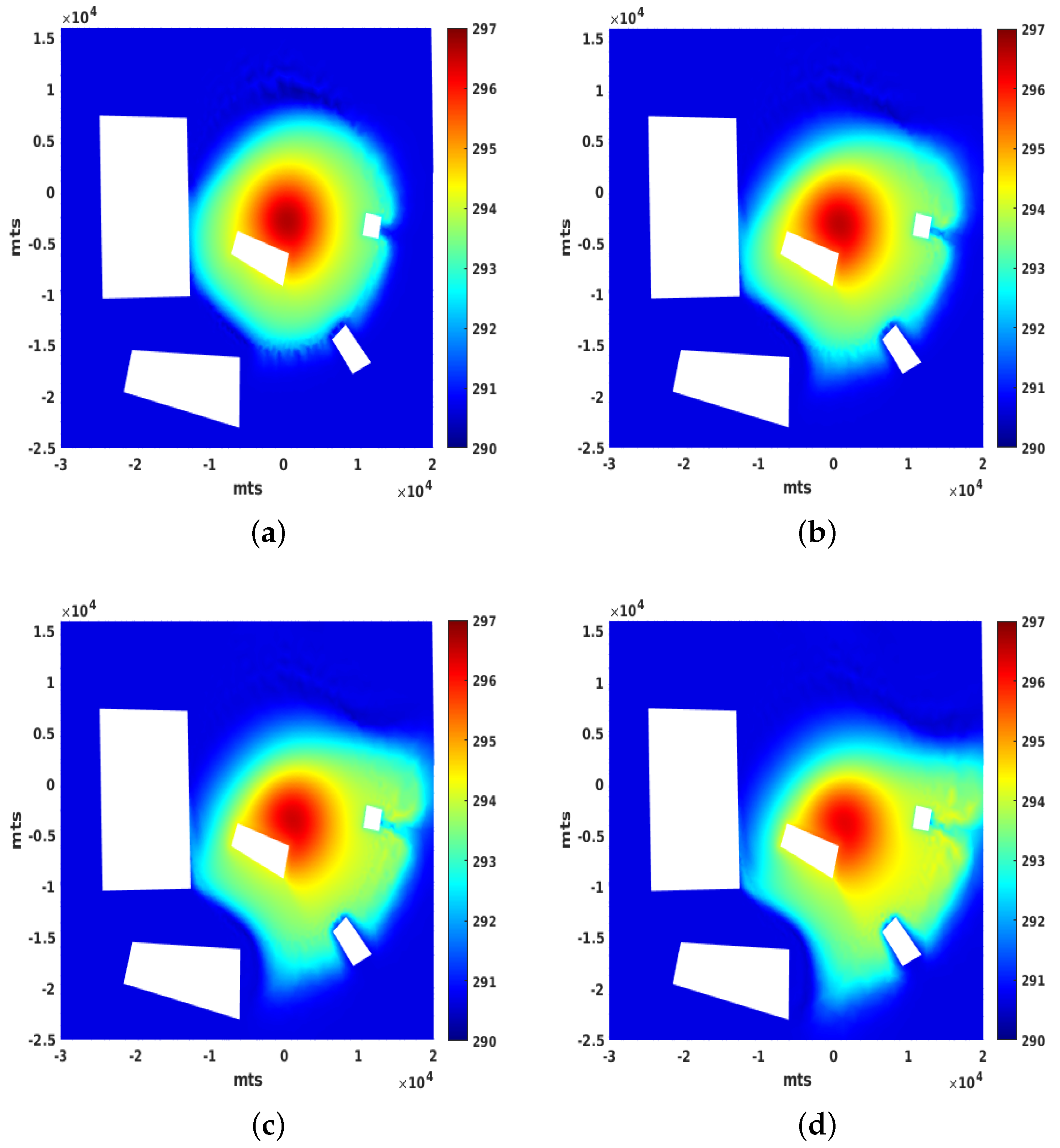
3.3. Influence of the Wind and the Need for Numerical Stabilization
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Symbol/Formula | Definition | Value/Units |
|---|---|---|
| Global solar radiation | W m | |
| Fluid density | kg m | |
| Air density | 1.1614 kg m | |
| Urban soil density | 2.11 × 10 kg m | |
| Rural soil density | 8.4 × 10 kg m | |
| Specific heat of air | 1005 J kg K | |
| Specific heat of urban soil | 920 J kg K | |
| Specific heat of rural soil | 3600 J kg K | |
| Specific heat of steam | 1952 J kg K | |
| Air conductivity | 0.0263 J s m K | |
| Urban soil conductivity | 0.41 J s m K | |
| Rural soil conductivity | 1.47 J s m K | |
| Air convection coefficient | 1 J s m K | |
| Urban soil convection coefficient | 0.4 J s m K | |
| Rural soil convection coefficient | 0.2 J s m K | |
| Urban albedo | ||
| Rural albedo | ||
| Urban soil emissivity | ||
| Rural soil emissivity | ||
| Sky emissivity | ||
| Urban soil roughness | 7 m | |
| Rural soil roughness | 1 m | |
| Urban friction velocity | 0.2 ms | |
| Rural friction velocity | 0.5 ms | |
| Urban Bowen radius | ||
| Rural Bowen radius | ||
| Air layer thickness | 2.0 m | |
| Soil layer thickness | 1.0 m | |
| k | Von Karman constant | |
| Nusselt number | 1 | |
| Stephan–Boltzmann constant | 5.6703 × 10 W m K | |
| r | Urban radius | 13,250.0 m |
| Urban center coordinates | (0, −2500) m | |
| d | Diameter of spheres | 1 m |
| Forchheimer coefficient | ||
| Gaussian distribution variances | (10, 10) | |
| Permeability | ||
| Soil resistance | s m | |
| Air resistance | s m | |
| Air radiation interchange coefficient | m s K | |
| Air convective interchange coefficient | m s | |
| Soil convective interchange coefficient | m s | |
| Air thermal diffusivity | ms | |
| Soil thermal diffusivity | ms |
References
- Oke, T.R.; Johnson, G.T.; Steyn, D.G.; Watson, I.D. Simulation of surface urban heat islands under ideal conditions at night part 2: Diagnosis of causation. Bound.-Layer Meteorol. 1991, 56, 339–358. [Google Scholar] [CrossRef]
- Johnson, G.T.; Oke, T.R.; Lyons, T.J.; Steyn, D.G.; Watson, I.D.; Voogt, J.A. Simulation of surface urban heat islands under ideal conditions at night part 1: Theory and tests against field data. Bound.-Layer Meteorol. 1991, 56, 275–294. [Google Scholar] [CrossRef]
- Oke, T. Boundary Layer Climates; Taylor & Francis: Boca Raton, FL, USA, 2002. [Google Scholar]
- Sportisse, B. Fundamentals in Air Pollution; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar] [CrossRef]
- Arifwidodo, S.D.; Chandrasiri, O.; Abdulharis, R.; Kubota, T. Exploring the effects of urban heat island: A case study of two cities in Thailand and Indonesia. APN Sci. Bull. 2019, 9. [Google Scholar] [CrossRef]
- Ward, K.; Lauf, S.; Kleinschmit, B.; Endlicher, W. Heat waves and urban heat islands in Europe: A review of relevant drivers. Sci. Total Environ. 2016, 569–570, 527–539. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhou, Y.; Yu, S.; Jia, G.; Li, H.; Li, W. Urban heat island impacts on building energy consumption: A review of approaches and findings. Energy 2019, 174, 407–419. [Google Scholar] [CrossRef]
- Cui, Y.; Xiao, S.; Giometto, M.G.; Li, Q. Effects of Urban Surface Roughness on Potential Sources of Microplastics in the Atmospheric Boundary Layer. Bound.-Layer Meteorol. 2022. [Google Scholar] [CrossRef]
- Ulpiani, G. On the linkage between urban heat island and urban pollution island: Three-decade literature review towards a conceptual framework. Sci. Total Environ. 2020, 751, 141727. [Google Scholar] [CrossRef]
- Basu, R.; Samet, J.M. Relation between Elevated Ambient Temperature and Mortality: A Review of the Epidemiologic Evidence. Epidemiol. Rev. 2002, 24, 190–202. [Google Scholar] [CrossRef]
- Taha, H. Urban climates and heat islands: Albedo, evapotranspiration, and anthropogenic heat. Energy Build. 1997, 25, 99–103. [Google Scholar] [CrossRef]
- Wang, H.; Peng, C.; Li, W.; Ding, C.; Ming, T.; Zhou, N. Porous media: A faster numerical simulation method applicable to real urban communities. Urban Clim. 2021, 38, 100865. [Google Scholar] [CrossRef]
- Mirzaei, P.A.; Haghighat, F. Approaches to study Urban Heat Island—Abilities and limitations. Build. Environ. 2010, 45, 2192–2201. [Google Scholar] [CrossRef]
- Mirzaei, P.A. Recent challenges in modeling of urban heat island. Sustain. Cities Soc. 2015, 19, 200–206. [Google Scholar] [CrossRef]
- Tian, L.; Li, Y.; Lu, J.; Wang, J. Review on Urban Heat Island in China: Methods, Its Impact on Buildings Energy Demand and Mitigation Strategies. Sustainability 2021, 13, 762. [Google Scholar] [CrossRef]
- Ming, T.; Lian, S.; Wu, Y.; Shi, T.; Peng, C.; Fang, Y.; de Richter, R.; Wong, N.H. Numerical Investigation on the Urban Heat Island Effect by Using a Porous Media Model. Energies 2021, 14, 4681. [Google Scholar] [CrossRef]
- Saitoh, T.; Shimada, T.; Hoshi, H. Modeling and simulation of the Tokyo urban heat island. Atmos. Environ. 1996, 30, 3431–3442. [Google Scholar] [CrossRef]
- Saitoh, T.S.; Yamada, N. Experimental and numerical investigation of thermal plume in urban surface layer. Exp. Therm. Fluid Sci. 2004, 28, 585–595. [Google Scholar] [CrossRef]
- Hang, J.; Li, Y. Wind Conditions in Idealized Building Clusters: Macroscopic Simulations Using a Porous Turbulence Model. Bound.-Layer Meteorol. 2010, 136, 129–159. [Google Scholar] [CrossRef]
- Hu, Z.; Yu, B.; Chen, Z.; Li, T.; Liu, M. Numerical investigation on the urban heat island in an entire city with an urban porous media model. Atmos. Environ. 2012, 47, 509–518. [Google Scholar] [CrossRef]
- Das, M.K.; Mukherjee, P.P.; Muralidhar, K. Modeling Transport Phenomena in Porous Media with Applications; Springer International Publishing: Zurich, Switwerland, 2018. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Hoekman, D.H.; Roebeling, R. A Methodology for the Assessment of Surface Resistance and Soil Water Storage Variability at Mesoscale Based on Remote Sensing Measurements: A Case Study with HAPEX-EFEDA Data; IAHS Special Publication, International Association of Hydrological Sciences: Wageningen, The Netherlands, 1994. [Google Scholar]
- Feddes, R.; Menenti, M.; Kabat, P.; Bastiaanssen, W. Is large-scale inverse modelling of unsaturated flow with areal average evaporation and surface soil moisture as estimated from remote sensing feasible? J. Hydrol. 1993, 143, 125–152. [Google Scholar] [CrossRef]
- Buttar, N.A.; Yongguang, H.; Shabbir, A.; Lakhiar, I.A.; Ullah, I.; Ali, A.; Aleem, M.; Yasin, M.A. Estimation of evapotranspiration using Bowen ratio method. IFAC-PapersOnLine 2018, 51, 807–810. [Google Scholar] [CrossRef]
- Hossein Ashktorab, W.; Pruitt, K.; Paw, U.; George, W. Energy balance determinations close to the soil surface using a micro-Bowen ratio system. Agric. For. Meteorol. 1989, 46, 259–274. [Google Scholar] [CrossRef]
- Larson, M.G.; Bengzon, F. The Finite Element Method: Theory, Implementation, and Applications; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Pan, H.; Rui, H. Mixed Element Method for Two-Dimensional Darcy–Forchheimer Model. J. Sci. Comput. 2011, 52, 563–587. [Google Scholar] [CrossRef]
- Gunzburger, M.D.; Bochev, P.B. Least-Squares Finite Element Methods; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Cocquet, P.H.; Rakotobe, M.; Ramalingom, D.; Bastide, A. Error analysis for the finite element approximation of the Darcy–Brinkman–Forchheimer model for porous media with mixed boundary conditions. J. Comput. Appl. Math. 2021, 381, 113008. [Google Scholar] [CrossRef]
- Salas, J.J.; López, H.; Molina, B. An analysis of a mixed finite element method for a Darcy–Forchheimer model. Math. Comput. Model. 2013, 57, 2325–2338. [Google Scholar] [CrossRef]
- Chorin, A. Numerical solution of the navier-stokes equations. Math. Comput. 1968, 22, 745–762. [Google Scholar] [CrossRef]
- Cockburn, B.; Shu, C.W. Runge–Kutta Discontinuous Galerkin Methods for Convection-Dominated Problems. J. Sci. Comput. 2001, 16, 173–261. [Google Scholar] [CrossRef]
- Li, Q.B. Discontinuous Finite Elements in Fluid Dynamics and Heat Transfer; Springer: Berlin, Germany, 2006. [Google Scholar] [CrossRef]
- Zhou, T.; Li, Y.; Shu, C.W. Numerical Comparison of WENO Finite Volume and Runge–Kutta Discontinuous Galerkin Methods. J. Sci. Comput. 2001, 16, 145–171. [Google Scholar] [CrossRef]
- Aram, F.; Higueras García, E.; Solgi, E.; Mansournia, S. Urban green space cooling effect in cities. Heliyon 2019, 5, e01339. [Google Scholar] [CrossRef]
- Fernández, F.; Alvarez-Vázquez, L.; García-Chan, N.; Martínez, A.; Vázquez-Méndez, M. Optimal location of green zones in metropolitan areas to control the urban heat island. J. Comput. Appl. Math. 2015, 289, 412–425. [Google Scholar] [CrossRef]
- Besir, A.B.; Cuce, E. Green roofs and facades: A comprehensive review. Renew. Sustain. Energy Rev. 2018, 82, 915–939. [Google Scholar] [CrossRef]
- Villarreal-Olavarrieta, C.E.; García-Chan, N.; Vázquez-Méndez, M.E. Simulation of Heat and Water Transport on Different Tree Canopies: A Finite Element Approach. Mathematics 2021, 9, 2431. [Google Scholar] [CrossRef]
- Vásquez-Álvarez, P.E.; Flores-Vázquez, C.; Cobos-Torres, J.C.; Cobos-Mora, S.L. Urban Heat Island Mitigation through Planned Simulation. Sustainability 2022, 14, 8612. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Chan, N.; Licea-Salazar, J.A.; Gutierrez-Ibarra, L.G. Urban Heat Island Dynamics in an Urban–Rural Domain with Variable Porosity: Numerical Methodology and Simulation. Mathematics 2023, 11, 1140. https://doi.org/10.3390/math11051140
García-Chan N, Licea-Salazar JA, Gutierrez-Ibarra LG. Urban Heat Island Dynamics in an Urban–Rural Domain with Variable Porosity: Numerical Methodology and Simulation. Mathematics. 2023; 11(5):1140. https://doi.org/10.3390/math11051140
Chicago/Turabian StyleGarcía-Chan, Néstor, Juan A. Licea-Salazar, and Luis G. Gutierrez-Ibarra. 2023. "Urban Heat Island Dynamics in an Urban–Rural Domain with Variable Porosity: Numerical Methodology and Simulation" Mathematics 11, no. 5: 1140. https://doi.org/10.3390/math11051140
APA StyleGarcía-Chan, N., Licea-Salazar, J. A., & Gutierrez-Ibarra, L. G. (2023). Urban Heat Island Dynamics in an Urban–Rural Domain with Variable Porosity: Numerical Methodology and Simulation. Mathematics, 11(5), 1140. https://doi.org/10.3390/math11051140






