Ensemble Methods in Customer Churn Prediction: A Comparative Analysis of the State-of-the-Art
Abstract
:1. Introduction
- We provide a comprehensive overview of the state-of-the-art ensemble methods in CCP and conduct the largest benchmark study to date. More specifically, we compare 6 single classifiers, 14 homogeneous ensembles, and 13 heterogeneous ensembles across 11 public and private data sets. By using several open-source data sets we ensure that our results are replicable and generalizable.
- We include several novel classifiers that have not yet been included in large scale benchmark studies. Especially, gradient boosting implementations such as lightGBM and catboost have received comparatively little attention in CCP. However, these models have empirically demonstrated to outperform other classifiers in other domains (e.g., [18,19]).
- We develop novel heterogeneous ensembles using a wide variety of base classifiers and advanced classifier selection methods that have not been used in previous work. For the base classifier pool, we apply several powerful classifiers into the heterogeneous ensemble framework [20]. For the classifier selection methods, research has mainly adopted heuristic search procedures such as hill climbing [21]. To the best of our knowledge, we are the first to compare advanced meta-heuristic and statistical optimization procedures to perform classifier selection.
- We use five different types of evaluation metrics that each measure a different aspect of CCP model performance, namely, overall statistical performance, performance for top ranked would-be churners, and profit-driven performance.
2. Related Work
2.1. Ensemble Methods
2.2. Ensemble Methods in Customer Churn
| Classifiers 1 | Evaluation 2 | Tests 3 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Study | Single | Hm | Ht | No 4 | D | I | P | No | Stat | B |
| Buckinx and Van den Poel 2005 [39] | X | X | 3 | X | X | 2 | ||||
| Lemmens and Croux 2006 [8] | X | X | 4 | X | X | 3 | ||||
| Burez and Van den Poel 2007 [29] | X | X | 3 | X | X | X | 3 | |||
| Coussement and Van den Poel 2008 [40] | X | X | 3 | X | X | 3 | X | |||
| Burez and Van den Poel 2009 [41] | X | X | 2 | X | X | 3 | X | |||
| Tsai and Lu 2009 [32] | X | X | 3 | X | 3 | X | ||||
| Xie et al., 2009 [42] | X | 4 | X | 2 | ||||||
| De Bock and Van den Poel 2011 [43] | X | 5 | X | X | 4 | X | ||||
| Ballings and Van den Poel 2012 [4] | X | X | 3 | X | 1 | X | ||||
| De Bock and Van den Poel 2012 [44] | X | X | 6 | X | X | 4 | X | |||
| Kim et al., 2012 [45] | X | X | 6 | X | 1 | |||||
| Verbeke et al., 2012 [2] | X | X | 16 | X | X | X | 3 | X | ||
| Coussement and De Bock 2013 [7] | X | X | 4 | X | 2 | X | ||||
| Idriss et al., 2012 [46] | X | X | 5 | X | 4 | |||||
| Baumann et al., 2015 [33] | X | X | 15 | X | 1 | X | ||||
| Vafeiadis et al., 2015 [6] | X | X | 6 | X | 4 | |||||
| Coussement et al., 2017 [27] | X | X | 9 | X | X | 2 | X | |||
| Idriss and Khan 2017 [47] | X | X | X | 5 | X | X | 2 | |||
| Oskarsdottir et al., 2017 [35] | X | X | 3 | X | X | X | 4 | X | ||
| Zhu et al., 2018 [48] | X | 3 | X | 1 | X | |||||
| Zhu et al., 2017 [49] | X | X | X | 7 | X | X | X | 3 | X | |
| De Caigny et al., 2018 [13] | X | X | 5 | X | X | 2 | X | |||
| Zhu et al., 2018 [50] | X | X | 4 | X | X | X | 3 | X | ||
| Ullah et al., 2019 [10] | X | X | 11 | X | X | 6 | ||||
| Jain et al., 2020 [51] | X | X | 2 | X | X | 8 | ||||
| Bhujbal and Bavdane 2021 [52] | X | X | X | 7 | X | 1 | ||||
| Chowdhury et al., 2021 [53] | X | 4 | X | X | 2 | |||||
| Deng et al., 2021 [54] | X | 3 | X | X | 3 | |||||
| De Bock and De Caigny 2021 [38] | X | X | 8 | X | X | 2 | X | |||
| Janssens et al., 2022 [55] | X | X | 7 | X | X | X | 3 | X | ||
| Karuppaiah and Palanisamy 2021 [56] | X | X | X | 5 | X | X | 2 | |||
| Kiguchi et al., 2022 [57] | X | X | 3 | X | X | 2 | ||||
| Lessmann et al., 2021 [21] | X | X | X | 18 | X | X | X | 3 | X | |
| Sagala and Permai 2021 [58] | X | 3 | X | X | 2 | |||||
| Vo et al., 2021 [59] | X | X | 4 | X | 4 | X | ||||
| Wu et al., 2021 [11] | X | X | 6 | X | X | 5 | ||||
| Gattermann and Thonemann 2021 [60] | X | X | 3 | X | X | 2 | ||||
| Mirkovic et al., 2022 [28] | X | X | 3 | X | X | 2 | ||||
| Our study | X | X | X | 33 | X | X | X | 5 | X | X |
2.3. Conclusions of the Related Work
3. Materials and Methods
3.1. Single Classifiers
3.2. Homogeneous Ensembles
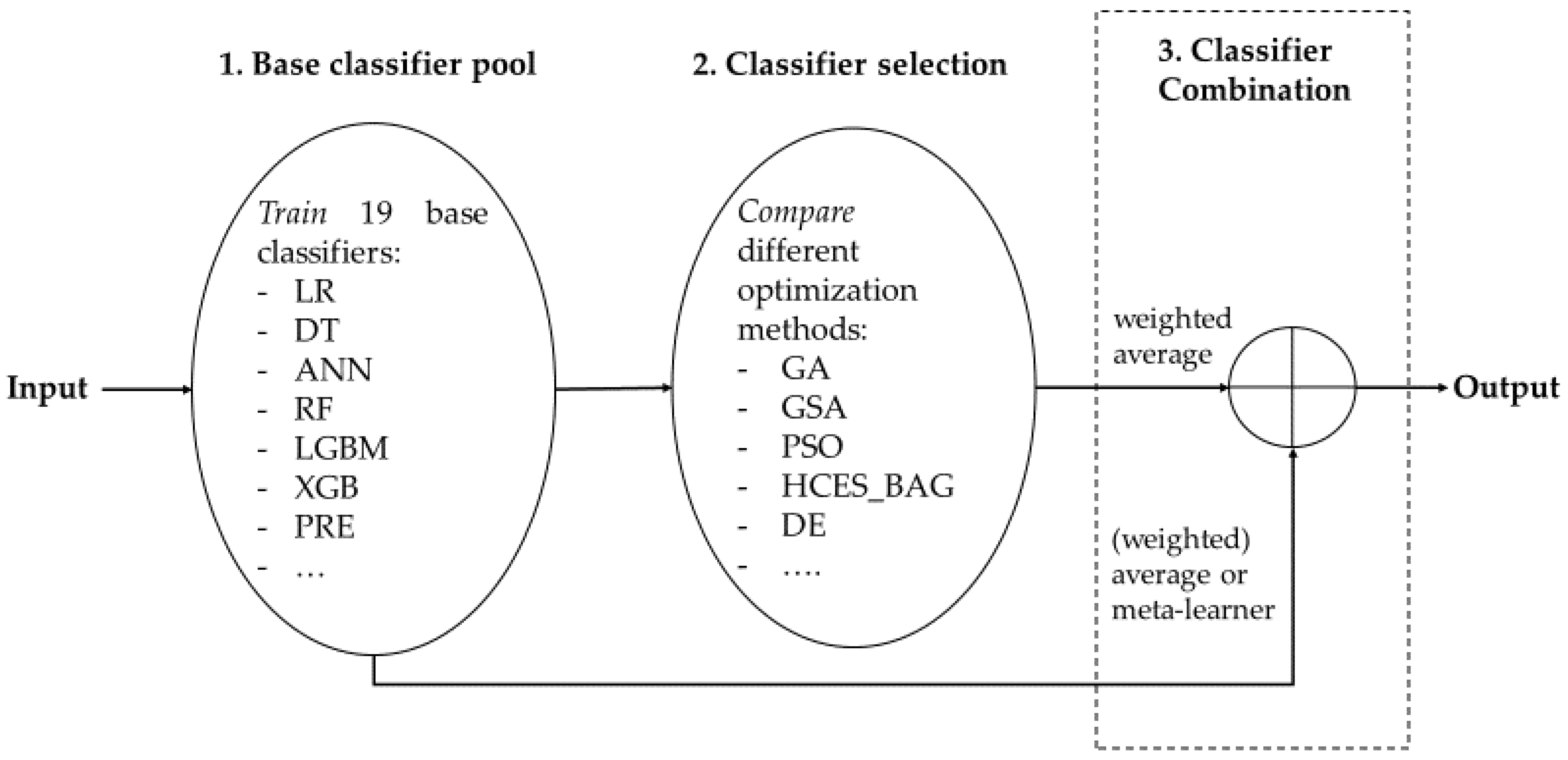
3.3. Heterogeneous Ensembles
3.3.1. Classifier Selection
3.3.2. Classifier Combination
4. Experiment Set-Up
4.1. Data and Cross-Validation
4.2. Data Preprocessing
4.3. Evaluation Metrics
4.4. Classifier Comparison
5. Results
6. Discussion
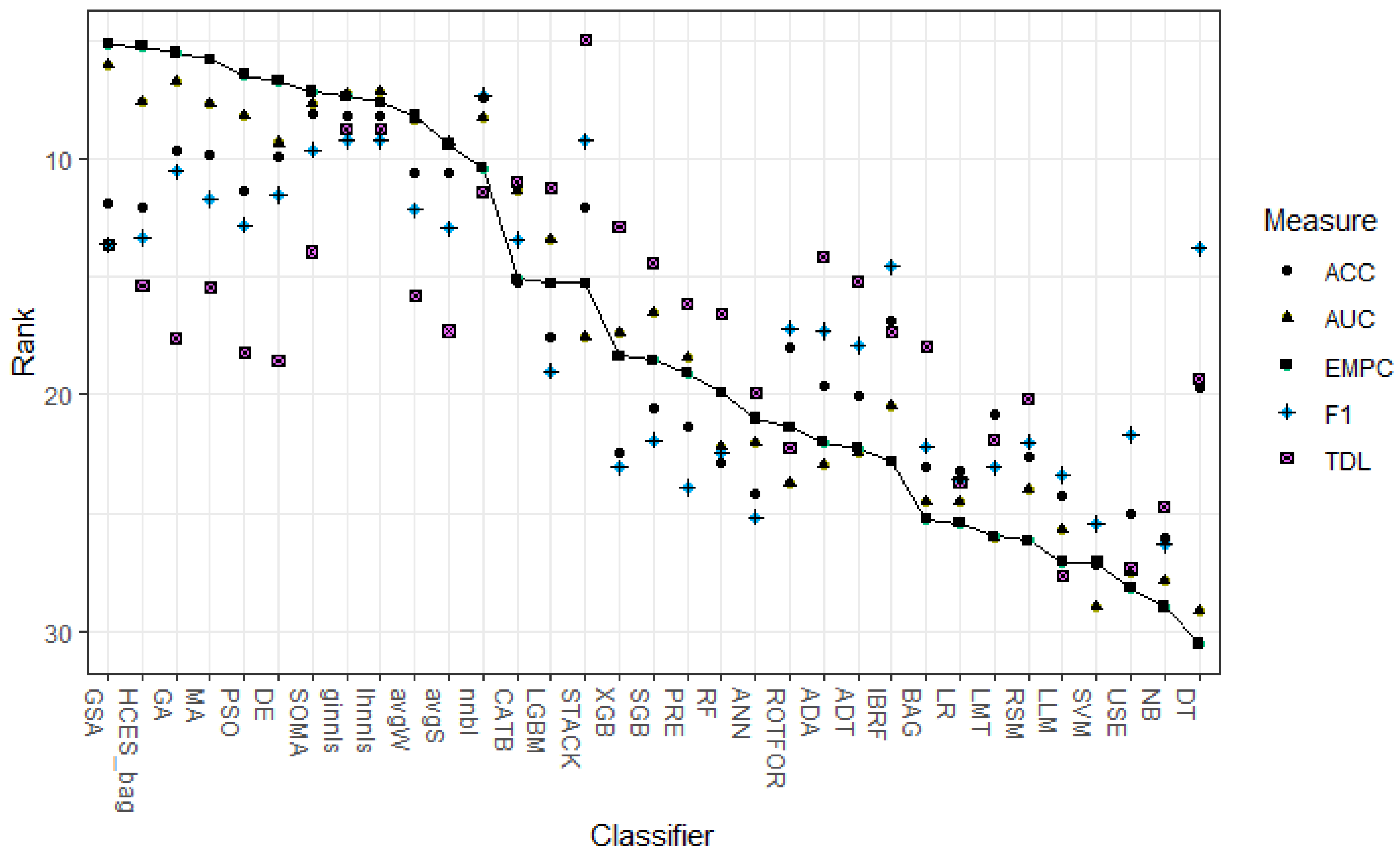
- We show that different performance measures yield different results to which classifier is most effective. For example, the statistical classifier combination methods (i.e., NNBL, LHNNLS, and GINNLS) work well for the threshold dependent metrics such as accuracy and F1 measure. These combination methods search for the coefficients that minimize the error rate, which explains their superior performance for statistical error-based metrics. For threshold independent metrics such as the AUC and EMPC, we observe that meta-heuristic search procedures (i.e., GSA, and GA) and HCES_BAG are among the top performers. These algorithms are direct optimization methods that maximize a specific metric by finding the optimal set of classifiers [94]. Hence, for threshold independent and profit/cost-based performance metrics, our results favor general purpose solvers.
- The classifiers rankings are quite robust across different sectors. A high correlation between all sectors, the telecommunications sector, and the other remaining ones is observed in terms of AUC and EMPC. For the threshold dependent metrics, the rankings vary the most between the telecommunications and other sectors. When looking at the top performing classifiers, there are variations between performance measures and sectors. Overall, the finding that statistical combination methods work best for error-based performance measures and meta-heuristics for profits still holds.
- Future studies who want to propose novel classifiers in the field of CCP should carefully benchmark their proposed method against competitive classifiers. Whereas logistic regression and random were considered the gold standard for single classifiers and homogeneous ensemble [27], our study indicates that these methods are outperformed by ANN and catboost or light GBM. Therefore, outperforming LR or RF cannot be considered as a methodological improvement. It might even be more difficult to outperform heterogeneous ensemble with GSA classifier selection, however, there is no off-the-shelf library available. Moreover, a large number of base classifiers have to be trained which can further refrain researchers from including a heterogeneous ensemble into their classifier set.
- Heterogeneous ensembles have not received much attention in CCP, and current studies mostly rely on the results of Lessmann et al. [9] and use the HCES_BAG algorithm as their default implementation. Our results, however, indicate that HCES_BAG is competitive but always outperformed by another method. Both in terms of AUC and expected profits, our results favor a heterogeneous ensemble with simulated annealing classifier selection for the local search procedures and a genetic algorithm selection for the population-based methods. For the other measures, statistical classifier selection methods such as NNBL outperform HCES_BAG. Hence, researchers that want to implement a heterogeneous ensemble method are advised to consider other methods than hill climbing. Our benchmark results can serve as a guideline for future studies.
- Our study clearly shows that putting time and effort in designing proper heterogeneous ensembles pays off: (1) adding powerful algorithms to the candidate models such as CATB and LGBM and (2) searching for the best classifier selection methods clearly increases the performance of heterogeneous ensembles.
- From a practical point of view, we show a clear trade-off between implementing simple but less accurate prediction methods (e.g., LR) or investing in advanced methods (e.g., heterogeneous ensembles) to have more accurate and profitable predictions. The results of both the statistical and Bayesian testing procedures also show that off-the-shelf methods such as CATB do not perform significantly worse than customized heterogeneous ensembles. Hence, managers should decide whether increased performance and/or profits of complex models is worth the effort.
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ACRM | Analytical customer relationship management |
| ACC | Accuracy |
| ADA | Adaboost |
| ADT | Alternating decision trees |
| ANN | Artificial neural networks |
| AUC | Area under the receiver operating characteristic curve |
| AVGS | Standard average |
| AVGW | Weighted average |
| BAG | Bagging |
| CATB | Catboost |
| CCP | Customer churn prediction |
| CART | Classification and regression trees |
| DE | Differential evolution |
| DT | Decision tree |
| EMPC | Expected maximum profit for customer churn |
| F1 | F1 measure |
| GA | Genetic algorithm |
| GINNLS | Goldfarb-Idnani non-negative least squares |
| GSA | Generalized simulated annealing |
| HCES_BAG | Hill-climbing ensemble selection with bagging |
| IBRF | Improved balance random forest |
| LHNNLS | Lawson-Hanson non-negative least squares |
| LLM | Logit leaf model |
| LGBM | Light GBM |
| LMT | Logistic model tree |
| LR | Logistic regression |
| MA | Memetic algorithm |
| NB | Naïve Bayes |
| NHST | Null-hypothesis statistical testing |
| NNBL | Non-negative binomial likelihood |
| PSO | Particle swarm optimization |
| PRE | Prediction rule-based ensembles |
| RF | Random forest |
| ROPE | Region of practical equivalence |
| ROTFOR | Rotation Forest |
| SGB | Stochastic gradient boosting |
| SOMA | Self-organizing migrating algorithm |
| STACK | Stacking |
| SVM | Support vector machines |
| USE | Uniform subsampled ensemble |
| XGB | XGBoost |
References
- Poel, D.V.D.; Larivière, B. Customer attrition analysis for financial services using proportional hazard models. Eur. J. Oper. Res. 2004, 157, 196–217. [Google Scholar] [CrossRef]
- Verbeke, W.; Dejaeger, K.; Martens, D.; Hur, J.; Baesens, B. New insights into churn prediction in the telecommunication sector: A profit driven data mining approach. Eur. J. Oper. Res. 2012, 218, 211–229. [Google Scholar] [CrossRef]
- Ahn, J.; Hwang, J.; Kim, D.; Choi, H.; Kang, S. A Survey on Churn Analysis in Various Business Domains. IEEE Access 2020, 8, 220816–220839. [Google Scholar] [CrossRef]
- Ballings, M.; Poel, D.V.D. Customer event history for churn prediction: How long is long enough? Expert Syst. Appl. 2012, 39, 13517–13522. [Google Scholar] [CrossRef] [Green Version]
- Neslin, S.A.; Gupta, S.; Kamakura, W.; Lu, J.; Mason, C.H.; Wang, C.-H.; Fong, H.-Y.; Backiel, A.; Baesens, B.; Claeskens, G.; et al. Defection Detection: Measuring and Understanding the Predictive Accuracy of Customer Churn Models. J. Mark. Res. 2006, 43, 204–211. [Google Scholar] [CrossRef] [Green Version]
- Vafeiadis, T.; Diamantaras, K.; Sarigiannidis, G.; Chatzisavvas, K. A comparison of machine learning techniques for customer churn prediction. Simul. Model. Pract. Theory 2015, 55, 1–9. [Google Scholar] [CrossRef]
- Coussement, K.; De Bock, K.W. Customer churn prediction in the online gambling industry: The beneficial effect of ensemble learning. J. Bus. Res. 2013, 66, 1629–1636. [Google Scholar] [CrossRef]
- Lemmens, A.; Croux, C. Bagging and Boosting Classification Trees to Predict Churn. J. Mark. Res. 2006, 43, 276–286. [Google Scholar] [CrossRef] [Green Version]
- Lessmann, S.; Baesens, B.; Seow, H.-V.; Thomas, L.C. Benchmarking state-of-the-art classification algorithms for credit scoring: An update of research. Eur. J. Oper. Res. 2015, 247, 124–136. [Google Scholar] [CrossRef] [Green Version]
- Ullah, I.; Raza, B.; Malik, A.K.; Imran, M.; Islam, S.U.; Kim, S.W. A Churn Prediction Model Using Random Forest: Analysis of Machine Learning Techniques for Churn Prediction and Factor Identification in Telecom Sector. IEEE Access 2019, 7, 60134–60149. [Google Scholar] [CrossRef]
- Wu, S.; Yau, W.-C.; Ong, T.-S.; Chong, S.-C. Integrated Churn Prediction and Customer Segmentation Framework for Telco Business. IEEE Access 2021, 9, 62118–62136. [Google Scholar] [CrossRef]
- Baesens, B.; Van Gestel, T.; Viaene, S.; Stepanova, M.; Suykens, J.; Vanthienen, J. Benchmarking state-of-the-art classification algorithms for credit scoring. J. Oper. Res. Soc. 2003, 54, 627–635. [Google Scholar] [CrossRef]
- de Caigny, A.; Coussement, K.; de Bock, K.W. A new hybrid classification algorithm for customer churn prediction based on logistic regression and decision trees. Eur. J. Oper. Res. 2018, 269, 760–772. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3147–3155. Available online: https://proceedings.neurips.cc/paper/2017/hash/6449f44a102fde848669bdd9eb6b76fa-Abstract.html (accessed on 5 August 2022).
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. Catboost: Unbiased boosting with categorical features. Adv. Neural Inf. Process. Syst. 2018, 31, 6638–6648. [Google Scholar]
- Verbraken, T.; Verbeke, W.; Baesens, B. A Novel Profit Maximizing Metric for Measuring Classification Performance of Customer Churn Prediction Models. IEEE Trans. Knowl. Data Eng. 2012, 25, 961–973. [Google Scholar] [CrossRef]
- Gunnarsson, B.R.; Broucke, S.; Baesens, B.; Óskarsdóttir, M.; Lemahieu, W. Deep learning for credit scoring: Do or don’t? Eur. J. Oper. Res. 2021, 295, 292–305. [Google Scholar] [CrossRef]
- Xia, Y. A Novel Reject Inference Model Using Outlier Detection and Gradient Boosting Technique in Peer-to-Peer Lending. IEEE Access 2019, 7, 92893–92907. [Google Scholar] [CrossRef]
- Ma, X.; Sha, J.; Wang, D.; Yu, Y.; Yang, Q.; Niu, X. Study on a prediction of P2P network loan default based on the machine learning LightGBM and XGboost algorithms according to different high dimensional data cleaning. Electron. Commer. Res. Appl. 2018, 31, 24–39. [Google Scholar] [CrossRef]
- Xia, Y.; Zhao, J.; He, L.; Li, Y.; Niu, M. A novel tree-based dynamic heterogeneous ensemble method for credit scoring. Expert Syst. Appl. 2020, 159, 113615. [Google Scholar] [CrossRef]
- Lessmann, S.; Haupt, J.; Coussement, K.; De Bock, K.W. Targeting customers for profit: An ensemble learning framework to support marketing decision-making. Inf. Sci. 2021, 557, 286–301. [Google Scholar] [CrossRef]
- García, S.; Fernández, A.; Luengo, J.; Herrera, F. Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: Experimental analysis of power. Inf. Sci. (N. Y.) 2010, 180, 2044–2064. [Google Scholar] [CrossRef]
- Benavoli, A.; Corani, G.; Demšar, J.; Zaffalon, M. Time for a Change: A Tutorial for Comparing Multiple Classifiers through Bayesian Analysis. J. Mach. Learn. Res. 2017, 136–181. [Google Scholar]
- Woźniak, M.; Graña, M.; Corchado, E. A survey of multiple classifier systems as hybrid systems. Inf. Fusion 2014, 16, 3–17. [Google Scholar] [CrossRef] [Green Version]
- Dietterich, T.G. Ensemble Methods in Machine Learning. In Multiple Classifier Systems: First International Workshop, MCS 2000 Proceedings 1, Cagliari, Italy, 21–23 June 2000; Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 1857 LNCS; Springer: Berlin/Heidelberg, Germany, 2000; pp. 1–15. [Google Scholar]
- Nascimento, D.S.; Coelho, A.L.; Canuto, A.M. Integrating complementary techniques for promoting diversity in classifier ensembles: A systematic study. Neurocomputing 2014, 138, 347–357. [Google Scholar] [CrossRef]
- Coussement, K.; Lessmann, S.; Verstraeten, G. A comparative analysis of data preparation algorithms for customer churn prediction: A case study in the telecommunication industry. Decis. Support Syst. 2017, 95, 27–36. [Google Scholar] [CrossRef]
- Mirkovic, M.; Lolic, T.; Stefanovic, D.; Anderla, A.; Gracanin, D. Customer Churn Prediction in B2B Non-Contractual Business Settings Using Invoice Data. Appl. Sci. 2022, 12, 5001. [Google Scholar] [CrossRef]
- Burez, J.; Poel, D.V.D. CRM at a pay-TV company: Using analytical models to reduce customer attrition by targeted marketing for subscription services. Expert Syst. Appl. 2007, 32, 277–288. [Google Scholar] [CrossRef] [Green Version]
- Hung, S.-Y.; Yen, D.C.; Wang, H.-Y. Applying data mining to telecom churn management. Expert Syst. Appl. 2006, 31, 515–524. [Google Scholar] [CrossRef] [Green Version]
- Moeyersoms, J.; Martens, D. Including high-cardinality attributes in predictive models: A case study in churn prediction in the energy sector. Decis. Support Syst. 2015, 72, 72–81. [Google Scholar] [CrossRef]
- Tsai, C.-F.; Lu, Y.-H. Customer churn prediction by hybrid neural networks. Expert Syst. Appl. 2009, 36, 12547–12553. [Google Scholar] [CrossRef]
- Baumann, A.; Lessmann, S.; Coussement, K.; De Bock, K.W.; Bock, D. Maximize What Matters: Predicting Customer Churn with Decision-Centric Ensemble Selection; Association for Information Systems AIS Electronic Library (AISeL): Münster, Germany, 2015; pp. 1–15. [Google Scholar]
- Bogaert, M.; Ballings, M.; Poel, D.V.D. Evaluating the importance of different communication types in romantic tie prediction on social media. Ann. Oper. Res. 2016, 263, 501–527. [Google Scholar] [CrossRef]
- Óskarsdóttir, M.; Bravo, C.; Verbeke, W.; Sarraute, C.; Baesens, B.; Vanthienen, J. Social network analytics for churn prediction in telco: Model building, evaluation and network architecture. Expert Syst. Appl. 2017, 85, 204–220. [Google Scholar] [CrossRef] [Green Version]
- Demšar, J. Statistical Comparisons of Classifiers over Multiple Data Sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Xia, Y.; Liu, C.; Da, B.; Xie, F. A novel heterogeneous ensemble credit scoring model based on bstacking approach. Expert Syst. Appl. 2018, 93, 182–199. [Google Scholar] [CrossRef]
- de Bock, K.W.; de Caigny, A. Spline-rule ensemble classifiers with structured sparsity regularization for interpretable customer churn modeling. Decis. Support Syst. 2021, 150, 113523. [Google Scholar] [CrossRef]
- Buckinx, W.; Poel, D.V.D. Customer base analysis: Partial defection of behaviourally loyal clients in a non-contractual FMCG retail setting. Eur. J. Oper. Res. 2005, 164, 252–268. [Google Scholar] [CrossRef]
- Coussement, K.; Poel, D.V.D. Churn prediction in subscription services: An application of support vector machines while comparing two parameter-selection techniques. Expert Syst. Appl. 2008, 34, 313–327. [Google Scholar] [CrossRef]
- Burez, J.; Van den Poel, D. Handling class imbalance in customer churn prediction. Expert Syst. Appl. 2009, 36, 4626–4636. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.; Li, X.; Ngai, E.; Ying, W. Customer churn prediction using improved balanced random forests. Expert Syst. Appl. 2009, 36, 5445–5449. [Google Scholar] [CrossRef]
- De Bock, K.W.; Poel, D.V.D. An empirical evaluation of rotation-based ensemble classifiers for customer churn prediction. Expert Syst. Appl. 2011, 38, 12293–12301. [Google Scholar] [CrossRef]
- De Bock, K.W.; Poel, D.V.D. Reconciling performance and interpretability in customer churn prediction using ensemble learning based on generalized additive models. Expert Syst. Appl. 2012, 39, 6816–6826. [Google Scholar] [CrossRef]
- Kim, N.; Jung, K.-H.; Kim, Y.S.; Lee, J. Uniformly subsampled ensemble (USE) for churn management: Theory and implementation. Expert Syst. Appl. 2012, 39, 11839–11845. [Google Scholar] [CrossRef]
- Idris, A.; Rizwan, M.; Khan, A. Churn prediction in telecom using Random Forest and PSO based data balancing in combination with various feature selection strategies. Comput. Electr. Eng. 2012, 38, 1808–1819. [Google Scholar] [CrossRef]
- Idris, A.; Khan, A. Churn Prediction System for Telecom using Filter–Wrapper and Ensemble Classification. Comput. J. 2016, 60, 410–430. [Google Scholar] [CrossRef]
- Zhu, B.; Broucke, S.; Baesens, B.; Maldonado, S. Improving Resampling-based Ensemble in Churn Prediction. In Proceedings of the Machine Learning Research, PMLR, London, UK, 11 October 2017; Volume 74, pp. 79–91. Available online: http://proceedings.mlr.press/v74/zhu17a.html (accessed on 9 August 2021).
- Zhu, B.; Baesens, B.; vanden Broucke, S.K. An empirical comparison of techniques for the class imbalance problem in churn prediction. Inf. Sci. 2017, 408, 84–99. [Google Scholar] [CrossRef] [Green Version]
- Zhu, B.; Baesens, B.; Backiel, A.; Broucke, S.K.L.M.V. Benchmarking sampling techniques for imbalance learning in churn prediction. J. Oper. Res. Soc. 2018, 69, 49–65. [Google Scholar] [CrossRef] [Green Version]
- Jain, H.; Khunteta, A.; Srivastava, S. Churn Prediction in Telecommunication using Logistic Regression and Logit Boost. Procedia Comput. Sci. 2020, 167, 101–112. [Google Scholar] [CrossRef]
- Bhujbal, N.S.; Bavdane, G.P. Leveraging the efficiency of Ensembles for Customer Retention. In Proceedings of the 5th International Conference on I-SMAC (IoT in Social, Mobile, Analytics and Cloud), I-SMAC 2021, Palladam, India, 11–13 November 2021; pp. 1675–1679. [Google Scholar]
- Chowdhury, A.; Kaisar, S.; Rashid, M.; Shafin, S.S.; Kamruzzaman, J. Churn Prediction in Telecom Industry using Machine Learning Ensembles with Class Balancing. In Proceedings of the 2021 IEEE Asia-Pacific Conference on Computer Science and Data Engineering (CSDE), Brisbane, Australia, 8–10 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Deng, Y.; Li, D.; Yang, L.; Tang, J.; Zhao, J. Analysis and prediction of bank user churn based on ensemble learning algorithm. In Proceedings of the 2021 IEEE International Conference on Power Electronics, Computer Applications (ICPECA), Shenyang, China, 22–24 January 2021. [Google Scholar] [CrossRef]
- Janssens, B.; Bogaert, M.; Bagué, A.; van den Poel, D. B2Boost: Instance-dependent profit-driven modelling of B2B churn. Ann. Oper. Res. 2022, 1–27. [Google Scholar] [CrossRef]
- Karuppaiah, K.S.; Palanisamy, N.G. WITHDRAWN: Heterogeneous ensemble stacking with minority upliftment (HESMU) for churn prediction on imbalanced telecom data. Mater. Today Proc. 2021. [Google Scholar] [CrossRef]
- Kiguchi, M.; Saeed, W.; Medi, I. Churn prediction in digital game-based learning using data mining techniques: Logistic regression, decision tree, and random forest. Appl. Soft. Comput. 2022, 118, 108491. [Google Scholar] [CrossRef]
- Sagala, N.T.M.; Permai, S.D. Enhanced Churn Prediction Model with Boosted Trees Algorithms in The Banking Sector. In Proceedings of the 2021 International Conference on Data Science and Its Applications (ICoDSA), Bandung, Indonesia, 6–7 October 2021; pp. 240–245. [Google Scholar] [CrossRef]
- Vo, N.N.; Liu, S.; Li, X.; Xu, G. Leveraging unstructured call log data for customer churn prediction. Knowl.-Based Syst. 2021, 212, 106586. [Google Scholar] [CrossRef]
- Gattermann-Itschert, T.; Thonemann, U.W. How training on multiple time slices improves performance in churn prediction. Eur. J. Oper. Res. 2021, 295, 664–674. [Google Scholar] [CrossRef]
- Corani, G.; Benavoli, A. A Bayesian approach for comparing cross-validated algorithms on multiple data sets. Mach. Learn. 2015, 100, 285–304. [Google Scholar] [CrossRef] [Green Version]
- Van Belle, R.; Baesens, B.; De Weerdt, J. CATCHM: A novel network-based credit card fraud detection method using node representation learning. Decis. Support Syst. 2022, 164, 113866. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Nie, G.; Rowe, W.; Zhang, L.; Tian, Y.; Shi, Y. Credit card churn forecasting by logistic regression and decision tree. Expert Syst. Appl. 2011, 38, 15273–15285. [Google Scholar] [CrossRef]
- Ballings, M.; Poel, D.V.D. Kernel Factory: An ensemble of kernel machines. Expert Syst. Appl. 2013, 40, 2904–2913. [Google Scholar] [CrossRef]
- Porwik, P.; Doroz, R.; Wrobel, K. An ensemble learning approach to lip-based biometric verification, with a dynamic selection of classifiers. Expert Syst. Appl. 2019, 115, 673–683. [Google Scholar] [CrossRef]
- Bryll, R.; Gutierrez-Osuna, R.; Quek, F. Attribute bagging: Improving accuracy of classifier ensembles by using random feature subsets. Pattern Recognit. 2003, 36, 1291–1302. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Bogaert, M.; Ballings, M.; Poel, D.V.D.; Oztekin, A. Box office sales and social media: A cross-platform comparison of predictive ability and mechanisms. Decis. Support Syst. 2021, 147, 113517. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Ballings, M.; Poel, D.V.D. CRM in social media: Predicting increases in Facebook usage frequency. Eur. J. Oper. Res. 2015, 244, 248–260. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Landwehr, N.; Hall, M.; Frank, E. Logistic Model Trees. Mach. Learn. 2005, 59, 161–205. [Google Scholar] [CrossRef] [Green Version]
- Fokkema, M. Fitting Prediction Rule Ensembles with R Package pre. J. Stat. Softw. 2020, 92, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Freund, Y.; Mason, L. The alternating decision tree learning algorithm. In ICML; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1999; Volume 99, pp. 124–133. [Google Scholar]
- Wang, R.; Na Cheng, M.; Loh, Y.M.; Wang, C.; Cheung, C.F. Ensemble learning with a genetic algorithm for surface roughness prediction in multi-jet polishing. Expert Syst. Appl. 2022, 207, 118024. [Google Scholar] [CrossRef]
- Rahman, A.; Verma, B. Ensemble classifier generation using non-uniform layered clustering and Genetic Algorithm. Knowl.-Based Syst. 2013, 43, 30–42. [Google Scholar] [CrossRef]
- Ballings, M.; Poel, D.V.D.; Bogaert, M. Social media optimization: Identifying an optimal strategy for increasing network size on Facebook. Omega 2016, 59, 15–25. [Google Scholar] [CrossRef]
- Zhou, Z.-H.; Wu, J.; Tang, W. Ensembling neural networks: Many could be better than all. Artif. Intell. 2002, 137, 239–263. [Google Scholar] [CrossRef] [Green Version]
- Xue, B.; Zhang, M.; Browne, W.N. Particle swarm optimisation for feature selection in classification: Novel initialisation and updating mechanisms. Appl. Soft Comput. 2014, 18, 261–276. [Google Scholar] [CrossRef]
- Zainudin, M.; Sulaiman, M.; Mustapha, N.; Perumal, T.; Nazri, A.; Mohamed, R.; Manaf, S. Feature Selection Optimization using Hybrid Relief-f with Self-adaptive Differential Evolution. Int. J. Intell. Eng. Syst. 2017, 10, 21–29. [Google Scholar] [CrossRef]
- Meiri, R.; Zahavi, J. Using simulated annealing to optimize the feature selection problem in marketing applications. Eur. J. Oper. Res. 2006, 171, 842–858. [Google Scholar] [CrossRef]
- Molina, D.; Lozano, M.; García-Martínez, C.; Herrera, F. Memetic Algorithms for Continuous Optimisation Based on Local Search Chains. Evol. Comput. 2010, 18, 27–63. [Google Scholar] [CrossRef] [PubMed]
- Ballings, M. Advances and Applications in Ensemble Learning; Ghent University, Faculty of Economics and Business Administration: Ghent, Belgium, 2014. [Google Scholar]
- Coussement, K.; Buckinx, W. A probability-mapping algorithm for calibrating the posterior probabilities: A direct marketing application. Eur. J. Oper. Res. 2011, 214, 732–738. [Google Scholar] [CrossRef]
- Cheng, N.; Wang, H.; Tang, X.; Zhang, T.; Gui, J.; Zheng, C.-H.; Xia, J. An Ensemble Framework for Improving the Prediction of Deleterious Synonymous Mutation. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 2603–2611. [Google Scholar] [CrossRef]
- De, S.; Prabu, P. A Sampling-Based Stack Framework for Imbalanced Learning in Churn Prediction. IEEE Access 2022, 10, 68017–68028. [Google Scholar] [CrossRef]
- Bin, Y.; Zhang, W.; Tang, W.; Dai, R.; Li, M.; Zhu, Q.; Xia, J. Prediction of Neuropeptides from Sequence Information Using Ensemble Classifier and Hybrid Features. J. Proteome Res. 2020, 19, 3732–3740. [Google Scholar] [CrossRef]
- Amin, A.; Al-Obeidat, F.; Shah, B.; Adnan, A.; Loo, J.; Anwar, S. Customer churn prediction in telecommunication industry using data certainty. J. Bus. Res. 2019, 94, 290–301. [Google Scholar] [CrossRef]
- Ahmed, M.; Siddiqi, I.; Afzal, H.; Khan, B. MCS: Multiple classifier system to predict the churners in the telecom industry. In Proceedings of the 2017 Intelligent Systems Conference (IntelliSys), London, UK, 7–8 September 2017; pp. 678–683. [Google Scholar] [CrossRef]
- Bogaert, M.; Lootens, J.; Poel, D.V.D.; Ballings, M. Evaluating multi-label classifiers and recommender systems in the financial service sector. Eur. J. Oper. Res. 2019, 279, 620–634. [Google Scholar] [CrossRef]
- Schetgen, L.; Bogaert, M.; Poel, D.V.D. Predicting donation behavior: Acquisition modeling in the nonprofit sector using Facebook data. Decis. Support Syst. 2021, 141, 113446. [Google Scholar] [CrossRef]
- Carrasco, J.; García, S.; del Mar Rueda, M.; Herrera, F. rNPBST: An R Package Covering Non-parametric and Bayesian Statistical Tests. In Hybrid Artificial Intelligent Systems: 12th International Conference, HAIS 2017 Proceedings 12, La Rioja, Spain, 21–23 June 2017; Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 10334 LNCS; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 281–292. [Google Scholar]
- De Bock, K.W.; Coussement, K.; Lessmann, S. Cost-sensitive business failure prediction when misclassification costs are uncertain: A heterogeneous ensemble selection approach. Eur. J. Oper. Res. 2020, 285, 612–630. [Google Scholar] [CrossRef]
- Benk, G.Y.; Badur, B.; Mardikyan, S. A New 360° Framework to Predict Customer Lifetime Value for Multi-Category E-Commerce Companies Using a Multi-Output Deep Neural Network and Explainable Artificial Intelligence. Information 2022, 13, 373. [Google Scholar] [CrossRef]
- Abellán, J.; Castellano, J.G. A comparative study on base classifiers in ensemble methods for credit scoring. Expert Syst. Appl. 2017, 73, 1–10. [Google Scholar] [CrossRef]

| Classifier | Abbreviation | Description | Hyperparameters |
|---|---|---|---|
| Logistic regression | LR | LR is considered the gold standard in churn prediction, due to its ease-of-implementation, reasonable performance and interpretability [5,51]. | Lasso = true Lambda = 2^{−14, −12, −10, …, 10, 12, 14} |
| Decision tree | DT | The main idea is to partition the data using rules that maximize the homogeneity of the prediction class in the nodes after each split [4]. The CART trees use the Gini index as a splitting criterion, and are easy to interpret [63,64]. | Minimal leaf size = number of instances×(0.01, 0.025, 0.05, 0.1, 0.25, 0.5) Prune = true, false with CP = 0.01 |
| Naïve Bayes | NB | NB uses the Bayes’ theorem with an independence assumption for the features, which implies that all features are equally important to predict churn. It then estimates the class-conditional probabilities per feature to come up with final predictions [34]. | / |
| Support vector machines | SVM | SVM uses the kernel trick to map the input to a high dimensional feature space [65]. Given a certain kernel function, the model then constructs a hyperplane that maximizes the margin between the classes. | Kernel = RBF C = 2−5, 2−1, 23, 27, 211, 215 ϒ = 2−15, 2−11, 2−7, 2−3, 21, 23 |
| Logit leaf model | LLM | The core idea is that decision trees create different segments of the data on which logistic regression models are built. By doing so, the LLM combines comprehensibility with accuracy [13]. | Minimal leaf size = 100 |
| Prune = 0.25 | |||
| Artificial neural networks | ANN | We implement a Multi-Layer Perceptron (MLP), which is a network that is organized in at least three layers: input, hidden, and output layer. The nodes of the input layer correspond with the independent variables and the dependent variable is represented in the output layer. The hidden layer is fully connected with the input and output layer and captures non-linearity of the data [17]. MLPs are trained using the back-propagation algorithm and the sigmoid activation function is used [17]. | Max number of weights = 5000 Max number of iterations = 5000 Decay = 0.001, 0.01, 0.1 Size = 2, 3,…, 20 |
| Classifier | Abbreviation | Description | Hyperparameters |
|---|---|---|---|
| Bagging | BAG | Bagging stands for bootstrap aggregating and was invented by Leo Breiman [63]. The idea is to train independent classifiers on bootstrap samples of the original data set. This is often performed by growing CART on the bootstrap samples. However, bagging can be combined with any base classifier. | Number of bootstrap samples = 10, 20, 30,…, 100 |
| Uniform subsampled ensemble | USE | USE is a variation on bagging, where the training samples are uniformly divided without replacement, and thus less data is needed to train the model [45]. | Number of uniform samples = 10, 15 Kernel = RBF |
| Random subspace method | RSM | RSM trains different samples of the data using random subsets of the features [67]. | Number of samples = 100 |
| Random forest | RF | RF combines bagging and random subspace method with CART as a base classifier [68]. The main idea is to decorrelate the trees in the ensemble, thereby decreasing the variance [69]. | Number of predictors to consider (m) = sqrt(number of variables) Number of trees = 500 |
| Improved balance random forest | IBRF | IBRF is a combination of weighted random forest, where the minority class has a higher prediction weight, and balanced random forests, where the minority class is oversampled [42]. The idea is that the best features are learned iteratively by changing the class distributions such that a higher penalty is given to misclassifications of the minority class. | Number of trees = 50 m = 0.5 d = 0.1 |
| Adaboost | ADA | The original boosting algorithm adaboost sequentially gives more weight to misclassified observations in order to boost the performance of the final ensemble [8]. | Number of iterations = 10, 50, 100, 250, 500, 1000 |
| Stochastic gradient boosting | SGB | Gradient boosting iteratively fits additive models on the residual error to minimize a certain loss function [70]. Stochastic gradient boosting is an extension that adds randomness to each iteration by training on a random subsample of the data. | Number of iterations = 50, 100, 250, 500 Maximum depth = 4, 6, 8 Shrinkage = 0.1 |
| XGBoost | XGB | XGB is a computational and mathematical improvement over the gradient boosting algorithm [71]. XGB calculates the second-order derivative of the loss function to speed up convergence and adds a penalty term to the individual trees to avoid overfitting. | Same as SGB |
| Light GBM | LGBM | LGBM is a powerful and light-weighted implementation of gradient boosting [14]. The main innovation of LGBM lies in the use of leaf-wise tree building and a histogram-based greedy search. By using these two techniques, the training time and memory usage is significantly decreased. | Same as SGB |
| Catboost | CATB | CATB is the most recent gradient boosting alternative and is designed to work particularly well with categorical features [15]. CATB proposes ordered gradient boosting to improve the training process and ordered target statistics to effectively handle categorical features. | Same as SGB |
| Logistic model tree | LMT | LMT uses a combination of decision trees and LogitBoost to create predictions [72]. LogitBoost is equivalent to adaboost with the exception that it uses a logistic loss function. LMT start by constructing a LogitBoost model at the root node and then splits the data using the C4.5 splitting rules and creates new LogitBoost models on the child splits. | Number of iterations = 200 |
| Rotation forest | ROTFOR | Rotation-based classifiers rotate the training data of the base classifiers by applying a rotation of the axes. The most well-known algorithm in this case is rotation forest, which applies principal components analysis on each bootstrap sample [43]. | Number of samples = 100 Number of predictors to consider = 3 |
| Alternating decision trees | ADT | ADT is a combination of prediction and decision nodes, where the final prediction is the sum of the prediction along the path of the tree that a customer has followed [73]. | Number of iterations = 10, 20, 30, 40, 50 |
| Prediction rule-based ensembles | PRE | PRE combines the benefits of tree-based ensemble methods with the interpretability of simple rules [74]. PRE create an initial set of rules from a gradient boosting model and retain a sparse set of rules by using lasso regression. The original variables are also added to the final regression by using linear basis functions. | Base ensemble = gradient boosting Rule inductor = conditional inference tree |
| Method | Abbreviation | Hyperparameters |
|---|---|---|
| Standard average | AVGS | / |
| Weighted average | AVGW | / |
| Stacking | STACK | Meta-learner = Random forest |
| Genetic algorithm | GA | Selection method = binary tournament selection Population size = 7 × number of variables Mutation chance = 0.033, 1/Population size Number of generations = 500 Elitism = max(1, 0.05 × Population size) |
| Hill-climbing ensemble selection with bagging | HCES-BAG | Number of iterations = 5, 25 |
| Non-negative binomial likelihood | NNBL | / |
| Goldfarb-Idnani Non-Negative Least Squares | GINNLS | / |
| Lawson-Hanson Non-Negative Least Squares | LHNNLS | / |
| Differential evolution | DE | Crossover probability = 0.5, 0.6938 Step size = 0.9314 Population size = 20, 100 Number of generations = 50, 500 |
| Particle swarm optimization | PSO | Swarm size = 30, 40 Iterations = 100, 500 |
| Generalized simulated annealing | GSA | Iterations = 500 Temperature = 0.5 Maximum calls = 1 × 107 Visiting parameter = 2.7 Acceptance parameter = −5 |
| Memetic algorithm | MA | Population size = 60 Local search = CMA-ES Iterations = 300 Effort = 0.5 Alpha = 0.5 Threshold = 10 × 10−8 |
| Self-organizing migrating algorithm | SOMA | Path length = 3 Step length = 0.11 Perturbation chance = 0.1 Minimum absolute step = 0 Minimum relative step = 0.001 Number of migrations = 300 Population size = 10 |
| Name | Source | Sector | #Instances | #Numeric Features | #Discrete Features | Churn rate (%) | Example Variables |
|---|---|---|---|---|---|---|---|
| D1 | Private | Newspaper | 1178 | 440 | 0 | 27 |
|
| D2 | Private | Racing | 14,179 | 4 | 0 | 78 |
|
| D3 | Private | B2B | 41,739 | 44 | 3 | 4 |
|
| D4 | Kaggle 1 | Telecom | 3333 | 17 | 3 | 14 |
|
| D5 | Kaggle 2 | Bank | 10,000 | 6 | 4 | 20 |
|
| D6 | KDD 3 | Telecom | 46,933 | 3 | 4 | 7 |
|
| D7 | Kaggle 4 | Telecom | 3333 | 8 | 2 | 14 |
|
| D8 | Kaggle 5 | Telecom | 7043 | 3 | 16 | 27 |
|
| D9 | Kaggle 6 | Telecom | 2000 | 9 | 4 | 50 |
|
| D10 | Kaggle 7 | Telecom | 51047 | 35 | 21 | 29 |
|
| D11 | UCI 8 | Telecom | 5000 | 15 | 3 | 14 |
|
| Family | Classifier | AUC | TDL | ACC | F1 | EMPC | Average | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rank | p-Value | Rank | p-Value | Rank | p-Value | Rank | p-Value | Rank | p-Value | Rank | Rank per Family | ||
| Single | LR | 24.545 | 0.000 | 23.727 | 0.000 | 23.273 | 0.003 | 23.545 | 0.002 | 25.455 | 0.000 | 24.109 | 24.779 |
| DT | 29.182 | 0.000 | 19.318 | 0.012 | 19.682 | 0.051 | 13.818 | 1.000 | 30.545 | 0.000 | 22.509 | ||
| SVM | 29.000 | 0.000 | 27.045 | 0.000 | 27.182 | 0.000 | 25.455 | 0.000 | 27.091 | 0.000 | 27.155 | ||
| NB | 27.909 | 0.000 | 24.727 | 0.000 | 26.091 | 0.000 | 26.364 | 0.000 | 29.000 | 0.000 | 26.818 | ||
| ANN | 22.000 | 0.002 | 19.909 | 0.007 | 24.182 | 0.001 | 25.182 | 0.000 | 21.000 | 0.002 | 22.455 | ||
| LLM | 25.727 | 0.000 | 27.636 | 0.000 | 24.273 | 0.001 | 23.409 | 0.003 | 27.091 | 0.000 | 25.627 | ||
| Homogeneous | BAG | 24.545 | 0.000 | 17.955 | 0.033 | 23.045 | 0.004 | 22.182 | 0.007 | 25.273 | 0.000 | 22.600 | 19.949 |
| USE | 27.545 | 0.000 | 27.364 | 0.000 | 25.045 | 0.001 | 21.682 | 0.010 | 28.182 | 0.000 | 25.964 | ||
| RF | 22.182 | 0.002 | 16.591 | 0.077 | 22.864 | 0.004 | 22.455 | 0.006 | 19.909 | 0.006 | 20.800 | ||
| IBRF | 20.455 | 0.009 | 17.364 | 0.048 | 16.909 | 0.290 | 14.591 | 1.000 | 22.818 | 0.000 | 18.427 | ||
| ADA | 23.000 | 0.001 | 14.182 | 0.228 | 19.636 | 0.051 | 17.318 | 0.254 | 22.000 | 0.001 | 19.227 | ||
| XGB | 17.364 | 0.092 | 12.909 | 0.324 | 22.500 | 0.006 | 23.091 | 0.003 | 18.364 | 0.020 | 18.845 | ||
| CATB | 11.364 | 1.000 | 11.000 | 0.589 | 15.273 | 0.717 | 13.455 | 1.000 | 15.091 | 0.197 | 13.236 | ||
| LGBM | 13.455 | 0.941 | 11.273 | 0.589 | 17.545 | 0.204 | 19.000 | 0.085 | 15.273 | 0.197 | 15.309 | ||
| SGB | 16.545 | 0.153 | 14.455 | 0.214 | 20.591 | 0.027 | 21.909 | 0.008 | 18.545 | 0.019 | 18.409 | ||
| LMT | 26.091 | 0.000 | 21.909 | 0.001 | 20.864 | 0.023 | 23.091 | 0.003 | 26.000 | 0.000 | 23.591 | ||
| RSM | 24.000 | 0.000 | 20.182 | 0.006 | 22.636 | 0.005 | 22.000 | 0.008 | 26.182 | 0.000 | 23.000 | ||
| ROTFOR | 23.727 | 0.000 | 22.227 | 0.001 | 17.955 | 0.165 | 17.182 | 0.262 | 21.364 | 0.002 | 20.491 | ||
| ADT | 22.455 | 0.001 | 15.182 | 0.145 | 20.091 | 0.039 | 17.909 | 0.179 | 22.273 | 0.001 | 19.582 | ||
| PRE | 18.455 | 0.045 | 16.182 | 0.098 | 21.364 | 0.015 | 23.909 | 0.002 | 19.091 | 0.012 | 19.800 | ||
| Heterogeneous | GA | 6.727 | 1.000 | 17.636 | 0.040 | 9.682 | 1.000 | 10.545 | 1.000 | 5.545 | 1.000 | 10.027 | 10.234 |
| HCES_BAG | 7.636 | 1.000 | 15.364 | 0.143 | 12.045 | 1.000 | 13.364 | 1.000 | 5.273 | 1.000 | 10.736 | ||
| AVGS | 9.318 | 1.000 | 17.318 | 0.048 | 10.636 | 1.000 | 12.955 | 1.000 | 9.409 | 1.000 | 11.927 | ||
| AVGW | 8.364 | 1.000 | 15.818 | 0.119 | 10.591 | 1.000 | 12.182 | 1.000 | 8.182 | 1.000 | 11.027 | ||
| STACK | 17.545 | 0.085 | 5.000 | - | 12.045 | 1.000 | 9.273 | 1.000 | 15.273 | 0.197 | 11.827 | ||
| NNBL | 8.318 | 1.000 | 11.409 | 0.589 | 7.409 | - | 7.318 | - | 10.409 | 1.000 | 8.973 | ||
| GINNLS | 7.273 | 1.000 | 8.773 | 0.720 | 8.227 | 1.000 | 9.227 | 1.000 | 7.364 | 1.000 | 8.173 | ||
| LHNNLS | 7.182 | 1.000 | 8.773 | 0.720 | 8.227 | 1.000 | 9.227 | 1.000 | 7.636 | 1.000 | 8.209 | ||
| DE | 9.364 | 1.000 | 18.545 | 0.022 | 9.909 | 1.000 | 11.545 | 1.000 | 6.727 | 1.000 | 11.218 | ||
| PSO | 8.182 | 1.000 | 18.182 | 0.028 | 11.409 | 1.000 | 12.818 | 1.000 | 6.455 | 1.000 | 11.409 | ||
| GSA | 6.091 | - | 13.636 | 0.248 | 11.864 | 1.000 | 13.636 | 1.000 | 5.182 | - | 10.082 | ||
| MA | 7.727 | 1.000 | 15.455 | 0.143 | 9.818 | 1.000 | 11.727 | 1.000 | 5.818 | 1.000 | 10.109 | ||
| SOMA | 7.727 | 1.000 | 13.955 | 0.234 | 8.136 | 1.000 | 9.636 | 1.000 | 7.182 | 1.000 | 9.327 | ||
| AUC | |||
|---|---|---|---|
| AUC All | AUC Telco | AUC Other | |
| AUC All | 1.000 | 0.989 | 0.958 |
| AUC Telco | 0.989 | 1.000 | 0.904 |
| AUC Other | 0.958 | 0.904 | 1.000 |
| TDL | |||
| TDL All | TDL Telco | TDL Other | |
| TDL All | 1.000 | 0.963 | 0.853 |
| TDL Telco | 0.963 | 1.000 | 0.682 |
| TDL Other | 0.853 | 0.682 | 1.000 |
| ACC | |||
| ACC All | ACC Telco | ACC Other | |
| ACC All | 1.000 | 0.960 | 0.781 |
| ACC Telco | 0.960 | 1.000 | 0.575 |
| ACC Other | 0.781 | 0.575 | 1.000 |
| EMPC | |||
| EMPC All | EMPC Telco | EMPC Other | |
| EMPC All | 1.000 | 0.993 | 0.978 |
| EMPC Telco | 0.992 | 1.000 | 0.945 |
| EMPC Other | 0.978 | 0.945 | 1.000 |
| F1 | |||
| F1 All | F1 Telco | F1 Other | |
| F1 All | 1.000 | 0.946 | 0.722 |
| F1 Telco | 0.946 | 1.000 | 0.458 |
| F1 Other | 0.722 | 0.458 | 1.000 |
| All | Telco | Other | |
|---|---|---|---|
| AUC | GSA | NNBL | GSA |
| TDL | STACK | STACK | STACK |
| ACC | NNBL | NNBL | DE |
| EMPC | GSA | NNBL | DE |
| F1 | GSA | DE | HCES_BAG |
| Family | Classifier | AUC | TDL | ACC | F1 | EMPC | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Score | ROPE | Score | ROPE | Score | ROPE | Score | ROPE | Score | ROPE | ||
| Single | LR | 0.754 | 0.004 | 1.906 | 0.000 | 0.820 | 0.016 | 0.815 | 0.041 | 10.219 | 0.001 |
| DT | 0.700 | 0.000 | 2.780 | 0.032 | 0.845 | 0.274 | 0.842 | 0.474 | 10.177 | 0.000 | |
| SVM | 0.736 | 0.000 | 2.465 | 0.000 | 0.781 | 0.000 | 0.792 | 0.000 | 10.442 | 0.000 | |
| NB | 0.723 | 0.000 | 1.922 | 0.000 | 0.801 | 0.000 | 0.796 | 0.001 | 10.255 | 0.000 | |
| ANN | 0.777 | 0.116 | 2.688 | 0.043 | 0.843 | 0.224 | 0.826 | 0.163 | 10.779 | 0.066 | |
| LLM | 0.722 | 0.000 | 2.021 | 0.000 | 0.805 | 0.001 | 0.788 | 0.000 | 9.948 | 0.000 | |
| Homogeneous | BAG | 0.770 | 0.053 | 2.861 | 0.113 | 0.845 | 0.257 | 0.827 | 0.175 | 10.726 | 0.009 |
| USE | 0.732 | 0.000 | 2.016 | 0.000 | 0.793 | 0.000 | 0.802 | 0.007 | 10.136 | 0.000 | |
| RF | 0.775 | 0.099 | 2.885 | 0.152 | 0.840 | 0.179 | 0.811 | 0.019 | 10.905 | 0.057 | |
| IBRF | 0.786 | 0.248 | 2.877 | 0.090 | 0.840 | 0.185 | 0.832 | 0.277 | 10.850 | 0.032 | |
| ADA | 0.771 | 0.067 | 3.039 | 0.311 | 0.831 | 0.075 | 0.835 | 0.339 | 10.793 | 0.019 | |
| XGB | 0.793 | 0.378 | 3.034 | 0.366 | 0.842 | 0.206 | 0.815 | 0.038 | 10.934 | 0.205 | |
| CATB | 0.800 | 0.446 | 2.998 | 0.257 | 0.848 | 0.307 | 0.843 | 0.481 | 11.011 | 0.242 | |
| LGBM | 0.796 | 0.405 | 3.043 | 0.355 | 0.855 | 0.433 | 0.836 | 0.353 | 10.987 | 0.237 | |
| SGB | 0.793 | 0.372 | 2.941 | 0.340 | 0.850 | 0.359 | 0.832 | 0.275 | 10.925 | 0.156 | |
| LMT | 0.755 | 0.005 | 2.490 | 0.001 | 0.840 | 0.174 | 0.820 | 0.085 | 10.389 | 0.006 | |
| RSM | 0.762 | 0.021 | 2.258 | 0.000 | 0.835 | 0.104 | 0.828 | 0.207 | 10.357 | 0.011 | |
| ROTFOR | 0.739 | 0.000 | 2.623 | 0.002 | 0.848 | 0.304 | 0.835 | 0.345 | 10.809 | 0.003 | |
| ADT | 0.782 | 0.172 | 2.821 | 0.081 | 0.838 | 0.142 | 0.837 | 0.377 | 10.759 | 0.095 | |
| PRE | 0.791 | 0.332 | 2.810 | 0.235 | 0.841 | 0.201 | 0.826 | 0.165 | 10.907 | 0.049 | |
| Heterogeneous | GA | 0.804 | 0.477 | 2.936 | 0.109 | 0.860 | 0.485 | 0.833 | 0.307 | 11.109 | 0.272 |
| HCES_BAG | 0.804 | 0.480 | 2.959 | 0.171 | 0.860 | 0.491 | 0.835 | 0.332 | 11.111 | - | |
| AVGS | 0.803 | 0.477 | 2.929 | 0.112 | 0.861 | 0.498 | 0.837 | 0.379 | 11.084 | 0.277 | |
| AVGW | 0.803 | 0.465 | 2.948 | 0.134 | 0.861 | 0.500 | 0.837 | 0.389 | 11.087 | 0.270 | |
| STACK | 0.786 | 0.250 | 3.140 | - | 0.853 | 0.425 | 0.849 | - | 11.020 | 0.073 | |
| NNBL | 0.804 | 0.473 | 3.012 | 0.202 | 0.863 | - | 0.844 | 0.522 | 11.106 | 0.279 | |
| GINNLS | 0.805 | 0.481 | 3.062 | 0.356 | 0.862 | 0.495 | 0.845 | 0.524 | 11.102 | 0.273 | |
| LHNNLS | 0.805 | - | 3.062 | 0.343 | 0.862 | 0.493 | 0.845 | 0.503 | 11.102 | 0.279 | |
| DE | 0.803 | 0.470 | 2.927 | 0.090 | 0.861 | 0.486 | 0.835 | 0.347 | 11.094 | 0.273 | |
| PSO | 0.803 | 0.463 | 2.929 | 0.110 | 0.860 | 0.495 | 0.835 | 0.345 | 11.107 | 0.278 | |
| GSA | 0.805 | 0.471 | 2.976 | 0.195 | 0.861 | 0.484 | 0.837 | 0.379 | 11.109 | 0.273 | |
| MA | 0.804 | 0.485 | 2.953 | 0.138 | 0.861 | 0.501 | 0.837 | 0.384 | 11.105 | 0.275 | |
| SOMA | 0.804 | 0.478 | 2.956 | 0.155 | 0.863 | 0.483 | 0.840 | 0.437 | 11.084 | 0.273 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bogaert, M.; Delaere, L. Ensemble Methods in Customer Churn Prediction: A Comparative Analysis of the State-of-the-Art. Mathematics 2023, 11, 1137. https://doi.org/10.3390/math11051137
Bogaert M, Delaere L. Ensemble Methods in Customer Churn Prediction: A Comparative Analysis of the State-of-the-Art. Mathematics. 2023; 11(5):1137. https://doi.org/10.3390/math11051137
Chicago/Turabian StyleBogaert, Matthias, and Lex Delaere. 2023. "Ensemble Methods in Customer Churn Prediction: A Comparative Analysis of the State-of-the-Art" Mathematics 11, no. 5: 1137. https://doi.org/10.3390/math11051137
APA StyleBogaert, M., & Delaere, L. (2023). Ensemble Methods in Customer Churn Prediction: A Comparative Analysis of the State-of-the-Art. Mathematics, 11(5), 1137. https://doi.org/10.3390/math11051137






