Abstract
Aiming at the shortcomings of non-optimal fuel consumption and low accuracy of Geosynchronous orbit (GEO) satellites in the east/west station keeping (EWSK) at the current stage, a micro-thrust EWSK algorithm for GEO satellites based on a single-synovial surface is proposed. This algorithm has the characteristics of low fuel consumption and high control precision. However, when this algorithm performs GEO station switching under the condition of limited velocity increment, the mean longitude capture path may not be optimal, the capture time of the mean longitude is too long, and the engineering applicability is not good. In view of the above problems, a micro-thrust EWSK for GEO satellites based on dual synovial surfaces is proposed. Through the advance planning of the mean longitude, the control lag caused by the limited velocity increment is eliminated, the optimal path-planning problem of the mean longitude is solved, and the capture time of the mean longitude is greatly shortened. The two EWSK algorithms proposed in this paper have the advantages of small calculation amount, optimal fuel consumption, high precision and strong stability, which have good engineering application value.
MSC:
85-10
1. Introduction
Geosynchronous equatorial orbit (GEO) satellites [1,2] are high-orbit satellites located above the equator. They have the characteristics of wide ground coverage and fixed pointing to the ground, and are widely used in communication, navigation, meteorological observation, and other fields.
However, under the action of various natural perturbations, satellites in GEO will gradually drift away from the original orbit, which will not only reduce the work efficiency of satellites, but may also cause satellites in GEO to collide. Therefore, keeping control of the GEO satellite orbit is required on a regular basis to keep the GEO satellite near its designed orbital position. The station keeping (SK) of the GEO satellite is divided into north/south station keeping (NSSK) and east/west station keeping (EWSK). The NSSK is also called orbital inclination keeping, which is the out-of-plane control; the EWSK includes the mean longitude keeping and the eccentricity vector keeping, which is the orbital in-plane control [3]. In the literature [3], we have studied the NSSK method with high precision and low fuel consumption. A method of micro-thrust low-fuel consumption, and high-precision east/west station keeping control for GEO satellites will be studied in this study.
Some scholars have studied the use of micro-thrust for SK in recent years, and it has been applied to GEO satellites such as Boeing 702 satellites [4,5]. Weiss et al. [6], Lin et al. [7], Caverly et al. [8], Weiss et al. [9], Walsh et al. [10] and others used model prediction (MPC) method to realize the SK of the GEO satellites. This algorithm requires that the thrust of the electric thruster be continuously adjustable, which requires too much computing power and is not friendly to spaceborne implementation. In addition, Frederik et al. [11], Gazzino et al. [12,13,14,15], Sukhanov et al. [16], Roth et al. [17] and others used various optimization algorithms to realize the SK of the GEO satellites.
However, the above research on pulse thrust and micro-thrust SK control have the disadvantages of low SK accuracy and high fuel consumption, and all require open-loop control of the satellite–ground loop, which is not autonomous [18]. As the number of satellites increases, there is an increasing need for SK accuracy of the GEO satellites [19]. Additionally, higher control accuracy requires more frequent control, which increases the burden on the ground station [20].
In view of the above background, this paper proposes a micro-thrust mean longitude-keeping method based on the single-synovial variable structure algorithm. However, the mean longitude-keeping algorithm based on a single-synovial surface assumes pulsed thrust, which is suitable for the longitude-keeping capture with low fuel consumption. Additionally, the mean longitude capture time is not optimal in some working conditions, which will lead to the control lag problem. Therefore, on the basis of the single-synovial algorithm, by adding a synovial surface to optimize the mean longitude capture time, not only is the fuel usage the most economical, but the optimum mean longitude capture time under all working conditions can also be achieved. In addition, by planning and activating tangential SK control in advance, rapid capture of longitude can be achieved, so as to solve the control lag problem. The block diagram of the proposed algorithm is shown in Figure 1.
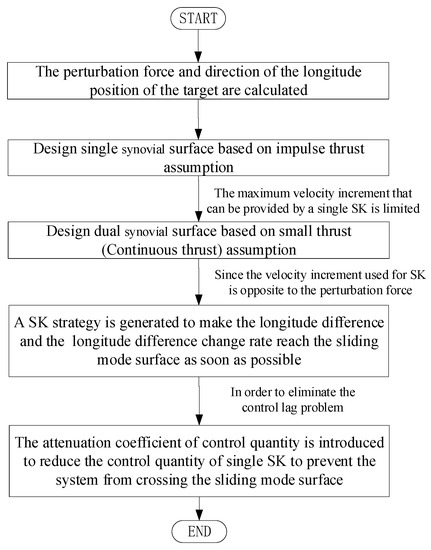
Figure 1.
The block diagram of the proposed algorithm.
The method proposed in this note can achieve mean longitude quickly, capture and stable EWSK with minimum fuel consumption, and is suitable for on-board autonomous control. The EWSK method proposed in this paper is simple and effective, and has great engineering application value.
The structure of this paper is as follows: Section 2 presents the method of mean longitude keeping by single-synovial surface, introduces the strategy for the mean longitude keeping and the calculation method of the control amount, and analyzes the stability and adaptability of the algorithm. Section 3 presents the method of mean longitude keeping by double-synovial surface, introduces the strategy for the mean longitude keeping and the calculation method of the control amount, and analyzes the stability and adaptability of the algorithm. The two synovial control algorithms are verified by simulation in Section 4. The full text is summarized in Section 5.
2. Mean Longitude Keeping Based on Single-Synovial Surface
The EWSK can be regarded as the problem of the orbital keeping control of the chief satellite relative to the target satellite, and the goal is to make the distance between the chief satellite and the target satellite tend to zero. The EWSK includes the mean longitude keeping and the eccentricity vector keeping, while mean longitude keeping is the most important part in the EWSK. The mean longitude keeping is realized, which means that the mean longitude drift rate is zero, so the orbital semi-major axis keeping is also realized. On the contrary, if the orbital semi-major axis keeping is realized, the satellite may still have a deviation of the mean longitude drift rate. Therefore, orbital semi-major axis and mean longitude keeping may also be referred to as mean longitude keeping.
The following five functional requirements and design constraints need to be met for mean longitude keeping:
- (1)
- The mean longitude keeping frequency is about once a day;
- (2)
- The thruster deviation angle is basically unchanged during the mean longitude keeping;
- (3)
- In order to achieve optimal fuel orbital capture and keeping, the velocity increment required for the mean longitude keeping is only used to overcome the orbital perturbation;
- (4)
- The longitude of the satellite satisfies the condition: ;
- (5)
- There is no constraint on the duration of capturing the target.
The mean longitude keeping of the chief satellite relative to the target satellite is essentially by offsetting the environmental interference along the tangential direction, changing the orbital semi-major axis, and then changing the satellite longitude drift rate to achieve the mean longitude capture and keeping. Therefore, when calculating the control strategy, not only the mean longitude difference, but also the change rate of the mean longitude is considered. When the mean longitude is kept in a stable state, the arc length of the mean longitude keeping using micro-thrust only accounts for about 5.8% of the arc length of the complete GEO, so the mean longitude keeping can also be regarded as pulse orbital change.
2.1. Mean Longitude Keeping Strategy
The relationship between mean longitude difference and the mean longitude drift rate is shown in Figure 2.
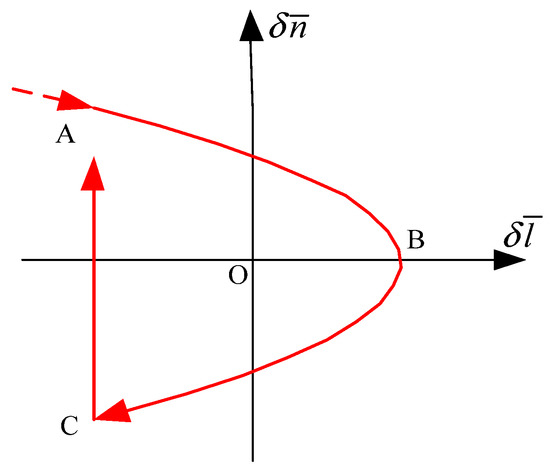
Figure 2.
Ideal phase plane of the mean longitude difference and the mean longitude drift rate.
When the envelope of the parabola is the largest, the right boundary (unit rad) of the mean longitude keeping satisfies:
where, is the mean angular acceleration, which is the orbital angular acceleration of the chief satellite relative to the target satellite, in rad/s2; T is orbital period of GEO satellites, which is about 86,400 s. Since the orbital angular acceleration of the target satellite is zero, is also equal to the orbital angular acceleration of the chief satellite.
As shown in Figure 2, after mean longitude keeping at the control point (C), the curve enters the standard synovial surface (point A). Under the action of the natural perturbation force along the synovial surface, the curve passes through point B and returns to point C again, forming a complete closed loop, that is, a unilateral limit cycle. All control amounts in the unilateral limit cycle are canceled with environmental disturbances, so it is also the most fuel-efficient control method.
The mean longitude drift rate at the control time is calculated as:
where,
is the time of the current position to the center of the target position;
is the difference of the average angular velocity between the chief satellite and the target satellite, which is called the right ascension drift rate of the chief satellite relative to the target satellite, in rad/s. The calculation formula of is:
where,
is the mean semi-major axis of the chief satellite, in m;
is the semi-major axis of the target satellite, in m;
is the average angular velocity of the target satellite, in rad/s.
The formula for calculating the mean longitude difference at the control time is:
where,
is the difference of the mean longitude between the chief satellite and target satellite, it is hereinafter referred to as the “mean longitude difference,” in rad.
The mean longitude difference and the mean longitude drift rate are respectively described in the time domain coordinate system, as shown in Figure 3.
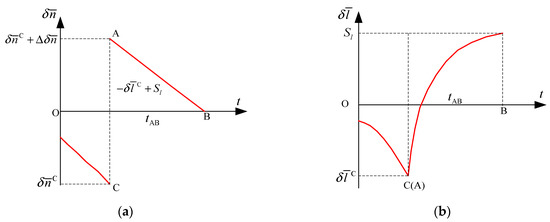
Figure 3.
Variation of the mean longitude difference and the mean longitude drift rate over time. (a) Variation of the mean longitude drift rate over time; (b) Variation in the mean longitude difference over time.
The definitions of points A, B and C in Figure 2 are the same as those in Figure 2. In Figure 3a, the abscissa is time, and the ordinate is the mean longitude drift rate. In Figure 3b, the abscissa is time, and the ordinate is the mean longitude difference.
Then, we have:
where,
is the mean longitude drift rate at the control point, in rad/s;
is the mean longitude difference at the control point, in rad/s;
is the change amount of the mean longitude drift rate caused by the SK, in rad/s;
is the time required for the mean longitude drift rate to decay to zero after orbital control, in s. When in the ideal state as shown in Figure 2, .
In Formula (5), and are unknowns, and the control amount of the mean longitude drift rate required for SK can be obtained by solving the quadratic equation system in one variable:
The relationship between the mean angular acceleration and the orbital semi-major axis is:
Combining Equations (6) and (7), the control amount of the semi-major axis required for SK can be obtained as:
The pulse thrust control equation of major semi-axis is:
Combining Equations (8) and (9), the tangential velocity increment for mean longitude control can be obtained as:
It can be seen from Equation (10) that once the control point is on the parabola, there is no need to perform mean longitude keeping control, because the control point can slide to along the synovial surface under the action of the natural perturbation force. However, this has a disadvantage. Once there is a trajectory prediction error, an orbital calculation error or an actuator error, the control point may fall into the forbidden SK zone. Once it falls into the forbidden SK zone, according to the principle of the most economical fuel, under the action of no active SK, the mean longitude difference will exceed , causing control overshoot and affecting the convergence time of .
The solutions to the above-mentioned defects are as follows. When the initial mean longitude difference is negative and the absolute value is large, the tangential control ability is abundant. At this time, the synovial surface is not changed, and a longitude keeping attenuation coefficient is introduced. Then, a large tangential control is decomposed into multiple small control, and the control point is always below the synovial surface until it falls into the stable SK point . Therefore, Equation (10) can be rewritten as:
For the mean longitude keeping based on a single-synovial surface, the smaller is, the more obvious the delay effect caused by the control after the introduction of the attenuation coefficient , so the velocity increment used for orbital correction in the path planning process is also larger, and vice versa. Considering the planning path and overshoot, generally . Under the action of Equation (11), the process in which the mean longitude of the chief satellite gradually approaches the mean longitude of the target satellite can be regarded as a path-planning process based on the synovial surface, and a small amount of orbital control can be regarded as a path-correction process.
2.2. Calculation of Control Amount
When using Formula (11) to calculate the velocity increment, it is required that no singularity occurs, that is, the number of squared roots is not less than zero, so the following formula must be satisfied:
Since , Equation (12) becomes:
The zone that does not satisfy Formula (13) is called the “mean longitude forbidden SK zone one” (it is hereinafter referred to as the ‘forbidden SK zone one’). At this time, , as shown in the red shaded area in Figure 4.
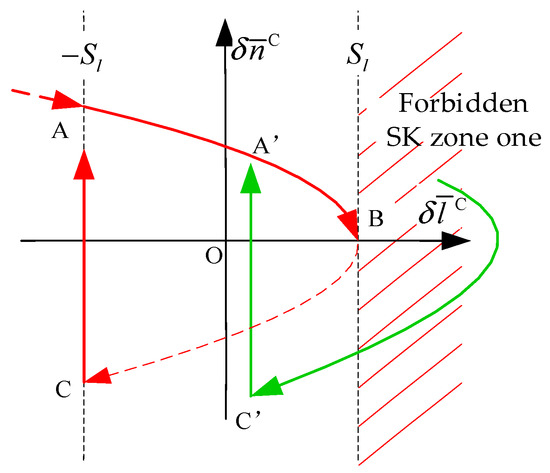
Figure 4.
Mean longitude forbidden SK zone one.
When the initial mean longitude difference is in the “forbidden SK zone one,” as shown by the green curve in Figure 4, as long as the mean longitude satisfies , , orbital control is not required at this time. Under the action of the earth’s non-spherical gravitational force, the orbit of the chief satellite is lifted, causing the westward retreat effect of the mean longitude, that is , so sooner or later, the necessary condition for the SK will be satisfied, corresponding to the C’ point in the green curve. At this time, it is only necessary to adjust the orbital semi-major axis, so that the mean longitude difference and the mean longitude drift rate returns to the point A’. Then, the mean longitude can be captured and kept. This process realizes the mean longitude keeping using the non-spherical gravity of the Earth. It can be seen that not being in the “forbidden SK zone one” is a necessary but not sufficient condition to satisfy the SK condition.
Additionally, fuel economy means that the tangential velocity increments from the control action are only used to counteract the velocity increments from the earth’s non-aspherical gravitational perturbations. When , the semi-major axis of the GEO satellite will continue to increase under the action of the earth’s non-spherical gravitational force. Therefore, the velocity increment produced by the control action must be in the opposite direction of the satellite’s flight, reducing the orbital altitude. The formula for calculating the tangential velocity for mean longitude keeping is:
It is required that the above formula does not occur in singularity; it must satisfy:
The zone that does not satisfy Formula (15) is called the “mean longitude forbidden SK zone two” (it is hereinafter referred to as the ‘forbidden SK zone two’), as shown in the red shaded area in Figure 4.
It is required that Equation (15) does not occur in singularity, the following equation must be satisfied, that is there is no overlap between the forbidden SK zone one and forbidden SK zone two.
It can be seen from Figure 5 that when the initial mean longitude difference is in the forbidden SK zone two, even if no SK control is applied, under the action of the earth’s non-spherical gravitational force, the mean longitude difference will reach or exceed . Therefore, when the initial mean longitude difference is in the forbidden SK zone two, without exerting control, it will automatically enter the forbidden SK zone one, and then enter the stable zone.
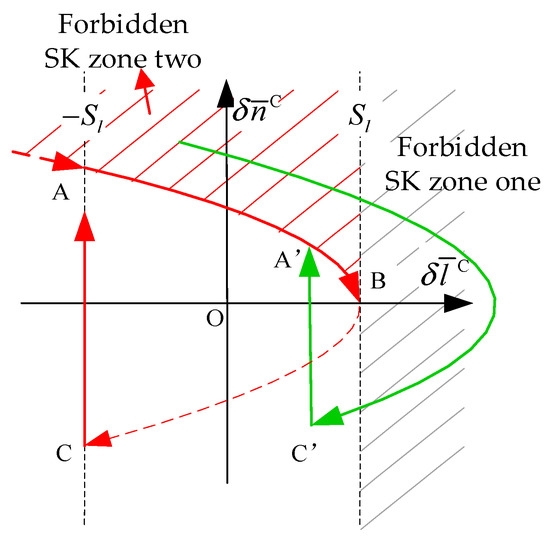
Figure 5.
Mean longitude of the forbidden SK zone two.
Equation (16) is a sufficient and necessary condition for mean longitude keeping. The non-shaded part in Figure 4 and Figure 5 is the controllable zone for the mean longitude keeping, that is, the mean longitude is returned to the synovial surface AB through the control action.
In summary, the control strategy of the mean longitude keeping based on single-synovial surface is:
2.3. Stability Analysis of Control Strategy
The stability of the single-synovial surface control system is proved by Lyapunov stability theorem, and the proof process is as follows:
Take the Lyapunov function of the control system as:
The first derivative of the above equation with respect to time t is:
As shown Figure 3, in Equation (19), , < 0. However, before controlling. Therefore, before controlling. According to Lyapunov stability theorem, the system is unstable.
After controlling, . From Formula (6), it can be obtained that:
Therefore, after controlling. According to Lyapunov stability theorem, the system is stable.
It can be seen from the above proof that the system is not a real-time stable system. It is unstable until control is exerted. However, when control is applied, the system is asymptotically stable. Even if the system goes beyond the synovial surface due to control overshoot or other uncertain factors, it will eventually return to a stable synovial surface over time, and the whole system will not diverge. The process of returning to the synovial surface when the system exceeds the synovial surface will be described in detail next.
Assuming that the mean longitude of the chief satellite satisfies , at this time, the tangential acceleration generated by the earth’s non-spherical gravitational force makes the orbital height continue to rise, and the mean longitude drift rate continues to decrease. The Cartesian coordinate system formed by the mean longitude difference and the mean longitude drift rate can be divided into three zones, corresponding to the following three situations:
- (1)
- As shown in Figure 4, when the initial mean longitude difference and the mean longitude drift rate is located at C’ (in the SK zone). Under the action of the tangential velocity increment, the mean longitude drift rate will change sign, and finally intersect with the synovial surface AB, and converge along the synovial surface AB to the vicinity of point B, achieving stable mean longitude keeping.
- (2)
- As shown in Figure 4, when the initial mean longitude difference and the mean longitude drift rate is located in the forbidden SK zone one, under the action of the earth’s non-spherical gravitational force, the curve will move along the green parabola until it entry SK controllable zone, which becomes the case (1). Then it goes through the same process of case (1) to achieve stable mean longitude keeping.
- (3)
- As shown in Figure 5, when the initial mean longitude difference and the mean longitude drift rate is in the forbidden SK zone two, under the action of the earth’s non-aspherical gravitational force, the curve will move along the green parabola to the forbidden SK zone one, which becomes case (2), and then entry SK controllable zone, which becomes the case (1). Finally, it goes through the same process of case (1) and achieve stable mean longitude keeping.
It can be seen that when the mean longitude of the chief satellite satisfies , regardless of the initial mean longitude difference and the mean longitude drift rate, a stable mean longitude keeping can be achieved in the end theoretically.
It is worth noting that when the mean longitude of the target satellite is close to the equilibrium point (75.1° E, 165.1° E), the effect of the earth’s non-aspherical gravitational force in the tangential direction is too small, and the minimum unilateral limit cycle is unstable, resulting in the occurrence of algorithm error. Once the mean longitude of the chief satellite exceeds zone , the direction of the tangential acceleration generated by the earth’s non-aspherical gravitational force will switch. In the absence of orbital control, the chief satellite will gradually move away from the mean longitude of the target satellite, causing the mean longitude to run out of control.
2.4. Adaptive Analysis of Control Strategy
When the mean longitude of the chief satellite is close to the equilibrium point (75.1° E, 165.1° E), the mean longitude is easily disturbed and out of control. In addition, if the mean longitude of the target satellite is switched near the equilibrium point, the mean longitude will naturally drift slowly, and the mean longitude capture time will also be greatly increased. To sum up, it is suggested that the mean longitude of the target satellite should be within the range of (85.1° E, 155.1° E).
In addition to the target mean longitude requirements, the algorithm applicability is also related to the orbital semi-major axis of the chief satellite. Due to the limited control capability of electric propulsion, if the absolute value of the difference between the current orbital semi-major axis and the nominal orbital semi-major axis is too large, the initial capture of the mean longitude may fail. Therefore, the orbital semi-major axis of the chief satellite should meet the conditions of the quasi-synchronous orbit, that is, the semi-major axis is ±35 km of the semi-major axis of the standard GEO.
In order to make the capture time of the target mean longitude as short as possible, the initial mean longitude and the mean longitude drift rate should meet the following conditions as much as possible: first, the difference between the target mean longitude and the current mean longitude should be as small as possible; second, the initial mean longitude and the mean longitude drift rate should be as close as possible to the synovial surface of natural drift; third, on the basis of the second rule, the initial mean longitude and mean longitude drift rate should be located below the synovial surface. Because the mean longitude is in a continuously controlled state at this time, the target mean longitude can be approached in the way of path planning to achieve rapid capture of the target mean longitude. Otherwise, if the initial mean longitude and mean longitude drift rate are located above the synovial surface, the mean longitude is in an uncontrolled state, and it is necessary to pass through the forbidden SK zone two and forbidden SK zone one in Figure 4 in turn, then arrive below the synovial surface so the target mean longitude capture can be realized. In the whole process, the overshoot of the mean longitude capture process is large, and the capture time is long.
3. Mean Longitude Keeping Based on Dual Synovial Surface
The mean longitude-keeping algorithm based on a single-synovial surface assumes pulsed thrust, which is suitable for the steady state longitude keeping with low fuel consumption. Both the mean longitude keeping and the mean longitude capture are optimal for fuel, but the mean longitude capture time is not optimal in some working conditions.
Therefore, on the basis of the single-synovial algorithm, by adding a synovial surface to optimize the mean longitude capture time, not only is the fuel the most economical, but also the optimum mean longitude capture time under all working conditions can be achieved. In addition, by planning and activating tangential SK control in advance, rapid capture of longitude can be achieved, so as to solve the control lag problem.
3.1. Mean Longitude Keeping Strategy
When the initial orbital semi-major axis or the initial mean longitude has a large deviation, the mean longitude keeping requires a large tangential velocity increment. However, in practice, the daily tangential velocity increments that can be provided for mean longitude keeping are limited, and tangential velocity increments need to be applied for several consecutive days. In fact, after the control effect of SK cancels the perturbation interference, the phase plane of the mean longitude difference and the mean longitude drift rate also takes the form of a synovial surface, and the direction of the mean longitude drift is opposite to the natural drift direction of the mean longitude.
In addition, when , theoretically, the perturbation force of the earth’s non-aspherical gravitational gravity in the tangential direction will continue to raise the orbital height. However, in different mean longitudes, the magnitude of the perturbation force of the earth’s non-aspherical gravitational gravity in the tangential direction is also different. For example, when the mean longitude is about 120°, the tangential perturbation force has the greatest effect, corresponding to a 2 m/s velocity increment per year for the mean longitude keeping; when the mean longitude is 75° or 165°, the tangential perturbation force is zero. The maximum value of the tangential velocity increment of the single SK can be regarded as unchanged. Therefore, in the process of large-scale transfer of the mean longitude, with the continuous change of the perturbation force of the earth’s non-aspherical gravitational gravity in the tangential direction, the synovial surface is in a dynamic change process. Therefore, the mean longitude-keeping algorithm in this section is also called the dynamic dual synovial mean longitude-keeping algorithm.
In response to the above problems, in addition to meeting the five requirements mentioned in Section 3, a new requirement for fast capture of the target mean longitude is added. In order to achieve this goal, it is necessary to optimize the mean longitude-keeping algorithm to reduce the capture time of the mean longitude.
The dual synovial surfaces mentioned above are: ① the mean longitude difference and mean longitude drift rate caused by the perturbation force of the earth’s non-spherical gravitational force in the tangential direction; ② the mean longitude difference and mean longitude drift rate caused by the combined action of the perturbation force of the earth’s non-spherical gravitational force in the tangential direction and the control force of the mean longitude keeping. For different synovial surfaces, the calculation of the control amount is also different.
The mean longitude-keeping strategy based on the dual synovial surface is shown in Figure 6.
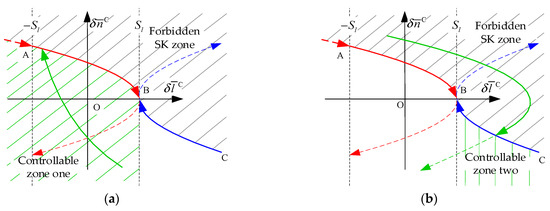
Figure 6.
The mean longitude keeping strategy based on the dual synovial surface. (a) represents the controllable zone one, representing the first expression in Equation (25). (b) represents the controllable zone two, representing the second expression in Equation (25).
In Figure 6, the red curve AB is the synovial surface of the mean longitude difference and the mean longitude drift rate caused by the tangential perturbation force of the earth’s non-aspherical gravitational force, which is the part of the red parabola. The blue curve CB is the synovial surface of the mean longitude difference and the mean longitude drift under the combined action of the SK control force and the earth’s non-spherical gravitational force, which is the part of the red parabola. The two curves are tangent at their vertices, with slopes of +∞ and −∞, respectively. The upper part of the connecting line between the two synovial surfaces is the forbidden SK zone. In the forbidden SK zone, performing a tangential SK in a negative flight direction will cause the mean longitude difference to exceed its right boundary.
Figure 6a is the controllable zone corresponding to the synovial surface AB, which is located below the synovial surface AB, and its goal is to make the controlled object enter the AB synovial surface as soon as possible. Figure 6b shows the controllable zone corresponding to the synovial surface CB, which is located below the synovial surface CB, and its goal is to make the controlled object enter the CB synovial surface as soon as possible.
3.2. Calculation of Control Amount
The controllable zone corresponding to the synovial surface AB in Figure 6a has the same SK strategy as the synovial surface AB, corresponding to Figure 4 in Section 3, and the calculation of the SK control amount is also consistent.
For the controllable zone corresponding to the synovial surface CB in Figure 6b, the tangential velocity increment used for the mean longitude keeping control is:
where, is the equivalent mean angular acceleration when the velocity increment of daily SK is the largest, the unit is rad/s2, and its expression is:
where,
is the maximum value of the tangential velocity increment that can be provided in the east-west direction, in m/s;
is the daily velocity increment generated by the earth’s non-aspherical gravitational force in the tangential direction at different geographic longitudes, unit m/s:
In the Formula (21), is the right boundary of the controllable zone two in Figure 6b, the unit is rad, and its expression is:
Combining Equations (21) and (24), the control strategy for the mean longitude keeping based on the dual synovial surface is:
It should be noted that the attenuation coefficient of the mean longitude keeping of the synovial surface AB acts directly on the velocity increment and does not affect the path planning of mean longitude capture. However, the attenuation coefficient of the mean longitude keeping of the synovial surface CB acts on the path planning in order to prevent overshoot caused by insufficient orbit control capability. Therefore, the path planning timing is advanced to ensure that the control capability has a certain margin, so as to ensure that the mean longitude capture can be completed quickly on the synovial surface CB.
3.3. Stability Analysis of Control Strategy
The stability proof of dual-synovial surface control is the same as that of single-synovial surface control. Similarly, the system is not a real-time stable system. It is unstable until control is exerted. However, when control is applied, the system is asymptotically stable. Even if the system goes beyond the synovial surface due to control overshoot or other uncertain factors, it will eventually return to a stable synovial surface over time, and the whole system will not diverge. The process of returning to the synovial surface when the system exceeds the synovial surface will be described in detail next.
Assuming that the mean longitude of the chief satellite satisfies , at this time, the tangential acceleration generated by the earth’s non-spherical gravitational force makes the orbital height continue to rise, and the mean longitude drift rate continues to decrease. The Cartesian coordinate system formed by the mean longitude difference and the mean longitude drift rate can be divided into three zones, corresponding to the following three situations:
- (1)
- As shown in Figure 6a, when the initial mean longitude difference and the mean longitude drift rate is located in the controllable zone one, the same as the mean longitude based on a single-synovial surface, under the action of the tangential velocity increment, the sign of the mean longitude drift rate will change, and intersects with the synovial surface AB, and finally converges along the synovial surface AB near point B, forming a stable mean longitude keeping.
- (2)
- As shown in Figure 6b, when the initial mean longitude difference and the mean longitude drift rate is located in the controllable zone two, under the action of the tangential velocity increment, the mean longitude drift rate will change its sign and approach the synovial surface CB. If the synovial surface CB can be tracked in the controllable zone two, it will converge to the vicinity of point B along the synovial surface CB, forming a stable longitude keeping. If the synovial surface CB cannot be tracked in the controllable zone two, the control strategy switches to the controllable zone one, and finally converges along the synovial surface AB to the vicinity of point B, forming a stable longitude keeping.
- (3)
- As shown in Figure 6b, when the initial mean longitude difference and the mean longitude drift rate is located in the forbidden SK zone and is far away from the synovial surface AB and CB, under the action of the earth’s non-spherical gravitational force, the curve will move along the green parabola to the “controllable zone two”, which becomes the situation (2), and then becomes the situation (1), and finally realizes the stable mean longitude keeping. In addition, when the initial mean longitude difference and the mean longitude drift rate is located in the forbidden SK zone and is close to the synovial surface AB, it may be due to the surface modeling error of the synovial film, the curve will intersect with the synovial surface AB, and it will directly become the situation (1), and finally converge along the synovial surface AB to the vicinity of point B, forming a stable mean longitude keeping.
It can be seen that when the mean longitude of the chief satellite satisfies , regardless of the initial mean longitude difference and the mean longitude drift rate, a stable mean longitude keeping can be achieved in the end theoretically.
Same as mean longitude keeping with single-synovial surface, when the mean longitude of the target satellite is close to the equilibrium point (75.1° E, 165.1° E), the effect of the earth’s non-aspherical gravitational force in the tangential direction is too small, and the minimum unilateral limit cycle is unstable, resulting in the occurrence of algorithm error. Once the mean longitude of the chief satellite exceeds zone , the direction of the tangential acceleration generated by the earth’s aspherical gravitational force will switch. In the absence of orbital control, the chief satellite will gradually move away from the mean longitude of the target satellite, causing the mean longitude to run out of control.
3.4. Adaptive Analysis of Control Strategy
Same as the mean longitude keeping with single-synovial plane, it is suggested that the mean longitude of the target satellite should be within the range of (85.1° E, 155.1° E). The semi-major axis of the chief satellite is ±35 km of the semi-major axis of the standard GEO.
Compared with the mean longitude keeping with single-synovial surface, the mean longitude keeping with dual synovial surface increases the controllable zone two, the curve responds in advance, and the capture time of the target mean longitude can be greatly reduced without increasing the fuel consumption.
The smaller the difference between the target mean longitude and the current mean longitude, the shorter the capture time of the target mean longitude. The closer the initial mean longitude and mean longitude drift rate are to the natural drift synovial surface (including the synovial surface AB and CB in Figure 6), the shorter the capture time of the target mean longitude.
It is worth noting that when the difference between the target and the current mean longitude is large, the addition of controllable zone two can make the model of the mean longitude keeping switch from pulse approximation to continuous thrust approximation. The accuracy of the control model is improved, so the capture time of the target mean longitude can be significantly shortened, and it has strong engineering application value.
4. Simulation and Analysis
4.1. Mean Longitude Keeping with Single-Synovial Surface
The environment used for simulations is Simulink, and the dynamic model used in the simulations is described in Table 1. Four simulation conditions are designed to cover the four zones of the phase plane of the mean longitude difference and the mean longitude drift rate, as shown in Table 2. In the following simulations, the maximum deflection angle of the thrust from the positive and negative normal directions to the positive and negative tangential directions is .

Table 1.
Dynamic model used in the simulations.

Table 2.
Simulation conditions of the mean longitude keeping with single-synovial surface.
4.1.1. Example One
The initial orbital values used in example one are shown in Table 3.

Table 3.
The initial simulation value of the example one of the mean longitude keeping with single-synovial surface.
The results are shown in Figure 7. It can be seen from Figure 7a that although the semi-major axis keeping and capture are realized, the capture and keeping of the semi-major axis has a small amount of overshoot.
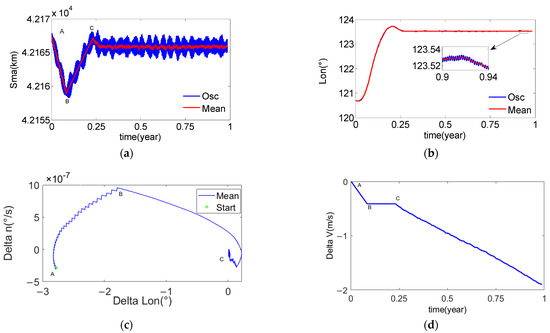
Figure 7.
The example one of the mean longitude keeping with single-synovial surface. (a) Orbital semi-major axis of the chief satellite; (b) Mean longitude of the chief satellite; (c) The phase plane formed by the mean longitude difference and the mean longitude drift rate; (d) The desired velocity increment for the mean longitude keeping.
It can be seen from Figure 7b,c that although the mean longitude capture and keeping is completed, the capture time of the mean longitude is about 3.5 months, and the process of mean longitude capture occurs overshoot. The process of overshoot is as follows: in Figure 7c, the velocity increment in point B is excessively large, so that the mean longitude difference and the mean longitude drift rate are located above the synovial surface. They pass through the forbidden SK zone two and forbidden SK zone one in turn, and finally reach the controllable zone, completing the mean longitude capture.
It can be seen from Figure 7d that all tangential velocity Increments are used to reduce the orbital semi-major axis. It shows that this strategy is the most fuel-saving strategy for the mean longitude keeping, and the velocity increment used for mean longitude keeping in one year is about 2 m/s. In addition, there is no tangential direction control amount during the period from B to C, indicating that there is no orbital control amount correction in this process.
4.1.2. Example Two
The initial orbital values used in this example are same as example one, but changed from 1 to 0.8. The results are shown in Figure 8.
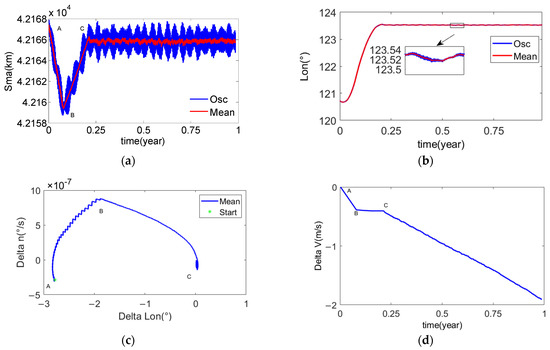
Figure 8.
The example two of the mean longitude keeping with single-synovial surface. (a) Orbital semi-major axis of the chief satellite; (b) Mean longitude of the chief satellite; (c) The phase plane formed by the mean longitude difference and the mean longitude drift rate; (d) The desired velocity increment for the mean longitude keeping.
It can be seen from Figure 8a that the semi-major axis keeping and capture are realized, and there is no overshoot in the process of the semi-major axis capture and keeping.
It can be seen from Figure 8b,c that the initial mean longitude and the longitude drift rate are located below the synovial surface, which is the controllable zone. There is no overshoot in the process of the target mean longitude capture, and the capture time is only about three months. Compared with example one, it can be regarded as a fast capture of the target mean longitude.
It can be seen from Figure 8d that all tangential velocity Increments are used to reduce the orbital semi-major axis. It shows that this strategy is the most fuel-saving strategy for the mean longitude keeping, and the velocity increment used for mean longitude keeping in one year is about 2 m/s. In addition, there is a small control amount in the tangential direction during the period from B to C, which means that there is always a small amount of orbital adjustment in the process to ensure that the mean longitude approaches the target mean longitude according to the specified path. It achieves fast capture of the mean longitude without overshoot and shows that the mean longitude attenuation coefficient is useful.
4.1.3. Example Three
The initial orbital values used in example three are shown in Table 4.

Table 4.
The initial simulation value of the example three of the mean longitude keeping with single-synovial surface.
The results are shown in Figure 9. It can be seen from Figure 9a that the semi-major axis keeping and capture are realized.
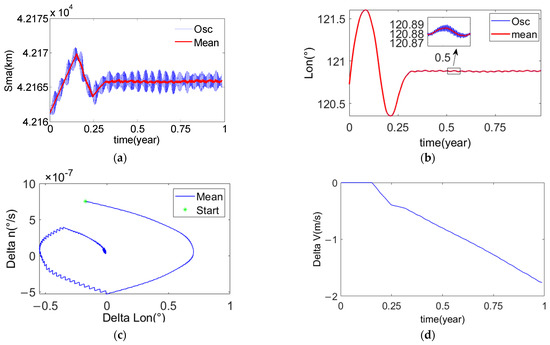
Figure 9.
The example three of the mean longitude keeping with single-synovial surface. (a) Orbital semi-major axis of the chief satellite; (b) Mean longitude of the chief satellite; (c) The phase plane formed by the mean longitude difference and the mean longitude drift rate; (d) The desired velocity increment for the mean longitude keeping.
It can be seen from Figure 9b,c that the initial mean longitude and mean longitude drift rate are located in the forbidden SK zone two. At this time, it is necessary to use the natural drift of the mean longitude to enter the forbidden SK zone one from the forbidden SK zone two to reach the controllable zone. Therefore, the capture time of the mean longitude is longer, about four months.
It can be seen from Figure 9d that all tangential velocity increments are used to reduce the orbital semi-major axis. It shows that this strategy is the most fuel-saving strategy for the mean longitude keeping. The velocity increment used for mean longitude keeping in one year is about 1.7 m/s, which is slightly less than that of example one. This is because the initial orbital altitude is about 5 km lower, thus reducing the need for velocity increments of the mean longitude keeping.
Compared with example two, the capture time of the target mean longitude of the example three is longer, which is consistent with the analysis in Section 3.4.
4.1.4. Example Four
The initial orbital values used in example four are shown in Table 5.

Table 5.
The initial simulation value of the example four of the mean longitude keeping with single-synovial surface.
The results are shown in Figure 10. It can be seen from Figure 10a that the semi-major axis keeping and capture are realized.
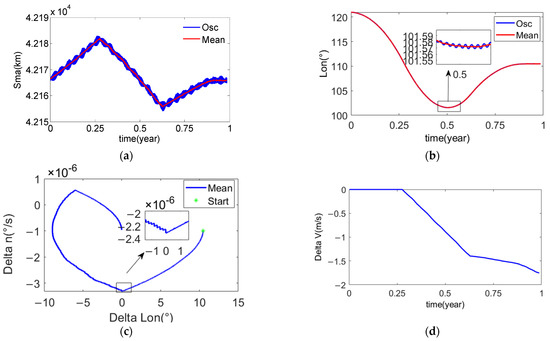
Figure 10.
The example four of the mean longitude keeping with single-synovial surface. (a) Orbital semi-major axis of the chief satellite; (b) Mean longitude of the chief satellite; (c) The phase plane formed by the mean longitude difference and the mean longitude drift rate; (d) The desired velocity increment for the mean longitude keeping.
It can be seen from Figure 10b that this algorithm achieves the capture of about 12° of mean longitude. However, due to the overshoot in the capture process, the mean longitude capture took a long time, and it took about 10 months to complete the mean longitude capture.
It can be seen from Figure 10c that the initial mean longitude and mean longitude drift rate are located in the forbidden SK zone one. At this time, it is necessary to use the natural drift of the mean longitude to enter the controllable zone from the forbidden SK zone one. It is consistent with the analysis in Section 3.4.
It can be seen from Figure 10d that all tangential velocity increments are used to reduce the orbital semi-major axis. It shows that this strategy is the most fuel-saving strategy for the mean longitude keeping. The velocity increment used for mean longitude keeping in one year is about 2 m/s.
The above four examples show that the mean longitude keeping with single-synovial surface has good stability, and can quickly achieve mean longitude capture and keeping with minimum fuel consumption.
It can be seen from example one and example two that after introducing the mean longitude keeping attenuation coefficient , there is no overshoot in the mean longitude capture process, and the time required to capture the target mean longitude is shorter.
It can be seen from examples three and four that there is an overshoot in the capture of the mean longitude and the semi-major axis, and the algorithm has room for optimization.
4.2. Mean Longitude Keeping with Dual Synovial Surface
The environment used for simulations is Simulink, and the dynamic model used in the simulations is described in Table 1. Three simulation conditions are designed to cover the three zone of the phase plane of the mean longitude difference and the mean longitude drift rate, as shown in Table 6. In the following simulations, the maximum deflection angle of the thrust from the positive and negative normal directions to the positive and negative tangential directions is .

Table 6.
Simulation conditions of the mean longitude keeping with dual-synovial surface.
4.2.1. Example One
The initial orbital values used in example one are shown in Table 7.

Table 7.
The initial simulation value of the example one of the mean longitude keeping with dual synovial surface.
The results are shown in Figure 10. It can be seen from Figure 11a that although the semi-major axis keeping and capture are realized, the capture and keeping of the semi-major axis has a small amount of overshoot.
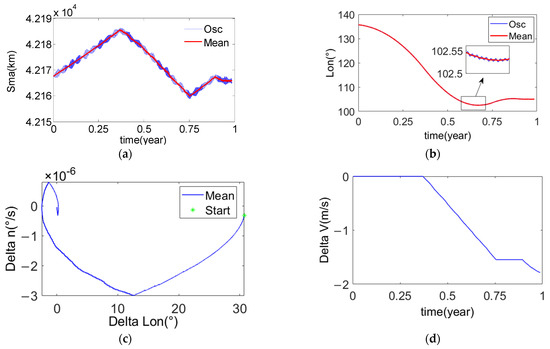
Figure 11.
The example one of the mean longitude keeping with dual synovial surface. (a) Orbital semi-major axis of the chief satellite; (b) Mean longitude of the chief satellite; (c) The phase plane formed by the mean longitude difference and the mean longitude drift rate; (d) The desired velocity increment for the mean longitude keeping.
It can be seen from Figure 11b,c that the capture time from 135° to 105° in mean longitude is about 10 months, and the capture process appears to overshoot. Because the synovial surface planning does not consider the margin, the SK control cannot strictly track the synovial surface, so overshoot occurs, which prolongs the capture time of the target mean longitude.
It can be seen from Figure 11d that all tangential velocity increments are used to reduce the orbital semi-major axis. It shows that this strategy is the most fuel-saving strategy of the mean longitude keeping. The velocity increment used for mean longitude keeping in one year is about 1.8 m/s.
4.2.2. Example Two
The initial orbital values used in this example are same as example one, but changed from 1 to 0.8. The results are shown in Figure 11.
It can be seen from Figure 12a that the semi-major axis keeping and capture are realized, and there is no overshoot in the process of the semi-major axis capture and keeping.
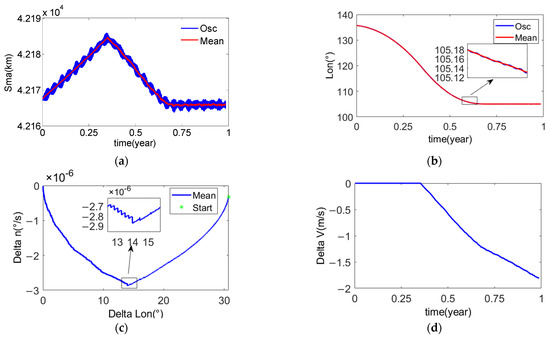
Figure 12.
The example two of the mean longitude keeping with dual synovial surface. (a) Orbital semi-major axis of the chief satellite; (b) Mean longitude of the chief satellite; (c) The phase plane formed by the mean longitude difference and the mean longitude drift rate; (d) The desired velocity increment for the mean longitude keeping.
It can be seen from Figure 12b,c that there is no overshoot in the capture process of mean longitude from 135° to 105°, and the capture time is about 7.5 months, which is about 2.5 months faster than example one. It turns out that the introduction of the mean longitude-keeping attenuation coefficient is useful.
It can be seen from Figure 12d that all tangential velocity increments are used to reduce the orbital semi-major axis. It shows that this strategy is the most fuel-saving strategy of the mean longitude keeping. The velocity increment used for mean longitude keeping in one year is about 1.8 m/s.
4.2.3. Example Three
The initial orbital values used in example three are shown in Table 8.

Table 8.
The initial simulation value of the example three of the mean longitude keeping with dual-synovial surface.
The results are shown in Figure 13. It can be seen from Figure 13a that the semi-major axis keeping and capture are realized, and there is no overshoot in the process of the semi-major axis capture and keeping.
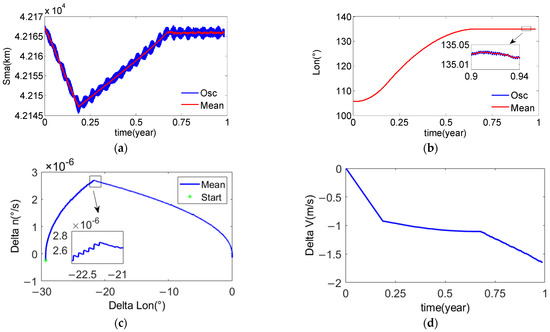
Figure 13.
The example three of the mean longitude keeping with dual synovial surface. (a) Orbital semi-major axis of the chief satellite; (b) Mean longitude of the chief satellite; (c) The phase plane formed by the mean longitude difference and the mean longitude drift rate; (d) The desired velocity increment for the mean longitude keeping.
It can be seen from Figure 13b,c that there is no overshoot in the capture process of mean longitude from 135° to 105°, and the capture time is about 7.5 months.
It can be seen from Figure 13d that all tangential velocity increments are used to reduce the orbital semi-major axis. It shows that this strategy is the most fuel-saving strategy for mean longitude keeping. The velocity increment used for mean longitude keeping in one year is about 1.6 m/s.
The above three examples show that the mean longitude keeping with dual synovial surface has good stability, and can quickly achieve mean longitude capture and keeping with minimum fuel consumption.
It can be seen from example one and example two that after introducing the mean longitude-keeping attenuation coefficient , there is no overshoot in the mean longitude-capture process, and the time required to capture the target mean longitude is shorter.
Example two and example three illustrate that the mean longitude keeping with dual synovial surface can achieve the transfer and keeping of the mean longitude of in about 7.5 months without consuming additional fuel.
5. Conclusions
In this paper, a high-precision micro-thrust EWSK control method for GEO satellites based on two control algorithms of single-synovial surface and dual synovial surface is proposed. The algorithm proposed in this paper has high precision, low fuel consumption, strong stability, and is suitable for on-board autonomous control. The velocity increment used for mean longitude keeping in one year is less than 2 m/s, and the control accuracy of mean longitude is better than 0.01°. Moreover, the dual-synovial surface control method is not only suitable for stable keeping of mean longitude, but also for fast capture of mean longitude under the condition of limited velocity increment, which solves the control lag problem of the single-synovial surface control method. In particular, in view of the constraint of finite tangential velocity of single SK, based on the single-synovial surface algorithm, the dual-synovial surface algorithm eliminates the control lag caused by finite velocity increment by planning the starting time of tangential SK thrust in advance, and realizes the fast capture of longitude from west to east without overshooting. Then, the fast capture with no overshoot of longitude is realized.
Author Contributions
Methodology, L.Y., F.L.; software, L.Y.; writing—original draft & review & editing, C.L.; data curation, H.Y.; Validation, J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Nature Science Foundation of China, grant number U20B2056.
Data Availability Statement
Not applicable.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Chao, C.C. Applied Orbit Perturbation and Maintenance; The Aerospace Press: El Segundo, CA, USA, 2005. [Google Scholar]
- Wang, Z.C.; Xing, G.H.; Zhang, H.W. Handbook of Geostationary Orbits; National Defense Industry Press: Beijing, China, 1999. [Google Scholar]
- Ye, L.; Liu, C.; Zhu, W.; Yin, H.; Liu, F.; Baoyin, H. North/south Station Keeping of the GEO Satellites in Asymmetric Configuration by Electric Propulsion with Manipulator. Mathematics 2022, 10, 2340. [Google Scholar] [CrossRef]
- Possner, M.P.; Almendra, M.; Garcia, G. A New Flight Dynamics Solution for Operations of the Boeing 702 Satellite. In Proceedings of the AIAA Space 2008 Conference & Exposition, San Diego, CA, USA, 9–11 September 2008. [Google Scholar]
- Feuerborn, S.A.; Neary, D.A.; Perkins, J.M. Finding a way: Boeing’s All Elecric Propulsion Satellite. In Proceedings of the 49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, San Jose, CA, USA, 14–17 July 2013. [Google Scholar]
- Weiss, A.; Cairano, D. Station Keeping and Momentum Management of Low-thrust Satellites Using MPC. Aerosp. Sci. Technol. 2018, 76, 229–241. [Google Scholar] [CrossRef]
- Lin, S.Y.; Li, M.; Yang, Z. Position maintenance and momentum wheel unloading control of electric propulsion satellites based on model prediction and orbit recursion. In Proceedings of the 4th Annual Conference on High Resolution Earth Observation, Wuhan, China, 17–18 September 2017. [Google Scholar]
- Caverly, R.; Cairano, D.; Weiss, A. Split-Horizon MPC for Coupled Station Keeping, Attitude Control, and Momentum Management of GEO Satellites using Electric Propulsion. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018. [Google Scholar]
- Weiss, A.; Kalabic, U.; Cairano, S. Model Predictive Control for Simultaneous Station keeping and Momentum Management of Low-thrust Satellites. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015. [Google Scholar]
- Walsh, A.; Cairano, D.; Weiss, A. MPC for coupled station keeping, attitude control, and momentum management of low-thrust geostationary satellites. In Proceedings of the 2016 Annual American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016. [Google Scholar]
- Frederik, J.; Bruijn, D. Geostationary Satellite Station-Keeping Using Convex Optimization. J. Guid. Control Dyn. 2015, 39, 605–616. [Google Scholar]
- Gazzino, C.; Arzelier, D.; Cerri, L.; Losa, D.; Louembet, C.; Pittet, C. A Three-step Decomposition Method for Solving the Minimum-fuel Geostationary Station Keeping of Satellites Equipped with Electric Propulsion. Acta Astronatica 2019, 158, 12–22. [Google Scholar] [CrossRef]
- Gazzino, C.; Arzelier, D.; Losa, D.; Louembet, C.; Pittet, C.; Cerri, L. Optimal Control for Minimum-fuel Geostationary Station Keeping of Satellites Equipped with Electric Propulsion. IFAC Pap. Online 2016, 49, 379–384. [Google Scholar] [CrossRef]
- Gazzino, C.; Louembet, C.; Arzelier, D.; Jozefowiez, N.; Losa, D.; Cerri, C.P. Interger Programming for Optimal Control of Geostationary Station Keeping of Low-thrust Satellites. In Proceedings of the 20th IFAC World Congress 2017, Toulouse, France, 9–14 July 2017. [Google Scholar]
- Gazzino, C.; Arzelier, D.; Cerri, L.; Pittet, C.; Losa, D. Long-Term Electric-Propulsion Geostationary Station-Keeping via Integer Programming. J. Guid. Control Dyn. 2019, 42, 976–991. [Google Scholar] [CrossRef]
- Sukhanov, A.A.; Prado, A.F. On one Approach to the Optimization of Low-thrust Station Keeping Manoeuvres. Adv. Space Res. 2012, 50, 1478–1488. [Google Scholar] [CrossRef]
- Roth, M. Strategies for Geostationary Spacecraft Orbit SK Using Electrical Propulsion Only. Ph.D. Thesis, Czech Technical University, Prague, Czech Republic, 2020. [Google Scholar]
- Ogawa, N.; Terui, F.; Mimasu, Y.; Yoshikawa, K.; Ono, G.; Yasuda, S.; Matsushima, K.; Masuda, T.; Hihara, H.; Sano, J.; et al. Image-based autonomous navigation of Hayabusa2 using artificial landmarks: The design and brief in-flight results of the first landing on asteroid Ryugu. Astrodyn 2020, 4, 89–103. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, S. Non-equatorial equilibrium points around an asteroid with gravitational orbit-attitude coupling perturbation. Astrodyn 2020, 4, 1–16. [Google Scholar] [CrossRef]
- Zhang, T.J.; Wolz, D.; Shen, H.X.; Luo, Y.-Z. Spanning tree trajectory optimization in the galaxy space. Astrodyn 2021, 5, 1–16. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).