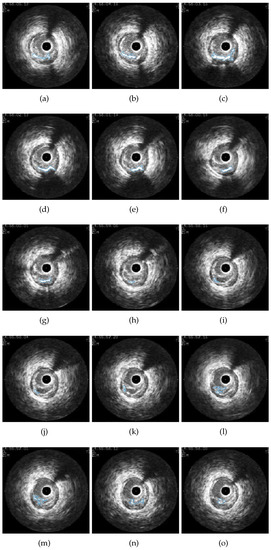
Abstract
The occurrence of atheroma plaques in the arteries can eventually obstruct them, leading to diseases such as atherosclerosis, which can cause, among others, a myocardial infarction or a stroke. As a consequence, it is necessary to shorten the time spent in locating and reconstructing the atheroma plaque that can be developed in an artery. This localization is usually conducted manually from the contours located on the cross-sectional radiographs of the artery and then reconstructed by creating the volumes using different techniques. This paper presents a 3-D reconstruction of the atheroma plaque by applying an image processing algorithm ad-hoc developed in order to obtain the boundaries of the atheroma, from a set of intravascular ultrasound images. The advantage of the approach developed in this paper is that it can be implemented in common medical procedures, as an important complementary decision-support tool. By reconstructing the atheroma instead of the artery, this work provides a different approach to improve its location and treatment. Results presented herein can be implemented in machine-learning-based algorithms, able to predict the growth and extent of incipient atheroma plaques, which ultimately contribute to an early detection of this pathology.
MSC:
68W99
1. Introduction
Currently, the link between engineering and medicine is well consolidated, as evidenced by the development of one of the most recent branches of engineering: biomedicine. The union of these two sciences helps with the diagnosis or treatment of many diseases. Numerous advances in biomedicine have been developed in recent decades. Within the medical context, these techniques have been also successfully applied to different clinical applications, for instance; diagnosis of cancer or melanomas [1,2,3], personalization of drug doses [4], and generation of synthetic dataset of microbial colonies [5]. They have been also used in the cardiovascular field, for instance; treating cardiovascular diseases [6,7], cardiovascular tissue characterisation [8,9] and for the interpretation of electrocardiography signals [10]. The present work focuses on cooperation with the field of cardiology and, within this, on the study of a lesion, the atheroma plaque.
An atheroma can be defined as a deposit of low-density lipoprotein (LDL) particles, located in the walls of the arteries, to which monocytes (a type of leukocyte) adhere. Atheromatosis or atherosclerosis are diseases caused by an obstruction of the arteries due to the appearance of atheroma plaques that, over time, narrow the arteries until they become obstructed. These diseases may lead to a myocardial infarction or a stroke [11], being therefore necessary to shorten the time dedicated to the localization and reconstruction of the atheroma plaque that can be generated in an artery.
3-D reconstruction is the process that allows real objects or shapes to be reproduced in the memory of a computer, faithfully imitating their physical characteristics such as dimension or volume. Although there are many 3D reconstruction techniques, not all of them provide results with the same quality. This quality is strongly influenced by the set of points chosen for the representation, which in turn depends on the efficiency, in terms of computational execution, of the selected 3D reconstruction algorithm [12,13]. The 3-D reconstruction has been applied in several fields and using different software techniques. For example, it has been used in the domain of architecture [14], in civil engineering [15], for the reconstruction of geographic data and aerial imagery [16] and handling occlusions in augmented reality in [17].
The localization of the atheroma plaque is usually performed manually from the contours located in the cross-section radiographs of the artery by performing its reconstruction. There exist several techniques for 3-D reconstruction of the affected arteries by means of 2-D images such as 3D transesophageal echocardiography [18,19], or also reconstruction from computed tomography images [20]. Still, most studies focus on reconstruction from localised contours on the images. Once the contours are located, there are several ways to create the volumes. To achieve this 3-D reconstruction, it is necessary to previously apply techniques to obtain images from inside the artery itself and to be able to see its cross-section.
One of the most outstanding advances is the development of IVUS (IntraVascular UltraSound). IVUS is a minimally invasive, high-resolution imaging technique that provides cross-sectional images of the structure of the vascular wall. It consists of introducing a catheter into the artery carrying a transducer that emits ultrasound at high frequencies, obtaining a high-resolution cross-sectional image [21]. Once the cross-sectional images have been obtained, the 3D reconstruction can be performed. Prior to IVUS, the technique used was contrast-enhanced coronary angiography [22], but images were obtained with low resolution and poor information. The benefits of using IVUS as a primary imaging tool have been confirmed by studies such as in [23].
Most studies focus on the reconstruction from the contours located in the images to subsequently create the volumes using different techniques. Sanz et al. in [24] obtained the boundaries of the contours through the active contours or `snakes’ technique. Afterwards, they used a grayscale criterion to distinguish each region and identify the atheroma plaque and performed the 3-D reconstruction using the overlapping contour technique, giving each of them a thickness. On the other hand, several studies, such as those in [25,26], start from an initial contour defined by the user and use segmentation algorithms based on the application of deformable models or `snakes’ to process the images and detect the arterial walls. The 3-D mesh can be generated by applying the Delaunay triangulation method [27,28].
Lo Vercio et al. [25] apply a triangulation method to generate the mesh that consists of joining the vertices of the successive contours in the sequence, selecting for each point of a contour the closest point of the next one. From these points, triangles are created using the neighbouring points until the contour is complete. Long et al. [26] use spline interpolation techniques along the vessel length.
In the present study, a 3-D reconstruction of an atheroma is performed from a series of IVUS images. Since most of the research focuses on the reconstruction of the artery, this project, based on the reconstruction of the atheroma plaque, provides a different approach that seeks to obtain a greater amount of information. As a consequence, an improvement in the localization and treatment of this atheroma plaque would be achieved, reducing the diseases caused by its accumulation in the walls of the artery. Therefore, the purpose of this work is to provide an improvement in the diagnosis of atheroma, going from a set of 2-D radiographs to a reasonably precise 3-D reconstruction carried out with two techniques.
2. Methodology
In this section, we demonstrate the materials used to obtain the images for this study (Section 2.1), then we introduce the information relative to the participants in the study (Section 2.2). Finally, the algorithm used is presented (Section 2.3).
2.1. Materials
An in vivo IVUS set of images of a real patient-specific geometry of a left coronary artery with atherosclerosis disease was obtained. The artery, which belongs to a 50-year-old male patient, was imaged using an automatic pullback with a speed of 0.5 mm/s from the distal part of the lesion to the tip of the guiding catheter. In total, twenty 2-D cross sections were obtained. The 3-D plaque geometry of the patient is reconstructed by piling up and following the trajectory of the center of the catheter.
2.2. Participants
The images and data used in this article were anonymously loaned by the Lozano Blesa Clinical University Hospital of Zaragoza (Spain) to scientific or academic purposes. The personal data of the patient are totally unknown by the authors of this study.
2.3. Algorithms/Methods
In this section, the main reconstruction algorithm is described. In order to obtain the boundaries of the atheroma, an image processing algorithm that consists of the following steps is used:
- Reading.
- Preprocessing.
- Extraction of the atheroma at each cross-sectional image.
- Extraction of the atheroma border.
- Postprocessing.
To reconstruct the atheroma, a set of cross-sectional images , of the artery is taken. Each image undergoes through each of the previous steps. Since image does not contain information on the previous cross-sectional image, a special procedure is followed.
The procedure is semi-automatic since the intervention of a specialist is required to fix three key points. First, the colour corresponding to the atheroma, then the rectangle where the atheroma could be and the identification of the first atheroma. Therefore, it works in an automatic mode once some data is introduced: the grayscale level of the atheroma as well as the window of search and the initial atheroma plaque. This knowledge is introduced by an specialist, generally a doctor in vascular medicine.
2.3.1. Preprocessing
First, the image is read from the repository (see, i.e., the current repository for this work shown by Figure A1) and transformed to standard grayscale () from the (RGB) triplet (see [29]). Let the grayscale image be . Then, the is prepared in order to improve the following steps of the algorithm (shown in Figure 1). First, the color intensity is modified to capture the color of the region of interest (). In a second step, the image is binarised:
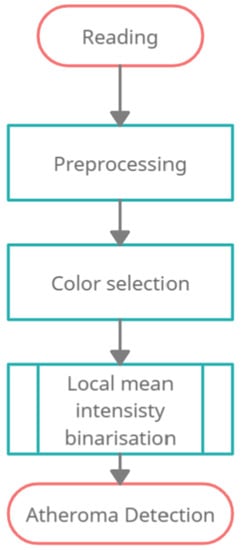
Figure 1.
Flowchart of the preprocessing step.
- Before starting the algorithm, the specialist is requested to provide the intensity of the atheroma . If the atheroma is not the brightest region of the image (i.e., ), then each pixel of the image is transformed following a tent-like map given by the function:In such way, it is ensured that the brightest region is the region that needs to be selected. Figure 2 gives an example of such map with a value . Once the transformation is used, the algorithm extracts the whitest regions in the next step.
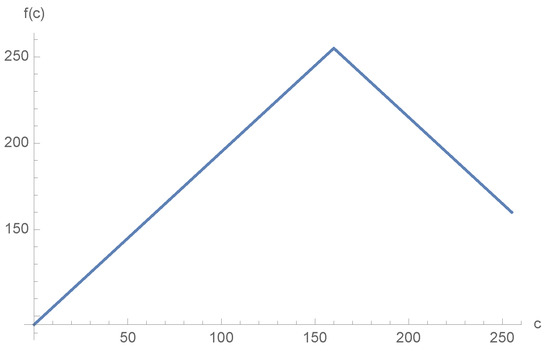 Figure 2. Example of tent-like map for .
Figure 2. Example of tent-like map for . - Binarisation of the image. The image is binarised by following an adaptive threshold based on the local mean intensity. In such way, the resulting image is smoother and less dependent on difference of light due to the noise that can be introduced by the capture device. Other methods have been implemented and tested, such as the Otsu filter or a fixed threshold value in order to decide whether the pixel is white or black. However, the extraction obtained is not as precise as with the adaptative threshold when comparing against the extraction made by a specialist. Thanks to the tent-like transformation, the intensity corresponding to the atheroma is always captured and is never lost due to the effects of the local mean intensity.
Let the binarised image be .
2.3.2. Detection of the Atheroma at Each Cross-Sectional Image
Once the the binarised image is obtained, the search region must be determined. This step is conducted in a semi-assisted way and following two different strategies according to the cross section considered. See Figure 3 for the flowchart of this step.
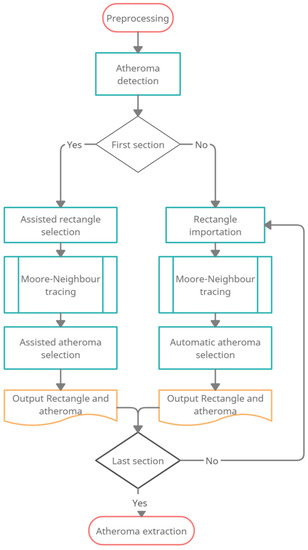
Figure 3.
Flowchart of the atheroma detection step.
For the first cross section, the specialist must select a rectangle were the artery is located. This fixes a working framework, where the atheroma is searched. This selection allows restricting the search region and improving the execution time of the procedure. Once the region is selected, the Moore-Neighbour tracing algorithm [30] is executed. This step highlights all the possible boundaries detected in the image. Finally, the specialist must select which of the boundaries detected corresponds to the atheroma. As a result of this step, the pixels corresponding to the atheroma () at the first cross section image are saved, as well as the pixels forming the boundary of the atheroma ().
Once the first cross sectional image is processed, the procedure works automatically. When analyzing the ith cross-sectional image, the framework rectangle for is fixed to for all the cross-sectional images. Then, the Moore-Neighbour tracing algorithm is conducted over the selected region to obtain m different neighbourhoods in . The atheroma at the ith step is considered such that the intersection between and is bigger. Given
where measures the size of the set, the pixels of the atheroma at step i are defined as and the boundary of the atheroma as the border of .
The intersection is used based on the heuristics that if two consecutive slices are close enough, then the atheroma will occupy the same region on the picture. Therefore, the intersection must be high.
2.3.3. Extraction of the Atheroma Edge
In the previous step, thanks to the Moore-Neighbour tracing algorithm, the set of pixels in the boundary of the atheroma plaque is detected. The pixels are automatically ordered by the algorithm. The next step consists in making uniform the number of points on the atheroma boundary at each cross-sectional image. Using the following algorithm, the m boundary points are transformed into exactly N points located along the boundary, and equally spaced:
- Compute , where we set to close the boundary. l gives the total length of the boundary following a piecewise connection.
- Compute the step .
- Fix , and .
- For ,
- (a)
- Compute the accumulated distance .
- (b)
- While a new point should be added. Use the following steps:
- Use linear interpolation to add the next boundary point to the uniformised boundary:Where .
- Increase .
Using such algorithm, it is possible that the number of points in the final boundary is enlarged or decreased. Since all the layers has exactly the same number of points, the resulting triangulation will be smoother and there will not be any boundary point with more than four triangles associated to it. The final output of this step is the set containing the N points in the boundary for the corresponding layer i.
2.3.4. Postprocessing
Once all the cross-sectional images are processed and all the boundaries are obtained with the same number of points in each individual boundary, the reconstruction of the atheroma is achieved by two different methodologies: (1) triangulation and (2) cubic spline surface reconstruction.
- Triangulation.After the last step for each image , the points at the boundary of the atheroma have been selected. We follow the triangulation (see flowchart in Figure 4b), as follows:
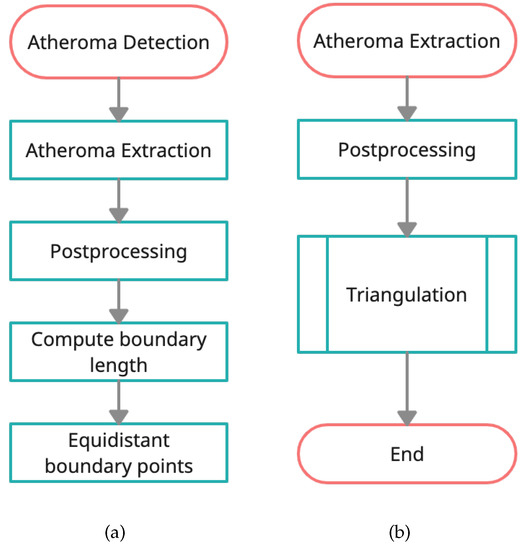 Figure 4. (a) Flowchart of the atheroma extraction step; (b) Flowchart of the postprocessing step.
Figure 4. (a) Flowchart of the atheroma extraction step; (b) Flowchart of the postprocessing step.- Connect each layer with the layer by adding triangles using the vertices:
- –
- and .
- –
- and .
- Once layer i is connected, proceed with the next layer, .
In such way, each layer is connected to the previous one by triangulation. The boundary of the atheroma is a 2-dimensional manifold; therefore, it can be covered by a mesh of triangles to join triplets of points. We note to the reader that here triangulation does not refer to the location of a point in the 3D space given two or more images but to cover a shape by a mesh of triangles. For each set of four points (, , and ). The triangles and are stored in order to reconstruct the 3D figure. With this, the atheroma is reconstructed. - Cubic spline surface reconstruction.Following the previous method, an additional attempt was made to reconstruct the surface of the atheroma from a set of splines that approximated its contour. Thus, using the initial vertical discretization (i.e., the 15 contours with 100 points per level), clusters of 15 points in the z-direction were used to fit a set of 100 cubic splines that had individually described functions that fit the lateral surface and allowed an improved discretization. Final atheroma’s reconstruction is achieved by joining adjacent points, which are the result of a denser sampling based on the previously obtained functions, with straight lines.
2.4. Reconstruction of the Artery
The artery can be reconstructed as a cylinder centered at the center of the prove and radius fixed by the specialist.
3. Results
The algorithm has been implemented using Matlab 2021.b and the ’Image Processing’ toolbox contained in that version. All the experiments have been executed in a Intel(R) Core i7-9700CPU 3.00 GHz with 16 Gb Ram in Windows 10 Pro. In order to clarify the process, the results demonstrated in that section correspond to an example of the reconstruction of a atheromatous plaque. It has also been tested in other situations with similar results.
Figure 5 shows the steps to extract the information for the first layer according to the following steps of the algorithm:
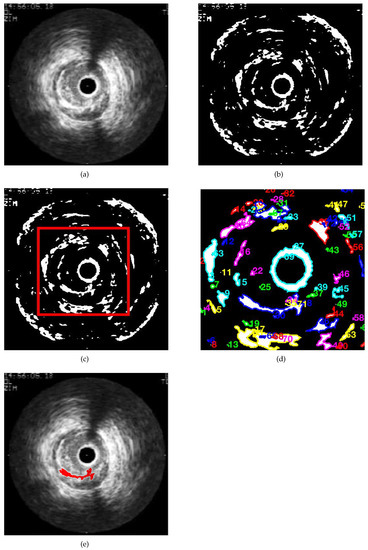
Figure 5.
Steps to extract the information for the first layer according to the proposed algorithm: (a) Initial image; (b) Binarised image; (c) Selected zone for the analysis; (d) Boundaries detected by the Moore-Neighbour algorithm; (e) Atheroma spot selected by the pathologist.
- First, the initial figure is obtained by the specialist.
- Then, the binarised image is shown.
- The user select the red square in the third.
- Finally, the boundaries of the possible regions are highlighted by the method. The user must select the one of interest to start the process.
The selection of the spot corresponding to the atheroma is always made by an expert pathologist, based on the spot size (normally, the largest one). It has to be noted that the pathologist indicates the atheromatous plaque spot only in the first image, the selection being automatic in the other images.
Once the first image of the set is analysed, the procedure works automatically. Figure 6 illustrates how the procedure selects the region of interest for the second and further images of the set. The top left plot shows the result of the first step: the binarised cross sectional image with the selected atheromeous region in red. The procedure considers the new cross sectional image that is binarised following the same strategy than in the first case (top right image in Figure 6). The zone of interest is selected to be the same as that of step 3. Step 4 is conducted automatically by the knowledge of the previous image. In Figure 6 bottom left plot, the set selected in the previous image is overlapped (red/blue pixels) on the binarised image. Red points are those corresponding to white pixels in the new image, while blue points are those corresponding to black pixels. The region selected for the new image is that one in which the intersection is larger, i.e., there are more red pixels. The resulting set is shown in red in the bottom right image of Figure 6.
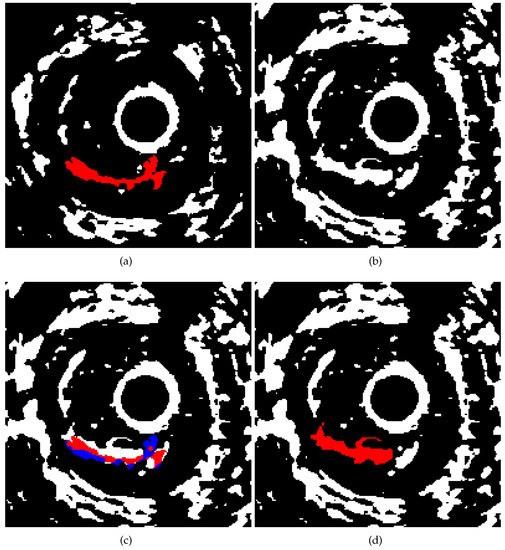
Figure 6.
(a) Binarised image in the first cross sectional image with the ateroma selected in red; (b) Binarised second image in the search region; (c) Binarised image with the pixels selected in the previous steps overlapped (red: the pixel is binarised and selected in the previous step, blue: the pixel is not binarised and was selected in the previous step); (d) Selected region according to the maximum number of coincidences.
The next step obtains the border of the region selected, as described in Section 2.3.3. In Figure 7, it is shown the border extracted in the first region (blue) and the result of the uniformization to 100 boundary points. The uniformization allows the posterior regularisation of the system. This step can be observed as a reparametrization of the border.
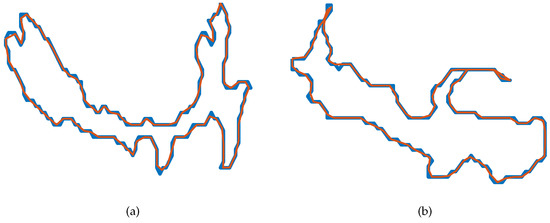
Figure 7.
Border obtained the Moore-Neighbour tracing algorithm (blue) and the reparametrization of the border to 100 border points (red): (a) Application for the first image; (b) application for the second image.
Once all the border of the region contains the same number of points for all the images, the algorithms reconstruct the atheroma plaque, as described in Section 2.3.4. Figure 8 shows the reconstruction of the atheroma from the full set of images, for triangulation (a,c) and cubic spline surface approximation (b,d).
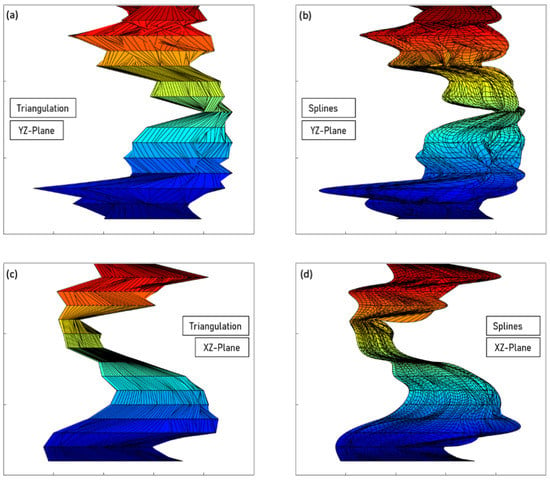
Figure 8.
Reconstruction of the atheroma through a triangulation (a,c) and cubic spline surface approximation (b,d).
4. Discussion
In this study, an algorithm to reconstruct atheroma plaques has been implemented. The works on the reconstruction of artery affections focus on the reconstruction of the anomaly once it has been detected by the specialist. First, the pathologist must select the pixels of the image affected by the illness and then the algorithm reconstructs the plaque. Using the algorithm proposed here, the pathologist is only asked to locate the atheroma in one cross-sectional image. From that point on, the algorithm works automatically. The user does not have to select which pixels are affected.
Recently, the segmentation of the vessels has been achieved using convolutional neural networks (for instance in [31]). However, the reconstruction is conducted from computed tomography angiographies, which do not provide enough precision and contrast in the image in order to detect the atheromatous region. In addition, the convolutional neural network is not able to explain the selection criterion. With the presented technique, the specialist supervises the procedure. This allows him to understand the selection.
This study has revealed interesting and promising results. However, some limitations have been found, the main one being the need of the cardiovascular pathologist intervention in order to identify the region of interest for the method.
5. Conclusions
In this paper, we present a self-developed algorithm able to reconstruct atheromatous plaques from intravascular ultrasound (IVUS) images. The main feature of this work is that it focuses on the reconstruction of the atheroma, instead of the artery and lumen geometrical features.
A semi-automatic tool was developed and successfully tested with real in-vivo IVUS images, able to reasonably reconstruct the atheromatous plaque. Two techniques (triangulation and cubic spline surface approximation) were implemented, through which reasonable 3D representations of the atheroma could be obtained.
This methodology can be implemented in common medical procedures, assisting pathologists in the identification of atheromatous material and serving as a complementary decision-making tool.
The fact of having available a delimited geometry of the atheromatous plaque at different stages of its development, may be of help when predicting the buildup and growth of these deposits, i.e., through machine-learning-based algorithms. Additionally, the obtained geometry can also be implemented in numerical simulations to assess changes in the blood flow due to this pathology.
Author Contributions
Conceptualization, J.M., M.C. and I.P.-R.; methodology, J.M., N.G. and M.C. software, J.M., D.P.-P. and A.L.; formal analysis, D.P.-P., N.G. and M.C.; writing—original draft preparation, D.P.-P., N.G. and I.P.-R.; writing—review and editing, J.M. and A.L. All authors have read and agreed to the published version of the manuscript.
Funding
The work of Ana Larrañaga has been supported by the 2020 predoctoral grant of the University of Vigo.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and the protocol was approved by the Ethics Committee of the project “Modelado y Simulación del envejecimiento de arterias debido a Aterosclerosis—Modelling and Simulation of arterial aging due to Atherosclerosis” (PRI-AIBDE-2011-1216).
Informed Consent Statement
All subjects gave their informed consent for inclusion before they participated in the study. All the images used in this study are anonymous and do not include any delicate nor compromising information or personal data that may affect the integrity of the source patients.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Handels, H.; Ross, T.; Kreusch, J.; Wolff, H.H.; Pöppl, S.J. Feature selection for optimized skin tumor recognition using genetic algorithms. Artif. Intell. Med. 1999, 16, 183–197. [Google Scholar] [CrossRef] [PubMed]
- Gniadecka, M.; Philipsen, P.A.; Sigurdsson, S.; Wessel, S.; Nielsen, O.F.; Christensen, D.H.; Hercogova, J.; Rossen, K.; Thomsen, H.K.; Gniadecki, R.; et al. Melanoma diagnosis by Raman spectroscopy and neural networks: Structure alterations in proteins and lipids in intact cancer tissue. J. Investig. Dermatol. 2004, 122, 443–449. [Google Scholar] [CrossRef] [PubMed]
- Huang, T.M.; Kecman, V. Gene extraction for cancer diagnosis by support vector machines—An improvement. Artif. Intell. Med. 2005, 35, 185–194. [Google Scholar] [CrossRef]
- Tan, B.K.J.; Teo, C.B.; Tadeo, X.; Peng, S.; Soh, H.P.L.; Du, S.D.X.; Luo, V.W.Y.; Bandla, A.; Sundar, R.; Ho, D.; et al. Personalised, Rational, Efficacy-Driven Cancer Drug Dosing via an Artificial Intelligence SystEm (PRECISE): A Protocol for the PRECISE CURATE.AI Pilot Clinical Trial. Front. Digit. Health 2021, 3, 635524. [Google Scholar] [CrossRef] [PubMed]
- Pawłowski, J.; Majchrowska, S.; Golan, T. Generation of microbial colonies dataset with deep learning style transfer. Sci. Rep. 2022, 12, 5212. [Google Scholar] [CrossRef]
- Itchhaporia, D.; Almassy, R.; Kaufman, L.; Snow, P.; Oetgen, W. Artificial Neural Networks Can Predict Significant Coronary Disease. J. Am. Coll. Cardiol. 1995, 25, 328A. [Google Scholar] [CrossRef]
- Poli, R.; Cagnoni, A.; Livi, R.; Coppini, G.; Valli, G. A neural network expert system for diagnosing and treating hypertension. Computer 1991, 24, 64–71. [Google Scholar] [CrossRef]
- Cilla, M.; Pérez-Rey, I.; Martínez, M.A.; Peña, E.; Martínez, J. On the use of Machine Learning Techniques for the Mechanical Characterization of Soft Biological Tissues. Int. J. Numer. Methods Biomed. Eng. 2018, e3121, 1–12. [Google Scholar] [CrossRef]
- Martínez, J.; Pérez-Rey, I.; Cilla, M. What are the possibilities of machine learning techniques on the mechanical characterization of biological tissues? Int. J. Biosens. Bioelectron. 2020, 6, 1–2. [Google Scholar]
- Jambukia, S.H.; Dabhi, V.K.; Prajapati, H.B. Classification of ECG signals using machine learning techniques: A survey. In Proceedings of the 2015 International Conference on Advances in Computer Engineering and Applications, Ghaziabad, India, 19–20 March 2015; pp. 714–721. [Google Scholar]
- Stary, H.C.; Chandler, A.B.; Dinsmore, R.E.; Fuster, V.; Glagov, S.; Insull, W.J.; Rosenfeld, M.E.; Schwartz, C.J.; Wagner, W.D.; Wissler, R.W. A definition of advanced types of atherosclerotic lesions and a histological classification of atherosclerosis. A report from the Committee on Vascular Lesions of the Council on Arteriosclerosis, American Heart Association. Circulation 1995, 92, 1355–1374. [Google Scholar] [CrossRef]
- Grandón-Pastén, N.; Aracena-Pizarro, D.; Tozzi, C.L. Reconstrucción de objeto 3D a partir de imágenes calibradas. Ingeniare Rev. Chil. Ing. 2007, 15, 158–168. [Google Scholar] [CrossRef]
- Piquer, A.; Company, P. Situación Actual de la Reconstrucción 3D de Dibujos Lineales. Inf. Tecnol. 2004, 15, 71–80. [Google Scholar] [CrossRef]
- Liritzis, I.; Volonakis, P.; Vosinakis, S. 3D Reconstruction of Cultural Heritage Sites as an Educational Approach. The Sanctuary of Delphi. Appl. Sci. 2021, 11, 3635. [Google Scholar] [CrossRef]
- Zingoni, A.; Diani, M.; Cosrini, G.; Masini, A. Real-time 3D reconstruction from images taken from an UAV. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2015, XL-3/W3, 313–319. [Google Scholar] [CrossRef]
- Maurer, M.; Rumpler, M.; Wendel, A.; Hoppe, C.; Irschara, A.; Bischof, H. Geo-referenced 3D reconstruction: Fusing public geographic data and aerial imagery. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 3557–3558. [Google Scholar]
- Tian, Y.; Long, Y.; Xia, D.; Yao, H.; Zhang, J. Handling occlusions in augmented reality based on 3D reconstruction method. Neurocomputing 2015, 156, 96–104. [Google Scholar] [CrossRef]
- Tsang, W.; Piazzese, C.; Kronzon, I.; Sotaquira, M.; Weinert, L.; Lang, R.M.; Caiani, E. Semi-automated detection and quantification of aortic atheromas from 3d transesophageal echocardiography. J. Am. Coll. Cardiol. 2013, 61, E974. [Google Scholar] [CrossRef]
- Bender, K.; Matoq, A.; Nelson, J.S. Transesophageal echocardiography in congenital heart surgery: Perioperative considerations. Prog. Pediatr. Cardiol. 2020, 58, 101263. [Google Scholar] [CrossRef]
- Kigka, V.B.; Rigas, G.; Sakellarios, A.; Siogkas, P.; Andrikos, I.O.; Exarchos, T.P.; Loggitsi, D.; Anagnostopoulos, C.D.; Michalis, L.K.; Negliaf, D.; et al. 3D reconstruction of coronary arteries and atherosclerotic plaques based on computed tomography angiography images. Biomed. Signal Process. Control 2018, 40, 286–294. [Google Scholar] [CrossRef]
- Vásquez, S.H.; Vesga, B.E.; Hernández, H.J. Imagenología coronaria: Ultrasonido intravascular (IVUS). Rev. Colomb. Cardiol. 2017, 24, 101–106. [Google Scholar] [CrossRef]
- Salido, L.; Mestre, J.L.; Jiménez-Mena, M.; Hernández, R.; Zamorano, J.L. Disección coronaria espontánea multivaso posparto. Rev. Argent. Cardiol. 2015, 83, 152–154. [Google Scholar] [CrossRef]
- Mariani, J., Jr.; Guedes, C.; Soares, P.; Zalc, S.; Campos, C.M.; Lopes, A.C.; Spadaro, A.G.; Perin, M.A.; Filho, A.E.; Takimura, C.K.; et al. Intravascular ultrasound guidance to minimize the use of iodine contrast in percutaneous coronary intervention: The MOZART (Minimizing cOntrast utiliZation with IVUS Guidance in coRonary angioplasTy) randomized controlled trial. J. Am. Coll. Cardiol. Cardiovasc. Interv. 2014, 7, 1287–1293. [Google Scholar] [CrossRef] [PubMed]
- Sanz, R.; Bodí, V.; Sanchís, J.; Moratal, D.; Núñez, J.; Palau, P.; García, D.; Rieta, J.J.; Sanchís, J.M.; Chorro, F.J.; et al. Desarrollo de software para la reconstrucción tridimensional y cuantificación automática de secuencias de ultrasonido intravascular. Experiencia inicial. Rev. Esp. Cardiol. 2006, 59, 879–888. [Google Scholar] [CrossRef] [PubMed]
- Lo Vercio, L.; Arguiñarena, E.; Romero, L.; Jonas, I.; del Fresno, M.; Vénere, M. Reconstrucción Arterial a partir de Ultrasonido Intravascular Sincronizado con Electrocardiograma. Mec. Comput. 2012, XXXI, 3053–3060. [Google Scholar]
- Long, Q.; Ariff, B.; Zhao, S.Z.; Thom, S.A.; Hughes, A.D.; Xu, X.Y. Reproducibility study of 3D geometrical reconstruction of the human carotid bifurcation from magnetic resonance images. Magn. Reson. Med. 2003, 49, 665–674. [Google Scholar] [CrossRef] [PubMed]
- Delaunay, B. Sur la sphère vide. A la mémoire de Georges Voronoï. Bulletin de l’Académie des Sciences de l’URSS. VII Série. 1934, pp. 793–800. Available online: http://mi.mathnet.ru/im4937 (accessed on 18 October 2022).
- Cazals, F.; Giesen, J. Delaunay Triangulation Based Surface Reconstruction: Ideas and Algorithms; No. 5393; INRIA: Rocquencourt, France, 2004.
- Burger, W.; Burge, M.J. Principles of Digital Image Processing Core Algorithms; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E.; Eddins, S.L. Digital Image Processing Using MATLAB; Gatesmark Publishing: Knoxville, TN, USA, 2009. [Google Scholar]
- Fu, F.; Wei, J.; Zhang, M.; Yu, F.; Xiao, Y.; Rong, D.; Shan, Y.; Li, Y.; Zhao, C.; Liao, F.; et al. Rapid vessel segmentation and reconstruction of head and neck angiograms using 3D convolutional neural network. Nat. Commun. 2020, 11, 4829. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).