Abstract
The ontology knowledge base (KB) can be divided into two parts: TBox and ABox, where the former models schema-level knowledge within the domain, and the latter is a set of statements of assertions or facts about instances. ABox reasoning is a process of discovering implicit knowledge in ABox based on the existing KB, which is of great value in KB applications. ABox reasoning is influenced by both the complexity of TBox and scale of ABox. The traditional logic-based ontology reasoning methods are usually designed to be provably sound and complete but suffer from long algorithm runtimes and do not scale well for ontology KB represented by OWL DL (Description Logic). In some application scenarios, the soundness and completeness of reasoning results are not the key constraints, and it is acceptable to sacrifice them in exchange for the improvement of reasoning efficiency to some extent. Based on this view, an approximate reasoning method for large-scale ABox in OWL DL KBs was proposed, which is named the ChunfyReasoner (CFR). The CFR introduces neural-symbolic learning into ABox reasoning and integrates the advantages of symbolic systems and neural networks (NNs). By training the NN model, the CFR approximately compiles the logic deduction process of ontology reasoning, which can greatly improve the reasoning speed while ensuring higher reasoning quality. In this paper, we state the basic idea, framework, and construction process of the CFR in detail, and we conduct experiments on two open-source ontologies built on OWL DL. The experimental results verify the effectiveness of our method and show that the CFR can support the applications of large-scale ABox reasoning of OWL DL KBs.
Keywords:
neural-symbolic learning; approximate reasoning; large-scale ABox reasoning; neural network; ontology reasoning; OWL DL MSC:
68T01; 68T07; 68T20; 68T27; 68T30; 68T99
1. Introduction
Ontology is an important form of modeling existing human knowledge through symbols, and it is the core of the Semantic Web technology framework [1]. OWL DL (Description Logic) is an ontology language recommended by W3C, which is widely used in practical applications [2,3] (unless otherwise specified, ontology in the following paragraphs refers to ontology built on OWL DL). An ontology knowledge base (KB) can be divided into two parts: TBox and ABox, where the former is the schema-level knowledge of the KB, which is used to describe the recognized concepts and roles, while the latter is a collection of assertions or factual statements of instances in the domain. Reasoning is the core technology in KB-based systems, and the process of reasoning new implicit knowledge in ABox based on the existing KB is called ABox reasoning [4] (also known as ABox materialization), which has important value in KB applications. Recently, with the explosive growth of data and the improvement of knowledge extraction technology, the ontology KBs containing large-scale ABox are becoming more common than before, and reasoning tasks for them have attracted increasing attention [5,6,7,8].
The ontology reasoning method based on logical deduction can ensure the soundness and completeness of the reasoning results, but it is a computationally intensive operation and cannot meet the need of scalability of the large-scale ABox reasoning in OWL DL [9]. On the one hand, ontology reasoning is constrained by the complexity of TBox. In the OWL DL, its reasoning complexity is at least EXPTIME-complete, and it is NEXPTIME-complete under the worst situations (http://www.cs.man.ac.uk/~ezolin/dl/, accessed on 1 October 2022). On the other hand, the scale of ABox influences the efficiency of ontology reasoning. The mainstream algorithms for ontology reasoning, such as Tableau algorithms [10] and their extensions, are all in-memory algorithms, whose reasoning is to detect the consistency of ontology by building models as well as define other reasoning tasks as a consistency check. For the ontology KBs containing large-scale ABox, the Tableau process needs to build a large number of abstract models, which either causes the reasoning failure due to memory overflow or decreases the reasoning efficiency due to a large number of frequent internal and external storage data exchanges. Therefore, the traditional ontology reasoning methods are not suitable for the large-scale ABox reasoning in OWL DL KBs.
KBs containing large-scale ABox can be seen as knowledge graphs (KGs) [11]. Although the KG completion method (KGC) [12,13] has good scalability toward large-scale KG reasoning, it can neither efficiently learn the axiom in ontology nor learn the materialization process of logical deduction. The basic idea of KGC is to train a semantic model by the existing knowledge in the KG and represent the entities and relations in the graph into low-dimensional vectors of real values while preserving the structure and semantic information of the KG as much as possible, and it also infers implicit assertions by vector operation. Due to the support of computer devices and various deep learning frameworks for vector computation, the KGC method has high computational efficiency and reasoning speed, and it scales well for large-scale ABox. However, the KGC method can only learn and induce frequent patterns that already exist in ABox, and it rarely considers the constraints of ontology axioms on the underlying assertions and deductive process of logical reasoning, so the reasoning quality is often poor [14]. Although some methods [15,16,17] tried to design new vector space to encode the axioms in ontology, most of them are suitable for simple ontology with poor expressive ability, and there is still a lack of a suitable approach to ontology represented in OWL DL.
In recent years, the emergence of neural-symbolic learning methods provides a new way to solve the large-scale ABox reasoning in KBs [18,19,20,21]. The symbolic system and neural network (NN) system (also known as the subsymbolic system) are complementary—the strength of NN is the weakness of symbolic system, and vice versa—the organic integration of the two can obtain a stronger problem-solving ability [22]. Using neural-symbolic learning to realize large-scale ABox reasoning and training a neural network model to approximate the deductive process of compiled logical reasoning, on the one hand, high-quality approximate deductive reasoning can be achieved, and on the other hand, high reasoning speed response can be obtained. Presumably, this form of reasoning would not be sound and complete, but it would trade correctness and soundness guarantees with higher runtime efficiency, in the spirit of approximate reasoning, which is reasonable in practical applications [23]. First, in the different application fields of semantic web technology, the need for a reasoning service can be totally different; in some scenarios, soundness and completeness are key constraints. For example, in the disease diagnosis, misdiagnosis or missed diagnosis will pay a very high cost. While in some scenarios, if a less precise answer leads to a faster reasoning response, it can be acceptable and will bring great convenience, such as in network security, information retrieval and other services. Second, in practical KBs, especially those with large-scale ABox, even the KBs sophisticatedly built by experts cannot ensure that all knowledge is correct. Therefore, it is permissible to sacrifice the theoretical soundness and completeness of reasoning results in exchange for the flexibility of applications and the improvement of practical efficiency. Thus, neural-symbolic learning has vital potential value in the reasoning applicaitons of KBs containing large-scale ABox.
Most of the existing ABox reasoning methods based on neural-symbolic learning consider ontologies with weak expressive ability, but the ontology with strong expressive ability built on OWL DL is less considered, which still needs further research. In this paper, we propose an approximate reasoning method for large-scale ABox for OWL DL based on neural-symbolic learning, which is named the ChunfyReasoner (CFR). The basic idea of the CFR is to regard deductive reasoning as a mapping function. The input is the original KB, and the output is the extended KB (the KB inferred by logic reasoning). Through the training of the NN model, the mapping relationship between the original KB and the extended KB is learned, allowing the NN model to approximately compile the process of deductive reasoning so as to achieve approximate ABox reasoning. In this paper, we state the basic idea, framework and construction process of the CFR in detail and verify the effectiveness of our method through experiments. The main contributions are as follows:
(1) We state the basic idea of the CFR in detail. As far as we know, this is the first time we explicitly propose a regression model that uses NN to model ABox reasoning into mapping relation learning. The CFR integrates ontology reasoning, graph data processing, knowledge representation, NNs, parallel computing and other technologies, which is a cross-innovation method. The basic idea of the CFR can also be used for reference in other reasoning tasks.
(2) We exhaustively demonstrate the overall framework and construction method of the CFR, which provides a novel and feasible technical approach for the large-scale ABox reasoning of OWL DL KBs.
(3) Experiments are conducted on two open-source ontologies built on OWL DL to verify the effectiveness of the CFR. The experimental results show that CFR can achieve high reasoning quality and efficiency, and it can effectively support large-scale ABox reasoning applications in OWL DL KBs.
This paper is organized as follows: in Section 2, related works are introduced. In Section 3, we state the basic idea, overall framework and construction method of CFR in detail. In Section 4, relevant experimental analysis is carried out. In Section 5, we discuss the limitations of the CFR, and Section 6 is the conclusion of this paper.
2. Related Work
In this paper, we mainly investigate and analyze three ABox reasoning methods for KBs: ABox reasoning based on logical deduction, ABox reasoning by KGC, and approximate ABox reasoning based on neural-symbolic learning.
2.1. ABox Reasoning Based on Logical Deduction
Description logic is the basis of OWL DL [9]. Common description logic is mainly obtained by adding or deleting different constructors on the basis of , and these constructors become the main basis for distinguishing different specific description logics: for example, adding the number restrictions in to obtain , and adding the functionality to obtain . In practical applications, it is not only necessary to describe concepts but also to enhance the expressive ability of roles. For example, with role transitivity is called ; if the axiom of role hierarchy is added, the language will be obtained. OWL DL corresponding to is the most expressive ontology language that can be decidable at present. The reasoning of OWL DL is high in complexity, even for the smallest propositionally closed DL (which only provides the class constructors ┐C, , , and ), the complexity of logical entailment is EXPTIME, and as for with high expressive ability, its reasoning complexity is NEXPTIME [24]. This means that increasingly large ontologies may, in the worst case, require exponentially increasing computing resources to reason. Therefore, traditional reasoning tools supporting OWL DL KBs such as Pellet [25] and Hermit [26] are not suitable for the reasoning tasks of large-scale ABox.
In order to balance the contradiction between expressive ability and reasoning efficiency and gain support for efficient reasoning, researchers try to seek a compromise between expressive ability and reasoning complexity and put forward some lightweight ontology languages, but it is difficult to be widely used in practice. W3C recommends some tractable description logic languages, such as OWL EL, Horn DL, and DL-lite, which respectively correspond to three sub-languages of OWL, which are OWL2 EL, OWL2 RL, and OWL2 QL [27]. Among these sub-languages, the standard time complexity of the reasoning problem is PTIME complete. Meanwhile, targeted reasoners for these sub-languages were also developed. For example, ELK [28] and RDFox [29] can perform efficient reasoning toward ontology expressed by OWL EL and OWL RL. However, the problem is that knowledge in the real world is not limited to these languages, and forcing ontology engineers to use these language will result in them having to give up knowledge that would otherwise require complex expressive ability. As a result, many ontologies in the real world exceed the expressive ability of any sub-language and still require reasoners for OWL DL to reasoning [23].
2.2. ABox Reasoning by KGC
The ontology KBs containing large-scale ABox can be regarded as KGs, and the KGC method can obtain efficient ABox reasoning, but KGC take less account of axioms in ontology, and it often has low reasoning quality. Distance-models are classical methods of KGC, such as TransE [30] and TransH [31]. They use existing knowledge in the KG to express the entities and relationships as continuous real value vectors in low-dimensional space and then define a score function to evaluate the probability of potential triples by calculating the spatial distance between different entities. However, for the KB with ontology constraints, the reasoning quality of these representation learning methods is not high. Some methods try to express axioms in ontology by constructing new vector spaces. For example, the EL encoding method [15] models description logic axioms as geometric construction models, using vectors to represent entities and relationships, using high-dimensional spheres to represent concepts, and using high-dimensional spheres to represent implication, mutual exclusion and overlapping relationships among concepts. Based on the spatial geometry constraints, the axiom is transformed into the loss function constraint to represent the learning model, and the ontology can be transformed into the learning model by training. However, this method cannot express the rules of role constructors and role axioms, and it has limited ability to express complex axioms in OWL DL. In addition, there are some similar methods, such as RotatE [16] and DensE [17], trying to learn the axioms in ontology by changing the form of different spatial coordinates. However, the axioms that these methods can deal with are still weak and cannot fully express the axioms contained in OWL DL.
Using NN to build a semantic model is a common method of KGC. Researchers have proposed a variety of NN models, such as traditional NN models such as ParamE [32] and NTN [33], CNN-based models such as ConvE [34] and ConvKB [35], and GCN-based models such as R-GCN [36], etc. We will not discuss these at length here; for details, please refer to [12,37]. Although these NNs have strong learning ability to capture the semantic features in ABox, their training process does not introduce logical reasoning as supervision (label), which brings two defects in ABox reasoning. First, the NN model can only learn the existing frequent patterns in ABox, and these existing frequent patterns are natural attributes contained in the KG, which usually cannot fully reflect the axioms in the ontology and do not contain the deductive mapping relationship from the top-level patterns to the bottom-level implicit assertions. Therefore, even if the NN model is fully trained, it is difficult to adequately learn the axioms in the ontology, and it cannot approximate the process of logical reasoning. Second, under the open world assumption (OWA) (the OWA is the assumption that what is not stated is unknown. Both the ontologies represented by OWL and the KBs represented by RDF are based on the OWA. The closed-world assumption (CWA) is the opposite of the OWA; it assumes that what is not currently known is false), the assertions not stated in the KG are unknown, and the judgment of the accuracy of the reasoning assertions output by the neural network model is vague due to the lack of logical reasoning results as a benchmark, while in the ABox reasoning of the ontology KB, it is more expected to obtain deterministic reasoning results. Therefore, ABox reasoning based on an NN model alone cannot achieve the desired results.
2.3. ABox Reasoning Based on Neural-Symbolic Learning
In recent years, with the development of Artificial Intelligence (AI) and cognitive science, researchers began to explore a new way to achieve symbolic reasoning based on NNs and proposed the neural-symbolic learning method [21,38]. Approaches in AI based on artificial NNs differ fundamentally from approaches that leverage knowledge bases to perform logical deduction and reasoning, but they are rather complementary to each other. Neural-symbol learning organically integrates the advantages of symbolic systems and NNs, has stronger problem-solving ability, and addresses fundamental problems related to building a technical bridge between the symbolic and subsymbolic sides of the divide, which is a more robust intelligent system [18,22]. In the ABox reasoning of the KBs, the advantages of the symbolic system include ensuring the soundness and completeness of the reasoning results, but the reasoning efficiency is low and cannot scale well for large-scale ABox. The advantages of the NN are that it has high computational efficiency and can realize fast reasoning. It is generally robust against noise in training or input data. However, its disadvantage is that it cannot effectively learn the complex axioms in TBox and a logical deduction process, and the quality of reasoning results is poor. ABox reasoning is based on neural-symbolic learning; it discards the shortcomings of both and integrates their advantages, which not only has higher reasoning efficiency but also can obtain high-quality results similar to symbolic reasoning. It has important reference value for solving large-scale ABox reasoning applications in KBs.
Some studies have used neural-symbolic learning for ABox reasoning. Ref. [18] combined symbolic methods (in particular, knowledge representation using symbolic logic and automated reasoning) with NNs to generate embeddings for nodes that encode related information within biological KGs, and then, they applied these embeddings to the prediction of edges in the KG. Although their method achieved outstanding results, to improve its scalability, they chose the ontologies represented by OWL EL as the research objects and used ELK to realize logical reasoning. For ontologies based on OWL DL, it is difficult to construct a training corpus, so these methods cannot be applied to ABox reasoning in OWL DL KBs. NMT4RDFS [39] performs ABox reasoning using an RDF-scheme (RDF(s)) based on KG embeddings. However, RDF(s) is an ontology model with weak expression ability; for the complex ontologies in this paper, NMT4RDFS cannot be applied. ReasonKGE [40] proposed an iterative method that dynamically identifies the inconsistent predictions produced by a given embedding model via symbolic reasoning and feeds them as negative samples for retraining the model. To address the scalability problem that arises when integrating ontological reasoning into the training processes of embedding models, the authors considered ontologies in OWL DL-Lite. However, under the OWA, most assertions are unknown rather than false, and logical inference is performed every time negative examples are obtained. Therefore, for complex ontologies, the cost of obtaining negative examples increases greatly, and ReasonKGE converges very slowly or even fails to converge. The recursive reasoning network [41] synthesizes a KB and extends it through Datalog reasoning and then employs the KB and its extended set as input data and target data to train a NN model. However, the recursive reasoning network was designed based on the CWA and cannot be used for ABox reasoning under the OWA. Many related studies are still being conducted on neural-symbolic learning, and we cannot enumerate them; it is strongly recommended to refer to the reviews in [38,42].
Recent studies have shown that for ABox in KBs, fast approximate reasoning can be achieved with the help of neural-symbolic learning. However, existing methods are oriented to performing knowledge reasoning under the CWA or operating on simple ontologies under the OWA. Further research is still needed for conducting ABox reasoning over OWL DL KBs, including complex ontologies under the OWA.
3. Construction Method of the CFR
In this part, firstly, the basic idea of the CFR is introduced, and then, its specific process and implementation method is elaborated in detail. Finally, the evaluation metrics of reasoning performance is put forward.
3.1. Basic Idea of the CFR
The reasoning task of large-scale ABox reasoning is mainly considered, so we presume the TBox of a given ontology KB is correct and complete. In order to formally describe the basic idea of the CFR, the definitions of related concepts are given at first.
Definition 1.
For a given OWL DL ontology KB, it is called origin KB, denoted as , and the knowledge base obtained based on logic reasoning is called extensional KB, denoted as . Ignoring the specific details, the reasoning process based on description logic is called ontology reasoning, which is denoted as .
According to Definition 1, the process of ABox reasoning can be expressed as:
If ontology reasoning is regarded as a function in a broad sense, the above formula can be converted into:
where the input is and the output is ; can be thought of as a mapping function from input to output.
The theory has proved that the deep neural network can effectively approximate to functions [43]. For an NN model , if is used as the input and is used as the supervision (output), where:
Under the condition that the expression ability and learning ability of are strong enough, after sufficient training, the mapping relationships from to can be effectively learned. It can be considered that the parameter learning of the is an approximate compilation of the deduction process of ontology reasoning, which is expressed as:
With the support of computer software and hardware for tensor computing and parallel computing of deep learning, the has higher computing efficiency and better scalability for large-scale ABox reasoning than .
The above idea is theoretically feasible, but it still faces two major challenges. Firstly, the input of the model is real-valued vectors, and ABox is usually represented by symbols, so how to input ABox into the is a problem. Secondly, the input layer parameters of the are fixed and usually should not be overmuch, so how to input a large-scale ABox into the is another problem.
Definition 2.
A class assertion indicates that instance e is the instance of class C; a role assertion represents that there is a relation r between instances s and o. A collection of class assertions and relation assertions is called an assertional box (ABox).
Let us start with the first challenge. In Definition 2, there are two kinds of assertions in ABox, class assertion and role (or relation) assertion , where class C and role r are defined in TBox. Class assertion is a unary predicate, and role assertion is a binary predicate. Both can be uniformly expressed as RDF [44] triple representation, which is a very common expression in semantic web and a lossless transformation. Then, these two assertions can be expressed as:
Based on the triple representation, ABox can be converted into numeric values. The common method is KG representation learning, but this is a lossy transformation. We expect to achieve a greater degree of approximation of the reasoning process, so the form of adjacency matrix is adopted. The adjacency matrix can only represent a single role among entities; however, there are many kinds of roles in ABox, so we adopt the method of a multi-layer adjacency matrix [39]; that is, the assertion involved in each type of role in ABox is expressed as an adjacency matrix, and finally, all the adjacency matrices are assembled to form a multi-layer adjacency matrix, the number of layers is equal to the role number in ABox, including the class assertion -A. At the same time, in order to realize end-to-end learning, it is necessary to record the corresponding role and entity dictionary of each layer of the adjacency matrix in the process of encoding a multi-layer adjacency matrix so as to ensure the reversible process from the multi-layer adjacency matrix to ABox. The concept definition is given below.
Definition 3.
The process of encoding ABox in ontology KB into a multi-layer adjacency matrix is called multi-layer adjacency matrix encoding, which is recorded as . The inverse process is called multi-layer adjacency matrix decoding, which is denoted as .
Then comes the second challenge. For large-scale ABox, if we input it to the at one time, this will result in two defects. First, the scale of ontology KB used for model training and the real KB that need to be inferred may be inconsistent, and the scale of ABox of KB in the real world may change constantly, which makes it difficult to fix the parameters of input layers of the . Second, large-scale ABox is usually difficult to input at one time due to the limitation of computer characteristics, and even if it can be input, it will lead to too many parameters in the input layer of the , which is difficult to train. We alleviate these defects by segmenting subgraphs of instances. The subgraph of instances is defined as follows.
Definition 4.
Let e be an instance in a given ontology KB; then, the subgraph formed by its adjacency entities and roles (or relations) centered on e in ABox is called the subgraph of instance e, which is named .
According to Definition 4, if all instances in the KB are traversed, ABox in the KB can be expressed as:
where represents the ID of instances in the KB, , and N represents the number of instances in ABox.
The input of large-scale ABox can be solved by subgraph segmentation. The reason is that even though the scale of ABox of training data and real KB are quite different, the sizes of those subgraph are usually not much different for a single instance. In addition, through subgraph segmentation, the number of training data can be increased, so training effect of the can be improved, since it is data-driven.
Definition 5.
For a given ontology KB, which is denoted as , let e be an instance in ABox and its corresponding subgraph be . If holds, then is called the extended subgraph corresponding to instance e.
The training of the depends on the supervision. We take the extended subgraph as the supervision data to train the , as shown in Definition 5. The extended subgraph of an instance is obtained by ontology reasoning under the complete TBox, which can ensure that it is correct and complete. Thanks to subgraph segmentation, the size of the subgraph of each instance is relatively small, so the cost of obtaining an extended subgraph will be greatly reduced.
Obviously, the establishment of the above formula requires a precondition: that is, whether the ABox reasoning result on the whole ABox can be approximated by the collection of extended subgraphs. Ref. [7] gives relevant verification and proves that this approximation is established.
We regard corresponding to the instance as a piece of training data, where the subgraph is the input data and the extended subgraph is the supervision data, so a total of N pieces of training data can be constructed on the whole ABox. According to Definition 5, every training data contains a complete logical deduction process. If the is constructed to learn the mapping relationships from the subgraph of an instance to its extended subgraph, that is:
Then, the can learn the general logical deduction calculus: that is, the process of deductive reasoning. Although the subgraph of each instance contains only fragmentary information in ABox, the complete deductive reasoning process can be learned by the trained on the subgraph of all instances for many cycles.
In the testing (or reasoning) phase of the , if a subgraph of an instance is input, then its corresponding extended subgraph is output, which is:
Then, after traversing the subgraphs corresponding to all instances in the test data, the extended ABox (Equation (7)) can be expressed as:
In the above formula, is the extended ABox reasoning result obtained through the NN method. We think it is an effective approximation of the reasoning result to the ontology reasoning, the structure and parameters of the approximately compile the deductive process of logical reasoning.
3.2. Framework of the CFR
In this section, we introduce the overall framework of the CFR. The framework is shown in Figure 1. It is mainly divided into two parts: model training and reasoning (or testing). In the figure, indicates the number of instances in the synthetic ABox, indicates the number of instances in the ABox of the real KB, and the meanings of other notations are the same as those in Section 3.1.
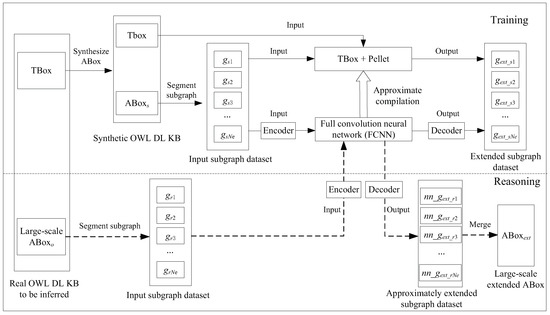
Figure 1.
Overall framework of the CFR.
In model training, the large-scale ABox is synthesized based on the TBox to form the synthetic ontology KB. On this basis, the subgraphs of in the synthetic ontology KB are divided to obtain the subgraph for each instance, and all the subgraphs constitute the input subgraph dataset. Then, the subgraph in the input subgraph dataset are merged with the complete TBox, and the corresponding extended subgraph is obtained by the ontology reasoner Pellet, thus forming the extended subgraph dataset. The subgraph and its correspondingly extended subgraph constitute a piece of training data. With the help of and , a reversible mapping from the symbol to the multi-layer adjacency matrix is constructed, and a fully convolutional neural network (FCNN) [45] is trained to learn the mapping relationships from the input subgraph to the extended subgraph.
In model reasoning (or testing), ABox in the real OWL DL KB is divided into subgraphs by the same method, and the subgraph of each instance is obtained, forming the input subgraph dataset. Each subgraph is encoded in turn by the and is input to the FCNN; then, the output result is decoded by the . By restoring the result into RDF triple representation and then obtaining the extended subgraph corresponding to each subgraph, we form the approximately extended subgraph dataset. Finally, all the extended subgraphs are merged to obtain a large-scale extended . With the above framework, the CFR implements the approximate reasoning task for large-scale ABox.
3.3. Process of the CFR
In this part, the ABox synthesis method, subgraph segmentation and dataset construction method, encoding and decoding method, and the structure of FCNN involved in the framework are described in detail in turn.
3.3.1. ABox Synthesis Method
The CFR synthesizes ABox based on TBox in ontology KB to train the FCNN. There are two main reasons. First, the NN model is data-driven, and the training process needs a lot of data to support it. In practical applications, it is costly to acquire a large-scale real ABox, and synthetic ABox can effectively alleviate the shortage of training data. Second, the assertions in ABox are strictly constrained by TBox, and the logically consistent synthetic ABox can ensure a high similarity with the real ABox. At the same time, various patterns defined in the TBox can be effectively simulated by synthesizing an ABox, which makes the generalization ability of the NN model stronger and effectively alliviates the unbalanced distribution of assertions and the pattern missing in the real ABox.
How to synthesize logically consistent ABox based on TBox under the OWA is a difficult problem. In this paper, the method of graph data synthesis in [46] is used to synthesize a logically consistent ABox. The specific process is shown in Algorithm 1, which can be roughly divided into the following three stages.
- The first stage is to obtain a set of class assertions by generating instances of each class and then reason over the set of class assertions. First, a given number of instances are generated according to the class in TBox to obtain a set of class assertions. Then, the ontology reasoner named Pellet is employed to perform a logical reasoning on the set of class assertions based on the TBox. The -A relation between the instance and the class is generalized to obtain the -A relation between the instance and the parent or parent-of-parent class and thus obtain the set of reasoned class assertions;
- The second stage is to generate the set of role assertions. According to the relation definition and class constraints, as well as the set of reasoned class assertions, the relation between instances is randomly established. The union of the set of class assertions and the set of relation assertions is the synthesized ABox with noise;
- The third stage is to remove conflict sets from the synthesized ABox with noise to obtain a logically consistent ABox. A set of relation assertions that randomly built may conflict with the set of axioms of the TBox. Based on the minimal conflict set discovery method, all the minimal conflict sets can be obtained from the synthesized ABox with noise and eliminated, and finally, a synthesized ABox with consistent logical expression is obtained.
| Algorithm 1: The ABox synthesis method based on TBox |
|
3.3.2. Subgraph Segmentation and Dataset Construction
Each piece of training data of the FCNN consists of the subgraph corresponding to the instance and its extended subgraph, which is, i.e., . Subgraph segmentation and ontology reasoning are needed to construct a train dataset based on synthesized ABox. The subgraph segmentation is conducted with the aid of the SPARQL (Simple Protocol and RDF Query Language) [47], and ontology reasoning is performed with the help of Pellet. The specific process is shown in Algorithm 2.
| Algorithm 2: Subgraph segmentation and dataset construction |
|
It should be noted that although the ontology reasoner is used in both Algorithms 1 and 2, the roles of the ontology reasoner in the two algorithms are different. In Algorithm 1, the role of ontology reasoner is to check and ensure the consistency of the assertions and the axioms of ontology in the synthesized ABox. In Algorithm 2, the function of the ontology reasoner is to carry out logical reasoning, to integrate the process of deductive reasoning into the data, and to produce supervision data for the training of the FCNN.
3.3.3. Encoding and Decoding Methods
ABox can be viewed as a heterogeneous graph with multiple relations, and its structure and information cannot be directly expressed by an adjacency matrix. The CFR draws lessons from the concept of a “channel” in CV (Computer Vision), regarding each role in ABox as a channel, and slicing ABox according to the channel; only one role is contained in each slice. Each slice is transformed into an adjacency matrix, and all slices are spliced to form an adjacency matrix layered according to roles, which is called a multi-layer adjacency matrix. It should be noted that each subgraph only contains the neighbor nodes and relations of the instance, and different instances have different neighbor nodes. Therefore, the entity dictionary of each graph should be recorded when encoding the subgraph so as to realize the inverse process from the multi-layer adjacency matrix to the extended subgraph in the decoding stage. The detailed process of subgraph encoding is shown in Algorithm 3.
The output of the FCNN is the multi-layer adjacency matrix, which is restored to the form of the extended subgraph by the decoder. The specific process is shown in Algorithm 4. It should be noted that the CFR is applicable to regression fitting when learning the object relational mapping, so the threshold (t) is a very important parameter, and the reconciliation of the quality and efficiency of the reasoning result can be realized by adjusting t. This parameter will be analyzed in detail in the experiment, and it will not be described here.
| Algorithm 3: The of a multi-layer adjacency matrix |
|
| Algorithm 4: The of a multi-layer adjacency matrix |
|
3.3.4. Structure of the FCNN
The CFR uses a FCNN, which is inspired by the successful application of FCNNs in computer vision. The model framework of the FCNN is shown in Figure 2. The input is the multi-layer adjacency matrix of the input subgraph, and the output is the multi-layer adjacency matrix of the extended subgraph. In the figure, represents the number of roles in the ontology KB, and d is the dimension of the adjacency matrix.
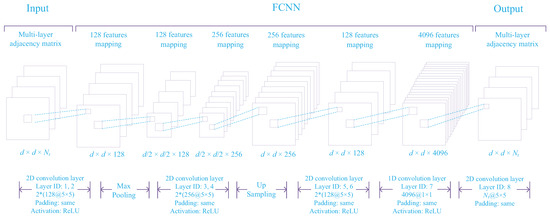
Figure 2.
Structure of the FCNN.
As can be seen from Figure 2, the CFR uses 8-layer FCNN model, where indicates that there are a convolutional layers connected, each layer contains b convolutional kernels, and the size of the convolutional kernel is . In the FCNN, the padding type of each convolutional layer is the “same”, meaning that the input and output feature maps are guaranteed to have the same dimensions. The activation function is not used for convolutional layer ID 8, and ReLU [48] is used for the other convolutional layers. In addition, the CFR uses one-dimensional convolution instead of the fully connected layer, as shown in convolutional layer ID 7 in the figure. The advantage of the FCNN is that the model parameters can be reduced effectively, the efficiency of training and reasoning can be improved, and the consistency of structure between the input and output can be improved while ensuring that the neural network model captures the global information.
It can also be seen from the figure that the input and output of the FCNN have the same dimension. In fact, the FCNN learns the object relational mapping from the input subgraph to the extended subgraph, and this object relational mapping is the embodiment of the logical deduction process of ontology reasoning under a specific TBox. The FCNN realizes the end-to-end representation and learning of the symbolic logical reasoning process by means of the hierarchical adjacency matrix encoder and decoder.
The equation for the convolutional computation in the network can be expressed as:
where the input is , the convolutional kernel is , and the output is . denotes the input size of the convolutional layer, C denotes the number of input channels, denotes the size of the convolutional kernel, denotes the number of the convolutional kernels, denotes the size of the output feature maps, and the FCNN in the CFR adopts the same size filling, so , denotes the index of the central node of the convolution block, and denotes rounding down.
The CFR uses the mean square error (MSE) as the loss function, and its specific formula is as follows:
where represents the number of roles in the ontology KB, d is the dimension of the adjacency matrix, represents the real value in the adjacency matrix, and represents the prediction value of the FCNN on the corresponding position. The CFR uses the Adam algorithm [49] for optimization training.
3.4. Evaluation Criterions of the CFR
In view of the soundness and completeness of logic-based ontology reasoning, the reasoning result of the ontology reasoning method is selected as the benchmark to define the evaluation criterions of the CFR. The evaluation criterions of approximate ABox reasoning of the CFR include , and , which are used to evaluate the accuracy, completeness and comprehensive performance of the CFR, respectively.
The input subgraph dataset is , the extended subgraph dataset obtained by ontology reasoning is , and is the subgraph dataset obtained by the CFR, where represents the number of instances in the KB. In reasoning results, the number of the triples that are correctly reasoned can be expressed as:
where , , denotes RDF triples, and denotes the length of the set.
The refers to the proportion of the correct triple in the output of the CFR, which can be expressed as:
The refers to the proportion of the correct triple in all correct triples in the reasoning result, which can be expressed as:
is used as the comprehensive evaluation criterion of and , which is also the comprehensive evaluation of approximate reasoning quality, and it is defined as:
4. Experiments
In this section, the experimental verification and result analysis of the CFR are carried out. Firstly, the experimental data and parameter settings of the CFR are introduced in detail. Then, we evaluate the reasoning quality of the CFR through experiments. Since the results of ontology reasoning are sound and complete, we selected results of Pellet as the benchmark and selected NMT4RDFS [39] as the comparison to analyze the reasoning , and of the CFR.
4.1. Experimental Data and Parameter Settings
The experimental environment mainly includes a deep learning workstation with 32 GB of memory, a CPU frequency of 2.90 GHz × 12, and a GeForce GTX 1080 GPU. The interaction interface between the CFR and ontology KBs is built based on rdflib and owlready2; the computational framework of the CFR is based on Keras and Tensorflow.
There are two open-source ontologies used in the experiment: one is family.swrl (http://protege.cim3.net/file/pub/ontologies/family.swrl.owl/family.swrl.owl, accessed on 1 March 2019) released by the Ontology Base of Stanford University, which is a family relation ontology, hereinafter referred to as “Family”, and the other is time-qualitative-only (https://github.com/sbatsakis/TemporalRepresentations, accessed on 20 May 2020) released by Batsakis et al., which is a time ontology hereinafter referred to as “Time”. We remove the SWRL rules in the two ontologies so that it only retains the relevant axioms of OWL DL. The statistical information and the complexity of the above ontologies are given in Table 1. In the table, “#” indicates the number of corresponding elements. Family and Time have different representation abilities, and their numbers of concepts, relations and axioms are also quite different, representing two different OWL DL ontologies.

Table 1.
Statistics of the Ontologies Used in the Experiments.
It is difficult to obtain a large amount of high-quality data for training in reality, so we train and evaluate our model on synthetic data. We synthesize the train and test dataset based on the two ontologies, respectively, with the scale shown in Table 2. In the table, “# CA”, “# RA”, and ”# A” indicate the number of class assertions, role assertions, and all assertions in ABox of the synthetic OWL DL KBs, respectively. “Ratio” shows the split ratio of the training set, verification set and test set, and “# Subgraphs” indicates the number of subgraphs in the corresponding dataset.

Table 2.
Statistical information of ABox and dataset split in synthetic OWL DL KBs.
In addition, in order to further analyze the generalization of the CFR to new data and the scalability to a large-scale ABox, we independently synthesized eight test sets of different scales on the two ontologies, as shown in Table 3, # F1∼# F8 and # T1∼ # T8, with their scales gradually increasing. It should be noted that the independently synthesized test data means that these data and train data and different test data are completely different from each other and do not interact with each other except that they share the same TBox, so this independent test set contains brand new data.

Table 3.
Statistics of the Independent Test Dataset Used in the Experiments.
In the evaluation of reasoning qulity of the CFR, we choose NMT4RDFS as the comparison method. This method is chosen for two reasons. First, the original design of this method is similar to that of the proposed CFR; both try to use an NN to achieve approximate logical reasoning, so the two methods are comparable. Second, unlike the CFR, NMT4RDFS is oriented toward ontology KBs (domain-specific KGs) constructed based on RDF(s). Compared with the ontologies constructed by OWL DL, the expressive ability of RDFs is weaker. Therefore, through a comparison with NMT4RDFS, the reasoning ability of the CFR for OWL DL ontologies can be demonstrated. The open-source implementation of NMT4RDFS can be downloaded from GitHub (https://github.com/Bassem-Makni/NMT4RDFS, accessed on 15 April 2021).
On all datasets, the CFR and NMT4RDFS use the same data for training and testing and then compare their reasoning , and . Their parameter settings are shown in Table 4. In the table, “d” indicates the dimension of the adjacency matrix, the “HOPE dimension” is the dimension compressed by NMT4RDFS using the HOPE method, and ”t” is the threshold for reconstructing the extended subgraph by the CFR.

Table 4.
Parameter Settings of the CFR and NMT4RDFS in the Experiments.
4.2. Reasoning Quality of the CFR
In this section, we verify the reasoning quality of the CFR by comparing and analyzing the , and of the CFR and NMT4RDFS on different test sets. The experimental results are shown in Table 5. In the table, “-” indicates that there is no inference assertion, because there are only two mutually exclusive classes in Time, so no inference assertion can be obtained.

Table 5.
The , and of class assertions (CA), role assertions (RA) and all assertions (A) of the CFR and NMT4RDFS.
As can be seen from Table 5, the reasoning quality of the CFR is much higher than that of NMT4RDFS. On the test set named Family, the of the CFR in term of class assertions, role assertions, and all assertions is 0.9428, 0.9652, and 0.9555, respectively, while that of NMT4RDFS is only 0.5102, 0.5119, and 0.5113. The CFR achieves superior reasoning accuracies. In addition, the reasoning results of the CFR are also highly complete, the of class assertions, role assertions and all assertions is 0.9282, 0.9946, and 0.9651, respectively, while that of NMT4RDFS is only 0.4592, 0.5917, and 0.5329. The of the CFR in assertion reasoning is 0.9603, while that of NMT4RDFS is only 0.5218. Obviously, the comprehensive performance of the CFR is much better than NMT4RDFS. Similar results have also been obtained on the test set named Time. The of the CFR is 0.9493, while that of NMT4RDFS is 0.7997. On the test sets of the two ontologies, the CFR achieves much better approximate reasoning results than NMT4RDFS. It is worth noting that the comprehensive reasoning performance of the CFR on the two ontologies is roughly the same ( is 0.9603 for Family and 0.9493 for Time), while the reasoning performance of NMT4RDFS is quite different ( is 0.5218 for Family and 0.7997 for Time), which also shows that the CFR has better applicability to OWL DL ontology KBs with different expression capabilities.
In order to further verify the reasoning quality of the CFR, we evaluate the reasoning quality of the CFR and NMT4RDFS on independently synthesized test sets of different scales (Table 3). The reasoning , and of the CFR and NMT4RDFS on all assertions are shown in Table 6. It can be found that the CFR achieves higher , and on all test datasets of Family and Time. For # F1∼# F8 on Family, the of the CFR is not less than 0.94, the is not less than 0.99, and the exceeds 0.97. For # T1∼# T8 on Time, the of the CFR is not less than 0.97, the is not less than 0.94, and the exceeds 0.96. The reasoning quality of the CFR is much higher than that of NMT4RDFS, which is close to the soundness and completeness of ontology reasoning. This shows that the CFR proposed has better reasoning ability for OWL DL ontology KBs, the CFR reasoning mechanism can learn the deep domain knowledge modeled in OWL DL ontologies more accurately, so it can more accurately approximate and compile the logical reasoning processes of complex ontologies, while NMT4RDFS targets RDF(s) ontologies, so it has limitations when addressing complex ontologies.

Table 6.
The , and of all assertions (A) of the CFR and NMT4RDFS on independent synthetic test datasets.
It can be seen from the horizontal comparison between Table 5 and Table 6 that the CFR has a strong generalization ability for new data. On the one hand, the reasoning quality of the CFR between independent test sets is similar, and the evaluation results are roughly the same as those on training sets. For # F1∼# F8, the is about 0.95, the is about 0.99, and the is about 0.97; For # T1∼# T8, the is about 0.98, the is about 0.95, and the is about 0.96. On the other hand, the CFR has excellent generalization ability for datasets of different sizes. Although the size of independent test sets varies greatly, the CFR still achieves similar reasoning results on all independent test sets, and the reasoning quality does not decrease with the growth of data size. For example, the scale of #T8 in Table 6 has far exceeded the scale of train data and other test datasets, but it still has the same reasoning quality as small-scale test sets such as #T1∼#T7. The CFR has good generalization ability because it is essentially an approximation of ontology reasoning process. Ontology reasoning is a top–down deductive reasoning. Its reasoning process is a logical deduction from pattern knowledge to underlying assertions, which depends on TBox rather than a specific ABox, and it is independent of the scale of ABox. The generalization of the CFR shows that it has learned the approximate process of ontology reasoning, and it has the approximate deduction ability that does not depend on the specific assertion data and its scale, but it only depends on the pattern knowledge.
In practical applications, different occasions may put forward different requirements for the soundness and completeness of reasoning results. The reasoning and of the CFR can be adjusted according to the application requirements of different occasions. It can be seen from Table 5 and Table 6 that the CFR shows slightly different performance on the Family and Time test datasets. The of the CFR on the Family test sets is slightly lower than that of Time, but the is relatively higher, which indicates that the CFR has achieved relatively high completeness on the Family, yet it shows high soundness on the Time ontology. We can achieve a compromise between the soundness and completeness of the CFR reasoning results via threshold(t) in the . With #F5 and #T5 being selected as the test sets, the curve of , and of the CFR reasoning result as the threshold(t) changes will be shown in Figure 3.
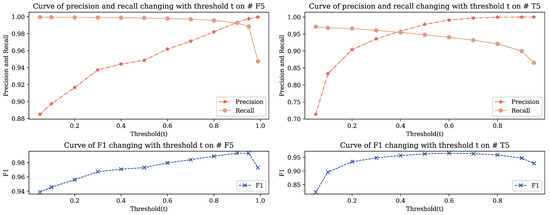
Figure 3.
Curve of , and of the CFR changing with threshold (t).
As it can be seen from the figure, for different ontologies, the , and of the CFR are slightly different under a certain threshold (t), but they show the same trend. The of the CFR will rise with the increase of threshold (t), the will decrease with the increase of threshold (t), and the will increase first and then decrease with the increase of threshold (t). The contradiction between soundness and completeness can be balanced by adjusting threshold (t). In applications, a larger threshold (t) can be set when the application has higher requirements on the soundness of reasoning results. For example, when the threshold (t) = 0.9, the of the CFR on the #F5 and #T5 are 0.9934 and 0.9999, respectively. If the threshold (t) continues to increase, the can even reach 100%, but the corresponding will be much lower. When the completeness of reasoning results is required, a smaller threshold (t) can be set. For example, when the threshold (t) = 0.1, the of the CFR on the two test sets are 0.9994 and 0.9681, respectively. If there is no special requirement for soundness and completeness, the threshold (t) maximizing can be selected, and the CFR has the best comprehensive performance at present. For example, for the test sets #F5 and #T5, the threshold (t) is set to 0.9 and 0.6, the values of the CFR are 0.9931 and 0.9651, respectively, and the corresponding values are 0.9934 and 0.9912, while the values are 0.9927 and 0.9404, respectively. From the above analysis, it can be found that the CFR can trade off the different emphasis between soundness and completeness by adjusting the threshold (t) in the process of reconstructing the extended subgraph, which can further improve the applicability of the CFR to meet different reasoning application scenarios.
In this section, we verify the reasoning quality of the CFR on test datasets of Family and Time through experimental analysis, analyze the generalization of the CFR on the new ABox and the ABox of different scales, and further explain that the CFR achieves a compromise between and through parameter adjustment. The experimental results show that the CFR can achieve high , and on test datasets of OWL DL ontology KBs, has superb generalization ability, and has better applicability to ABox reasoning in different occasions.
4.3. Reasoning Efficiency of the CFR
In this section, we illustrate the reasoning efficiency by comparing the reasoning time consumption of the CFR and ontology reasoning. In the experiment, two logical-based ontology reasoners are chosen as the benchmarks, namely, Pellet and Hermit. Both are widely used ontology reasoners and are relatively representative.
The reasoning time consumption of the CFR and ontology reasoning methods on the test datasets #F1 ∼ #F8 and #T1 ∼ #T8 is shown in Table 7. The reasoning time consumption in the table is the average of the three reasoning times on the corresponding test sets. “-” means that the reasoning cannot be performed due to memory overflow or the reasoning results can not obtained for more than 12 h. We do not discuss the differences between ontology reasoners (refer to [50]) but only illustrate the efficiency of the CFR by comparing the reasoning time. It needs to be explained that the Pellet and Hermit are relatively mature products, which have been optimized by a large number of researchers to improve the reasoning efficiency, while the CFR is only a prototype algorithm. If the CFR is optimized, the inference speed can be further improved.

Table 7.
Time consumption of the CFR and ontology reasoners on independent synthetic test datasets.
It can be found from the table that the CFR has a greater reasoning speed advantage than ontology reasoners. For all independent synthetic test datasets, the reasoning time consumption of Pellet, HermiT and the CFR will increase with the growth of the scale of the ABox, but the difference is that the reasoning time consumption of Pellet and HermiT increases significantly faster than that of the CFR. It is worth noting that with the growth of the scale of ABox, the reasoning time consumption of Pellet and Hermit is far greater than that of the CFR. The larger the scale of ABox is, the more obvious the advantage of reasoning speed of the CFR. For example, for #F6, the reasoning time consumption of Pellet and HermiT is about 655 times and 1158 times longer than that of the CFR, respectively. For the test datasets on Time, Pellet shows worse applicability, which can only obtain reasoning results on the #T1∼ #T5. Although HermiT can obtain the results on all the test datasets, its reasoning time consumption is much longer than that of the CFR. For example, in the largest test set #T8, HermiT took 5067 s to finish reason, while the CFR only took 355 s, showing the former is about 14 times slower than the latter. In order to analyze the trend of the reasoning time consumption of the CFR more directly, the curves of the reasoning time trends of different reasoning methods on the test is drawn, as shown in Figure 4. Since the number of class assertions in different datasets varies greatly, the abscissa in the figure is the logarithmic coordinate.
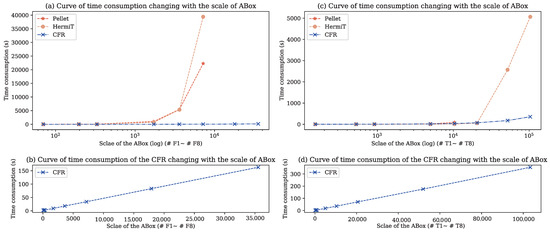
Figure 4.
Curve of time consumption of Pellet, HermiT and the CFR changing with the scale of ABox.
It can be seen from Figure 4a,b that the reasoning time consumption of Pellet and HermiT on #F6 has increased dramatically, which is about 4.1 times and 7.4 times that of #F5, respectively, and the scale of #F6 is only about two times that of #F5. Thus, it can be seen that the reasoning time consumption of ontology reasoning methods does not increase linearly with the growth of the scale of ABox, but it tends to increase exponentially. The reasoning time consumption of the CFR is almost a straight line with the growth of the scale of ABox, indicating that the reasoning time of the CFR rises linearly with the scale of ABox in OWL DL KBs. Figure 4c,d compare the curve of reasoning time consumption of different reasoning methods on the Time, showing a similar change trend to those on Family, which indicates that the proposed CFR has universality to some extent and shows similar reasoning efficiency on different ontologies.
The traditional OWL DL-oriented ontology reasoners, such as Pellet and HermiT, are usually based on classic Tableau algorithms and their extensions, both of which are in-memory algorithms. Theoretical research has proven that for an ontology represented by OWL DL, the complexity of its reasoning process is at least ExpTime-complete. Therefore, for Pellet and HermiT, when the scale of ABox grows, both the memory resources occupied and the time consumed increase exponentially. The CFR takes subgraphs of instances as input, and once the NN model is determined, for each subgraph, only one operation is triggered and each operation can be calculated in a constant amount of time. Therefore, the time consumption of the CFR is linear in the number of instances, that is, , where indicates the scale of the instance in an OWL DL KB. Compared with traditional ontology reasoners, the CFR has higher reasoning efficiency and faster response speed, and it has better scalability for a large-scale ABox in OWL DL KBs.
In this part, the reasoning time consumptions of ontology reasoning methods and the CFR are analyzed and compared by experiments. Experimental results show that the CFR has higher reasoning efficiency and faster reasoning speed than ontology reasoning. With the growth of the scale of ABox, the reasoning time consumption increases linearly: the larger the scale of ABox, the more obvious the advantage of its reasoning speed.
5. Discussion
Although the reasoning quality and efficiency of the CFR proposed are verified by experiments, there are still some challenges to discuss that may affect the applicability and limitations of our method.
Firstly, the CFR has some limitations on long chain reasoning. In the ontology KB built on OWL DL, chained reasoning is inevitably involved, such as roles with transitivity. Let us take the role named “” ( means that s is the ancestor of o) as an example; if the following assertions exist in the KB, , and , we can infer the implicit assertion . If we expect the CFR to obtain such reasoning results, we should ensure that instances a and d appear in a subgraph at the same time, which is often not guaranteed when using the method in this paper to perform subgraph segmentation. Therefore, if there is a lot of chained reasoning in the KB, the completeness of reasoning results of the CFR may be negatively affected. If we adopt a higher-order subgraph segmentation (refer to [7]), it can ensure that the instances involved in chain reasoning are in a subgraph, but it will lead to the rapid growth of the scale of the subgraph, increase the difficulty of NN training, and affect the quality of approximate reasoning. We choose #F5 to illustrate this limitation by comparing the reasoning performance of the CFR on one-hop and two-hop subgraphs. The results are shown in Figure 5. It can be seen from the figure that the reasoning performance of the CFR on two-hop subgraphs is slightly reduced, and no matter the , or is slightly lower than the reasoning result of one-hop subgraphs. This is because for two-hop subgraphs, the adjacency matrix will be larger and more sparse, reducing the efficiency of information encoding and making the training of NNs more difficult. Although some methods such as HOPE [39] can reduce the dimension of the adjacency matrix, there will be information loss, and we cannot completely reconstruct the adjacency matrix. Therefore, the reasoning performance of the CFR may be limited for the KBs containing a large number of long-chain reasoning, and we will explore more appropriate subgraph encoding methods to alleviate this problem in subsequent research.
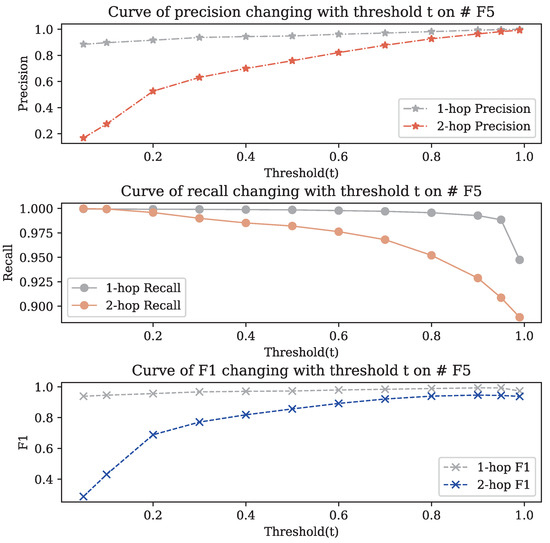
Figure 5.
Curve of , and of the CFR changing with threshold(t) on 1-hop and 2-hop subgraphs.
Secondly, we should pay attention to the case where ABox contains super nodes. The super nodes are instances that are associated with many other instances, such as an instance of a school in LUBM (http://krr-nas.cs.ox.ac.uk/ontologies/lib/LUBM/, accessed on 20 April 2021) ontology, which may be associated with thousands of student instances. In the reasoning process of the CFR, if there are many super-nodes, the scale of the subgraph centered on the super-node will be much larger than that of other nodes, and the multi-layer adjacency matrix corresponding to the super-node will be very large and sparse, which will lead to a lot of parameters in the input layer of the NN, making the NN model difficult to train. However, in practice, the influence of super-nodes is limited, because the information of all subgraphs is redundant, such as assertions (indicating that student s study in school o), then this assertion will appear in the subgraph corresponding to instances s and o, respectively. If we discard the subgraph of super-node o, it will not cause information loss from a global perspective. Therefore, in reasoning applications of the CFR, the subgraphs corresponding to super nodes can be appropriately discarded.
6. Conclusions
The OWL DL KB containing large-scale ABox is becoming more and more common; ABox reasoning has gradually become a bottleneck restricting its further application. The existing reasoning methods are difficult to adapt to the reasoning needs of large-scale ABox. Aiming at these shortcomings, we introduce neural-symbolic learning into ABox reasoning and propose an approximate reasoning method, called the CFR, which implements approximate deductive reasoning on OWL DL KB by approximately compiling the logical deduction process of ontology reasoning through neural network. We formalize the basic idea of the CFR, introduce the overall framework and specific process in detail, and carry out experiments on two open-source ontologies built on OWL DL. The experimental results show that the CFR can not only achieve higher approximate reasoning quality but also has higher reasoning efficiency and a faster reasoning response, which effectively illustrates the effectiveness of the CFR. The CFR is expected to effectively support large-scale ABox reasoning applications in OWL DL KBs.
In the future, we will continue to conduct further research on the characteristics of the CFR, mainly including the following aspects. The first is to use the generalization of NN to further explore the ability of the CFR to perform transfer reasoning and incremental reasoning. The second is to further explore the reasoning ability of the CFR in large-scale ABox containing noise by using the robustness of an NN. The third is to try to realize the interpretability of reasoning results of the CFR by using arguments of ontology reasoning as the supervision. We hope that the CFR can provide useful reference for exploring more large-scale ABox reasoning methods.
Author Contributions
Conceptualization, X.Z., B.L., Z.D. and L.Y.; methodology, X.Z.; formal analysis, X.Z.; investigation, X.Z.; data curation, B.L. and Z.D.; writing—original draft preparation, X.Z.; writing—review and editing, B.L. and C.Z.; funding acquisition, C.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Foundation (NSF) of China OF FUNDER grant number 71571186, 61273322.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are openly available in Gitee at https://gitee.com/x-x-zhu/the-data-of-cfr.git, accessed on 16 November 2022.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Guarino, N.; Oberle, D.; Staab, S. What Is an Ontology? Handbook on Ontologies; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–17. [Google Scholar] [CrossRef]
- Jorge, C.; Sheth, A. The Semantic Web and its applications. In Semantic Web Services, Processes and Applications; Springer: Boston, MA, USA, 2006; pp. 3–33. [Google Scholar] [CrossRef]
- Horrocks, I. Owl: A description logic based ontology language. In Proceedings of the 11th International Conference on Principles and Practice of Constraint Programming, Sitges, Spain, 1–5 October 2005; pp. 5–8. [Google Scholar] [CrossRef]
- De Giacomo, G.; Lenzerini, M. TBox and ABox reasoning in expressive description logics. KR 1996, 96, 316–327. [Google Scholar]
- Ren, Y.; Pan, J.Z.; Lee, K. Parallel ABox Reasoning of EL Ontologies. In Proceedings of the Joint International Semantic Technology Conference, Hangzhou, China, 4–7 December 2011; pp. 17–32. [Google Scholar] [CrossRef]
- Klarman, S.; Endriss, U.; Schlobach, S. ABox Abduction in the Description Logic . J. Autom. Reason. 2011, 46, 43–80. [Google Scholar] [CrossRef]
- Zhu, X.; Lin, B.; Ding, Z.; Yao, L.; Zhu, C. Implementing Large-Scale ABox Materialization Using Subgraph Reasoning. In Proceedings of the International Conference on Knowledge Science, Engineering and Management, Singapore, 6–8 August 2022; pp. 627–643. [Google Scholar] [CrossRef]
- Cui, Z.; Chen, H.; Cui, L.; Liu, S.; Liu, X.; Xu, G.; Yin, H. Reinforced KGs reasoning for explainable sequential recommendation. World Wide Web 2022, 25, 631–654. [Google Scholar] [CrossRef]
- Baader, F.; Horrocks, I.; Sattler, U. Description logics. Handbook on Ontologies; Springer: Berlin/Heidelberg, Germany, 2004; pp. 3–28. [Google Scholar] [CrossRef]
- Zese, R.; Bellodi, E.; Riguzzi, F.; Cota, G.; Lamma, E. Tableau reasoning for description logics and its extension to probabilities. Ann. Math. Artif. Intell. 2018, 82, 101–130. [Google Scholar] [CrossRef]
- Abu-Salih, B. Domain-specific knowledge graphs: A survey. J. Netw. Comput. Appl. 2021, 185, 103076. [Google Scholar] [CrossRef]
- Shen, T.; Zhang, F.; Cheng, J. A comprehensive overview of knowledge graph completion. Knowl.-Based Syst. 2022, 255, 109597. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Y.; Zhao, B.; Cheng, J.; Zhao, X.; Duan, Z. Knowledge graph completion: A review. IEEE Access 2020, 8, 192435–192456. [Google Scholar] [CrossRef]
- Wiharja, K.; Pan, J.Z.; Kollingbaum, M.J.; Deng, Y. Schema aware iterative Knowledge Graph completion. J. Web Semant. 2020, 65, 100616. [Google Scholar] [CrossRef]
- Kulmanov, M.; Liu-Wei, W.; Yan, Y.; Hoehndorf, R. El embeddings: Geometric construction of models for the description logic EL++. In Proceedings of the 28th International Joint Conferences on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 6103–6109. [Google Scholar] [CrossRef]
- Sun, Z.; Deng, Z.H.; Nie, J.Y.; Tang, J. Rotate: Knowledge graph embedding by relational rotation in complex space. In Proceedings of the 7th International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar] [CrossRef]
- Lu, H.; Hu, H.; Lin, X. DensE: An enhanced non-commutative representation for knowledge graph embedding with adaptive semantic hierarchy. Neurocomputing 2022, 476, 115–125. [Google Scholar] [CrossRef]
- Alshahrani, M.; Khan, M.A.; Maddouri, O.; Kinjo, A.R.; Queralt-Rosinach, N.; Hoehndorf, R. Neuro-symbolic representation learning on biological knowledge graphs. Bioinformatics 2017, 33, 2723–2730. [Google Scholar] [CrossRef]
- Franklin, N.T.; Norman, K.A.; Ranganath, C.; Zacks, J.M.; Gershman, S.J. Structured Event Memory: A neuro-symbolic model of event cognition. Psychol. Rev. 2020, 127, 327–361. [Google Scholar] [CrossRef]
- Belle, V. Symbolic logic meets machine learning: A brief survey in infinite domains. In Proceedings of the International Conference on Scalable Uncertainty Management, Bozen-Bolzano, Italy, 23–25 September 2020; pp. 3–16. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Eberhart, A.; Bianchi, F.; Hitzler, P. Towards bridging the neuro-symbolic gap: Deep deductive reasoners. Appl. Intell. 2021, 51, 6326–6348. [Google Scholar] [CrossRef]
- Hitzler, P.; Bianchi, F.; Ebrahimi, M.; Sarker, M.K. Neural-symbolic integration and the semantic web. Semant. Web 2020, 11, 3–11. [Google Scholar] [CrossRef]
- Rudolph, S.; Tserendorj, T.; Hitzler, P. What is approximate reasoning? In Proceedings of the International Conference on Web Reasoning and Rule Systems, Karlsruhe, Germany, 31 October–November 1 2008; pp. 150–164. [Google Scholar] [CrossRef]
- Pan, J.Z.; Thomas, E. Approximating owl-dl ontologies. In Proceedings of the 22nd National Conference on Artificial Intelligence, Vancouver, BC, Canada, 22–26 July 2007; pp. 1434–1439. [Google Scholar]
- Sirin, E.; Parsia, B.; Grau, B.C.; Kalyanpur, A.; Katz, Y. Pellet: A practical owl-dl reasoner. J. Web Semant. 2007, 5, 51–53. [Google Scholar] [CrossRef]
- Glimm, B.; Horrocks, I.; Motik, B.; Stoilos, G.; Wang, Z. HermiT: An OWL 2 reasoner. J. Autom. Reason. 2014, 53, 245–269. [Google Scholar] [CrossRef]
- Krötzsch, M. OWL 2 profiles: An introduction to lightweight ontology languages. In Proceedings of the Reasoning Web-Semantic Technologies for Advanced Query Answering, Vienna, Austria, 3–8 September 2012; pp. 112–183. [Google Scholar] [CrossRef]
- Kazakov, Y.; Krötzsch, M.; Simančík, F. The incredible elk. J. Autom. Reason. 2014, 53, 1–61. [Google Scholar] [CrossRef]
- Nenov, Y.; Piro, R.; Motik, B.; Horrocks, I.; Wu, Z.; Banerjee, J. RDFox: A highly-scalable RDF store. In Proceedings of the 14th International Semantic Web Conference, Bethlehem, PA, USA, 11–15 October 2015; pp. 3–20. [Google Scholar] [CrossRef]
- Bordes, A.; Usunier, N.; Garcia-Duran, A.; Weston, J.; Yakhnenko, O. Translating embeddings for modeling multi-relational data. In Proceedings of the 26th International Conference on Neural Information Processing Systems, South Lake Tahoe, CA, USA, 5–10 December 2013; pp. 2787–2795. [Google Scholar]
- Wang, Z.; Zhang, J.; Feng, J.; Chen, Z. Knowledge graph embedding by translating on hyperplanes. In Proceedings of the 28th AAAI Conference on Artificial Intelligence, Québec City, QC, Canada, 27–31 July 2014; pp. 1112–1119. [Google Scholar] [CrossRef]
- Che, F.; Zhang, D.; Tao, J.; Niu, M.; Zhao, B. Parame: Regarding neural network parameters as relation embeddings for knowledge graph completion. In Proceedings of the 34th AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 2774–2781. [Google Scholar] [CrossRef]
- Socher, R.; Chen, D.; Manning, C.D.; Ng, A. Reasoning with neural tensor networks for knowledge base completion. In Proceedings of the 26th International Conference on Neural Information Processing Systems, South Lake Tahoe, CA, USA, 5–10 December 2013; pp. 926–934. [Google Scholar]
- Dettmers, T.; Minervini, P.; Stenetorp, P.; Riedel, S. Convolutional 2d knowledge graph embeddings. In Proceedings of the 32nd AAAI conference on artificial intelligence, New Orleans, LA, USA, 2–7 February 2018; pp. 1811–1818. [Google Scholar] [CrossRef]
- Nguyen, D.Q.; Nguyen, T.D.; Nguyen, D.Q.; Phung, D. A novel embedding model for knowledge base completion based on convolutional neural network. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, New Orleans, LA, USA, 1–6 June 2018; pp. 327–333. [Google Scholar] [CrossRef]
- Schlichtkrull, M.; Kipf, T.N.; Bloem, P.; Berg, R.V.D.; Titov, I.; Welling, M. Modeling relational data with graph convolutional networks. In Proceedings of the 15th European Semantic Web Conference, Heraklion, Greece, 3–7 June 2018; pp. 593–607. [Google Scholar] [CrossRef]
- Ji, S.; Pan, S.; Cambria, E.; Marttinen, P.; Philip, S.Y. A survey on knowledge graphs: Representation, acquisition, and applications. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 494–514. [Google Scholar] [CrossRef]
- Garcez, A.D.; Bader, S.; Bowman, H.; Lamb, L.C.; de Penning, L.; Illuminoo, B.V.; Poon, H.; Zaverucha, G. Neural-symbolic learning and reasoning: A survey and interpretation. Neuro-Symb. Artif. Intell. State Art 2022, 342, 1–51. [Google Scholar] [CrossRef]
- Makni, B.; Hendler, J. Deep learning for noise-tolerant RDFS reasoning. Semant. Web 2019, 10, 823–862. [Google Scholar] [CrossRef]
- Jain, N.; Tran, T.K.; Gad-Elrab, M.H.; Stepanova, D. Improving knowledge graph embeddings with ontological reasoning. In Proceedings of the 20th International Semantic Web Conference, Virtual Event, 24–28 October 2021; pp. 410–426. [Google Scholar] [CrossRef]
- Hohenecker, P.; Lukasiewicz, T. Ontology reasoning with deep neural networks. J. Artif. Intell. Res. 2020, 68, 503–540. [Google Scholar] [CrossRef]
- Hitzler, P.; Eberhart, A.; Ebrahimi, M.; Sarker, M.K.; Zhou, L. Neuro-symbolic approaches in artificial intelligence. Natl. Sci. Rev. 2022, 9, nwac035. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Ting, T.O.; Man, K.L.; Guan, S.U. Investigation of neural networks for function approximation. Procedia Comput. Sci. 2013, 17, 586–594. [Google Scholar] [CrossRef]
- Sakr, S.; Al-Naymat, G. Relational processing of RDF queries: A survey. ACM SIGMOD Rec. 2010, 38, 23–28. [Google Scholar] [CrossRef]
- Yamashita, R.; Nishio, M.; Do, R.K.; Togashi, K. Convolutional neural networks: An overview and application in radiology. Insights Imaging 2018, 9, 611–629. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Chen, H.; Lu, M.; Zhu, X.; Yao, L.; Ding, Z.; Zhu, C.; Zhu., X. Yizhong Tushuju Hecheng Fangfa, Zhuangzhi, Jisuanji Shebei He Cunchu Jiezhi. Hunan Province. CN112231422B, 26 February 2021. (In Chinese). [Google Scholar]
- Pérez, J.; Arenas, M.; Gutierrez, C. Semantics and complexity of SPARQL. ACM Trans. Database Syst. 2009, 34, 1–45. [Google Scholar] [CrossRef]
- Dubey, S.R.; Singh, S.K.; Chaudhuri, B.B. Activation functions in deep learning: A comprehensive survey and benchmark. Neurocomputing 2022, 503, 92–108. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Dahou, A.; Abualigah, L.; Yu, L.; Alshinwan, M.; Khasawneh, A.M.; Lu, S. Advanced metaheuristic optimization techniques in applications of deep neural networks: A review. Neural Comput. Appl. 2021, 33, 14079–14099. [Google Scholar] [CrossRef]
- Parsia, B.; Matentzoglu, N.; Gonçalves, R.S.; Glimm, B.; Steigmiller, A. The OWL reasoner evaluation (ORE) 2015 competition report. J. Autom. Reason. 2017, 59, 455–482. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).