1. Introduction
If one considers the operations of classical algebraic structures (such as groups, rings, fields, …) by looking at their graphs, then one sees that they satisfy two fundamental assumptions: they are left total and functional. In other words, these properties can be spelled out as operations being
everywhere defined (i.e., the operation can be applied to any two elements to obtain at least one result) and
single-valued (i.e., an application of the operation to any two elements yields at most one result). A hyperfield is a field-like structure where the latter property is relaxed for the additive operation. In the literature, such structures appear perhaps more than one would expect: hyperfields are of interest, e.g., in tropical geometry [
1,
2,
3], symmetrization [
4,
5,
6], projective geometry [
7], valuation theory [
8,
9,
10,
11], and ordered algebra [
12,
13,
14]. There are even reasons to believe that their theory generalizes field theory in ways that can be used to tackle deep problems such as the description of
, the “field of characteristic one” (cf. [
7,
15]).
More generally, since the pioneer papers [
16,
17,
18] of F. Marty, structures with multivalued operations (also called hyperstructures) generalizing classical single-valued structures have been the object of several research projects. For example, modules with a multivalued operation and a scalar multiplication over Krasner hyperrings (the old brothers of hyperfields) have been studied, e.g., in [
19,
20,
21]. In addition, hypergroups are mentioned in a journal of theoretical physics, in [
22].
In this article, we focus on valued hyperfields, generalizing valued fields: the object of study of classical valuation theory. In [
23], after having introduced valued hyperfields for the first time, Krasner associates to any valued field
a projective system
of valued hyperfields, indexed by the non-negative elements of the value group of
. Krasner proves that the projective limit of the system
is isomorphic (as a valued field) to the valuation-theoretic completion of
. His proof makes heavy use of a metric structure of the hyperfields in
, which is induced by the canonical valuation metric on
K. On the other hand, while axioms of valuation maps generalize readily to the setting of hyperfields, these are not anymore sufficient to induce a metric in the general case. Krasner’s approach to this obstacle has been to postulate one further axiom for valued hyperfields, which becomes tautological in the case of a single-valued addition. Nevertheless, examples of hyperfields with interesting valuation maps that do not induce a metric as required by Krasner are now known. Among these examples, particularly important for the present article are the
generalized tropical hyperfields ([
24] Example 2.14), which naturally encode ordered abelian groups as valued hyperfields and include
the tropical hyperfield, which became a fundamental object of study in tropical geometry (cf. [
1,
2,
3]). Other such examples can be found in [
8] (Example 4.3) or [
25].
In addition, without the metric condition, valuation maps on (hyper)fields are nothing but homomorphisms (with a specific target) in the category of valued hyperfields and their homomorphisms, making a natural framework for classical valuation theory too.
The main aims of this article are the following:
To generalize the above-mentioned limit construction of Krasner to valued fields of any (finite or infinite) Archimedean rank.
To describe the generalized limit construction in respecting the principle of equivalence (i.e., avoiding elements-dependent arguments, including Krasner’s metric arguments).
While the first aim does not present relevant difficulties, the possibility of achieving the second aim may, at first glance, raise some doubts. We will prove that the necessary metric-dependent properties of the systems are a reflection of the fact that the limit construction of Krasner is performed locally in . The latter means that these properties can be deduced by seeing as a diagram in the slice categories of over-generalized tropical hyperfields. In this slice category, Krasner’s result is in fact nothing but the computation of limit cones over completely determined diagrams. A category-theoretic characterization of the full subcategory of whose objects are generalized tropical hyperfields has not been fully achieved yet. We shall give our reasons to believe that this is possible and to which other research problems this one is connected in the conclusions section.
This article starts with a brief review in
Section 2 of the necessary category-theoretic background as well as the notation adopted. A survey of the algebraic theory of hyperfields follows in
Section 3, with the above-mentioned generalization of Krasner’s construction of the projective systems
to arbitrary Archimedean rank. The category
of valued hyperfields is also defined in this section. In addition, the embedding of the category of ordered abelian groups and order-preserving group homomorphisms into
via generalized tropical hyperfields is described. In the main
Section 4, the transition to slice categories is formalized by proving that the diagram
descends to the slice category
, for all ordered abelian group extensions
of the value group
and that the vertex of a limit cone over the latter diagram, is isomorphic to the valuation-theoretic completion of
in
, as well as, consequently, in
and in the category of valued fields and value-preserving field-homomorphisms. The conclusive
Section 5 describes related open problems, tracing lines for future investigations.
2. Category-Theoretic Preliminaries and Terminology
Many references for category theory may be cited, which cover the necessary background for the scope of this paper. The classic [
26] is certainly one of them, and we found particularly useful the following books as well [
27,
28,
29].
Since we believe that one way to better appreciate our contribution is to be as precise as possible with terminology and notation, we shall assume only some familiarity with the concepts of category, small category, and functor in this preliminary section.
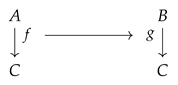
As for basic notations, for a category , we write to mean that A is an object in , and for any ordered pair of objects in , we denote the set of arrows in by . For the composition of arrows, the symbol ∘ will be employed, and the identity -arrow of will be written as .
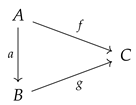
If
C is an object in
, then the
slice category
has
-arrows
, with
, as objects, while a
-arrow
is an arrow
in
if and only if the following triangular diagram
is commutative in
, i.e.,
.
The concept of a limit in a category is fundamental and, partly due to its generality, admits many equivalent definitions. The terminology we adopt for limits is similar to that of [
29], which seemed to be the most appropriate in this case. Let us go through a brief recap.
Limits
Fix a category
. If
is a small category, then a functor
is called a
diagram in of shape . A
cone on a diagram
consists of an object
V in
, called the
vertex of the cone, together with a family, indexed by the collection of objects in
,
of
-arrows, called the
sides of the cone such that the following triangular diagram
is commutative, for all arrows
.
A cone with vertex
L and sides
over a diagram
is called a
limit cone if it satisfies the following
universal property: for any cone on
D as in (
1), there exists a unique arrow
such that
holds, for all
.
By a limit of a diagram , we mean the vertex of a limit cone over D.
An isomorphism between objects in a category is a -arrow with the property that a -arrow exists such that and . The notation used for this arrow suggests that from the mere existence, uniqueness follows too, which is in fact well known to be the case.
The uniqueness of the arrows whose existence is guaranteed by the universal property of limit cones implies that, when they exist, limit cones are unique up to (a unique) isomorphism (of cones). In particular, limits in a category are unique up to (a unique) -isomorphism. It is up to this isomorphism that we speak of the limit of a diagram.
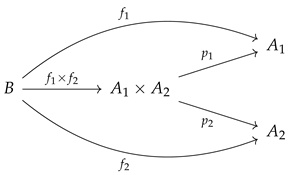
The sides of limit cones are often called
projections. This name comes from the analogy with the limit of diagrams of shape
, that is, the category consisting of 2 objects with their identity arrows solely. The latter specially shaped limits are called
(binary) products. In fact, in the category
of sets and functions, their vertex is the familiar Cartesian product of sets, while their sides are nothing but the projections onto its components. For the product
of two objects
, where
denote the projections (
), the universal property of limits has the following form: for any object
B in
admitting two arrows
(
) in
, there exists a unique arrow
such that the following diagram
is commutative.
Another specially shaped limit, which is named terminal object, is defined in a category as the limit cone of the unique diagram , where ∅ denotes the category with no objects and, consequently, no arrows (the empty category). If T is a terminal object in , then the universal property of limits has the following form: for any object C in , there exists a unique arrow .
When limit cones on diagrams of a certain shape exist in a category , then one says that has limits of shape . One then usually simplifies the terminology further in case the particular shape has been given a name. For instance, phrases like “ has products” or “ has a terminal object” mean that has limits of shape and ∅, respectively.
Remark 1. It is important to keep in mind that uniqueness up to isomorphism does not necessarily mean absolute uniqueness (following the remark on terminology in the preface of [30], one may phrase this as “categorial uniqueness is not categorical”). For example, in the category of sets and functions, where isomorphisms are bijections, all singleton sets are terminal objects. 3. Valued Fields and Hyperfields
Let
be a field and
a linearly ordered abelian group (always denoted additively) (Note that we use the same symbols to denote the additive structure of
K and the abelian group structure of
. This is standard practice and will cause no confusion). That is,
is an abelian group equipped with a linear order relation ≤ and an abelian group structure whose operation + is compatible with ≤, i.e., the following implication:
holds, for all
. A map
, where
∞ is a symbol such that
for all
, is called a
(Krull) valuation on K if and only if it satisfies all of the following three properties:
- (VAL1)
if and only if , for all .
- (VAL2)
, for all .
- (VAL3)
, for all .
If a valuation
v on a field
K is given, then
is called a
valued field, while the image of
v in
, denoted by
, is called the
value group of . The
value of
will be written as
whenever no risk of confusion arises. If
is a valued field, then
is a subring of
K, called the
valuation ring of
. It determines the valuation map
v up to valuation equivalence, i.e., up to composition with an order-preserving isomorphism of the value group. The prime ideals of the valuation ring
are linearly ordered by set inclusion and have the following form:
where
is a convex subgroup of
(see [
31] Lemma 2.3.1). The ideal
, corresponding to the trivial convex subgroup
of
, is the unique maximal ideal of
. The field
, defined as the quotient ring
, is called the
residue field of
.
A homomorphism of valued fields from to can be defined as a homomorphism of fields such that . The latter condition is sometimes phrased as “ preserves the valuation”. Since homomorphisms of valued fields are in particular homomorphisms of fields, they are automatically injective and will thus sometimes be called embeddings. We say that is a valued field extension of if and the inclusion map is an embedding of valued fields. In this way, valued fields and their homomorphisms form a category , which is a subcategory of . By an isomorphism of valued fields, we mean an isomorphism in , namely, a bijective homomorphism of valued fields whose inverse (as a function) is an arrow in too. This can be spelled out further as follows: a function is an isomorphism of valued fields if and only if it is an isomorphism of fields such that .
Fix now a valued field . There is a smallest ordinal (such ordinal is usually called the cofinality of ) serving as the index set of a sequence that is cofinal in , i.e., such that for each there exists such that . We say that a sequence of elements of K is a Cauchy sequence if and only if for every there exists such that if , then .
A sequence is, instead, said to be convergent to an element x belonging to some valued field extension of if and only if for every there exists such that if , then .
If the latter property happens to hold, then we also say that the sequence converges in L. If is a valued field extension of , then we say that K lies dense in L if every Cauchy sequence in K converges in L, while is called complete if and only if every Cauchy sequence in K converges in K.
Fact 1 (Theorem 2.4.3 in [
31]).
Every valued field admits one and (up to isomorphism of valued fields) only one valued field extension —called the completion
of —which is complete and in which K lies dense. An important consequence of the fact that
K lies dense in
is that the value group
and the residue field
of
are (canonically) isomorphic to
and
, respectively (cf. [
31] Proposition 2.4.4).
Krasner Hyperfields
Hyperfields first appeared in [
23]. In introducing them, Krasner was motivated by his interest in certain structures obtained from valued fields by means of the “factor (or quotient) construction”, which he himself described for the first time in the same article and later in [
32]. For the algebraic definition of hyperfields, we refer to [
24] (Definition 2.7) and the references therein. A more categorial treatment of these structures within the category of sets and (total) relations can be found in [
33].
The following definition of homomorphism for hyperfields has become standard in the literature.
Definition 1. Let be hyperfields. A functionis called a homomorphism of hyperfields
if , its restriction to the multiplicative groups is a homomorphism of groups, and in addition,holds, for all . We now define a projective system of hyperfields associated with any valued field of arbitrary Archimedean rank (see also [
9,
10]).
For a valued field
and an element
such that
, consider the group of the
1-units of level γ in
:
It can be easily verified that
for all
, so that the valuation map
v on
K factors through the quotient group
and yields a map
, where
. We follow the notation of [
9] and denote the multiplicative coset
of
in
as
(in particular,
) and call the
valued γ-hyperfield associated with the hyperfield
, where
The verification of the fact that the above defined structures
are in fact hyperfields, for all
such that
, is analogous to Krasner’s one for the Archimedean rank 1 case. The same conclusion also follows from the more general quotient construction described in [
32]. The use of the term “valued” is motivated once one observes that the map
satisfies (VAL1), (VAL2) and the following property analogous to (VAL3):
- (VAL3*)
, for all and all
see also [
8,
24,
34]. More generally, we shall call
a
valued hyperfield whenever
v is a map from the hyperfield
H to an ordered abelian group
(with the addition of
∞) satisfying (VAL1), (VAL2) and (VAL3*). These requirements are equivalent (cf., e.g., [
24] Lemma 3.4) to
v being a homomorphism of hyperfields
, where
denotes the
generalized tropical hyperfield associated with
:
Example 1 (Example 2.14 in [
24]).
Let ∞ be a symbol such that for all . For , we denote by the closed interval containing all satisfying . Then, by setting for all and:It is not difficult to check that is a hyperfield, called generalized tropical hyperfield associated with Γ
. Moreover, the identity homomorphism is a valuation on . Finally, note that the order of Γ
can be recovered as follows:and that this observation yields an embedding of the category of ordered abelian groups and order-preserving group homomorphisms into the category of hyperfields and their homomorphisms. Example 2 (Trivial valuation). Let H be any hyperfield, Γ any ordered abelian group, and be defined as and for all . Then, v is a valuation on H, called the trivial valuation.
It is well known that finite fields only admit the trivial valuation. Among infinite fields, another known example is the algebraic closures of finite fields. The next example describes a class containing finite and infinite hyperfields that all only admit the trivial valuation.
Example 3 ([
35]).
The following multivalued operation ⊞
on a set with a distinguished element , is defined by Massouros in [35] as follows:In [35] (Proposition 2), it is proved that any abelian group structure on such that , for all , yields a hyperfield . Let be a valuation on and suppose that satisfies . Then, in particular, , and since , we obtain that by definition. On the other hand, by standard arguments in valuation theory (see, e.g., [8] Lemma 4.5(4)) from and , we deduce the contradicting statement . Thus, only admits the trivial valuation, as contended. Remark 2. The hyperfields of the form were introduced by Massouros’ as an example that negatively answers the question (posed in [32]) whether all hyperfields can be obtained from fields with a multiplicative quotient construction. The question whether all hyperfields admitting non-trivial valuations can be obtained from fields with that multiplicative quotient construction is, to our knowledge, open. This particular problem is more extensively discussed in [10]. In [
24] (Section 3), the author shows that, as in the case of fields, the set
of the elements in a valued hyperfield
with non-negative value under
v determines the valuation map (up to valuation-equivalence). As a consequence, homomorphisms of valued hyperfields are defined analogously to arrows in
, and a category
is thus obtained. A field
K with additive operation + can be viewed as a hyperfield with additive operation ⊞ defined by the formula
. Conversely, any hyperfield with a
singlevalued additive operation, i.e., such that
is a singleton for all
, can be viewed as a field. We have described an embedding of
into
. By the observations made in Example 1 above, a valuation
on a hyperfield
H is, equivalently, a
-arrow
.
Let us now fix a valued field . The following statement contains a number of fundamental properties of the valued -hyperfields associated with , where .
Lemma 1 (Lee Lemma). Take for some positive integer k, and let be such that . The following assertions hold:
- (i)
If , then .
- (ii)
If x and y are not both 0, then - (iii)
If x and y are not both 0, then - (iv)
.
- (v)
If are not all 0, then
Proof. See [
9] (Lemma 3.1) or [
34] (Lemma 3.3). □
From the above fundamental properties, we now wish to isolate the following important consequences.
Proposition 1. Take , where denotes the valued γ-hyperfield of for some such that . Then, all elements of have the same value under , unless .
Proof. See [
23] (§ 3) or [
34] (Proposition 3.19). □
The above proposition permits to induce from
an ultrametric distance on
, which we denote by
(see, e.g., [
24] Definition 4.1).
Proposition 2. Let be the valued γ-hyperfield of a valued field , where . If x and y are not both 0, then is the open ultrametric ball of radius around with respect to .
Proof. See [
23] (§ 3) or [
34] (Proposition 3.26). □
4. Main Results
For the rest of the paper:
denotes a valued field.
denotes an ordered abelian group containing as a substructure in the language of ordered groups.
In the first result of this final section, we highlight another consequence of the fact that a valued field lies dense in its completion. As usual, if a homomorphism of hyperfields is bijective and its inverse is a homomorphism of hyperfields as well, then is called an isomorphism of hyperfields.
Lemma 2. Let be the completion of and identify K and with the subsets of and to which they are canonically isomorphic. Then, for all such that , there is an isomorphism of hyperfields such that holds, for all .
Proof. Fix such that . Just for this proof, we will denote by the class of in and by the class of in . It follows from Lemma 1 that, for all nonzero , we have that , as a subset of , is an open ultrametric ball (with respect to the ultrametric induced on by ). Since K lies dense in , there is such that . On the other hand, is an equivalence class in with respect to an equivalence relation whose restriction to K has among its equivalence classes. Consequently, as subsets of and if satisfies as well, then and thus must hold. Since all belong to the class in , this proves that the assignment defines a bijective function . From the definitions and the inclusion , it easily follows at this point that is an isomorphism of hyperfields satisfying the assertion of the lemma. □
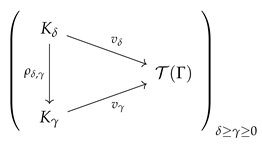
The next result is that the valued
-hyperfields of
, form a diagram
(of shape the poset category associated with
) in the slice category
.
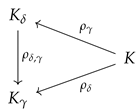
Lemma 3. If satisfy , then the functionsare arrows in the slice category . Furthermore, if are non-negative elements of , then Proof. First we show that
is well defined for all
as in the statement. To this end, assume that
. Then, there exists
such that
. Since
, we have that
, so we obtain that
for some
and thus
It is clear that
holds. Furthermore, the following computation:
for all
with
, shows that the restriction of
to
is a homomorphism of groups (with codomain
). In addition, we have that
where
and
denote the additive operation of
and
, respectively, and we used again the fact that
. We have proved that
is a homomorphism of hyperfields.
We deduce that
is an arrow in
by noticing that the following chain of equalities:
holds, for all
, by the definition of the valuations
and
. The last assertion of the lemma follows immediately from the definition of the functions
(
). □
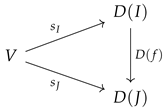
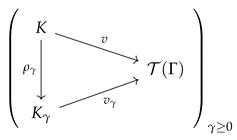
The assignment
defines a function
, for all non-negative
. It follows from the definitions that these functions are homomorphisms of valued hyperfields such that
for all
, i.e., the following triangular diagrams:
commute in
. Therefore, the functions
are arrows in the slice category
. Moreover, they respect the functions
in the sense that, for all non-negative
, we have that the following diagram
commutes in
. The above discussion shows that
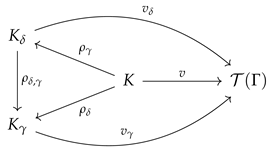
is the vertex of a cone over the diagram (
3) in
, i.e., the following diagram
is commutative in
. Now consider the completion
of
. If, as before, we identify
with the subset of
to which it is canonically isomorphic, then from Lemma 2, we deduce that
too is the vertex of a cone over the same diagram (
3). In addition,
K embeds as a valued field in
by Fact 1, and such an embedding can be seen to be an arrow in
. Before moving forward, let us prove the following useful lemma, which states that (with the right choice of
) all cones in
over the diagram (
3) are (valued) fields.
Lemma 4. Let be a valued hyperfield such that there are order-preserving group-embeddings , and assume that is the vertex of a cone in over the diagram (3). Then, H is a field, i.e., for all , we have that is a singleton, where ⊞ denotes the additive operation of the hyperfield H. Proof. We work up to the given embeddings of ordered abelian groups. Fix
such that
. We denote by
the sides of the given cone in
. Pick
and
. We claim that
, where
. Since
is an an arrow in the slice category
, we obtain that
holds in
, where
denotes the additive operation of the hyperfield
. In addition, we obtain that the equalities
and
hold in
. Thus, by Proposition 2, we have that
is an open ultrametric ball in
of radius
. Let now
be an increasing and cofinal sequence of non-negative elements of
, and take an arbitrary
. We consider some
that is large enough so that
holds in
. If we suppose that
, then by Proposition 1, and since
is a homomorphism of hyperfields, we obtain that for any
, the value
is larger than
. Since
is arbitrary in
, this implies that
and so
. We deduce that
This contradiction shows that must hold in , and as a consequence, we obtain that . Furthermore, since is an arrow in , we have that , and by enlarging (if necessary), we can ensure that as well. Now, for all , we obtain that and, again by Proposition 2, is an open ultrametric ball of radius and center . Therefore, will be larger than , and since is arbitrary in , it follows that anyway. At this point, our claim is proved, and follows. The proof is complete. □
By the following theorem, the valued field extensions of a valued field that embed in its completion are characterized in terms of the diagram (
3).
Theorem 1. Let be a valued field extension of such that there is an order-preserving group-embedding . Then, the following statements are equivalent:
- (i)
embeds as a valued field into .
- (ii)
For all such that , there is an isomorphism in :
Proof. We begin by proving that implies . Since L contains K, which lies dense in , it follows that L lies dense in too. Hence, follows as in the proof of Lemma 2.
For the implication from
to
, a little more effort is needed. First, we need to fix an increasing and cofinal sequence of non-negative elements
in the value group
, as we have shown in the proof of Lemma 4. Then, for any
and all
, we set
to be a representative for the class
. By the assumption
and the definition of the hyperfield valuations
and
, we deduce that
holds in
for all
. In addition, since
is increasing, Lemma 1
yields that
holds in
, for all
. Now, by the cofinality of
in
, the latter inequality implies that
is a Cauchy sequence in
K, which then converges to some
.
We claim that
y does not depend on the choice of the representatives
, but only on the class
. For let
be such that
be another choice. As above,
is a Cauchy sequence in
K and we denote by
its limit in
. If
and
are such that
and
hold in
, then, by Lemma 1
, and since
, we obtain that
and then
hold in
. Since
is arbitrary in
, we may conclude that
, i.e.,
holds in
.
Our next claim is that the assignment
defines an embedding of valued fields
To see why this holds, most of the efforts are devoted to the verification that
preserves the additive operations. Take
, and assume without loss of generality that
. If
are such that
,
and
for all
, then, as before, these elements form Cauchy sequences in
K. Let us then denote by
z,
a and
b their limits in
, respectively. By definition of
, we have that
,
and
. Our aim now will be to prove that
holds in
. We first obtain from Lemma 1
that
holds, for all
. Therefore, if we fix any
and let
be large enough so that
and
hold in
, then an application of Lemma 1
yields that
holds in
, where we used the fact that
for all
. Thus, we obtain that
and, consequently,
hold in
. Since
is arbitrary in
and
, we deduce that
and, consequently,
, as contended.
Now, it suffices to recall that and that if , then hold in to immediately deduce that and that must hold in . We have proved that is a homomorphism of fields and, as such, an embedding.
Finally, since holds in , for all and all (as we have already shown above) it can be easily verified from the definition of convergent sequences, that the element , to which the Cauchy sequence in K converges, satisfies , for all . We conclude that holds, for all . In particular, we have that is an embedding of valued fields. □
In the proof of the implication from to in the above theorem, we have used the assumption that is an extension of only for identifying and with a canonical subset of . However, in the final analysis, this identification is not necessary and is performed only for a smoother exposition of the reasonings in the proof.
Scholium 1 (The term ‘scholium’ (literally, a marginal note) is used, e.g., in [
36] to denote something that follows directly from the
proof of a preceding result, as opposed to a corollary that follows directly from the
statement of the preceding result). If
is any valued field such that there is an order-preserving group-embedding and, up to this embedding, Condition of Theorem 1 holds, then there is a -arrow . Now, under the assumptions of the above result, for a valued hyperfield
, we deduce, first, that
L is a field by Lemma 4. Then, we denote by
and by
the projections onto the valued
-hyperfields associated with
of
and
, respectively. It is so straightforward to verify that the embedding
that we have constructed in the proof of Theorem 1 is unique with the property that
for all
such that
. Indeed, this conclusion follows from the fact that for any
, the classes
form a chain of ultrametric balls in
L of increasing radii and, moreover, the set of this radii is cofinal in
. We have now fully proved Krasner’s result [
23] (§ 4) in a purely categorial language:
Theorem 2. The completion of is (-isomorphic to) the limit of Diagram (
3)
in , for any ordered abelian group extension Γ
of . We note moreover, that in the above setting the assumption is a posteriori not restrictive.
Corollary 1. is complete if and only if it is the limit of the diagram (
3)
, with , in . We conclude by describing the above abstract and general constructions and results in one concrete example.
Example 4 (t-adic valuations on formal Laurent series fields). Let K be a field and t any transcendental over K. We denote by the polynomial ring, by the field of rational functions, by the formal power series ring and by the field of formal Laurent series, i.e., the fraction field of .
A map is defined on a non-zero power series as the exponent of the highest power of t dividing f. The restriction of to is extended to a discrete valuation , called the t-adic valuation
, by setting:for all . It is well known that the completion of the valued field with respect to is and throughout this example, we shall denote again by . By definition, a principal unit of level has the form:with . Thus, the elements (with non-negative value) of the valued n-hyperfield H associated with correspond to truncated power series.
That is, two power series in are in the same class in H if and only if all of their coefficients up to the n-th coincide. While, since , the product in descends to H, the additive operation does not as some cancellations may occur that cannot be determined on the basis of the coefficients of degree . For instance, while certainly contains as holds in , by a distinct choice of representatives we also find that contains, e.g., the class of:which has value under and is hence is not . The multivalued operation of H is defined as to include all possibilities given by the indeterminacy caused by the above mentioned cancellations of terms of order greater than n.
From a metric perspective, two power series are close to each other in if their difference can be divided by a high power of t. Thus, the above-described truncations correspond to an identification of power series that are closer to each other than a fixed finite distance.
An application of Lemma 2 in this case shows that for all and any non-zero power series , a rational function exists whose power series expansion has the coefficients of equal to those of f for all , respectively.
The limit construction culminated in Theorem 2 above, is a general and formal form of the intuitive idea that when “truncations” at all finite levels are known, then the additive indeterminacy can be resolved and full information on the power series ring —and consequently on the valued field —can be derived. On the other hand, due to the density of in , the just-described procedure cannot be used to identify the valued subfield .
Several deep open questions in mathematics are related to the study of valuations of (finite or infinite) Archimedean rank
(see, e.g., [
37] and the references therein). The above example on valuations of rank 1 includes fields as
(where
p is a prime number), which are as well sources of deep unresolved problems on which intuitions often struggle in dealing with unexpected counterexamples (cf. [
38]).
In this article, which certainly constitutes a tiny drop in the ocean, the intuitive idea of truncation of power series described in Example 4 is formally extended to the general case, showing at the same time that it constitutes a fundamental and deep property shared by all (non-trivially) valued fields. Our approach is in line with other extension results, such as the fractal geometry induced on the power series rings
by
t-adic valuations ([
39], Example 3), which has been generalized to discretely valued fields in [
39] (Proposition 5).