A Result of Krasner in Categorial Form

Abstract

In 1957, M. Krasner described a complete valued field $(K,v)$ as the inverse limit of a system of certain structures, called hyperfields, associated with $(K,v)$. We put this result in purely category-theoretic terms by translating it into a limit construction in certain slice categories of the category of valued hyperfields and their homomorphisms. We replace the original metric-dependent arguments employed by Krasner with a clean and elegant transition to certain slice categories.

1. Introduction

If one considers the operations of classical algebraic structures (such as groups, rings, fields, …) by looking at their graphs, then one sees that they satisfy two fundamental assumptions: they are left total and functional. In other words, these properties can be spelled out as operations being everywhere defined (i.e., the operation can be applied to any two elements to obtain at least one result) and single-valued (i.e., an application of the operation to any two elements yields at most one result). A hyperfield is a field-like structure where the latter property is relaxed for the additive operation. In the literature, such structures appear perhaps more than one would expect: hyperfields are of interest, e.g., in tropical geometry [1,2,3], symmetrization [4,5,6], projective geometry [7], valuation theory [8,9,10,11], and ordered algebra [12,13,14]. There are even reasons to believe that their theory generalizes field theory in ways that can be used to tackle deep problems such as the description of ${\mathbb{F}}_1$, the “field of characteristic one” (cf. [7,15]).

More generally, since the pioneer papers [16,17,18] of F. Marty, structures with multivalued operations (also called hyperstructures) generalizing classical single-valued structures have been the object of several research projects. For example, modules with a multivalued operation and a scalar multiplication over Krasner hyperrings (the old brothers of hyperfields) have been studied, e.g., in [19,20,21]. In addition, hypergroups are mentioned in a journal of theoretical physics, in [22].

In this article, we focus on valued hyperfields, generalizing valued fields: the object of study of classical valuation theory. In [23], after having introduced valued hyperfields for the first time, Krasner associates to any valued field $(K,v)$ a projective system $\mathcal{H}=\mathcal{H}(K,v)$ of valued hyperfields, indexed by the non-negative elements of the value group of $(K,v)$. Krasner proves that the projective limit of the system $\mathcal{H}$ is isomorphic (as a valued field) to the valuation-theoretic completion of $(K,v)$. His proof makes heavy use of a metric structure of the hyperfields in $\mathcal{H}$, which is induced by the canonical valuation metric on K. On the other hand, while axioms of valuation maps generalize readily to the setting of hyperfields, these are not anymore sufficient to induce a metric in the general case. Krasner’s approach to this obstacle has been to postulate one further axiom for valued hyperfields, which becomes tautological in the case of a single-valued addition. Nevertheless, examples of hyperfields with interesting valuation maps that do not induce a metric as required by Krasner are now known. Among these examples, particularly important for the present article are the generalized tropical hyperfields $\mathcal{T}\left(\mathsf{\Gamma }\right)$ ([24] Example 2.14), which naturally encode ordered abelian groups as valued hyperfields and include the tropical hyperfield, which became a fundamental object of study in tropical geometry (cf. [1,2,3]). Other such examples can be found in [8] (Example 4.3) or [25].

In addition, without the metric condition, valuation maps on (hyper)fields are nothing but homomorphisms (with a specific target) in the category $\mathbf{vHyp}$ of valued hyperfields and their homomorphisms, making $\mathbf{vHyp}$ a natural framework for classical valuation theory too.

The main aims of this article are the following:

• To generalize the above-mentioned limit construction of Krasner to valued fields of any (finite or infinite) Archimedean rank.
• To describe the generalized limit construction in $\mathbf{vHyp}$ respecting the principle of equivalence (i.e., avoiding elements-dependent arguments, including Krasner’s metric arguments).

While the first aim does not present relevant difficulties, the possibility of achieving the second aim may, at first glance, raise some doubts. We will prove that the necessary metric-dependent properties of the systems $\mathcal{H}$ are a reflection of the fact that the limit construction of Krasner is performed locally in $\mathbf{vHyp}$. The latter means that these properties can be deduced by seeing $\mathcal{H}$ as a diagram in the slice categories of $\mathbf{vHyp}$ over-generalized tropical hyperfields. In this slice category, Krasner’s result is in fact nothing but the computation of limit cones over completely determined diagrams. A category-theoretic characterization of the full subcategory of $\mathbf{vHyp}$ whose objects are generalized tropical hyperfields has not been fully achieved yet. We shall give our reasons to believe that this is possible and to which other research problems this one is connected in the conclusions section.

This article starts with a brief review in Section 2 of the necessary category-theoretic background as well as the notation adopted. A survey of the algebraic theory of hyperfields follows in Section 3, with the above-mentioned generalization of Krasner’s construction of the projective systems $\mathcal{H}(K,v)$ to arbitrary Archimedean rank. The category $\mathbf{vHyp}$ of valued hyperfields is also defined in this section. In addition, the embedding of the category of ordered abelian groups and order-preserving group homomorphisms into $\mathbf{vHyp}$ via generalized tropical hyperfields is described. In the main Section 4, the transition to slice categories is formalized by proving that the diagram $\mathcal{H}(K,v)$ descends to the slice category $\mathbf{vHyp}/\mathcal{T}\left(\mathsf{\Gamma }\right)$, for all ordered abelian group extensions $\mathsf{\Gamma }$ of the value group $vK$ and that the vertex of a limit cone over the latter diagram, is isomorphic to the valuation-theoretic completion of $(K,v)$ in $\mathbf{vHyp}/\mathcal{T}\left(\mathsf{\Gamma }\right)$, as well as, consequently, in $\mathbf{vHyp}$ and in the category of valued fields and value-preserving field-homomorphisms. The conclusive Section 5 describes related open problems, tracing lines for future investigations.

2. Category-Theoretic Preliminaries and Terminology

Many references for category theory may be cited, which cover the necessary background for the scope of this paper. The classic [26] is certainly one of them, and we found particularly useful the following books as well [27,28,29].

Since we believe that one way to better appreciate our contribution is to be as precise as possible with terminology and notation, we shall assume only some familiarity with the concepts of category, small category, and functor in this preliminary section.

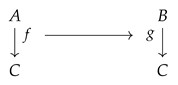
As for basic notations, for a category $\mathcal{C}$, we write $A\in Ob\left(\mathcal{C}\right)$ to mean that A is an object in $\mathcal{C}$, and for any ordered pair $(A,B)$ of objects in $\mathcal{C}$, we denote the set of arrows $f:A⟶B$ in $\mathcal{C}$ by $\mathcal{C}(A,B)$. For the composition of arrows, the symbol ∘ will be employed, and the identity $\mathcal{C}$-arrow of $A\in Ob\left(\mathcal{C}\right)$ will be written as $1_A:A⟶A$.

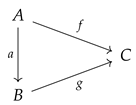
If C is an object in $\mathcal{C}$, then the slice category $\mathcal{C}/C$ has $\mathcal{C}$-arrows $f:A⟶C$, with $A\in Ob\left(\mathcal{C}\right)$, as objects, while a $\mathcal{C}$-arrow $a:A⟶B$ is an arrow

in $\mathcal{C}/C$ if and only if the following triangular diagram

is commutative in $\mathcal{C}$, i.e., $g\circ a=f$.

The concept of a limit in a category is fundamental and, partly due to its generality, admits many equivalent definitions. The terminology we adopt for limits is similar to that of [29], which seemed to be the most appropriate in this case. Let us go through a brief recap.

Limits

Fix a category $\mathcal{C}$. If $\mathcal{S}$ is a small category, then a functor $D:\mathcal{S}⟶\mathcal{C}$ is called a diagram in $\mathcal{C}$ of shape $\mathcal{S}$. A cone on a diagram $D:\mathcal{S}⟶\mathcal{C}$ consists of an object V in $\mathcal{C}$, called the vertex of the cone, together with a family, indexed by the collection of objects in $\mathcal{S}$,

$${\left(V\stackrel{ s_I }{\to }D\left(I\right)\right)}_{I\in Ob\left(\mathcal{S}\right)}$$

(1)

of $\mathcal{C}$-arrows, called the sides of the cone such that the following triangular diagram

is commutative, for all arrows $f\in \mathcal{S}(I,J)$.

A cone with vertex L and sides $p_I$ over a diagram $D:\mathcal{S}⟶\mathcal{C}$ is called a limit cone if it satisfies the following universal property: for any cone on D as in (1), there exists a unique arrow $h:V⟶L$ such that $p_I\circ h=s_I$ holds, for all $I\in Ob\left(\mathcal{S}\right)$.

By a limit of a diagram $D:\mathcal{S}⟶\mathcal{C}$, we mean the vertex of a limit cone over D.

An isomorphism between objects $A,B$ in a category $\mathcal{C}$ is a $\mathcal{C}$-arrow $f:A⟶B$ with the property that a $\mathcal{C}$-arrow $f^{-1}:B⟶A$ exists such that $f^{-1}\circ f=1_A$ and $f\circ f^{-1}=1_B$. The notation $f^{-1}$ used for this arrow suggests that from the mere existence, uniqueness follows too, which is in fact well known to be the case.

The uniqueness of the arrows whose existence is guaranteed by the universal property of limit cones implies that, when they exist, limit cones are unique up to (a unique) isomorphism (of cones). In particular, limits in a category $\mathcal{C}$ are unique up to (a unique) $\mathcal{C}$-isomorphism. It is up to this isomorphism that we speak of the limit of a diagram.

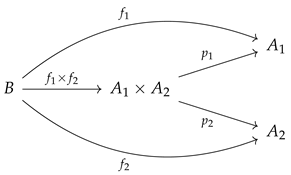
The sides of limit cones are often called projections. This name comes from the analogy with the limit of diagrams of shape $\mathbf{2}$, that is, the category consisting of 2 objects with their identity arrows solely. The latter specially shaped limits are called (binary) products. In fact, in the category $\mathbf{Set}$ of sets and functions, their vertex is the familiar Cartesian product of sets, while their sides are nothing but the projections onto its components. For the product $(A\times B,p_1,p_2)$ of two objects $A_1,A_2\in Ob\left(\mathcal{C}\right)$, where $p_i:A_1\times A_2⟶A_i$ denote the projections ($i=1,2$), the universal property of limits has the following form: for any object B in $\mathcal{C}$ admitting two arrows $f_i:B⟶A_i$ ($i=1,2$) in $\mathcal{C}$, there exists a unique arrow $f_1\times f_2:B⟶A_1\times A_2$ such that the following diagram

is commutative.

Another specially shaped limit, which is named terminal object, is defined in a category $\mathcal{C}$ as the limit cone of the unique diagram $\mathsf{\varnothing }⟶\mathcal{C}$, where ∅ denotes the category with no objects and, consequently, no arrows (the empty category). If T is a terminal object in $\mathcal{C}$, then the universal property of limits has the following form: for any object C in $\mathcal{C}$, there exists a unique arrow ${!}_C:C⟶T$.

When limit cones on diagrams of a certain shape $\mathcal{S}$ exist in a category $\mathcal{C}$, then one says that $\mathcal{C}$ has limits of shape $\mathcal{S}$. One then usually simplifies the terminology further in case the particular shape has been given a name. For instance, phrases like “$\mathcal{C}$ has products” or “$\mathcal{C}$ has a terminal object” mean that $\mathcal{C}$ has limits of shape $\mathbf{2}$ and ∅, respectively.

Remark 1.

It is important to keep in mind that uniqueness up to isomorphism does not necessarily mean absolute uniqueness (following the remark on terminology in the preface of [30], one may phrase this as “categorial uniqueness is not categorical”). For example, in the category $\mathbf{Set}$ of sets and functions, where isomorphisms are bijections, all singleton sets are terminal objects.

3. Valued Fields and Hyperfields

Let $(K,+,·,0,1)$ be a field and $(\mathsf{\Gamma },\le ,+,0)$ a linearly ordered abelian group (always denoted additively) (Note that we use the same symbols to denote the additive structure of K and the abelian group structure of $\mathsf{\Gamma }$. This is standard practice and will cause no confusion). That is, $\mathsf{\Gamma }$ is an abelian group equipped with a linear order relation ≤ and an abelian group structure whose operation + is compatible with ≤, i.e., the following implication:

$$\gamma \le \delta \Rightarrow \gamma +\epsilon \le \delta +\epsilon$$

holds, for all $\gamma ,\delta ,\epsilon \in \mathsf{\Gamma }$. A map $v:K⟶\mathsf{\Gamma }\cup \{\infty \}$, where ∞ is a symbol such that $\gamma +\infty =\infty +\gamma =\infty >\gamma$ for all $\gamma \in \mathsf{\Gamma }$, is called a (Krull) valuation on K if and only if it satisfies all of the following three properties:

(VAL1)

$v\left(x\right)=\infty$ if and only if $x=0$, for all $x\in K$.

(VAL2)

$v\left(xy\right)=v\left(x\right)+v\left(y\right)$, for all $x,y\in K$.

(VAL3)

$v(x+y)\ge min\left\{v\right(x),v(y\left)\right\}$, for all $x,y\in K$.

If a valuation v on a field K is given, then $(K,v)$ is called a valued field, while the image of v in $\mathsf{\Gamma }$, denoted by $vK$, is called the value group of $(K,v)$. The value $v\left(x\right)$ of $x\in K$ will be written as $vx$ whenever no risk of confusion arises. If $(K,v)$ is a valued field, then

$${\mathcal{O}}_v:=\{x\in K\mid vx\ge 0\}$$

is a subring of K, called the valuation ring of $(K,v)$. It determines the valuation map v up to valuation equivalence, i.e., up to composition with an order-preserving isomorphism of the value group. The prime ideals of the valuation ring ${\mathcal{O}}_v$ are linearly ordered by set inclusion and have the following form:

$${\mathfrak{m}}_v^{\mathsf{\Delta }}:=\{x\in K\mid vx>\delta ,\mathrm{for}\mathrm{all}\delta \in \mathsf{\Delta }\},$$

where $\mathsf{\Delta }$ is a convex subgroup of $vK$ (see [31] Lemma 2.3.1). The ideal ${\mathfrak{m}}_v:={\mathfrak{m}}_v^{\left\{0\right\}}$, corresponding to the trivial convex subgroup $\left\{0\right\}$ of $vK$, is the unique maximal ideal of ${\mathcal{O}}_v$. The field $Kv$, defined as the quotient ring ${\mathcal{O}}_v/{\mathfrak{m}}_v$, is called the residue field of $(K,v)$.

A homomorphism of valued fields from $(K,v)$ to $(L,w)$ can be defined as a homomorphism of fields $\sigma :K⟶L$ such that $\sigma \left({\mathcal{O}}_v\right)\subseteq {\mathcal{O}}_w$. The latter condition is sometimes phrased as “$\sigma$ preserves the valuation”. Since homomorphisms of valued fields are in particular homomorphisms of fields, they are automatically injective and will thus sometimes be called embeddings. We say that $(L,w)$ is a valued field extension of $(K,v)$ if $K\subseteq L$ and the inclusion map is an embedding of valued fields. In this way, valued fields and their homomorphisms form a category $\mathbf{vFld}$, which is a subcategory of $\mathbf{Set}$. By an isomorphism of valued fields, we mean an isomorphism in $\mathbf{vFld}$, namely, a bijective homomorphism of valued fields whose inverse (as a function) is an arrow in $\mathbf{vFld}$ too. This can be spelled out further as follows: a function $\sigma :K⟶L$ is an isomorphism of valued fields $(K,v)\simeq (L,w)$ if and only if it is an isomorphism of fields $K\simeq L$ such that $\sigma \left({\mathcal{O}}_v\right)={\mathcal{O}}_w$.

Fix now a valued field $(K,v)$. There is a smallest ordinal (such ordinal $\kappa$ is usually called the cofinality of $vK$) $\kappa$ serving as the index set of a sequence ${\left({\gamma }_{\nu }\right)}_{\nu <\kappa }$ that is cofinal in $vK$, i.e., such that for each $\delta \in vK$ there exists $\nu <\kappa$ such that $\delta <{\gamma }_{\nu }$. We say that a sequence ${\left(x_{\nu }\right)}_{\nu <\kappa }$ of elements of K is a Cauchy sequence if and only if for every $\gamma \in vK$ there exists ${\nu }_0<\kappa$ such that if ${\nu }_0\le \nu ,\mu <\kappa$, then $v(x_{\nu }-x_{\mu })>\gamma$.

A sequence ${\left(x_{\nu }\right)}_{\nu <\kappa }$ is, instead, said to be convergent to an element x belonging to some valued field extension $(L,w)$ of $(K,v)$ if and only if for every $\gamma \in wL$ there exists ${\nu }_0<\kappa$ such that if ${\nu }_0\le \nu <\kappa$, then $w(x-x_{\nu })>\gamma$.

If the latter property happens to hold, then we also say that the sequence ${\left(x_{\nu }\right)}_{\nu <\kappa }$ converges in L. If $(L,w)$ is a valued field extension of $(K,v)$, then we say that K lies dense in L if every Cauchy sequence in K converges in L, while $(K,v)$ is called complete if and only if every Cauchy sequence in K converges in K.

Fact 1

(Theorem 2.4.3 in [31]). Every valued field $(K,v)$ admits one and (up to isomorphism of valued fields) only one valued field extension $(K^c,v^c)$—called the completion of $(K,v)$—which is complete and in which K lies dense.

An important consequence of the fact that K lies dense in $K^c$ is that the value group $v^c{K}^c$ and the residue field $K^c{v}^c$ of $(K^c,v^c)$ are (canonically) isomorphic to $vK$ and $Kv$, respectively (cf. [31] Proposition 2.4.4).

Krasner Hyperfields

Hyperfields first appeared in [23]. In introducing them, Krasner was motivated by his interest in certain structures obtained from valued fields by means of the “factor (or quotient) construction”, which he himself described for the first time in the same article and later in [32]. For the algebraic definition of hyperfields, we refer to [24] (Definition 2.7) and the references therein. A more categorial treatment of these structures within the category of sets and (total) relations can be found in [33].

The following definition of homomorphism for hyperfields has become standard in the literature.

Definition 1.

Let $(H,⊞,·,0,1),(H^{\prime },{⊞}^{\prime },{·}^{\prime },0^{\prime },1^{\prime })$ be hyperfields. A function

$$\sigma :H⟶H^{\prime }$$

is called a homomorphism of hyperfields if $\sigma \left(0\right)=0^{\prime }$, its restriction to the multiplicative groups is a homomorphism of groups, and in addition,

$$\sigma (x⊞y)\subseteq \sigma \left(x\right){⊞}^{\prime }\sigma \left(y\right)$$

(2)

holds, for all $x,y\in H$.

We now define a projective system of hyperfields associated with any valued field of arbitrary Archimedean rank (see also [9,10]).

For a valued field $(K,v)$ and an element $\gamma \in vK$ such that $\gamma \ge 0$, consider the group of the 1-units of level γ in $K^{\times }$:

$${\mathcal{U}}_v^{\gamma }:=\{u\in K\mid v(u-1)>\gamma \}.$$

It can be easily verified that $vu=0$ for all $u\in {\mathcal{U}}_v^{\gamma }$, so that the valuation map v on K factors through the quotient group $K_{\gamma }^{\times }:=K^{\times }/{\mathcal{U}}_v^{\gamma }$ and yields a map $v_{\gamma }:K_{\gamma }⟶vK\cup \{\infty \}$, where $K_{\gamma }:=K_{\gamma }^{\times }\cup \left\{{\left[0\right]}_{\gamma }\right\}$. We follow the notation of [9] and denote the multiplicative coset $x{\mathcal{U}}_v^{\gamma }$ of $x\in K$ in $K_{\gamma }$ as ${\left[x\right]}_{\gamma }$ (in particular, ${\left[0\right]}_{\gamma }=\left\{0\right\}$) and call the valued γ-hyperfield associated with $(K,v)$ the hyperfield $(K_{\gamma },⊞,·,{\left[0\right]}_{\gamma },{\left[1\right]}_{\gamma })$, where

$${\left[x\right]}_{\gamma }⊞{\left[y\right]}_{\gamma }:=\{{[x+yu]}_{\gamma }\mid u\in {\mathcal{U}}_v^{\gamma }\}\mathrm{and}{\left[x\right]}_{\gamma }·{\left[y\right]}_{\gamma }:={\left[xy\right]}_{\gamma }.$$

The verification of the fact that the above defined structures $K_{\gamma }$ are in fact hyperfields, for all $\gamma \in vK$ such that $\gamma \ge 0$, is analogous to Krasner’s one for the Archimedean rank 1 case. The same conclusion also follows from the more general quotient construction described in [32]. The use of the term “valued” is motivated once one observes that the map $v_{\gamma }$ satisfies (VAL1), (VAL2) and the following property analogous to (VAL3):

(VAL3*)

$v_{\gamma }{\left[z\right]}_{\gamma }\ge min\{v_{\gamma }{\left[x\right]}_{\gamma },v{\left[x\right]}_{\gamma }\}$, for all ${\left[x\right]}_{\gamma },{\left[y\right]}_{\gamma }\in K_{\gamma }$ and all ${\left[z\right]}_{\gamma }\in {\left[x\right]}_{\gamma }⊞{\left[y\right]}_{\gamma }$

see also [8,24,34]. More generally, we shall call $(H,v)$ a valued hyperfield whenever v is a map from the hyperfield H to an ordered abelian group $\mathsf{\Gamma }$ (with the addition of ∞) satisfying (VAL1), (VAL2) and (VAL3*). These requirements are equivalent (cf., e.g., [24] Lemma 3.4) to v being a homomorphism of hyperfields $H⟶\mathcal{T}\left(\mathsf{\Gamma }\right)$, where $\mathcal{T}\left(\mathsf{\Gamma }\right)$ denotes the generalized tropical hyperfield associated with $\mathsf{\Gamma }$:

Example 1

(Example 2.14 in [24]). Let ∞ be a symbol such that $\gamma +\infty =\infty +\gamma =\infty >\gamma$ for all $\gamma \in \mathsf{\Gamma }$. For $\gamma ,\delta \in \mathsf{\Gamma }\cup \{\infty \}$, we denote by $[\gamma ,\delta ]$ the closed interval containing all $\epsilon \in \mathsf{\Gamma }\cup \{\infty \}$ satisfying $\gamma \le \epsilon \le \delta$. Then, by setting $\gamma ⊞\infty =\infty ⊞\gamma =\left\{\gamma \right\}$ for all $\gamma \in \mathcal{T}\left(\mathsf{\Gamma }\right)$ and:

$$\gamma ⊞\delta :=\left\{\begin{array}{cc}\{min\{\gamma ,\delta \left\}\right\}\hfill & \mathrm{if}\gamma \ne \delta ,\hfill \\ \gamma ,\infty ]\hfill & \mathrm{if}\gamma =\delta .\hfill \end{array}\right.(\gamma ,\delta \in \mathcal{T}\left(\mathsf{\Gamma }\right))$$

It is not difficult to check that $\left(\mathcal{T}\right(\mathsf{\Gamma }),⊞,+,\infty ,0)$ is a hyperfield, called generalized tropical hyperfield associated with Γ. Moreover, the identity homomorphism $\mathcal{T}\left(\mathsf{\Gamma }\right)\to \mathcal{T}\left(\mathsf{\Gamma }\right)$ is a valuation on $\mathcal{T}\left(\mathsf{\Gamma }\right)$. Finally, note that the order of Γ can be recovered as follows:

$$\gamma \le \delta \iff \delta \in \gamma ⊞\gamma$$

and that this observation yields an embedding of the category of ordered abelian groups and order-preserving group homomorphisms into the category of hyperfields and their homomorphisms.

Example 2

(Trivial valuation). Let H be any hyperfield, Γ any ordered abelian group, and $v:H\to \mathcal{T}\left(\mathsf{\Gamma }\right)$ be defined as $v\left(0\right)=\infty$ and $vx=0$ for all $x\in H\backslash \left\{0\right\}$. Then, v is a valuation on H, called the trivial valuation.

It is well known that finite fields only admit the trivial valuation. Among infinite fields, another known example is the algebraic closures of finite fields. The next example describes a class containing finite and infinite hyperfields that all only admit the trivial valuation.

Example 3

([35]). The following multivalued operation ⊞ on a set $\mathbb{M}$ with a distinguished element $0\in \mathbb{M}$, is defined by Massouros in [35] as follows:

$$x⊞y=\left\{\begin{array}{cc}\{x,y\}\hfill & \mathrm{if}x,y\ne 0\mathit{and}x\ne y,\hfill \\ \mathbb{M}\backslash \left\{x\right\}\hfill & \mathrm{if}y=x\ne 0,\hfill \\ \left\{x\right\}\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

In [35] (Proposition 2), it is proved that any abelian group structure $(\mathbb{M}\backslash \{0\},·,1)$ on $\mathbb{M}$ such that $0·x=x·0=0$, for all $x\in \mathbb{M}$, yields a hyperfield $(\mathbb{M},⊞,·,0,1)$.

Let $v:\mathbb{M}\to \mathcal{T}\left(\mathsf{\Gamma }\right)$ be a valuation on $\mathbb{M}$ and suppose that $x\in \mathbb{M}\backslash \left\{0\right\}$ satisfies $vx>v\left(1\right)$. Then, in particular, $x\ne 1$, and since $x\ne 0$, we obtain that $x⊞1=\{x,1\}$ by definition. On the other hand, by standard arguments in valuation theory (see, e.g., [8] Lemma 4.5(4)) from $x\in x⊞1$ and $vx>v\left(1\right)$, we deduce the contradicting statement $vx=v\left(1\right)$. Thus, $\mathbb{M}$ only admits the trivial valuation, as contended.

Remark 2.

The hyperfields of the form $\mathbb{M}$ were introduced by Massouros’ as an example that negatively answers the question (posed in [32]) whether all hyperfields can be obtained from fields with a multiplicative quotient construction.

The question whether all hyperfields admitting non-trivial valuations can be obtained from fields with that multiplicative quotient construction is, to our knowledge, open. This particular problem is more extensively discussed in [10].

In [24] (Section 3), the author shows that, as in the case of fields, the set ${\mathcal{O}}_v$ of the elements in a valued hyperfield $(H,v)$ with non-negative value under v determines the valuation map (up to valuation-equivalence). As a consequence, homomorphisms of valued hyperfields are defined analogously to arrows in $\mathbf{vFld}$, and a category $\mathbf{vHyp}$ is thus obtained. A field K with additive operation + can be viewed as a hyperfield with additive operation ⊞ defined by the formula $x⊞y:=\{x+y\}$. Conversely, any hyperfield with a singlevalued additive operation, i.e., such that $x⊞y$ is a singleton for all $x,y\in H$, can be viewed as a field. We have described an embedding of $\mathbf{vFld}$ into $\mathbf{vHyp}$. By the observations made in Example 1 above, a valuation $v:H⟶\mathsf{\Gamma }\cup \{\infty \}$ on a hyperfield H is, equivalently, a $\mathbf{vHyp}$-arrow $(H,v)⟶(\mathcal{T}\left(\mathsf{\Gamma }\right),1_{\mathcal{T}\left(\mathsf{\Gamma }\right)})$.

Let us now fix a valued field $(K,v)$. The following statement contains a number of fundamental properties of the valued $\gamma$-hyperfields associated with $(K,v)$, where $0\le \gamma \in vK$.

Lemma 1

(Lee Lemma). Take $x,y,x_0,\dots ,x_k\in K$ for some positive integer k, and let $\gamma \in vK$ be such that $\gamma \ge 0$. The following assertions hold:

(i)

If $x\ne 0$, then ${\left[x\right]}_{\gamma }=\{y\in K\mid v(x-y)>\gamma +vx\}$.

(ii)

If x and y are not both 0, then

$$\bigcup ({\left[x\right]}_{\gamma }⊞{\left[y\right]}_{\gamma })=\{z\in K\mid v(z-(x+y))>\gamma +min\{vx,vy\}\}.$$

(iii)

If x and y are not both 0, then

$$0\in \bigcup ({\left[x\right]}_{\gamma }⊞{\left[y\right]}_{\gamma })\iff \bigcup ({\left[x\right]}_{\gamma }⊞{\left[y\right]}_{\gamma })=\left\{z\in K\mid vz>\gamma +min\{vx,vy\}\right\}.$$

(iv)

${[x_0+\dots +x_k]}_{\gamma }\in {\left[x_0\right]}_{\gamma }⊞\dots ⊞{\left[x_k\right]}_{\gamma }$.

(v)

If $x_0,\dots ,x_k\in {\mathcal{O}}_v$ are not all 0, then

$${\left[y\right]}_{\gamma }\in {\left[x_0\right]}_{\gamma }⊞\dots ⊞{\left[x_k\right]}_{\gamma }\Rightarrow v(x_0+\dots +x_k-y)>\gamma .$$

Proof. 

See [9] (Lemma 3.1) or [34] (Lemma 3.3). □

From the above fundamental properties, we now wish to isolate the following important consequences.

Proposition 1.

Take ${\left[x\right]}_{\gamma },{\left[y\right]}_{\gamma }\in K_{\gamma }$, where $(K_{\gamma },v_{\gamma })$ denotes the valued γ-hyperfield of $(K,v)$ for some $\gamma \in vK$ such that $\gamma \ge 0$. Then, all elements of ${\left[x\right]}_{\gamma }⊞{\left[y\right]}_{\gamma }$ have the same value under $v_{\gamma }$, unless ${\left[0\right]}_{\gamma }\in {\left[x\right]}_{\gamma }⊞{\left[y\right]}_{\gamma }$.

Proof. 

See [23] (§ 3) or [34] (Proposition 3.19). □

The above proposition permits to induce from $v_{\gamma }$ an ultrametric distance on $K_{\gamma }$, which we denote by $d_{\gamma }$ (see, e.g., [24] Definition 4.1).

Proposition 2.

Let $(K_{\gamma },v_{\gamma })$ be the valued γ-hyperfield of a valued field $(K,v)$, where $0\le \gamma \in vK$. If x and y are not both 0, then ${\left[x\right]}_{\gamma }⊞{\left[y\right]}_{\gamma }$ is the open ultrametric ball of radius $\delta :=\gamma +min\{vx,vy\}$ around ${[x+y]}_{\gamma }\in K_{\gamma }$ with respect to $d_{\gamma }$.

Proof. 

See [23] (§ 3) or [34] (Proposition 3.26). □

4. Main Results

For the rest of the paper:

• $(K,v)$ denotes a valued field.
• $(\mathsf{\Gamma },\le ,+,0)$ denotes an ordered abelian group containing $(vK,\le ,+,0)$ as a substructure in the language $\{\le ,+,0\}$ of ordered groups.

In the first result of this final section, we highlight another consequence of the fact that a valued field lies dense in its completion. As usual, if a homomorphism of hyperfields $\sigma$ is bijective and its inverse is a homomorphism of hyperfields as well, then $\sigma$ is called an isomorphism of hyperfields.

Lemma 2.

Let $(K^c,v^c)$ be the completion of $(K,v)$ and identify K and $vK$ with the subsets of $K^c$ and $v^c{K}^c$ to which they are canonically isomorphic. Then, for all $\gamma \in vK$ such that $\gamma \ge 0$, there is an isomorphism of hyperfields ${\sigma }_{\gamma }:K_{\gamma }⟶K_{\gamma }^c$ such that $v_{\gamma }\left({\sigma }_{\gamma }\left(a\right)\right)=v_{\gamma }^c\left(a\right)$ holds, for all $a\in K_{\gamma }^c$.

Proof. 

Fix $\gamma \in vK$ such that $\gamma \ge 0$. Just for this proof, we will denote by ${\left[x\right]}^c$ the class of $x\in K^c$ in $K_{\gamma }^c$ and by $\left[y\right]$ the class of $y\in K$ in $K_{\gamma }$. It follows from Lemma 1$\left(i\right)$ that, for all nonzero $x\in K^c$, we have that ${\left[x\right]}^c$, as a subset of $K^c$, is an open ultrametric ball (with respect to the ultrametric induced on $K^c$ by $v^c$). Since K lies dense in $K^c$, there is $y\in K$ such that $y\in {\left[x\right]}^c$. On the other hand, ${\left[x\right]}^c$ is an equivalence class in $K^c$ with respect to an equivalence relation whose restriction to K has $\left[y\right]$ among its equivalence classes. Consequently, ${\left[y\right]}^c={\left[x\right]}^c$ as subsets of $K^c$ and if $y^{\prime }\in K$ satisfies $y^{\prime }\in {\left[x\right]}^c$ as well, then ${\left[y\right]}^c={\left[x\right]}^c={\left[y^{\prime }\right]}^c$ and thus $\left[y\right]=\left[y^{\prime }\right]$ must hold. Since all $x\in K$ belong to the class ${\left[x\right]}^c$ in $K_{\gamma }^c$, this proves that the assignment $\left[x\right]\mapsto {\left[x\right]}^c$ defines a bijective function ${\sigma }_{\gamma }:K_{\gamma }⟶K_{\gamma }^c$. From the definitions and the inclusion ${\mathcal{U}}_v^{\gamma }\subseteq {\mathcal{U}}_{v^c}^{\gamma }$, it easily follows at this point that ${\sigma }_{\gamma }$ is an isomorphism of hyperfields satisfying the assertion of the lemma. □

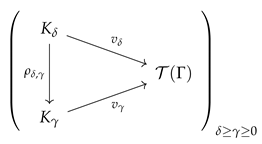
The next result is that the valued $\gamma$-hyperfields of $(K,v)$, form a diagram

(3)

(of shape the poset category associated with $v{K}_{\ge 0}$) in the slice category $\mathbf{vHyp}/\mathcal{T}\left(\mathsf{\Gamma }\right)$.

Lemma 3.

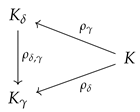
If $\gamma ,\delta \in vK\subseteq \mathsf{\Gamma }$ satisfy $0\le \gamma \le \delta$, then the functions

$$\begin{array}{cc}\hfill {\rho }_{\delta ,\gamma }:K_{\delta }\stackrel{ }{\to }& K_{\gamma }\\ \hfill [x{]}_{\delta }\stackrel{ }{\mapsto }& [x{]}_{\gamma }\end{array}$$

are arrows in the slice category $\mathbf{vHyp}/\mathcal{T}\left(\mathsf{\Gamma }\right)$. Furthermore, if $\gamma \le \delta \le \epsilon$ are non-negative elements of $vK$, then

$${\rho }_{\epsilon ,\gamma }={\rho }_{\delta ,\gamma }\circ {\rho }_{\epsilon ,\delta }.$$

Proof. 

First we show that ${\rho }_{\delta ,\gamma }$ is well defined for all $\gamma ,\delta$ as in the statement. To this end, assume that ${\left[x\right]}_{\delta }={\left[y\right]}_{\delta }$. Then, there exists $t\in {\mathcal{U}}_v^{\delta }$ such that $x=yt$. Since $\gamma \le \delta$, we have that ${\mathcal{U}}_v^{\delta }\subseteq {\mathcal{U}}_v^{\gamma }$, so we obtain that $x=yt$ for some $t\in {\mathcal{U}}_v^{\gamma }$ and thus

$${\rho }_{\delta ,\gamma }\left({\left[x\right]}_{\delta }\right)={\left[x\right]}_{\gamma }={\left[y\right]}_{\gamma }={\rho }_{\delta ,\gamma }\left({\left[y\right]}_{\delta }\right).$$

It is clear that ${\rho }_{\delta ,\gamma }{\left[0\right]}_{\delta }={\left[0\right]}_{\gamma }$ holds. Furthermore, the following computation:

$${\rho }_{\delta ,\gamma }\left({\left[x\right]}_{\delta }{\left[y\right]}_{\delta }^{-1}\right)={\rho }_{\delta ,\gamma }\left({\left[x{y}^{-1}\right]}_{\delta }\right)={\left[x{y}^{-1}\right]}_{\gamma }={\left[x\right]}_{\gamma }{\left[y\right]}_{\gamma }^{-1}={\rho }_{\delta ,\gamma }\left({\left[x\right]}_{\delta }\right){\rho }_{\delta ,\gamma }{\left({\left[y\right]}_{\delta }\right)}^{-1},$$

for all $x,y\in K$ with $y\ne 0$, shows that the restriction of ${\rho }_{\delta ,\gamma }$ to $K_{\delta }^{\times }$ is a homomorphism of groups (with codomain $K_{\gamma }^{\times }$). In addition, we have that

$$\begin{array}{cc}\hfill {\rho }_{\delta ,\gamma }\left({\left[x\right]}_{\delta }{⊞}_{\delta }{\left[y\right]}_{\delta }\right)& =\{{\rho }_{\delta ,\gamma }\left({[x+yt]}_{\delta }\right)\mid t\in {\mathcal{U}}_v^{\delta }\}\hfill \\ \hfill & =\{{[x+yt]}_{\gamma }\mid t\in {\mathcal{U}}_v^{\delta }\}\hfill \\ \hfill & \subseteq \{{[x+yt]}_{\gamma }\mid t\in {\mathcal{U}}_v^{\gamma }\}\hfill \\ \hfill & ={\left[x\right]}_{\gamma }{⊞}_{\gamma }{\left[y\right]}_{\gamma }\hfill \\ \hfill & ={\rho }_{\delta ,\gamma }\left({\left[x\right]}_{\delta }\right){⊞}_{\gamma }{\rho }_{\delta ,\gamma }\left({\left[y\right]}_{\delta }\right).\hfill \end{array}$$

where ${⊞}_{\delta }$ and ${⊞}_{\gamma }$ denote the additive operation of $K_{\delta }$ and $K_{\gamma }$, respectively, and we used again the fact that ${\mathcal{U}}_v^{\delta }\subseteq {\mathcal{U}}_v^{\gamma }$. We have proved that ${\rho }_{\delta ,\gamma }$ is a homomorphism of hyperfields.

We deduce that ${\rho }_{\delta ,\gamma }$ is an arrow in $\mathbf{vHyp}/\mathcal{T}\left(\mathsf{\Gamma }\right)$ by noticing that the following chain of equalities:

$$v_{\delta }{\left[x\right]}_{\delta }=vx=v_{\gamma }{\left[x\right]}_{\gamma }=v_{\gamma }\left({\rho }_{\delta ,\gamma }{\left[x\right]}_{\delta }\right)$$

holds, for all ${\left[x\right]}_{\delta }\in K_{\delta }$, by the definition of the valuations $v_{\gamma }$ and $v_{\delta }$. The last assertion of the lemma follows immediately from the definition of the functions ${\rho }_{\delta ,\gamma }$ ($\delta \ge \gamma \ge 0$). □

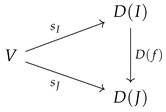
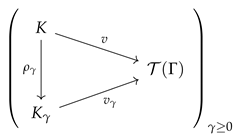
The assignment $x\mapsto {\left[x\right]}_{\gamma }$ defines a function ${\rho }_{\gamma }:K⟶K_{\gamma }$, for all non-negative $\gamma \in vK$. It follows from the definitions that these functions are homomorphisms of valued hyperfields such that $vx=v_{\gamma }{\left[x\right]}_{\gamma }$ for all $x\in K$, i.e., the following triangular diagrams:

commute in $\mathbf{vHyp}$. Therefore, the functions ${\rho }_{\gamma }$ are arrows in the slice category $\mathbf{vHyp}/\mathcal{T}\left(\mathsf{\Gamma }\right)$. Moreover, they respect the functions ${\rho }_{\delta ,\gamma }$ in the sense that, for all non-negative $\gamma ,\delta \in vK$, we have that the following diagram

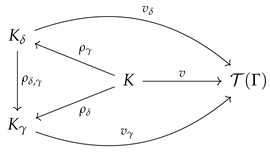
commutes in $\mathbf{vHyp}$. The above discussion shows that $(K,v)$ is the vertex of a cone over the diagram (3) in $\mathbf{vHyp}/\mathcal{T}\left(\mathsf{\Gamma }\right)$, i.e., the following diagram

is commutative in $\mathbf{vHyp}$. Now consider the completion $(K^c,v^c)$ of $(K,v)$. If, as before, we identify $vK$ with the subset of $v^c{K}^c$ to which it is canonically isomorphic, then from Lemma 2, we deduce that $K^c$ too is the vertex of a cone over the same diagram (3). In addition, K embeds as a valued field in $K^c$ by Fact 1, and such an embedding can be seen to be an arrow in $\mathbf{vHyp}/\mathcal{T}\left(\mathsf{\Gamma }\right)$. Before moving forward, let us prove the following useful lemma, which states that (with the right choice of $\mathsf{\Gamma }$) all cones in $\mathbf{vHyp}/\mathcal{T}\left(\mathsf{\Gamma }\right)$ over the diagram (3) are (valued) fields.

Lemma 4.

Let $(H,w)$ be a valued hyperfield such that there are order-preserving group-embeddings $vK\hookrightarrow wH\hookrightarrow \mathsf{\Gamma }$, and assume that $(H,w)$ is the vertex of a cone in $\mathbf{vHyp}/\mathcal{T}\left(\mathsf{\Gamma }\right)$ over the diagram (3). Then, H is a field, i.e., for all $x,y\in H$, we have that $x⊞y$ is a singleton, where ⊞ denotes the additive operation of the hyperfield H.

Proof. 

We work up to the given embeddings of ordered abelian groups. Fix $\gamma \in vK$ such that $\gamma \ge 0$. We denote by $f_{\gamma }:H⟶K_{\gamma }$ the sides of the given cone in $\mathbf{vHyp}/\mathcal{T}\left(\mathsf{\Gamma }\right)$. Pick $x,y\in H^{\times }$ and $z,z^{\prime }\in x⊞y$. We claim that $0\in z^{\prime }⊞z^{-}$, where $z^{-}$. Since $f_{\gamma }$ is an an arrow in the slice category $\mathbf{vHyp}/\mathcal{T}\left(\mathsf{\Gamma }\right)$, we obtain that $f_{\gamma }\left(z\right),f_{\gamma }\left(z^{\prime }\right)\in f_{\gamma }\left(x\right){⊞}_{\gamma }{f}_{\gamma }\left(y\right)$ holds in $K_{\gamma }$, where ${⊞}_{\gamma }$ denotes the additive operation of the hyperfield $K_{\gamma }$. In addition, we obtain that the equalities $wx=v_{\gamma }{f}_{\gamma }\left(x\right)$ and $wy=v_{\gamma }{f}_{\gamma }\left(y\right)$ hold in $\mathsf{\Gamma }$. Thus, by Proposition 2, we have that $f_{\gamma }\left(x\right){⊞}_{\gamma }{f}_{\gamma }\left(y\right)$ is an open ultrametric ball in $K_{\gamma }$ of radius $\gamma +min\{wx,wy\}$. Let now ${\left({\gamma }_{\nu }\right)}_{\nu <\kappa }$ be an increasing and cofinal sequence of non-negative elements of $vK$, and take an arbitrary $\delta \in vK$. We consider some $\nu <\kappa$ that is large enough so that ${\gamma }_{\nu }+min\{wx,wy\}>\delta$ holds in $\mathsf{\Gamma }$. If we suppose that ${\left[0\right]}_{{\gamma }_{\nu }}\notin f_{{\gamma }_{\nu }}\left(z^{\prime }\right){⊞}_{{\gamma }_{\nu }}{f}_{{\gamma }_{\nu }}{\left(z\right)}^{-}$, then by Proposition 1, and since $f_{{\gamma }_{\nu }}$ is a homomorphism of hyperfields, we obtain that for any $a\in z^{\prime }-z^{-}$, the value $wa=v_{{\gamma }_{\nu }}{f}_{{\gamma }_{\nu }}\left(a\right)\in vK\cup \{\infty \}$ is larger than $\delta$. Since $\delta$ is arbitrary in $vK$, this implies that $wa=\infty$ and so $a=0$. We deduce that

$${\left[0\right]}_{{\gamma }_{\nu }}=f_{{\gamma }_{\nu }}\left(a\right)\in f_{{\gamma }_{\nu }}\left(z^{\prime }\right){⊞}_{{\gamma }_{\nu }}{f}_{{\gamma }_{\nu }}{\left(z\right)}^{-}.$$

This contradiction shows that ${\left[0\right]}_{{\gamma }_{\nu }}\in f_{{\gamma }_{\nu }}\left(z^{\prime }\right){⊞}_{{\gamma }_{\nu }}{f}_{{\gamma }_{\nu }}{\left(z\right)}^{-}$ must hold in $K_{{\gamma }_{\nu }}$, and as a consequence, we obtain that $f_{{\gamma }_{\nu }}\left(z^{\prime }\right)=f_{{\gamma }_{\nu }}\left(z\right)$. Furthermore, since $f_{{\gamma }_{\nu }}$ is an arrow in $\mathbf{vHyp}/\mathcal{T}\left(\mathsf{\Gamma }\right)$, we have that $w{z}^{\prime }=wz$, and by enlarging $\nu$ (if necessary), we can ensure that ${\gamma }_{\nu }+wz>\delta$ as well. Now, for all $a\in z^{\prime }⊞z^{-}$, we obtain that $f_{{\gamma }_{\nu }}\left(a\right)\in f_{{\gamma }_{\nu }}\left(z^{\prime }\right){⊞}_{{\gamma }_{\nu }}{f}_{{\gamma }_{\nu }}{\left(z\right)}^{-}$ and, again by Proposition 2, $f_{{\gamma }_{\nu }}\left(z^{\prime }\right){⊞}_{{\gamma }_{\nu }}{f}_{{\gamma }_{\nu }}{\left(z\right)}^{-}$ is an open ultrametric ball of radius ${\gamma }_{\nu }+wz$ and center ${\left[0\right]}_{{\gamma }_{\nu }}$. Therefore, $wa=v_{{\gamma }_{\nu }}{f}_{{\gamma }_{\nu }}\left(a\right)\in vK\cup \{\infty \}$ will be larger than $\delta$, and since $\delta$ is arbitrary in $vK$, it follows that $a=0$ anyway. At this point, our claim is proved, and $z^{\prime }=z$ follows. The proof is complete. □

By the following theorem, the valued field extensions of a valued field that embed in its completion are characterized in terms of the diagram (3).

Theorem 1.

Let $(L,w)$ be a valued field extension of $(K,v)$ such that there is an order-preserving group-embedding $wL\hookrightarrow \mathsf{\Gamma }$. Then, the following statements are equivalent:

(i)

$(L,w)$ embeds as a valued field into $(K^c,v^c)$.

(ii)

For all $\gamma \in vK$ such that $\gamma \ge 0$, there is an isomorphism in $\mathbf{vHyp}/\mathcal{T}\left(\mathsf{\Gamma }\right)$:

$$\begin{array}{cc}\hfill {\sigma }_{\gamma }:(L_{\gamma },w_{\gamma })\stackrel{ }{\to }& (K_{\gamma },v_{\gamma }).\end{array}$$

Proof. 

We begin by proving that $\left(i\right)$ implies $\left(ii\right)$. Since L contains K, which lies dense in $K^c$, it follows that L lies dense in $K^c$ too. Hence, $\left(ii\right)$ follows as in the proof of Lemma 2.

For the implication from $\left(ii\right)$ to $\left(i\right)$, a little more effort is needed. First, we need to fix an increasing and cofinal sequence of non-negative elements ${\left({\gamma }_{\nu }\right)}_{\nu <\kappa }$ in the value group $vK$, as we have shown in the proof of Lemma 4. Then, for any $x\in L^{\times }$ and all $\nu <\kappa$, we set $y_{\nu }\in K^{\times }$ to be a representative for the class ${\sigma }_{{\gamma }_{\nu }}\left({\left[x\right]}_{{\gamma }_{\nu }}\right)\in K_{{\gamma }_{\nu }}^{\times }$. By the assumption $\left(ii\right)$ and the definition of the hyperfield valuations $v_{{\gamma }_{\nu }}$ and $w_{{\gamma }_{\nu }}$, we deduce that $v{y}_{\nu }=wx$ holds in $\mathsf{\Gamma }$ for all $\nu <\kappa$. In addition, since ${\left({\gamma }_{\nu }\right)}_{\nu <\kappa }$ is increasing, Lemma 1$\left(i\right)$ yields that

$$v(y_{\nu }-y_{\mu })>{\gamma }_{\nu }+wx$$

holds in $\mathsf{\Gamma }$, for all $\nu <\mu <\kappa$. Now, by the cofinality of ${\left({\gamma }_{\nu }\right)}_{\nu <\kappa }$ in $vK$, the latter inequality implies that ${\left(y_{\nu }\right)}_{\nu <\kappa }$ is a Cauchy sequence in K, which then converges to some $y\in K^c$.

We claim that y does not depend on the choice of the representatives $y_{\nu }\in K$, but only on the class $\sigma \left({\left[x\right]}_{{\gamma }_{\nu }}\right)\in K_{\gamma }^{\times }$. For let $y_{\nu }^{\prime }\in K$ be such that ${\left[y_{\nu }^{\prime }\right]}_{{\gamma }_{\nu }}={\sigma }_{{\gamma }_{\nu }}\left({\left[x\right]}_{{\gamma }_{\nu }}\right)$ be another choice. As above, ${\left(y_{\nu }^{\prime }\right)}_{\nu <\kappa }$ is a Cauchy sequence in K and we denote by $y^{\prime }$ its limit in $K^c$. If $\delta \in vK$ and $\nu <\kappa$ are such that ${\gamma }_{\nu }+wx>\delta$ and $v^c(y-y_{\nu }),v^c(y_{\nu }^{\prime }-y^{\prime })>\delta$ hold in $\mathsf{\Gamma }$, then, by Lemma 1$\left(i\right)$, and since $v{y}_{\nu }^{\prime }=wx=v{y}_{\nu }$, we obtain that

$$v(y_{\nu }-y_{\nu }^{\prime })>{\gamma }_{\nu }+wx>\delta$$

and then

$$\begin{array}{cc}\hfill v^c(y-y^{\prime })& =v^c(y-y_{\nu }+y_{\nu }-y_{\nu }^{\prime }+y_{\nu }^{\prime }-y^{\prime })\hfill \\ \hfill & \ge min\{v^c(y-y_{\nu }),v^c(y_{\nu }-y_{\nu }^{\prime }),v^c(y_{\nu }^{\prime }-y^{\prime })\}>\delta \hfill \end{array}$$

hold in $\mathsf{\Gamma }$. Since $\delta$ is arbitrary in $vK=v{K}^c$, we may conclude that $v^c(y-y^{\prime })=\infty$, i.e., $y^{\prime }=y$ holds in $K^c$.

Our next claim is that the assignment $x\mapsto y$ defines an embedding of valued fields

$$\begin{array}{cc}\hfill \sigma :(L,w)\stackrel{ }{\to }& (K^c,v^c).\end{array}$$

To see why this holds, most of the efforts are devoted to the verification that $\sigma$ preserves the additive operations. Take $x,y\in L$, and assume without loss of generality that $wx\le wy$. If $z_{\nu },a_{\nu },b_{\nu }\in K$ are such that ${\left[z_{\nu }\right]}_{{\gamma }_{\nu }}={[x+y]}_{{\gamma }_{\nu }}$, ${\left[a_{\nu }\right]}_{{\gamma }_{\nu }}={\left[x\right]}_{{\gamma }_{\nu }}$ and ${\left[b_{\nu }\right]}_{{\gamma }_{\nu }}={\left[y\right]}_{{\gamma }_{\nu }}$ for all $\nu <\kappa$, then, as before, these elements form Cauchy sequences in K. Let us then denote by z, a and b their limits in $K^c$, respectively. By definition of $\sigma$, we have that $\sigma (x+y)=z$, $\sigma \left(x\right)=a$ and $\sigma \left(y\right)=b$. Our aim now will be to prove that $z=a+b$ holds in $K^c$. We first obtain from Lemma 1$\left(iv\right)$ that

$$z_{\nu }\in \bigcup ({\left[a_{\nu }\right]}_{{\gamma }_{\nu }}+{\left[b_{\nu }\right]}_{{\gamma }_{\nu }})$$

holds, for all $\nu <\kappa$. Therefore, if we fix any $\delta \in vK$ and let $\nu <\kappa$ be large enough so that ${\gamma }_{\nu }+wx>\delta$ and

$$v^c(a-a_{\nu }),v^c(b-b_{\nu }),v^c(z-z_{\nu })>\delta$$

hold in $\mathsf{\Gamma }$, then an application of Lemma 1$\left(ii\right)$ yields that

$$v(a_{\nu }+y_{\nu }-z_{\nu })>{\gamma }_{\nu }+wx>\delta$$

holds in $\mathsf{\Gamma }$, where we used the fact that $v{a}_{\nu }=wx$ for all $\nu <\kappa$. Thus, we obtain that

$$\begin{array}{cc}\hfill v^c(a_{\nu }+b_{\nu }-z)& =v^c(a_{\nu }+b_{\nu }-z_{\nu }+z_{\nu }-z)\hfill \\ \hfill & \ge min\{v^c(a_{\nu }+b_{\nu }-z_{\nu }),v^c(z_{\nu }-z)\}>\delta \hfill \end{array}$$

and, consequently,

$$\begin{array}{cc}\hfill v^c(a+b-z)& =v^c(a-a_{\nu }+b-b_{\nu }+a_{\nu }+b_{\nu }-z)\hfill \\ \hfill & \ge min\{v^c(a-a_{\nu }),v^c(b-b_{\nu }),v^c(a_{\nu }+b_{\nu }-z)\}>\delta \hfill \end{array}$$

hold in $\mathsf{\Gamma }$. Since $\delta$ is arbitrary in $vK$ and $v^c(a+b-z)\in vK\cup \{\infty \}$, we deduce that $v^c(a+b-z)=\infty$ and, consequently, $z=a+b$, as contended.

Now, it suffices to recall that ${[-x]}_{\gamma }=-{\left[x\right]}_{\gamma }$ and that if $y\ne 0$, then ${\left[x{y}^{-1}\right]}_{\gamma }={\left[x\right]}_{\gamma }{\left[y\right]}_{\gamma }^{-1}$ hold in $L_{\gamma }$ to immediately deduce that $\sigma (-x)=\sigma {\left(x\right)}^{-}$ and that $\sigma \left(a{b}^{-1}\right)=\sigma \left(a\right)\sigma {\left(b\right)}^{-1}$ must hold in $K_{\gamma }^c$. We have proved that $\sigma$ is a homomorphism of fields and, as such, an embedding.

Finally, since $v{y}_{\nu }=wx$ holds in $\mathsf{\Gamma }$, for all $x\in L^{\times }$ and all $\nu <\kappa$ (as we have already shown above) it can be easily verified from the definition of convergent sequences, that the element $\sigma \left(x\right)\in K^c$, to which the Cauchy sequence ${\left(y_{\nu }\right)}_{\nu <\kappa }$ in K converges, satisfies $v^c\left(\sigma \left(x\right)\right)=v{y}_{\nu }$, for all $\nu <\kappa$. We conclude that $v\left(\sigma \right(x\left)\right)=wx$ holds, for all $x\in L$. In particular, we have that $\sigma$ is an embedding of valued fields. □

In the proof of the implication from $\left(ii\right)$ to $\left(i\right)$ in the above theorem, we have used the assumption that $(L,w)$ is an extension of $(K,v)$ only for identifying $vK$ and $v^c{K}^c$ with a canonical subset of $wL$. However, in the final analysis, this identification is not necessary and is performed only for a smoother exposition of the reasonings in the proof.

Scholium 1

(The term ‘scholium’ (literally, a marginal note) is used, e.g., in [36] to denote something that follows directly from the proof of a preceding result, as opposed to a corollary that follows directly from the statement of the preceding result). If $(L,w)$ is any valued field such that there is an order-preserving group-embedding $wL\hookrightarrow \mathsf{\Gamma }$ and, up to this embedding, Condition $\left(ii\right)$ of Theorem 1 holds, then there is a $\mathbf{vHyp}/\mathcal{T}\left(\mathsf{\Gamma }\right)$-arrow $(L,w)⟶(K^c,v^c)$.

Now, under the assumptions of the above result, for a valued hyperfield $(L,w)$, we deduce, first, that L is a field by Lemma 4. Then, we denote by $f_{\gamma }:L\to L_{\gamma }\simeq K_{\gamma }$ and by ${\tilde{\rho }}_{\gamma }:K^c\to K_{\gamma }^c\simeq K_{\gamma }$ the projections onto the valued $\gamma$-hyperfields associated with $(K,v)$ of $(L,w)$ and $(K^c,v^c)$, respectively. It is so straightforward to verify that the embedding $\sigma$ that we have constructed in the proof of Theorem 1 is unique with the property that $f_{\gamma }={\tilde{\rho }}_{\gamma }\circ \sigma$ for all $\gamma \in vK$ such that $\gamma \ge 0$. Indeed, this conclusion follows from the fact that for any $x\in L^{\times }$, the classes ${\left({\left[x\right]}_{\gamma }\right)}_{\gamma \in v{K}_{\ge 0}}$ form a chain of ultrametric balls in L of increasing radii and, moreover, the set of this radii is cofinal in $vK$. We have now fully proved Krasner’s result [23] (§ 4) in a purely categorial language:

Theorem 2.

The completion $(K^c,v^c)$ of $(K,v)$ is ($\mathbf{vHyp}$-isomorphic to) the limit of Diagram (3) in $\mathbf{vHyp}/\mathcal{T}\left(\mathsf{\Gamma }\right)$, for any ordered abelian group extension Γ of $vK$.

We note moreover, that in the above setting the assumption $\mathsf{\Gamma }=vK=wL$ is a posteriori not restrictive.

Corollary 1.

$(K,v)$ is complete if and only if it is the limit of the diagram (3), with $\mathsf{\Gamma }=vK$, in $\mathbf{vHyp}/\mathcal{T}\left(\mathsf{\Gamma }\right)$.

We conclude by describing the above abstract and general constructions and results in one concrete example.

Example 4

(t-adic valuations on formal Laurent series fields). Let K be a field and t any transcendental over K. We denote by $K\left[t\right]$ the polynomial ring, by $K\left(t\right)$ the field of rational functions, by $K\left[\right[t\left]\right]$ the formal power series ring and by $K\left(\right(t\left)\right)$ the field of formal Laurent series, i.e., the fraction field of $K\left[\right[t\left]\right]$.

A map $v_t$ is defined on a non-zero power series $f\in K\left[\right[t\left]\right]$ as the exponent $v_t\left(f\right)\in {\mathbb{Z}}_{\ge 0}$ of the highest power of t dividing f. The restriction of $v_t$ to $K\left[t\right]$ is extended to a discrete valuation $v_t:K\left(t\right)\to \mathbb{Z}\cup \{\infty \}$, called the t-adic valuation, by setting:

$$v_t\left(\frac{f}{g}\right):=v_t\left(f\right)-v_t\left(g\right)$$

for all $f,g\in K\left[t\right]$. It is well known that the completion of the valued field $(K\left(t\right),v_t)$ with respect to $v_t$ is $K\left(\right(t\left)\right)$ and throughout this example, we shall denote $v_t^c$ again by $v_t$.

By definition, a principal unit $u\in K\left(\right(t\left)\right)$ of level $n\in \mathbb{N}={\left(v_{t}K\left(\left(t\right)\right)\right)}_{\ge 0}$ has the form:

$$1+t^n\left(\sum _{i=1}^{+\infty }{a}_i{t}^i\right)\in K\left[\left[t\right]\right]$$

with $a_i\in K$.

Thus, the elements (with non-negative value) of the valued n-hyperfield H associated with $(K\left(\left(t\right)\right),v_t)$ correspond to truncated power series. That is, two power series in $K\left[\right[t\left]\right]$ are in the same class in H if and only if all of their coefficients up to the n-th coincide. While, since $n\ge 0$, the product in $K\left(\right(t\left)\right)$ descends to H, the additive operation does not as some cancellations may occur that cannot be determined on the basis of the coefficients of degree $\le n$. For instance, while ${\left[1\right]}_n⊞{[-1]}_n$ certainly contains ${\left[0\right]}_n$ as $1-1=0$ holds in $K\left(\right(t\left)\right)$, by a distinct choice of representatives we also find that ${\left[1\right]}_n⊞{[-1]}_n$ contains, e.g., the class of:

$$1+t^{n+1}-(1-t^{n+1})=2t^{n+1}$$

which has value $n+1<\infty$ under $v_t$ and is hence is not ${\left[0\right]}_n$.

The multivalued operation of H is defined as to include all possibilities given by the indeterminacy caused by the above mentioned cancellations of terms of order greater than n.

From a metric perspective, two power series are close to each other in $(K\left(\left(t\right)\right),v_t)$ if their difference can be divided by a high power of t. Thus, the above-described truncations correspond to an identification of power series that are closer to each other than a fixed finite distance.

An application of Lemma 2 in this case shows that for all $n\in \mathbb{N}$ and any non-zero power series $f\in K\left[\right[t\left]\right]$, a rational function exists whose power series expansion has the coefficients of $t^i$ equal to those of f for all $i\le n$, respectively.

The limit construction culminated in Theorem 2 above, is a general and formal form of the intuitive idea that when “truncations” at all finite levels are known, then the additive indeterminacy can be resolved and full information on the power series ring $K\left[\right[t\left]\right]$—and consequently on the valued field $(K\left(\left(t\right)\right),v_t)$—can be derived. On the other hand, due to the density of $K\left(t\right)$ in $K\left(\right(t\left)\right)$, the just-described procedure cannot be used to identify the valued subfield $(K\left(t\right),v_t)$.

Several deep open questions in mathematics are related to the study of valuations of (finite or infinite) Archimedean rank $>1$ (see, e.g., [37] and the references therein). The above example on valuations of rank 1 includes fields as ${\mathbb{F}}_p\left(\left(t\right)\right)$ (where p is a prime number), which are as well sources of deep unresolved problems on which intuitions often struggle in dealing with unexpected counterexamples (cf. [38]).

In this article, which certainly constitutes a tiny drop in the ocean, the intuitive idea of truncation of power series described in Example 4 is formally extended to the general case, showing at the same time that it constitutes a fundamental and deep property shared by all (non-trivially) valued fields. Our approach is in line with other extension results, such as the fractal geometry induced on the power series rings ${\mathbb{F}}_p\left[\left[t\right]\right]$ by t-adic valuations ([39], Example 3), which has been generalized to discretely valued fields in [39] (Proposition 5).

5. Conclusions and Future Work

We trace below possible future developments.

• A diagram of the form (3) as above can be associated with any non-trivially valued hyperfield (cf. [10] Proposition 1.17). As a corollary to the results presented in this article, we may deduce the following statement:

  If among the cones over the diagram (3), where $(K,v)$ is only assumed to be a non-trivially valued hyperfield, there is one whose vertex is a valued field $(L,w)$, then the limit cone of that shape exists in $\mathbf{vHyp}$ and its vertex is isomorphic to the valuation-theoretic completion of $(L,w)$.

  Let us note that the hypothesis of the above assertion holds under weaker assumptions on $(K,v)$ than that of K being a field. For instance, by [10] (Proposition 1.27), it suffices that v satisfies Krasner’s further assumption (such valuations are called Krasner valuations in [24] (Section 4)). The problem of whether the just mentioned assumption on $(K,v)$ is also necessary is outside the scope of this work and left open for future investigations. This is also related to the open problem mentioned in Remark 2 above.
• Generalized tropical hyperfields are characterized in [24] (Theorem 5.2). This characterization result relates the problem of isolating the full subcategory of $\mathbf{vHyp}$, whose objects are generalized tropical hyperfields, to the broader class of stringent hyperfields. These have been characterized in [40], but the current form of Bowler and Su’s characterization theorem is not yet fully element-independent.
• In conclusion, let us note that the recent theory of enriched valuations mentioned in [25], Example 3.16 suggests further extensions of our approach, where the target of an (enriched) valuation is taken from a wider class of hyperfields than that of generalized tropical hyperfields or stringent hyperfields.