High-Dimensional Mediation Analysis for Time-to-Event Outcomes with Additive Hazards Model
Abstract
:1. Introduction
2. Model and Notations
3. Multiple Testing-Based Mediator Selection
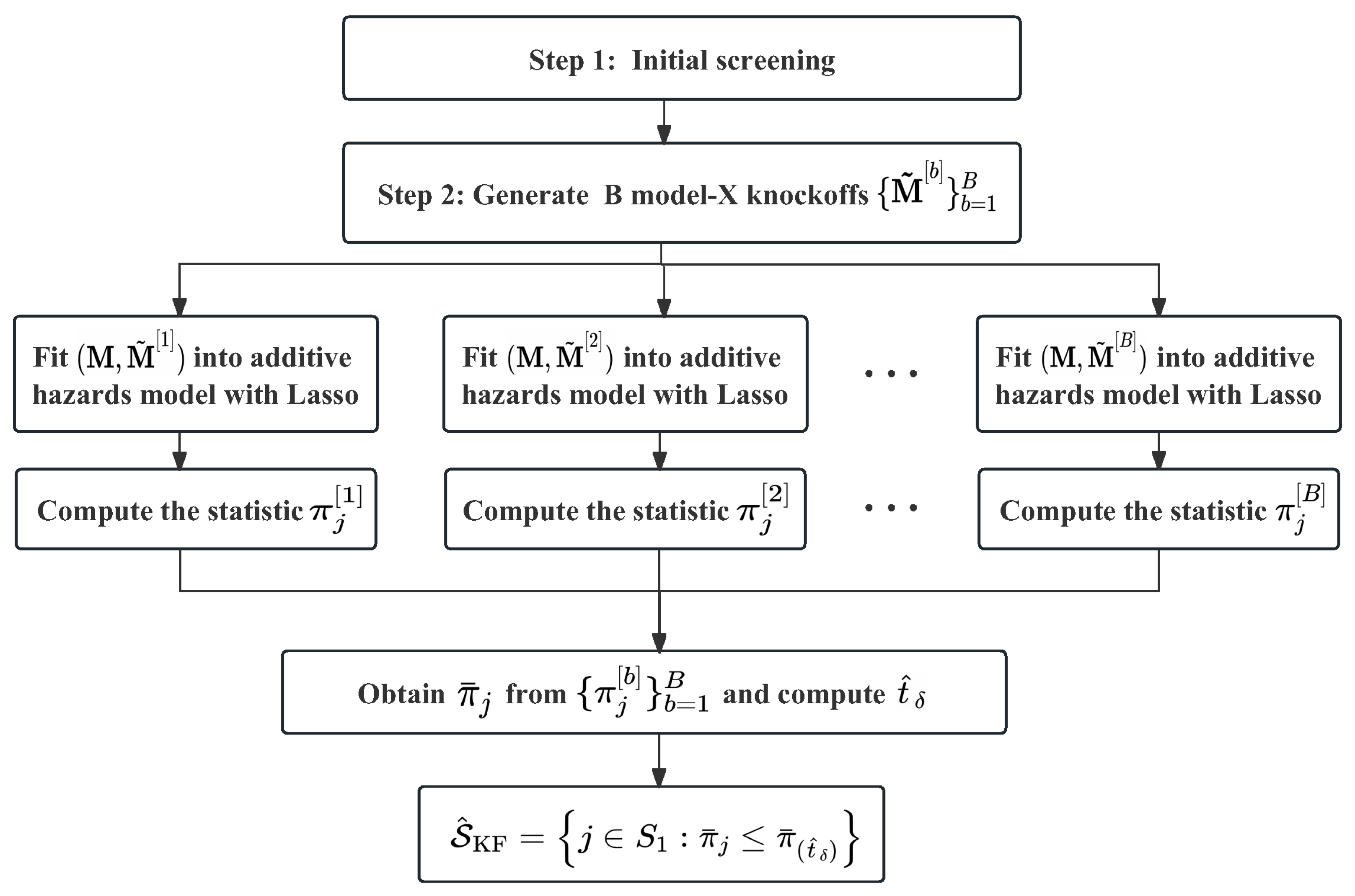
4. Knockoff Filter for High-Dimensional Mediators
5. Simulation Studies
6. Application
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Baron, R.M.; Kenny, D.A. The moderator–mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. J. Personal. Soc. Psychol. 1986, 51, 1173. [Google Scholar] [CrossRef] [PubMed]
- Valeri, L.; VanderWeele, T.J. Mediation analysis allowing for exposure-mediator interactions and causal interpretation: Theoretical assumptions and implementation with SAS and SPSS macros. Psychol. Methods 2013, 18, 137. [Google Scholar] [CrossRef] [PubMed]
- VanderWeele, T.J. Mediation analysis: A practitioner’s guide. Annu. Rev. Public Health 2016, 37, 17–32. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Zhou, X.; Zhang, M.; Zhao, W.; Liu, Y.; Kardia, S.L.R.; Roux, A.V.D.; Needham, B.L.; Smith, J.A.; Mukherjee, B. Bayesian Shrinkage Estimation of High Dimensional Causal Mediation Effects in Omics Studies. Biometrics 2020, 76, 700–710. [Google Scholar] [CrossRef] [PubMed]
- Dowling, C.M.; Hayes, S.L.; Phelan, J.J.; Cathcart, M.C.; Finn, S.P.; Mehigan, B.J.; McCormick, P.H.; Coffey, J.C.; O’Sullivan, J.N.; Kiely, P. Expression of protein kinase C gamma promotes cell migration in colon cancer. Oncotarget 2017, 8, 72096–72107. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.T. Joint significance tests for mediation effects of socioeconomic adversity on adiposity via epigenetics. Ann. Appl. Stat. 2018, 12, 1535–1557. [Google Scholar] [CrossRef]
- Charalambous, A.; Giannakopoulou, M.; Bozas, E.; Paikousis, L. Parallel and serial mediation analysis between pain, anxiety, depression, fatigue and nausea, vomiting and retching within a randomised controlled trial in patients with breast and prostate cancer. BMJ Open 2019, 9, e026809. [Google Scholar] [CrossRef]
- Zhang, H.; Zheng, Y.; Zhang, Z.; Gao, T.; Joyce, B.T.; Yoon, G.; Zhang, W.; Schwartz, J.D.; Just, A.C.; Colicino, E.; et al. Estimating and testing high-dimensional mediation effects in epigenetic studies. Bioinformatics 2016, 32, 3150–3154. [Google Scholar] [CrossRef]
- Zhao, Y.; Lindquist, M.A.; Caffo, B.S. Sparse principal component based high-dimensional mediation analysis. Comput. Stat. Data Anal. 2020, 142, 106835. [Google Scholar] [CrossRef]
- Derkach, A.; Pfeiffer, R.M.; Chen, T.H.; Sampson, J.N. High dimensional mediation analysis with latent variables. Biometrics 2019, 75, 745–756. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, J.; Feng, Y.; Wang, C.; Li, H.; Liu, L. Mediation effect selection in high-dimensional and compositional microbiome data. Stat. Med. 2021, 40, 885–896. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Chen, J.; Li, Z.; Liu, L. Testing for mediation effect with application to human microbiome data. Stat. Biosci. 2021, 13, 313–328. [Google Scholar] [CrossRef] [PubMed]
- Zeng, P.; Shao, Z.; Zhou, X. Statistical methods for mediation analysis in the era of high-throughput genomics: Current successes and future challenges. Comput. Struct. Biotechnol. J. 2021, 19, 3209–3224. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Hou, L.; Liu, L. A review of high-dimensional mediation analyses in DNA methylation studies. In Epigenome-Wide Association Studies: Methods and Protocols; Weihua, G., Ed.; Springer: Berlin/Heidelberg, Germany, 2022; Volume 2432. [Google Scholar] [CrossRef]
- Valeri, L.; Lin, X.; VanderWeele, T.J. Mediation analysis when a continuous mediator is measured with error and the outcome follows a generalized linear model. Stat. Med. 2014, 33, 4875–4890. [Google Scholar] [CrossRef] [PubMed]
- Gaynor, S.M.; Schwartz, J.; Lin, X. Mediation analysis for common binary outcomes. Stat. Med. 2019, 38, 512–529. [Google Scholar] [CrossRef]
- Tein, J.Y.; MacKinnon, D.P. Estimating mediated effects with survival data. In New Developments in Psychometrics: Proceedings of the International Meeting of the Psychometric Society (IMPS2001), Osaka, Japan, 15–19 July 2001; Springer: Berlin/Heidelberg, Germany, 2003; pp. 405–412. [Google Scholar]
- Gelfand, L.A.; MacKinnon, D.P.; DeRubeis, R.J.; Baraldi, A.N. Mediation analysis with survival outcomes: Accelerated failure time vs. proportional hazards models. Front. Psychol. 2016, 7, 423. [Google Scholar] [CrossRef] [PubMed]
- Luo, C.; Fa, B.; Yan, Y.; Wang, Y.; Zhou, Y.; Zhang, Y.; Yu, Z. High-dimensional mediation analysis in survival models. PLoS Comput. Biol. 2020, 16, e1007768. [Google Scholar] [CrossRef]
- Zhang, H.; Zheng, Y.; Hou, L.; Zheng, C.; Liu, L. Mediation analysis for survival data with high-dimensional mediators. Bioinformatics 2021, 37, 3815–3821. [Google Scholar] [CrossRef]
- Yu, Z.; Cui, Y.; Wei, T.; Ma, Y.; Luo, C. High-dimensional mediation analysis with confounders in survival models. Front. Genet. 2021, 12, 688871. [Google Scholar] [CrossRef]
- Tian, P.; Yao, M.; Huang, T.; Liu, Z. CoxMKF: A knockoff filter for high-dimensional mediation analysis with a survival outcome in epigenetic studies. Bioinformatics 2022, 38, 5229–5235. [Google Scholar] [CrossRef]
- Cui, Y.; Luo, C.; Luo, L.; Yu, Z. High-dimensional mediation analysis based on additive hazards model for survival data. Front. Genet. 2021, 12, 771932. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Wu, L.; Zhang, H. A space-time spectral order sinc-collocation method for the fourth-order nonlocal heat model arising in viscoelasticity. Appl. Math. Comput. 2023, 457, 128192. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y.; Yang, X. An efficient ADI difference scheme for the nonlocal evolution problem in three-dimensional space. J. Appl. Math. Comput. 2023, 69, 651–674. [Google Scholar] [CrossRef]
- Tian, Q.; Yang, X.; Zhang, H.; Xu, D. An implicit robust numerical scheme with graded meshes for the modified Burgers model with nonlocal dynamic properties. Comput. Appl. Math. 2023, 42, 246. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, H.; Jiang, X.; Yang, X. A high-order and efficient numerical technique for the nonlocal neutron diffusion equation representing neutron transport in a nuclear reactor. Ann. Nucl. Energy 2024, 195, 110163. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, H.; Yang, X. H1-norm error analysis of a robust ADI method on graded mesh for three-dimensional subdiffusion problems. In Numerical Algorithms; Springer: Berlin/Heidelberg, Germany, 2023; pp. 1–19. [Google Scholar]
- Huang, Y.T.; Yang, H.I. Causal mediation analysis of survival outcome with multiple mediators. Epidemiology 2017, 28, 370–378. [Google Scholar] [CrossRef]
- Lin, D.Y.; Ying, Z. Semiparametric analysis of the additive risk model. Biometrika 1994, 81, 61–71. [Google Scholar] [CrossRef]
- Fan, J.; Lv, J. Sure independence screening for ultrahigh dimensional feature space. J. R. Stat. Soc. Ser. 2008, 70, 849–911. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Hao, N.; Zhang, H.H. Oracle p-values and variable screening. Electron. J. Stat. 2017, 11, 3251–3271. [Google Scholar] [CrossRef]
- Dai, J.Y.; Stanford, J.L.; LeBlanc, M. A multiple-testing procedure for high-dimensional mediation hypotheses. J. Am. Stat. Assoc. 2022, 117, 198–213. [Google Scholar] [CrossRef] [PubMed]
- Barber, R.F.; Candès, E.J. Controlling the false discovery rate via knockoffs. Ann. Stat. 2014, 43, 2055–2085. [Google Scholar] [CrossRef]
- Candès, E.J.; Fan, Y.; Janson, L.; Lv, J. Panning for gold: ‘Model-X’ knockoffs for high dimensional controlled variable selection. J. R. Stat. Soc. Ser. (Stat. Methodol.) 2016, 80, 551–577. [Google Scholar] [CrossRef]
- Nguyen, T.B.; Chevalier, J.A.; Thirion, B.; Arlot, S. Aggregation of multiple knockoffs. Int. Conf. Mach. Learn. 2020, 119, 7283–7293. [Google Scholar]
- Meinshausen, N.; Meier, L.; Bühlmann, P. p-Values for High-Dimensional Regression. J. Am. Stat. Assoc. 2008, 104, 1671–1681. [Google Scholar] [CrossRef]
- Govindan, R.; Ding, L.; Griffith, M.; Subramanian, J.; Dees, N.D.; Kanchi, K.L.; Maher, C.A.; Fulton, R.S.; Fulton, L.; Wallis, J.W.; et al. Genomic Landscape of Non-Small Cell Lung Cancer in Smokers and Never-Smokers. Cell 2012, 150, 1121–1134. [Google Scholar] [CrossRef]
- Matouk, I.J.; Halle, D.; Gilon, M.; Hochberg, A. The non-coding RNAs of the H19-IGF2 imprinted loci: A focus on biological roles and therapeutic potential in Lung Cancer. J. Transl. Med. 2015, 13, 113. [Google Scholar] [CrossRef]

| Sample Size | CR = 20% | CR = 50% | |||||
|---|---|---|---|---|---|---|---|
| Cui | HDMT | Knockoff | Cui | HDMT | Knockoff | ||
| MS | 3.05 | 4.42 | 5.902 | 1.276 | 2.018 | 4.638 | |
| CMR | 0.032 | 0.078 | 0.524 | 0 | 0.008 | 0.202 | |
| FDP | 0.032 | 0.083 | 0.039 | 0.035 | 0.066 | 0.034 | |
| TPR | 0.481 | 0.637 | 0.937 | 0.193 | 0.286 | 0.739 | |
| MS | 5.162 | 6.276 | 6.222 | 3.042 | 4.088 | 5.866 | |
| CMR | 0.362 | 0.396 | 0.71 | 0.044 | 0.106 | 0.536 | |
| FDP | 0.028 | 0.092 | 0.039 | 0.039 | 0.075 | 0.041 | |
| TPR | 0.83 | 0.923 | 0.989 | 0.479 | 0.603 | 0.93 | |
| MS | 6.044 | 6.59 | 6.238 | 4.9 | 5.852 | 6.252 | |
| CMR | 0.728 | 0.594 | 0.786 | 0.25 | 0.314 | 0.736 | |
| FDP | 0.027 | 0.077 | 0.033 | 0.019 | 0.075 | 0.039 | |
| TPR | 0.975 | 0.996 | 1 | 0.796 | 0.883 | 0.993 | |
| Sample Size | CR = 20% | CR = 50% | |||||
|---|---|---|---|---|---|---|---|
| Cui | HDMT | Knockoff | Cui | HDMT | Knockoff | ||
| n = 300 | MS | 3.47 | 5.744 | 7.184 | 1.012 | 2.304 | 5.872 |
| CMR | 0.066 | 0.454 | 0.18 | 0 | 0.032 | 0.118 | |
| FDP | 0.025 | 0.063 | 0.168 | 0.019 | 0.042 | 0.133 | |
| TPR | 0.554 | 0.875 | 0.978 | 0.159 | 0.338 | 0.833 | |
| n = 500 | MS | 5.292 | 6.376 | 7.78 | 1.962 | 4.666 | 6.87 |
| CMR | 0.362 | 0.69 | 0.098 | 0.002 | 0.232 | 0.152 | |
| FDP | 0.025 | 0.053 | 0.216 | 0.013 | 0.059 | 0.164 | |
| TPR | 0.855 | 0.994 | 0.998 | 0.317 | 0.702 | 0.941 | |
| n = 800 | MS | 5.974 | 6.362 | 7.976 | 3.482 | 6.174 | 7.382 |
| CMR | 0.784 | 0.73 | 0.09 | 0.064 | 0.522 | 0.15 | |
| FDP | 0.017 | 0.048 | 0.232 | 0.015 | 0.068 | 0.182 | |
| TPR | 0.976 | 0.999 | 0.999 | 0.567 | 0.942 | 0.989 | |
| CpGs | Chromosome | Gene | (se) | (se) | |
|---|---|---|---|---|---|
| cg21926276 | Chr11 | H19 | |||
| cg24200525 | Chr22 | SBF1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, M.; Zhang, H. High-Dimensional Mediation Analysis for Time-to-Event Outcomes with Additive Hazards Model. Mathematics 2023, 11, 4891. https://doi.org/10.3390/math11244891
An M, Zhang H. High-Dimensional Mediation Analysis for Time-to-Event Outcomes with Additive Hazards Model. Mathematics. 2023; 11(24):4891. https://doi.org/10.3390/math11244891
Chicago/Turabian StyleAn, Meng, and Haixiang Zhang. 2023. "High-Dimensional Mediation Analysis for Time-to-Event Outcomes with Additive Hazards Model" Mathematics 11, no. 24: 4891. https://doi.org/10.3390/math11244891
APA StyleAn, M., & Zhang, H. (2023). High-Dimensional Mediation Analysis for Time-to-Event Outcomes with Additive Hazards Model. Mathematics, 11(24), 4891. https://doi.org/10.3390/math11244891





