Sparse Diffusion Least Mean-Square Algorithm with Hard Thresholding over Networks
Abstract
:1. Introduction
2. Algorithm Formulation
2.1. Derivation of Sparse Diffusion LMS with Hard Thresholding
2.2. Guideline for Determining Thresholds
3. Performance Analysis
3.1. Assumptions
3.2. Mean Stability Analysis
3.3. Transient Analysis in Mean Square
3.4. Steady-State Analysis in Mean Square
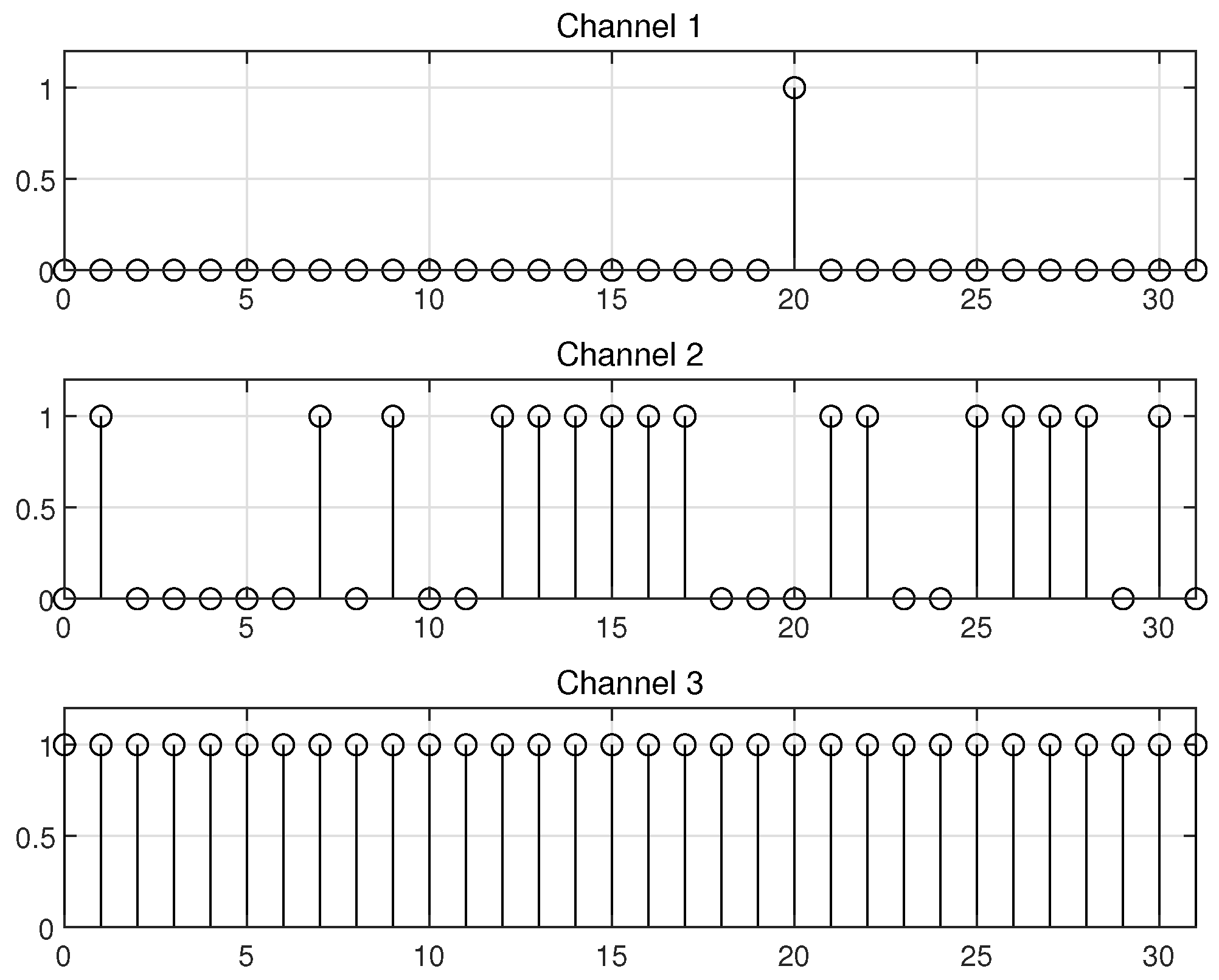
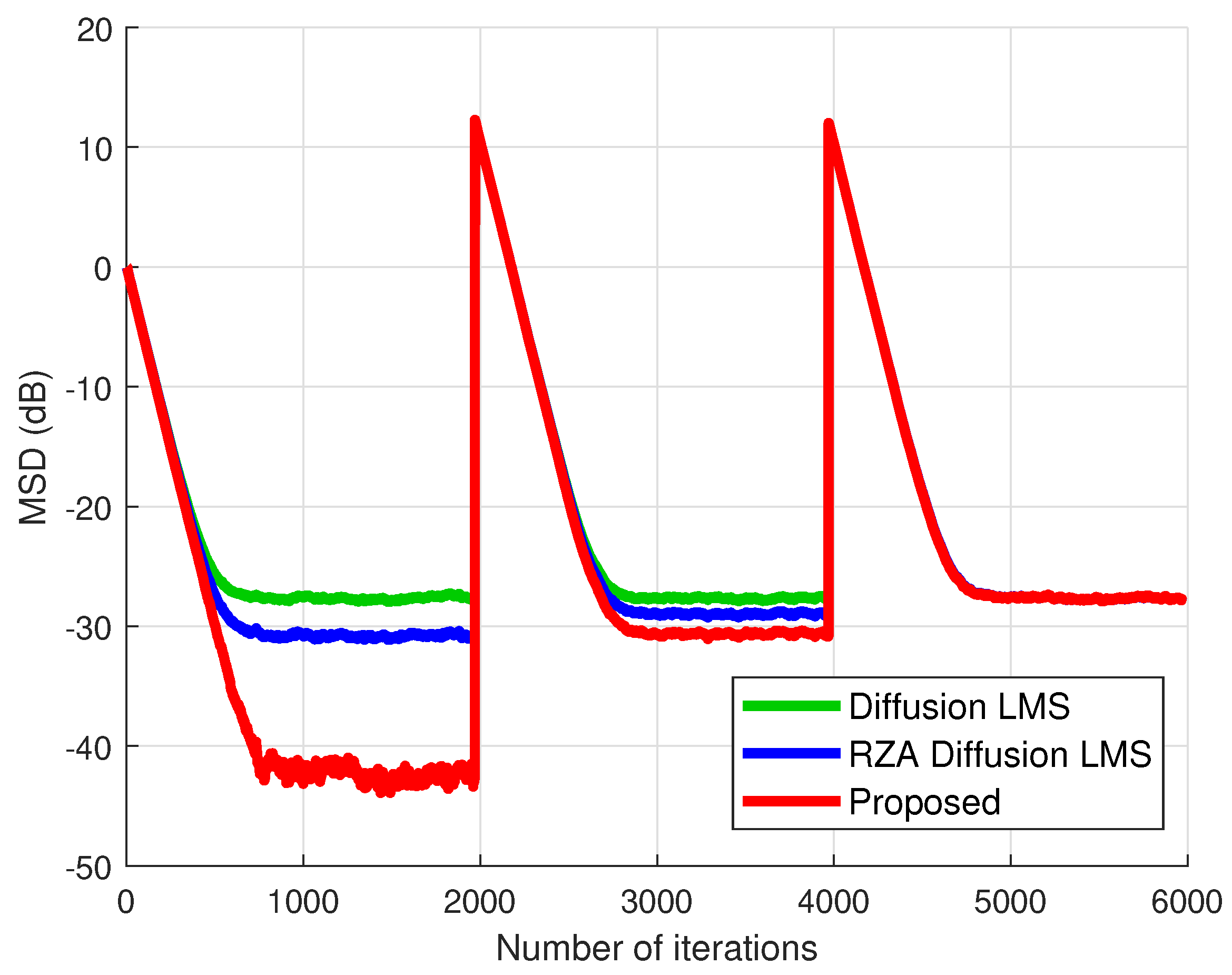
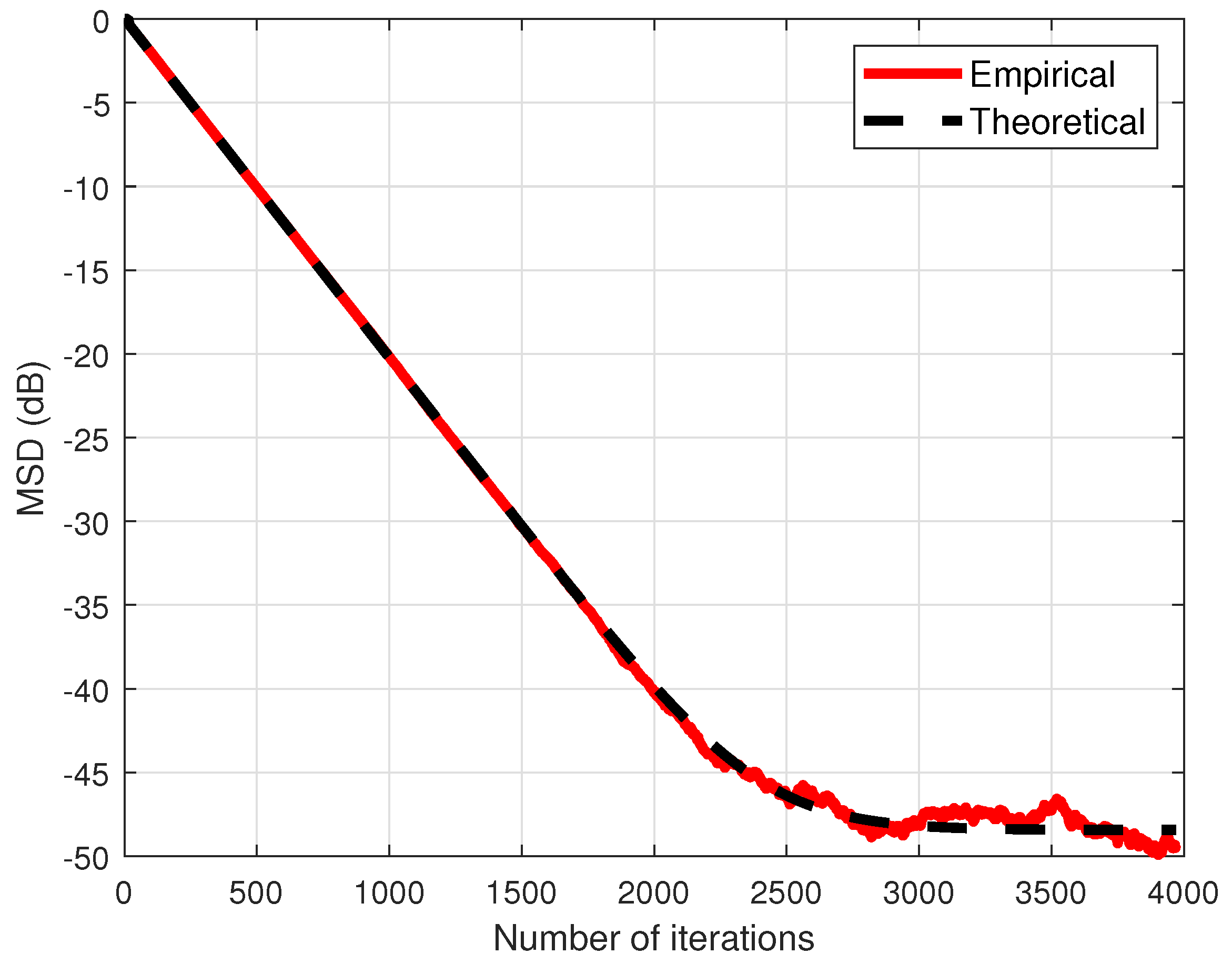
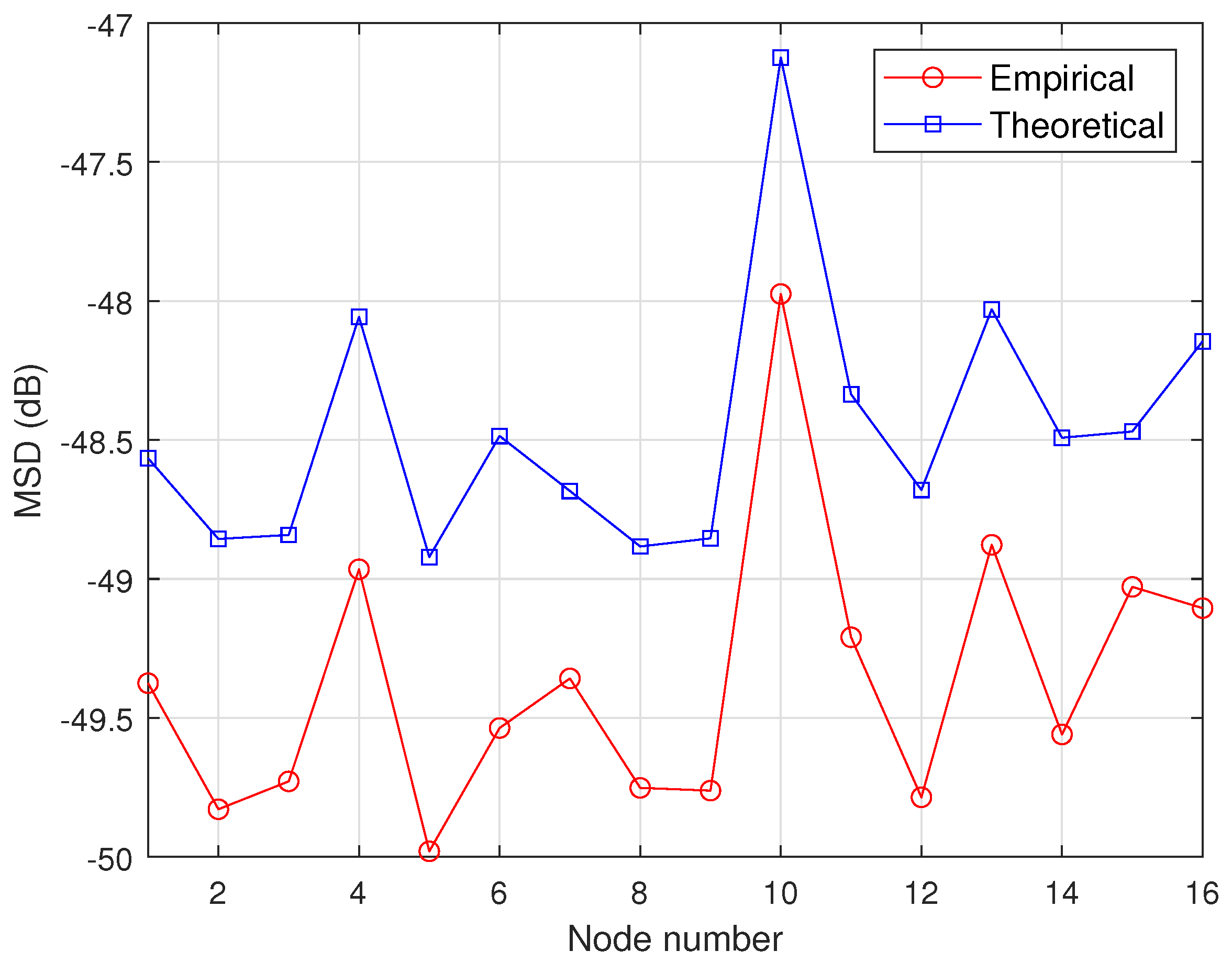
4. Simulation Results
4.1. Performance Comparison
4.2. Theoretical Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Sayed, A.H. Adaptation, learning, and optimization over networks. Found. Trends Mach. Learn. 2014, 7, 311–801. [Google Scholar] [CrossRef]
- Lopes, C.G.; Sayed, A.H. Incremental adaptive strategies over distributed networks. IEEE Trans. Signal Process. 2007, 55, 4064–4077. [Google Scholar] [CrossRef]
- Schizas, I.D.; Mateos, G.; Giannakis, G.B. Distributed LMS for consensus-based in-network adaptive processing. IEEE Trans. Signal Process. 2009, 57, 2365–2382. [Google Scholar] [CrossRef]
- Soatti, G.; Nicoli, M.; Savazzi, S.; Spagnolini, U. Consensus-based algorithms for distributed network-state estimation and localization. IEEE Trans. Signal Inf. Process. Netw. 2016, 3, 430–444. [Google Scholar] [CrossRef]
- Lopes, C.G.; Sayed, A.H. Diffusion least-mean squares over adaptive networks: Formulation and performance analysis. IEEE Trans. Signal Process. 2008, 56, 3122–3136. [Google Scholar] [CrossRef]
- Cattivelli, F.S.; Sayed, A.H. Diffusion LMS strategies for distributed estimation. IEEE Trans. Signal Process. 2010, 58, 1035–1048. [Google Scholar] [CrossRef]
- Liu, Y.; Li, C.; Zhang, Z. Diffusion sparse least-mean squares over networks. IEEE Trans. Signal Process. 2012, 60, 4480–4485. [Google Scholar] [CrossRef]
- Sayed, A.H. Diffusion adaptation over networks. In Academic Press Library Signal Processing; Elsevier: Amsterdam, The Netherlands, 2014; Volume 3, pp. 323–453. [Google Scholar]
- Tu, S.Y.; Sayed, A.H. Diffusion strategies outperform consensus strategies for distributed estimation over adaptive networks. IEEE Trans. Signal Process. 2012, 60, 6217–6234. [Google Scholar] [CrossRef]
- Lee, J.W.; Kim, S.E.; Song, W.J.; Sayed, A.H. Spatio-temporal diffusion strategies for estimation and detection over networks. IEEE Trans. Signal Process. 2012, 60, 4017–4034. [Google Scholar] [CrossRef]
- Jung, S.M.; Seo, J.H.; Park, P. A variable step-size diffusion normalized least-mean-square algorithm with a combination method based on mean-square deviation. Circuits Syst. Signal Process. 2015, 34, 3291–3304. [Google Scholar] [CrossRef]
- Yu, Y.; He, H.; Yang, T.; Wang, X.; de Lamare, R.C. Diffusion normalized least mean M-estimate algorithms: Design and performance analysis. IEEE Trans. Signal Process. 2020, 68, 2199–2214. [Google Scholar] [CrossRef]
- Cattivelli, F.S.; Lopes, C.G.; Sayed, A.H. Diffusion recursive least-squares for distributed estimation over adaptive networks. IEEE Trans. Signal Process. 2008, 56, 1865–1877. [Google Scholar] [CrossRef]
- Li, L.; Chambers, J.A. Distributed adaptive estimation based on the APA algorithm over diffusion networks with changing topology. In Proceedings of the IEEE Statistical Signal Processing Workshop, Cardiff, UK, 31 August–3 September 2009; pp. 757–760. [Google Scholar]
- Takahashi, N.; Yamada, I.; Sayed, A.H. Diffusion least-mean squares with adaptive combiners: Formulation and performance Analysis. IEEE Trans. Signal Process. 2010, 58, 4795–4810. [Google Scholar] [CrossRef]
- Lee, H.S.; Kim, S.E.; Lee, J.W.; Song, W.J. A variable step-size diffusion LMS algorithm for distributed estimation. IEEE Trans. Signal Process. 2015, 63, 1808–1820. [Google Scholar] [CrossRef]
- Chu, Y.; Chan, S.C.; Zhou, Y.; Wu, M. A new diffusion variable spatial regularized LMS algorithm. Signal Process. 2021, 188, 108207. [Google Scholar] [CrossRef]
- Shi, K.; Shi, P. Convergence analysis of sparse LMS algorithms with l1-norm penalty based on white input signal. Signal Process. 2010, 90, 3289–3293. [Google Scholar] [CrossRef]
- Wagner, K.; Doroslovacki, M. Proportionate-type normalized least mean square algorithms with gain allocation motivated by mean-square error minimization for white input. IEEE Trans. Signal Process. 2011, 59, 2410–2415. [Google Scholar] [CrossRef]
- Murakami, Y.; Yamagishi, M.; Yukawa, M.; Yamada, I. A sparse adaptive filtering using time-varying soft-thresholding techniques. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Dallas, TX, USA, 14–19 March 2010; pp. 3734–3737. [Google Scholar]
- Su, G.; Jin, J.; Gu, Y.; Wang, J. Performance analysis of l_0 norm constraint least mean square algorithm. IEEE Trans. Signal Process. 2012, 60, 2223–2235. [Google Scholar] [CrossRef]
- Chen, Y.; Gu, Y.; Hero III, A.O. Sparse LMS for system identification. In Proceedings of the IEEE Internatinal Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 3125–3128. [Google Scholar]
- Lee, H.S.; Lee, J.W.; Song, W.J.; Kim, S.E. Adaptive algorithm for sparse system identification based on hard-thresholding techniques. IEEE Trans. Circuits Syst. II Exp. Briefs 2020, 67, 3597–3601. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Yang, X.; Wu, L.; Zhang, H. A space-time spectral order sinc-collocation method for the fourth-order nonlocal heat model arising in viscoelasticity. Appl. Math. Comput. 2023, 457, 128192. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, H.; Jiang, X.; Yang, X. A high-order and efficient numerical technique for the nonlocal neutron diffusion equation representing neutron transport in a nuclear reactor. Ann. Nucl. Energy 2023, 195, 110163. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, J.; Wang, W.; Zhang, H. A predictor-corrector compact difference scheme for a nonlinear fractional differential equation. Fractal Fract. 2023, 7, 521. [Google Scholar] [CrossRef]
- Yim, S.H.; Lee, H.S.; Song, W.J. Proportionate diffusion LMS algorithm for sparse distributed estimation. IEEE Trans. Circuits Syst. II Exp. Briefs 2015, 62, 992–996. [Google Scholar] [CrossRef]
- Lee, H.S.; Yim, S.H.; Song, W.J. z2-proportionate diffusion LMS algorithm with mean square performance analysis. Signal Process. 2017, 131, 154–160. [Google Scholar] [CrossRef]
- Lorenzo, P.D.; Sayed, A.H. Sparse distributed learning based on diffusion adaptation. IEEE Trans. Signal Process. 2013, 61, 1419–1433. [Google Scholar] [CrossRef]
- Das, B.K.; Chakraborty, M.; Arenas-García, J. Sparse distributed estimation via heterogeneous diffusion adaptive networks. IEEE Trans. Circuits Syst. II Exp. Briefs 2016, 63, 1079–1083. [Google Scholar] [CrossRef]
- Kumar, K.S.; George, N.V. Polynomial sparse adaptive estimation in distributed networks. IEEE Trans. Circuits Syst. II Exp. Briefs 2018, 65, 401–405. [Google Scholar]
- Nautiyal, M.; Bhattacharjee, S.S.; George, N.V. Robust and sparse aware diffusion adaptive algorithms for distributed estimation. IEEE Trans. Circuits Syst. II Exp. Briefs 2022, 69, 239–243. [Google Scholar] [CrossRef]
- Huang, W.; Chen, C.; Yao, X.; Li, Q. Diffusion fused sparse LMS algorithm over networks. Signal Process. 2020, 171, 107497. [Google Scholar] [CrossRef]
- Huang, W.; Shan, H.; Xu, J.; Yao, X. Adaptive diffusion pairwise fused Lasso LMS algorithm over networks. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 5816–5827. [Google Scholar] [CrossRef] [PubMed]
- Martin, R.K.; Sethares, W.A.; Williamson, R.C.; Johnson, C.R. Exploiting sparsity in adaptive filters. IEEE Trans. Signal Process. 2002, 50, 1883–1894. [Google Scholar] [CrossRef]
- Krishnan, D.; Fergus, R. Fast image deconvolution using hyper-Laplacian priors. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 6–11 December 2009; pp. 1033–1041. [Google Scholar]
- Zuo, W.; Meng, D.; Zhang, L.; Feng, X.; Zhang, D. A generalized iterated shrinkage algorithm for non-convex sparse coding. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 217–224. [Google Scholar]
- Haykin, S.S. Adaptive Filter Theory; Pearson Education India: Noida, India, 2005. [Google Scholar]
- Haddad, D.B.; Petraglia, R. Transient and steady-state MSE analysis of the IMPNLMS algorithm. Digital Signal Process. 2014, 33, 50–59. [Google Scholar] [CrossRef]
- Saeed, M.O.B.; Zerguine, A.; Zunmo, S.A. A variable step-size strategy for distributed estimation over adaptive networks. EURASIP J. Adv. Signal Process. 2013, 1, 135. [Google Scholar] [CrossRef]

| Notations | Description |
|---|---|
| Euclidean norm of its argument | |
| -norm of its argument | |
| -norm of its argument (maximum norm) | |
| Mathematical expectation | |
| Largest eigenvalue of a matrix | |
| Trace operator | |
| Transposition | |
| Hermitian transposition | |
| Column vector with its entries | |
| Diagonal matrix with its entries | |
| Stack the columns of its matrix argument on top of each other | |
| I | Identity matrix |
| ⊗ | Kronecker product operation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.-S.; Jin, C.; Shin, C.; Kim, S.-E. Sparse Diffusion Least Mean-Square Algorithm with Hard Thresholding over Networks. Mathematics 2023, 11, 4638. https://doi.org/10.3390/math11224638
Lee H-S, Jin C, Shin C, Kim S-E. Sparse Diffusion Least Mean-Square Algorithm with Hard Thresholding over Networks. Mathematics. 2023; 11(22):4638. https://doi.org/10.3390/math11224638
Chicago/Turabian StyleLee, Han-Sol, Changgyun Jin, Chanwoo Shin, and Seong-Eun Kim. 2023. "Sparse Diffusion Least Mean-Square Algorithm with Hard Thresholding over Networks" Mathematics 11, no. 22: 4638. https://doi.org/10.3390/math11224638
APA StyleLee, H.-S., Jin, C., Shin, C., & Kim, S.-E. (2023). Sparse Diffusion Least Mean-Square Algorithm with Hard Thresholding over Networks. Mathematics, 11(22), 4638. https://doi.org/10.3390/math11224638






