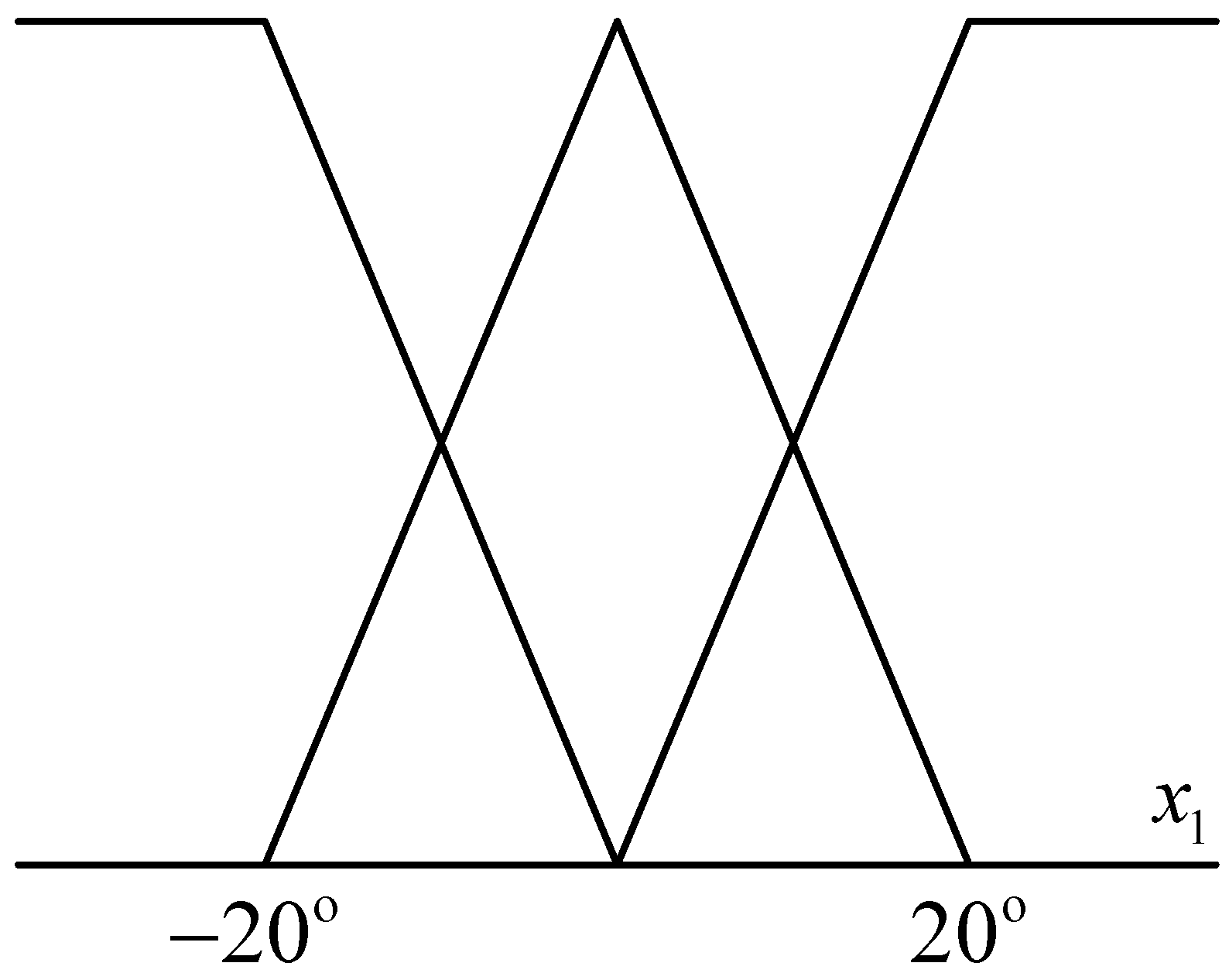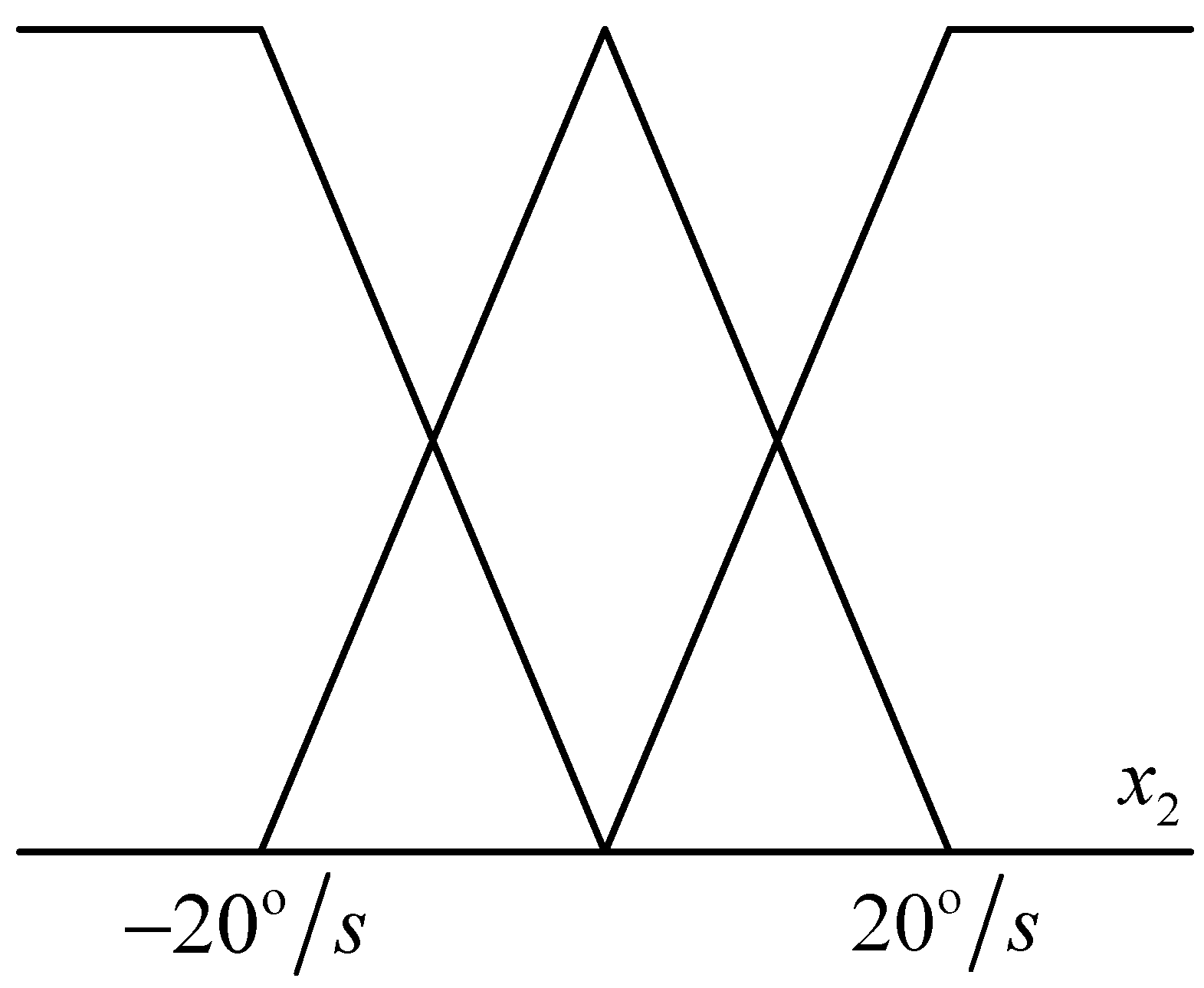Passive Stabilization of Static Output Feedback of Disturbed Nonlinear Stochastic System

Abstract

This paper investigates the Static Output (SO) control issue of the disturbed nonlinear stochastic system, which achieves passivity. Through the application of fuzzy sets and the stochastic differential equation, a Takagi–Sugeno (T-S) fuzzy model with the terms of multiplicative noise and external disturbance can be constructed to describe the considered systems. Furthermore, the Parallel Distributed Compensation (PDC) concept is used to design a fuzzy controller exhibiting an SO feedback scheme structure. To attenuate the effect of external disturbance, the PDC-based SO fuzzy controller is designed to exhibit passivity. During the derivation of some sufficient conditions, a line-integral Lyapunov function is utilized to avoid the conservative term produced using the derivative membership function. Using converting technologies, a stability criterion belonging to Linear Matrix Inequality (LMI) forms is proposed such that the derived conditions are convex hull problems and are solved through an optimization algorithm. Then, the proposed criterion is used to discuss the problem of SO controller design of ship fin stabilizing systems with added disturbance and noise.

1. Introduction

A Static Output (SO) feedback structure is a realistic and straightforward control method for stabilizing systems. Generally, the states of a dynamical state–space system do not possess measurable signals during operating processes. In [1,2,3], the SO feedback scheme was applied to discuss the controller synthesis problem of nonlinear systems via the Takagi–Sugeno (T-S) fuzzy model. Moreover, based on the T-S fuzzy model [4,5], the nonlinear control problems can also be discussed via linear theories to guarantee stability. Most control problems of nonlinear systems have usually been discussed and investigated using the Lyapunov function [1] for guaranteeing stability. Furthermore, the Parallel Distributed Compensation (PDC) concept was proposed by [6] to establish the corresponding fuzzy controller. Regarding the structure of the T-S fuzzy model, the PDC-based fuzzy controller is established by blending several sub-controllers that are designed for the corresponding linear sub-system and the same membership function, which is same as that of the fuzzy model. The literature [6] shows the successful case of using the PDC concept to extensively design fuzzy controllers for nonlinear systems. Nevertheless, during stability analysis, the SO control problem is more difficult to solve than the regular feedback control problem in using the convex optimization algorithm. Especially, it is more difficult to convert the sufficient condition [7,8] for the SO control problem to Linear Matrix Inequality (LMI) problems [9]. It is generally known that the calculation process of the convex optimization algorithm requires the LMI form described by a convex hull. To obtain this form, several technologies and inequalities [4,5,8,10] have been employed by ignoring some natural relaxations. However, the algorithm is a popular and effective tool to solve the control problem. And the recent works [4,5,10,11,12] still applied the convex optimization algorithm to discuss the control problems they considered. In [7,11,12], an extra algorithm was provided in solving the SO control problem via iterative calculations. It is well known that those equalities and extra algorithms cause some conservatism in discussing the Static Output control problem. Therefore, an effective and relaxed SO feedback controller design method is an issue of interest by investigating the realistic stabilization problems of nonlinear systems.

In existing works, numerous technologies have been proposed to reduce the conservatism of SO stability criteria. In accordance with the structure of the T-S fuzzy model, the Lyapunov function with a parameter-dependent structure [12,13,14] was provided to reduce the conservatism of stability analysis. In that Lyapunov function, the number matrices representing the weighting of system energy is dependent on the number of fuzzy rules. Based on [13,14], the Lyapunov function in the parameter-dependent case provides a less conservative result than the regular case in analyzing the stability of T-S fuzzy models. However, a latent conservatism in the parameter-dependent Lyapunov function is brought by the derivative term in the membership function. To avoid the conservatism, a Lyapunov function constructed using the line-integral concept was developed by [15] for eliminating the derivative membership function during the stability analysis. Referring to [16,17,18,19], some diagonal matrices and an off-diagonal matrix are required for forming the positive definite matrices in the line-integral Lyapunov function owing to the path-independent property. Because of the unique structure of positive definite matrices, the difficulty of obtaining LMI conditions is increased. Referring to [17], an iterative LMI algorithm was provided to find feasible solutions separately. Although the iterative LMI algorithm offers a solution to solve the bilinear matrix inequality problem, some necessary initial scalars are strictly required and set to increase the solvability of the sufficient conditions. Therefore, a practical and straightforward criterion derived by using the line-integral Lyapunov function is necessary to design an SO feedback controller.

Stochastic behavior naturally appears in the real environment due to unmeasured and unpredicted signals. In most existing control results, this stochastic behavior is usually ignored or represented as an external disturbance. However, the property of stochastic behavior is unpredictability. In [20,21], a stochastic differential equation was proposed to describe stochastic systems. The works in the literature [22,23,24] have discussed the control problems of stochastic systems. A nonlinear stochastic system represented by the T-S fuzzy model was widely applied to discuss their stability analysis and controller synthesis. In [22], the authors described the stochastic behavior using a differential equation that consisted of an ordinary differential equation and a term with multiplicative noise [21,22]. Brownian motion builds the multiplicative noise term [21] and states. On the other hand, the root-mean-square concept is always applied to discuss the stability of stochastic systems because of their unpredictability [22]. Moreover, the Itô formula [24] is required to manifest the unpredicted energy caused by stochastic behavior and to analyze the time-derivative trend. Furthermore, the attenuation of the T-S fuzzy model with multiplicative noise was investigated by [25,26] for achieving passivity. Referring to [27], the passivity can be reduced through methods such as positive theory, $H_2$ control, $H_{\infty }$ control, and passivity. Studying the existing results, only a few works have investigated and researched the SO control result in nonlinear stochastic systems. Thus, it is an exciting issue and is considered in this paper.

Inspired by the above illustrations, the SO feedback stability criterion of nonlinear stochastic systems is proposed in this paper through the T-S fuzzy model and the stochastic differential equation. And the PDC concept is employed to establish the SO feedback controller such that the stability is guaranteed in the mean square. For the goal, the Lyapunov function in the line-integral case is chosen and the Itô formula is used to find some sufficient conditions while avoiding the term of the derivative membership function. According to the convex optimization algorithm, sufficient LMI conditions are required to build the stability criterion. Moreover, the passivity is also considered to include several levels of attenuation. Finally, the disturbed ship fin stabilizing stochastic system is applied to verify the proposed stability criterion.

The structure of this paper is as follows: Section 2 provides the control problem of the considered T-S fuzzy model. In Section 3, a stability criterion is proposed to guarantee stability and passivity in the mean square. In Section 4, the numerical simulation result is presented. Some conclusions are given in Section 5.

$I$ denotes the identity matrix, $E\{·\}$ denotes the expected value of $·$, and $\ast$ denotes the symmetric parts in the block matrix.

2. System Description and Problem Formulations

In this section, a T-S fuzzy stochastic system with external disturbance is presented as follows:

If $x_1\left(t\right)$ is $M_1^{\alpha i1}$ and $x_2\left(t\right)$ is $M_2^{\alpha i2}$ and … and $x_n\left(t\right)$ is $M_n^{\alpha in}$, then

$$dx\left(t\right)=\left({\mathbf{A}}_{i}x\left(t\right)+{\mathbf{B}}_{i}u\left(t\right)+{\mathbf{U}}_{i}v\left(t\right)\right)dt+\left({\overline{\mathbf{A}}}_{i}x\left(t\right)+{\overline{\mathbf{B}}}_{i}u\left(t\right)+{\overline{\mathbf{U}}}_{i}v\left(t\right)\right)d\beta \left(t\right)$$

(1)

$$y\left(t\right)={\mathbf{C}}_{1i}x\left(t\right)$$

(2)

$$z\left(t\right)={\mathbf{C}}_{2i}x\left(t\right)+{\mathbf{D}}_{i}v\left(t\right)$$

(3)

where $x^T\left(t\right)\in {\mathbb{R}}^n$, $u^T\left(t\right)\in {\mathbb{R}}^m$, $y\left(t\right)\in {\mathbb{R}}^q$, $z\left(t\right)\in {\mathbb{R}}^r$, and $v\left(t\right)\in {\mathbb{R}}^s$ are the vectors of the state, control input, measured output, output, and external disturbance, respectively. The fuzzy set is set by $M_n^{\alpha ij}$ for the fuzzy rule as $i=\mathrm{1,2},\dots ,N$. The $x_j$-based fuzzy set on the i-th fuzzy rule is denoted as ${\alpha }_{ij}$. $\beta \left(t\right)$ is a scalar Brownian motion [21] with independent increment properties. ${\mathbf{A}}_i$, ${\mathbf{B}}_i$, ${\mathbf{U}}_i$, ${\overline{\mathbf{A}}}_i$, ${\overline{\mathbf{B}}}_i$, ${\overline{\mathbf{U}}}_i$, ${\mathbf{C}}_{1i}$, ${\mathbf{C}}_{2i}$, and ${\mathbf{D}}_i$ are constant matrices with compatible dimensions. Referring to [26], the nonlinear stochastic system described by (1) is also called the Itô form. The form can also be converted into a general engineering description [26] as a normal differential equation. However, in the engineering description, the term $d\beta \left(t\right)$ is changed as $d\beta \left(t\right)/dt=\dot{\beta }\left(t\right)$, which is the zero-mean-square noise with a variance of one. To fit in with the used formula, the Itô form for the stochastic system is used in this paper. Thus, the system in (1)–(3) can be further shown as follows:

$$dx\left(t\right)={\sum }_{i=1}^N{h}_i\left(t\right)\left\{\left({\mathbf{A}}_{i}x\left(t\right)+{\mathbf{B}}_{i}u\left(t\right)+{\mathbf{U}}_{i}v\left(t\right)\right)dt+\left({\overline{\mathbf{A}}}_{i}x\left(t\right)+{\overline{\mathbf{B}}}_{i}u\left(t\right)+{\overline{\mathbf{U}}}_{i}v\left(t\right)\right)d\beta \left(t\right)\right\}$$

(4)

$$y\left(t\right)={\sum }_{i=1}^N{h}_i\left(t\right){\mathbf{C}}_{1i}x\left(t\right)$$

(5)

$$z\left(t\right)=\sum _{i=1}^N{h}_i\left(t\right)\left\{{\mathbf{C}}_{2i}x\left(t\right)+{\mathbf{D}}_{i}v\left(t\right)\right\}$$

(6)

where ${\mu }_j^{{\alpha }_{ij}}\left(x_j\left(t\right)\right)=\frac{{\mu }_j^{{\alpha }_{ij}}\left(x\left(t\right)\right)}{{\sum }_{i=1}^N{\mu }_j^{{\alpha }_{ij}}\left(x\left(t\right)\right)}$, $h_i\left(t\right)={\prod }_{j=1}^n{\mu }_j^{\alpha ij}\left(x_j\left(t\right)\right)$, $0\le h_i\left(t\right)\le 1$, and ${\sum }_{i=1}^N{h}_i\left(t\right)=1$. For simplification, $x\left(t\right)\triangleq x$, $u\left(t\right)\triangleq u$, $y\left(t\right)\triangleq y$, $z\left(t\right)\triangleq z$, $v\left(t\right)\triangleq v$, $\beta \left(t\right)\triangleq \beta$, and $h_i\left(t\right)\triangleq h_i$.

With the same membership function, the following PDC-based SO fuzzy controller is provided for the system in (4)–(6).

If $x_1$ is $M_1^{\alpha i1}$, $x_2$ is $M_2^{\alpha i2}$, …, and $x_n$ is $M_n^{\alpha in}$, then

$$u=-{\mathbf{F}}_{i}y$$

(7)

or

$$u={\sum }_{i=1}^N{h}_i\left(-{\mathbf{F}}_{i}y\right)$$

(8)

According to the controller (8), one can easily infer the following closed-loop system from (4).

$$dx={\sum }_{i=1}^N{\sum }_{j=1}^N{\sum }_{k=1}^N{h}_i{h}_j{h}_k\left\{\left(\left({\mathbf{A}}_i-{\mathbf{B}}_i{\mathbf{F}}_j{\mathbf{C}}_{1k}\right)x+{\mathbf{U}}_{i}v\right)dt+\left(\left({\overline{\mathbf{A}}}_i-{\overline{\mathbf{B}}}_i{\mathbf{F}}_j{\mathbf{C}}_{1k}\right)x+{\overline{\mathbf{U}}}_{i}v\right)d\beta \right\}$$

$$={\sum }_{i=1}^N{\sum }_{j=1}^N{\sum }_{k=1}^N{h}_i{h}_j{h}_k\left\{\left({\mathbf{R}}_{ijk}x+{\mathbf{U}}_{i}v\right)dt+\left({\overline{\mathbf{R}}}_{ijk}x+{\overline{\mathbf{U}}}_{i}v\right)d\beta \right\}$$

(9)

where ${\mathbf{R}}_{ijk}={\mathbf{A}}_i-{\mathbf{B}}_i{\mathbf{F}}_j{\mathbf{C}}_{1k}$ and ${\overline{\mathbf{R}}}_{ijk}{=\overline{\mathbf{A}}}_i-{\overline{\mathbf{B}}}_i{\mathbf{F}}_j{\mathbf{C}}_{1k}$.

Remark 1.

In [18], the line-integral Lyapunov function was applied to develop the stability criterion for the stability in the mean square. However, the disturbance effect on the systems was not considered by [18]. To extend the result, passivity is used in this paper to guarantee the stability and attenuation of the nonlinear stochastic systems in the mean square.

Due to the stochastic behaviors, the case considered for stability is ensured by achieving the following definition.

Definition 1

([24]). For the solution of the closed-loop system, (9) is asymptotically stable in the mean square when $E\left\{x\right\}\to 0$ and $E\left\{x^{T}x\right\}\to 0$ as $t\to \infty$.

Definition 2

([26]). Given the matrices ${\mathit{S}}_1$, ${\mathit{S}}_2\ge 0$, and ${\mathit{S}}_3$, the system (9) is passive when the following inequality is satisfied by the disturbance $v$ and output $z$ in the terminal time $t_p>0$.

$$E\left\{2{\int }_0^{t_p}{z}^T{\mathbf{S}}_{1}vdt\right\}>E\left\{{\int }_0^{t_p}{z}^T{\mathbf{S}}_{2}zdt+{\int }_0^{t_p}{v}^T{\mathbf{S}}_{3}vdt\right\}$$

(10)

Through setting the different matrices as ${\mathit{S}}_1$, ${\mathit{S}}_2\ge 0$, and ${\mathit{S}}_3$, the passivity in (10) can be reduced to other cases for determining the kind of attenuation [27]. Furthermore, the following lemmas are applied to derive the sufficient conditions belonging to the LMI problem.

Lemma 1

([2]). For a positive definite matrix $\tilde{\mathit{R}}$, and matrices $\tilde{\mathit{A}}$ and $\tilde{\mathit{B}}$, the following inequality holds.

$${\tilde{\mathbf{A}}}^{\mathit{T}}\tilde{\mathbf{B}}+{\tilde{\mathbf{B}}}^{\mathit{T}}\tilde{\mathbf{A}}\le {\tilde{\mathbf{A}}}^{\mathit{T}}\tilde{\mathbf{R}}\tilde{\mathbf{A}}+{\tilde{\mathbf{B}}}^{\mathit{T}}{\tilde{\mathbf{R}}}^{-1}\tilde{\mathbf{B}}$$

(11)

Lemma 2

([2]). For a positive definite matrix $\tilde{\mathit{R}}$, the following inequality is held with a square matrix $\tilde{\mathit{X}}$ and a scalar $\alpha$.

$${\tilde{\mathbf{X}}}^T{\tilde{\mathbf{R}}}^{-1}\tilde{\mathbf{X}}\le {\alpha }^2\tilde{\mathbf{R}}\pm \alpha \tilde{\mathbf{X}}\pm \alpha {\tilde{\mathbf{X}}}^T$$

(12)

For the closed-loop system (9), the stability criterion is proposed in the next section to achieve the asymptotical stability and passivity in the mean square.

3. Passive Static Output Feedback Controller Design Method

The line-integral Lyapunov function and Itô formula are employed to derive the sufficient conditions in this section. According to the requirement of the convex optimization algorithm, the derived conditions are transferred into the LMI form.

Theorem 1.

With the given matrices ${\mathit{S}}_1$, ${\mathit{S}}_2\ge 0$, and ${\mathit{S}}_3$, if there exist feedback gains ${\mathit{F}}_i$ and positive definite matrix ${\tilde{\mathit{P}}}_i$ satisfying the following stability conditions, the asymptotical stability and passivity of closed-loop system (9) can be guaranteed in the mean square.

$$\left[\begin{array}{cc}{\mathsf{\Pi }}_1+{\overline{\mathbf{R}}}_{ijk}^T{\tilde{\mathbf{P}}}_i{\overline{\mathbf{R}}}_{ijk}& \mathit{*}\\ {\mathsf{\Pi }}_2& {\mathsf{\Pi }}_3\end{array}\right]+\coprod <0 \mathrm{f}\mathrm{o}\mathrm{r} i,j,k=1,2,\dots ,N$$

(13)

where $\coprod =\left[\begin{array}{cc}{\mathit{C}}_{2i}^T{\mathit{S}}_2{\mathit{C}}_{2i}& *\\ -{\mathit{S}}_1{\mathit{C}}_{2i}-{\mathit{D}}_i^T{\mathit{S}}_2{\mathit{C}}_{2i}& {\mathit{S}}_3-{\mathit{D}}_i^T{\mathit{S}}_1-{\mathit{S}}_1^T{\mathit{D}}_i+{\mathit{D}}_i^T{\mathit{S}}_1{\mathit{D}}_i\end{array}\right]$, ${\mathit{\Pi }}_3={\overline{\mathit{U}}}_i^T{\tilde{\mathit{P}}}_i{\overline{\mathit{U}}}_i$, ${\mathit{\Pi }}_1={\mathit{R}}_{ijk}^T{\tilde{\mathit{P}}}_i+{\tilde{\mathit{P}}}_i{\mathit{R}}_{ijk}$, ${\mathit{\Pi }}_2={\overline{\mathit{U}}}_i^T{\tilde{\mathit{P}}}_i+{\overline{\mathit{U}}}_i^T{\tilde{\mathit{P}}}_i{\overline{\mathit{R}}}_{ijk}$, ${\tilde{\mathit{P}}}_i=\overline{\mathit{P}}+{\mathit{W}}_i$, $\overline{\mathit{P}}=\left[\begin{array}{cccc}0& p_{12}& \cdots & p_{1n}\\ p_{12}& 0& \cdots & p_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ p_{1n}& p_{2n}& \cdots & 0\end{array}\right]$, and $\mathit{W}=\left[\begin{array}{cccc}{w}_{11}^{\alpha i1}& 0& \cdots & 0\\ 0& w_{22}^{\alpha i2}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & w_{nn}^{\alpha in}\end{array}\right]$.

Proof. 

The line-integral Lyapunov function, identical to [18], is chosen with the matrix ${\tilde{\mathbf{P}}}_i$ in this theorem. Using the Itô formula, the derivative along the trajectories of (9) is as follows:

$$dV\left(x\right)=LV\left(x\right)dt+2{\sum }_{i=1}^N{\sum }_{j=1}^N{\sum }_{k=1}^N{h}_i{h}_j{h}_k{x}^T\left\{\left({\tilde{\mathbf{P}}}_i{\overline{\mathbf{R}}}_{ijk}x+{\overline{\mathit{U}}}_{i}v\right)\right\}d\beta$$

(14)

where

$$\begin{gathered} LV\left(x\right)={\sum }_{i=1}^N{\sum }_{j=1}^N{\sum }_{k=1}^N{h}_i{h}_j{h}_k\left\{x^T\left({\mathbf{R}}_{ijk}^T{\tilde{\mathbf{P}}}_i+{\tilde{\mathbf{P}}}_i{\mathbf{R}}_{ijk}+{\overline{\mathbf{R}}}_{ijk}^T{\tilde{\mathbf{P}}}_i{\overline{\mathbf{R}}}_{ijk}\right)x\right.+ \\ \left.2x^T\left({\tilde{\mathbf{P}}}_i{\mathbf{U}}_i+{\overline{\mathbf{R}}}_{ijk}^T{\tilde{\mathbf{P}}}_i{\overline{\mathbf{U}}}_i\right)v+v^T{\overline{\mathbf{U}}}_i^T{\tilde{\mathbf{P}}}_i{\overline{\mathbf{U}}}_{i}v\right\} \end{gathered}$$

(15)

Since the independent increment property, the following equation is held by taking the expectation of (14).

$$E\left\{dV\left(x\right)\right\}=E\left\{LV\left(x\right)dt\right\}$$

(16)

Through arranging (16), the following equation is obtained.

$$E\left\{LV\left(x\right)dt\right\}={\sum }_{i=1}^N{\sum }_{j=1}^N{\sum }_{k=1}^N{h}_i{h}_j{h}_k\left[\begin{array}{c}{x}^T\\ v^T\end{array}\right]\left[\begin{array}{cc}{\mathsf{\Pi }}_1+{\overline{\mathbf{R}}}_{ijk}^T{\tilde{\mathbf{P}}}_i{\overline{\mathbf{R}}}_{ijk}& \mathit{*}\\ {\mathsf{\Pi }}_2& {\mathsf{\Pi }}_3\end{array}\right]\left[\begin{array}{c}x\\ v\end{array}\right]$$

(17)

Assuming $x\left(0\right)=0$, the following relationship is defined to discuss the disturbance effect on the system.

$$\begin{gathered} \mathsf{\Gamma }\left(x,v,t\right)=E\left\{{\int }_0^{t_p}{z}^T{\mathbf{S}}_{2}z+v^T{\mathbf{S}}_{3}v-2z^T{\mathbf{S}}_{1}vdt\right\} \\ =E\left\{{\int }_0^{t_p}{z}^T{\mathbf{S}}_{2}z+v^T{\mathbf{S}}_{3}v-2z^T{\mathbf{S}}_{1}v+LV\left(x\right)dt\right\}-V\left(x\left(t_p\right)\right) \\ \le E\left\{{\int }_0^{t_p}{z}^T{\mathbf{S}}_{2}z+v^T{\mathbf{S}}_{3}v-2z^T{\mathbf{S}}_{1}v+LV\left(x\right)dt\right\} \end{gathered}$$

$$=E\left\{{\int }_0^{t_p}\Phi \left(x,v,t\right)dt\right\}$$

(18)

in which $\mathsf{\Phi }\left(x,v,t\right)=z^T{\mathbf{S}}_{2}z+v^T{\mathbf{S}}_{3}v-2z^T{\mathbf{S}}_{1}v+LV\left(x\right)$.

With (17), we have the following equation from (18).

$$\mathsf{\Phi }\left(x,v,t\right)={\sum }_{i=1}^N{\sum }_{j=1}^N{\sum }_{k=1}^N{h}_i{h}_j{h}_k\left[\begin{array}{c}{x}^T\\ v^T\end{array}\right]\left(\left[\begin{array}{cc}{\mathsf{\Pi }}_1+{\overline{\mathbf{R}}}_{ijk}^T{\tilde{\mathbf{P}}}_i{\overline{\mathbf{R}}}_{ijk}& \mathit{*}\\ {\mathsf{\Pi }}_2& {\mathsf{\Pi }}_3\end{array}\right]+\coprod \right)\left[\begin{array}{c}x\\ v\end{array}\right]$$

(19)

If (15) holds, then $\mathsf{\Phi }\left(x,v,t\right)<0$ can be implied from (19). Also, the following inequalities can be inferred from (16) according to $\mathsf{\Phi }\left(x,v,t\right)<0$.

$$\mathsf{\Gamma }\left(x,v,t\right)<0$$

(20)

or

$$E\left\{2{\int }_0^{t_p}{z}^T{\mathbf{S}}_{1}vdt\right\}>E\left\{{\int }_0^{t_p}{z}^T{\mathbf{S}}_{2}zdt+{\int }_0^{t_p}{v}^T{\mathbf{S}}_{3}vdt\right\}$$

(21)

Since (21) is equal to (10), the closed-loop system (9) is passive in the mean square. In addition, the stability of the system is necessarily verified. Because (13) holds, $\mathsf{\Phi }\left(x,v,t\right)<0$ is guaranteed from (19). By assuming $v=0$, one has

$$E\left\{LV\left(x\left(t\right)\right)dt\right\}<{-\mathbf{C}}_{2i}^T{\mathbf{S}}_2{\mathbf{C}}_{2i}$$

(22)

Since ${\mathbf{S}}_2\ge 0$ and (22), the negativity of $E\left\{LV\left(x\left(t\right)\right)dt\right\}$ is easily found such that

$$E\left\{dV\left(x\left(t\right)\right)\right\}=E\left\{LV\left(x\left(t\right)\right)dt\right\}<0$$

(23)

Thus, the asymptotical stability of the closed-loop system (9) can be guaranteed by satisfying Definition 1 with $E\left\{dV\left(x\left(t\right)\right)\right\}<0$. The proof of Theorem 1 is completed. □

In Theorem 1, the asymptotical stability and passivity of the system (9) are achieved by holding the condition (13). However, the combination of variables shows the bilinear problems in (13). Therefore, the following theorem provides the LMI condition converted from (13) to find the feasible solutions.

Theorem 2.

With the given matrices ${\mathit{S}}_1$, ${\mathit{S}}_2\ge 0$, and ${\mathit{S}}_3$, and scalar $\alpha$, the system (9) is asymptotically stable and passive in the mean square if there exist the matrices $\mathit{M}$ and ${\mathit{N}}_j$, and the positive definite matrices ${\tilde{\mathit{P}}}_i$, ${\mathit{R}}_1$, ${\mathit{R}}_2$, and ${\mathit{R}}_3$ such that

$$\left[\begin{array}{ccc}{\mathsf{\Psi }}_{11}+\coprod ^{~}& \mathit{*}& \mathit{*}\\ {\mathsf{\Psi }}_{21}& -{\mathsf{\Psi }}_{22}& \mathit{*}\\ {\mathsf{\Psi }}_{31}& 0& {-\mathsf{\Psi }}_{33}\end{array}\right]<0$$

(24)

where ${\mathit{\Psi }}_{11}=\left[\begin{array}{ccc}{\tilde{\mathit{\Psi }}}_1& *& *\\ {\tilde{\mathit{\Psi }}}_2& {\prod }_3& *\\ {{\tilde{\mathit{P}}}_i\mathit{A}}_i-{\mathit{B}}_i{\mathit{N}}_j{\mathit{C}}_{1k}& 0& -{\tilde{\mathit{P}}}_i\end{array}\right]$, $\coprod ^{~}=\left[\begin{array}{cc}\coprod & *\\ 0& 0\end{array}\right]$, ${\mathit{\Psi }}_{22}=\left[\begin{array}{ccc}{\mathit{R}}_1& *& *\\ 0& {\mathit{R}}_2& *\\ 0& 0& {\mathit{R}}_3\end{array}\right]$, ${\mathit{\Psi }}_{22}=\left[\begin{array}{ccc}{\mathit{N}}_j{\mathit{C}}_{1i}& 0& 0\\ {\mathit{N}}_j{\mathit{C}}_{1i}& 0& 0\\ {\mathit{N}}_j{\mathit{C}}_{1i}& 0& 0\end{array}\right]$, ${\mathit{\Psi }}_{31}=\left[\begin{array}{ccc}{\left({\tilde{\mathit{P}}}_i{\mathit{B}}_i-{\mathit{B}}_i\mathit{M}\right)}^T& *& *\\ 0& {\left({\tilde{\mathit{P}}}_i{\overline{\mathit{B}}}_i-{\overline{\mathit{B}}}_i\mathit{M}\right)}^T{\overline{\mathit{U}}}_k& *\\ 0& 0& {\left({\tilde{\mathit{P}}}_i{\mathit{B}}_i-{\mathit{B}}_i\mathit{M}\right)}^T\end{array}\right]$, ${\mathit{\Psi }}_{33}=\left[\begin{array}{ccc}-{\alpha }^2{\mathit{R}}_1+\alpha \mathit{M}+\alpha {\mathit{M}}^T& *& *\\ 0& -{\alpha }^2{\mathit{R}}_2+\alpha \mathit{M}+\alpha {\mathit{M}}^T& *\\ 0& 0& -{\alpha }^2{\mathit{R}}_3+\alpha \mathit{M}+\alpha {\mathit{M}}^T\end{array}\right],$ ${\tilde{\mathit{\Psi }}}_1={{\tilde{\mathit{P}}}_i\mathit{A}}_i-{\mathit{B}}_i{\mathit{N}}_j{\mathit{C}}_{1k}+{\left({{\tilde{\mathit{P}}}_i\mathit{A}}_i-{\mathit{B}}_i{\mathit{N}}_j{\mathit{C}}_{1k}\right)}^T$, and ${\tilde{\mathit{\Psi }}}_2={\mathit{U}}_i^T{\tilde{\mathit{P}}}_i+{\overline{\mathit{U}}}_i^T{\tilde{\mathit{P}}}_i{\overline{\mathit{A}}}_i-{\overline{\mathit{U}}}_i^T{\overline{\mathit{B}}}_i{\mathit{N}}_j{\mathit{C}}_{1k}$.

Proof. 

The following inequality is inferred by using Lemma 2 on ${\mathsf{\Psi }}_{33}$ in (24).

$${-\overline{\mathsf{\Psi }}}_{33}\le {-\mathsf{\Psi }}_{33}$$

(25)

where ${\overline{\mathsf{\Psi }}}_{33}=\left[\begin{array}{ccc}{\mathbf{M}}^T{\mathbf{R}}_1^{-1}\mathbf{M}& \mathit{*}& \mathit{*}\\ 0& {\mathbf{M}}^T{\mathbf{R}}_2^{-1}\mathbf{M}& \mathit{*}\\ 0& 0& {\mathbf{M}}^T{\mathbf{R}}_3^{-1}\mathbf{M}\end{array}\right]$. According to (24) and (25), the following inequality can be held.

$$\left[\begin{array}{ccc}{\mathsf{\Psi }}_{11}+\coprod ^{~}& \mathit{*}& \mathit{*}\\ {\mathsf{\Psi }}_{21}& -{\mathsf{\Psi }}_{22}& \mathit{*}\\ {\mathsf{\Psi }}_{31}& 0& {-\overline{\mathsf{\Psi }}}_{33}\end{array}\right]<0$$

(26)

Applying the Schur complement to (26), one has

$${\mathsf{\Psi }}_{11}+\coprod ^{~}+{{\mathsf{\Psi }}_{21}^T{\mathsf{\Psi }}_{22}^{-1}\mathsf{\Psi }}_{21}+{{\mathsf{\Psi }}_{31}^T{\overline{\mathsf{\Psi }}}_{33}^{-1}\mathsf{\Psi }}_{31}<0$$

(27)

Setting ${\mathbf{F}}_i=-{\mathbf{M}}^{-1}{\mathbf{N}}_i$, one can find the following relationship.

$${{\mathsf{\Psi }}_{21}^T{\mathsf{\Psi }}_{22}^{-1}\mathsf{\Psi }}_{21}={{\tilde{\mathsf{\Psi }}}_{21}^T{{\mathbf{M}}^T\mathsf{\Psi }}_{22}^{-1}\mathbf{M}\tilde{\mathsf{\Psi }}}_{21}={{\tilde{\mathsf{\Psi }}}_{21}^T{\overline{\mathsf{\Psi }}}_{33}^{-1}\tilde{\mathsf{\Psi }}}_{21}$$

(28)

where ${\tilde{\mathsf{\Psi }}}_{21}=\left[\begin{array}{ccc}{-\mathbf{F}}_j{\mathbf{C}}_{1i}& 0& 0\\ {-\mathbf{F}}_j{\mathbf{C}}_{1i}& 0& 0\\ {-\mathbf{F}}_j{\mathbf{C}}_{1i}& 0& 0\end{array}\right]$.

With Lemma 1, the following inference is found by setting $\tilde{\mathbf{A}}={\mathsf{\Psi }}_{21}$, $\tilde{\mathbf{B}}={\tilde{\mathsf{\Psi }}}_{31}$, and $\tilde{\mathbf{R}}={\overline{\mathsf{\Psi }}}_{33}$.

$$\begin{gathered} {\tilde{\mathsf{\Psi }}}_{21}^T{\overline{\mathsf{\Psi }}}_{33}^{-1}{\tilde{\mathsf{\Psi }}}_{21}+{\mathsf{\Psi }}_{31}^T{\overline{\mathsf{\Psi }}}_{33}^{-1}{\mathsf{\Psi }}_{31}\ge {\tilde{\mathsf{\Psi }}}_{21}^T{\mathsf{\Psi }}_{31}+{\mathsf{\Psi }}_{31}^T{\tilde{\mathsf{\Psi }}}_{21}= \\ \left[\begin{array}{ccc}{-{\mathbf{C}}_{1i}^T{\mathbf{F}}_j^T\left({\tilde{\mathbf{P}}}_i{\mathbf{B}}_i-{\mathbf{B}}_i\mathbf{M}\right)}^T-\left({\tilde{\mathbf{P}}}_i{\mathbf{B}}_i-{\mathbf{B}}_i\mathbf{M}\right){\mathbf{F}}_j{\mathbf{C}}_{1i}& *& *\\ -{\overline{\mathbf{U}}}_k^T\left({\tilde{\mathbf{P}}}_i{\overline{\mathbf{B}}}_i-{\overline{\mathbf{B}}}_i\mathbf{M}\right){\mathbf{F}}_j{\mathbf{C}}_{1i}& 0& *\\ -\left({\tilde{\mathbf{P}}}_i{\mathbf{B}}_i-{\mathbf{B}}_i\mathbf{M}\right){\mathbf{F}}_j{\mathbf{C}}_{1i}& 0& 0\end{array}\right] \end{gathered}$$

(29)

According to (27) and (29), one can find the following equivalent inequalities.

$${\mathsf{\Psi }}_{11}+\coprod ^{~}+{\tilde{\mathsf{\Psi }}}_{21}^T{\mathsf{\Psi }}_{31}+{\mathsf{\Psi }}_{31}^T{\tilde{\mathsf{\Psi }}}_{21}<0$$

(30)

and

$${\tilde{\mathsf{\Psi }}}_{11}+\coprod ^{~}<0$$

(31)

where ${\tilde{\mathsf{\Psi }}}_{11}=\left[\begin{array}{ccc}{\mathsf{\Pi }}_1& \mathrm{*}& \mathrm{*}\\ {\mathsf{\Pi }}_2& {\mathsf{\Pi }}_3& \mathrm{*}\\ {\tilde{\mathbf{P}}}_i\left({\overline{\mathbf{A}}}_i-{\overline{\mathbf{B}}}_i{\mathbf{F}}_j{\mathbf{C}}_{1k}\right)& 0& {-\tilde{\mathbf{P}}}_i^{-1}\end{array}\right]$.

Applying the Schur complement to (31), one has

$$\left[\begin{array}{cc}{\mathsf{\Pi }}_1+{\overline{\mathbf{R}}}_{ijk}^T{\tilde{\mathbf{P}}}_i{\overline{\mathbf{R}}}_{ijk}& \mathit{*}\\ {\mathsf{\Pi }}_2& {\mathsf{\Pi }}_3\end{array}\right]+\coprod <0$$

(32)

Comparing with (13) and (32), the solutions are obviously realized in (24) satisfying condition (13) in Theorem 1. The proof of Theorem 2 is completed. □

Based on Theorem 2, the gain to build the SO feedback controller (8) can be obtained using the convex optimization algorithm to guarantee the asymptotical stability and passivity of (9) in the mean square.

4. Numerical Example

In this section, the SO control problem of a ship fin stabilizing system is discussed using the proposed stability criterion. Considering a sea wave causing the ship’s rolling motion, the sea waves’ main energy centralizes at a low frequency via spectrum theory. For the rolling damp and resilient moments, the nonlinearity of the ship fin stabilizing system is described in [28]. Using the modeling approach, one can find the corresponding T-S fuzzy model as follows:

$$dx={\sum }_{i=1}^9{h}_i\left\{\left({\mathbf{A}}_{i}x+\mathbf{B}u+\mathbf{U}v\right)dt+\left({\overline{\mathbf{A}}}_{i}x+\overline{\mathbf{B}}u+\overline{\mathbf{U}}v\right)d\beta \right\}$$

(33)

$$y={\mathbf{C}}_{1}x$$

(34)

$$z={\mathbf{C}}_{2}x+\mathbf{D}v$$

(35)

where ${\mathbf{A}}_1=\left[\begin{array}{cc}0& 1\\ -0.4874& -0.185\end{array}\right]$, ${\mathbf{A}}_2=\left[\begin{array}{cc}0& 1\\ -0.5073& -0.185\end{array}\right]$, ${\mathbf{A}}_3=\left[\begin{array}{cc}0& 1\\ -0.5272& -0.185\end{array}\right]$, ${\mathbf{A}}_4=\left[\begin{array}{cc}0& 1\\ -0.4874& -0.225\end{array}\right]$, ${\mathbf{A}}_5=\left[\begin{array}{cc}0& 1\\ -0.5073& -0.225\end{array}\right]$, ${\mathbf{A}}_6=\left[\begin{array}{cc}0& 1\\ -0.5272& -0.225\end{array}\right]$, $\mathbf{U}=\left[\begin{array}{c}0.1\\ 0\end{array}\right]$, ${\mathbf{A}}_7=\left[\begin{array}{cc}0& 1\\ -0.4874& -0.265\end{array}\right]$, ${\mathbf{A}}_8=\left[\begin{array}{cc}0& 1\\ -0.5073& -0.265\end{array}\right]$, ${\mathbf{A}}_9=\left[\begin{array}{cc}0& 1\\ -0.8272& -0.265\end{array}\right]$, $\overline{\mathbf{U}}=0.01\mathbf{U}$, $\mathbf{B}=\left[\begin{array}{c}0\\ 2.9084\end{array}\right]\times {10}^{-7},{\mathbf{C}}_1=\left[\begin{array}{cc}1& 0\end{array}\right],{\mathbf{C}}_2=\left[\begin{array}{cc}1& 0\end{array}\right]$, ${\overline{\mathbf{A}}}_i=0.01{\mathbf{A}}_i$, and $\overline{\mathbf{B}}=0.01\mathbf{B}$.

The membership functions for $x_1$ and $x_2$ are, respectively, shown in Figure 1 and Figure 2. $v$ is chosen as the zero mean white noise with a variance of 0.1. With the given $\alpha =0.1$ and setting the strict input passivity as ${\mathbf{S}}_1=\mathbf{I}$, ${\mathbf{S}}_2=0$, and ${\mathbf{S}}_3=\mathbf{I}$, the following feasible solutions are obtained by solving Theorem 2.

${\tilde{\mathbf{P}}}_1=\left[\begin{array}{cc}30.3856& 3.3195\\ 3.3195& 36.972\end{array}\right]$, ${\tilde{\mathbf{P}}}_2=\left[\begin{array}{cc}30.273& 3.3195\\ 3.3195& 36.9714\end{array}\right]$, ${\tilde{\mathbf{P}}}_3=\left[\begin{array}{cc}30.1605& 3.3195\\ 3.3195& 36.9708\end{array}\right]$, ${\tilde{\mathbf{P}}}_4=\left[\begin{array}{cc}30.3857& 3.3195\\ 3.3195& 35.0985\end{array}\right]$, ${\tilde{\mathbf{P}}}_5=\left[\begin{array}{cc}30.273& 3.3195\\ 3.3195& 36.9714\end{array}\right]$, ${\tilde{\mathbf{P}}}_6=\left[\begin{array}{cc}30.1605& 3.3195\\ 3.3195& 36.0974\end{array}\right]$, ${\tilde{\mathbf{P}}}_7=\left[\begin{array}{cc}30.3854& 3.3195\\ 3.3195& 33.2341\end{array}\right]$, ${\tilde{\mathbf{P}}}_8=\left[\begin{array}{cc}30.2728& 3.3195\\ 3.3195& 33.2336\end{array}\right]$, ${\tilde{\mathbf{P}}}_9=\left[\begin{array}{cc}30.1602& 3.3195\\ 3.3195& 33.2331\end{array}\right]$, ${\mathbf{F}}_1=3.3725\times {10}^5$, ${\mathbf{F}}_2=3.1251\times {10}^5$, ${\mathbf{F}}_3=2.8778\times {10}^5$, ${\mathbf{F}}_4=3.6002\times {10}^5$, ${\mathbf{F}}_5=3.3637\times {10}^5$, ${\mathbf{F}}_6=3.1272\times {10}^5$, ${\mathbf{F}}_7=3.8264\times {10}^5$, ${\mathbf{F}}_8=3.6007\times {10}^5$, ${\mathbf{F}}_9=3.375\times {10}^5$, $\mathbf{M}=117.8598$, and ${\mathbf{R}}_1={\mathbf{R}}_2={\mathbf{R}}_3=23.3386$.

Furthermore, the following PDC-based SO controller can be established via the obtained gains.

$$u={\sum }_{i=1}^9{h}_i\left(-{\mathbf{F}}_{i}y\right)$$

(36)

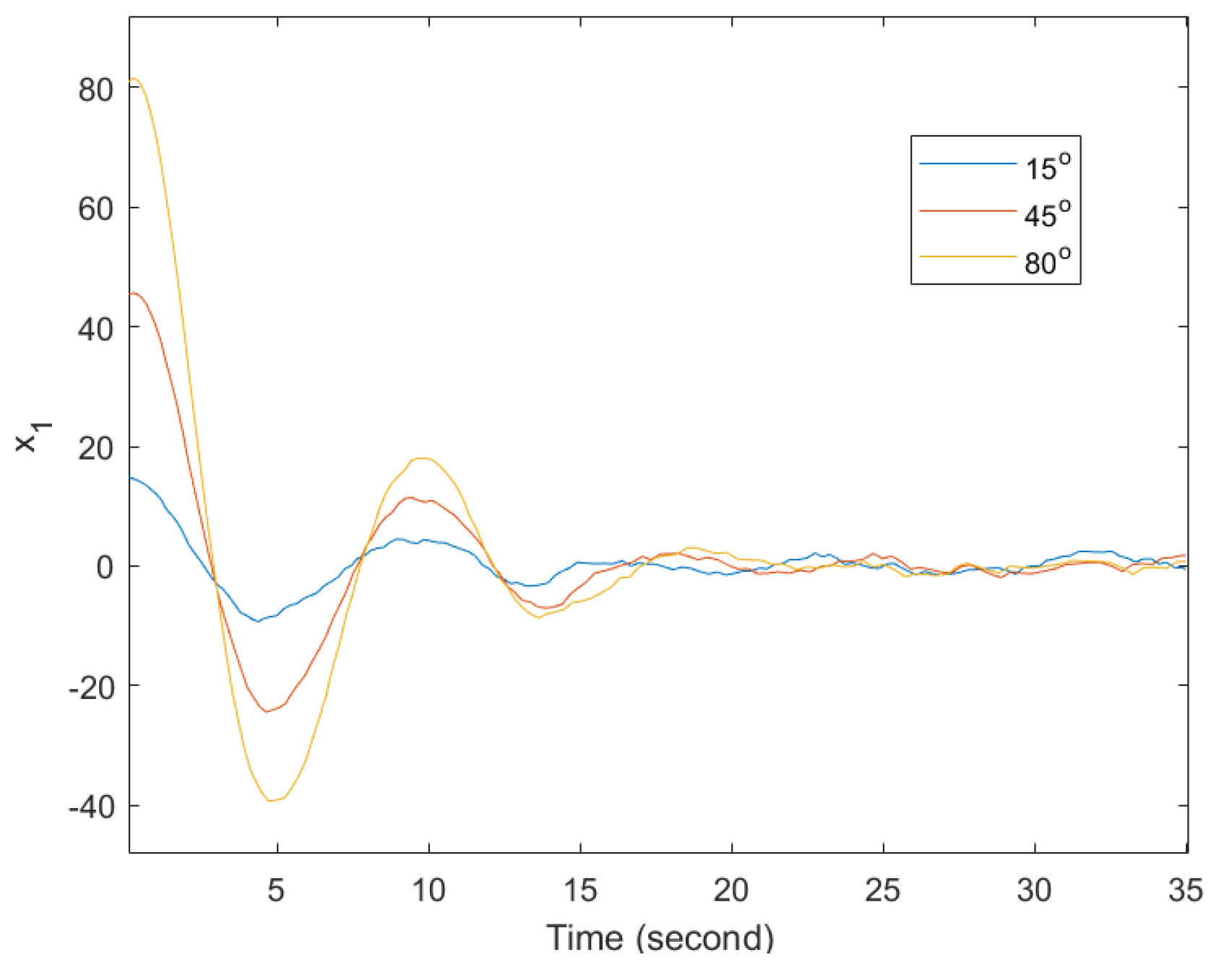
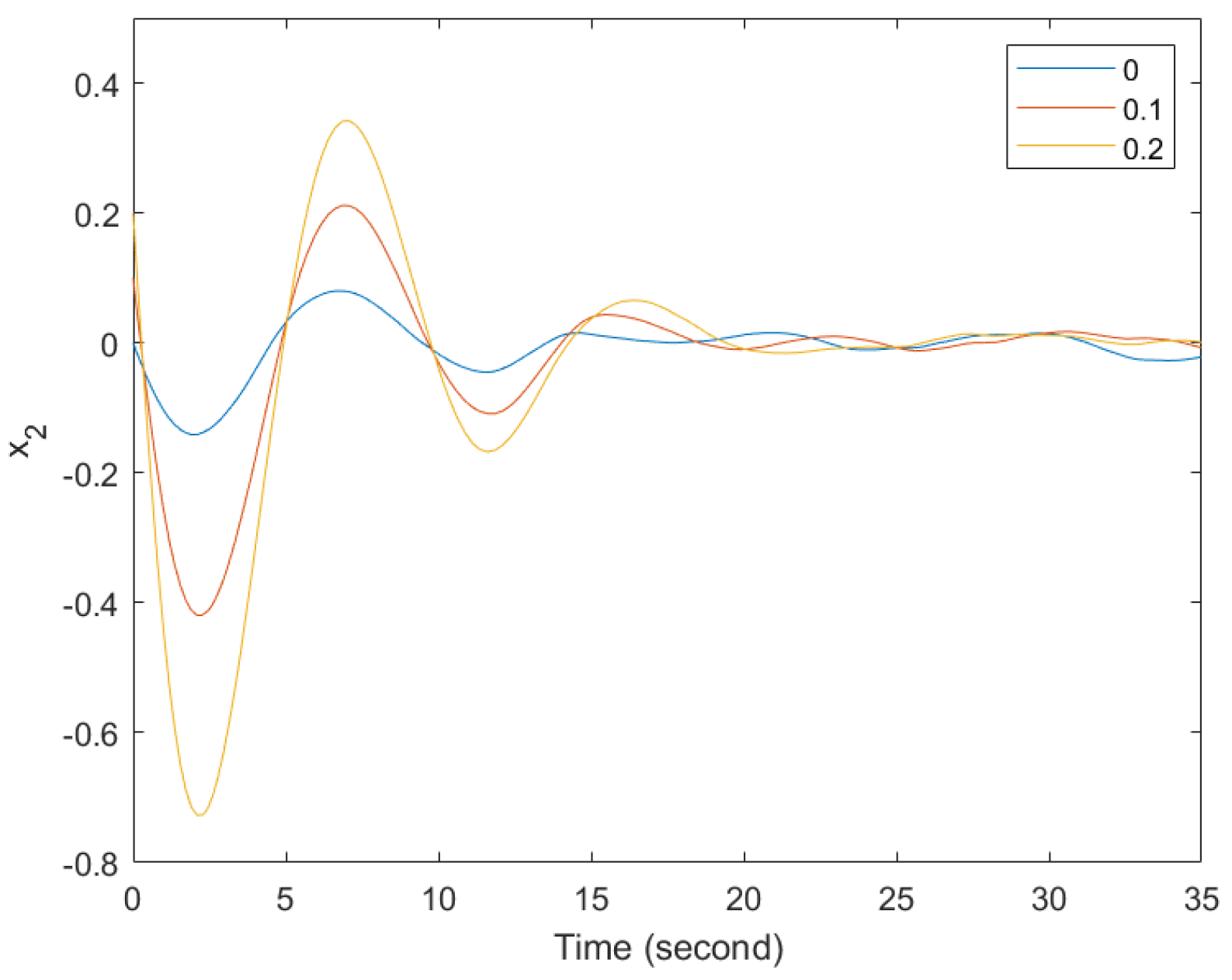
With the controller (36), the responses of the system (33) are stated in Figure 3 and Figure 4 with $x^T\left(0\right)=\left[\begin{array}{cc}15°& 0\end{array}\right]$, $x^T\left(0\right)=\left[\begin{array}{cc}45°& 0.1\end{array}\right]$, and $x^T\left(0\right)=\left[\begin{array}{cc}80°& 0.2\end{array}\right]$. From those results in the figures, the states converge to zero when time goes to infinity. According to Definition 1, the asymptotical stability of system (33) is achieved in the mean square. In addition, the following equation is given by introducing the simulated result to check the satisfaction of strict input passivity.

$$\frac{E\left\{2{\int }_0^{40}{z}^{T}vdt\right\}}{E\left\{{\int }_0^{40}{v}^{T}vdt\right\}}=2.001$$

(37)

The ratio value of (37) is larger than one; it is easily found that Definition 2 is satisfied. Therefore, the ship fin stabilizing system with the multiplicative noises achieves asymptotical stability and the strict input passivity constraint in the mean square using the designed SO controller.

Showing the robustness of the T-S fuzzy model, the other initial conditions of $x^T\left(0\right)=\left[\begin{array}{cc}15°& 0\end{array}\right]$, $x^T\left(0\right)=\left[\begin{array}{cc}45°& 0\end{array}\right]$, and $x^T\left(0\right)=\left[\begin{array}{cc}80°& 0\end{array}\right]$ are added to obtain the other simulation results in Figure 3 and Figure 4. From these result, it can be inferred that the different initial conditions influence the transient responses. However, the asymptotical stability of the closed-loop system is also guaranteed via the designed controller. And the effect of external disturbance on the system can be constrained by the controllers. Thus, the considered asymptotical stability and strict input passivity are also achieved via the designed SO fuzzy controller (36).

5. Conclusions

The SO control criterion for the disturbed nonlinear stochastic systems was provided to guarantee asymptotical stability and passivity. With the line-integral Lyapunov function, the term of the derivative membership function can be avoided when analyzing the stability. Based on the conversion technologies, the convex optimization algorithm can be applied to solve the sufficient conditions without extra iterations. Thus, the proposed design method is a simpler and more available solution to design the SO feedback controller for nonlinear stochastic systems. In the future, the proposed SO control technology will be applied to global dynamics analysis and control problems [29,30]. Furthermore, the novel topics of the finite-time L₂ control issue [31] and self-learning T-S fuzzy control problem [32] will be our topics of interest.