Statistical Beamforming for Multi-Set Space–Time Shift-Keying-Based Full-Duplex Millimeter Wave Communications

Abstract

Full-duplex (FD) communication has been shown to provide an increased achievable rate, while millimeter wave (mmWave) communications benefit from a large available bandwidth that further improves the achievable rate. On the other hand, the concept of multi-set space-time shift keying (MS-STSK) has been proposed to provide a flexible design trade-off between throughput and performance. Hence, in this work, we consider the design of an FD-aided MS-STSK transceiver for millimeter wave communications. However, a major challenge is that channel reciprocity is not valid in mmWave communications due to shorter channel coherence time. Thus, the uplink (UL) pilots cannot be utilized to estimate the downlink (DL) channel. To overcome this challenge, we propose a beamforming technique based on channel statistics without assuming channel reciprocity. For this purpose, a closed-form expression for the outage probability of the system is derived by employing the characterization of the ratio of the Indefinite Quadratic Form (IQF). The derived analytical expression is then utilized to design optimum beamforming weights using the Sequential Quadratic Programming (SQP)-based heuristic method. Moreover, an Iterative Statistical Method (ISM) of joint transmit and receive beamforming algorithm is also developed by utilizing Principle Eigenvector (PE) and Generalized Rayleigh Quotient (G-RQ) optimization techniques. Finally, we verify our simulation results with the theoretical analysis.

1. Introduction

Due to the increasing demand for larger data rates and lower latency, the next generation of wireless communication is looking for enhanced spectral efficiency with better latency performance [1]. Millimeter wave-based communications inherit a large available bandwidth ranging from 28 to 300 GHz and hence are capable of delivering higher data rates with larger coverage [2]. However, the performance of mmWave-based frequency systems is highly sensitive to atmospheric and weather conditions that result in higher propagation losses [2]. Hence, directional transmission is employed to mitigate the propagation losses, where large antenna arrays can be used for achieving beamforming gains [3,4].

Multiple-In-Multiple-Output (MIMO) systems have been shown to provide beneficial throughput and performance gains [5]. The concept of spatial modulation (SM) was proposed as a low-complexity MIMO design option for providing an improved performance versus complexity trade-off by potentially relying on a single RF chain [6,7]. Recently, the idea of space–time shift keying (STSK) was introduced to provide a more flexible transmission scheme versus conventional multiplexing gain design adjustments [8]. In STSK, the transmitting signal is spread over multiple time slots and transmit antennas using certain dispersion matrices. It was shown in [9] that the STSK scheme can improve the Bit Error Rate (BER) and throughput of the system. Additionally, the idea of STSK was further enhanced in [10] by incorporating both SM and STSK to come up with the method of multi-set STSK (MS-STSK). This scheme is capable of transmitting information by utilizing the indices of the complex-valued signal, the dispersion matrices, and the index of the antenna combination.

Despite the above advantages of the mmWave and the MS-STSK systems, the performance of these systems is highly affected by self-interference (SI). Therefore, in addition to the traditional SI suppression strategies, the SI cancellation relying on beamforming techniques is critical at mmWave frequency. On the other hand, the use of pilots increases the overhead, resulting in a lower spectral efficiency. This work aims to tackle these issues.

This paper is structured as follows. The literature review is presented in Section 2 after the introduction in Section 1. Next, the system model for the MS-STSK-based FD mmWave communication system is presented in Section 3. The derivation of outage probability is provided in Section 4. Our suggested statistical techniques for concurrently developing the transmit and receive beamformer weights are developed in Section 5. Simulation results are presented in Section 6. Finally, Section 7 provides concluding observations.

2. Literature Review

Due to the substantial self-interference that comes from the transmitter’s own transmission interfering with the received signal, the idea of simultaneous transmission and receiving in the same frequency band was deemed impracticable. However, it was shown in [11,12] that this is possible and it is termed full-duplex (FD) wireless communication. Hence, it can achieve twice the spectral efficiency in contrast to the conventional half-duplex communication, which was a great breakthrough [13,14,15].

Designing an FD mmWave communication system is a promising research direction for further improving the achievable rate as well as supporting a large number of users [16]. It was shown in [16] that careful beamforming design for FD mmWave systems can provide clear performance gains. Then, several works in the literature have been devoted to the design of transmit and receive beamforming techniques in FD and mmWave communication [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32]. A summary of these works with their approaches and shortcomings is provided in Table 1.

Table 1. Summary of Literature Review.

Task or Challenge	Approach and Assumptions	Shortcomings	Reference
Hybrid beamforming design for full-duplex mmWave communications	Constrained optimization approach using CSI	MSTSK is not considered Pilot transmission is required for estimating CSI	[16]
Frequency selective hybrid precoding in mmWave communications	Constrained optimization approach using CSI	MSTSK is not considered Receive beamforming is not considered Pilot transmission is required for estimating CSI	[17]
Transceiver design for full-duplex MIMO relay systems	Minimum Mean Square Error (MMSE) minimization using CSI	MSTSK is not considered Pilot transmission is required for estimating CSI	[18]
Hybrid beamforming for mmWave OFDM systems	Constrained optimization using CSI	FD is not considered MSTSK is not considered Pilot transmission is required for estimating CSI	[19]
Beamforming for full duplex mmWave communications	Throughput maximization with constrained optimization using CSI	MSTSK is not considered Pilot transmission is required for estimating CSI	[20,21,22,23]
Finite-Resolution Digital Beamforming for mmWave communications	Sum rate maximization with sum power constraints using CSI	MSTSK is not considered Pilot transmission is required for estimating CSI	[24]
Digital beamforming for mmWave communications	Hierarchical beamforming with codebook design using CSI Energy-efficiency optimization using CSI	FD is not considered MSTSK is not considered Pilot transmission is required for estimating CSI	[25,26,27,28,29,30,31,32]

2.1. Shortcomings in the Existing Works

The advantages of both the FD and the MSTSK techniques motivated us to deploy these at mmWaves in order to further enhance spectral efficiency. However, efficient beamforming in such a system has not been investigated in the existing works. Additionally, it is observed that most of the existing beamforming techniques are based on either perfect or imperfect Channel State Information (CSI) estimation requiring pilot transmission. This is usually completed with the assumption that channel reciprocity holds as long as the UL and the DL transmission occur within a channel’s coherence time. Thus, the base station (BS) can utilize that same CSI, which was obtained in UL transmission. However, the assumption of channel reciprocity is not valid in mmWave communications as the channel coherence time is very short [33], and thus, the UL CSI can not be utilized for the DL transmission. On the other hand, CSI estimation by the separate DL pilot transmission results in a larger overhead [34]. To overcome these challenges, we propose beamforming design relying only on channel statistics rather than requiring channel estimation using pilot transmissions and assuming channel reciprocity. Our major contributions are listed next.

2.2. Our Contributions and Paper Organization

The following are our work’s main contributions:

• With the aid of the IQF representation, we express the Signal-to-Interference Ratio (SINR) of the users’ signal at the BS of the MS-STSK-based FD mmWave communication system as the ratio of IQFs.
• We derive the outage probability expression for individual users in the MS-STSK-based FD mmWave communication system by utilizing the characterization of IQF ratio with the aid of conditional probability evaluation.
• We formulate a constrained optimization problem to design both transmit and receive beamforming weights in the MS-STSK-based FD mmWave communication system by minimizing the scalarized sum outage probability of the system while constraining the beamformer weights power to unity.
• We created two techniques to address the proposed constrained optimization problem: the first utilizes the SQP-based heuristic optimization technique and the second employs an iterative procedure of jointly designing the transmit and the receive beamforming algorithm with the aid of the PE and the G-RQ optimization techniques.

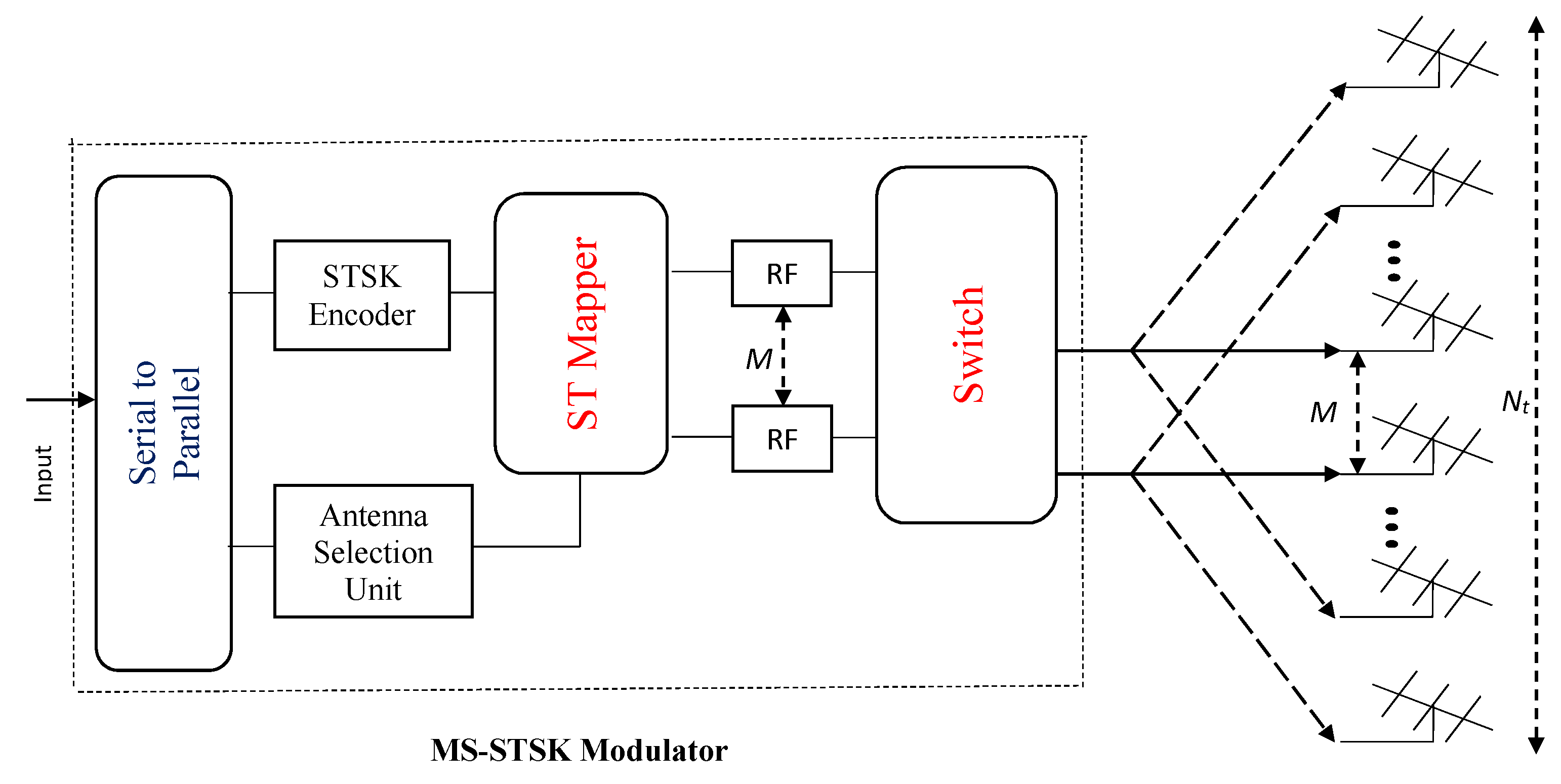
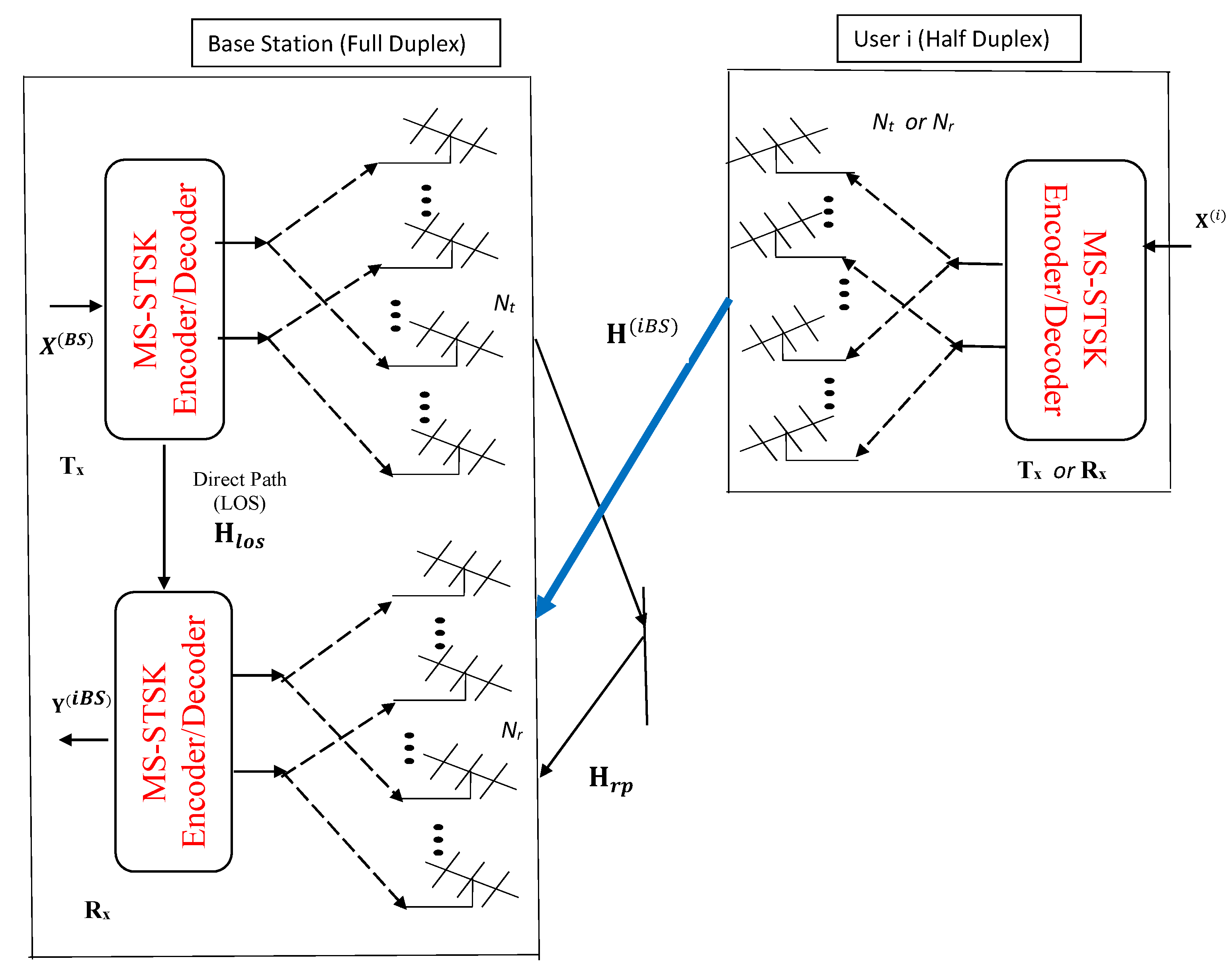
3. System Model

In this work, an FD MS-STSK-assisted BS communicating with multiple Half-Duplex (HD) users via a point-to-point link is considered as shown in Figure 1; that is, the BS is receiving signals from a single user only at a time. The BS is equipped with $N_t$ and $N_r$ antenna arrays (AAs) for the transmit mode and the receive mode, respectively. Each User Equipment (UE) is equipped with $N_r$ AAs (the number of transmitter AAs can be different for UEs, which can also be different from the number of receiver AAs at the BS. However, we kept the same AAs for simplicity of presentation, while all the proposed design is valid for variable AAs also), and each AA at the BS and the UE is equipped with K antenna elements (AEs). Moreover, there are M RF chains at the BS which are linked with M active AAs out of the total of $N_t$ available transmit AAs at any given time, as shown in Figure 1.

Figure 1. Block diagram of the MS-STSK modulator.

The BS is equipped with MS-STSK encoder/decoder which is utilized to map the input bit stream in order to form an MS-STSK codeword as illustrated in Figure 1. The complex-valued amplitude-phase modulation signal, the dispersion matrix, and the indexes of the activated transmit AAs are used to transmit the information in the input data (see [10] for further details). The codeword $\mathbf{X}$ transmitted for the $k^{th}$ APM symbol (denoted as $x_k$) by the MS-STSK encoder can be expressed as:

$$\mathbf{X}={\mathbf{A}}_{i,j}{x}_k,$$

(1)

where ${\mathbf{A}}_{i,j}$ is the $i^{th}$ dispersion matrix used for the $j^{th}$ transmit antenna combinations (AC).

After describing the MS-STSK system model employed at the BS, we consider the uplink signal, where a single HD UE communicates in a point-to-point link with the BS receiver using multiplexing-based MIMO transmission. Additionally, the BS is broadcasting and receiving simultaneously, since it is functioning in the FD mode, as indicated in Figure 2, which causes self-interference (SI). Thus, the received signal at the BS due to user i (denoted by ${\mathbf{Y}}^{\left(iBS\right)}$) of dimension $N_r\times T$ after combining with $K{N}_r\times N_r$ receive combiner matrix ${\mathbf{W}}^{\left(BS\right)}$ is given by

$$\begin{array}{ccc}\hfill {\mathbf{Y}}^{\left(iBS\right)}& =& \underset{\mathrm{desired}\mathrm{signal}}{\underbrace{{{\mathbf{W}}^{\left(BS\right)}}^H{\mathbf{H}}^{\left(iBS\right)}{\mathbf{F}}^{\left(i\right)}{\mathbf{X}}^{\left(i\right)}}}+\underset{\mathrm{self}-\mathrm{interference}}{\underbrace{{{\mathbf{W}}^{\left(BS\right)}}^H{\mathbf{H}}_{\mathrm{SI}}{\mathbf{F}}^{\left(BS\right)}{\mathbf{X}}^{\left(BS\right)}}}\hfill \\ & & +\underset{\mathrm{noise}}{\underbrace{{{\mathbf{W}}^{\left(BS\right)}}^H{\mathbf{V}}^{\left(BS\right)}}},\hfill \end{array}$$

(2)

where ${\mathbf{X}}^{\left(BS\right)}$ and ${\mathbf{X}}^{\left(i\right)}$ are the $N_t\times T$ the transmitted signal matrices of BS and user i, respectively, ${\mathbf{F}}^{\left(BS\right)}$ and ${\mathbf{F}}^{\left(i\right)}$ are the $K{N}_t\times N_t$ transmit precoder matrices of BS and user i, respectively, ${\mathbf{V}}^{\left(BS\right)}$ is the $K{N}_r\times T$ noise matrix at the BS receiver whose elements are independent and identically distributed (i.i.d.) with zero mean and variance ${\sigma }_v^2$, and ${\mathbf{H}}^{\left(iBS\right)}\in {\mathbb{C}}^{K{N}_r\times K{N}_t}$ is the channel matrix from user i to the BS and is given by

$${\mathbf{H}}^{\left(iBS\right)}=[{\mathbf{H}}_1^{\left(iBS\right)}{\mathbf{H}}_2^{\left(iBS\right)}\dots {\mathbf{H}}_{N_c}^{\left(iBS\right)}],$$

(3)

where ${\mathbf{H}}_{n_c}^{\left(iBS\right)}$ is the ${n_c}^{th}$ cluster sub-channel matrix of size $N_{r}K\times MK$, which is given by

$${\mathbf{H}}_{n_c}^{\left(iBS\right)}=\left[\begin{array}{cccc}{\mathbf{H}}_{n_c}^{11}& \dots & \dots & \dots {\mathbf{H}}_{n_c}^{1M}\\ ⋮& ⋮& ⋮& ⋮\\ {\mathbf{H}}_{n_c}^{N_{r}1}& \dots & \dots & {\mathbf{H}}_{n_c}^{N_{r}M}\end{array}\right],$$

Figure 2. Point-to-point communication between Full Duplex BS with MS-STSK modulator/ demodulator and Half-Duplex user.

Meanwhile, ${\mathbf{H}}_{n_c}^{mn}$ is the channel matrix of size $K\times K$ in the $n_c^{th}$ cluster linking between the $m^{th}$ AA and the $n^{th}$ AA at the receiver and the transmitter, respectively.

The statistical model used for the channel matrix ${\mathbf{H}}_{n_c}^{mn}$ is composed of $N_c^{\{m,n\}}$ clusters with $N_{\mathrm{ray}}^{\{m,n\}}$ rays, which is given by

$${\mathbf{H}}_{n_c}^{mn}=\sqrt{\frac{1}{N_c{N}_{\mathrm{ray}}}}\sum _{n_c=1}^{N_c^{\{m,n\}}}\sum _{n_{\mathrm{ray}}=1}^{N_{\mathrm{ray}}^{\{m,n\}}}{\alpha }_{n_c}^{n_{\mathrm{ray}}}{\mathbf{a}}_r\left({\varphi }_{n_c}^{n_{\mathrm{ray}}}\right){\mathbf{a}}_t^T\left({\varphi }_{n_c}^{n_{\mathrm{ray}}}\right),$$

(4)

where ${\mathbf{a}}_r\left({\varphi }_{n_c}^{n_{\mathrm{ray}}}\right)$ and ${\mathbf{a}}_t\left({\varphi }_{n_c}^{n_{\mathrm{ray}}}\right)$ are the response vectors for receive and transmit AAs, respectively. In this work, we consider uniform linear AAs, for which the response vectors ${\mathbf{a}}_r$ and ${\mathbf{a}}_t$ are given by [35]

$${\mathbf{a}}_r\left({\varphi }_r\right)={[1e^{j\frac{2\pi }{\lambda }dcos\left({\varphi }_r\right)}\dots e^{j\frac{2\pi }{\lambda }(K-1)dcos\left({\varphi }_r\right)}]}^T,$$

(5)

$${\mathbf{a}}_t\left({\varphi }_t\right)={[1e^{j\frac{2\pi }{\lambda }dcos\left({\varphi }_t\right)}\dots e^{j\frac{2\pi }{\lambda }(K-1)dcos\left({\varphi }_t\right)}]}^T,$$

(6)

where ${\varphi }_r$ and ${\varphi }_t$ represent, respectively, the angles of arrival and departure.

The second term in (2) is the interference due to the BS’s own transmission as the BS is operating in the FD mode, where it can transmit and receive at the same time. The self-interference channel matrix at the FD BS is denoted as ${\mathbf{H}}_{\mathrm{SI}}$, which is a near-field channel and can be represented as [16,20,36]

$${\mathbf{H}}_{\mathrm{SI}}=\sqrt{\frac{\kappa }{\kappa +1}}{\mathbf{H}}_{los}+\sqrt{\frac{1}{\kappa +1}}{\mathbf{H}}_{rp},$$

(7)

where $\kappa$ is the Rician factor, ${\mathbf{H}}_{\mathrm{los}}$ is the near-field channel’s line-of-sight (LOS) component, and ${\mathbf{H}}_{rp}$ is the reflected path of the SI channel for the BS, and it is modeled as in (4) [16]. Additionally, the ${(m,n)}^{th}$ entry of the LOS channel matrix denoted as ${\left[{\mathbf{H}}_{los}\right]}_{mn}$ is given by [16,20,36]

$${\left[{\mathbf{H}}_{los}\right]}_{mn}=\frac{\rho }{r_{mn}}exp\left(-j2\pi \frac{r_{mn}}{\lambda }\right),$$

(8)

where constant $\rho$ is utilized to achieve the power normalization, that is, $\parallel {\mathbf{H}}_{los}{\parallel }_F^2=1$. Here, the distance between the $m^{th}$ transmitting AE and the $n^{th}$ receiving AE is denoted as $r_{mn}$, which can be calculated as [16,20]:

$$\begin{array}{ccc}& & r_{mn}=\sqrt{r_x^2+r_y^2-2r_x{r}_{y}cos(\Theta )},\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill \text{where}& & r_x=\frac{D}{tan(\Theta )}+(n-1)\frac{\lambda }{2},\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill \text{and}& & r_y=\frac{D}{sin(\Theta )}+(m-1)\frac{\lambda }{2}.\hfill \end{array}$$

(11)

Here, D is the distance by which the AAs are separated and $\Theta$ is the angle of AAs. In the next section, we present the outage probability analysis, which is then used for the precoder and combiner design.

4. Outage Probability Analysis

Consider the system model defined in (2) employing the SI channel in (7); then, the received signal ${\mathbf{Y}}^{\left(BSi\right)}$ can be stated as

$$\begin{array}{ccc}\hfill & & {\mathbf{Y}}^{\left(iBS\right)}=\underset{\mathrm{desired}\mathrm{signal}}{\underbrace{{{\mathbf{W}}^{\left(BS\right)}}^H{\mathbf{H}}^{\left(iBS\right)}{\mathbf{F}}^{\left(i\right)}{\mathbf{X}}^{\left(i\right)}}}\hfill \\ & & +\underset{\mathrm{self}-\mathrm{interference}}{\underbrace{\sqrt{\frac{\kappa }{\kappa +1}}{{\mathbf{W}}^{\left(BS\right)}}^H{\mathbf{H}}_{los}{\mathbf{F}}^{\left(BS\right)}{\mathbf{X}}^{\left(BS\right)}+\sqrt{\frac{1}{\kappa +1}}{{\mathbf{W}}^{\left(BS\right)}}^H{\mathbf{H}}_{rp}{\mathbf{F}}^{\left(BS\right)}{\mathbf{X}}^{\left(BS\right)}}}\hfill \\ & & +\underset{\mathrm{noise}}{\underbrace{{{\mathbf{W}}^{\left(BS\right)}}^H{\mathbf{V}}^{\left(BS\right)}}}.\hfill \end{array}$$

(12)

Thus, the instantaneous SINR at the BS reception from the user i can be stated as

$${SINR}^{\left(iBS\right)}=\frac{{∥{{\mathbf{W}}^{\left(BS\right)}}^H{\mathbf{H}}^{\left(iBS\right)}{\mathbf{F}}^{\left(i\right)}{\mathbf{X}}^{\left(i\right)}∥}_F^2}{\frac{\kappa }{\kappa +1}{∥{{\mathbf{W}}^{\left(BS\right)}}^H{\mathbf{H}}_{los}{\mathbf{F}}^{\left(BS\right)}{\mathbf{X}}^{\left(BS\right)}∥}_F^2+\frac{1}{\kappa +1}{∥{{\mathbf{W}}^{\left(BS\right)}}^H{\mathbf{H}}_{rp}{\mathbf{F}}^{\left(BS\right)}{\mathbf{X}}^{\left(BS\right)}∥}_F^2+\mathbb{E}{∥{{\mathbf{W}}^{\left(BS\right)}}^H{\mathbf{V}}^{\left(BS\right)}∥}_F^2},$$

(13)

where ${∥{\mathbf{W}}^{\left(BS\right)}∥}_F^2$ shows the Frobenius norm of the matrix ${\mathbf{W}}^{\left(BS\right)}$ and $\mathbb{E}$ is the expectation operator.

At this stage, we denote ${\mathbf{w}}_k^{\left(BS\right)}$ as the $k^{th}$ column vector in ${\mathbf{W}}^{\left(BS\right)}$, ${\mathbf{F}}_j^{\left(i\right)}$ as the $j^{th}$ column vector in ${\mathbf{F}}^{\left(i\right)}$, and ${\mathbf{F}}_j^{\left(BS\right)}$ as the $j^{th}$ column vector in ${\mathbf{F}}^{\left(BS\right)}$. Additionally, let us denote ${\mathbf{X}}_{kj}^{\left(BS\right)}$ to represent the ${(k,j)}^{th}$ element in ${\mathbf{X}}^{\left(BS\right)}$, ${\mathbf{X}}_{kj}^{\left(i\right)}$ is the ${(k,j)}^{th}$ element in ${\mathbf{X}}^{\left(i\right)}$, and ${\mathbf{v}}_j^{\left(BS\right)}$ is the $j^{th}$ column vector in ${\mathbf{V}}^{\left(BS\right)}$ which is zero mean additive white noise having variance ${\sigma }_v^2$. Next, by using the vectorized version of the channel matrices, i.e., ${\mathbf{h}}^{\left(iBS\right)}=vec\left({\mathbf{H}}^{\left(iBS\right)}\right)$, ${\mathbf{h}}_{los}=vec\left({\mathbf{H}}_{los}\right)$, and ${\mathbf{h}}_{rp}=vec\left({\mathbf{H}}_{rp}\right)$ with the aid of linear algebra property, we can express the terms ${\mathbf{H}}^{\left(iBS\right)}{\mathbf{F}}_j^{\left(i\right)}$, ${\mathbf{H}}_{los}{\mathbf{F}}_j^{\left(BS\right)}$, and ${\mathbf{H}}_{rp}{\mathbf{F}}_j^{\left(BS\right)}$ as follows:

$$\begin{array}{ccc}\hfill {\mathbf{H}}^{\left(iBS\right)}{\mathbf{F}}_j^{\left(i\right)}& =& \left({\mathbf{I}}_{K{N}_r}\otimes {\mathbf{F}}_j^{{\left(i\right)}^T}\right){\mathbf{h}}^{\left(iBS\right)},\hfill \\ \hfill {\mathbf{H}}_{los}{\mathbf{F}}_j^{\left(BS\right)}& =& \left({\mathbf{I}}_{K{N}_r}\otimes {\mathbf{F}}_j^{{\left(BS\right)}^T}\right){\mathbf{h}}_{los},\hfill \\ \hfill {\mathbf{H}}_{rp}{\mathbf{F}}_j^{\left(BS\right)}& =& \left({\mathbf{I}}_{K{N}_r}\otimes {\mathbf{F}}_j^{{\left(BS\right)}^T}\right){\mathbf{h}}_{rp},\hfill \end{array}$$

(14)

where the notation ⊗ denotes the Kronecker product and ${\mathbf{I}}_{K{N}_r}$ is the $K{N}_r$-dimensional Identity matrix. Finally, using the whitening transformation for random channel vectors, i.e., ${\overline{\mathbf{h}}}^{\left(iBS\right)}={\mathbf{R}}_{{\mathbf{h}}^{\left(iBS\right)}}^{-H/2}{\mathbf{h}}^{\left(iBS\right)}$ and ${\overline{\mathbf{h}}}_{rp}={{\mathbf{R}}_{\mathbf{h}}}_{rp}^{-H/2}{\mathbf{h}}_{rp}$ where ${\mathbf{R}}_{{\mathbf{h}}^{\left(iBS\right)}}$ and ${{\mathbf{R}}_{\mathbf{h}}}_{rp}$ are the correlation matrices for ${\mathbf{h}}^{\left(iBS\right)}$ and ${\mathbf{h}}_{rp}$, respectively. Thus, the SINR given in (13) can be formulated as a ratio of IQF as follows:

$${\mathrm{SINR}}^{\left(iBS\right)}=\frac{\left|\right|{\overline{\mathbf{h}}}^{\left(iBS\right)}{\left|\right|}_{{\mathbf{A}}^{\left(iBS\right)}}^2}{\left|\right|{\overline{\mathbf{h}}}_{rp}{\left|\right|}_{{\mathbf{B}}^{\left(iBS\right)}}^2+{ϵ}^{\left(i\right)}},$$

(15)

where the notation ${\left|\right|\mathbf{x}\left|\right|}_{\mathbf{A}}^2$ denotes the weighted norm of vector $\mathbf{x}$ and is defined as ${\left|\right|\mathbf{x}\left|\right|}_{\mathbf{A}}^2={\mathbf{x}}^H\mathbf{A}\mathbf{x}$. The scalar term ${ϵ}^{\left(i\right)}$ and the matrices ${\mathbf{A}}^{\left(iBS\right)}$ and ${\mathbf{B}}^{\left(iBS\right)}$ appearing in (15) are defined as

$$\begin{array}{ccc}\hfill {\mathbf{A}}^{\left(iBS\right)}& =& T{\mathbf{R}}_{{\mathbf{h}}^{\left(iBS\right)}}^{1/2}\{\sum _{k=1}^{N_r}\sum _{j=1}^{N_t}\hfill \\ & & {\left({\mathbf{I}}_{K{N}_r}\otimes {{\mathbf{F}}_j^{\left(i\right)}}^T\right)}^H{\mathbf{w}}_k^{\left(BS\right)}{{\mathbf{w}}_k^{\left(BS\right)}}^H\left({\mathbf{I}}_{K{N}_r}\otimes {{\mathbf{F}}_j^{\left(i\right)}}^T\right)\}{\mathbf{R}}_{{\mathbf{h}}^{\left(iBS\right)}}^{H/2},\hfill \\ \hfill {\mathbf{B}}^{\left(iBS\right)}& =& \frac{T}{\kappa +1}{\mathbf{R}}_{{\mathbf{h}}_{rp}}^{1/2}\{\sum _{k=1}^{N_r}\sum _{j=1}^{N_t}\hfill \\ & & {\left({\mathbf{I}}_{K{N}_r}\otimes {{\mathbf{F}}_j^{\left(BS\right)}}^T\right)}^H{\mathbf{w}}_k^{\left(BS\right)}{{\mathbf{w}}_k^{\left(BS\right)}}^H\left({\mathbf{I}}_{K{N}_r}\otimes {{\mathbf{F}}_j^{\left(BS\right)}}^T\right)\}{\mathbf{R}}_{{\mathbf{h}}_{rp}}^{H/2},\hfill \\ \hfill {ϵ}^{\left(i\right)}& =& \frac{T\kappa }{\kappa +1}Tr\left(\sum _{k=1}^{N_r}\sum _{j=1}^{N_t}{\left({\mathbf{I}}_{K{N}_r}\otimes {{\mathbf{F}}_j^{\left(BS\right)}}^T\right)}^H\right.\hfill \\ & & \left.{\mathbf{w}}_k^{\left(BS\right)}{{\mathbf{w}}_k^{\left(BS\right)}}^H\left({\mathbf{I}}_{K{N}_r}\otimes {{\mathbf{F}}_j^{\left(BS\right)}}^T\right)\right)+T{\sigma }_v^2\sum _{k=1}^{N_r}\left|\right|{\mathbf{w}}_k^{\left(BS\right)}{\left|\right|}^2.\hfill \end{array}$$

(16)

To obtain the expression (15), we have used the fact that the input signals are unit power, that is $|{\mathbf{X}}_{kj}^{\left(BS\right)}{|}^2=1$ and $|{\mathbf{X}}_{kj}^{\left(i\right)}{|}^2=1$. In addition, we have used the fact that $\left|\right|{\mathbf{h}}_{los}{\left|\right|}^2=1$.

Next, using the definition that the outage probability is the likelihood that the SINR${}^{\left(iBS\right)}$ is below a specific power threshold, say ${\gamma }_{th}$, we can evaluate its outage probability as follows:

$$P_{out}^{\left(iBS\right)}\left({\gamma }_{th}\right)=Pr\left({\mathrm{SINR}}^{\left(iBS\right)}\le {\gamma }_{th}\right)=Pr\left(\frac{\left|\right|{\overline{\mathbf{h}}}^{\left(iBS\right)}{\left|\right|}_{{\mathbf{A}}^{\left(iBS\right)}}^2}{\left|\right|{\overline{\mathbf{h}}}_{rp}{\left|\right|}_{{\mathbf{B}}^{\left(iBS\right)}}^2+{ϵ}^{\left(i\right)}}\le {\gamma }_{th}\right).$$

(17)

Given the fact that the random vectors ${\overline{\mathbf{h}}}^{\left(iBS\right)}$ and ${\overline{\mathbf{h}}}_{rp}$ are independent, we can evaluate the probability in two steps: first, evaluate the conditional outage probability of SINR${}^{\left(iBS\right)}$ conditioned on ${\overline{\mathbf{h}}}_{rp}$ or equivalently conditioned on $z=\left|\right|{\overline{\mathbf{h}}}_{rp}{\left|\right|}_{{\mathbf{B}}^{\left(iBS\right)}}^2$ and then average the conditional probability over the PDF of z to evaluate the outage probability. In the first step, the conditional outage probability given z can be evaluated using the approach for characterizing the Indefinite Quadratic Forms provided in [37,38] and is given by

$$Pr\left({\mathrm{SINR}}^{\left(iBS\right)}\le {\gamma }_{th}|z\right)=u\left({\gamma }_{th}\right)-\sum _{j=1}^{K^2{N}_r{N}_t}\frac{{\lambda }_j^{K^2{N}_r{N}_t}{e}^{\frac{-{\gamma }_{th}\left(z+{ϵ}^{\left(i\right)}\right)}{{\lambda }_j}}}{{\displaystyle |{\lambda }_j|\prod _{i=1,i\ne j}^{K^2{N}_r{N}_t}\left({\lambda }_j-{\lambda }_i\right)}}u\left(\frac{{\gamma }_{th}(z+{ϵ}^{\left(i\right)})}{{\lambda }_j}\right),$$

(18)

where ${\lambda }_j$ is the $j^{\mathrm{th}}$ eigenvalue of the matrix ${\mathbf{A}}^{\left(iBS\right)}$. Next, using the approach of [37], the PDF of z can be shown to be

$$f_z\left(z\right)=\sum _{k=1}^{K^2{N}_r{N}_t}\frac{{\rho }_k^{K^2{N}_r{N}_t-1}{e}^{\frac{-z}{{\rho }_k}}}{{\displaystyle |{\rho }_k|\prod _{i=1,i\ne k}^{K^2{N}_r{N}_t}\left({\rho }_k-{\rho }_i\right)}}u\left(\frac{z}{{\rho }_k}\right),$$

(19)

where ${\rho }_k$ is the $k^{\mathrm{th}}$ eigenvalue of the matrix ${\mathbf{B}}^{\left(iBS\right)}$. Finally, by averaging the conditional probability $Pr\left({\mathrm{SINR}}^{\left(iBS\right)}\le {\gamma }_{th}|z\right)$ over $f_z\left(z\right)$ using the approach of [39], the required outage probability can be expressed as

$$\begin{array}{ccc}\hfill & & P_{out}^{\left(iBS\right)}\left({\gamma }_{th}\right)={\int }_{-\infty }^{\infty }Pr\left(\mathrm{SINR}\le {\gamma }_{th}|z\right)f_z\left(z\right)dz\hfill \\ & & =\sum _{k=1}^{K^2{N}_r{N}_t}{\beta }_{k}u\left({\gamma }_{th}\right)\left\{u\left({\rho }_k\right)u\left({ϵ}^{\left(i\right)}\right)+(1-u\left({\rho }_k\right))u\left({ϵ}^{\left(i\right)}\right)e^{\frac{{ϵ}^{\left(i\right)}}{{\rho }_k}}+u\left({\rho }_k\right)(1-u\left({ϵ}^{\left(i\right)}\right))e^{\frac{{ϵ}^{\left(i\right)}}{{\rho }_k}}\right\}\hfill \\ & & -\sum _{k=1}^{K^2{N}_r{N}_t}\sum _{j=1}^{K^2{N}_r{N}_t}\frac{{\beta }_k{\zeta }_j{\lambda }_j{e}^{-\frac{{\gamma }_{th}{ϵ}^{\left(i\right)}}{{\lambda }_j}}}{({\gamma }_{th}{\rho }_k+{\lambda }_j)}\{u\left({\rho }_k\right)u\left({\lambda }_j\right)u\left({ϵ}^{\left(i\right)}\right)+u\left({\rho }_k\right)u\left({\lambda }_j\right)(1-u\left({ϵ}^{\left(i\right)}\right))e^{\frac{{ϵ}^{\left(i\right)}({\gamma }_{th}{\rho }_k+{\lambda }_j)}{{\rho }_k{\lambda }_j}}\hfill \\ & & +u\left({\rho }_k\right)(1-u\left({\lambda }_j\right))(1-u\left({ϵ}^{\left(i\right)}\right))(1-e^{\frac{{ϵ}^{\left(i\right)}({\gamma }_{th}{\rho }_k+{\lambda }_j)}{{\rho }_k{\lambda }_j}})+(1-u\left({\rho }_k\right))u\left({\lambda }_j\right)u\left({ϵ}^{\left(i\right)}\right)(e^{\frac{{ϵ}^{\left(i\right)}({\gamma }_{th}{\rho }_k+{\lambda }_j)}{{\rho }_k{\lambda }_j}}-1)\},\hfill \end{array}$$

(20)

where

$${\beta }_k=\frac{{\rho }_k^{K^2{N}_r{N}_t}}{{\displaystyle |{\rho }_k|\prod _{i=1,i\ne k}^{K^2{N}_r{N}_t}\left({\rho }_k-{\rho }_i\right)}},$$

and

$${\zeta }_j=\frac{{\lambda }_j^{K^2{N}_r{N}_t}}{{\displaystyle |{\lambda }_j|\prod _{i=1,i\ne j}^{K^2{N}_r{N}_t}\left({\lambda }_j-{\lambda }_i\right)}}.$$

(21)

5. Design of Optimum Beamformer Weights

Here, we provide our suggested method for determining the transmit and receive beamformer weights for all users, i.e., ${\mathbf{W}}^{\left(BS\right)}$ and ${\mathbf{F}}^{\left(i\right)}$$\forall i$. Here, the objective is to develop an optimization problem that can provide the optimum beamforming solution for both the transmitter and the receiver by minimizing the outage probability for all system users. We propose to minimize the scalarized sum outage probability (denoted as $P_{out}^{sum}$) for $N_u$ total users using the approach of [40]. Thus, $P_{out}^{sum}$ can be stated as

$$P_{out}^{sum}=\frac{1}{N_u}\sum _{i=1}^{N_u}{P}_{out}^{\left(iBS\right)}\left({\gamma }_{th}\right),$$

(22)

In our work, the proposed objective is to minimize the sum outage probability with respect to the transmit and the receive beamforming weights of all users while constraining the powers of these beamforming weights to unity, that is,

$$\begin{array}{cccc}\hfill & \underset{{\{{\mathbf{W}}^{\left(BS\right)},{\mathbf{F}}^{\left(i\right)}\}}_{i=1}^{N_u}}{\mathrm{minimize}}\hfill & \hfill & P_{out}^{sum}\left({\gamma }_{th}\right),\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill & \hfill & {∥{\mathbf{W}}^{BS)}∥}_F^2=1\hfill \\ \hfill & \mathrm{and}\hfill & \hfill & {∥{\mathbf{F}}^{\left(i\right)}∥}_F^2=1,\forall i.\hfill \end{array}$$

(23)

Next, two methods to deal with the optimization problem in (23) are provided.

5.1. Heuristic Approach for Joint Optimization of Precoder and Beamformer

It can be observed that the objective function proposed in (23) is highly non-linear and non-convex in nature. Thus, a unique closed-form solution cannot be obtained using classical optimization tools. Therefore, we propose to use the sequential quadratic programming (SQP)-based solution which is a well-established technique in optimization theory [41].

5.2. Closed Form Iterative Solution

The heuristic approach presented in Section 5.1 to solve the optimization problem in (23) requires exhaustive search and hence has high computational complexity. Thus, a sub-optimal solution can be used to jointly optimize the transmit and receive beamforming weights, which has significantly reduced computational complexity. For this purpose, we develop an iterative solution that utilizes the “Principle Eigenvector” method [42] to obtain transmit beamformer weights (i.e., ${\mathbf{F}}^{\left(i\right)}\forall i$) using initialized receive beamformer weights (i.e., ${\mathbf{W}}^{\left(BS\right)}$) and then calculate the receive beamformer weights using the “Generalized Rayleigh Quotient (G-RQ)” method [40]. This process in iterations will be continued until the sum SINR is maximized. The design details are presented in the following sections.

5.2.1. Transmit Beamforming using Principle Eigenvector Method

In order to design the transmit beamformer weights ${\mathbf{F}}^{\left(i\right)}$, we utilize the approach of principle eigenvector [42] to find the solution that maximizes the capacity by maximizing the SINR. To achieve this, the desired signal component is maximized while the beam powers are limited to unity. For illustration, we use the case of our presented system model in (2), where the transmit beamforming weights ${\mathbf{F}}^{\left(i\right)}$ will be calculated using the following optimization strategy

$$\underset{\left\{{\mathbf{F}}_j^{\left(i\right)}\right\}}{\mathrm{maximize}}\sum _{k=1}^{N_r}\mathbb{E}\left[\right|{{\mathbf{w}}_k^{\left(BS\right)}}^H{\mathbf{H}}^{\left(iBS\right)}{\mathbf{F}}_j^{\left(i\right)}{|}^2],\forall j,$$

(24)

which can be equivalently expressed as

$$\underset{\left\{{\mathbf{F}}_j^{\left(i\right)}\right\}}{\mathrm{maximize}}{{\mathbf{F}}_j^{\left(i\right)}}^H\left\{\sum _{k=1}^{N_r}\mathbb{E}\left[{{\mathbf{H}}^{\left(iBS\right)}}^H{\mathbf{w}}_k^{\left(BS\right)}{{\mathbf{w}}_k^{\left(BS\right)}}^H{\mathbf{H}}^{\left(iBS\right)}\right]\right\}{\mathbf{F}}_j^{\left(i\right)},\forall j.$$

(25)

Next, using the fact that ${{\mathbf{H}}^{\left(iBS\right)}}^H{\mathbf{w}}_k^{\left(BS\right)}=\left({\mathbf{I}}_{K{N}_t}\otimes {{\mathbf{w}}_k^{\left(BS\right)}}^T\right){{\mathbf{h}}^{\left(iBS\right)}}^{*}$, where ${{\mathbf{h}}^{\left(iBS\right)}}^{*}$ is the vectorized version of ${{\mathbf{H}}^{\left(iBS\right)}}^H$, we can set up the above optimization task as

$$\underset{\left\{{\mathbf{F}}_j^{\left(2\right)}\right\}}{\mathrm{maximize}}{{\mathbf{F}}_j^{\left(i\right)}}^H\left\{\sum _{k=1}^{N_r}\left({\mathbf{I}}_{K{N}_t}\otimes {{\mathbf{w}}_k^{\left(BS\right)}}^T\right){\mathbf{R}}_{{{\mathbf{h}}^{\left(\mathbf{iBS}\right)}}^{*}}{\left({\mathbf{I}}_{K{N}_t}\otimes {{\mathbf{w}}_k^{\left(BS\right)}}^T\right)}^H\right\}{\mathbf{F}}_j^{\left(i\right)},\forall j$$

where ${\mathbf{R}}_{{{\mathbf{h}}^{\left(\mathbf{iBS}\right)}}^{*}}$ is the correlation matrix of ${{\mathbf{h}}^{\left(iBS\right)}}^{*}$. The solution of the above task is well established and is given by the eigenvector that corresponds to the largest eigenvalue of matrix ${\sum }_{k=1}^{N_r}\left({\mathbf{I}}_{K{N}_t}\otimes {{\mathbf{w}}_i^{largf\left(iBS\right)}}^{T}T\right){\mathbf{R}}_{{{\mathbf{h}}^{\left(\mathbf{iBS}\right)}}^{*}}{\left({\mathbf{I}}_{K{N}_t}\otimes {{\mathbf{w}}_i^{\left(iBS\right)}}^T\right)}^H$ [42], that is,

$${{\mathbf{F}}_j^{\left(i\right)}}^{opt}=\max \mathrm{eigenvector}\left(\sum _{k=1}^{N_r}\left({\mathbf{I}}_{K{N}_t}\otimes {{\mathbf{w}}_k^{\left(BS\right)}}^T\right){\mathbf{R}}_{{{\mathbf{h}}^{\left(\mathbf{iBS}\right)}}^{*}}{\left({\mathbf{I}}_{K{N}_t}\otimes {{\mathbf{w}}_k^{\left(BS\right)}}^T\right)}^H\right).$$

(26)

This method of evaluating ${{\mathbf{F}}_j^{\left(i\right)}}^{opt}$ given in (26) will be repeated for all j (i.e., for all columns in ${{\mathbf{F}}^{\left(i\right)}}^{opt}$) and all i (i.e., for all users $i=1,2,\cdots ,N_u$).

5.2.2. Receive Beamforming Using G-RQ Method

In order to use the G-RQ solution for our task, let us consider the $T^{th}$ dimensional received signal vector at the BS from user i via $k^{th}$ receive AA (denoted as ${\mathbf{y}}_k^{\left(iBS\right)}$), and it can be stated as

$$\begin{array}{ccc}\hfill & & {\mathbf{y}}_k^{\left(iBS\right)}=\underset{\mathrm{desired}\mathrm{signal}}{\underbrace{{{\mathbf{w}}_k^{\left(BS\right)}}^H{\mathbf{H}}^{\left(iBS\right)}{\mathbf{F}}^{\left(i\right)}{\mathbf{X}}^{\left(i\right)}}}\hfill \\ & & +\underset{\mathrm{self}-\mathrm{interference}}{\underbrace{\sqrt{\frac{\kappa }{\kappa +1}}{{\mathbf{w}}_k^{\left(BS\right)}}^H{\mathbf{H}}_{los}{\mathbf{F}}^{\left(BS\right)}{\mathbf{X}}^{\left(BS\right)}+\sqrt{\frac{1}{\kappa +1}}{{\mathbf{w}}_k^{\left(BS\right)}}^H{\mathbf{H}}_{rp}{\mathbf{F}}^{\left(BS\right)}{\mathbf{X}}^{\left(BS\right)}}}\hfill \\ & & +\underset{\mathrm{noise}}{\underbrace{{{\mathbf{w}}_k^{\left(BS\right)}}^H{\mathbf{V}}^{\left(BS\right)}}}.\hfill \end{array}$$

(27)

Then, the statistical SINR for the $i^{th}$ user signal at the BS via the $k^{th}$ receive AA can be expressed as

$$\mathbb{E}\left[{\mathrm{SINR}}_k^{\left(iBS\right)}\right]=\frac{{{\mathbf{w}}_k^{\left(BS\right)}}^H\left[T{\sum }_{j=1}^{N_t}{\mathbf{C}}_j^{\left(i\right)}\right]{\mathbf{w}}_k^{\left(BS\right)}}{{{\mathbf{w}}_k^{\left(BS\right)}}^H\left[\frac{T\kappa }{\kappa +1}{\sum }_{j=1}^{N_t}{{\mathbf{C}}_{los}^{\left(BS\right)}}_j+\frac{T}{\kappa +1}{\sum }_{j=1}^{N_t}{{\mathbf{C}}_{rp}^{\left(BS\right)}}_j+N_t{\sigma }_v^2\mathbf{I}\right]{\mathbf{w}}_k^{\left(BS\right)}}.$$

(28)

where

$$\begin{array}{ccc}\hfill {\mathbf{C}}_j^{\left(i\right)}& =& \left({\mathbf{I}}_{K{N}_r}\otimes {{\mathbf{F}}_j^{\left(i\right)}}^T\right){\mathbf{R}}_{{\mathbf{h}}^{\left(iBS\right)}}{\left({\mathbf{I}}_{K{N}_r}\otimes {{\mathbf{F}}_j^{\left(i\right)}}^T\right)}^H,\hfill \\ \hfill {{\mathbf{C}}_{los}^{\left(BS\right)}}_j& =& \left({\mathbf{I}}_{K{N}_r}\otimes {{\mathbf{F}}_j^{\left(BS\right)}}^T\right){\mathbf{h}}_{los}{{\mathbf{h}}_{los}}^H{\left({\mathbf{I}}_{K{N}_r}\otimes {{\mathbf{F}}_j^{\left(BS\right)}}^T\right)}^H,\hfill \\ \hfill and{{\mathbf{C}}_{rp}^{\left(BS\right)}}_j& =& \left({\mathbf{I}}_{K{N}_r}\otimes {{\mathbf{F}}_j^{\left(BS\right)}}^T\right){\mathbf{R}}_{{\mathbf{h}}_{rp}}{\left({\mathbf{I}}_{K{N}_r}\otimes {{\mathbf{F}}_j^{\left(BS\right)}}^T\right)}^H.\hfill \end{array}$$

The G-RQ method for obtaining ${\mathbf{W}}^{\left(BS\right)}$ can be formulated using the following constrained optimization task [40]:

$$\underset{{\left\{{\mathbf{w}}_k^{\left(BS\right)}\right\}}_{k=1}^{N_r}}{\mathrm{maximize}}\mathbb{E}\left[{\mathrm{SINR}}_k^{\left(iBS\right)}\right]\mathrm{subject}\mathrm{to}{∥{\mathbf{w}}_k^{\left(BS\right)}∥}^2=1.$$

(29)

The solution for this constrained optimization is well known [40] and is given by

$${{\mathbf{w}}_k^{\left(BS\right)}}^{opt}=\max \mathrm{eigenvector}\left({\mathbf{Q}}^{-1}\mathbf{P}\right),\forall i,$$

(30)

where $\mathbf{Q}=\frac{T\kappa }{\kappa +1}{\sum }_{j=1}^{N_t}{\mathbf{C}}_{\mathbf{los}j}^{\left(\mathbf{1}\right)}+\frac{T}{\kappa +1}{\sum }_{j=1}^{N_t}{{\mathbf{C}}_{\mathbf{rp}}^{\left(\mathbf{1}\right)}}_j+N_t{\sigma }_{v^{\left(1\right)}}^2\mathbf{I}$ and $\mathbf{P}=T{\sum }_{j=1}^{N_t}{\mathbf{C}}_j^{\left(2\right)}$.

A pseudo-code for the proposed iterative statistical method (denoted as ISM) to obtain beamforming in the MS-STSK-based FD mmWave system is specified as Algorithm 1.

Algorithm 1 Pseudo-code for the ISM algorithm.

Require: Set the precision level ($p^{th}$) and criteria for the algorithm’s termination. Require: Set the time index $n=0$.     Compute transmit beamfomer weights ${{\mathbf{F}}_j^{\left(i\right)}}^{opt},\forall j$ using (26) to obtain ${{\mathbf{F}}^{\left(i\right)}}^{opt}$.     Repeat the above step for all users, that is, evaluate ${{\mathbf{F}}^{\left(i\right)}}^{opt},\forall i$.     Compute the receive beamformer weights ${{\mathbf{w}}_k^{\left(BS\right)}}^{opt},\forall k$ using (30) to obtain ${{\mathbf{W}}^{\left(BS\right)}}^{opt}$.     Compute the objective function, i.e, ${\mathit{J}}_n={\sum }_{i=1}^{N_r}\mathbb{E}\left[{\mathrm{SINR}}_i\right]$ using (28).     $n=n+1$.     Evaluate ${\mathit{J}}_n$ using (28)     if$|{\mathit{J}}_n-{\mathit{J}}_{n-1}|\ge p^{th}$ then       update beamforming weights.     else       Termination condition = true.     end if

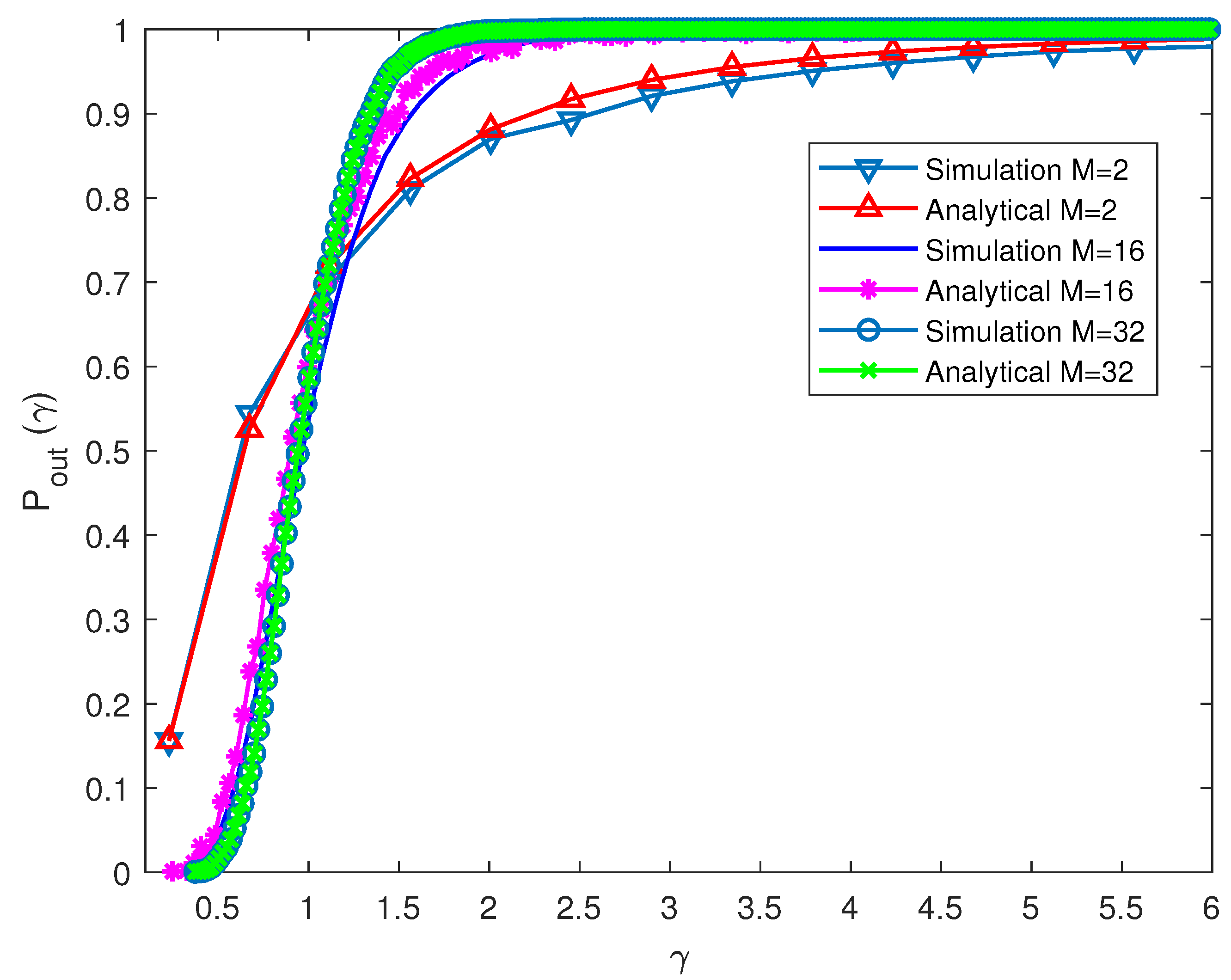
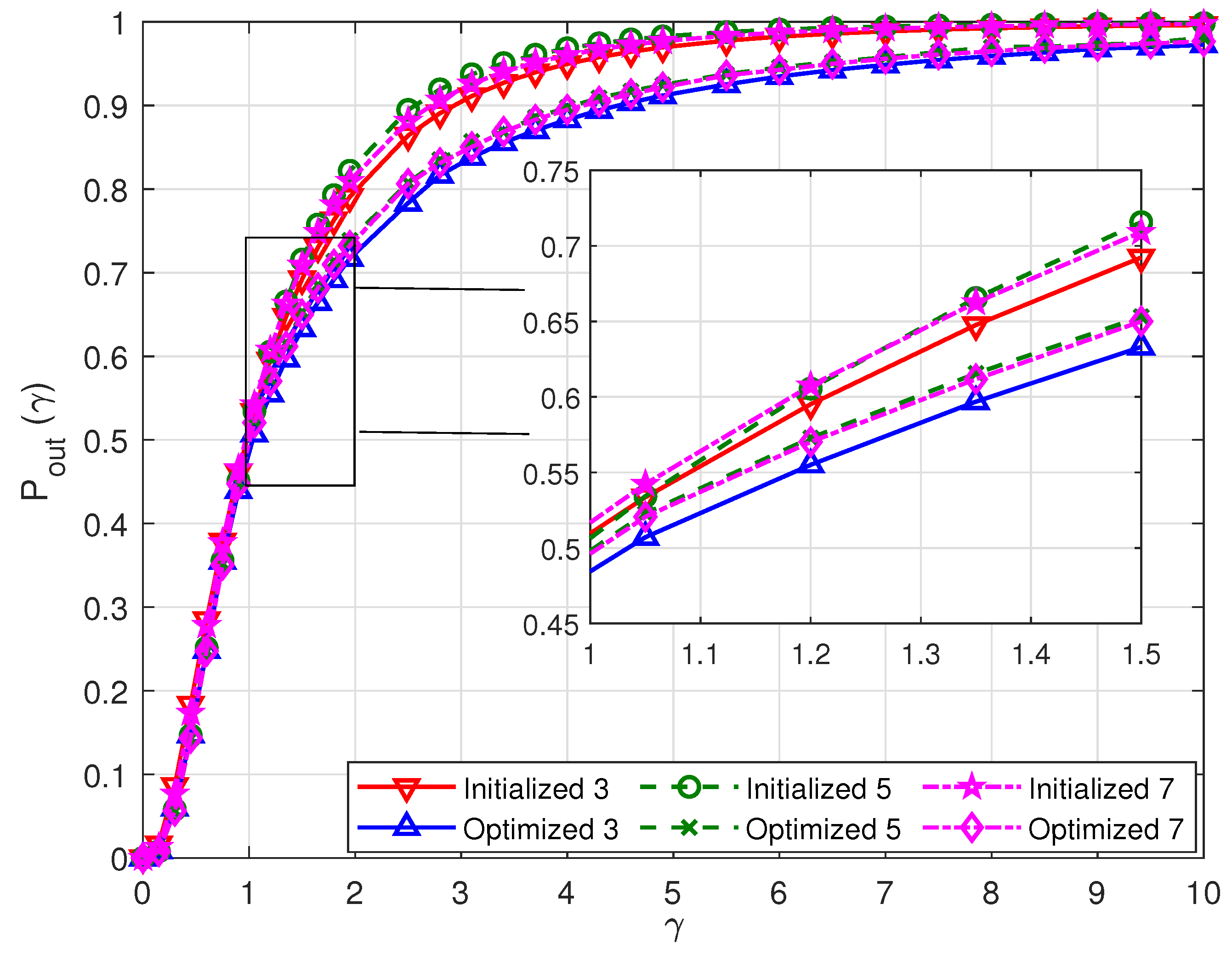
6. Simulation Results

Here, we provide the simulation results to confirm our theoretical analysis for the MS-STSK-based FD mmWave system. For this purpose, we use MATLAB software to implement the system model defined in (2). The channel matrices ${\mathbf{H}}^{\left(iBS\right)}$ and ${\mathbf{H}}_{SI}$ are generated using (3)–(6). Here, the angles of arrival and departure (${\varphi }_r$ and ${\varphi }_t$) are obtained randomly using uniform random variables in the range $[0,2\pi ]$. The cluster size ($N_c^{\{m,n\}}$) and the number of rays ($N_{\mathrm{ray}}^{\{m,n\}}$) are set to unity for all m and n. The results of the simulation are calculated by averaging 400 different Monte Carlo simulations. In our experiments, we consider a total two number of users, i.e., $N_u=2$.

First, we contrast user 1’s analytically calculated outage probability at the BS with the simulated one via Monte Carlo runs. For this purpose, the analytical outage probability is calculated using the derived expression in (20). In this particular experiment, the SNR value is kept at 20 dB. The antenna array size, the number of clusters, and the number of received antennas used are $K=10$, $N_c=1$, and $N_r=2$, respectively. The transmit and the receive beamformer weights (i.e., ${\mathbf{W}}^{\left(BS\right)}$ and ${\mathbf{F}}^{\left(i\right)}$ for all users (i = 1, 2) are generated randomly with complex entries. This comparison is reported in Figure 3 for three different values of the number of RF chains, that is, M = 2, M = 16, and M = 32. It can be easily depicted from the displayed results that the theoretical results match well with the simulations for all three values of M, which validates our derived analytical expressions for the outage probability.

Figure 3. Validation of analytical results for the BS outage probability due to user 1 via Monte Carlo simulations.

Next, in Figure 4, the performance of the SQP-based proposed heuristic method is compared for various values of antenna arrays K (i.e., K = 3, 5, 7). The transmit and the receive beamfomer weights are initialized with random complex values. The SQP-based proposed heuristic method is then employed to solve the constrained optimization task of (23). It is evident that the suggested SQP-based solution has reduced the likelihood of an outage. Secondly, it can be observed that the optimization gain in terms of reduction in outage probability is almost identical for all values of K. In addition, it can be observed that the outage probability reduction is significant using the designed beamforming. For example, at the threshold value of $\gamma$ = 2.5, the outage probability for K = 3 is reduced from 0.88 to 0.78, which is significant.

Figure 4. Performance of the proposed SQP-based method for $K=3,5,7$ with $N_t=2$ and $N_r=2$.

Finally, in Figure 5, we contrasted the proposed ISM algorithm’s performance with that of the SQP-based proposed heuristic method. For this experiment, we set the system parameters as used in Figure 3 except K = 3 and M = 16. It can be depicted from the result that both the proposed methods have minimized the outage probability as compared to the initial result. Additionally, it can be noticed that the proposed iterative ISM strategy has outperformed the proposed SQP-based heuristic approach. This may be due to the reason that the expression of outage probability is highly non-linear and non-convex, which makes it possible for the heuristic method to become trapped in a local minimum. Thus, it can be concluded that the proposed methods of beamforming design are capable of improving the system’s performance.

Figure 5. Performance comparison of the sum outage probabilities for the proposed methods.

7. Conclusions

In this work, we used the characterization of the IQF ratio to obtain a closed-form formula for the outage probability in the MS-STSK-based FD mmWave communication system. Additionally, by minimizing the obtained outage probability expression, we created two statistical techniques for generating transmit and receive beamforming weights. Our theoretical analysis has been validated using simulation findings. The fact that the suggested approaches solely rely on channel data and do not require pilot broadcast for channel estimation makes them bandwidth-efficient, which is a significant advantage.