Optimal Selection of Stock Portfolios Using Multi-Criteria Decision-Making Methods
Abstract
1. Introduction
2. Research Literature
2.1. Modern Portfolio Theory
- Investors are risk-averse and have increasing expected utility, and the final utility curve of their wealth is decreasing;
- Investors choose their stock portfolio based on the average and variance of expected returns. Therefore, their indifference curves are a function of the expected rate of return and variance;
- Every investment option is infinitely divisible;
- Investors have a “one-period” “time” horizon, and this is the same for all investors;
- Investors prefer higher returns at a certain level of risk, and vice versa; for a certain level of return, they want the lowest risk (anti-recession assumption).
2.2. Portfolio and MCDM Approaches
2.3. Optimization Algorithms
2.4. MADM Approaches
2.4.1. TOPSIS
2.4.2. ARAS
2.4.3. Taxonomy Method
2.4.4. VIKOR
2.4.5. COPRAS
2.4.6. WASPAS
2.4.7. DEA Method
2.4.8. Mean Rank Method
Borda Count Method
Copeland Method
3. Research Method
3.1. Population
3.2. Evaluation Metrics
4. Findings
5. Discussion and Conclusions
Research Limitations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- De la Torre-Torres, O.V.; Galeana-Figueroa, E.; Del Río-Rama, M.d.l.C.; Álvarez-García, J. Using Markov-Switching Models in US Stocks Optimal Portfolio Selection in a Black–Litterman Context (Part 1). Mathematics 2022, 10, 1296. [Google Scholar] [CrossRef]
- Mitra Thakur, G.S.; Bhattacharyya, R.; Sarkar (Mondal), S. Stock Portfolio Selection Using Dempster–Shafer Evidence Theory. J. King Saud Univ. -Comput. Inf. Sci. 2018, 30, 223–235. [Google Scholar] [CrossRef]
- Rasoulzadeh, M.; Edalatpanah, S.A.; Fallah, M.; Najafi, S.E. A Multi-Objective Approach Based on Markowitz and DEA Cross-Efficiency Models for the Intuitionistic Fuzzy Portfolio Selection Problem. Decis. Mak. Appl. Manag. Eng. 2022, 5, 241–259. [Google Scholar] [CrossRef]
- Akram, M.; Shah, S.M.U.; Ali Al-Shamiri, M.M.; Edalatpanah, S.A. Extended DEA Method for Solving Multi-Objective Transportation Problem with Fermatean Fuzzy Sets. AIMS Math. 2023, 8, 924–961. [Google Scholar] [CrossRef]
- Sorourkhah, A. Coping Uncertainty in the Supplier Selection Problem Using a Scenario-Based Approach and Distance Measure on Type-2 Intuitionistic Fuzzy Sets. Fuzzy Optim. Model. J. 2022, 3, 64–71. [Google Scholar] [CrossRef]
- Sorourkhah, A.; Babaie-Kafaki, S.; Azar, A.; Shafiei Nikabadi, M. A Fuzzy-Weighted Approach to the Problem of Selecting the Right Strategy Using the Robustness Analysis (Case Study: Iran Automotive Industry). Fuzzy Inf. Eng. 2019, 11, 39–53. [Google Scholar] [CrossRef]
- Song, Q.; Liu, A.; Yang, S.Y. Stock Portfolio Selection Using Learning-to-Rank Algorithms with News Sentiment. Neurocomputing 2017, 264, 20–28. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio Selection. J. Financ. 1952, 7, 77–91. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio Selection; Yale University Press: London, UK, 2009; ISBN 9789812833655. [Google Scholar]
- Jalilian, J.; Rasi, R.E. Multi Objective Portfolio Optimization for a Private Equity Investment Company under Data Insufficiency Condition. Int. J. Financ. Manag. Account. 2021, 6, 23–37. [Google Scholar]
- Li, B.; Zhang, R.; Sun, Y. Multi-Period Portfolio Selection Based on Uncertainty Theory with Bankruptcy Control and Liquidity. Automatica 2023, 147, 110751. [Google Scholar] [CrossRef]
- Wei, P.; Yang, C.; Zhuang, Y. Robust Consumption and Portfolio Choice with Derivatives Trading. Eur. J. Oper. Res. 2023, 304, 832–850. [Google Scholar] [CrossRef]
- Sorourkhah, A.; Edalatpanah, S.A. Considering the Criteria Interdependency in the Matrix Approach to Robustness Analysis with Applying Fuzzy ANP. Fuzzy Optim. 2021, 3, 22–33. [Google Scholar]
- Sorourkhah, A.; Edalatpanah, S.A. Using a Combination of Matrix Approach to Robustness Analysis (MARA) and Fuzzy DEMATEL-Based ANP (FDANP) to Choose the Best Decision. Int. J. Math. Eng. Manag. Sci. 2022, 7, 68–80. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; García-Segura, T.; Martí, J.V.; Yepes, V. A Review of Multi-Criteria Decision-Making Methods Applied to the Sustainable Bridge Design. Sustainability 2016, 8, 1295. [Google Scholar] [CrossRef]
- Li, W.; Yi, P.; Li, L. Superiority-Comparison-Based Transformation, Consensus, and Ranking Methods for Heterogeneous Multi-Attribute Group Decision-Making. Expert Syst. Appl. 2023, 213, 119018. [Google Scholar] [CrossRef]
- Daugherty, M.S.; Jithendranathan, T.; Vang, D.O. Portfolio Selection Using the Multiple Attribute Decision Making Model. Invest. Manag. Financ. Innov. 2021, 18, 155–165. [Google Scholar] [CrossRef]
- Broumi, S.; Ajay, D.; Chellamani, P.; Malayalan, L.; Talea, M.; Bakali, A.; Schweizer, P.; Jafari, S. Interval Valued Pentapartitioned Neutrosophic Graphs with an Application to MCDM. Oper. Res. Eng. Sci. Theory Appl. 2022, 5, 68–91. [Google Scholar] [CrossRef]
- Vásquez, J.A.; Escobar, J.W.; Manotas, D.F. AHP–TOPSIS Methodology for Stock Portfolio Investments. Risks 2022, 10, 4. [Google Scholar] [CrossRef]
- Wu, Q.; Liu, X.; Qin, J.; Zhou, L. Multi-Criteria Group Decision-Making for Portfolio Allocation with Consensus Reaching Process under Interval Type-2 Fuzzy Environment. Inf. Sci. 2021, 570, 668–688. [Google Scholar] [CrossRef]
- Mohammed, H.J. The Optimal Project Selection in Portfolio Management Using Fuzzy Multi-Criteria Decision-Making Methodology. J. Sustain. Financ. Invest. 2021, 13, 125–141. [Google Scholar] [CrossRef]
- Estrada-Padilla, A.; Gómez-Santillán, C.; Joaquín Fraire-Huacuja, H.; Cruz-Reyes, L.; Rangel-Valdez, N.; Lucila Morales-Rodríguez, M.; José Puga-Soberanes, H. GRASP/Δ: An Efficient Algorithm for the Multi-Objective Portfolio Optimization Problem. Expert Syst. Appl. 2023, 211, 118647. [Google Scholar] [CrossRef]
- Ekirapa, H.E. An Assessment of the Relationship between Risk and Return at the Nairobi Securities Exchange Using the Downside Risk Capital Asset Pricing Model; University of Nairobi: Nairobi, Kenya, 2015. [Google Scholar]
- Tabasi, H.; Yousefi, V.; Tamošaitienė, J.; Ghasemi, F. Estimating Conditional Value at Risk in the Tehran Stock Exchange Based on the Extreme Value Theory Using Garch Models. Adm. Sci. 2019, 9, 40. [Google Scholar] [CrossRef]
- Popović, M.; Savić, G.; Kuzmanović, M.; Martić, M. Using Data Envelopment Analysis and Multi-Criteria Decision-Making Methods to Evaluate Teacher Performance in Higher Education. Symmetry 2020, 12, 563. [Google Scholar] [CrossRef]
- Zhang, K.; Xie, Y.; Noorkhah, S.A.; Imeni, M.; Das, S.K. Neutrosophic Management Evaluation of Insurance Companies by a Hybrid TODIM-BSC Method: A Case Study in Private Insurance Companies. Manag. Decis. 2022. ahead-of-print. [Google Scholar] [CrossRef]
- Mohammadi, S.E.; Mohammadi, E.; Barzinpour, F. Portfolio Optimization in Tehran Stock Exchange by Using Data Envelopment Analysis and Symbiotic Organisms Search. Mod. Res. Decis. Mak. 2018, 3, 223–248. [Google Scholar]
- Jalota, H.; Mandal, P.K.; Thakur, M.; Mittal, G. A Novel Approach to Incorporate Investor’s Preference in Fuzzy Multi-Objective Portfolio Selection Problem Using Credibility Measure. Expert Syst. Appl. 2023, 212, 118583. [Google Scholar] [CrossRef]
- Brito, I. A Portfolio Stock Selection Model Based on Expected Utility, Entropy and Variance. Expert Syst. Appl. 2023, 213, 118896. [Google Scholar] [CrossRef]
- Ali, Y.; Mehmood, B.; Huzaifa, M.; Yasir, U.; Khan, A.U. Development of a New Hybrid Multi Criteria Decision-Making Method for a Car Selection Scenario. Facta Univ. Ser. Mech. Eng. 2020, 18, 357–373. [Google Scholar] [CrossRef]
- Hwang, C.-L.; Yoon, K. Methods for Multiple Attribute Decision Making; Hwang, C.-L., Yoon, K., Eds.; Springer: Berlin/Heidelberg, Germany, 1981; pp. 58–191. ISBN 978-3-642-48318-9. [Google Scholar]
- Pamucar, D.; Bozanic, D.; Kurtov, D. Fuzzification of the Saaty’s Scale and a Presentation of the Hybrid Fuzzy AHP-TOPSIS Model: An Example of the Selection of a Brigade Artillery Group Firing Position in a Defensive Operation. Vojnoteh. Glas. 2016, 64, 966–986. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z. A New Additive Ratio Assessment (ARAS) Method in Multicriteria Decision-Making. Technol. Econ. Dev. Econ. 2010, 16, 159–172. [Google Scholar] [CrossRef]
- Heidary Dahooie, J.; Estiri, M.; Zavadskas, E.K.; Xu, Z. A Novel Hybrid Fuzzy DEA-Fuzzy ARAS Method for Prioritizing High-Performance Innovation-Oriented Human Resource Practices in High Tech SME’s. Int. J. Fuzzy Syst. 2022, 24, 883–908. [Google Scholar] [CrossRef]
- Adanson, M. Familles des Plantes; Vincent: Paris, France, 1763. [Google Scholar]
- Diao, F.; Cai, Q.; Wei, G. Taxonomy Method for Multiple Attribute Group Decision Making Under the Spherical Fuzzy Environment. Informatica 2022, 33, 713–729. [Google Scholar] [CrossRef]
- Hellwig, Z. Application of the Taxonomic Method to the Typological Division of Countries Due to the Level of Their Development and the Structure of Qualified Personnel. Stat. Rev. 1986, 4, 307–327. [Google Scholar]
- Opricovic, S. Multicriteria Optimization of Civil Engineering Systems. Ph.D. Thesis, Faculty of Civil Engineering, Belgrade, Serbia, 1998. [Google Scholar]
- Büyüközkan, G.; Havle, C.A.; Feyzioğlu, O. Digital Competency Evaluation of Low-Cost Airlines Using an Integrated IVIF AHP and IVIF VIKOR Methodology. J. Air Transp. Manag. 2021, 91, 101998. [Google Scholar] [CrossRef]
- Hezer, S.; Gelmez, E.; Özceylan, E. Comparative Analysis of TOPSIS, VIKOR and COPRAS Methods for the COVID-19 Regional Safety Assessment. J. Infect. Public Health 2021, 14, 775–786. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Kildiene, S. State of Art Surveys of Overviews on MCDM/MADM Methods. Technol. Econ. Dev. Econ. 2014, 20, 165–179. [Google Scholar] [CrossRef]
- Tavana, M.; Shaabani, A.; di Caprio, D.; Amiri, M. An Integrated and Comprehensive Fuzzy Multicriteria Model for Supplier Selection in Digital Supply Chains. Sustain. Oper. Comput. 2021, 2, 149–169. [Google Scholar] [CrossRef]
- Balali, A.; Valipour, A.; Edwards, R.; Moehler, R. Ranking Effective Risks on Human Resources Threats in Natural Gas Supply Projects Using ANP-COPRAS Method: Case Study of Shiraz. Reliab. Eng. Syst. Saf. 2021, 208, 107442. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J.; Zakarevicius, A. Optimization of Weighted Aggregated Sum Product Assessment. Elektron. Elektrotech. 2012, 122, 3–6. [Google Scholar] [CrossRef]
- Deveci, M.; Canıtez, F.; Gökaşar, I. WASPAS and TOPSIS Based Interval Type-2 Fuzzy MCDM Method for a Selection of a Car Sharing Station. Sustain. Cities Soc. 2018, 41, 777–791. [Google Scholar] [CrossRef]
- Miç, P.; Antmen, Z.F. A Decision-Making Model Based on TOPSIS, WASPAS, and MULTIMOORA Methods for University Location Selection Problem. SAGE Open 2021, 11. [Google Scholar] [CrossRef]
- Pishgar-Komleh, S.H.; Zylowski, T.; Rozakis, S.; Kozyra, J. Efficiency under Different Methods for Incorporating Undesirable Outputs in an LCA+DEA Framework: A Case Study of Winter Wheat Production in Poland. J. Environ. Manage. 2020, 260, 110138. [Google Scholar] [CrossRef] [PubMed]
- Long, Q.; Song, K. Operational Performance Evaluation of E-Government Microblogs Under Emergencies Based on a DEA Method. Inf. Syst. Front. 2021, 24, 1–18. [Google Scholar] [CrossRef]
- Li, H.; Yang, W.; Zhou, Z.; Huang, C. Resource Allocation Models’ Construction for the Reduction of Undesirable Outputs Based on DEA Methods. Math. Comput. Model. 2013, 58, 913–926. [Google Scholar] [CrossRef]
- Roodposhti, F.R.; Jahromi, M.B.; Kamalzadeh, S. Portfolio Selection Using Analytic Hierarchy Process and Numerical Taxonomy Analysis: Case Study of Iran. Am. J. Financ. Account. 2018, 5, 394. [Google Scholar] [CrossRef]
- Mendonça, G.H.M.; Ferreira, F.G.D.C.; Cardoso, R.T.N.; Martins, F.V.C. Multi-Attribute Decision Making Applied to Financial Portfolio Optimization Problem. Expert Syst. Appl. 2020, 158, 113527. [Google Scholar] [CrossRef]
- Samaras, G.D.; Matsatsinis, N.F.; Zopounidis, C. A Multicriteria DSS for Stock Evaluation Using Fundamental Analysis. Eur. J. Oper. Res. 2008, 187, 1380–1401. [Google Scholar] [CrossRef]
- Chen, W. Artificial Bee Colony Algorithm for Constrained Possibilistic Portfolio Optimization Problem. Phys. A Stat. Mech. Appl. 2015, 429, 125–139. [Google Scholar] [CrossRef]
- González, Y.; Conde, A.; Treviño, J. New DOCR Coordination via Non-Conventional Time Curves to Achieve Bounded Relay Times. Int. J. Electr. Power Energy Syst. 2023, 146, 108775. [Google Scholar] [CrossRef]

| Metric | Formula | |
|---|---|---|
| 1 | Sales growth rate = | (Current period sales − prior period sales)/prior period sales |
| 2 | Net income growth rate = | (Current period net income − prior period net income)/prior period net income |
| 3 | EPS growth rate = | (Current period EPS − prior period EPS)/prior period EPS |
| 4 | EPS = | Net income/total number of shares |
| 5 | Net profit margin = | Net profits/net Sales |
| 6 | Operating margin = | Operating income/revenue (or sales) |
| 7 | ROA = | Net income/total assets |
| 8 | ROE = | Net income/total equity |
| 9 | Total asset turnover = | Net sales/total assets |
| 10 | Accounts receivable turnover = | Net sales/average account receivables |
| 11 | Inventory turnover = | Cost of goods sold/average inventories |
| 12 | Beta = | |
| 13 | Financial risk = | Total debts/total assets |
| 14 | Price to EPS = | Price per share EPS |
| 15 | Price to BVPS = | Price per share/total number of shares/equities |
| Companies Numbers | VIKOR | COPRAS | TOPSIS | WASPAS | Taxonomy |
|---|---|---|---|---|---|
| 1 | 2 | 24 | 6 | 23 | 1 |
| 2 | 11 | 19 | 13 | 22 | 12 |
| 3 | 16 | 14 | 19 | 9 | 11 |
| 4 | 5 | 7 | 4 | 3 | 3 |
| 5 | 10 | 5 | 5 | 6 | 4 |
| 6 | 24 | 16 | 12 | 20 | 24 |
| 7 | 4 | 10 | 22 | 5 | 16 |
| 8 | 20 | 15 | 16 | 14 | 19 |
| 9 | 22 | 22 | 24 | 24 | 22 |
| 10 | 18 | 21 | 17 | 17 | 14 |
| 11 | 15 | 11 | 11 | 11 | 6 |
| 12 | 7 | 1 | 1 | 1 | 21 |
| 13 | 21 | 9 | 9 | 19 | 20 |
| 14 | 8 | 20 | 18 | 7 | 9 |
| 15 | 12 | 4 | 3 | 10 | 7 |
| 16 | 3 | 23 | 20 | 15 | 15 |
| 17 | 13 | 8 | 8 | 13 | 13 |
| 18 | 14 | 12 | 21 | 18 | 17 |
| 19 | 19 | 3 | 7 | 12 | 18 |
| 20 | 1 | 6 | 10 | 2 | 2 |
| 21 | 23 | 2 | 2 | 16 | 23 |
| 22 | 6 | 18 | 23 | 8 | 5 |
| 23 | 9 | 13 | 15 | 4 | 8 |
| 24 | 17 | 17 | 14 | 21 | 10 |
| Companies Numbers | Taxonomy | ARAS | WASPAS | TOPSIS | COPRAS | VIKOR | Mean Rank | Final Rank |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 23 | 6 | 24 | 2 | 9.8 | 6 |
| 2 | 12 | 9 | 22 | 13 | 19 | 11 | 14.3 | 17 |
| 3 | 11 | 14 | 9 | 19 | 14 | 16 | 13.8 | 14 |
| 4 | 3 | 6 | 3 | 4 | 7 | 5 | 4.6 | 2 |
| 5 | 4 | 15 | 6 | 5 | 5 | 10 | 7.5 | 4 |
| 6 | 24 | 21 | 20 | 12 | 16 | 24 | 19.5 | 23 |
| 7 | 16 | 22 | 5 | 22 | 10 | 4 | 13.1 | 13 |
| 8 | 19 | 4 | 14 | 16 | 15 | 20 | 14.6 | 19 |
| 9 | 22 | 12 | 24 | 24 | 22 | 22 | 21 | 24 |
| 10 | 14 | 18 | 17 | 17 | 21 | 18 | 17.5 | 21 |
| 11 | 6 | 13 | 11 | 11 | 11 | 15 | 11.1 | 8 |
| 12 | 21 | 2 | 1 | 1 | 1 | 7 | 5.5 | 3 |
| 13 | 20 | 17 | 19 | 9 | 9 | 21 | 15.8 | 20 |
| 14 | 9 | 11 | 7 | 18 | 20 | 8 | 12.1 | 11 |
| 15 | 7 | 19 | 10 | 3 | 4 | 12 | 9.1 | 5 |
| 16 | 15 | 8 | 15 | 20 | 23 | 3 | 14 | 16 |
| 17 | 13 | 10 | 13 | 8 | 8 | 13 | 10.8 | 7 |
| 18 | 17 | 23 | 18 | 21 | 12 | 14 | 17.5 | 22 |
| 19 | 18 | 24 | 12 | 7 | 3 | 19 | 13.8 | 15 |
| 20 | 2 | 5 | 2 | 10 | 6 | 1 | 4.3 | 1 |
| 21 | 23 | 1 | 16 | 2 | 2 | 23 | 11.1 | 9 |
| 22 | 5 | 16 | 8 | 23 | 18 | 6 | 12.6 | 12 |
| 23 | 8 | 20 | 4 | 15 | 13 | 9 | 11.5 | 10 |
| 24 | 10 | 7 | 21 | 14 | 17 | 17 | 14.3 | 18 |
| Company 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | Total Wins | Borda Count | Difference between Wins and Losses | Copeland | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Company 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 17 | 5 | 15 | 4 | |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 14 | −8 | 15 | |
| 3 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 8 | 9 | −2 | 12 | |
| 4 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 19 | 3 | 17 | 3 | |
| 5 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 18 | 4 | 15 | 4 | |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 16 | −21 | 20 | |
| 7 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 7 | 10 | −1 | 11 | |
| 8 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 6 | 11 | −6 | 14 | |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 16 | −22 | 21 | |
| 10 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 14 | −13 | 18 | |
| 11 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 12 | 7 | 5 | 7 | |
| 12 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 23 | 1 | 23 | 1 | |
| 13 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 3 | 14 | −12 | 17 | |
| 14 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 8 | 9 | 2 | 9 | |
| 15 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 15 | 6 | 10 | 5 | |
| 16 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 5 | 12 | −8 | 15 | |
| 17 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 11 | 8 | 5 | 7 | |
| 18 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 15 | −15 | 19 | |
| 19 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 13 | −9 | 16 | |
| 20 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 20 | 2 | 19 | 2 | |
| 21 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 8 | 9 | 7 | 6 | |
| 22 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 8 | 9 | 1 | 10 | |
| 23 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 11 | 8 | 3 | 8 | |
| 24 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 | 12 | −5 | 13 | |
| Total losses | 2 | 11 | 10 | 2 | 3 | 21 | 8 | 12 | 22 | 16 | 7 | 0 | 15 | 6 | 5 | 13 | 6 | 17 | 13 | 1 | 1 | 7 | 8 | 10 | 216 |
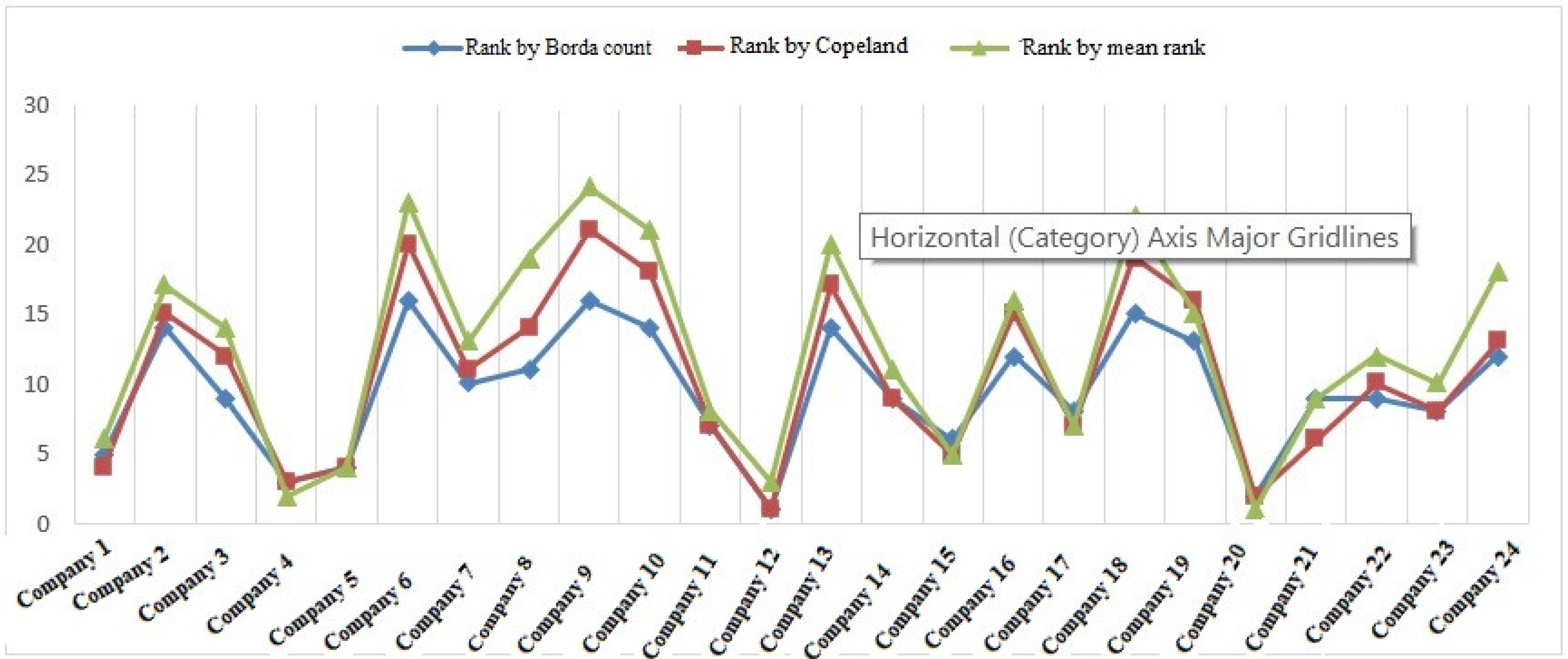
| Companies Number | Rank by Borda Count | Rank by Copeland | Rank by Mean Rank |
|---|---|---|---|
| 1 | 5 | 4 | 6 |
| 2 | 14 | 15 | 17 |
| 3 | 9 | 12 | 14 |
| 4 | 3 | 3 | 2 |
| 5 | 4 | 4 | 4 |
| 6 | 16 | 20 | 23 |
| 7 | 10 | 11 | 13 |
| 8 | 11 | 14 | 19 |
| 9 | 16 | 21 | 24 |
| 10 | 14 | 18 | 21 |
| 11 | 7 | 7 | 8 |
| 12 | 1 | 1 | 3 |
| 13 | 14 | 17 | 20 |
| 14 | 9 | 9 | 11 |
| 15 | 6 | 5 | 5 |
| 16 | 12 | 15 | 16 |
| 17 | 8 | 7 | 7 |
| 18 | 15 | 19 | 22 |
| 19 | 13 | 16 | 15 |
| 20 | 2 | 2 | 1 |
| 21 | 9 | 6 | 9 |
| 22 | 9 | 10 | 12 |
| 23 | 8 | 8 | 10 |
| 24 | 12 | 13 | 18 |
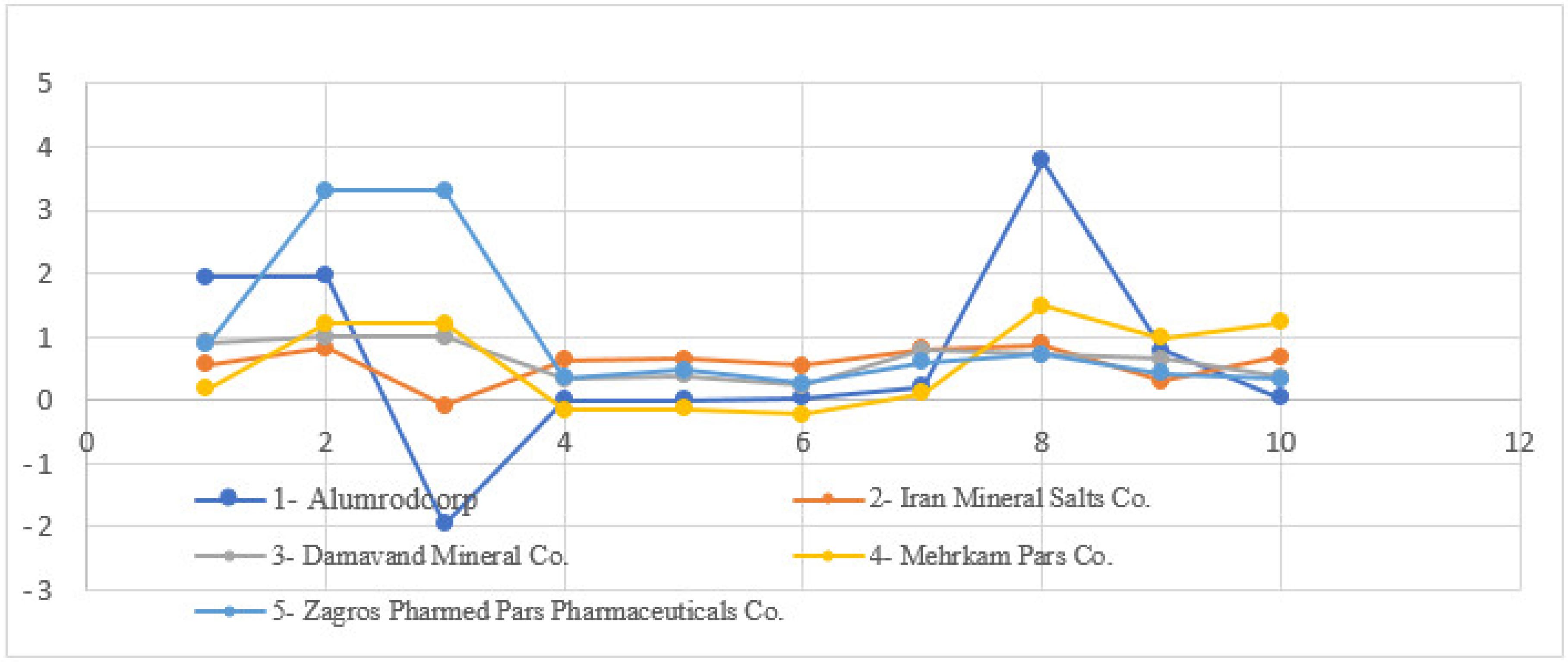
| Companies | Sales Growth (1) | Net Income Growth (2) | EPS Growth (3) | Net Profit Margin (4) | Operating Margin (5) | ROA (6) | ROE (7) | Total Assets Turnover (8) | Financial Risk (9) | β Coefficient (10) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1/9404 | 1/9611 | −1/9611 | 0/0074 | 0/0076 | 0/0430 | 0/2129 | 3/7761 | 0/7931 | 0/0399 |
| 4 | 0/5572 | 0/8219 | −0/0890 | 0/6213 | 0/6399 | 0/5423 | 0/8020 | 0/8728 | 0/3035 | 0/6841 |
| 5 | 0/9013 | 0/9935 | 0/9935 | 0/3286 | 0/3873 | 0/2339 | 0/7790 | 0/7118 | 0/6460 | 0/3720 |
| 12 | 0/1774 | 1/2144 | 1/2144 | −0/1549 | −0/1348 | −0/2298 | 0/0987 | 1/4829 | 0/9867 | 1/2314 |
| 20 | 0/8756 | 3/3155 | 3/3155 | 0/3543 | 0/4779 | 0/2550 | 0/5979 | 0/7197 | 0/4246 | 0/3366 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, D.; Imeni, M.; Edalatpanah, S.A.; Alburaikan, A.; Khalifa, H.A.E.-W. Optimal Selection of Stock Portfolios Using Multi-Criteria Decision-Making Methods. Mathematics 2023, 11, 415. https://doi.org/10.3390/math11020415
Jing D, Imeni M, Edalatpanah SA, Alburaikan A, Khalifa HAE-W. Optimal Selection of Stock Portfolios Using Multi-Criteria Decision-Making Methods. Mathematics. 2023; 11(2):415. https://doi.org/10.3390/math11020415
Chicago/Turabian StyleJing, Dongmei, Mohsen Imeni, Seyyed Ahmad Edalatpanah, Alhanouf Alburaikan, and Hamiden Abd El-Wahed Khalifa. 2023. "Optimal Selection of Stock Portfolios Using Multi-Criteria Decision-Making Methods" Mathematics 11, no. 2: 415. https://doi.org/10.3390/math11020415
APA StyleJing, D., Imeni, M., Edalatpanah, S. A., Alburaikan, A., & Khalifa, H. A. E.-W. (2023). Optimal Selection of Stock Portfolios Using Multi-Criteria Decision-Making Methods. Mathematics, 11(2), 415. https://doi.org/10.3390/math11020415









