An Image-Encipherment Algorithm Using a Combination of a One-Dimensional Chaotic Map and a Three-Dimensional Piecewise Chaotic Map

Abstract

One-dimensional and three-dimensional piecewise chaotic maps are used to propose an image-encipher technique in this article. First, the logistic map is used to construct the pseudo-random sequence. After that, this sequence is used to scramble the plain image. Next, the three-dimensional piecewise chaotic map has produced a mask of the chaotic sequence. After doing some preprocessing steps on the mask, a bit-wise XOR operation with the mask is applied to the shuffled image. The suggested algorithm is used to encipher and decipher a different range of images. To check the algorithm security and efficiency, the algorithm performance was calculated using multiple statistical tests and compared to several recent algorithms. Furthermore, numerical simulations and experimental data are also used to validate the proposed algorithm’s resistance to various attacks.

1. Introduction

Data-sharing across open networks and the Internet is growing exponentially, and keeping information secret is a major challenge. This information may include text, images, audio, video, etc. Most multimedia applications in today’s world include images. Image encipherment is one prospective way to hide an image’s information. Hence, different encipherment methods for protecting sensitive images from unauthorised users have been developed and used in recent years. In addition, chaotic maps are distinguished by their unpredictability, bifurcation, and acute susceptibility to initial restrictions and parameters of control. These characteristics allow chaotic maps to create a sequence of random numbers that are unpredictable without strictly specifying initial conditions and parameters of control. As a result, chaotic systems are increasingly being used in recent image-encipherment studies, because the secret key should be volatile, unforeseeable, and extremely sensitive to even little value changes.Most encipherment algorithms are dependent on permutation, substitution, or both. In any case, an image is enciphered and deciphered using the exact secret key. In fact, most authors now use the permutation/substitution model. Certainly, this would improve secrecy and make cracking the encipherment more difficult. The permutation/substitution model has two stages. First, permutation, or confusion, is often used to minimize pixel correlation. The value of the pixel is then modified using diffusion.

The first encipherment algorithm through the chaotic map was published in [1]. Many articles after that used chaotic maps of various types to produce strong image-encipherment algorithms. These chaotic maps are of different dimensions—maybe one, two, three, or more. Additionally, some of these are piecewise maps or non-piecewise maps. The researchers suggested an image technique dependent on a 1D chaotic economic map in [2,3]. In [4], a 1D chaotic map relying on the Beta function was presented, which was then used to create an image-encipherment algorithm. In [5], a new encipherment method dependent on the Rijndael architecture that employs a 1D chaotic map and a block cipher in an appropriate mode of operation is described. Ref. [6] used S-Box and a 1D logistic-sine chaotic map to suggest a novel encipherment scheme. Additionally in [7], the authors used a 1D sine-powered chaotic map to develop an encipher system. By combining the logistic map with the sine map, an enhanced 1D sinusoidal chaotic scheme was presented and used to construct a novel image-encipherment algorithm in [8]. All the prior works used non-piecewise 1D chaotic maps for the proposed encipherment algorithms. Ref. [9] presented an algorithm for image encipherment via a 1D piecewise chaotic tent map. In [10], the authors used a novel chaotic system composed of two 1D piecewise chaotic maps. This system uses one chaotic map to confuse another, then used the result as a basis of a novel image-encipherment algorithm. The authors suggested a new scheme to encipher images via a 1D piecewise chaotic map and the bisection method in [11]. A parallel image-encipher algorithm was present in [12]. This method uses a piecewise linear chaotic map (1D map) and a hyperchaotic map (4D non-piecewise map). The previous article employed a hybrid system that included piecewise and non-piecewise chaotic maps of different dimensions.

Since the system behavior is rapidly changing in the chaotic maps with high-dimensional and these have a huge key-space, they are safer than one-dimensional chaotic maps. Therefore, a lot of researchers have proposed algorithms based on high-dimensional maps, but most of them were non-piecewise chaotic maps. For example, if we look at the non-piecewise high-dimensional chaotic maps, we find a lot of articles as shown next. In [13], a new form of encipherment was presented. This form is based on 1D and 2D chaotic maps and genetic operations. A novel image-encipherment technique using keys generated from DNA and plain images via 1D and 2D chaotic maps was presented in [14]. Ref. [15] designed an encipherment system that depended on 2D chaotic economic and logistic maps. An encipherment algorithm using a recent 2D chaotic map that was derived from two 1D chaotic maps in [16]. In [17], the authors present an encipherment algorithm based on a 2D HCM (Henon–Chebyshev map). In [18], the authors created an encipherment technique based on the Henon chaotic map, the Lü 3D chaotic map, and double spiral scans. Ref. [19] took advantage of the Fisher–Yates shuffling algorithm and a 3D chaotic economic map to suggest an encipher scheme. Ref. [20] proposed an image-encipherment system based on the 3D Lorenz chaotic map. An image-encipherment approach using a three-dimensional chaotic map and DNA encoding is suggested in [21]. In [22], an image-encipherment algorithm via a 3D infinite collapse map was introduced. A 3D chaotic map and a strong S-Box were used to build an image-encipherment algorithm in [23]. A new image-encipherment method via the genetic algorithm-III (NSGA) and a four-dimensional chaotic map was presented in [24]. The authors in [25] used a 6D hyperchaotic map to propose an image-encipherment scheme.

In the field of cryptography, neural networks play a significant role. In particular, these algorithms have improved pseudorandomness and complexity. Many authors studied neural networks with image encryption. In [26], the authors introduced a chaotic coupled neural network image-encipherment algorithm. An image-encipherment algorithm based on a hyperchaotic memristive ring neural network is presented in [27]. In [28], the researchers suggested an image-encipherment algorithm via a multiscroll memeristive Hopfield neural network.

On the other hand, a few articles that used piecewise high-dimensional chaotic maps mention some of them as following. Ref. [29] combine the chaotic system with Brownian motion to design a new encipherment algorithm. This chaotic system is composed of two chaotic maps. The first one is a basin chaotic map, and this is a 2D non-piecewise chaotic map, but the other one is a gingerbread man chaotic map, and this is a 2D piecewise chaotic map. A novel coupled 2D piecewise chaotic map was introduced in [30], then used to propose a fast image cryptosystem. The authors in [31] suggested an image-encipherment scheme via a nonlinear 2D piecewise smooth chaotic map. Additionally in [32], a fast image-encipher algorithm via the chaotic baker map was suggested. This map is a 3D piecewise chaotic map.

From the above discussion, it was noticed that there are very few articles that use high-dimensional piecewise chaotic maps for image-encipherment algorithms. This is the reason for proposing an encipherment algorithm via a 3D piecewise chaotic map in the current article. This algorithm has two parts. The first part uses a 1D logistic map to permute the pixel positions to reduce the correlations between them. The other part used a 3D piecewise chaotic map to modify the pixel values of an image.

This article is separated into the sections mentioned below. In Section 2, a basic overview of a 3D piecewise chaotic map is introduced. Section 3 concentrates on the shuffling method that uses the sequence created via the logistic map. Section 4 discusses the suggested encipherment and decipherment algorithms in more detail. Security investigation and comparisons within the literature are given in Section 5 for related algorithms. In Section 6 the conclusion is addressed.

2. 3D Piecewise Chaotic Map (3DPCM)

The 3D piecewise chaotic map is defined by [33]:

$$f(x,y,z)=\left\{\begin{array}{c}\overline{x}\\ \overline{y}\\ \overline{z}\end{array}\right.=\left\{\begin{array}{c}y\\ z\\ c_0+c_{1}x+c_{2}y-\left|z\right|\end{array}\right.$$

(1)

where $c_0,c_1,c_2$ are bifurcation parameters and they are real numbers. Therefore, the state space $(x,y,z)\in R^3$. For some values of its bifurcation parameters, this map shows chaotic attractors. Suppose $x=z_{t-2},y=z_{t-1}$ and $z=z_t,$ such that $(x_t,y_t,z_t)$; $t=0,1,\dots$ be a trajectory of the map (1), the map can be converted into a difference equation of third order as:

$$z_{t+1}=c_0+c_1{z}_{t-2}+c_2{z}_{t-1}-\left|z_t\right|$$

(2)

Two linear zones can be separated in space because of the form of map (1)’s vector field f. Thus, map (1) can be rewritten as follows:

$$f(x,y,z)=\left\{\begin{array}{cc}\left(\begin{array}{c}y\\ z\\ c_0+c_{1}x+c_{2}y-z\end{array}\right)& ,z\ge 0\\ \left(\begin{array}{c}y\\ z\\ c_0+c_{1}x+c_{2}y+z\end{array}\right)& ,z<0\end{array}\right.$$

If $c_1+c_2-2\ne 0$ and $c_1+c_2\ne 0$, then map (1) has two fixed points computed by:

$$S_1=\frac{-c_0}{c_1+c_2-2}(1,1,1),S_1=\frac{-c_0}{c_1+c_2}(1,1,1)$$

If $c_0>0$ and $c_1<2-c_2$, the fixed point $S_1$ is stable if and only if the following requirements are met:

$$\left\{\begin{array}{c}-1<c_1<1\\ c_2<c_1<2-c_2<3-c_1-c_1^2\end{array}\right.$$

However, if $c_0<0$ and $c_1<2-c_2$, the fixed point $S_2$ is stable if and only if the following requirements are met:

$$\left\{\begin{array}{c}-1<c_1<1\\ c_2-2<c_1<-c_2<1+c_1-c_1^2\end{array}\right.$$

If $c_1+c_2\ne 2$ or $c_1+c_2\ne 0$, the map (1) has possible limited orbits, otherwise, all the orbits of the map (1) are unlimited [33]. Figure 1 shows the 3D piecewise chaotic map bifurcation diagram of x plotted versus $c_0\in [0,1.5]$ with $c_1=-0.29$ and $c_2=-0.9$. The Largest Lyapunov Exponent(LLE) of the 3D piecewise chaotic map versus $c_0\in [0,2]$ with $c_1=-0.29$ and $c_2=-0.9$ is presented in Figure 2.

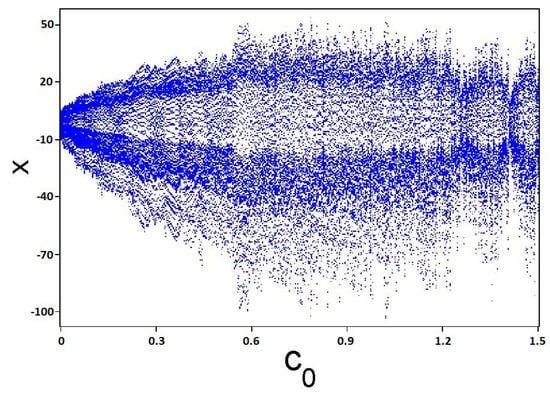
Figure 1. The 3D piecewise chaotic map bifurcation diagram of x plotted versus $c_0\in [0,1.5]$ with $c_1=-0.29$ and $c_2=-0.9$.

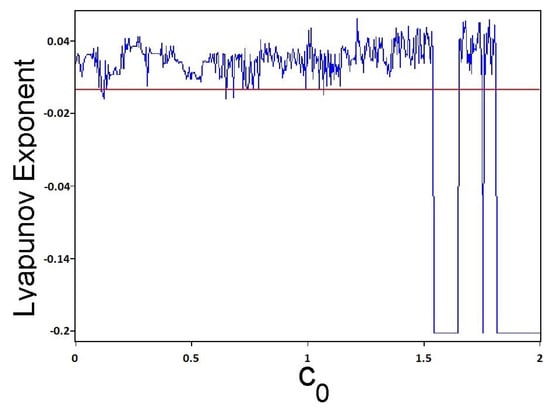
Figure 2. Changing of the LLE of the 3D piecewise chaotic map versus $c_0\in [0,2]$ with $c_1=-0.29$ and $c_2=-0.9$.

The randomness of sequences generated by the 3DPCM is tested via NIST statistical package. To do that, 100 sequences were generated by the 3DPCM and tested by NIST. Table 1 shows the results of all 15 statistical tests. All tests have been passed.

Table 1. The statistical tests of NIST for 3DPCM.

Statistical Test	3DPCM	Result
Frequency monobit test	100/100	√
Block frequency test	100/100	√
Rank test	99/100	√
Runs test	99/100	√
Longest runs test	98/100	√
Cumulative sums test	99/100	√
Discrete Fourier transform	100/100	√
Random excursion test	57/58	√
Random excursion variant test	56/58	√
Universal test	97/100	√
Approximate entropy	99/100	√
Linear complexity test	98/100	√
Serial	99/100	√
Non-Overlapping templates test	98/100	√
Overlapping templates test	100/100	√

3. Generate Shuffling Sequence Using Logistic Map

The plain image pixels are permuted to remove the strong correlations between pixels. In this work, using the sequence created by the logistic map, the pixels’ locations are permuted at random. To produce a random sequence of integer values via a logistic map, the following steps are taken:

1.

Generate $MN$ random fraction numbers using the logistic map $(x_{i+1}=\mu x_i(1-x_i))$ where the plain image has the size $M\times N$ and $\mu$ close to 4.

2.

Index the generated numbers from 1 to $MN$.

3.

Sort the indexed sequence in ascending order.

4.

Take the list of indices after sorting operation as a required sequence.

The $1\times 15$ size key generation is shown in Figure 3.

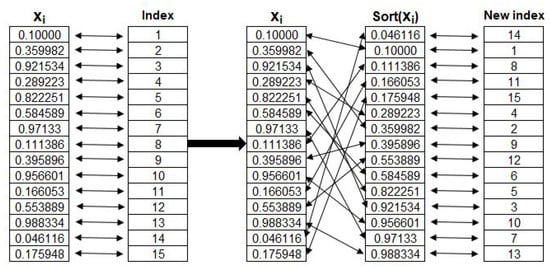
Figure 3. Generate random various values between 1 and 15 using logistic map $x_{i+1}=3.9998x_i(1-x_i)$ and $x_0=0.1$.

4. The Proposed Work

This section has been devoted to the generation of the key and the two image algorithms that are proposed. The first algorithm is to encipher the plain image, and the second is to decipher the encrypted image.

4.1. The Generated Secret Key

Let $\mathbf{A}=\left(a_{ij}\right),i=1,2,\dots ,M,j=1,2,\dots ,N.$ To compute the secret key, we use the factor of key mixing proportion (K) as follows [34]:

$$K=\frac{1}{256}mod\left(\frac{{\sum }_{i=1}^M{\sum }_{j=1}^N{a}_{ij}}{M\times N},256\right),$$

(3)

The initial conditions $x_0,y_0,z_0,x_{r}0,x_{c}0,$ as well as the logistic map and map (1) parameters are then evaluated using the following formulas:

$$\left.\begin{array}{cc}\hfill x_0& =\frac{(x_0+K)}{2},\hfill \\ \hfill y_0& =\frac{(y_0+K)}{2},\hfill \\ \hfill z_0& =\frac{(z_0+K)}{2},\hfill \\ \hfill x_{r0}& =\frac{(x_{r0}+K)}{2},\hfill \\ \hfill x_{c0}& =\frac{(x_{c0}+K)}{2},\hfill \\ \hfill c_0& =0.9+K\hfill \\ \hfill c_1& =-1.29+K\hfill \\ \hfill c_2& =-1.9+K\hfill \\ \hfill \mu & =3.99+0.008\ast K\hfill \end{array}\right\}$$

(4)

4.2. Encipherment Algorithm

Assume the plain image is $A=\left(a_{ij}\right),$ with $1\le i\le M,$ $1\le j\le N,$ and $a_{ij}$ being the pixel value at location $i,j$. The designed algorithm to encipher the image A is introduced in (Algorithm 1). This algorithm is denoted by 3DPCM algorithm from now. It consists of three steps. As described in Section 3, the plan image pixels are first shuffled via the logistic map. The second step is to create a random sequence using the 3D piecewise chaotic map in (1). The last step is to XOR the pixels of the shuffled image with the randomly generated sequence of the proposed map to diffuse them.

4.3. Decipherment Algorithm

This is the opposite of the encipherment algorithm and restores the plain image. Algorithm 2 is the suggested image-decipherment algorithm.   

Algorithm 1 Encipherment Algorithm

Input: Original image A, $x_{r0},x_{c0}$ for Logistic map shuffling and $c_0,c_1,c_2,x_0,y_0,z_0$ for map (1).  Output: Enciphered image E $=\left(e_{i,j}\right),i=1,2,\dots ,M,j=1,2,\dots ,N$.  Step 1: Input the Original image A then transform it to the grey image.  Step 2: Invoke a logistic map using initial values $x_{r0},x_{c0}$ to generate permutations of numbers at random $\{1,2,\dots ,M\}$ and $\{1,2,\dots ,N\},X_p$ and $Y_p$, respectively.  Step 3: Compute ${Shuf}_A$ as follows:     For $i_1=1ToM$, For $i_2=1ToN$          $A(X_p\left(i_1\right),Y_p\left(i_2\right))={Shuf}_A(i_1,i_2)$       End For, End For  Step 4: Change a ${Shuf}_A$ image into vector of size a $1\times MN$.  Step 5: Transform ${Shuf}_A$ to binary vector B = $\{b_1,b_2,\dots ,b_{MN}\}$.  Step 6: Generate $MN$ fractional values using 3D piecewise chaotic map and initial values $c_0,c_1$ and $c_2,$ as follows:     $x_1=y_0$,     $y_1=z_0$,     $z_1=c_0+c_1{x}_0+c_2{y}_0-\left|\left(z_0\right)\right|$,     $w_1=\frac{frac\left(x_1\right)+frac\left(y_1\right)+frac\left(z_1\right)}{3}$     For $i=1ToMN+499$           $x_{i+1}=y_i$, $y_{i+1}=z\left(i\right)$,     $z_{i+1}=c_0+c_{1}x\left(i\right)+c_{2}y\left(i\right)-\left|z\left(i\right)\right|$           $w_{i+1}=\frac{frac\left(x_{i+1}\right)+frac\left(y_{i+1}\right)+frac\left(z_{i+1}\right)}{3}$     End For  Step 7: For the values in Step 6, perform the following preprocessing:     $W=mod\left(floor(w(500:MN+499)\times {10}^{14},256)\right)$  Step 8: To compute the $\mathbf{Map}$, transform $\mathbf{W}$ to a binary vector.  Step 9: Perform ${\mathbf{B}}_{\mathbf{Map}}=XOR(\mathbf{B},\mathbf{Map})$.  Step 10: Transform ${\mathbf{B}}_{\mathbf{Map}}$ to decimal vector $\mathbf{D}=\{d_1,d_2,\dots ,d_{MN}\}$.  Step 11: Change $\mathbf{D}$ into $M\times N$ array, which we will call $\mathbf{E}$. $\mathbf{E}$ represents the enciphered image.  Step 12: End

Algorithm 2 Decipherment Algorithm

Input: Enciphered image $\mathbf{E},$$x_{r0},x_{c0}$ for logistic map shuffling and $c_0,c_1,c_2,x_0,y_0,z_0$ for 3D piecewise chaotic map (map (1)).  Output: Original image $\mathbf{A}$.  Step 1: Read the enciphered image and transform it into a vector with a size of $1\times MN$.  Step 2: Transform the array $\mathbf{E}$ to binary vector $\mathbf{B}=\{b_1,b_2,\dots ,b_{MN}\}$.  Step 3: Using initial values $c_0,c_1$ and $c_2,$ generate fractional values of size $MN$ via map (1) as follows:     $x_1=y_0$, $y_1=z_0$, $z_1=c_0+c_1{x}_0+c_2{y}_0-\left|z_0\right|$     $w_1=\frac{frac\left(x_1\right)+frac\left(y_1\right)+frac\left(z_1\right)}{3}$     For $i=1ToMN+499$         $x_{i+1}=y_i$, $y_{i+1}=z\left(i\right)$, $z_{i+1}=c_0+c_{1}x\left(i\right)+c_{2}y\left(i\right)-\left|z\left(i\right)\right|$         $w_{i+1}=\frac{frac\left(x_{i+1}\right)+frac\left(y_{i+1}\right)+frac\left(z_{i+1}\right)}{3}$     End For  Step 4: Modify Step 3’s values as follows: $W=mod\left(floor(w(500:MN+499)\times {10}^{14},256)\right)$  Step 5: Transform $\mathbf{W}$ to binary to evaluate the $\mathbf{Map}$ vector.  Step 6: Perform ${\mathbf{B}}_{\mathbf{Map}}=XOR(\mathbf{B},\mathbf{Map})$.  Step 7: Transform ${\mathbf{B}}_{\mathbf{Map}}$ to decimal vector $\mathbf{D}=\{d_1,d_2,\dots ,d_{MN}\}$.  Step 8: Change $\mathbf{D}$ into $M\times N$ array, say $Shu{f}_A$ as the Shuffling original image.  Step 9: Using initial values $x_{r0},x_{c0}$, invoke a logistic map using to generate permutations of numbers at random $\{1,2,\dots ,M\}$ and $\{1,2,\dots ,N\},X_p$ and $Y_p$, respectively.  Step 10: Compute A as follows:      For $i1=1ToM$, For $i2=1ToN$           $A(X_p\left(i1\right),Y_p\left(i2\right))={Shuf}_A(i1,i2)$       End For, End For  Step 11: End

5. Security Analyses

Samples of different images were enciphered using 3DPCM algorithm. Then, some statistical tests were applied to these enciphered images to check the security and performance of 3DPCM algorithm. All the plain images in this article were chosen from the image databases [35].

5.1. Histogram Analysis

Enciphered images must have a uniform pixel distribution according to the encipherment scheme. This means that the cryptanalysts are having trouble extracting accurate statistical data from the enciphered image. Histogram analysis of a set of several plain images and their enciphered images is displayed in Figure 4 and Figure 5. Original images and their histograms, and enciphered images and their histograms, are displayed, respectively.

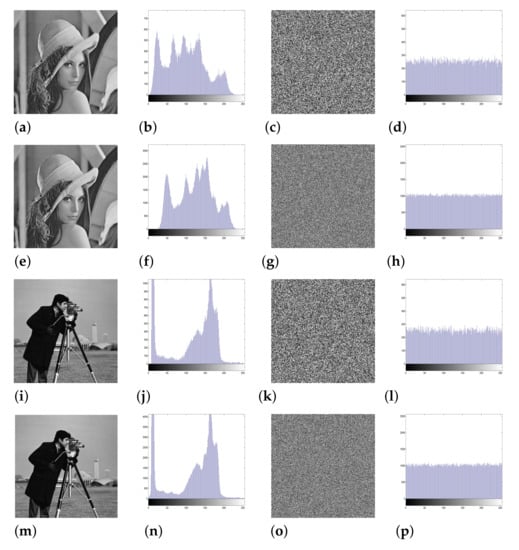
Figure 4. Histogram analysis: the plain images ((a) Lena${}_{(256\times 256)}$, (e) Lena${}_{(512\times 512)}$, (i) Cameraman${}_{(256\times 256)}$, and (m) Cameraman${}_{(512\times 512)}$) and their corresponding histograms (b,f,j,n), the corresponding enciphered images (c,g,k,o) and their corresponding histograms (d,h,l,p).

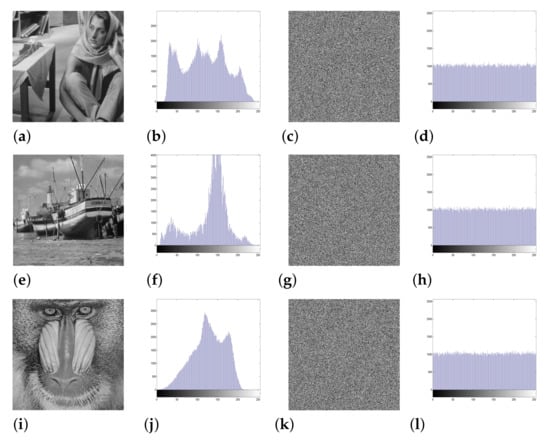
Figure 5. Histogram analysis: the plain images ((a) Barbara${}_{(512\times 512)}$, (e) Boat${}_{(512\times 512)}$, and (i) Mandrill${}_{(512\times 512)}$) and their corresponding histograms (b,f,j), the corresponding enciphered images (c,g,k) and their corresponding histograms (d,h,l).

The enciphered image histograms are uniformly distributed (the last column of Figure 4 and Figure 5). As a result, the 3DPCM Algorithm is immune to statistical attacks. Additionally, the ${\chi }^2$ test is applied to demonstrate the uniformity of the enciphered image histogram. The chi-square value of the image is calculated using the formula:

$${\displaystyle {\chi }^2=\sum _{i=0}^{255}\frac{{(P_i-\overline{F_i})}^2}{\overline{F_i}}}$$

(5)

where:

$P_i$: the occurrence frequency that has been observed of pixel value i,

$F_i$: the occurrence frequency that has been expected of pixel value i in uniform distribution, and it computes $(M\times N)/256$, where M represents the image height and N represents its width.

$\alpha =0.05$: the level of significance.

The ${\chi }^2$ values are given in Table 2 using the enciphered images. In Table 2, the measured ${\chi }^2$ values are below ${\chi }^2(255,0.05)\approx 293$. As a result, the enciphered image histograms have uniform distributions.

Table 2. ${\chi }^2$ values of plain and enciphered images at $c_0=1,c_1=-0.29,c_2=-0.9,x_0=2.10,$$y_0=2.10,z_0=2.10,x_{r0}=0.01,x_{c0}=0.02$ and $\mu =3.998$.

Image	${\mathit{\chi }}^2$
	Plain Image	Enciphered Image
Lena${}_{(256\times 256)}$	$3.0578\times {10}^4$	246.4531
Lena${}_{(512\times 512)}$	$1.5834\times {10}^5$	233.4883
Cameraman${}_{(256\times 256)}$	$1.1097\times {10}^5$	279.6250
Cameraman${}_{(512\times 512)}$	$4.1853\times {10}^5$	267.8730
Barbara${}_{(512\times 512)}$	$9.5549\times {10}^4$	288.1602
Boat${}_{(512\times 512)}$	$3.8397\times {10}^5$	274.2891
Mandrill${}_{(512\times 512)}$	$2.1137\times {10}^5$	265.9980

5.2. Information Entropy Analysis

Entropy is a useful metric for evaluating the degree of randomness in an image. With increasing image information entropy, the unpredictability of image information distribution increases and visual information decreases.

The entropy, H, is measured as follows:

$${\displaystyle H\left(Y\right)=-\sum _{i=0}^{2^n-1}p\left(y_i\right){log}_{2}p\left(y_i\right)}$$

(6)

where $p\left(y_i\right)$ is the probability of the ith possible value in Y; and the greyscale values are represented by bit number n.

To estimate the randomness, the global entropy (GE) and actual block entropy (ABE) are calculated. The image is separated into K non-intersecting blocks, each with a specified number of pixels (T), to determine the actual block entropy. After that, each block’s entropy is calculated, and the mean of the entropies for all blocks is computed to determine the actual block entropy. The global entropy and actual block entropy at $K=100$ and $T=16$ of some enciphered images are displayed in Table 3. Table 4 displays comparison between the global entropy of 3DPCM algorithm and some other new algorithms.

Table 3. Entropy of enciphered images at $c_0=1,c_1=-0.29,c_2=-0.9,x_0=2.10,y_0=2.10,$$z_0=2.10,x_{r0}=0.01,x_{c0}=0.02$ and $\mu =3.998$.

Image	GE	ABE	Theoretical ABE
			$\mathbf{\alpha }=\mathbf{0.01}$	$\mathbf{\alpha }=\mathbf{0.05}$
			7.1628	7.1663
Lena${}_{(256\times 256)}$	7.9973	7.2582	√	√
Lena${}_{(512\times 512)}$	7.9994	7.2602	√	√
Cameraman${}_{(256\times 256)}$	7.9969	7.2451	√	√
Cameraman${}_{(512\times 512)}$	7.9993	7.2968	√	√
Barbara${}_{(512\times 512)}$	7.9992	7.2889	√	√
Boat${}_{(512\times 512)}$	7.9992	7.2690	√	√
Mandrill${}_{(512\times 512)}$	7.9993	7.2422	√	√

Table 4. A comparison between GE via 3DPCM algorithm and some other new algorithms.

Image	3DPCM Algorithm	Ref. [6]	Ref. [14]	Ref. [16]
Lena	7.9994	7.9971	7.9897	7.9971
Cameraman	7.9993	7.9978	7.9890	7.9976

5.3. Correlation Analysis

Usually, plain images have strong correlations between adjacent pixels in three directions—horizontal, vertical, and diagonal. This must be reduced. Therefore, a good encipherment algorithm must produce an enciphered image that has a correlation close to zero between its neighbouring pixels. The correlation between two points is given by

$$r_{uv}=\frac{Cov(u,v)}{\sqrt{D\left(u\right)}\sqrt{D\left(v\right)}}$$

(7)

where

$${\displaystyle Cov(u,v)=\frac{1}{N}\sum _{i=1}^N(u_i-E\left(u\right))(v_i-E\left(v\right)),}$$

(8)

$${\displaystyle D\left(u\right)=\frac{1}{N}\sum _{i=1}^N{(u_i-E\left(u\right))}^2,}$$

(9)

and

$${\displaystyle E\left(u\right)=\frac{1}{N}\sum _{i=1}^N{u}_i.}$$

(10)

Figure 6 depicts the relationship distribution of two horizontally, vertically, and diagonally neighbouring pixels in Lena’s plain and enciphered images ($512\times$512).

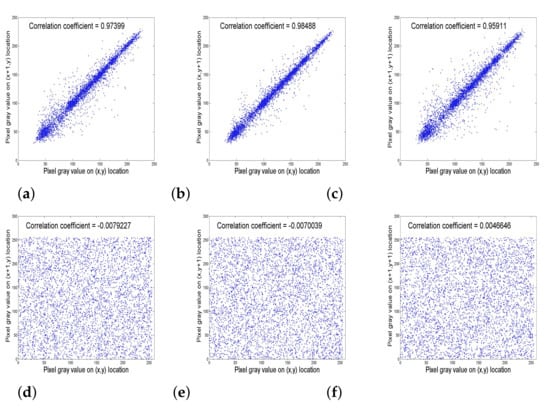
Figure 6. Correlation coefficients of neighbouring pixels for Lena${}_{(256\times 256)}$ image in (a) Horizontal, (b) Vertical and (c) Diagonal directions. Additionally, correlation coefficients of neighbouring pixels for the enciphered image of Lena${}_{(256\times 256)}$ in (d) Horizontal, (e) Vertical and (f) Diagonal directions.

Table 5 shows the correlations between neighbouring pixels in plain images and enciphered images in the three directions. The correlation of all enciphered images using the 3DPCM algorithm is close to zero, as shown in this table. In the plain images, it is near one. Table 6 proposed a comparison based on correlation between neighbouring pixels in the enciphered images between 3DPCM algorithm and some new encryption algorithms in the literature. As seen in this table, the 3DPCM algorithm produces better results.

Table 5. Two neighbouring pixels Correlation of plain and enciphered image at $a=1,b=-0.29,$$c=-0.9,x_0=2.1,y_0=2.1,z_0=2.1,x_{r0}=0.01,x_{c0}=0.02$ and $\mu =3.998$.

Image	Plain Image			Enciphered Image
	H	V	D	H	V	D
Lena${}_{(256\times 256)}$	0.9372	0.9671	0.9195	0.0231	0.0150	0.0017
Lena${}_{(512\times 512)}$	0.9740	0.9849	0.9591	−0.0079	−0.0070	0.0047
Cameraman${}_{(256\times 256)}$	0.9338	0.9579	0.9052	0.0162	0.0086	0.0045
Cameraman${}_{(512\times 512)}$	0.9846	0.9882	0.9742	−0.0002	−0.0008	0.0041
Barbara${}_{(512\times 512)}$	0.9126	0.9635	0.9042	−0.0034	−0.0116	0.0130
Boat${}_{(512\times 512)}$	0.9347	0.9714	0.9207	0.0130	0.0030	0.0143
Mandrill${}_{(512\times 512)}$	0.9379	0.9187	0.8742	−0.0053	0.0125	0.0140

Table 6. Correlations between two neighbouring pixels in the enciphered image Lena${}_{(512\times 512)}$ via the $\mathbf{3}\mathbf{DPCM}$ algorithm, as well as new encipherment algorithms.

	3DPCM Algorithm	Ref. [18]	Ref. [15]
H	−0.0079	−0.0685	−0.0091
V	−0.0070	0.0857	−0.0798
D	0.0047	0.0059	−0.0062

5.4. Sensitivity Analyses

The sensitivity of the encipherment algorithm to relatively few modifications in the plain image and in the secret key is discussed in this section. In the effective encipherment algorithm, any minor modifications in the plain image pixel values or the true secret key should be displayed as the output of the non-identical enciphered image.

5.4.1. Key Sensitivity Analysis

A good encipherment algorithm needs to be extremely sensitive to its secret key to withstand an intensive attack, which implies that even small changes in the secret key can produce completely different enciphered images. As a result, if the decipherment key and the encipherment key are slightly different, an enciphered image must be impossible to decipher using the 3DPCM algorithm or recover any patterns from the plain image.

To see how sensitive the secret key is, after the plain image was enciphered with the secret key, only one of the secret key parameters was updated by adding a very small value to its original value, while the other parameters remained unmodified. The enciphered image is then deciphered using the updated secret key.

To show the 3DPCM algorithm sensitivity to the secret key, a very small error ($+{10}^{-14}$) was added to just one parameter in the secret key, and the deciphered images with the updated secret key were displayed in Figure 7a–i. It can be proven that no meaningful information can be extracted from any deciphered image with the modified secret key. Therefore, the plain image is recovered via the original secret key, as shown in Figure 7j. The above discussion demonstrates the 3DPCM algorithm security.

Figure 7. Key sensitivity analysis result.

5.4.2. Plain Image Sensitivity Analysis

To avoid differential attacks, the encipherment algorithm should be particularly sensitive to the plain image. Consequently, if even one of the original image pixel is updated, practically all the enciphered image pixels will change as well. If this occurs, the algorithm is said to have the diffusion property. The efficiency to extend some small improvement in the plain image over the entire enciphered image is known as the diffusion property. NPCR and UACI are the two measurements used to compute the sensitivity of the 3DPCM algorithm to small modifications in the plain images. They are determined as follows:

$$NPCR=\frac{{\displaystyle \sum _{u,v}D(u,v)}}{M\times N}\times 100\%$$

(11)

$${\displaystyle UACI=\frac{1}{M\times N}\sum _{u,v}\frac{|E_1(u,v)-E_2(u,v)|}{255}\times 100\%}$$

(12)

where:

$$D(u,v)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}{E}_1(u,v)=E_2(u,v)\hfill \\ 1\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(13)

where the image dimensions are $M,N$, and $E_1$ and $E_2$ are the results of running the 3DPCM algorithm to a plain image and a plain image that has been changed by one pixel, respectively. NPCR has a theoretical value of 99.61% and UACI has a theoretical value of 33.46%. NPCR and UACI are calculated for various tested images in Table 7. NPCR has an average value of 99.6097% and UACI has an average value of 33.4666%, all of which are similar to theoretical values. The 3DPCM is compared to various other novel algorithms using NPCR and UACI measurements in Table 8.

Table 7. NPCR and UACI values for various tested images at $c_0=1,c_1=-0.29,c_2=-0.9,$$x_0=2.10,y_0=2.10,z_0=2.10,x_{r0}=0.01,x_{c0}=0.02$ and $\mu =3.998$.

Image	NPCR	UACI
Lena${}_{(256\times 256)}$	99.6033%	33.3807
Lena${}_{(512\times 512)}$	99.6101%	33.4906
Cameraman${}_{(256\times 256)}$	99.5956%	33.4710
Cameraman${}_{(512\times 512)}$	99.6078%	33.5240
Barbara${}_{(512\times 512)}$	99.6048%	33.4007
Boat${}_{(512\times 512)}$	99.6315%	33.4815
Mandrill${}_{(512\times 512)}$	99.6151%	33.5175
Average	99.6097%	33.4666

Table 8. NPCR and UACI average values in the 3DPCM algorithm and several other new algorithms.

Algorithm	NPCR	UACI
Theoretical value	99.610%	33.460
3DPCM algorithm	99.6097%	33.4666
Ref. [15]	99.607%	33.427
Ref. [16]	99.630%	33.400
Ref. [14]	90.955%	30.433
Ref. [6]	99.655%	33.467

5.5. Key-Space Analysis

The key-space for a strong encipherment algorithm must be large enough to survive a brute-force attack (≥$2^{100}$). The key-space in the 3DPCM algorithm is composed of the logistic map initial values and its parameter, the initial values of the 3D piecewise chaotic map, and their parameters. Therefore, the key-space will be ${10}^{140} (>>2^{100})$ if the accuracy was ${10}^{-14}$.

5.6. Noise Attack Analysis

A cryptanalyst can add noise or distribute it electronically via an enciphered image. The efficiency of the 3DPCM algorithm against noise attack is analyzed in this section. To test this, we add Gaussian noise with variances of $0.1$ and $0.01$ and Salt&Pepper noise with densities of $0.1$ and $0.05$ to the chosen enciphered image.

Figure 8 shows deciphered images for all cases. Since pixels that have been altered by noise do not spread throughout the deciphered image throughout the decipherment process, the 3DPCM algorithm is productive against noise. The peak signal-to-noise ratio (PSNR) and mean square error (MSE) are used to calculate the effect of noise on the enciphered image. The following formulas define PSNR and MSE:

$$PSNR=10lo{g}_{10}\left(\frac{{255}^2}{MSE}\right).$$

(14)

where

$${\displaystyle MSE=\frac{1}{M\times N}\sum _{i=1}^M\left(\sum _{j=1}^N{(P_{ij}-D_{ij})}^2\right),}$$

(15)

such that

Figure 8. Deciphered image by applying multiple forms of noise to the enciphered image Lena$(256\times 256)$.

$P_{ij}$: the pixel value of the plain image, $D_{ij}$: the pixel value of the deciphered image for the noisy enciphered image. Table 9 compares the 3DPCM algorithm and the other two algorithms based on MSE and PSNR values for Lena${}_{(256\times 256)}$ image. The findings of the 3DPCM algorithm are superior to those of the other two algorithms for a large amount of noise.

Table 9. Noise analysis.

Noise	3DPCM Algorithm		Ref. [15]		Ref. [19]
	MSE	PSNR	MSE	PSNR	MSE	PSNR
Gaussian noise $(\mu =0,{\sigma }^2=0.1)$	3212.2	13.1	5201.2	11.0	5272.1	10.9
Gaussian noise $(\mu =0,{\sigma }^2=0.01)$	2370.6	14.4	2321.4	14.5	2348.4	14.4
Salt&Pepper noise $(d=0.1)$	887.3	18.7	893.1	18.6	909.3	18.5
Salt&Pepper noise $(d=0.05)$	449.6	21.6	437.9	21.7	444.1	21.7

5.7. Chosen Plain-Text Attack Analysis (CPTAA)

Since the 3DPCM algorithm is very sensitive to the initial values and parameters of the logistic map and map (1), any update in the plain image pixel values causes a significant change in the generated sequences by those maps. As a result, the 3DPCM algorithm would be able to withstand this plain-text attack. To use this type of attack, the cryptanalyst needs the enciphered image and a limited amount of time to use the encipherment machine. Assuming P is the plain image, C is the corresponding enciphered image and $D=\left(d_{ij}\right);d_{ij}=0;i=1,2,\dots ,M;j=1,2,\dots ,N$ is the designed image to find the decimal array $C_D$. Then, the following steps are taken to measure the algorithm impedance to a CPA:

• Step 1: Encipher designed image D by 3DPCM Algorithm, the result is given the name $C_D$.
• Step 2: To restore the plain image, do a bit-wise XOR operation between the enciphered image C and the enciphered image $\left(CD\right)$. The result is named R.
• Step 3:P is compared to R.

Figure 9 shows the reconstructed plain image is completely different from the plain image. Consequently, the 3DPCM algorithm would be able to withstand the CPA.

Figure 9. CPTAA for Lena${}_{(256\times 256)}$ image.

5.8. Contrast Analysis

Contrast, in general, helps to identify the features in an image’s texture. An efficient algorithm must generate an enciphered image with a high degree of contrast. It is measured by:

$${\displaystyle C=\sum _{\alpha ,\beta }{|\alpha -\beta |}^2{p}_{\alpha ,\beta }}$$

(16)

such that the number of grey-level co-occurrence matrices was denoted by $p_{\alpha ,\beta }$. The enciphered image has a high degree of contrast because of the extent of the randomness provided by the logistic map and map (1) in the 3DPCM algorithm. The high contrast of different forms of enciphered images is displayed in Table 10.

Table 10. Contrast of some enciphered images at $c_0=1,c_1=-0.29,c_2=-0.9,x_0=2.10,$$y_0=2.10,$$z_0=2.10,x_{r0}=0.01,x_{c0}=0.02$ and $\mu =3.998$.

Image	Contrast
	Plain Image	Enciphered Image
Lena${}_{(256\times 256)}$	0.4511	10.4663
Lena${}_{(512\times 512)}$	0.2288	10.5194
Cameraman${}_{(256\times 256)}$	0.5872	10.5518
Cameraman${}_{(512\times 512)}$	0.1862	10.5399
Barbara${}_{(512\times 512)}$	0.7356	10.5091
Boat${}_{(512\times 512)}$	0.3799	10.5354
Mandrill${}_{(512\times 512)}$	0.3476	10.5102

5.9. NIST Statistical Tests

There are some popular tests used for randomness assessment. The NIST statistical tests are one of them. It has developed 15 tests to investigate the randomness of the sequences created by encipherment algorithms. To verify our findings, we enciphered 100 copies of the Lena${}_{(256\times 256)}$ image with random secret keys. Each enciphered image’s resulting sequence is 524288 bits long. NIST is applied to ensure that the sequences are random. The results are displayed in Table 11. We can see that all the sequences succeeded.

Table 11. NIST statistical test for 100 enciphered images via the 3DPCM algorithm at $c_0=1,$$c_1=-0.29,$$c_2=-0.9,x_0=2.10,y_0=2.10,z_0=2.10,x_{r0}=0.01,x_{c0}=0.02$ and $\mu =3.998$ and random values of $x_0$ between 0 and 1.

Statistical Test	3DPCM Algorithm	Result
Frequency monobit test	100/100	√
Block frequency test	100/100	√
Runs test	98/100	√
Longest runs test	100/100	√
Rank test	99/100	√
Fast Fourier transform	98/100	√
Cumulative sums test	99/100	√
Random excursion test	51/51	√
Random excursion variant test	51/51	√
Approximate entropy	100/100	√
Universal test	99/100	√
Serial	100/100	√
Linear complexity test	99/100	√
Non-Overlapping templates test	99/100	√
Overlapping templates test	99/100	√

5.10. Computational Complexity Analysis

The total number of operations that are used in image confusion and diffusion is used to compute the computational cost of the 3DPCM algorithm. The confusion process is needed to $(2\times M\times N)$ operations for the generating random sequence using the logistic map and the shuffling process needs $(M\times N)$ operations. Additionally, for constructing the sequences from the 3D piecewise chaotic map $(4\times M\times N+500)$ operations are required, and the preprocessing sequences needs $(M\times N)$ operations. Lastly, for the diffusion process, the XOR is needed for $(M\times N)$ operations. As a result, the 3DPCM algorithm computing cost is $\theta (M\times N)$.

5.11. Computational Time Analysis

MATLAB 2014a was used to evaluate the computational time on a laptop with a 2.20 GHz CPU, 8 GB of RAM. Table 12 shows the encipherment and decipherment times for some tested images.

Table 12. Computational time analysis at $c_0=1,c_1=-0.29,c_2=-0.9,x_0=2.10,y_0=2.10,$$z_0=2.10,$$x_{r0}=0.01,x_{c0}=0.02$ and $\mu =3.998$.

Image	Encipherment	Decipherment
	Time (s)	Time (s)
Lena${}_{(256\times 256)}$	0.2151	0.1917
Lena${}_{(512\times 512)}$	0.7336	0.7336
Cameraman${}_{(256\times 256)}$	0.1930	0.2554
Cameraman${}_{(512\times 512)}$	0.6993	0.6962
Barbara${}_{(512\times 512)}$	0.6982	0.7129
Boat${}_{(512\times 512)}$	0.7003	0.7160
Mandrill${}_{(512\times 512)}$	0.6797	0.6852

6. Conclusions

This article introduces a new encipherment technique that combines a 1D chaotic map with a 3D piecewise chaotic map. According to the results of the histogram, information entropy analysis, and NIST test, the suggested algorithm can be used to effectively encipher images. The key-space of the suggested algorithm is ${10}^{140}$, and the information entropies, the correlation coefficients, and the contrast of the enciphered images are close to 8, 0, and $10.5$, respectively. It is demonstrated that the suggested algorithm has a high degree of resistance to attacks based on the experimental analysis of key-space, various types of noise attacks, CPAA, and sensitivity analyses. In future work, a quantum encipherment based on a 3D piecewise chaotic map will be designed to improve the present algorithm security.