Abstract
This paper presents the design, modeling, simulation, and experimental testing of a novel 2-DOF precision micro-positioning stage. A compact parallel structure is proposed and the rotation stroke of the stage is improved by reducing the rotation radius. Compared with other positioning stages, the developed stage has the advantage of large rotation stroke, compact structure, and high resonant frequency, and it can realize various positioning functions with fewer piezoelectric actuators. The simplified flexibility equation of the composite bridge mechanism was obtained through the equivalent replacement of the composite hinge, and then the transmission ratio and input stiffness analysis model of the stage are further established. Then, the simulation and experiment verify the accuracy of the model. The significant size parameters of the stage are determined according to the sensitivity analysis and verified by FEA. To decouple the rotation and translation, we establish the scale factor. The experimental results reveal that the workspace of the stage is 22.90 mrad × 95.03 μm. The step response time is 80 ms and the rotation resolution is 5 μrad under open-loop control.
Keywords:
micro-positioning; piezoelectric actuation; compliant mechanisms; 2-DOF rotation-translation MSC:
74-10
1. Introduction
The high-precision positioning stage is the main equipment used in micro/nano manufacturing, which is widely used in microdevice processing, optical component alignment, atomic force microscopy, micro/nano operation, and other fields [1,2,3,4]. In the field of optical image stabilization, the micro-positioning stage driven by piezoelectric actuators (PEAs) is used to compensate for the linear and angular vibration displacement of the camera, which makes the image surface coincide with the photosensitive receiving element to improve the image quality [5,6,7]. Generally, only the multi-DOF positioning stage has the positioning ability of rotation and translation [8,9,10,11], but it has the disadvantages of high manufacturing cost, complex structure, large volume, and short rotation stroke. Therefore, it is hoped that the 2-DOF positioning stage with a simple structure and large stroke can be used to realize the positioning target of rotation and translation.
Leon Clark developed an in-plane 2-DOF (X, ) positioning stage with the ability of coupled rotational and translational motion, which has a working stroke of 10.31 μm in the X direction and 535.8 μrad in the direction [12]. Compared with the in-plane motion type stage, the out-of-plane motion type stage has better vertical stiffness in the Z-axis direction [13], but there is little research on the out-of-plane 2-DOF positioning stage. If there is a need for positioning in the Z and direction, the 3-DOF positioning stage is the only solution. For example, Kim et al. designed a vertical, out-of-plane,3-DOF positioning stage with a working stroke of 190 mm in translation and 0.5 mrad in rotation [10]. Lee et al. designed an out-of-plane 3-DOF positioning stage driven by 4 PEAs, which has a working stroke of 190 mm in translation and 4 mrad in rotation [11]. Compared with linear vibration, angular vibration is the main factor in reduced image quality [14]. However, these 3-DOF positioning stages have a short rotation stroke, and it is difficult to meet the needs of compensation for angular vibration. Therefore, it is necessary to design a novel 2-DOF positioning stage with a large working stroke in rotation.
In order to improve the working stroke of the stage, researchers have proposed different methods to drive the positioning stage, which can be divided into three categories. In the first category, the voice coil motor or linear motor is widely used as the driver because of its low cost and large working stroke [15,16,17], but it is vulnerable to external magnetic field disturbance [18,19]. In the second category, the PEA step actuator is used as the driver because of its advantage of resistance to magnets, large thrust, and fast response, but it requires multiple drivers to cooperate, has a complex structure, and has poor movement speed and accuracy [20]. In the third category, the displacement amplifying ratio of the amplification mechanism is increased to increase the working stroke of the stage [21,22,23], but the amplification ratio and the stiffness have to be balanced. Excessively raising the amplification ratio greatly reduces the rigidity of the platform and affects its load capacity [24]. In addition, directly increasing the size of the stage can effectively improve the working stroke [25,26], but it is contrary to the compact design concept and limits the application of the stage [27]. In summary, it is very challenging to greatly increase the rotation stroke of the stage without increasing the size and decreasing the stiffness.
In order to solve the contradiction between rotational stroke and stiffness, this study uses the method of reducing the rotation radius to increase the rotation stroke of the stage. According to reference [12,28], the angular displacement is approximately equal to the linear displacement divided by the radius of rotation, and a new compact parallel structure is designed, which has the conditions to greatly reduce the rotation radius. The two amplification mechanisms arranged in parallel are designed in reverse motion, forming a rotating couple to further reduce the rotation radius, thus further improving the rotation stroke of the stage.
Even so, it is not easy to realize the large stroke movement of the stage because only by accurately modeling the stage can we better predict and optimize the performance of the stage. The influence of the load stiffness on the output displacement of the amplifying mechanism cannot be ignored [29,30]. It is no longer applicable to calculate the amplification ratio of the commonly used translational stiffness and rotational stiffness [31]. So the flexibility matrix method is used to model the stage. When the flexibility matrix method is used to solve the parallel double chain structure in the compound amplification mechanism, the translation matrix and rotation matrix are often used to solve the problem [32,33,34,35]. Additionally, the calculation is complex and the process is cumbersome, which is not conducive to the calculation of the stage workspace and the optimization of the size parameters. Therefore, the composite flexure hinge is simplified as a single hinge, simplifying the calculation process. The theoretical calculation results are verified by simulation and experiment and have good accuracy.
This paper presents a novel 2-DOF precision micro-positioning stage. To achieve a large rotation stroke and a more compact structure, two compound bridge mechanisms with reverse motion are connected in parallel. To accurately calculate the motion stroke, the modeling method of the composite hinge is simplified, and the analytical model of the stage is further derived. In addition, due to the difference in the amplification mechanism, a scale factor is introduced through simulation analysis to achieve the decoupling of rotation and translation. Compared with other positioning stages, the developed stage has the advantages of large rotation stroke, compact structure, and high resonant frequency, and it can realize various positioning functions with fewer PEAs.
The rest of this paper is as follows: In Section 2, the mechanical design of increasing rotation stroke is introduced. In Section 3, the transmission ratio and input stiffness analysis model of the stage are derived, and the important dimensional parameters are determined by parameter sensitivity analysis. In Section 4, the finite element analysis (FEA) is used to verify the modeling results, and the scale factor of the decoupling of rotation and translation is established. In Section 5, a prototype is built and a series of experiments are carried out. Section 6 provides a summary of the article.
2. Machine Design
According to the analysis of the structure of the stage, we design a large stroke 2-DOF positioning stage, and Figure 1a shows the topology of the positioning stage. Under the condition of small displacement, the rotation angle equation of the stage can be expressed as:
where and are the angle of rotation and radius of rotation, respectively, and is the output displacement of the amplifying mechanism.
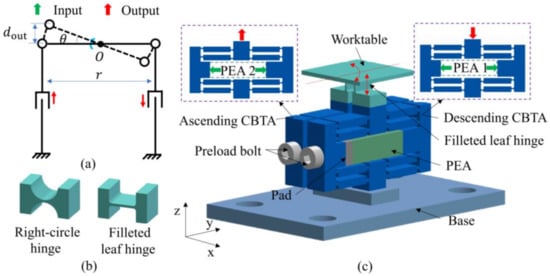
Figure 1.
(a) Platform topology. (b) Flexure hinges. (c) 2-DOF (, Z) positioning stage.
As discussed above, compared with increasing , it is a better way to increase the rotation travel of the stage by decreasing . The rotation of the stage in the direction of is realized by the rotation couple formed by two displacement amplification mechanisms that move in opposite directions, and the parallel arrangement reduces the rotation radius and greatly improves the rotation stroke.
2.1. Design of Flexure Hinge and Amplifying Mechanism
The rotational stroke is mainly affected by the type of flexure hinge. As shown in Figure 1b, the commonly used flexure hinges are right-circle hinges and filleted leaf hinges [36]. By comparing two types of flexure hinges, it is found that the filleted leaf hinge can avoid the problem of a deformation interval which is too short and can better satisfy the design requirements of large stroke rotation.
Because the output displacement of the PEA is only tens of microns, a displacement amplification mechanism is required to obtain a larger driving displacement [37]. Because of the bending moment caused by the parallel arrangement structure, the mechanical structure tilts and loses output displacement. To reduce the loss of output displacement, the amplification mechanism needs to have good stiffness. Commonly used amplification mechanisms include the lever mechanism, diamond mechanism, bridge mechanism, Scott–Russell mechanism, etc. As shown in Figure 2, the rhombic amplification mechanism (RTA) [25], the compound rhombic amplification mechanism (CRTA) [38], and the compound bridge amplification mechanism (CBTA) are analyzed and compared through FEA. We find that the CBTA has outstanding advantages in radial bending moment stiffness and higher resonance frequency.
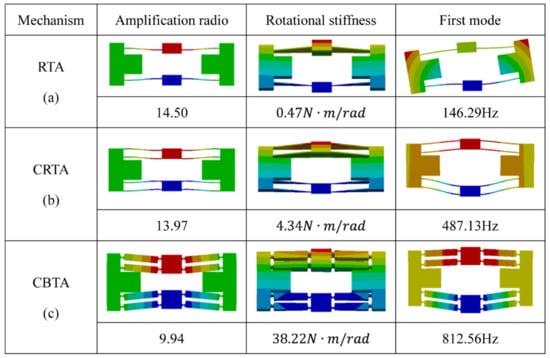
Figure 2.
Comparison of three displacement amplifying mechanisms. (a) RTA; (b) CRTA;(c) CBTA.
2.2. Stage Composition and Working Principle
As shown in Figure 1c, the stage is driven by two CBTA arranged vertically on the base plate. They are the ascending CBTA and descending CBTA, respectively, and are connected with the worktable through filleted leaf hinges and transfer the output displacement to the worktable.
The stage has a variety of positioning capabilities, such as half-stroke rotation, full-stroke rotation, translation, and the composite motion of rotation and translation. Specifically, when the platform is single driven, it is driven by one PEA, and has half of the full-rotation. When the stage is dual driven, it is driven by both PEAs and has full-stroke rotation. When the phase difference of the stage dual-driven signal is 180°, the worktable moves along the Z-axis in a certain deflection angle. By changing the phase difference or voltage of the input signal, the composite motion of rotation and translation can be realized.
3. Stage Modeling
In order to analyze the influence of the parameters on the stage performance, it is necessary to accurately model the stage and optimize the parameters.
3.1. Modeling of the CBTA
Because of the symmetry of the stage and CBTA, we can choose to model only parts of them and reduce the difficulty of calculation. As shown in Figure 3, because is small, the vertical compound right circular flexure hinge is equivalent to the horizontal compound right circular flexure hinge. By doubling the hinge width, that is, , the conversion of composite flexible hinge to single flexible hinge is realized, and the difficulty of calculation is reduced.
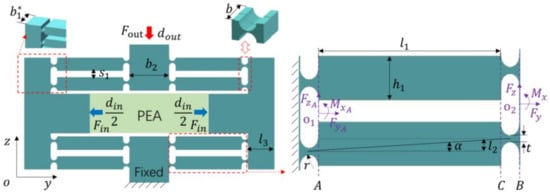
Figure 3.
Composite bridge mechanism.
It is too redundant to describe the deformation of the flexure hinge with the flexibility matrix of 6-DOF for the stage with 2-DOF, so the flexibility equation is established by simplifying the flexibility matrix of 3-DOF. The compliance equation for the composite flexure hinge is as follows:
where is the flexibility matrix, is the load vector , and is the displacement vector . According to reference [39], the compliance matrix parameters of the right circular flexure hinge are shown in the Table 1.

Table 1.
Flexibility matrix parameter.
According to the equilibrium theory of forces, the following equation can be obtained:
As shown in Figure 3, the displacement at point B is the superposition of the displacement at point A and the displacement at point C. Since the flexure hinges at both ends of the connecting rod bear the same force, their deformation is the same [24]. According to Equation (2), the displacement of point B is calculated as follows:
By arranging Equations (4) and (5), the following equation can be obtained:
According to the symmetry:, and Equations (6) and (7), the input–output matrix expression of CBTA can be obtained:
where , , , .
3.2. Calculation of the Stage Workspace
As shown in Figure 4, the polygon area enclosed by the point is the workspace of the worktable. is the moving range of the angular motion axis. The maximum rotation angle of the worktable is in single-driven mode, and in dual-driven mode. The worktable can move in translation from to with a height of , where .
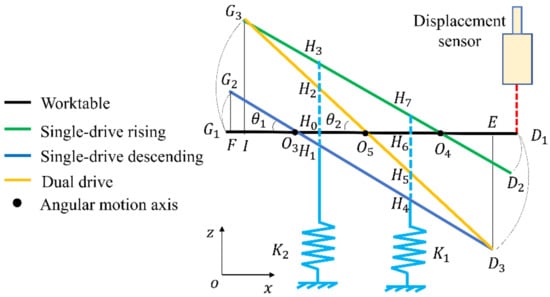
Figure 4.
Schematic diagram of worktable motion track.
As shown in Figure 5a, the rotation of the worktable is driven by a PEA. According to the rotation equation of beam, the rotation angle of the filleted leaf hinge is:
where is the rotational stiffness of the filleted leaf hinge and .
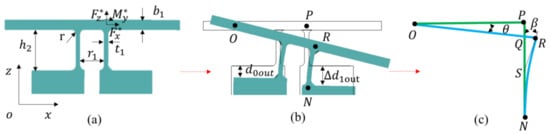
Figure 5.
(a) Worktable and rotation hinge. (b) Single-drive deformation diagram. (c) Single-drive deformation geometric relationship.
From Figure 5c, ∆ OPQ is similar to ∆ QRS:
because the rotation radius in the single-driven mode is twice that in the dual-driven mode, which can be obtained from (1) and (9):
Combine Equation (8) with Equation (11), and the rotation angle of the stage is calculated.
and the input stiffness of the stage is as follows:
However, due to the influence of load stiffness, the output displacement of the CBTA will be attenuated. Because the rigidity of the two CBTA is equal, , the output stiffness is equal to the load stiffness , and the output displacement under the load stiffness is:
where is the output displacement of the CBTA with load stiffness, and is the output displacement of the CBTA without load stiffness. Under the drive of PEA, the motion direction of the CBTA is consistent with its own working direction, so it is an active output. In the single-drive mode, the PEA-driven CBTA influences the CBTA which is not driven by PEA on the other side and generates a passive output displacement which is opposite to the direction of its own movement, and and can be obtained from Equations (8) and (11):
where active output is positive and passive output is negative. As shown in Figure 5b, when the stage is driven by one PEA, is not completely translated into the rotation of the stage due to the effect of the coupled motion. The effective rotational displacement of the stage can be calculated as:
The single-driven rotation angle equation is obtained by combining Equation (17), Equation (11), and Equation (8):
The transmission ratio of the single-drive rotation is:
Without considering the influence of load stiffness and coupling displacement, the input stiffness of single-drive rotation is obtained from Equation (13).
When the worktable is in dual-driven mode, the output displacement is all converted into the translation stroke. The translation stroke is the sum of and for the same bridge mechanism, which can be obtained from Equations (15) and (16):
It can be seen that the translation stroke is affected by the CBTA and has nothing to do with the filleted leaf hinge, and the transmission ratio of translation motion is:
At the highest point and the lowest point of the stage translation motion, the stage is driven by PEA, which is similar to the single-driven rotation. Therefore, the input stiffness is equal, and the translation input stiffness is given by Equation (13).
The rotation angle of the dual-driven rotation can be obtained by the Equations (1) and (11):
where is the output displacement of the CBTA under the load stiffness.
The dual-drive stage rotation angle is given by Equations (8) and (22):
The transmission ratio of the dual-drive rotation is:
The calculation process of the input stiffness of the dual-driven rotation is similar to the single-driven rotation, and its rotation radius is the half of single-driven rotation:
Because the input stiffness affects the output displacement of the PEA, the output displacement of the stage attenuates.
where is the no-load output displacement of the PEA. is the equivalent stiffness of the PEA. Substituting Equations (18)–(21) and (23), (24), (26), the maximum working stroke of the stage is as follows:
It should be pointed out that is an ideal transmission ratio and has the following relationship with the actual transmission ratio :
3.3. Transmission Ratio and Input Stiffness Analysis
From Equations (27) and (28), it can be seen that the rotational and translational strokes are affected by the input stiffness and transmission ratio. In Figure 6, the effect of various dimensional parameters on the transmission ratio and input stiffness is analyzed, and the rotation stroke is the main optimization object.
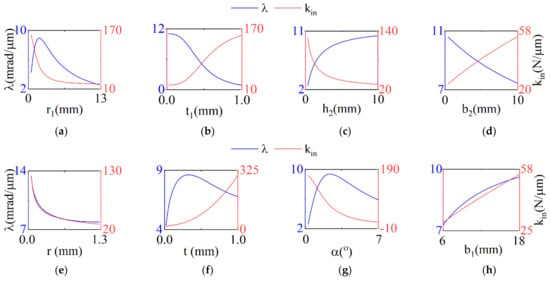
Figure 6.
Effect of major dimensional parameter on input stiffness and transmission ratio. (a) Rotation radius. (b) Thickness of the leaf hinge. (c) Leaf hinge height. (d) Leaf hinge width. (e) Minimum thickness of right-circle hinge. (f) Radius of right-circle hinge. (g) Angle of connecting rod. (h) Width of the CBTA.
Figure 6a–d shows the relationship between the dimensional parameters of the filleted leaf hinge and transmission ratio and input stiffness, and Figure 6e–h shows the relationship between the dimensional parameters of the CBTA and transmission ratio and input stiffness. The input stiffness in Figure 6a,c,f,g and the transmission ratio in Figure 6b,d,f both have the same trend, which falls with the increase in the size parameters. The input stiffness in Figure 6b,d,e,h and the transmission ratio in Figure 6c,h both have the same trend, which rises with the increase in the size parameters; the maximum value of the transmission ration appears in Figure 6a,e,g.
3.4. Parameter Sensitivity Analysis
In order to obtain a larger rotation stroke, sensitivity analysis of the transmission ratio and input stiffness is carried out to determine the main dimensional parameters of the stage. As shown in Figure 7, , the thickness of the filleted leaf hinge, is the most sensitive parameter to the transmission ratio and the input stiffness, and the right-circle hinge thickness of the CBTA is also a sensitive parameter to the input stiffness.
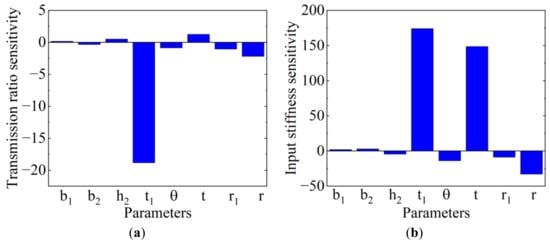
Figure 7.
Sensitivity analysis results. (a) Transmission ratio sensitivity. (b) Input stiffness sensitivity.
3.5. Parameter Determination
The dimension of PEA is 6 × 6 × 18 mm3, and the axial stiffness of piezoelectric actuator is = 60 N/μm. In order to facilitate the alignment and installation of PEA, the width of the bridge mechanism is consistent with the width of the piezoelectric ceramic, which is determined as = 6 mm, = 12 mm, and the width of the leaf hinge is determined to be = 6 mm, which is consistent with the width of the CBTA. The length of the connecting rod has to meet the following inequality , which is set to be 10 mm. The stage can be driven by the PEA only if the following condition is met: . In order to obtain a larger rotation stroke of the stage, it is necessary to make the input stiffness as small as possible and the transmission ratio as large as possible when determining the dimensional parameters. According to Figure 6a,e,g, the values of , t, and shall be selected to maximize the transmission ratio. Therefore, they are determined as = 3 mm, t = 0.3 mm, and . The input stiffness should be set as an appropriate value and is set as , and the values of , and are determined as , , = 0.5 mm. Since and have been determined, can be obtained and the height of connecting rod can also be determined as 2 mm by the inequality . is set to be 1 mm. The total height of the CBTA is determined to be 17 mm according to the inequality . When is 4 mm, the total length L of the CBTA is 38 mm.
The dimensional parameters of the stage are listed in Table 2, and the mechanical property parameters of the material Al7075 are listed in Table 3. Under the voltage of 150 V, the output displacement of the PEA is 10 μm, and the theoretical calculation results of the stage are shown in Table 4.

Table 2.
Dimensional parameters of stage, unit: mm.

Table 3.
Physical and mechanical parameters of Al7075 material.

Table 4.
Theoretical calculation result.
4. Model Validation with Simulation
Finite element analysis is used to study the characteristics of the stage under single-driven mode and dual-driven mode. The stage was geometrically modeled by employing SOLIDWORKS 2020 software and the static analysis was implemented with the software ANSYS Workbench 2020R2. Adaptive mesh division was adopted and the smoothing were high. The calculating results were proven to be convergent and accurate enough. During the simulation, the base of the stage was fixed, and the input displacements were applied to the input ends. When the rotation is single-driven and the input displacement is 10 μm, and the ascending CBTA is working, as shown in Figure 8a, the active output displacement is 67.65 μm, the passive output displacement is 29.63 μm, the stage rotation angle is 12.15 mrad, and the input stiffness is 35.80 N/μm. When the descending CBTA is working, as shown in Figure 8b, the active output displacement is 76.68 μm, the passive output displacement is 33.05 μm, the stage rotation angle is 13.94 mrad, and the input stiffness is 36.97 N/μm. According to the simulation results of single-driven rotation, the moving range of the angular axis in the X direction is [−3985.15 μm~3957.20 μm] with the center of the stage as the origin. When the rotation is dual-driven, as shown in Figure 8c, the maximum rotation angle is , the transmission ratio is 3.1 mrad/μm, and the input stiffness is 42.92 N/μm. As shown in Figure 8d, whether the stage is single driven or dual driven, the maximum stress is at the flexure hinge of the CBTA, and the maximum stress is 127.17 MPa, which is far below the yield strength of the material.

Figure 8.
Stage static analysis. (a) Single-drive ascending rotation. (b) Single-drive descending rotation. (c) Dual-drive rotation. (d) Stage stress distribution.
The amplification ratios of the two CBTAs are 6.77 and 7.67, respectively. The difference between the two CBTAs causes rotational coupling in translation motion if no adjustment is made. It is difficult to make two amplification mechanisms have the same amplification ratio, and it is difficult to achieve the expected result after processing and assembly. So, a simpler method is proposed. Even if the PEA has hysteresis, there is a functional relationship between input voltage and output displacement. Therefore, the following proportional equation can be obtained:
where is the scale factor, is the input voltage of PEA1, is the input voltage of PEA2. The amplitude of two input voltages are adjusted by using to make two CBTAs have the same movement speed and output displacement. When the two input signals are as shown in Figure 9a, the maximum displacement of the CBTA are 10 and 11.3, respectively, and the translation simulation result of the stage is as shown in Figure 9b. The worktable moves periodically under a certain initial angle, in which the rotation angle at the lowest point is 16.35 mrad and the rotation angle at the highest point is 16.34 mrad. The height differences between the two sides of the worktable are 93.73 μm and 93.48 μm, respectively. After a rising period, the worktable has almost no deflection, the decoupling of rotation and translation is realized, and the maximum translation stroke is 93.61 μm.
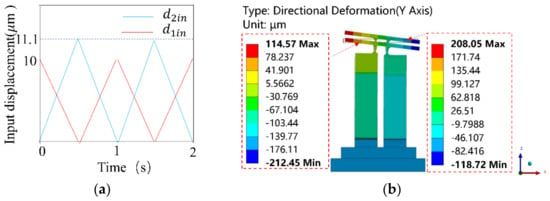
Figure 9.
(a) Translation displacement input signal. (b) Dual-drive translation.
Modal analysis verifies the dynamic performance of the stage. Figure 10 shows the first two modal analysis results. The first mode and the second mode of natural frequency are 699.38 Hz and 881.25 Hz, respectively, which proves that the stage has outstanding dynamic characteristics and can be applied to high-frequency operational tasks.
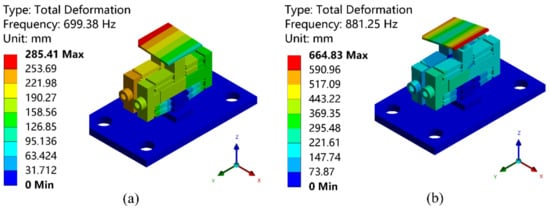
Figure 10.
Natural frequency. (a) First natural frequency of 699.38 Hz; (b) Second natural frequency of 881.25 Hz.
5. Experimental Study
5.1. Prototype Processing
The prototype of the stage is processed by WEDM. Limited to the manufacturer’s processing capacity, integrated processing is difficult, so the model is cut modularly and assembled with bolts. Excluding the fixed base, the volume of the prototype is . The material is AL7075, which has the advantages of high elasticity, high yield strength, and light weight.
5.2. Experimental Apparatus and Measuring Method
As shown in Figure 11, the experiment equipment includes a 2-DOF positioning stage, a spectral confocal displacement sensor (CDS-500, THINKFOCUS, Shanghai, China), a signal generator (AFG1022, Tektronix Corporation, Beaverton, OR, USA), a voltage amplifier (E00. A4, COREMORROW, Harbin, China), an oscilloscope (TBS2000, Tektronix Corporation, Beaverton, OR, USA), and a vibration isolation platform. The displacement sensor is fixed on bracket to measure the displacement of the edges on two sides of the worktable. The selected two measuring points are symmetrical about the worktable, which ensures the position accuracy and measurement accuracy of the rotating shaft.

Figure 11.
Experimental setup.
In order to more intuitively describe the performance of the worktable, the displacement measured by the sensor is converted into the rotation angle of the worktable. To reduce the error caused by conversion, the conversion formula is derived accurately. Based on the similar triangles and in Figure 4:
where , and , to determine the position of the angular motion axis, the radius of rotation is calculated as:
The angle in is calculated as:
where and are the displacement measured by the sensor.
5.3. Sweep Frequency Analysis
Precision impedance analyzer (LCR Meter 6630, MICROTEST, Taiwan, China) is used to run the sweep frequency analysis on the stage. As shown in Figure 12a, at the input voltage of 0.2 V and the sweep frequency of 10~1000 Hz, the first peak is 662.70 Hz and the second peak is 837.80 Hz. Compared with the result of FEA simulation, the relative error is 5.53% and 5.18%, respectively. When the two PEAs are connected in parallel and loaded with a 6 V sine wave, the output displacement decreases with the increase in the input signal frequency. As shown in Figure 12b, three displacement measurement values at 580 Hz, 655 Hz, and 700 Hz are selected, except that the displacement value at 655 Hz is affected by resonance, the displacement decreases with the increase in input signal frequency.
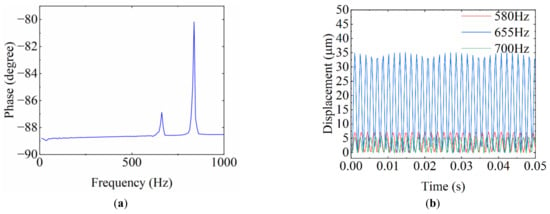
Figure 12.
(a) Response frequency. (b) Amplitude test.
5.4. Working Stroke of the Stage
First, the working stroke under single-driven mode is tested. A 150 V trapezoidal wave is applied to PEA1 and PEA2, and the output rotation angle is shown in Figure 13a. The maximum rotation angles are = 12.50 mrad and = 10.53 mrad. The movement interval of the angular motion axis obtained by Equation (32) is [−4745.27 μm~4542.45 μm].
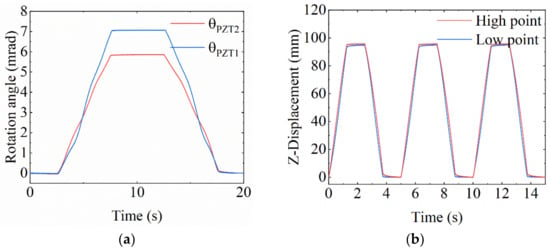
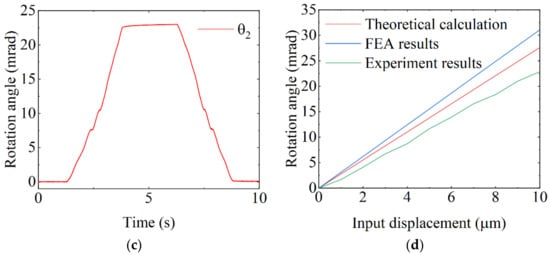
Figure 13.
(a) Single-drive rotation. (b) Double-drive translation. (c) Double-drive rotation (d) Transmission ratio analysis.
Then, the working stroke under dual-driven is tested. The results of translation stroke test are shown in Figure 13b, and the maximum lifting height is 95.03 μm. The maximum rotation stroke of the stage can be obtained when the two trapezoidal voltages and are both 150 V and the phase difference is . The results of rotation stroke test are shown in Figure 13c, and the maximum rotation angle is 22.90 mrad.
The transmission ratio of rotation is 2.29, and the Figure 13d shows the difference between the theoretical result, simulation result, and experimental result of the transmission ratio. Because of the energy loss of lever arm bending and flexure hinge stretching, the transmission ratio in the experimental result is lower than the theoretical result and simulation result, and the results of the theoretical calculations, FEA, and experiment are listed in Table 5.

Table 5.
Comparison of theoretical, simulation, and experimental results.
5.5. Stage Performance Analysis
The parallel PEAs are control by a step signal of 75 V, and the step response time of the stage is shown in Figure 14a. Because of the effect of creep, the PEA needs a stable time of 80 ms. When a continuous square wave signal is input, the stage tracking test result is as shown in Figure 14b. The result shows that the stable time in the tracking test is the same as the stable time in the step response test. Different weights are placed on the worktable to study the influence of different loads on the performance of the stage. As shown in Figure 14c, the vibration amplitude of the worktable increases with the increase in the load, and the steady-state time required for the worktable is also gradually prolonged. The stage is used in the field of micro/nano operation, and the load is usually very small, so the stage meets the general engineering requirements.
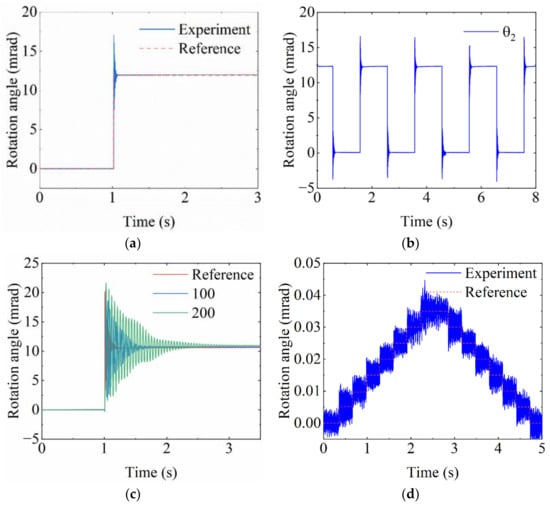
Figure 14.
(a) Step response. (b) Tracking test. (c) Load test. (d) Resolution.
Under the open-loop control, the stage rotation resolution is tested with the step wave of gradually decreasing voltage. As shown in Figure 14d, the plateau trapezoidal response profile can be clearly seen at a voltage of 1.5 V, and the resolution at this time is 5 μrad.
The stage is controlled by two voltage signals, and the voltages are adjusted according to the scale factor in Equation (30). Driven by 132 V and 150 V and a 5 Hz sine wave with zero phase difference, the stage starts to rotate, and the performance of the stage is shown in Figure 15a. The lifting height of the edge of the two sides is the same, and the angular motion axis is in the center of symmetry. When the phase difference is adjusted to , the motion of the stage changes to translation. The translation of the stage is detected by three non-colinear points. As shown in Figure 15b, the three curves representing displacement almost coincide, indicating that translation and rotation are decoupled. Figure 15c shows that the translation stroke decreases with the increase in frequency. The maximum lifting height of 94.14 at 5 Hz decreases to 89.03 at 100 Hz. As shown in Figure 15d, when the frequency is 10 Hz, the coupling displacement of the stage in X and Y directions is detected. The coupling displacement values in X and Y are 8.78 and 6.70 , respectively. The coupling displacement is caused by the assembly error and manufacturing process.

Figure 15.
(a) Symmetrical rotation. (b) 5 Hz translation. (c) 100 Hz translation. (d) Parasitic motion. (e) Alternating translational rotation. (f) Simultaneous translational rotation.
The compound motion of rotation and translation is tested. Driven by two triangular wave voltage signals which satisfy and phase difference , the stage moves alternately in a compound motion of rotation and translation, as shown in Figure 15e. When the two triangular wave voltage signals satisfy , and the phase difference , the speed of the two sides are different and the rotation and the translation are carried out simultaneously as shown in Figure 15f. By changing the signal, the desired other types of compound motion can be achieved.
5.6. Performance Comparison Analysis
There are many indexes to evaluate the performance of the micro-positioning stage, including stage volume, stroke range, natural frequency, and degree of freedom. The differences between the stage presented in this paper and other stages are listed in Table 6, and the result shows that the stage presented in this paper has outstanding advantages in structure size, first-order natural frequency, and rotation stroke.

Table 6.
Performance comparison with other stages.
6. Conclusions
This paper presents the design, modeling, simulation, and experimental testing of a novel 2-DOF precision micro-positioning stage. A compact parallel structure is innovatively proposed, and the rotation stroke of the stage is greatly improved by reducing the rotation radius. Compared with other positioning stages, this stage has outstanding advantages in compact structure, large rotation stroke, high resonance frequency, and multiple motion functions. Under the condition of two PEA drives, the stage can realize multiple positioning functions such as rotation, translation, and compound motion of rotation and translation superposition. In addition, the simulation and experimental results prove that the simplification process in the modeling process of the composite hinge is accurate and reliable, and the stage analytical model established on this basis successfully predicts the performance of the stage. The main size parameters were determined based on sensitivity analysis. The scale factor is established through finite element simulation, which makes up the difference of the amplification mechanism and realizes the decoupling of rotation and translation. The experimental results reveal that the first resonant frequency of the stage is 662.70 Hz, the maximum angle under single-driven mode is 12.50 mrad, the moving interval of the angular axis is [−4745.27 μm~4542.45 μm], and the maximum translational displacement under dual-driven mode is 95.03 μm. The maximum rotation angle under dual-driven mode is 22.90 mrad. The step response time is 80 ms and the rotation resolution is under open-loop control. In the future, on the basis of this study, it can be developed into multiple-degree-of-freedom hybrid positioning stage. It is installed on the top of the 2-DOF or 3-DOF positioning stage to build a mixed type of multiple-degree-of-freedom micro-positioning stage.
Author Contributions
Conceptualization, W.H. and D.A.; methodology, W.H. and D.A.; software, Y.L. and Y.S.; investigation, W.H. and Y.L.; data curation, W.H. and Y.L.; writing—original draft preparation, Y.L. and Y.S.; writing—review and editing, W.H., D.A. and Z.L.; visualization, Y.L. and Y.S.; supervision, W.H. and D.A.; project administration, W.H., D.A. and Z.L.; funding acquisition W.H., D.A. and Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No.52105177,52075108,51975136), the Natural Science Foundation of Guangdong Province, China (Grant No.2022A1515011875), the young innovative talents project of general colleges and universities in Guangdong Province, China (Grant No.2021KQNCX067).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Parameters | Symbol |
| Output displacement of the amplifying mechanism | |
| Output displacement of the CBTA without load stiffness | |
| Output displacement of the CBTA with load stiffness | |
| Effective rotational displacement of the stage single-drive mode | |
| Output displacement of CBTA in dual-drive mode |
References
- Das, T.K.; Shirinzadeh, B.; Al-Jodah, A.; Ghafarian, M.; Pinskier, J. A novel compliant piezoelectric actuated symmetric microgripper for the parasitic motion compensation. Mech. Mach. Theory 2020, 155, 104069. [Google Scholar] [CrossRef]
- Mohith, S.; Upadhya, A.R.; Navin, K.P.; Kulkarni, S.M.; Rao, M. Recent trends in piezoelectric actuators for precision motion and their applications: A review. Smart Mater. Struct. 2020, 30, 013002. [Google Scholar] [CrossRef]
- Chen, W.; Yang, S.; Liu, J.; Chen, W.; Jin, Y. Design of a novel 5-DOF flexure-based compound alignment stage for Roll-to-Roll Printed Electronics. Rev. Sci. Instrum. 2017, 88, 025002. [Google Scholar] [CrossRef]
- Wang, Y.; Yan, P. A novel bidirectional complementary-type inchworm actuator with parasitic motion based clamping. Mech. Syst. Signal Process. 2019, 134, 106360. [Google Scholar] [CrossRef]
- Zhong, X.; Liu, C.; Di, Z.; Fang, H. Optimization and Experiment of Two-Dimensional Parallel Decoupling Image Stabilization Mechanism. Int. J. Precis. Eng. Manuf. 2020, 21, 1965–1974. [Google Scholar] [CrossRef]
- Tan, X.; Zhu, F.; Wang, C.; Yu, Y.; Shi, J.; Qi, X.; Yuan, F.; Tan, J. Two-Dimensional Micro-/Nanoradian Angle Generator with High Resolution and Repeatability Based on Piezo-Driven Double-Axis Flexure Hinge and Three Capacitive Sensors. Sensors 2017, 17, 2672. [Google Scholar] [CrossRef]
- Liu, P.; Yan, P.; Özbay, H. Design and trajectory tracking control of a piezoelectric nano-manipulator with actuator saturations. Mech. Syst. Signal Process. 2018, 111, 529–544. [Google Scholar] [CrossRef]
- Zhang, D.; Li, P.; Zhang, J.; Chen, H.; Guo, K.; Ni, M. Design and Assessment of a 6-DOF Micro/Nanopositioning System. IEEE/ASME Trans. Mechatron. 2019, 24, 2097–2107. [Google Scholar] [CrossRef]
- Lin, C.; Yu, J.; Wu, Z.; Shen, Z. Decoupling and control of micromotion stage based on hysteresis of piezoelectric actuation. Microsyst. Technol. 2019, 25, 3299–3309. [Google Scholar] [CrossRef]
- Kim, H.; Kim, J.; Ahn, D.; Gweon, D. Development of a Nanoprecision 3-DOF Vertical Positioning System with a Flexure Hinge. IEEE Trans. Nanotechnol. 2013, 12, 234–245. [Google Scholar] [CrossRef]
- Lee, H.-J.; Kim, H.-C.; Kim, H.-Y.; Gweon, D.-G. Optimal design and experiment of a three-axis out-of-plane nano positioning stage using a new compact bridge-type displacement amplifier. Rev. Sci. Instrum. 2013, 84, 115103. [Google Scholar] [CrossRef] [PubMed]
- Clark, L.; Shirinzadeh, B.; Bhagat, U.; Smith, J.; Zhong, Y. Development and control of a two DOF linear–angular precision positioning stage. Mechatronics 2015, 32, 34–43. [Google Scholar] [CrossRef]
- Lee, J.-C.; Lee, K.-I.; Yang, S.-H. Development of compact three-degrees-of-freedom compensation system for geometric errors of an ultra-precision linear axis. Mech. Mach. Theory 2016, 99, 72–82. [Google Scholar] [CrossRef]
- Guo, L.; Li, W.; Li, X.; Hong, G.; Zhu, J.; Zeng, X.; Tang, Y.; Xing, M. Analysis of angle vibration effects on imaging quality of synthetic aperture ladar. Optik 2017, 157, 298–305. [Google Scholar] [CrossRef]
- Al-Jodah, A.; Shirinzadeh, B.; Ghafarian, M.; Das, T.K.; Pinskier, J.; Tian, Y.; Zhang, D. Modeling and a cross-coupling compensation control methodology of a large range 3-DOF micropositioner with low parasitic motions. Mech. Mach. Theory 2021, 162, 104334. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Q. Design, fabrication and testing of a novel symmetrical 3-DOF large-stroke parallel micro/nano-positioning stage. Robot. Comput. Manuf. 2018, 54, 162–172. [Google Scholar] [CrossRef]
- Chen, C.-C. An optical image stabilization using novel ultrasonic linear motor and fuzzy sliding-mode controller for portable digital camcorders. IEEE Trans. Consum. Electron. 2017, 63, 343–349. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, Q. Survey on Recent Designs of Compliant Micro-/Nano-Positioning Stages. Actuators 2018, 7, 5. [Google Scholar] [CrossRef]
- Gao, X.; Yang, J.; Wu, J.; Xin, X.; Li, Z.; Yuan, X.; Shen, X.; Dong, S. Piezoelectric Actuators and Motors: Materials, Designs, and Applications. Adv. Mater. Technol. 2020, 5, 1–26. [Google Scholar] [CrossRef]
- Li, J.; Huang, H.; Morita, T. Stepping piezoelectric actuators with large working stroke for nano-positioning systems: A review. Sens. Actuators A: Phys. 2019, 292, 39–51. [Google Scholar] [CrossRef]
- Tian, Y.; Lu, K.; Wang, F.; Zhou, C.; Ma, Y.; Jing, X.; Yang, C.; Zhang, D. A Spatial Deployable Three-DOF Compliant Nano-Positioner With a Three-Stage Motion Amplification Mechanism. IEEE/ASME Trans. Mechatron. 2020, 25, 1322–1334. [Google Scholar] [CrossRef]
- Ling, M.; Cao, J.; Jiang, Z.; Lin, J. Theoretical modeling of attenuated displacement amplification for multistage compliant mechanism and its application. Sens. Actuators A: Phys. 2016, 249, 15–22. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.; Xie, Y.; Wang, R. Design and analysis of new ultra compact decoupled XYZθ stage to achieve large-scale high precision motion. Mech. Mach. Theory 2021, 167, 104527. [Google Scholar] [CrossRef]
- Liu, P.; Yan, P. A new model analysis approach for bridge-type amplifiers supporting nano-stage design. Mech. Mach. Theory 2016, 99, 176–188. [Google Scholar] [CrossRef]
- Ling, M.; Cao, J.; Jiang, Z.; Zeng, M.; Li, Q. Optimal design of a piezo-actuated 2-DOF millimeter-range monolithic flexure mechanism with a pseudo-static model. Mech. Syst. Signal Process. 2019, 115, 120–131. [Google Scholar] [CrossRef]
- Chen, G.; Ma, Y.; Li, J. A tensural displacement amplifier employing elliptic-arc flexure hinges. Sens. Actuators A Phys. 2016, 247, 307–315. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, Q. Design, optimization and testing of a compact XY parallel nanopositioning stage with stacked structure. Mech. Mach. Theory 2018, 126, 171–188. [Google Scholar] [CrossRef]
- Bhagat, U.; Shirinzadeh, B.; Clark, L.; Chea, P.; Qin, Y.; Tian, Y.; Zhang, D. Design and analysis of a novel flexure-based 3-DOF mechanism. Mech. Mach. Theory 2013, 74, 173–187. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhao, J.; Peng, Y.; Pu, H.; Yang, Y. A novel amplification ratio model of a decoupled XY precision positioning stage combined with elastic beam theory and Castigliano’s second theorem considering the exact loading force. Mech. Syst. Signal Process. 2019, 136, 106473. [Google Scholar] [CrossRef]
- Ling, M.; Cao, J.; Jiang, Z.; Lin, J. Modular kinematics and statics modeling for precision positioning stage. Mech. Mach. Theory 2017, 107, 274–282. [Google Scholar] [CrossRef]
- Xu, Q.; Li, Y. Analytical modeling, optimization and testing of a compound bridge-type compliant displacement amplifier. Mech. Mach. Theory 2011, 46, 183–200. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Q. Development and Assessment of a Novel Decoupled XY Parallel Micropositioning Platform. IEEE/ASME Trans. Mechatron. 2009, 15, 125–135. [Google Scholar] [CrossRef]
- Wang, F.; Huo, Z.; Liang, C.; Shi, B.; Tian, Y.; Zhao, X.; Zhang, D. A Novel Actuator-Internal Micro/Nano Positioning Stage With an Arch-Shape Bridge-Type Amplifier. IEEE Trans. Ind. Electron. 2018, 66, 9161–9172. [Google Scholar] [CrossRef]
- Liang, C.; Wang, F.; Huo, Z.; Shi, B.; Tian, Y.; Zhao, X.; Zhang, D. A 2-DOF Monolithic Compliant Rotation Platform Driven by Piezoelectric Actuators. IEEE Trans. Ind. Electron. 2019, 67, 6963–6974. [Google Scholar] [CrossRef]
- Pham, M.T.; Yeo, S.H.; Teo, T.J. Three-Legged Compliant Parallel Mechanisms: Fundamental Design Criteria to Achieve Fully Decoupled Motion Characteristics and a State-of-the-Art Review. Mathematics 2022, 10, 1414. [Google Scholar] [CrossRef]
- Tian, Y.; Shirinzadeh, B.; Zhang, D.; Zhong, Y. Three flexure hinges for compliant mechanism designs based on dimensionless graph analysis. Precis. Eng. 2009, 34, 92–100. [Google Scholar] [CrossRef]
- Wang, S.; Rong, W.; Wang, L.; Xie, H.; Sun, L.; Mills, J.K. A survey of piezoelectric actuators with long working stroke in recent years: Classifications, principles, connections and distinctions. Mech. Syst. Signal Process. 2019, 123, 591–605. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, Q. Design, Fabrication, and Testing of a New Compact Piezo-Driven Flexure Stage for Vertical Micro/Nanopositioning. IEEE Trans. Autom. Sci. Eng. 2018, 16, 908–918. [Google Scholar] [CrossRef]
- Koseki, Y.; Tanikawa, T.; Koyachi, N.; Arai, T. Kinematic analysis of a translational 3-d.o.f. micro-parallel mechanism using the matrix method. Adv. Robot. 2002, 16, 251–264. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).