Robustness of the cμ-Rule for an Unreliable Single-Server Two-Class Queueing System with Constant Retrial Rates
Abstract
:1. Introduction
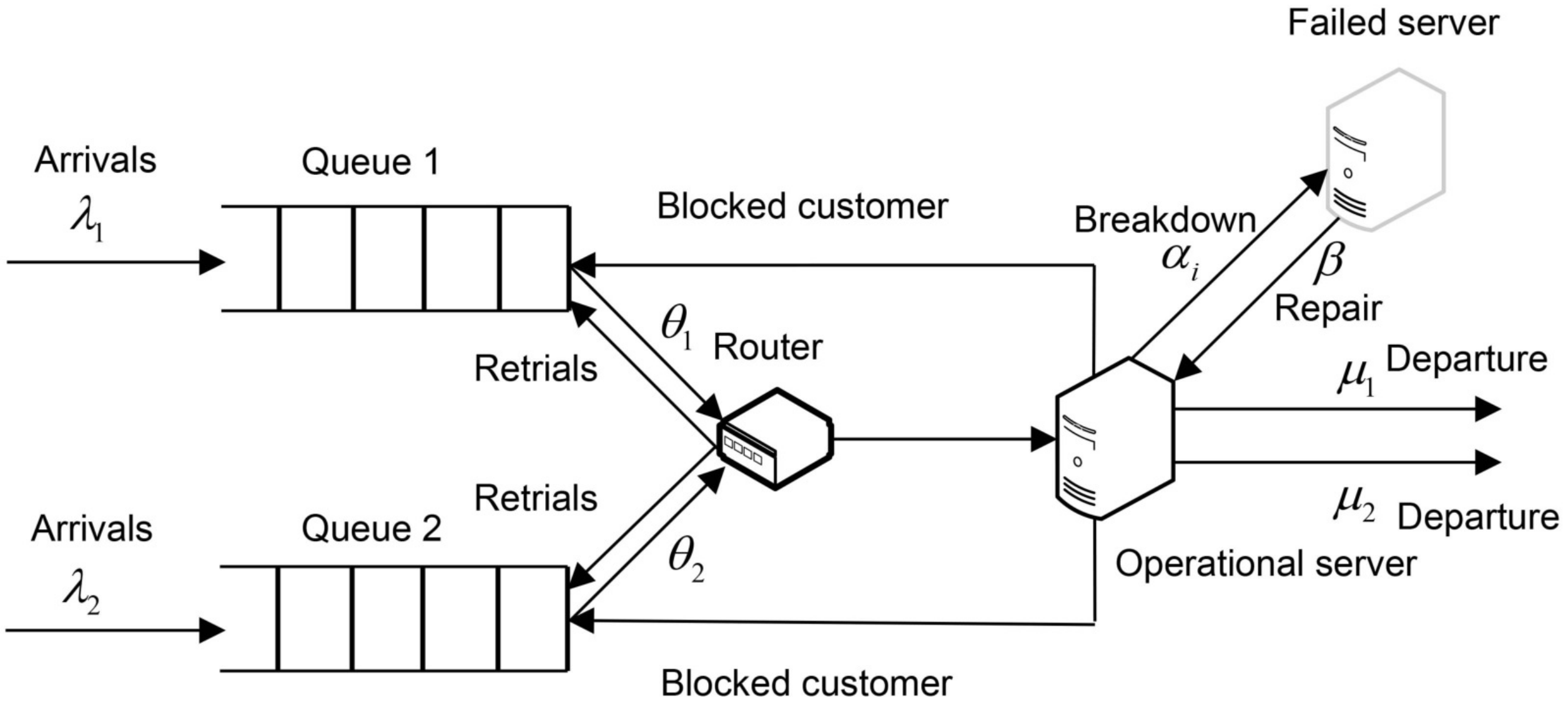
2. Model Description
3. Optimal Allocation Problem
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FIFO | First-In-First-Out |
| QBD | Quasi-Birth-and-Death |
| MDP | Markov Decision Process |
References
- Buyukkoc, C.; Varaiya, P.; Walr, J. The cμ rule revisited. Adv. Appl. Probab. 1985, 17, 237–238. [Google Scholar] [CrossRef]
- Cox, D.R.; Smith, W.L. Queues; Methuen: London, UK, 1961. [Google Scholar]
- Hirayama, T.; Kijima, M.; Nishimura, S. Further results for dynamic scheduling of multiclass G/G/1 queues. J. Appl. Probab. 1989, 26, 595–603. [Google Scholar] [CrossRef]
- Invernizzi, P.; Ripanti, S. A Generalized cμ-Rule for Scheduling Multiclass Queueing Systems with Dependent Arrival Rates. Master’s Thesis, Politecnico di Milano, Milan, Italy, 2018. Available online: https://www.politesi.polimi.it/bitstream/10589/139990/3/2018_04_Invernizzi_Ripanti.pdf (accessed on 15 September 2023).
- Van Mieghem, J.A. Dynamic scheduling with convex delay costs: The generalized cμ-rule. Ann. Appl. Probab. 1995, 5, 809–833. [Google Scholar] [CrossRef]
- Baras, J.S.; Dorsey, A.J.; Makowski, A.M. Two competing queues with linear costs and geometric service requirements: The μc-rule is often optimal. Adv. Appl. Probab. 1985, 17, 186–209. [Google Scholar] [CrossRef]
- Kebarighotbi, A.; Cassandras, C.G. Revisiting the optimality of the cμ-rule with Stochastic Flow Models. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC) Held Jointly with 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009. [Google Scholar]
- Winkler, A. Dynamic scheduling of a single-server two-class queue with constant retrial policy. Ann. Oper. Res. 2013, 202, 197–210. [Google Scholar] [CrossRef]
- Krishnasamy, S.; Arapostathis, A.; Johari, R.; Shakkottai, S. On Learning the cμ Rule in Single and Parallel Server Networks. In Proceedings of the 56th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 2–5 October 2018; pp. 153–154. [Google Scholar]
- Artalejo, J. A classified bibliography of research on retrial queues: Progress in 1990–1999. Top 1999, 7, 187–211. [Google Scholar] [CrossRef]
- Yang, T.; Templeton, J.G.C. A survey on retrial queues. Queueing Syst. 1987, 2, 201–233. [Google Scholar] [CrossRef]
- Fayolle, G. A simple telephone exchange with delayed feedbacks. In Proceedings of the International Seminar on Teletraffic Analysis and Computer Performance Evaluation, Amsterdam, The Netherlands, 2–6 June 1986; pp. 245–253. [Google Scholar]
- Economou, A.; Kanta, S. Equilibrium customer strategies and social-profit maximization in the single-server constant retrial queue. Nav. Res. Logist. 2011, 58, 107–122. [Google Scholar] [CrossRef]
- Efrosinin, D.; Winkler, A. Queueing system with a constant retrial rate, non-reliable server and threshold-based recovery. Eur. J. Oper. Res. 2011, 210, 594–605. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, X.; Huang, P. Strategic behavior and social optimization in a constant retrial queue with the N-policy. Eur. J. Oper. Res. 2017, 256, 841–849. [Google Scholar] [CrossRef]
- Avrachenkov, K.; Morozov, E.; Nekrasova, R.; Steyaert, B. Stability analysis and simulation of n-class retrial system with constant retrial rates and poisson inputs. Asia Pac. J. Oper. Res. 2014, 31, 1440002. [Google Scholar] [CrossRef]
- Dimitriou, I. A two-class queueing system with constant retrial policy and general class dependent service times. Eur. J. Oper. Res. 2018, 270, 1063–1073. [Google Scholar] [CrossRef]
- Nekrasova, R.; Morozov, E.; Efrosinin, D.; Stepanova, N. Stability analysis of a two-class system with constant retrial rate and unreliable server. Ann. Oper. Res. 2023. [Google Scholar] [CrossRef]
- Neuts, M.F. Matrix-Geometric Solutions in Stochastic Models: An Algorithmic Approach; Johns Hopkins University Press: Baltimore, MD, USA, 1981. [Google Scholar]
- Howard, R.A. Dynamic Programming and Markov Processes (Technology Press Research Monographs), 1st ed.; MIT Press: Cambridge, UK, 1960. [Google Scholar]
- Puterman, M.L. Markov Decision Processes: Discrete Stochastic Dynamic Programming; Wiley-Interscience: New York, NY, USA, 1994. [Google Scholar]
- Sennott, L.T. Stochastic Dynamic Programming and the Control of Queueing Systems; Wiley Series in Probability and Statistics: Applied Probability and Statistics; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Özkan, E.; Kharoufeh, J. Optimal control of a two-server queueing system with failures. Probab. Eng. Informational Sci. 2014, 28, 489–527. [Google Scholar] [CrossRef]
| 0.30 | 5 | 3 | 0.55 | 0.5 | 0.10 | 1.00 | 25.657 | 29.403 |
| 0.26 | 5 | 3 | 0.70 | 0.40 | 0.10 | 2.00 | 36.909 | 34.238 |
| 0.26 | 5 | 3 | 0.70 | 0.43 | 0.12 | 1.64 | 18.223 | 18.291 |
| 0.30 | 3 | 5 | 0.51 | 0.5 | 0.10 | 1.00 | 25.430 | 22.955 |
| 0.30 | 3 | 5 | 0.51 | 0.5 | 0.10 | 0.90 | 23.421 | 24.709 |
| 0.30 | 5 | 3 | 0.55 | 0.5 | 0.10 | 1.20 | 33.348 | 31.610 |
| \ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ⋯ |
| 0 | 0 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | ... |
| 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | ... |
| 2 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | ... |
| 3 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | ... |
| 4 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | ... |
| 5 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | ... |
| 6 | 1 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | ... |
| 7 | 1 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ... |
| 8 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ... |
| 9 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ... |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋱ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Efrosinin, D.; Stepanova, N.; Sztrik, J. Robustness of the cμ-Rule for an Unreliable Single-Server Two-Class Queueing System with Constant Retrial Rates. Mathematics 2023, 11, 4002. https://doi.org/10.3390/math11184002
Efrosinin D, Stepanova N, Sztrik J. Robustness of the cμ-Rule for an Unreliable Single-Server Two-Class Queueing System with Constant Retrial Rates. Mathematics. 2023; 11(18):4002. https://doi.org/10.3390/math11184002
Chicago/Turabian StyleEfrosinin, Dmitry, Natalia Stepanova, and Janos Sztrik. 2023. "Robustness of the cμ-Rule for an Unreliable Single-Server Two-Class Queueing System with Constant Retrial Rates" Mathematics 11, no. 18: 4002. https://doi.org/10.3390/math11184002
APA StyleEfrosinin, D., Stepanova, N., & Sztrik, J. (2023). Robustness of the cμ-Rule for an Unreliable Single-Server Two-Class Queueing System with Constant Retrial Rates. Mathematics, 11(18), 4002. https://doi.org/10.3390/math11184002






