A Multi-Stage Methodology for Long-Term Open-Pit Mine Production Planning under Ore Grade Uncertainty
Abstract
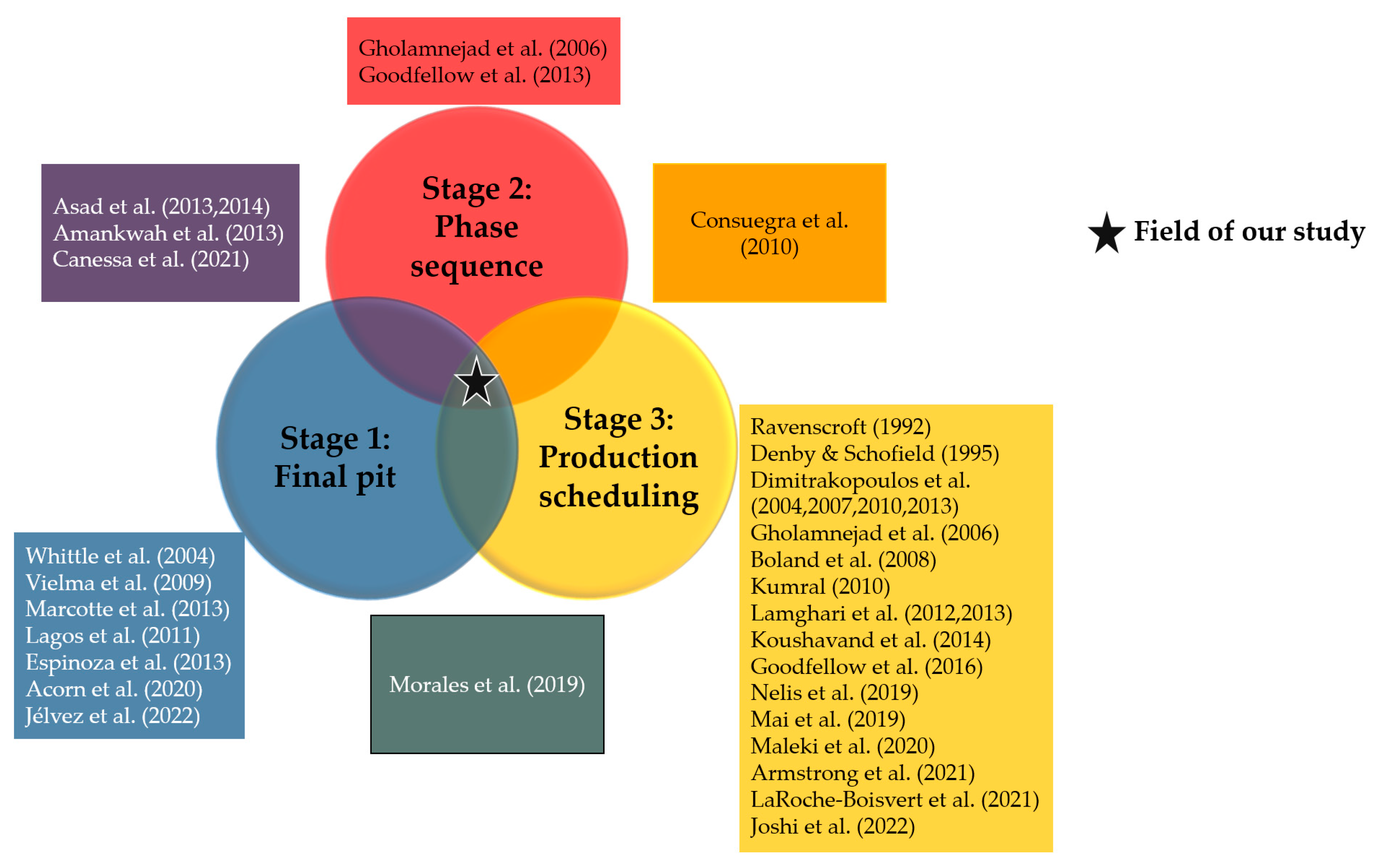
:1. Introduction
- Economic evaluation. For each block, an economic evaluation representing the net economic value of mining it (and potentially processing it) is calculated. This evaluation depends on the block’s mineral content, the price of the ore, and the associated costs of mining and processing the block. Thus, an economic block model is obtained.
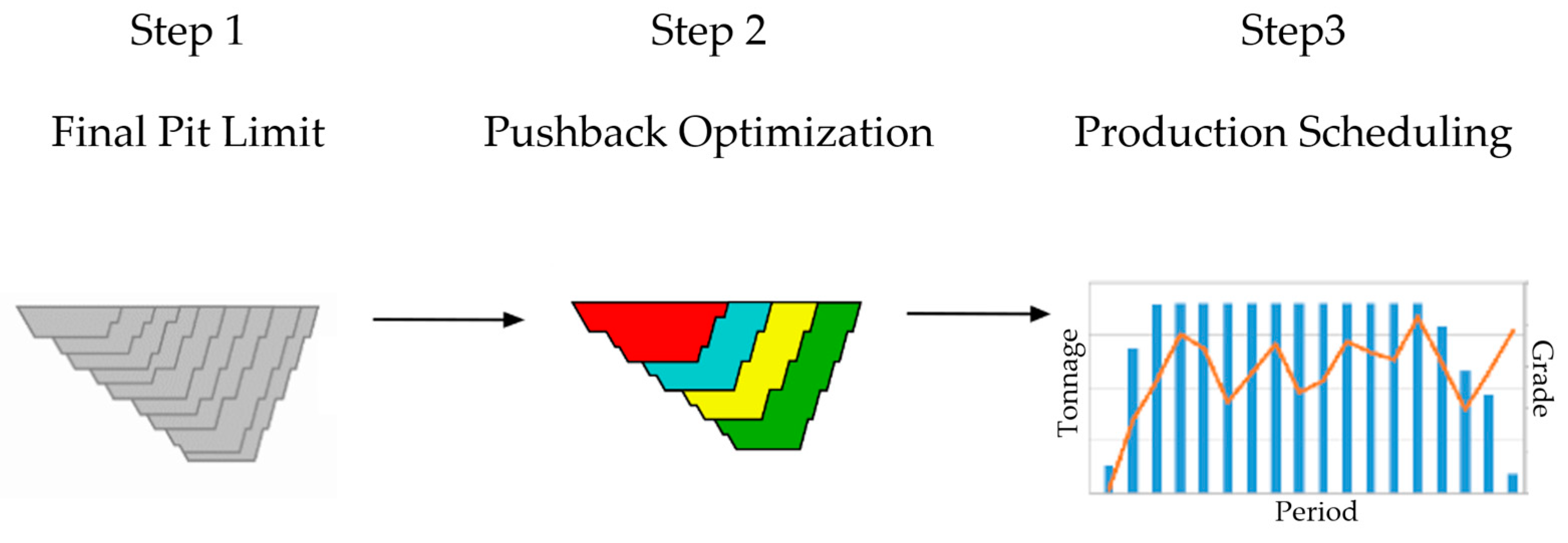
- Final pit. With this main input, in addition to a series of technical parameters, the region of the mine where the exploitation will be carried out is defined; this is known as the final pit (first stage). This key step in the planning process provides an estimation of the economic value and tonnage of the mining project in its early stages.
- Pushback optimization. Within the final pit, many incremental nested pits are generated using the Lerchs and Grossmann methodology [4]. Among these nested pits, some are chosen to define the mining phases (second stage), and the volumes between consecutive phases are called pushbacks. The selection of the phases (equivalently, the pushbacks) is performed based on selected criteria, such as the minimum operational width that must be maintained to ensure an operative design and similar ore tonnage [5,6,7,8].
- A mathematical model to optimize the final pit considering the geological uncertainty. The model optimizes the pit value minus the conditional value at risk (CVaR).
- A mathematical model for pushback optimization in an uncertainty setting. In the application in this paper, the model selects pushbacks from nested pits such that the total tonnages are similar, but it can be modified to accommodate other criteria.
- A mixed-integer program to schedule bench phases under uncertainty to minimize deviations from production targets based on an existing set of pushbacks.
- The integration of the previous contributions as a multi-stage strategic optimization approach and its application in a real case study.
2. Materials and Methods
2.1. General Notation
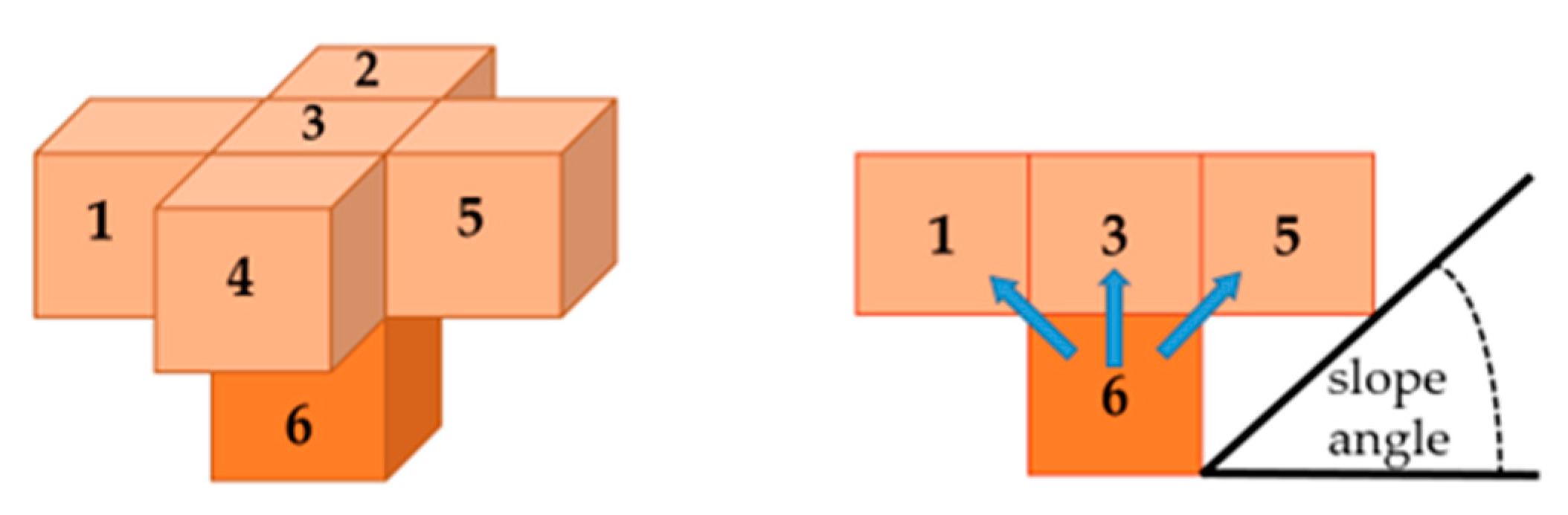
2.2. Stage 1: Final Pit Limit Problem
| (6) | |||
| s.t. | (7) | ||
| (8) | |||
| (9) | |||
| (10) | |||
| (11) | |||
| (12) |
2.3. Stage 2: Pushback Optimization
2.3.1. Computation of Stochastic Nested Pits
2.3.2. Pushback Selection from the Stochastic Nested Pits
| (18) | |||
| s.t. | (19) | ||
| (20) | |||
| (21) | |||
| (22) | |||
| (23) | |||
| (24) | |||
| (25) | |||
| (26) |
2.4. Stage 3: Production Scheduling
| (P3) | (36) | ||
| s. t. | (37) | ||
| (38) | |||
| (39) | |||
| (40) | |||
| (41) | |||
| (42) | |||
| (43) | |||
| (44) | |||
| (45) | |||
| (46) | |||
| (47) | |||
| (48) | |||
| (49) | |||
| (50) | |||
| (51) | |||
| (52) | |||
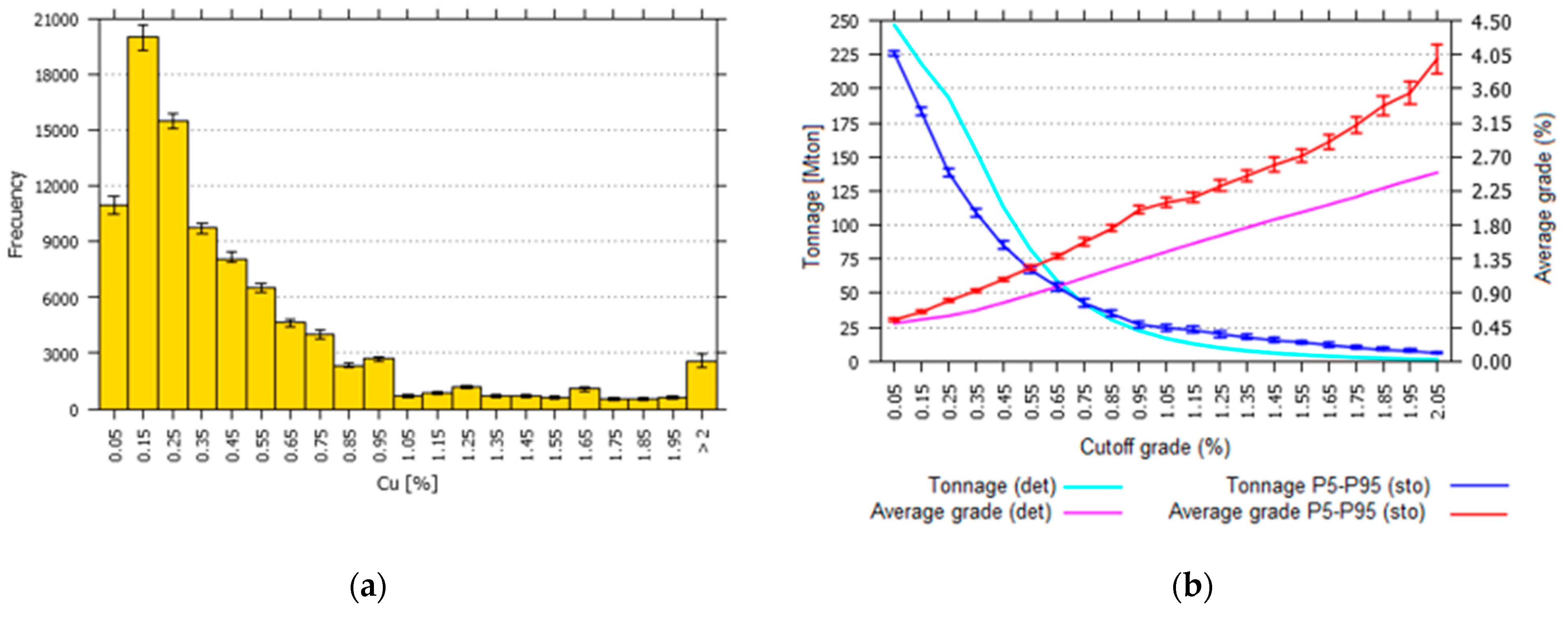
2.5. Case Study
3. Results
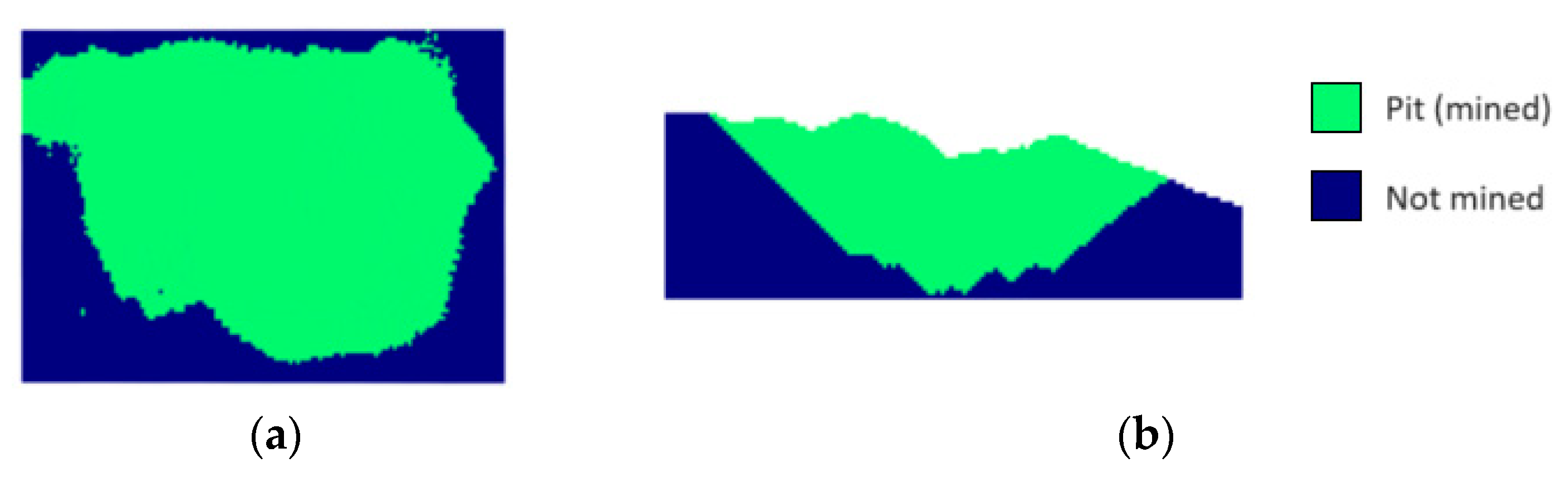
3.1. Final Pit
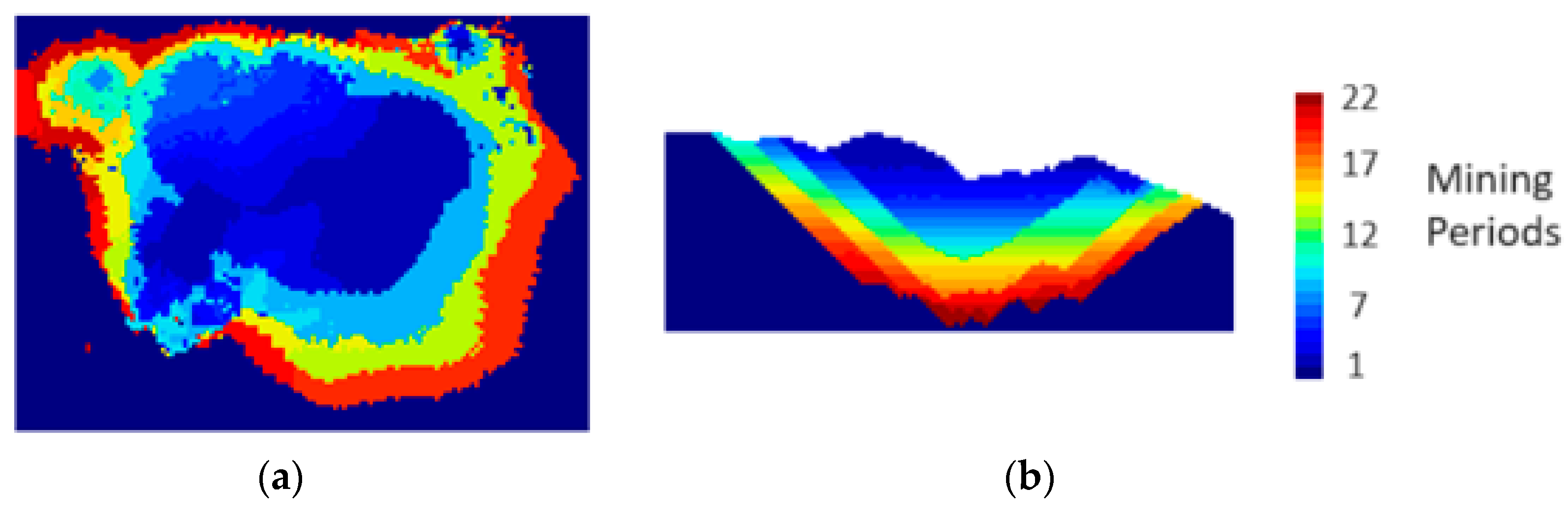
3.2. Pushback Optimization
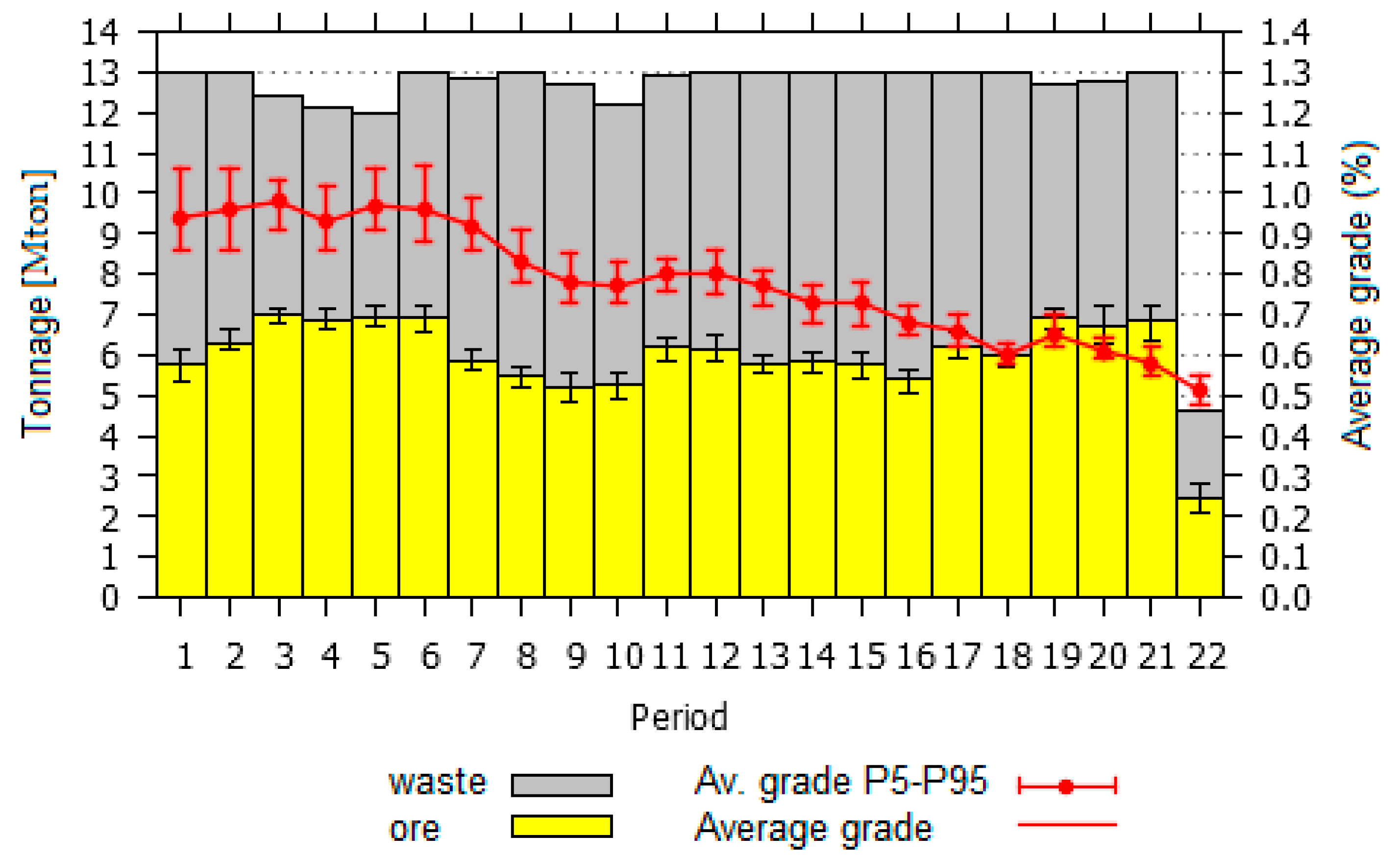
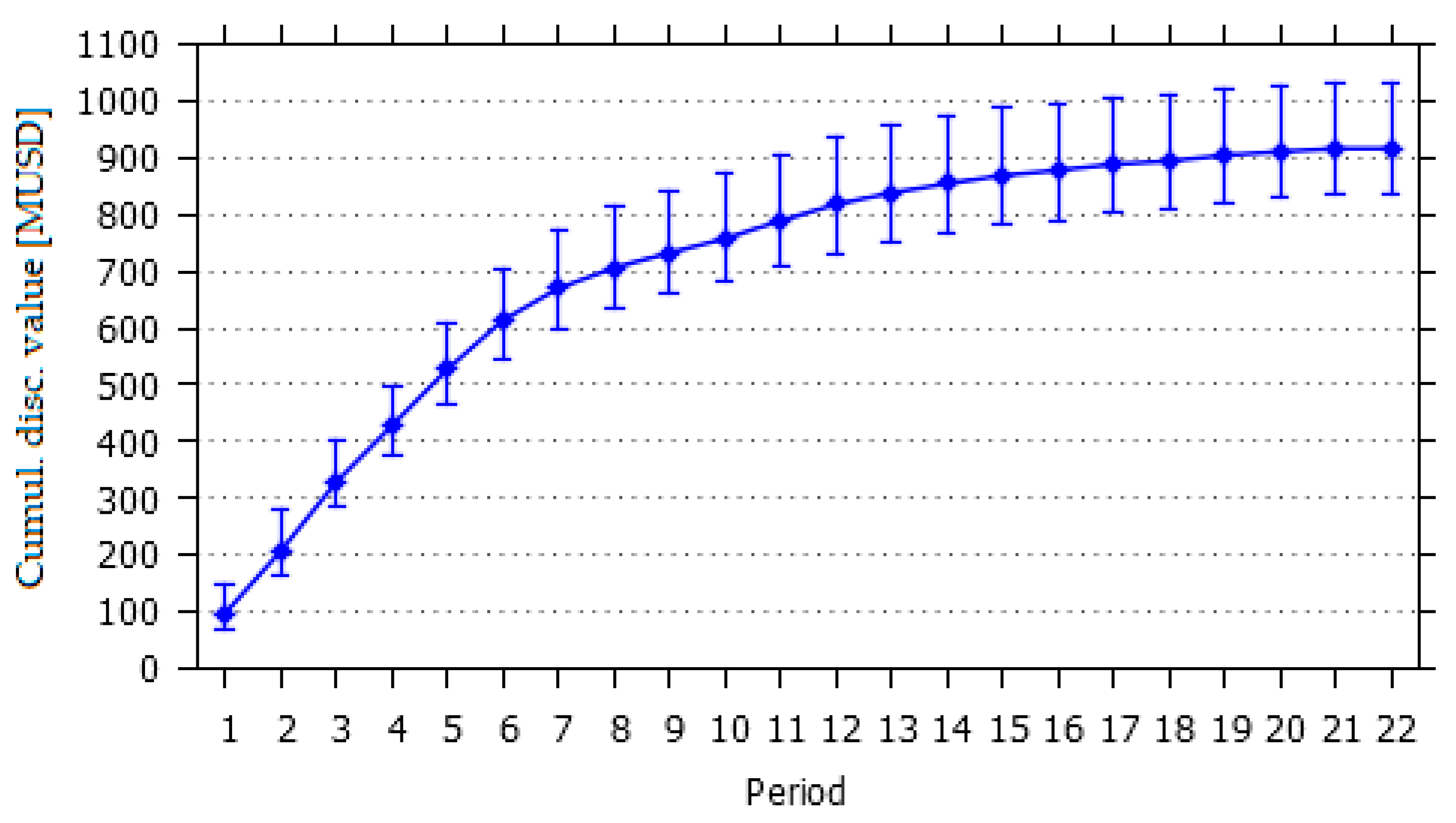
3.3. Production Scheduling
3.4. Impact of Grade Uncertainty at Each of the Planning Stages
- Fully deterministic, “”: In this case, the multi-stage methodology is applied without considering grade uncertainty, i.e., under a deterministic approach. This is considered the “base case”.
- Stochastic 3rd stage, “”: This case aims to evaluate the effect of incorporating grade uncertainty in production scheduling only. For this, we consider grade uncertainty only in stage 3, deterministic final pit, and pushback optimization.
- Deterministic 1st stage, “”: In this case, the final pit limit is chosen under a deterministic approach, but pushback optimization and production scheduling are stochastic.
- Fully stochastic, “”: In this case, the multi-stage methodology is applied, considering grade uncertainty at all stages. This case aims to evaluate the contribution of Stage 1 under grade uncertainty when compared with. Additionally, this case shows the added value of the complete proposed methodology.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hustrulid, W.A.; Kuchta, M.; Martin, R.K. Open Pit Mine Planning and Design, Two Volume Set & CD-ROM Pack; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar] [CrossRef]
- Chilès, J.-P.; Delfiner, P. Geostatistics Modeling Spatial Uncertainty; John Wiley & Sons: New York, NY, USA, 2012; Available online: http://internationalscholarvoxcom/book/88813008 (accessed on 24 June 2018).
- Tabesh, M.; Mieth, C.; Nasab, H.A. A multi-step approach to long-term open-pit production planning. Int. J. Min. Miner. Eng. 2014, 5, 273. [Google Scholar] [CrossRef]
- Lerchs, H.; Grossmann, I.F. Optimum Design of Open-Pit Mines, Transactions. Can. Inst. Min. 1965, 58, 17–24. [Google Scholar]
- Meagher, C.; Dimitrakopoulos, R.; Avis, D. Optimized open pit mine design, pushbacks and the gap problem—A review. J. Min. Sci. 2014, 50, 508–526. [Google Scholar] [CrossRef]
- Jélvez, E.; Morales, N.; Askari-Nasab, H. A new model for automated pushback selection. Comput. Oper. Res. 2020, 115, 104456. [Google Scholar] [CrossRef]
- Nancel-Penard, P.; Morales, N. Optimizing pushback design considering minimum mining width for open pit strategic planning. Eng. Optim. 2022, 54, 1494–1508. [Google Scholar] [CrossRef]
- Morales, N.; Nancel-Penard, P.; Espejo, N. Development and analysis of a methodology to generate operational open-pit mine ramp designs automatically. Optim. Eng. 2022, 24, 711–741. [Google Scholar] [CrossRef]
- Chicoisne, R.; Espinoza, D.; Goycoolea, M.; Moreno, E.; Rubio, E. A New Algorithm for the Open-Pit Mine Production Scheduling Problem. Oper. Res. 2012, 60, 517–528. [Google Scholar] [CrossRef]
- Letelier, O.R.; Espinoza, D.; Goycoolea, M.; Moreno, E.; Muñoz, G. Production Scheduling for Strategic Open Pit Mine Planning: A Mixed-Integer Programming Approach. Oper. Res. 2020, 68, 1425–1444. [Google Scholar] [CrossRef]
- Nancel-Penard, P.; Morales, N.; Cornillier, F. A recursive time aggregation-disaggregation heuristic for the multidimensional and multiperiod precedence-constrained knapsack problem: An application to the open-pit mine block sequencing problem. Eur. J. Oper. Res. 2022, 303, 1088–1099. [Google Scholar] [CrossRef]
- Morales, N.; Seguel, S.; Cáceres, A.; Jélvez, E.; Alarcón, M. Incorporation of Geometallurgical Attributes and Geological Uncertainty into Long-Term Open-Pit Mine Planning. Minerals 2019, 9, 108. [Google Scholar] [CrossRef]
- Upadhyay, S.; Askari-Nasab, H. Simulation and optimization approach for uncertainty-based short-term planning in open pit mines. Int. J. Min. Sci. Technol. 2018, 8, 153–166. [Google Scholar] [CrossRef]
- Abdel Sabour, S.A.; Dimitrakopoulos, R.G.; Kumral, M. Mine design selection under uncertainty. Min. Technol. 2008, 117, 53–64. [Google Scholar] [CrossRef]
- Dowd, P.A.; Xu, C.; Coward, S. Strategic mine planning and design: Some challenges and strategies for addressing them. Min. Technol. 2016, 125, 22–34. [Google Scholar] [CrossRef]
- Dimitrakopoulos, R. Advances in Applied Strategic Mine Planning; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Ortiz, J.M.; Deutsch, C.V. Indicator Simulation Accounting for Multiple-Point Statistics. Math. Geol. 2004, 36, 545–565. [Google Scholar] [CrossRef]
- Emery, X.; Lantuéjoul, C. TBSIM: A computer program for conditional simulation of three-dimensional Gaussian random fields via the turning bands method. Comput. Geosci. 2006, 32, 1615–1628. [Google Scholar] [CrossRef]
- Maleki, M.; Madani, N.; Jélvez, E. Geostatistical Algorithm Selection for Mineral Resources Assessment and its Impact on Open-pit Production Planning Considering Metal Grade Boundary Effect. Nat. Resour. Res. 2021, 30, 4079–4094. [Google Scholar] [CrossRef]
- Whittle, D. A Bozorgebrahimi, Hybrid Pits—Linking Conditional Simulation and Lerchs-Grossmann Through Set Theory. In Proceedings of the Symposium on Orebody Modelling and Strategic Mine Planning, Perth, Australia, 22–24 November 2004; pp. 399–404. [Google Scholar]
- Marcotte, D.; Caron, J. Ultimate open pit stochastic optimization. Comput. Geosci. 2013, 51, 238–246. [Google Scholar] [CrossRef]
- Vielma, J.P.; Espinoza, D.; Moreno, E. Risk control in ultimate pits using conditional simulations. In Proceedings of the 34th APCOM Conference, Vancouver, BC, Canada, 6–9 October 2009; pp. 107–114. [Google Scholar]
- Lagos, G.; Espinoza, D.; Moreno, E.; Amaya, J. Robust Planning for an Open-Pit Mining Problem under Ore-Grade Uncertainty. Electron. Notes Discret. Math. 2011, 37, 15–20. [Google Scholar] [CrossRef]
- Espinoza, D.; Lagos, G.; Moreno, E.; Vielma, J. Risk averse approaches in open-pit production planning under ore grade uncertainty: An ultimate pit study. In Proceedings of the 36th International Symposium on the Applications of Computers and Operations Research in the Mineral Industry (APCOM), Alegre, Brazil, 4–8 November 2013; pp. 492–501. [Google Scholar]
- Acorn, T.; Boisvert, J.B.; Leuangthong, O. Managing Geologic Uncertainty in Pit Shell Optimization Using a Heuristic Algorithm and Stochastic Dominance, Mining. Metall. Explor. 2020, 37, 375–386. [Google Scholar] [CrossRef]
- Jelvez, E.; Morales, N.; Ortiz, J.M. Stochastic Final Pit Limits: An Efficient Frontier Analysis under Geological Uncertainty in the Open-Pit Mining Industry. Mathematics 2021, 10, 100. [Google Scholar] [CrossRef]
- Dimitrakopoulos, R.; Martinez, L.; Ramazan, S. A maximum upside/minimum downside approach to the traditional optimization of open pit mine design. J. Min. Sci. 2007, 43, 73–82. [Google Scholar] [CrossRef]
- Gholamnejad, J.; Osanloo, M. Incorporation of ore grade uncertainty into the push back design process. J. South. Afr. Inst. Min. Metall. 2007, 107, 177–185. [Google Scholar]
- Goodfellow, R.; Dimitrakopoulos, R. Algorithmic integration of geological uncertainty in pushback designs for complex multiprocess open pit mines. Min. Technol. 2013, 122, 67–77. [Google Scholar] [CrossRef]
- Ravenscroft, P. Risk analysis for mine scheduling by conditional simulation. Trans. Inst. Min. Metall. Sect. A Min. Ind. 1992, 101, A104–A108. [Google Scholar]
- Denby, B.; Schofield, D. Inclusion of risk assessment in open-pit design and scheduling. Int. J. Rock. Mech. Min. Sci. Geomech. Abstr. 1995, 5, 230A. [Google Scholar]
- Dimitrakopoulos, R.; Farrelly, C.T.; Godoy, M. Moving forward from traditional optimization: Grade uncertainty and risk effects in open-pit design. Min. Technol. 2002, 111, 82–88. [Google Scholar] [CrossRef]
- Dimitrakopoulos, R.; Ramazan, S. Uncertainty based production scheduling in open pit mining. SME Trans. 2004, 316, 106–112. [Google Scholar]
- Dimitrakopoulos, R. Stochastic optimization for strategic mine planning: A decade of developments. J. Min. Sci. 2011, 47, 138–150. [Google Scholar] [CrossRef]
- Dimitrakopoulos, R.; Jewbali, A. Joint stochastic optimisation of short and long term mine production planning: Method and application in a large operating gold mine. Min. Technol. 2013, 122, 110–123. [Google Scholar] [CrossRef]
- Koushavand, B.; Askari-Nasab, H.; Deutsch, C.V. A linear programming model for long-term mine planning in the presence of grade uncertainty and a stockpile. Int. J. Min. Sci. Technol. 2014, 24, 451–459. [Google Scholar] [CrossRef]
- Mai, N.L.; Topal, E.; Erten, O.; Sommerville, B. A new risk-based optimisation method for the iron ore production scheduling using stochastic integer programming. Resour. Policy 2019, 62, 571–579. [Google Scholar] [CrossRef]
- Maleki, M.; Jélvez, E.; Emery, X.; Morales, N. Stochastic Open-Pit Mine Production Scheduling: A Case Study of an Iron Deposit. Minerals 2020, 10, 585. [Google Scholar] [CrossRef]
- LaRoche-Boisvert, M.; Dimitrakopoulos, R. An Application of Simultaneous Stochastic Optimization at a Large Open-Pit Gold Mining Complex under Supply Uncertainty. Minerals 2021, 11, 172. [Google Scholar] [CrossRef]
- Boland, N.; Dumitrescu, I.; Froyland, G. A multistage stochastic programming approach to open pit mine production scheduling with uncertain geology. Optim. Online 2008, 1–33. [Google Scholar]
- Nelis, G.; Morales, N.; Widzyk-Capehart, E. Comparison of Different Approaches to Strategic Open-Pit Mine Planning Under Geological Uncertainty. In Proceedings of the 27th International Symposium on Mine Planning and Equipment Selection-MPES 2018, Calgary, AL, Canada, 4–22 August 2018; Widzyk-Capehart, E., Hekmat, A., Singhal, R., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 95–105. [Google Scholar] [CrossRef]
- Armstrong, M.; Lagos, T.; Emery, X.; Homem-de-Mello, T.; Lagos, G.; Sauré, D. Adaptive open-pit mining planning under geological uncertainty. Resour. Policy 2021, 72, 102086. [Google Scholar] [CrossRef]
- Kumral, M. Robust stochastic mine production scheduling. Eng. Optim. 2010, 42, 567–579. [Google Scholar] [CrossRef]
- Lamghari, A.; Dimitrakopoulos, R. Progressive hedging applied as a metaheuristic to schedule production in open-pit mines accounting for reserve uncertainty. Eur. J. Oper. Res. 2016, 253, 843–855. [Google Scholar] [CrossRef]
- Goodfellow, R.C.; Dimitrakopoulos, R. Global optimization of open pit mining complexes with uncertainty. Appl. Soft Comput. 2016, 40, 292–304. [Google Scholar] [CrossRef]
- Chatterjee, S.; Dimitrakopoulos, R. Production scheduling under uncertainty of an open-pit mine using Lagrangian relaxation and branch-and-cut algorithm. Int. J. Min. Reclam. Environ. 2020, 34, 343–361. [Google Scholar] [CrossRef]
- Lamghari, A.; Dimitrakopoulos, R. Hyper-heuristic approaches for strategic mine planning under uncertainty. Comput. Oper. Res. 2020, 115, 104590. [Google Scholar] [CrossRef]
- Tolouei, K.; Moosavi, E.; Tabrizi, A.H.; Afzal, P.; Bazzazi, A.A. An optimisation approach for uncertainty-based long-term production scheduling in open-pit mines using meta-heuristic algorithms. Int. J. Min. Reclam. Environ. 2021, 35, 115–140. [Google Scholar] [CrossRef]
- Joshi, D.; Paithankar, A.; Chatterjee, S.; Equeenuddin, S.M. Integrated Parametric Graph Closure and Branch-and-Cut Algorithm for Open Pit Mine Scheduling under Uncertainty. Mining 2022, 2, 32–51. [Google Scholar] [CrossRef]
- Asad, M.W.; Dimitrakopoulos, R. Implementing a parametric maximum flow algorithm for optimal open pit mine design under uncertain supply and demand. J. Oper. Res. Soc. 2013, 64, 185–197. [Google Scholar] [CrossRef]
- Asad, M.W.; Dimitrakopoulos, R.; van Eldert, J. Stochastic production phase design for an open pit mining complex with multiple processing streams. Eng. Optim. 2014, 46, 1139–1152. [Google Scholar] [CrossRef]
- Amankwah, H.; Larsson, T.; Textorius, B. Open-Pit Mining with Uncertainty: A Conditional Value-at-Risk Approach. In Optimization Theory, Decision Making, and Operations Research Applications; Migdalas, A., Sifaleras, A., Georgiadis, C.K., Papathanasiou, J., Stiakakis, E., Eds.; Springer: New York, NY, USA, 2013; pp. 117–139. [Google Scholar] [CrossRef]
- Canessa, G.; Moreno, E.; Pagnoncelli, B.K. The risk-averse ultimate pit problem. Optim. Eng. 2021, 22, 2655–2678. [Google Scholar] [CrossRef]
- Consuegra, F.R.; Dimitrakopoulos, R. Algorithmic approach to pushback design based on stochastic programming: Method, application and comparisons. Min. Technol. 2010, 119, 88–101. [Google Scholar] [CrossRef]
- Osanloo, M.; Gholamnejad, J.; Karimi, B. Long-term open pit mine production planning: A review of models and algorithms, International Journal of Mining. Reclam. Environ. 2008, 22, 3–35. [Google Scholar] [CrossRef]
- Fathollahzadeh, K.; Asad, M.W.; Mardaneh, E.; Cigla, M. Review of Solution Methodologies for Open Pit Mine Production Scheduling Problem. Int. J. Min. Reclam. Environ. 2021, 35, 564–599. [Google Scholar] [CrossRef]
- Zeng, L.; Liu, S.Q.; Kozan, E.; Corry, P.; Masoud, M. A comprehensive interdisciplinary review of mine supply chain management. Resour. Policy 2021, 74, 102274. [Google Scholar] [CrossRef]
- Dimitrakopoulos, R.; Lamghari, A. Simultaneous stochastic optimization of mining complexes-mineral value chains: An overview of concepts, examples and comparisons. Int. J. Min. Reclam. Environ. 2022, 36, 443–460. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Uryasev, S. Optimization of conditional value-at-risk. JOR 2000, 2, 21–41. [Google Scholar] [CrossRef]
- Krokhmal, P.; Uryasev, S.; Palmquist, J. Portfolio optimization with conditional value-at-risk objective and constraints. JOR 2001, 4, 43–68. [Google Scholar] [CrossRef]
- Espinoza, D.; Goycoolea, M.; Moreno, E. A Newman, MineLib: A library of open pit mining problems. Ann. Oper. Res. 2013, 206, 93–114. [Google Scholar] [CrossRef]
- Dimitrakopoulos, R.; Ramazan, S. Stochastic integer programming for optimising long term production schedules of open pit mines: Methods, application and value of stochastic solutions. Min. Technol. 2008, 117, 155–160. [Google Scholar] [CrossRef]
- Leite, A.; Dimitrakopoulos, R. Stochastic optimization of mine production scheduling with uncertain ore/metal/waste supply. Int. J. Min. Sci. Technol. 2014, 24, 755–762. [Google Scholar] [CrossRef]
- de Carvalho, J.; Dimitrakopoulos, R. Effects of High-Order Simulations on the Simultaneous Stochastic Optimization of Mining Complexes. Minerals 2019, 9, 210. [Google Scholar] [CrossRef]
- Lambert, W.B.; Brickey, A.; Newman, A.M.; Eurek, K. Open-Pit Block-Sequencing Formulations: A Tutorial. Interfaces 2014, 44, 127–142. [Google Scholar] [CrossRef]
- Mitchell, S.; OSullivan, M.; Dunning, I. PuLP: A Linear Programming Toolkit for Python; The University of Auckland: Auckland, New Zealand, 2011. [Google Scholar]
- Gurobi Optimization, LCC. Gurobi Optimizer Reference Manual 2022. 2022. Available online: http://www.gurobi.com (accessed on 30 June 2022).




| Parameter | Symbol | Value |
|---|---|---|
| Copper price (USD/ton) | Price | 5511.55 |
| Metallurgical recovery | Rec | 0.85 |
| Mining cost (USD/ton) | Mcost | 3.2 |
| Processing cost (USD/ton) | Pcost | 9.0 |
| Parameter | Symbol | Value |
|---|---|---|
| Max. mining capacity (Mton) | 13.0 | |
| Min. mining capacity (Mton) | 0.0 | |
| Max. processing capacity (Mton) | 7.0 | |
| Min. processing capacity (Mton) | 6.0 | |
| Max. average grade (%) | ||
| Min. average grade (%) | 0.8–0.5 | |
| Maximum depth (benches) | 8 | |
| Horizon planning (years) | 22 | |
| Discount rate | 1/(1 + 10%) | |
| Number of destinations | 2 | |
| Number of scenarios | 50 | |
| Cost over-production ore (USD/ton) | 18.5 | |
| Cost under-production ore (USD/ton) | 18.5 | |
| Cost over-production metal (USD/ton) | 0 | |
| Cost under-production metal (USD/ton) | 39.0 |
| VaR [MUSD] | CVaR [MUSD] | Exptd. Value [MUSD] | Opt. Gap (%) | Time [s] |
|---|---|---|---|---|
| 144.99 | 166.00 | 2078.06 | 0.1 | 14,881 |
| Expected Tonnage [Mton] | Cutoff Grade | Difference [Ton] | Relative Variation % | |
|---|---|---|---|---|
| Fixed | Dynamic | |||
| Ore | 137.52 | 131.72 | 5.80 | 4.4 |
| Waste | 135.67 | 141.47 | −5.80 | −4.1 |
| Total (rock) | 273.19 | 273.19 | 0.00 | 0.0 |
| Case | ENPV [MUSD] | Relative Variation of ENPV (%) | ETCU [MUSD] | Relative Variation of ETCU (%) |
|---|---|---|---|---|
| 904.7 | - | 86.5 | - | |
| 915.4 | 0.9 | 41.8 | −51.7 | |
| 917.8 | 1.1 | 34.2 | −60.5 | |
| 923.8 | 2.1 | 26.7 | −69.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jelvez, E.; Ortiz, J.; Varela, N.M.; Askari-Nasab, H.; Nelis, G. A Multi-Stage Methodology for Long-Term Open-Pit Mine Production Planning under Ore Grade Uncertainty. Mathematics 2023, 11, 3907. https://doi.org/10.3390/math11183907
Jelvez E, Ortiz J, Varela NM, Askari-Nasab H, Nelis G. A Multi-Stage Methodology for Long-Term Open-Pit Mine Production Planning under Ore Grade Uncertainty. Mathematics. 2023; 11(18):3907. https://doi.org/10.3390/math11183907
Chicago/Turabian StyleJelvez, Enrique, Julian Ortiz, Nelson Morales Varela, Hooman Askari-Nasab, and Gonzalo Nelis. 2023. "A Multi-Stage Methodology for Long-Term Open-Pit Mine Production Planning under Ore Grade Uncertainty" Mathematics 11, no. 18: 3907. https://doi.org/10.3390/math11183907
APA StyleJelvez, E., Ortiz, J., Varela, N. M., Askari-Nasab, H., & Nelis, G. (2023). A Multi-Stage Methodology for Long-Term Open-Pit Mine Production Planning under Ore Grade Uncertainty. Mathematics, 11(18), 3907. https://doi.org/10.3390/math11183907







