Bifurcation Analysis Software and Chaotic Dynamics for Some Problems in Fluid Dynamics Laminar–Turbulent Transition
Abstract
1. Introduction
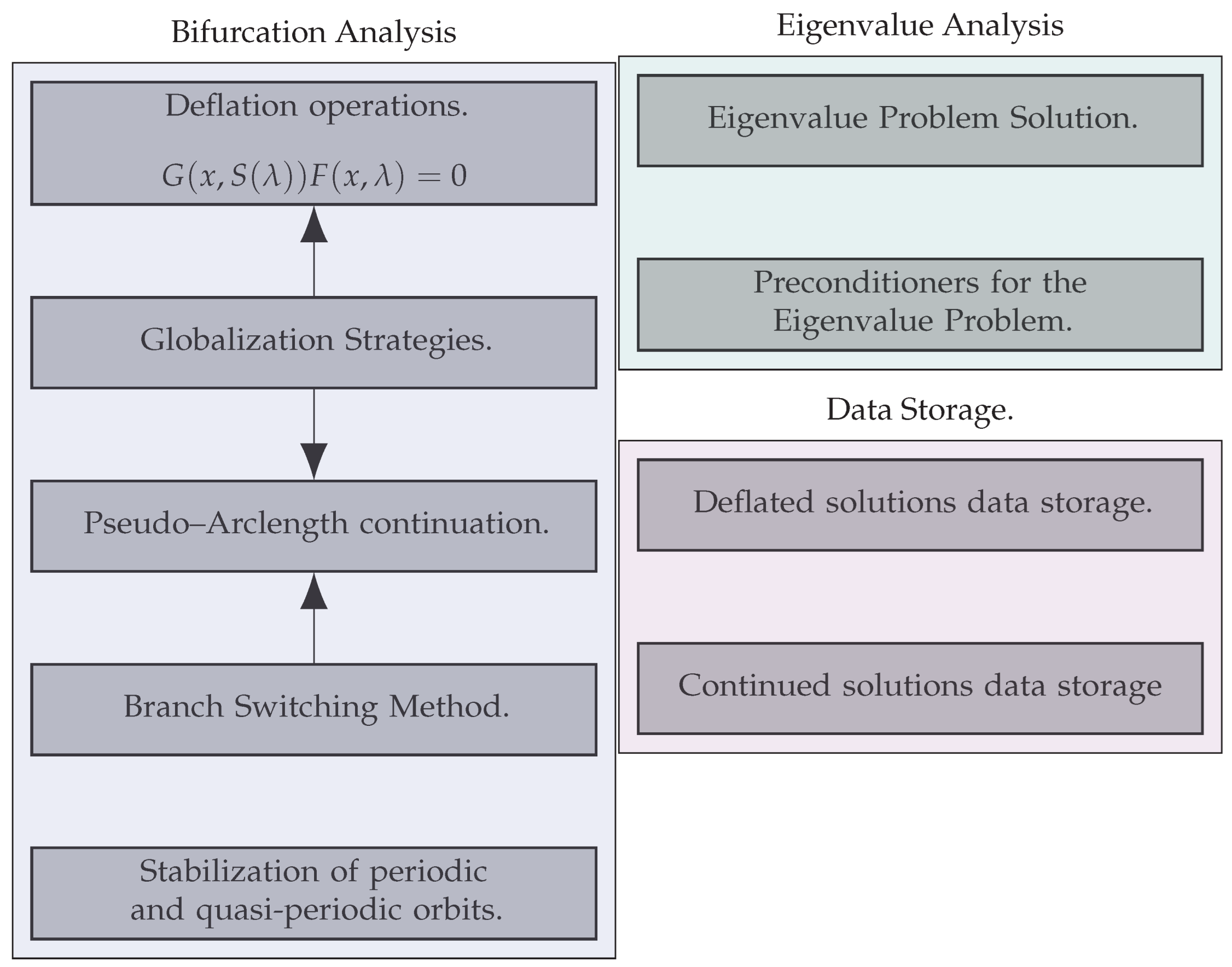
- Find a solution of (2) that can be traced from for some variation of to obtain using the continuation process, and apply stabilization methods if the solution is linear unstable.
- Obtain the linearization of the system (2) at and find the leading eigenvalues of the linearized system (these can be eigenvalues with the largest real parts for stationary solutions or the largest magnitude eigenvalues for periodic solutions).
- Find where the leading eigenvalues cross an imaginary axis or cross the unit circle for exponential mapping.
- Identify the bifurcation type.
- Check if there are other solutions that exist for the system at , then set such solutions as , and go to Step 1.
- Deflation of the solutions.
- Continuation of the solutions through bifurcation points.
- Stabilization of the stationary points of the original system (stationary solutions).
- Stabilization of periodic orbits (for example, by the stabilization of the fixed points in the Poincare mapping).
- Obtaining the leading eigenvalues of either the original system or of the return Poincare mapping.
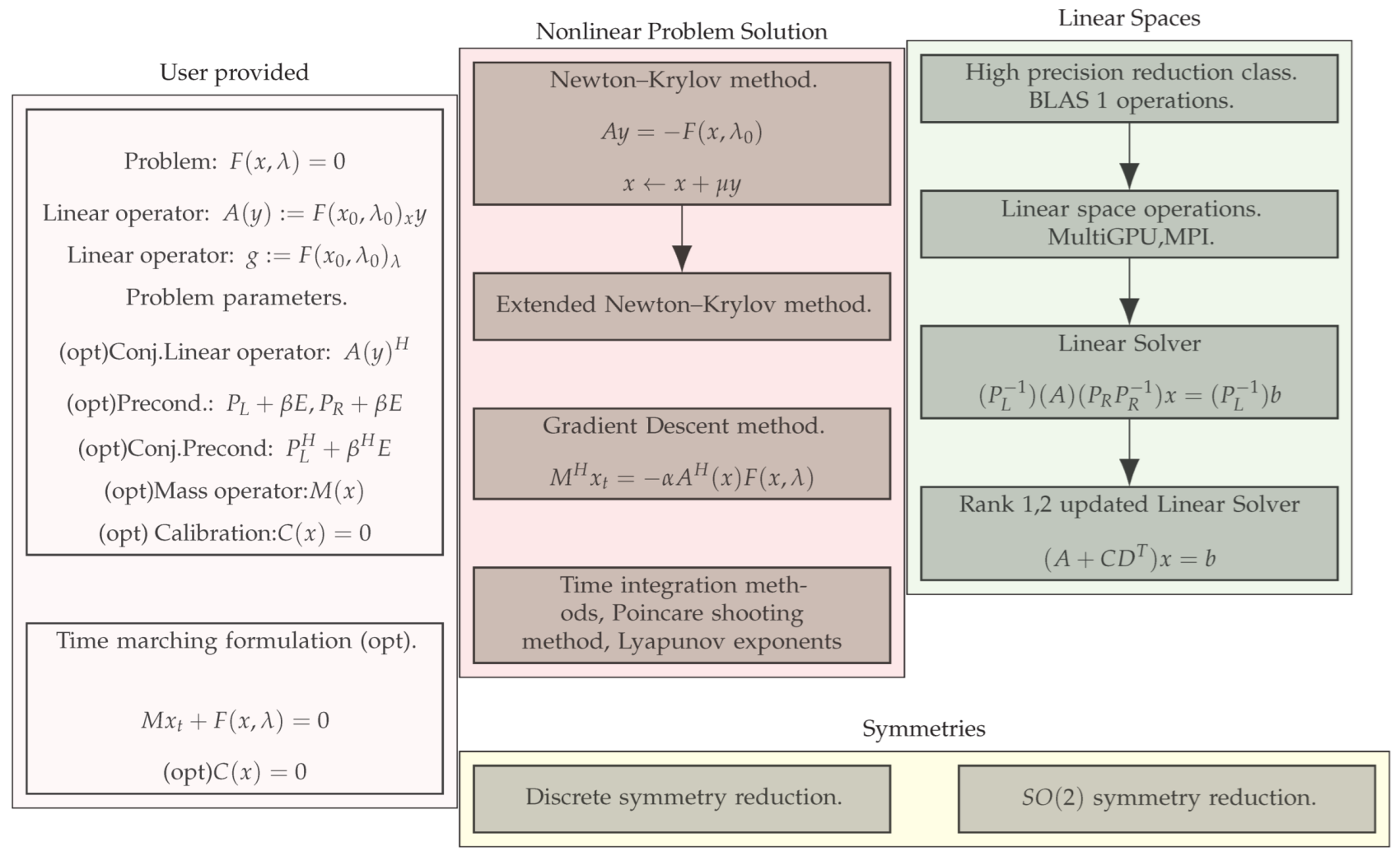
2. Numerical Methods and Software
2.1. Time Marching Integration
- ;
- ;
- and , there exist constants and s.t. .
| Algorithm 1 Error-free addition s.t. , , and . |
|
| Algorithm 2 Error-free multiplication s.t.: , , and |
|
| Algorithm 3 Compensated explicit autonomous Runge–Kutta method single-step from n to . All variables are presented in the base floating-point precision. |
|
2.2. Deflation with Discrete Symmetry
3. Bifurcation Analysis and Chaotic Dynamics in ABC Flow
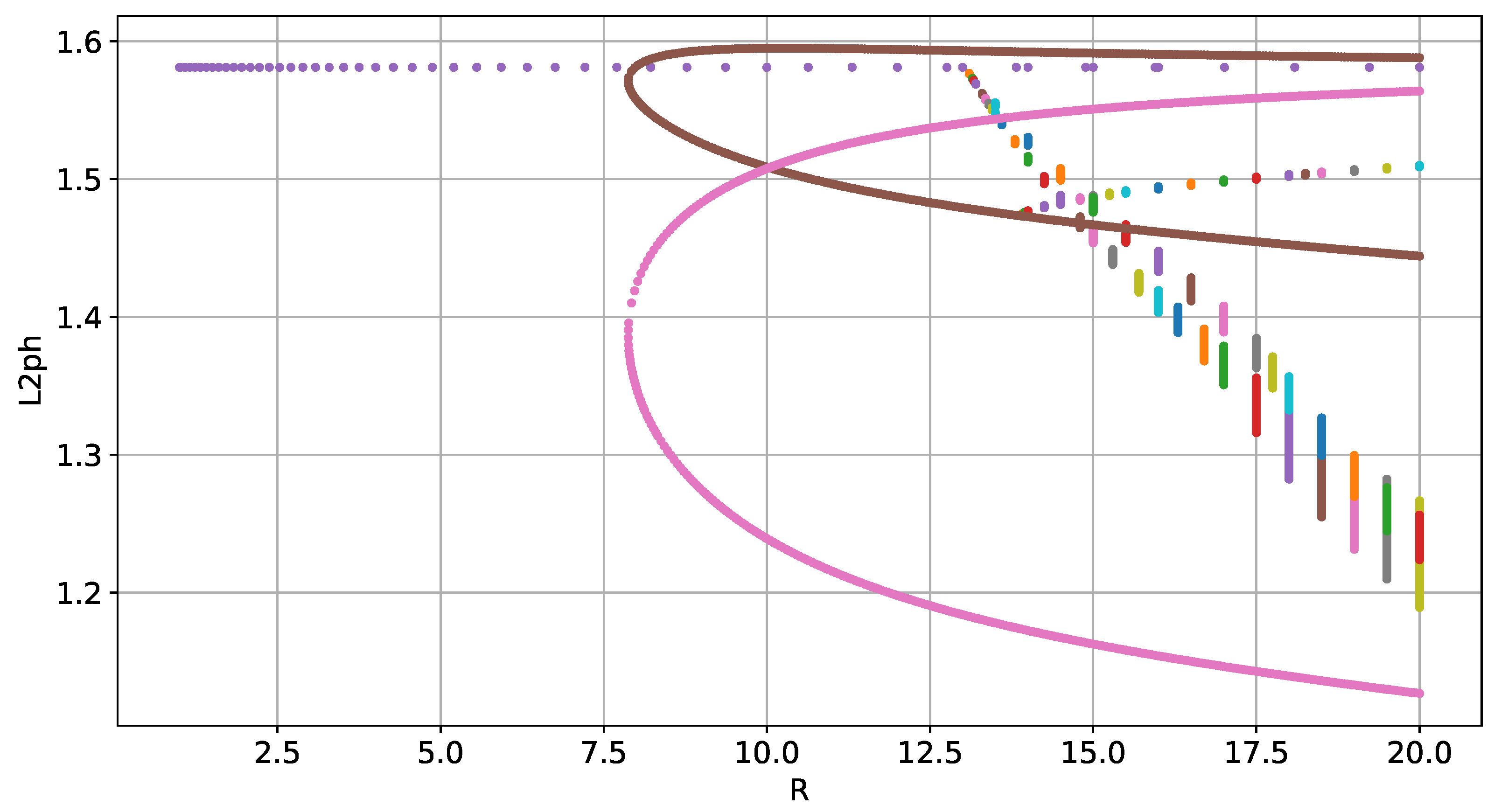
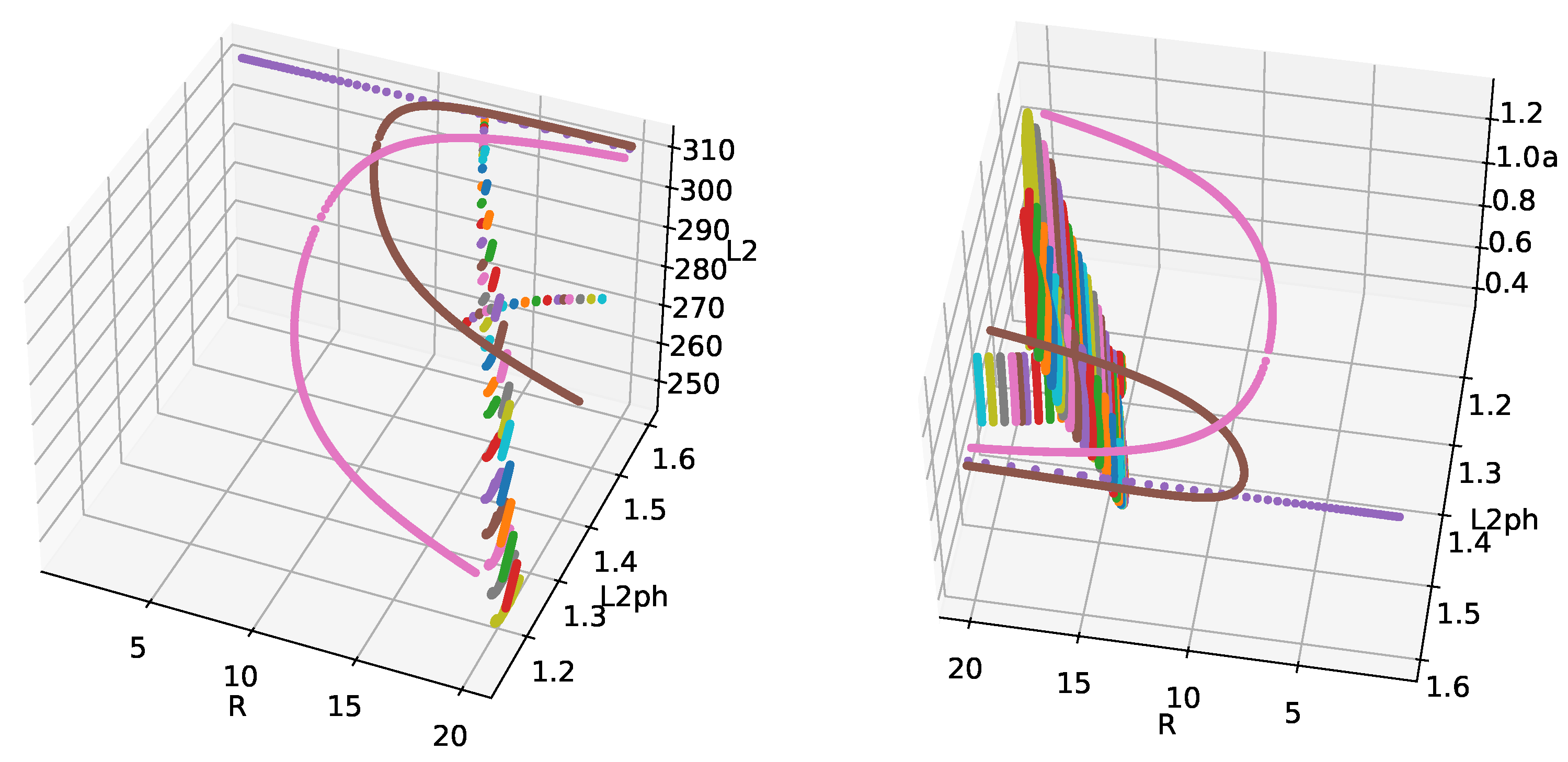
3.1. Bifurcation Analysis
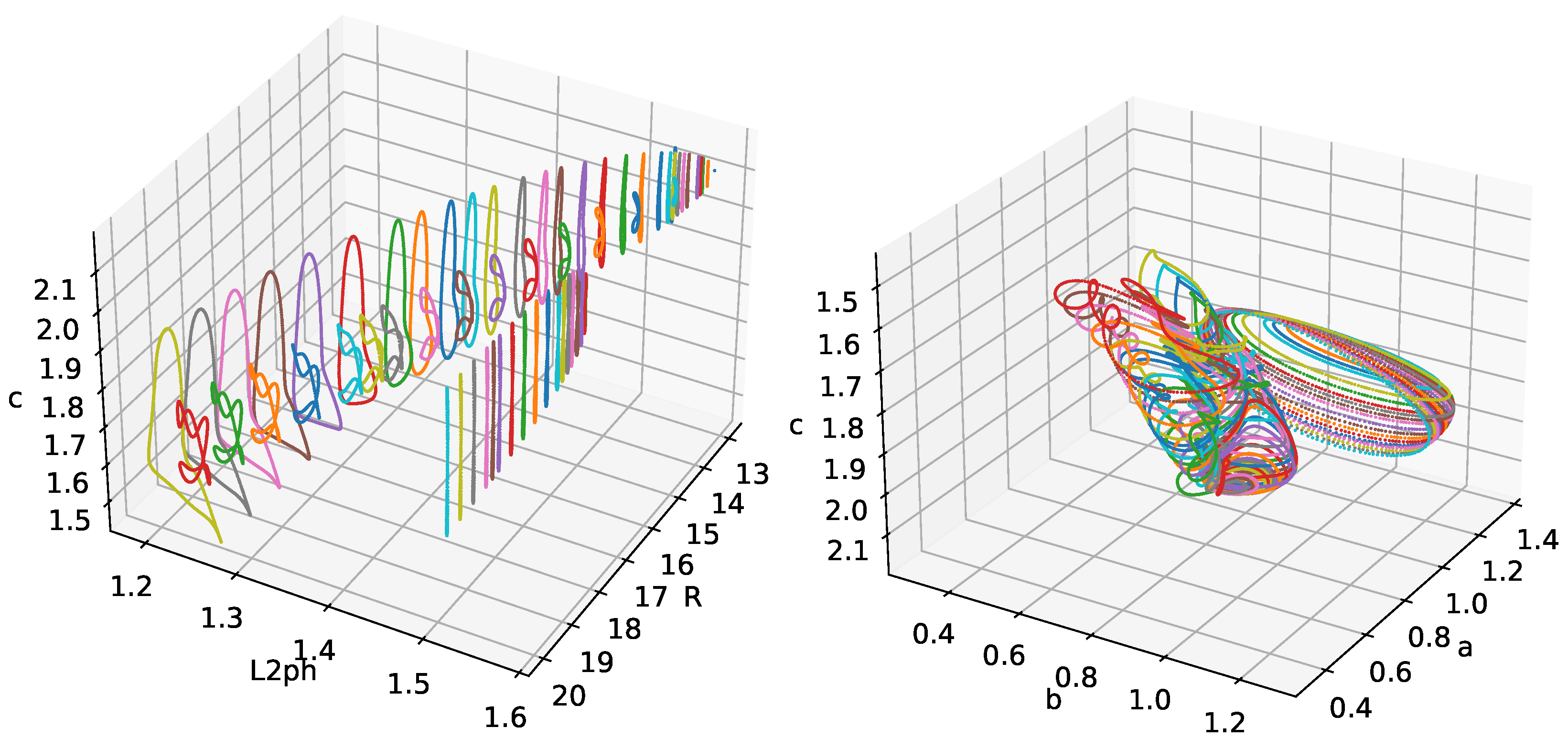
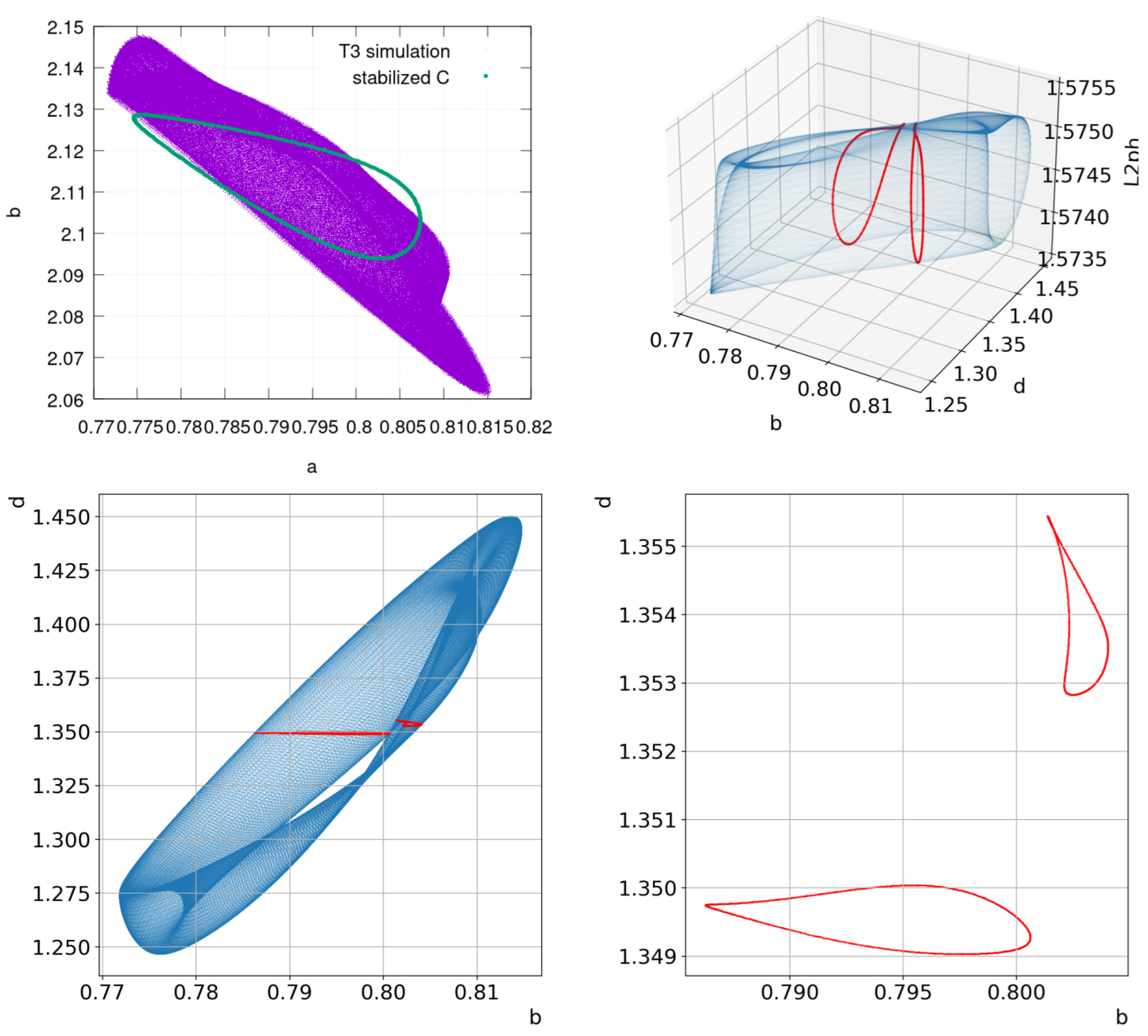
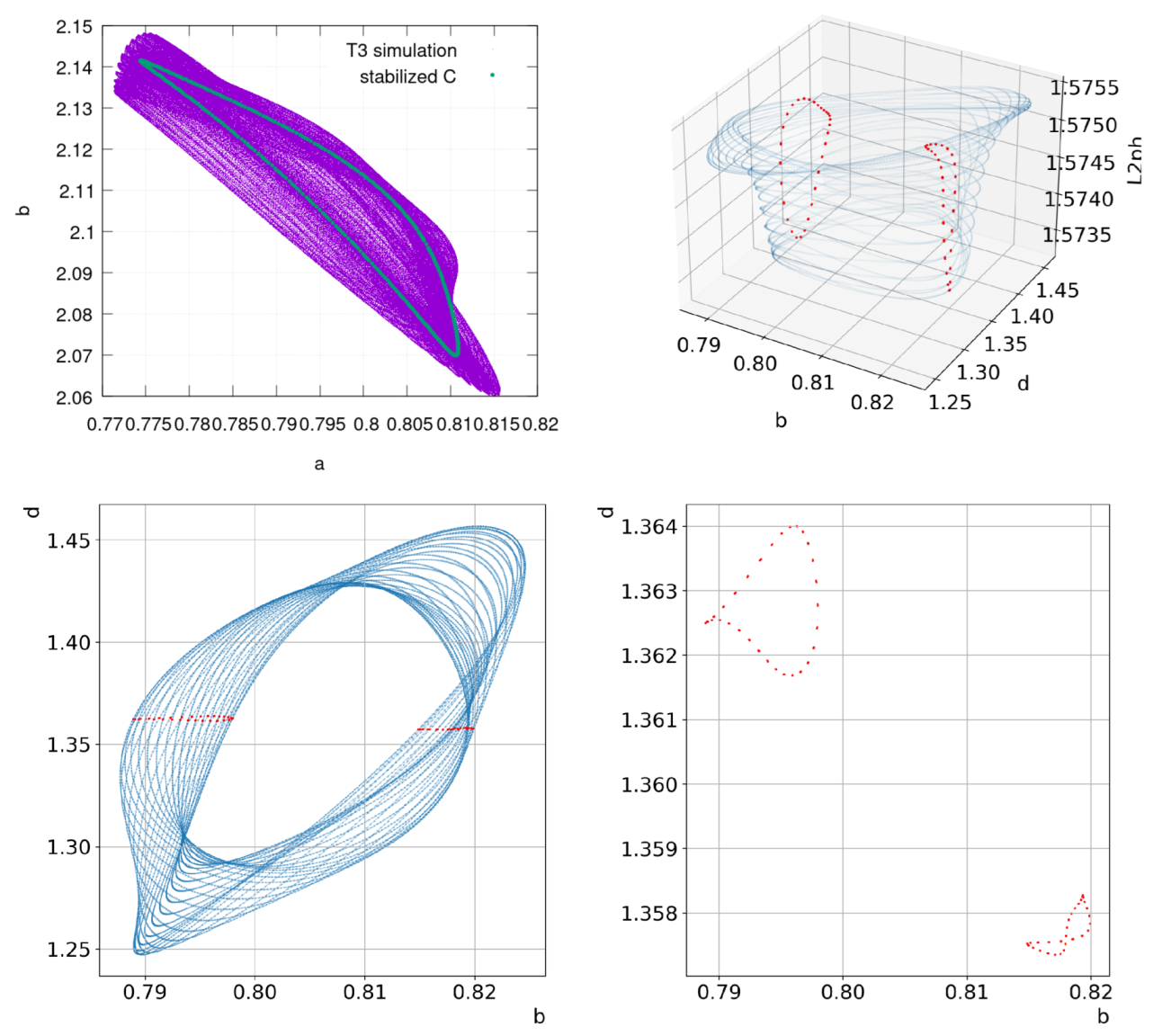
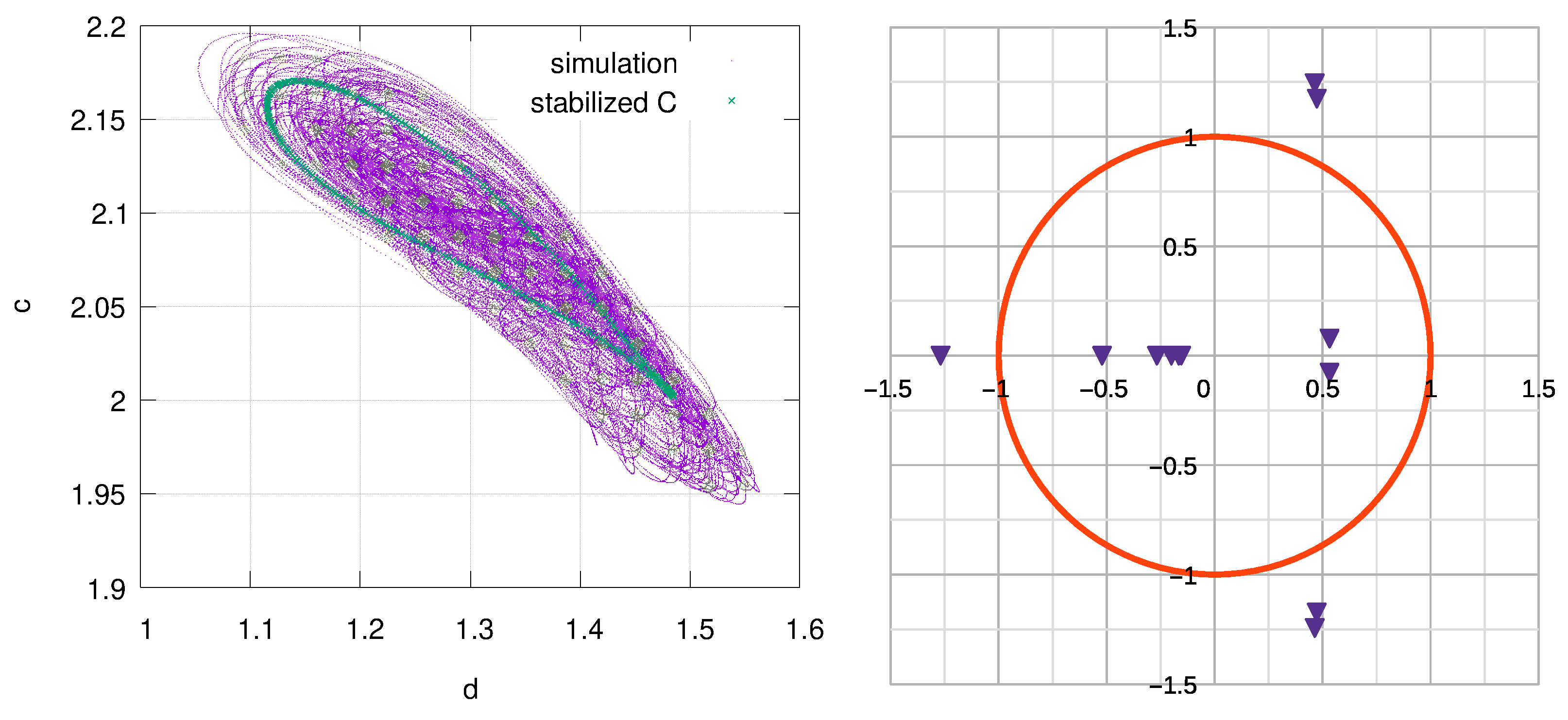
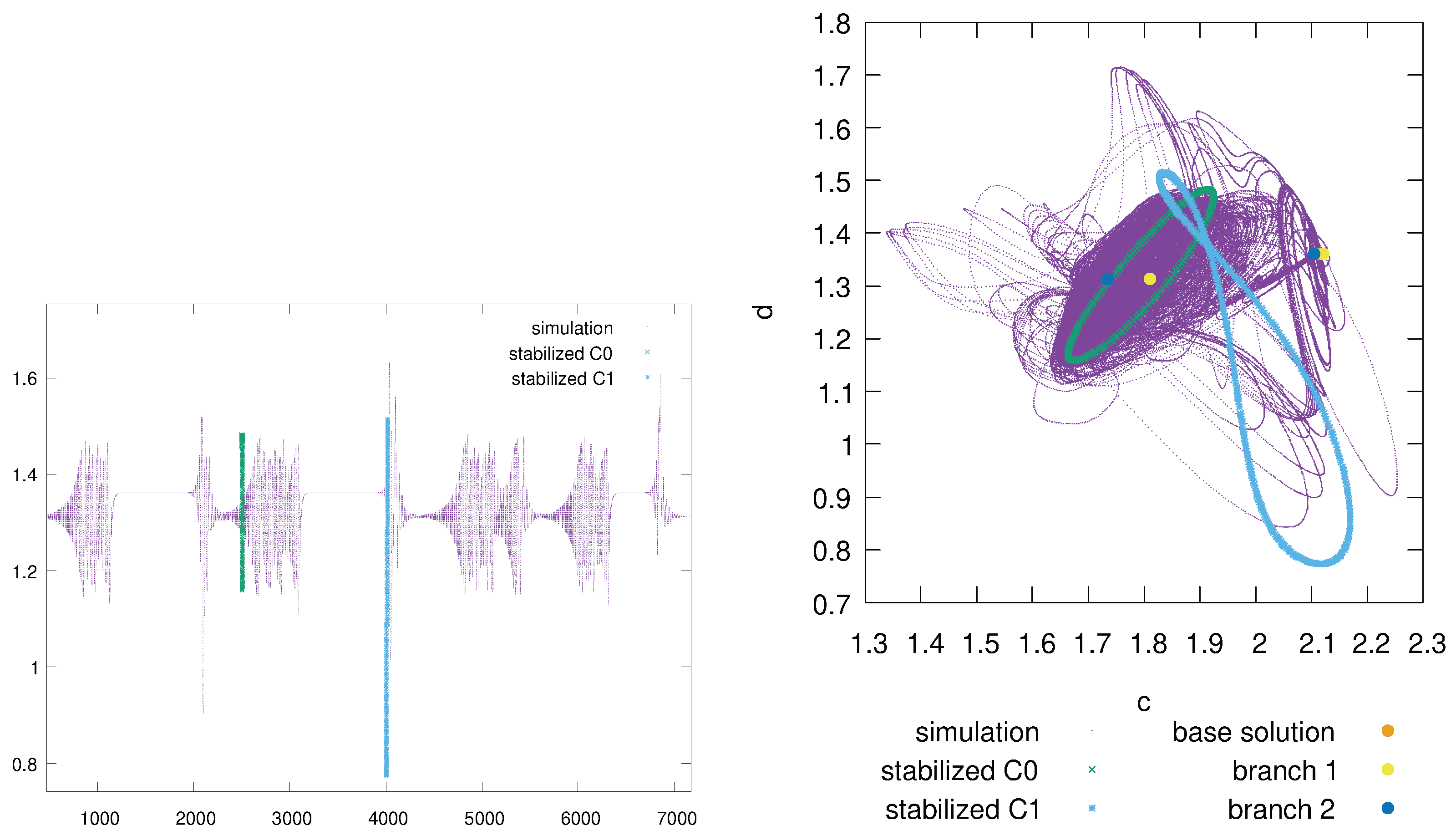
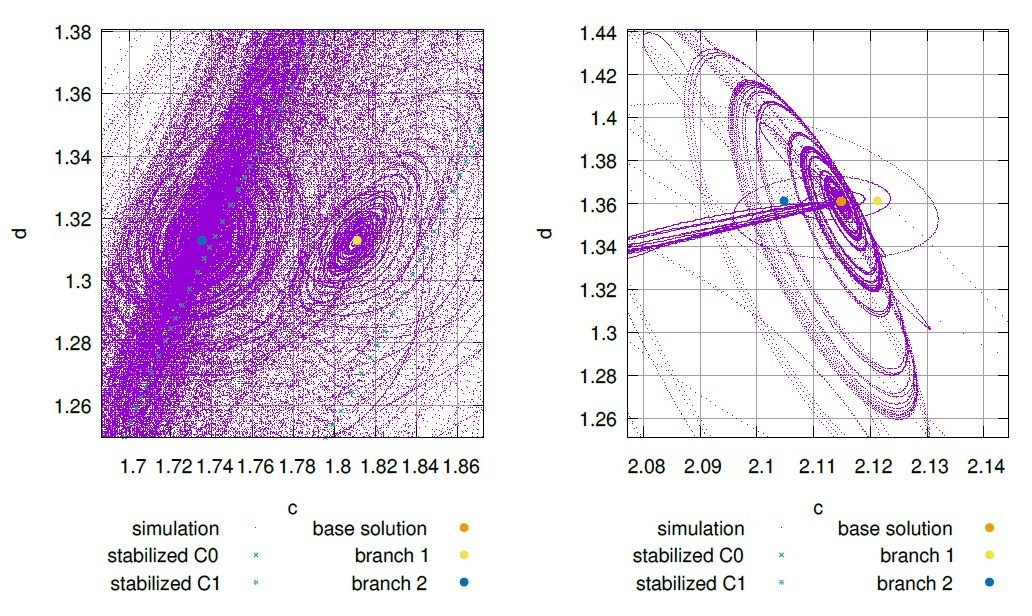
3.2. Analysis of Chaotic Regimes
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GPU | Graphics Processing Unit |
| CPU | Central Processing Unit |
| RK | Runge–Kutta method |
| DIRK | Diagonally Implicit Runge–Kutta method |
| SDIRK | Singly Diagonally Implicit Runge–Kutta method |
| IMEX | Implicit–Explicit Method |
| IM | Inertial Manifold |
| DOFs | Degrees Of Freedom |
| SSP | Strong Stability-Preserving |
| ODE | Ordinary Differential Equation |
| RK3SSP | RK explicit Third-order SSP |
| ABC | Arnold–Beltrami–Childress flow |
| CUDA | Compute Unified Device Architecture |
| OpenMP | Open Multi-Processing |
| MPI | Message-Passing Interface |
| DNS | Direct Numerical Simulation |
References
- Salahifard, H.; Vaezpour, S.M. Bifurcation problems for noncompact operators. Miskolc Math. Notes 2016, 17, 571. [Google Scholar] [CrossRef]
- Elhajji, S.; Errachid, M. Analysis of a bifurcation problem. Math. Comput. Simul. 2002, 58, 231–245. [Google Scholar] [CrossRef]
- Guo, S.; Wu, J. Lyapunov–Schmidt Reduction. In Applied Mathematical Sciences; Springer: New York, NY, USA, 2013; pp. 119–151. [Google Scholar] [CrossRef]
- Carr, J. Applications of Centre Manifold Theory; Springer US: Greer, SC, USA, 1981. [Google Scholar] [CrossRef]
- Temam, R. Infinite-Dimensional Dynamical Systems in Mechanics and Physics; Springer: New York, NY, USA, 1997. [Google Scholar] [CrossRef]
- Golubitsky, M.; Stewart, I.; Schaeffer, D.G. Singularities and Groups in Bifurcation Theory; Springer: New York, NY, USA, 1988. [Google Scholar] [CrossRef]
- Temple, B.; Young, R. A Liapunov-Schmidt Reduction for Time-Periodic Solutions of the Compressible Euler Equations. Methods Appl. Anal. 2010, 17, 225–262. [Google Scholar] [CrossRef]
- Yudovich, V. Non-stationary flow of an ideal incompressible liquid. USSR Comput. Math. Math. Phys. 1963, 3, 1407–1456. [Google Scholar] [CrossRef]
- Judovič, V.I. An Example of Loss of Stability and Generation of a Secondary Flow in a Closed Vessel. Math. USSR Sb. 1967, 3, 519–533. [Google Scholar] [CrossRef]
- Kurakin, L.G.; Yudovich, V.I. On Equilibrium Bifurcations in the Cosymmetry Collapse of a Dynamical System. Sib. Math. J. 2004, 45, 294–310. [Google Scholar] [CrossRef]
- Agrachev, A.A.; Sarychev, A.V. Controllability of 2D Euler and Navier–Stokes Equations by Degenerate Forcing. Commun. Math. Phys. 2006, 265, 673–697. [Google Scholar] [CrossRef]
- Sapronov, Y. Modelling Liquid Flows in Diffusers by Reduced Equations. Bull. Susu. MMP 2014, 7, 74–86. [Google Scholar] [CrossRef]
- Rehman, K.U.; Malik, M. On Lie symmetry mechanics for Navier–Stokes equations unified with non-Newtonian fluid model: A classical directory. Phys. A Stat. Mech. Its Appl. 2019, 535, 122469. [Google Scholar] [CrossRef]
- Edwards, W.; Tuckerman, L.; Friesner, R.; Sorensen, D. Krylov Methods for the Incompressible Navier–Stokes Equations. J. Comput. Phys. 1994, 110, 82–102. [Google Scholar] [CrossRef]
- Tuckerman, L.S.; Barkley, D. Bifurcation Analysis for Timesteppers. In The IMA Volumes in Mathematics and Its Applications; Springer: New York, NY, USA, 2000; pp. 453–466. [Google Scholar] [CrossRef]
- Barkley, D.; Tuckerman, L.S. Stokes preconditioning for the inverse power method. In Fifteenth International Conference on Numerical Methods in Fluid Dynamics; Springer: Berlin/Heidelberg, Geramny, 1997; pp. 75–76. [Google Scholar] [CrossRef]
- Tuckerman, L.S.; Huepe, C.; Brachet, M.E. Numerical methods for bifurcation problems. In Instabilities and Nonequilibrium Structures IX; Springer: Dordrecht, The Netherlands, 2004; pp. 75–83. [Google Scholar] [CrossRef]
- Sorensen, D.C. Implicitly Restarted Arnoldi/Lanczos Methods for Large Scale Eigenvalue Calculations. In ICASE/LaRC Interdisciplinary Series in Science and Engineering; Springer: Dordrecht, The Netherlands, 1997; pp. 119–165. [Google Scholar] [CrossRef]
- Borońska, K.; Tuckerman, L.S. Extreme multiplicity in cylindrical Rayleigh-Bénard convection. I. Time dependence and oscillations. Phys. Rev. E 2010, 81. [Google Scholar] [CrossRef] [PubMed]
- Borońska, K.; Tuckerman, L.S. Extreme multiplicity in cylindrical Rayleigh-Bénard convection. II. Bifurcation diagram and symmetry classification. Phys. Rev. E 2010, 81. [Google Scholar] [CrossRef] [PubMed]
- Tuckerman, L.S. Computational Challenges of Nonlinear Systems. In Emerging Frontiers in Nonlinear Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 249–277. [Google Scholar] [CrossRef]
- Sanchez, J.; Marques, F.; Lopez, J. A Continuation and Bifurcation Technique for Navier–Stokes Flows. J. Comput. Phys. 2002, 180, 78–98. [Google Scholar] [CrossRef][Green Version]
- Sánchez, J.; Net, M.; Garcia-Archilla, B.; Simo, C. Newton–Krylov continuation of periodic orbits for Navier–Stokes flows. J. Comput. Phys. 2004, 201, 13–33. [Google Scholar] [CrossRef]
- Sánchez, J.; Net, M.; Simó, C. Computation of invariant tori by Newton–Krylov methods in large-scale dissipative systems. Phys. D Nonlinear Phenom. 2010, 239, 123–133. [Google Scholar] [CrossRef]
- Chen, W.; Wang, Q.; Hesthaven, J.S.; Zhang, C. Physics-informed machine learning for reduced-order modeling of nonlinear problems. J. Comput. Phys. 2021, 446, 110666. [Google Scholar] [CrossRef]
- Pichi, F.; Ballarin, F.; Rozza, G.; Hesthaven, J.S. An artificial neural network approach to bifurcating phenomena in computational fluid dynamics. Comput. Fluids 2023, 254, 105813. [Google Scholar] [CrossRef]
- Farrell, P.E.; Birkisson, Á.; Funke, S.W. Deflation Techniques for Finding Distinct Solutions of Nonlinear Partial Differential Equations. SIAM J. Sci. Comput. 2015, 37, A2026–A2045. [Google Scholar] [CrossRef]
- Kalantonis, V.; Perdios, E.; Perdiou, A.; Ragos, O.; Vrahatis, M. Deflation techniques for the determination of periodic solutions of a certain period. Astrophys. Space Sci. 2003, 288, 591–599. [Google Scholar] [CrossRef]
- Davidenko, D. On a new method of numerical solution of systems of nonlinear equations. Dokladi AN USSR (Russian) 1953, 88, 601–602. [Google Scholar]
- Evstigneev, N.M. On the Convergence Acceleration and Parallel Implementation of Continuation in Disconnected Bifurcation Diagrams for Large-Scale Problems. In Communications in Computer and Information Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 122–138. [Google Scholar] [CrossRef]
- Evstigneev, N.M. Deflation of Periodic Orbits in Large-Scale Systems: Algorithm and Parallel Implementation. In Communications in Computer and Information Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2021; pp. 76–91. [Google Scholar] [CrossRef]
- Boullé, N.; Dallas, V.; Farrell, P.E. Bifurcation analysis of two-dimensional Rayleigh-Bénard convection using deflation. Phys. Rev. E 2022, 105. [Google Scholar] [CrossRef] [PubMed]
- Evstigneev, N.M. Disconnected stationary solutions for 2D Kolmogorov flow problem in periodic domain. J. Phys. Conf. Ser. 2021, 1730, 012078. [Google Scholar] [CrossRef]
- Evstigneev, N.M. Disconnected stationary solutions for 3D Kolmogorov flow problem: Preliminary results. J. Phys. Conf. Ser. 2021, 2090, 012046. [Google Scholar] [CrossRef]
- Evstigneev, N.M.; Magnitskii, N.A.; Silaev, D.A. Qualitative analysis of dynamics in Kolmogorov’s problem on a flow of a viscous incompressible fluid. Diff. Equat. 2015, 51, 1292–1305. [Google Scholar] [CrossRef]
- Evstigneev, N.M.; Magnitskii, N.A. Nonlinear Dynamics of Laminar-Turbulent Transition in Generalized 3D Kolmogorov Problem for Incompressible Viscous Fluid at Symmetric Solution Subset. J. Appl. Nonlinear Dyn. 2017, 6, 345–353. [Google Scholar] [CrossRef]
- Evstigneev, N.; Magnitskii, N.; Ryabkov, O. Numerical Bifurcation Analysis in 3D Kolmogorov Flow Problem. J. Appl. Nonlinear Dyn. 2019, 8, 595–619. [Google Scholar] [CrossRef]
- Evstigneev, N.; Magnitskii, N.; Sidorov, S. Nonlinear dynamics of laminar–turbulent transition in three dimensional Rayleigh–Benard convection. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2851–2859. [Google Scholar] [CrossRef]
- Evstigneev, N.M.; Magnitskii, N.A. Numerical Analysis of Laminar-Turbulent Bifurcation Scenarios in Kelvin–Helmholtz and Rayleigh–Taylor Instabilities for Compressible Flow. In Turbulence Modelling Approaches—Current State, Development Prospects, Applications; InTech: Rijeka, Croatia, 2017; pp. 29–59. [Google Scholar] [CrossRef]
- DoedelJanuary, E.J. Auto94p: An Experimental Parallel Version of Auto; California Institute of Technology: Pasadena, CA, USA, 1995. [Google Scholar]
- Dhooge, A.; Govaerts, W.; Kuznetsov, Y.A. MATCONT. ACM Trans. Math. Softw. 2003, 29, 141–164. [Google Scholar] [CrossRef]
- Back, A.; Guckenheimer, J.M.; Myers, M.; Wicklin, F.J.; Worfolk, P.A. Dstool: Computer assisted exploration of dynamical systems. Notices Am. Math. Soc. 1992, 39, 303–309. [Google Scholar]
- Guillot, L.; Cochelin, B.; Vergez, C. A generic and efficient Taylor series–based continuation method using a quadratic recast of smooth nonlinear systems. Int. J. Numer. Methods Eng. 2019, 119, 261–280. [Google Scholar] [CrossRef]
- Guillot, L.; Lazarus, A.; Thomas, O.; Vergez, C.; Cochelin, B. A purely frequency based Floquet-Hill formulation for the efficient stability computation of periodic solutions of ordinary differential systems. J. Comput. Phys. 2020, 416, 109477. [Google Scholar] [CrossRef]
- Soares, F.; Vergez, C.; Antunes, J.; Cochelin, B.; Debut, V.; Silva, F. Bifurcation analysis of cantilever beams in channel flow. J. Sound Vib. 2023, 567, 117951. [Google Scholar] [CrossRef]
- Lust, K.; Roose, D. An Adaptive Newton–Picard Algorithm with Subspace Iteration for Computing Periodic Solutions. SIAM J. Sci. Comput. 1998, 19, 1188–1209. [Google Scholar] [CrossRef]
- Veltz, R. BifurcationKit.jl. 2020. Available online: https://hal.archives-ouvertes.fr/hal-02346 (accessed on 5 September 2023).
- Evstigneev, N.M.; Ryabkov, O.I. On the mixed approximation type pressure correction method for incompressible Navier–Stokes equations. J. Phys. Conf. Ser. 2018, 1141, 012119. [Google Scholar] [CrossRef]
- Evstigneev, N.M.; Ryabkov, O.I. Pressure—Velocity projection method with mixed type approximation for Oseen discrete operator. J. Phys. Conf. Ser. 2019, 1391, 012072. [Google Scholar] [CrossRef]
- Evstigneev, N.M. Implementation of Implicitly Restarted Arnoldi Method on MultiGPU Architecture with Application to Fluid Dynamics Problems. In Communications in Computer and Information Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 301–316. [Google Scholar] [CrossRef]
- Evstigneev, N.M. Inexact matrix exponential preconditioner for implicitly restarted Arnoldi method in fluid dynamics stability problems for parallel heterogeneous architecture. J. Phys. Conf. Ser. 2018, 1141, 012121. [Google Scholar] [CrossRef]
- Evstigneev, N.M. Numerical analysis of Krylov multigrid methods for stationary advection-diffusion equation. J. Phys. Conf. Ser. 2019, 1391, 012080. [Google Scholar] [CrossRef]
- Bocharov, A.; Evstigneev, N.; Petrovskiy, V.; Ryabkov, O.; Teplyakov, I. Implicit method for the solution of supersonic and hypersonic 3D flow problems with Lower-Upper Symmetric-Gauss-Seidel preconditioner on multiple graphics processing units. J. Comput. Phys. 2020, 406, 109189. [Google Scholar] [CrossRef]
- Evstigneev, N.; Ryabkov, O.; Bocharov, A.; Petrovskiy, V.; Teplyakov, I. Compensated summation and dot product algorithms for floating-point vectors on parallel architectures: Error bounds, implementation and application in the Krylov subspace methods. J. Comput. Appl. Math. 2022, 414, 114434. [Google Scholar] [CrossRef]
- Evstigneev, N.M. Analysis of Block Stokes-Algebraic Multigrid Preconditioners on GPU Implementations. In Communications in Computer and Information Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2022; pp. 116–130. [Google Scholar] [CrossRef]
- Ascher, U.M.; Ruuth, S.J.; Spiteri, R.J. Implicit-explicit Runge–Kutta methods for time-dependent partial differential equations. Appl. Numer. Math. 1997, 25, 151–167. [Google Scholar] [CrossRef]
- Koto, T. IMEX Runge–Kutta schemes for reaction–diffusion equations. J. Comput. Appl. Math. 2008, 215, 182–195. [Google Scholar] [CrossRef]
- Chertock, A.; Cui, S.; Kurganov, A.; Wu, T. Steady State and Sign Preserving Semi-Implicit Runge–Kutta Methods for ODEs with Stiff Damping Term. SIAM J. Numer. Anal. 2015, 53, 2008–2029. [Google Scholar] [CrossRef]
- Temam, R. Inertial manifolds. Math. Intell. 1990, 12, 68–74. [Google Scholar] [CrossRef]
- Temam, R. Inertial manifolds and slow manifolds. In The Mathematics of Models for Climatology and Environment; Springer: Berlin/Heidelberg, Geramny, 1997; pp. 181–214. [Google Scholar] [CrossRef]
- Temam, R. Approximation of attractors, large eddy simulations and multiscale methods. Proc. R. Soc. Lond. A 1991, 434, 23–39. [Google Scholar] [CrossRef]
- Evstigneev, N.; Magnitskii, N. FSM Scenarios of Laminar-Turbulent Transition in Incompressible Fluids. In Nonlinearity, Bifurcation and Chaos—Theory and Applications; InTech: Rijeka, Croatia, 2012. [Google Scholar] [CrossRef]
- Butcher, J.C. Numerical Methods for Ordinary Differential Equations; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Boldo, S.; Faissole, F.; Chapoutot, A. Round-Off Error and Exceptional Behavior Analysis of Explicit Runge–Kutta Methods. IEEE Trans. Comput. 2020, 69, 1745–1756. [Google Scholar] [CrossRef]
- Nakayama, T.; Takahashi, D. Implementation of Multiple-Precision Floating-Point Arithmetic Library for GPU Computing. In Proceedings of the Parallel and Distributed Computing and Systems, ACTAPRESS, Dallas, TX, USA, 14–16 December 2011. [Google Scholar] [CrossRef]
- Arnold, V.I. Sur la topologie des écoulements stationnaires des fluides parfaits. In Vladimir I. Arnold—Collected Works; Springer: Berlin/Heidelberg, Germany, 1965; pp. 15–18. [Google Scholar] [CrossRef]
- Podvigina, O.M. Spatially-periodic steady solutions to the three-dimensional Navier–Stokes equation with the ABC-force. Phys. D Nonlinear Phenom. 1999, 128, 250–272. [Google Scholar] [CrossRef]
- Ashwin, P.; Podvigina, O. Hopf bifurcation with cubic symmetry and instability of ABC flow. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 2003, 459, 1801–1827. [Google Scholar] [CrossRef]
- Podvigina, O.; Ashwin, P.; Hawker, D. Modelling instability of ABC flow using a mode interaction between steady and Hopf bifurcations with rotational symmetries of the cube. Phys. D Nonlinear Phenom. 2006, 215, 62–79. [Google Scholar] [CrossRef]
- Podvigina, O.M. Investigation of the ABC flow instability with application of centre manifold reduction. Dyn. Syst. 2006, 21, 191–208. [Google Scholar] [CrossRef]
- Magnitskii, N.A. Universal Bifurcation Chaos Theory and Its New Applications. Mathematics 2023, 11, 2536. [Google Scholar] [CrossRef]
- Skokos, C.; Gottwald, G.A.; Laskar, J. (Eds.) Chaos Detection and Predictability; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Parker, J.P.; Schneider, T.M. Invariant tori in dissipative hyperchaos. Chaos 2022, 32, 113102. [Google Scholar] [CrossRef] [PubMed]
- Lucas, D.; Kerswell, R. Spatiotemporal dynamics in two-dimensional Kolmogorov flow over large domains. J. Fluid Mech. 2014, 750, 518–554. [Google Scholar] [CrossRef]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Evstigneev, N.M.; Magnitskii, N.A. Bifurcation Analysis Software and Chaotic Dynamics for Some Problems in Fluid Dynamics Laminar–Turbulent Transition. Mathematics 2023, 11, 3875. https://doi.org/10.3390/math11183875
Evstigneev NM, Magnitskii NA. Bifurcation Analysis Software and Chaotic Dynamics for Some Problems in Fluid Dynamics Laminar–Turbulent Transition. Mathematics. 2023; 11(18):3875. https://doi.org/10.3390/math11183875
Chicago/Turabian StyleEvstigneev, Nikolay M., and Nikolai A. Magnitskii. 2023. "Bifurcation Analysis Software and Chaotic Dynamics for Some Problems in Fluid Dynamics Laminar–Turbulent Transition" Mathematics 11, no. 18: 3875. https://doi.org/10.3390/math11183875
APA StyleEvstigneev, N. M., & Magnitskii, N. A. (2023). Bifurcation Analysis Software and Chaotic Dynamics for Some Problems in Fluid Dynamics Laminar–Turbulent Transition. Mathematics, 11(18), 3875. https://doi.org/10.3390/math11183875





