On a Generalized Wave Equation with Fractional Dissipation in Non-Local Elasticity
Abstract
:1. Introduction
2. Mathematical Model
- is the strain measure used in [16];
- , since ;
3. Notations
4. Solutions to the Cauchy Problem (17), (18)
- withand where
- ,
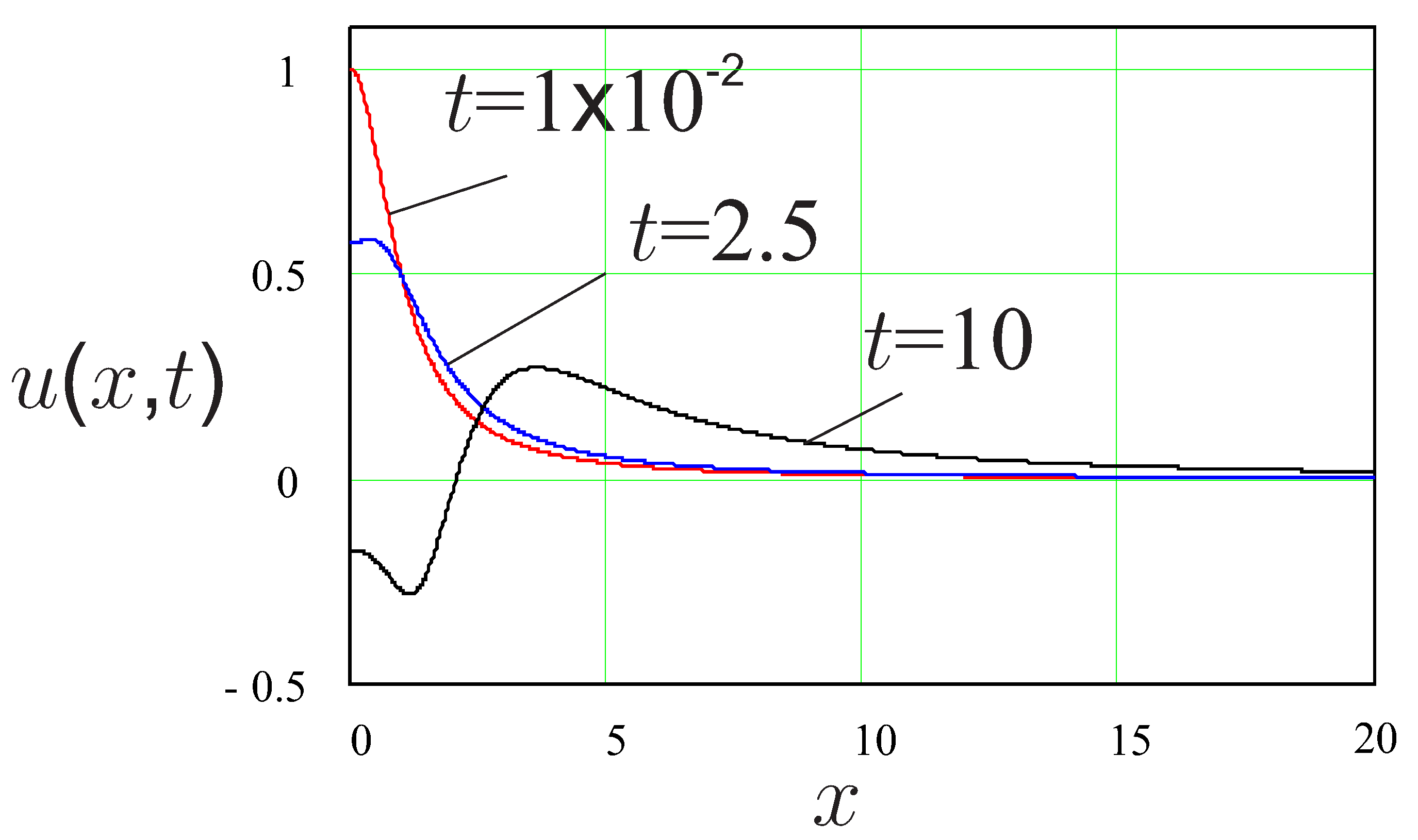
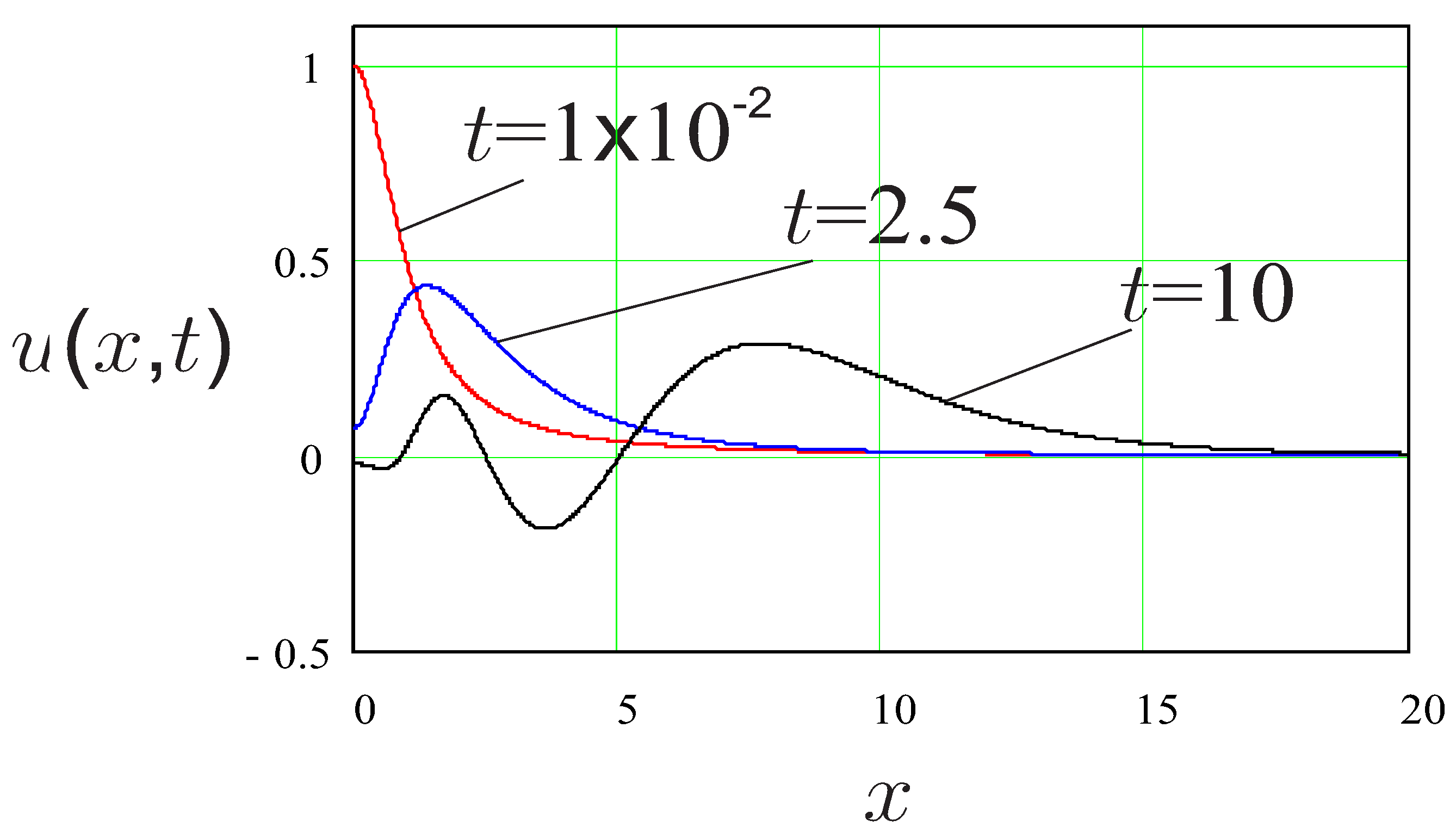
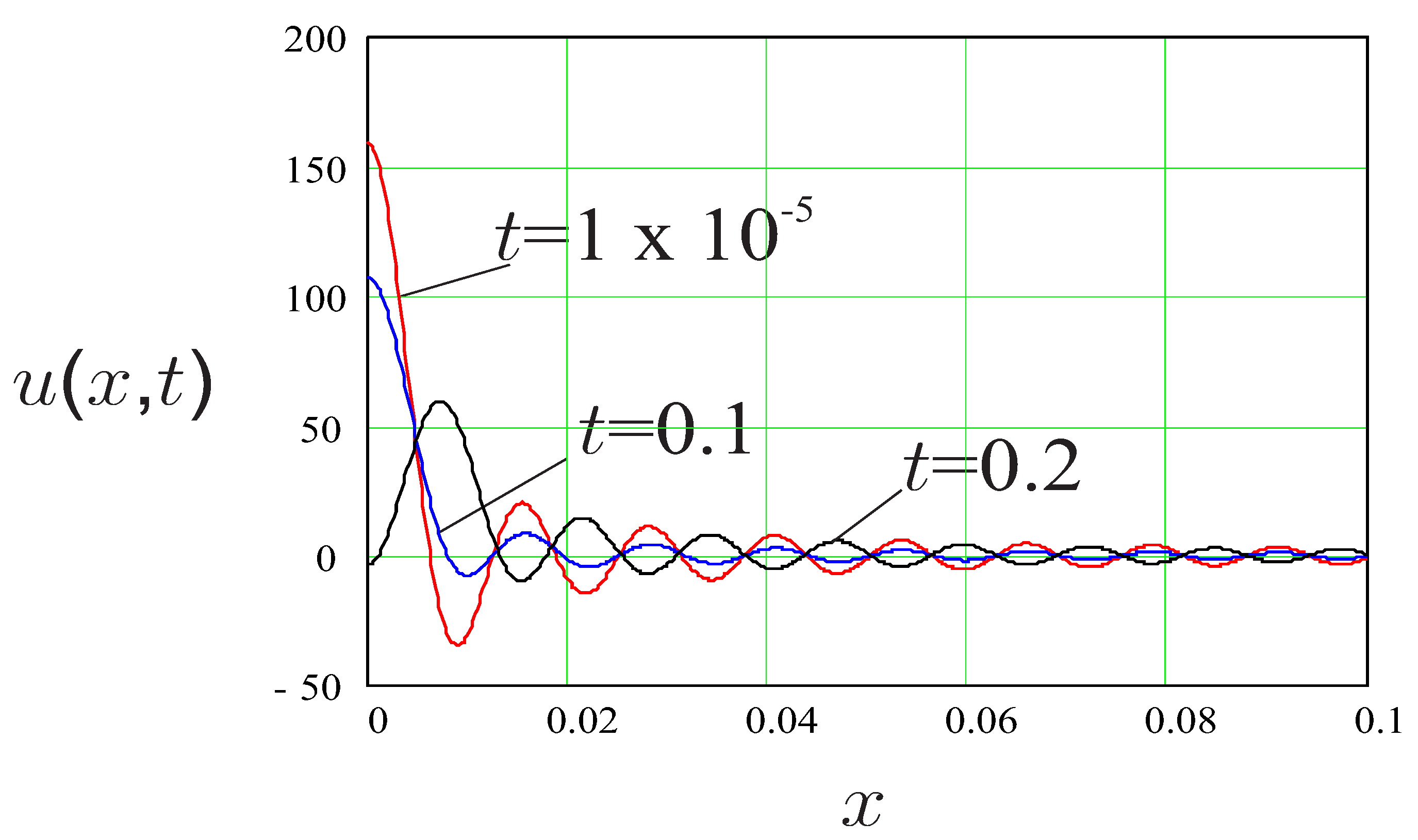
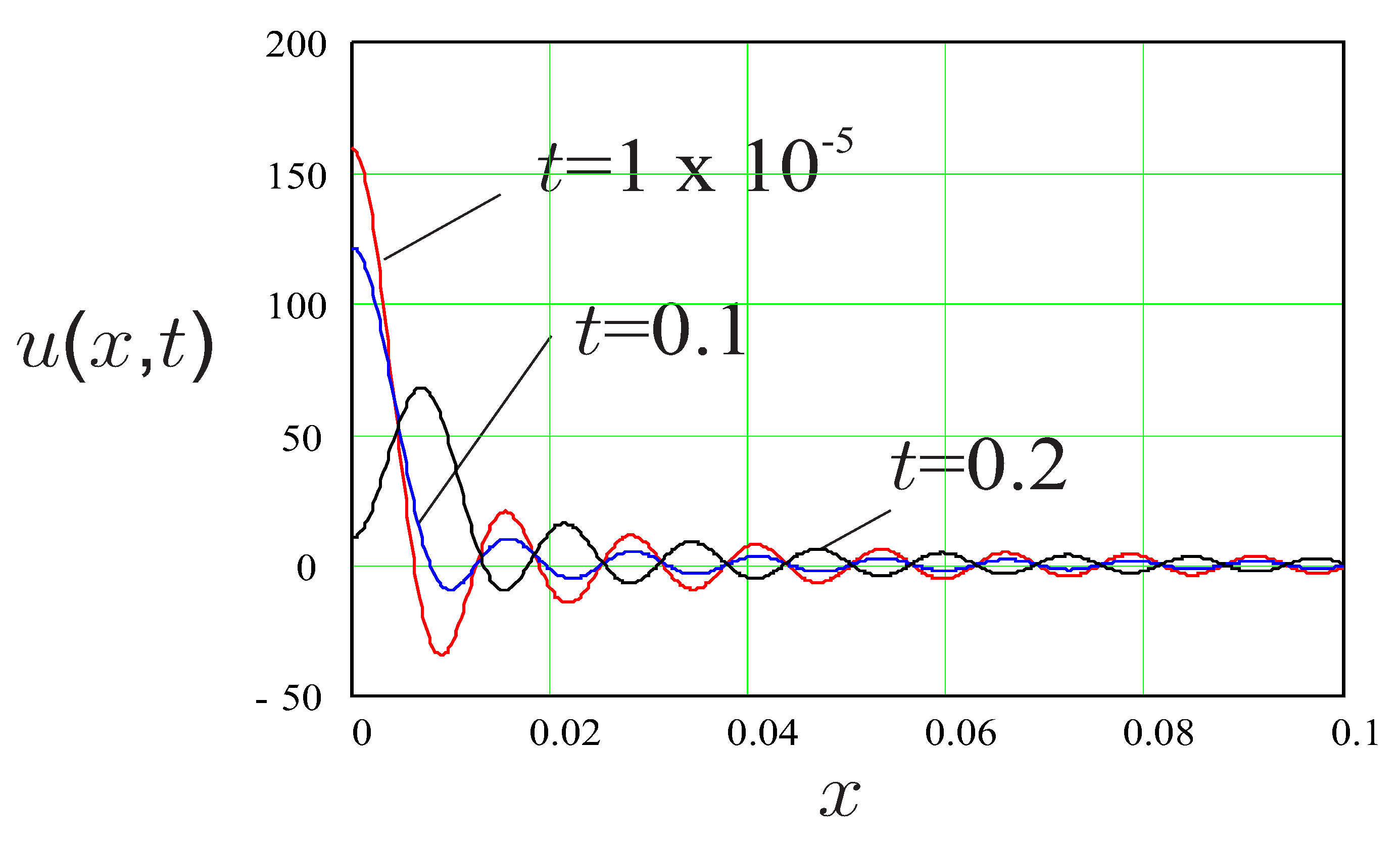
5. Numerical Examples
6. Conclusions
- 1.
- We introduced a new measure of deformation, generalizing the classical one-dimensional strain. It is non-local and contains two parameters, and In the special case , it is reduced to classical or the strain measure or the generalized strain measure used in [16]. We note that a similar formalism was used in [28] in the context of classical particle mechanics, i.e., a finite number of degrees of freedom.
- 2.
- 3.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Gorenflo, R.; Mainardi, F. Fractional Calculus, Integral and Differential Equations of Fractional Order. In Fractional Calculus in Continuum Mechanics; Carpinteri, A., Mainardi, F., Eds.; Springer: Berlin/Heidelberg, Germany, 1977; pp. 223–276. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Gordon and Breach: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.I. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Lazopulos, K.A. Non-local Continuum Mechanics and Fractional Calculus. Mech. Res. Commun. 2006, 33, 753–757. [Google Scholar] [CrossRef]
- Sandev, T.; Chechkin, A.; Kantz, H.; Metzler, R. Diffusion and Fokker-Planck-Smoluchowski equations with Generalized memory kernel. Fract. Calc. Appl. Anal. 2015, 18, 1006–1038. [Google Scholar] [CrossRef]
- Tarasov, V.E. General Fractional Dynamics. Mathematics 2021, 9, 1464. [Google Scholar] [CrossRef]
- Diethelm, K.; Kiryakova, V.; Luchko, Y.; Tenreiro Machado, J.A.; Tarasov, T.E. Trends, directions for further research, and some open problems of fractional calculus. Nonlinear Dyn. 2022, 107, 3245–3270. [Google Scholar] [CrossRef]
- Tarasov, V.E. General Non-Local Continuum Mechanics: Derivation of Balance Equations. Mathematics 2022, 10, 1427. [Google Scholar] [CrossRef]
- Sandev, T.; Sokolov, I.M.; Metzler, R.; Chechkin, A. Beyond monofractional kinetics. Chaos Solitons Fractals 2017, 102, 210–217. [Google Scholar] [CrossRef]
- Molina-Garcia, D.; Sandev, T.; Safdari, H.; Pagnini, G.; Chechkin, A.; Metzler, R. Crossover from anomalous to normal diffusion: Truncated power-law noise correlations and applications to dynamics in lipid bilayers. New J. Phys. 2018, 20, 103027. [Google Scholar] [CrossRef]
- Atanackovic, T.M.; Guran, A. Theory of Elasticity for Scientists and Engineers; Birkhauser: Boston, MA, USA, 2000. [Google Scholar]
- Tarasov, V.E. General Fractional Calculus in Multi-Dimensional Space: Riesz Form. Mathematics 2023, 11, 1651. [Google Scholar] [CrossRef]
- Atanackovic, T.M.; Stankovic, B. Generalized Wave Equation in Non-local Elasticity. Acta Mech. 2009, 208, 1–10. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A New Definition of Fractional Derivative without Singular Kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Atanackovic, T.M.; Pilipovic, S.; Zorica, D. Properties of the Caputo–Fabrizio Fractional Derivative and Its Distributional Settings. Fract. Calc. Appl. Anal. 2018, 21, 29–44. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series and Products; Academic Press: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Stein, E.M. Singular Integrals and Differentiability Properties of Functions; Princeton University Press: Princeton, NJ, USA, 1970. [Google Scholar]
- Schwartz, L. Théorie des Distributions; Hermann: Paris, France, 1957. [Google Scholar]
- Schwartz, L. Méthodes Mathématiques pour les Sciences Physiques; Hermann: Paris, France, 1961. [Google Scholar]
- Szmydt, Z. Fourier Transformation and Linear Differential Equations; Reidel Publishing Company: Dordrecht, The Netherlands, 1977. [Google Scholar]
- Vladimirov, V.S. Generalized Functions in Mathematical Physics; Mir Publishers: Moscow, Russia, 1979. [Google Scholar]
- Titchmarsh, E.C. Introduction to the Theory of Fourier Integrals; Clarendon Press: Oxford, UK, 1948. [Google Scholar]
- Baclic, B.S.; Atanackovic, T.M. Stability and Creep of a Fractional Derivative Order Viscoelastic Rod. Bulletin 2000, 25, 115–131. [Google Scholar]
- Magnus, W.; Oberhettinger, F. Formeln und Sätze für die Speziellen Funktionen der Mathematischen Physik; Springer: Berlin/Heidelberg, Germany, 1948. [Google Scholar]
- Klimek, M. Fractional Sequential Mechanics—Models with Symmetric Fractional Derivative. Czechoslov. J. Phys. 2001, 51, 1348–1354. [Google Scholar] [CrossRef]
- Area, I.; Losada, J.; Nieto, J.J. On Fractional Derivatives and Primitives of Periodic Functions. Abstr. Appl. Anal. 2014, 2014, 392598. [Google Scholar]
- Garrappa, R.; Kaslik, E.; Popolizio, M. Evaluation of Fractional Integrals and Derivatives of Elementary Functions: Overview and Tutorial. Mathematics 2019, 7, 407. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atanackovic, T.M.; Djekic, D.D.; Gilic, E.; Kacapor, E. On a Generalized Wave Equation with Fractional Dissipation in Non-Local Elasticity. Mathematics 2023, 11, 3850. https://doi.org/10.3390/math11183850
Atanackovic TM, Djekic DD, Gilic E, Kacapor E. On a Generalized Wave Equation with Fractional Dissipation in Non-Local Elasticity. Mathematics. 2023; 11(18):3850. https://doi.org/10.3390/math11183850
Chicago/Turabian StyleAtanackovic, Teodor M., Diana Dolicanin Djekic, Ersin Gilic, and Enes Kacapor. 2023. "On a Generalized Wave Equation with Fractional Dissipation in Non-Local Elasticity" Mathematics 11, no. 18: 3850. https://doi.org/10.3390/math11183850
APA StyleAtanackovic, T. M., Djekic, D. D., Gilic, E., & Kacapor, E. (2023). On a Generalized Wave Equation with Fractional Dissipation in Non-Local Elasticity. Mathematics, 11(18), 3850. https://doi.org/10.3390/math11183850





