Enhancing Medical Image Segmentation: Ground Truth Optimization through Evaluating Uncertainty in Expert Annotations

Abstract

The surge of supervised learning methods for segmentation lately has underscored the critical role of label quality in predicting performance. This issue is prevalent in the domain of medical imaging, where high annotation costs and inter-observer variability pose significant challenges. Acquiring labels commonly involves multiple experts providing their interpretations of the “true” segmentation labels, each influenced by their individual biases. The blind acceptance of these noisy labels as the ground truth restricts the potential effectiveness of segmentation algorithms. Here, we apply coupled convolutional neural network approaches to a small-sized real-world dataset of bovine cumulus oocyte complexes. This is the first time these methods have been applied to a real-world annotation medical dataset, since they were previously tested only on artificially generated labels of medical and non-medical datasets. This dataset is crucial for healthy embryo development. Its application revealed an important challenge: the inability to effectively learn distinct confusion matrices for each expert due to large areas of agreement. In response, we propose a novel method that focuses on areas of high uncertainty. This approach allows us to understand the individual characteristics better, extract their behavior, and use this insight to create a more sophisticated ground truth using maximum likelihood. These findings contribute to the ongoing discussion of leveraging machine learning algorithms for medical image segmentation, particularly in scenarios involving multiple human annotators.

1. Introduction

The task of segmenting anatomical structures in medical images is known to be challenged by significant inter-reader variability, which can impact the performance of subsequent supervised machine learning models. This issue is particularly pressing in the medical and biological domains, where labeled data are often limited due to the high costs associated with expert annotations. Across diverse fields and applications, differing biases and levels of expertise among annotators lead to considerable variations in segmentation annotations of structures in medical images [1]. For instance, in the realm of assisted reproduction, expert annotators are primarily responsible for the segmentation of relevant structures, both in human and other mammalian data. For this kind of tasks, the UNet architecture [2] has been used extensively in several medical and biological fields [3]. Despite their expertise, disagreements and inconsistencies in annotations are not uncommon, adding another layer of complexity to the already challenging task. As a result, despite the proliferation of digital medical imaging data over the past couple of decades, access to data with curated labels that can be readily used for machine learning remains relatively scarce [4]. This underlines the pressing need for advanced methodologies capable of robust learning from such noisy annotations.

Various pre-processing techniques are routinely employed to reconcile inter-reader variations and curate segmentation annotations by merging labels from multiple experts. A particularly common and straightforward approach utilizes the majority-vote approach [5], whereby the ground truth is derived from the most frequently occurring opinion among the experts. This method has been effectively applied in various contexts, including Assisted Reproductive Technology (ART) for COC, as demonstrated by Athanasiou et al. [6]. Furthermore, an advanced variant of this method, which considers class similarities, has demonstrated effectiveness in the aggregation of brain tumor segmentation labels [1]. However, a primary limitation of these approaches is the assumption that all experts hold equal reliability. To circumvent this, Warfield et al. [7] proposed a label fusion technique, known as STAPLE, which explicitly models the individual reliability of each expert and leverages this information to ‘weight’ their opinions during the label aggregation process. Due to its consistent superiority over traditional majority-vote pre-processing across various applications, STAPLE has emerged as the preferred label fusion method.

Recently, STAPLE has seen numerous enhancements, particularly in the context of multi-atlas segmentation problems [8]. These enhancements particularly shine when image registration transfers segments from labeled images (“atlases”) to a new scan. A notable improvement, known as STEPS, was introduced by Cardoso et al. [9]. This approach took things a step further by incorporating the local morphological similarity between atlases and target images. Numerous extensions of this approach, such as in the work of Asman et al. [10], have since been explored. However, a shared limitation across these label fusion methods is the absence of a mechanism allowing information integration across different training images. This restriction essentially limits the applicability of these methods to cases where each image comes with a substantial number of annotations from multiple experts. In practice, obtaining such many annotations can be prohibitively expensive. Moreover, these methods often utilize relatively simplistic functions to model the relationship between observed noisy annotations, true labels, and expert reliability. As a result, they may fall short of capturing the complex characteristics of human annotators.

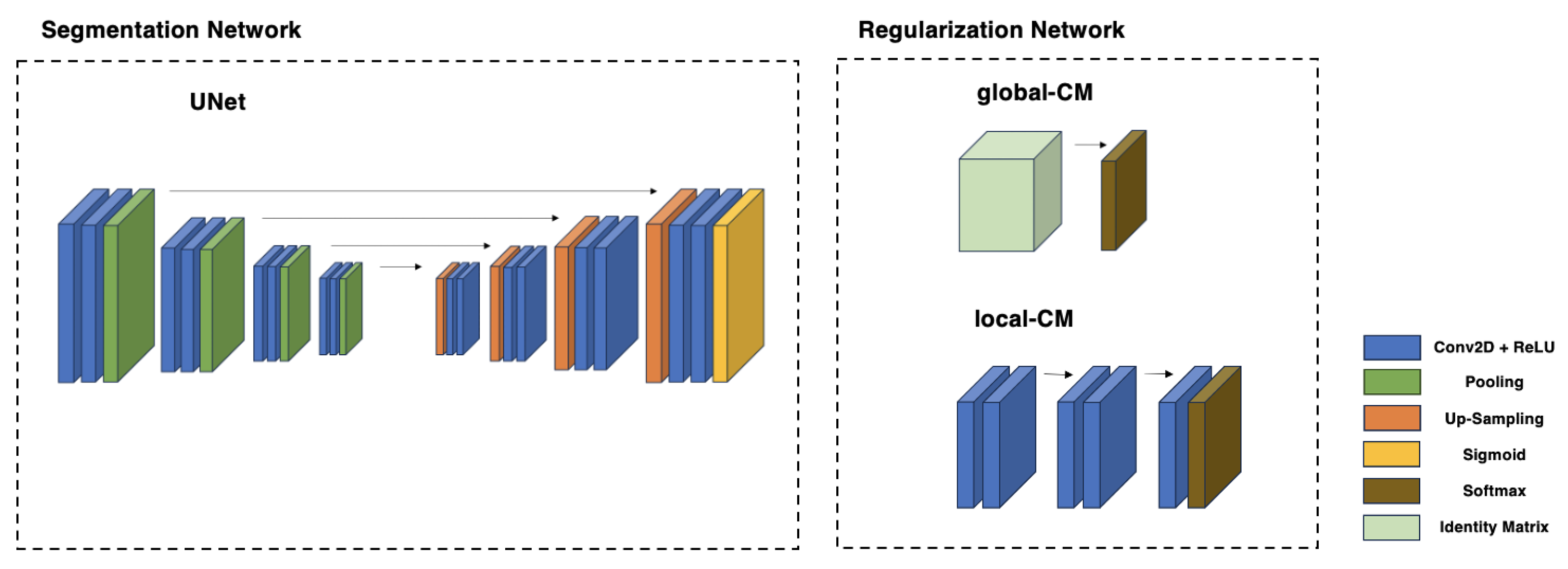
Several studies suggest solutions to these challenges by devising models that execute an end-to-end supervised segmentation process. This process aims to simultaneously determine the reliability of multiple human annotators and the true segmentation labels using only noisy labels. The proposed architectures [11,12,13,14] involve two integrated CNNs. The first one calculates the true segmentation probabilities. In contrast, the second characterizes individual annotators (e.g., tendencies to over-segment, mix-ups between different classes, etc.) by computing the pixel-wise confusion matrices (CMs) on a per-image basis. These models purport to outperform methods such as STAPLE and its variants by employing deep neural networks to unravel the complex mappings from the input images to the behaviors of the annotators and to the actual segmentation labels. Moreover, the CNNs’ parameters are “global variables” optimized over multiple image samples. This feature empowers the model to disentangle the true labels from the annotators’ errors robustly, drawing on correlations between analogous image samples. This robustness holds even when the number of available annotations per image is minimal (e.g., a single annotation per image). However, these techniques have not been tested on actual medical data yet, where challenges such as the absence of clear-cut differences among experts may occur, unlike in the artificially created data used in their previous studies. Furthermore, the feasibility of these architectures on small-sized datasets, with their unique challenges, has not been investigated yet. In this study, we implement the methods suggested in the literature [12] on a small-sized dataset of COC, annotated by three experts. This marks the first instance where such techniques are employed with real-world medical data and masks from multiple experts, and not synthetic masks as in the previously mentioned work. Our findings reveal that while these techniques have potential, they may not be entirely effective in this context, and several challenges emerge, suggesting room for refinement in these proposals. Venturing a step further, we turn our attention towards areas of high uncertainty, as the majority of the areas exhibit considerable agreement among experts. By concentrating on these areas with high predictive uncertainty, we succeed in crafting a unique confusion matrix for each expert. This matrix serves as a signature of each expert’s annotation style within the field of Assisted Reproductive Technology.

We also establish a similar ‘identity’ for the final Deep Learning model and compare the behaviors of the model and human experts. Ultimately, we use these ‘identities’ within the uncertain areas to derive a new ground truth. This novel ground truth proves to be more reliable than the commonly employed majority-vote or STAPLE methods in the literature, thereby providing a promising direction for future work in this domain.

The structure of this paper is as follows: Following the introduction, we delve into related work in the field in Section 2. This is followed by a detailed description of the methodology we adopted in Section 3. Subsequently, we present our findings and engage in a thoughtful discussion about the implications and significance of our results in Section 4. Finally, in Section 5, we draw conclusions from our study and suggest possible directions for future work.

2. Related Work

Image segmentation in medical data has witnessed numerous advancements due to the introduction and utilization of the UNet architecture [2]. There are numerous cases in the literature demonstrating the effectiveness of utilizing the UNet [3]. Assessing the efficacy of image segmentation techniques is a longstanding challenge. Interactive segmentation by expert annotators is a commonly accepted practice, yet it introduces variability between different experts. A variety of methods has been put forth to estimate annotator skills and establish ground truth labels. These approaches can be broadly categorized into two groups: (i) two-stage approaches [7,15,16,17] and (ii) simultaneous approaches [12,13,18,19,20].

In two-stage approaches, label aggregation and supervised model training occur independently. Initially, noisy labels are consolidated using a probabilistic model that incorporates unknown variables—annotator skills and ground truth labels. A machine learning model is then trained on ground truth labels to perform the task. Unfortunately, these methods often neglect raw input information during label aggregation, impacting estimated true labels.

The STAPLE algorithm was introduced by Warfield et al. [15] in 2002. It characterizes each annotator w through a confusion matrix ${\theta }_w\in {\mathbb{R}}^{L\times L}$, where L is the number of classes, and ${\theta }_{w,c^{\prime },c}$ denotes the probability that expert w labels a pixel as $c^{\prime }$ given c in consensus. STAPLE employs Expectation Maximization [7] for maximum likelihood consensus segmentation. Enhancements followed, including Spatial STAPLE [16] and Local MAP STAPLE [17]. Non-Local STAPLE (NLS) [10] proposed by Asman and Landman addresses intensity inclusion in consensus computation. MOJITO [21] minimizes Fréchet variance to counter STAPLE sensitivity. Carass et al. [22] used STAPLE for a challenge, revealing experts’ superiority over algorithms.

Simultaneous approaches combine supervised model prediction with noisy label handling for enhanced accuracy. Employing expectation maximization, these methods require ample labels. However, real-life label collection constraints limit their practicality.

This category simultaneously curates labels and train models, achieving synergy. Despite favoring basic classification, these approaches improve predictive power and sample efficiency over the first category. Yet, structured prediction tasks with high-dimensional outputs lack attention. Zhang et al. [12] introduced a supervised segmentation method that estimated annotator reliability and true labels using noisy data. While they evaluate their methodology in several synthetic scenarios, it has not been tested on real medical data with masks from multiple annotators. Zhang et al. [13] refined this approach with crowdsourcing. Liu et al. [18] shifted their focus to learning dynamics—a concept previously studied in classification problems but scarcely explored in the realm of image segmentation. They propose the ADELE model, but the results provided are not grounded in the core issue of multiple annotators with varying annotation methods. Other methods were proposed [19,20,23,24], but none handle real medical data from multiple experts.

Our work represents the first attempt at implementing a simultaneous approach to this tangible problem, using data directly provided by three distinct experts in the field.

3. Materials and Methods

3.1. Dataset

Images from 100 COCs were captured both at the immature stage (0 h of maturation) and at the mature stage (22 h post maturation). This was accomplished using an Olympus stereomicroscope coupled with a ToupCam camera and facilitated by ToupView software (version 3.7.13270.20181102). All images were acquired with a consistent magnification of 56×, centering a single oocyte’s zona pellucida in the middle of the field of focus. Images were stored as .png files with a resolution of 2592 × 1944 pixels in RGB format. A total of 100 paired images of COCs were presented to three experts to annotate the COC area, using the ImageJ (version 1.53j) software. Finally, a total of 200 images and 200 × 3 masks were collected. The images and the masks were downscaled to reach the final dimensions of 192 × 240 × 1. The method of majority-vote [5] was used to compute a GT and use it for evaluation purposes.

An example of the data provided by the Department of Internal Medicine, Reproduction and Population Medicine, Ghent University (https://www.ugent.be/di/irp/en, accessed on 9 November 2021), is available in Figure 1.

3.2. Architecture

Our proposed approach has been deployed utilizing the PyTorch framework. The network dedicated to segmentation tasks employs the UNet structure, featuring a depth of five layers. The number of channels in these layers scales up progressively, starting from 32, then to 64, 128, 256, and finally reaching 512. The annotating network uses a Softmax [25] function for the simpler case of having a global CM, or, for the more complicated local CM case, a double convolutional block, with a convolution function followed by a ReLU function (Figure 2). The dataset, consisting of 200 images, was divided into three subsets: 80% for the training set, 10% for the validation set, and 10% for the test set. It is trained for 100 epochs, with a learning rate starting at 1 $\times {10}^{-3}$ and going down to 1 $\times {10}^{-6}$ progressively. The training batch size was set to 16, and the optimizer to Adam [26].

3.2.1. Segmentation Network

The segmentation model is undertaken by a UNet architecture [2]. It is parameterized by $\theta$ and outputs a predicted probability distribution denoted as $p_{\theta }\left(\mathbf{X}\right)\in {[0,1]}^{WxHxL}$, with W being the width of the image, H the height of the image, and L being the number of classes. This distribution represents the likelihood of a pixel belonging to a specific class. For this application, there are only 2 classes $(L=2)$ since there is only the COC area and the background. UNet, with its distinctive U-shaped layout, has become the network of choice for medical image segmentation since this architecture is adept at extracting both low-level and high-level features, thus enhancing the segmentation accuracy. It has been also used previously for similar tasks with COC [6]. Additionally, UNet demonstrates superior performance with smaller datasets, making it the best choice for the current problem. The UNet is available on the left side of Figure 2, linked to the following regularization network.

3.2.2. Regularization Network

Following [12], the regularization network (Figure 2) is parameterized by $\varphi$, and its primary goal is to recover the true segmentation probability distribution. This is achievable by emulating the distinct behavior of the three annotators (Figure 3). The term ‘behavior’ refers to each annotator’s unique inclination toward specific “false” segmentation patterns, such as the tendency to assume pixels to be part of the COC area and not of the background. These behaviors are captured using confusion matrices (CMs). Assuming that the true label is previously known, then the CM is constructed as follows:

$$a_{ij}^{\left(m\right)}\left(\mathbf{x}\right)=p(y^{\left(m\right)}=i\mid y_{GT}=j,\mathbf{x})$$

(1)

where $a_{ij}^{\left(m\right)}$ stands for the element in the $(i,j)$ cell of the CM for expert m. In an image of size $WxH$, for every pixel w∈W, h∈H, the CM could be the same among all pixels (global-CM case), or it could change for each pixel (w, h) of each image $\mathbf{x}$ (local-CM case). Consequently, in global CM cases, there is only one CM representing the whole image, while in local CM cases, there is a CM for each pixel. $y_{GT}$ refers to the GT mask used for this process, and $y^{\left(m\right)}$ refers to the mask provided by annotator m. The GT here is not observable, so the model is disentangled to reach its own GT, and the CM is not able to be computed in a straightforward way.

Thus, a regularization network is implemented, which serves to model the confusion matrices. Each of these matrices is the output from a CNN that takes the COC image $\mathbf{x}$ as its input. The CNN is characterized by $\varphi \left(m\right)$ and shares the same architecture for every CM branch, while it is independently optimized following random initialization. The probability distribution prediction, $p_{\varphi }\left(\mathbf{x}\right)$, is provided by the segmentation network, as can be seen in the schemas (Figure 3 and Figure 4). By performing element-wise multiplication of the CMs and this predicted probability distribution, we derive the estimated probability distributions corresponding to each annotator:

$$p_{\theta ,\varphi }^{\left(m\right)}\left(\mathbf{x}\right)=A_{\varphi }^{\left(m\right)}\left(\mathbf{x}\right)·p_{\theta }\left(\mathbf{x}\right)$$

(2)

where $A_{\varphi }^{\left(m\right)}$ is the total of the CMs with $m\in \{1,2,3\}$, and ‘·’ operator denotes the element-wise matrix multiplication in $(w,h)$, where needed.

In essence, the creation of the ideal confusion matrix and the corresponding estimated probability distribution is accomplished through a joint optimization process involving both the segmentation network and the regularization network.

3.3. Loss Function and Evaluation Metrics

In this section, we provide a detailed explanation of how we perform a combined optimization of the segmentation network parameters denoted as $\theta$ and the annotator network parameters denoted as $\varphi$. We also discuss the evaluation metrics employed in our study.

To assess the performance of the proposed segmentation, the dice coefficient [27] is selected. The dice coefficient quantifies the spatial concurrence between two regions, providing a range from 0 to 1, where 0 implies no overlap whatsoever, while 1 indicates complete agreement. The corresponding equation is given below (3):

$$dice(f,\mathbf{x},y)=\frac{2{\sum }_{ij}f{\left(\mathbf{x}\right)}_{ij}{y}_{ij}}{{\sum }_{ij}f{\left(\mathbf{x}\right)}_{ij}+{\sum }_{ij}{y}_{ij}}$$

(3)

with y being the ground truth, $\mathbf{x}$ being the input image, and $f\left(\mathbf{x}\right)$ being the prediction of the model.

To ensure that the estimated probability distribution, incorporating annotator behaviors, closely aligns with the actual annotations, we utilize dice loss. Dice loss for binary segmentation is formulated as follows:

$${\mathcal{L}}_{dice}(f,\mathbf{x},y)=1-dice(f,\mathbf{x},y)$$

(4)

Following this, we integrate a regularization term based on the trace norm theorem [11]. The theorem implies that, given a dominant trace of the confusion matrix, the operation of (2) will aim to minimize this trace. This minimization facilitates the alignment of the estimated confusion matrices of individual annotators with the true values. The optimization of the CM’s trace is accomplished via the loss function:

$${\mathcal{L}}_{trace}(f,\mathbf{x},y)=\sum _{m=1}^{3}tr\left(A_{\varphi }^{\left(m\right)}\left(\mathbf{x}\right)\right)$$

(5)

with $tr\left(A\right)$ denoting the trace of A.

Essentially, minimizing the trace promotes the highest degree of unreliability in the estimated annotators, whereas minimizing the dice loss secures fidelity to the observed annotator inputs. The overall loss function is formulated by integrating both the dice loss and the trace loss:

$${\mathcal{L}}_{total}^{\theta ,\varphi }={\mathcal{L}}_{dice}^{\theta }+\gamma {\mathcal{L}}_{trace}^{\varphi }$$

(6)

where $\gamma$ corresponds to a regularization term. To establish the optimal $\gamma$, several options are tested, followed by a quantitative comparison from $\gamma$ = 0.0 to $\gamma$ = 1.0 with a step of 0.1, while some options are above 1.0 to examine the case of assigning higher importance to the trace loss. By minimizing the combined loss function, the model learns the parameters $\theta$ and $\varphi$.

3.4. Methodology

In our study, we structure our approach into three key stages. Initially, we examine the methods outlined in the existing literature that are focused on training a supervised segmentation model using labels generated by several human experts (Section 3.4.1). This is particularly examined in the context of a limited dataset comprising COC images and associated binary masks annotated by three distinct experts. The primary objective here is to extract the true segmentation exclusively from this collection of noisy labels. Due to some poor results, we switch our focus toward areas of high uncertainty (Section 3.4.2). We further refine our analysis by extracting distinctive annotating behavior profiles for each expert. In the third and final stage (Section 3.4.3), we aim to optimize the ground truth. We underscore the areas of high uncertainty, thus augmenting the precision and reliability of the segmentation model.

The code is available on the following GitHub page: maximum-likelihood-gt (accessed on 19 July 2023).

3.4.1. Jointly Learning

In this research, we implement the suggested methodology [12] comprising of a pair of convolutional neural networks (CNNs). The unique function of these CNNs is to predict the confusion matrix for each expert, which is subsequently used for segmenting the area of the COC, eliminating the need for prior GT.

• Coupled CNN training: The initial approach was to implement a local CM model where each image pixel was assigned its individual CM. Given the high dimensionality involved with assigning a CM to each pixel—effectively a H × W × 2 × 2 dimensional problem—we decided to revise our strategy, with H being the height of the image, W being the width of it, and a 2 × 2 confusion matrix for each pixel. (Figure 3)
  To manage the high dimensionality, we adopted a different approach, reducing the multiple CMs to a single one (global CM) and aiming at capturing the behavior across the entire image. This effectively condensed the problem from a H × W × 2 × 2 dimension to a more manageable 2 × 2 CM. (Figure 4)
• Coupled CNN training with transfer learning: In order to assist the initial models, examining further options was necessitated. We adopted the method proposed by Athanasiou et al. [6] and trained a segmenting CNN model to segment the COC area proficiently. Subsequently, the weights of the model were saved to serve as a starting point for disentangling the process from the ground truth, negating the need to train both CNNs simultaneously and offering a promising starting point for the training.
  Upon revisiting the approach, two primary concepts stood out. The first entailed training with the pre-trained weights, allowing the models to optimize the weights for both CNNs. The second concept involved training with the pre-trained weights, freezing the segmentation CNN, and enabling the models to train the annotating CNN, thus learning the CMs.

3.4.2. Confusion Matrices on Uncertainty

To derive the confusion matrices in areas of uncertainty, a pre-trained deep learning model that has achieved a high dice score (Athanasiou et al. [6]) for segmenting the COC area is employed. This model is used to pinpoint areas of uncertainty by setting a threshold at 0.05. In this context, every pixel that falls between [0.05–0.95] is considered uncertain. Conversely, any pixel outside this range is deemed a certain segmentation where there should be agreement among experts.

The pixels of interest for each image are identified and directly compared with the GT. In this instance, the GT is defined as the majority-voted masks created by combining the masks provided by experts. By comparing the expert annotations with the majority-vote annotation solely on uncertain pixels, confusion matrices are constructed.

Specifically, for each pixel in the uncertainty range, if an expert annotates it as ‘1’ and the GT indicates ‘0’, it is recorded as a False Positive in the confusion matrix. If the expert marks it as ‘0’ and the GT indicates ‘1’, it is a False Negative. Conversely, if the expert’s annotation aligns with the GT, it is recorded as a True Positive or True Negative. This process is applied to all pixels in the uncertain areas of an image.

Following this, we normalize across the rows of actual values to obtain a confusion matrix for each annotator per image. To attain a total confusion matrix for each annotator, we compute the mean of their confusion matrices across all images.

3.4.3. Maximum Likelihood Ground Truth

Once the confusion matrices for each annotator are estimated, it is possible to estimate the ground truth by maximum likelihood. Next, we show how to put together the labels provided by each annotator and their confusion matrices to compute the Maximum Likelihood Ground Truth. Assume that for a pixel, the set of annotators is M, and for each annotator, $m\in M$ receives a label $y^{\left(m\right)}$. We have a CM, $A^{\left(m\right)}=(a_{ij}^{\left(m\right)})$, where $a_{ij}^{\left(m\right)}$ stands for the probability that annotator m labels the pixel as i when the real label for that pixel is j. Also, assume that we have a prior $\rho =({\rho }_1,\dots ,{\rho }_L)$, where ${\rho }_j$ describes how likely it is that this pixel is from class j, before receiving any annotation of this pixel. We want to compute $p(y_{GT}=j|y^{\left(M\right)},A^{\left(M\right)},\rho )$, which is the probability that the pixel is of class j given all the available information ($y^{\left(M\right)}=\left\{y^{\left(m\right)}\right|m\in M\}$ and $A^{\left(M\right)}=\left\{A^{\left(m\right)}\right|m\in M\}).$ Following the results presented in [28] (Equation (2.5)), we can compute it as

$$p(y_{GT}=j|y^{\left(M\right)},A^{\left(M\right)},\rho )=\frac{{\alpha }_j{\rho }_j}{{\sum }_{l\in L}{\alpha }_l{\rho }_l},$$

(7)

where ${\alpha }_j={\prod }_{m\in M}{a}_{y^{\left(m\right)}j}^{\left(m\right)}.$ For a straightforward application, we suggest defining ${\rho }_j$ as the frequency of label j in the set of annotations.

4. Results and Discussion

In the following section, we present and discuss the outcomes derived from the application of the methodology outlined in the previous sections. These results correspond to (i) the performance of the dual-CNN framework as depicted in existing literature, along with the modifications that we introduced, (ii) the extraction and understanding of the unique annotating behavior profile exhibited by each expert, and (iii) the advancements made in developing a more sophisticated ground truth, focused on the uncertain areas. This analysis aims to shed light on the effectiveness of our multi-faceted approach for addressing the challenges inherent in the segmentation task.

4.1. Performance Coupled CNNs

The performance of the dual-CNN structure did not meet the expectations formed by its previous applications on artificial data. This observation held true across all different iterations, irrespective of the use of global or local CMs and regardless of the use of transfer learning. Multiple factors contributed to this discordance between the expected potential of the methodology and the ultimate results achieved.

Two key challenges became evident during our study. Firstly, the nature of real-world medical problems, such as the present COC investigation, inherently restricts the size of available data. In our scenario, the dataset was composed of a maximum of 200 COC images. Secondly, experts in the medical fields typically exhibit high accuracy in identifying the regions of COCs, thereby diminishing the degree of disagreement amongst them. This relatively high consensus among experts further complicates the task of segmenting and distinguishing various expert behaviors.

Eventually, neither the local CM’s nor the global CM’s strategy allowed the dual-CNN model to learn the segmentation of COC areas successfully. In both cases, the model began to diverge after a few epochs. Various attempts were made to tackle this issue, including adjusting multiple hyperparameters and the exploration of different $\gamma$ values to manage the trace loss better. Despite these efforts, the performance remained poor, underscoring the challenge of adapting the model to this specific task.

In a preceding study by Athanasiou et al. [6], transfer learning emerged as an indispensable tool to achieve high performance in COC area segmentation. The first approach, despite starting from an advantageous position in training, could not sustain high performance for both the local CM and global CM implementations. The second approach involved freezing the segmenting CNN to ensure its high performance, shifting the focus towards learning the CMs on the annotating CNN.

While this model could learn three different CMs, the values were strikingly similar across the experts. The True Positive (TP) and True Negative (TN) parts were extremely close to 1.0, and the False Positive (FP) and False Negative (FN) parts were extremely close to 0.0. Upon further examination, we discovered that this was to be expected, as there was substantial agreement among the experts on the majority of the pixels forming either part of the image background or the COC itself.

The same poor results were achieved even when a pre-trained network (by Athanasiou et al. [6]) was used as the starting point for this approach. Despite its advantageous initial standing, the network could not maintain high performance when applied to either the local CM or global CM variants. In the latter approach, the segmentation CNN was ‘frozen’ to maintain its high performance, thus shifting the emphasis towards learning the CMs on the annotation CNN. Although this model was able to discern three different CMs, their values were strikingly alike across all the experts, with True Positive (TP) and True Negative (TN) values approximating 1.0 and False Positive (FP) and False Negative (FN) values near 0.0.

As it is already assumed, the high degree of consensus among experts on most of the pixels led to this poor outcome. Finally, we accepted that the proposed approach still needs improvements to fulfill the idea of their creators and alter our focus on the CMs.

4.2. Performance on CMs—Learning

In this phase of our work, our primary aim is to learn the unique CMs of each expert in areas of high uncertainty (Figure 5). Given that the experts largely agree in their assessments, the only viable approach to characterize their distinct annotating “behaviors” lies in these contentious areas. Initially, the areas of high uncertainty are pinpointed. This is achieved through the use of our deep learning model, which discerns the zones where there is an elevated level of indecision regarding pixel classification, as described in Section 3.4. Subsequently, we compare each pixel of every annotator’s mask to the majority-vote ground truth. This process is repeated five times, and ultimately, we synthesize a mean confusion matrix for each annotator drawn from the complete dataset. The resulting matrices, which shed light on the unique ‘identity’ of each expert, are illustrated in Figure 6.

At this point, the approach of each expert towards the ambiguous areas—those with the highest likelihood of disagreement—has become clear. The first expert scores significantly high on the True Negative metric but averages on the True Positive one, indicating a greater tendency to categorize a pixel as part of the background and stricter criteria for identifying a pixel as part of the COC. Conversely, the third expert shows a somewhat opposing approach. He appears more lenient in categorizing pixels as part of the COC, even at the risk of falsely including background pixels in the COC region, as evidenced by his high True Positive score and average True Negative score. Lastly, the second expert sits in between these two extremes, exhibiting a more balanced approach. He demonstrates relatively high accuracy in correctly identifying pixels as part of the COC when they indeed are, and as parts of the background when they are not.

4.3. Ground Truth

Using the maximum likelihood approach as described in Section 3.4.3, a new and more sophisticated method for computing the ground truth is proposed, incorporating the personal annotations of experts. An illustrative example of this novel ground truth computation is depicted in Figure 7.

The first approach utilizes a majority vote strategy (Figure 7a). In cases where three experts are involved, an uncertainty level of only 0.67 is achieved when two out of the three experts agree while the third expert disagrees. The second approach (Figure 7b), however, leverages the previously derived confusion matrices from the annotation processes to gain insight into the annotators’ behaviors. This knowledge is then utilized to enhance the certainty level for each pixel beyond 0.67, encompassing a range of 0.67–1. Consequently, the final ground truth determination is fortified, as it has the capacity to identify erroneous pixels that may have been produced by the majority vote method. Figure 7c exhibits the disparities in the areas of the image where the majority vote and maximum likelihood methods diverge.

The maximum likelihood method’s qualitative superiority over previous approaches is readily apparent. What makes our method stand out is how it tackles existing limitations. We have found that current methods fall short when applied to real-world annotation medical data from assisted reproduction. They were efficient with synthetic data or annotations by non-experts, but in real cases, they need improvement.

Our method is designed to address limitations that have been identified in current practices. It has come to light that these methods fall short when dealing with actual medical data from assisted reproduction, a significant departure from their performance with synthetic data or annotations by non-experts (crowdsourcing). A distinctive feature of our approach is its focus on creating customized profiles for each expert based on their annotations. These profiles, derived using confusion matrices, target areas where experts exhibit discrepancies or uncertainty. This capability is achieved by working with real-world annotation data that accurately capture genuine expert disagreement.

Furthermore, our approach allows us to discern the distinct annotation behaviors of each expert. This step holds importance as it enables the reuse of these behavioral patterns for future annotations, thereby sidestepping the need for repetitive experimentation. This not only conserves time and resources, but also bolsters model training accuracy. Notably, our approach does away with the prerequisite of an odd number of experts, which is a constraint imposed by prevailing methods.

A notable practical advantage of our methodology is its seamless integration into clinical and laboratory environments. This integration permits the preservation and application of personalized annotation profiles, streamlining the process of generating augmented results without the intricacies of sourcing and amalgamating numerous annotations.

In conclusion, our innovative approach revolutionizes the computation of ground truth. It actively addresses shortcomings in current methodologies while delivering tangible benefits in terms of precision and operational efficiency in medical image analysis.

5. Conclusions

The focus of the study was an exploration of multi-annotator segmentation using a COC dataset. This research consisted of three main steps: the application of a coupled CNN architecture to real medical data as proposed in the literature, a focus on uncertain areas to extract individual expert annotating profiles, and an attempt to optimize the ground truth by emphasizing areas of high uncertainty.

A primary finding of this investigation was the distinct disparity between results obtained from artificial data that have been used in previous works, and those from real-life medical datasets. Significantly, strategies that showed considerable success with artificial data proved unsatisfactory when applied to real-life medical data. This underscored the inherent complexities and unique characteristics of real-world annotation medical data, serving as a reminder that solutions developed in idealized environments may not necessarily translate directly to practical applications. Efforts to enhance the model’s performance using different strategies, such as transfer learning and variations in CMs, did not yield any notable improvements.

Another obstacle encountered was the difficulty in achieving a consensus among the experts. Although high agreement among experts is generally desirable, it presented a hurdle in the quest to improve the coupled CNN’s segmentation model using the individuals’ CMs, since minimal knowledge could be obtained in a highly agreeable environment. This suggests that models designed for scenarios with significant annotation disagreement may struggle when the discrepancies are minimal.

In response to these challenges, the focus shifted toward the regions of uncertainty within the data. An opportunity was found to delve deeper into understanding the individual behaviors of each expert, specifically in the context of these ambiguous areas. This introspection proved to be a fruitful endeavor, unveiling unique tendencies and preferences for each expert.

With this newfound understanding of annotator behaviors, a transition was made to redefine the ground truth (GT) from a more informed perspective. This was not an attempt to divorce the GT from expert annotations, but rather, it was a sophisticated endeavor to better integrate expert preferences into the construction of the GT. A novel GT was proposed and formulated based on maximum likelihood and with a specific focus on areas of uncertainty identified through the utilization of the deep learning model. This new approach surpasses the simplistic majority-vote strategy, providing a more sophisticated reflection of expert knowledge in the resulting GT.

The proposed method offers distinct advantages, primarily centered on addressing multi-labeling challenges by focusing on uncertain areas. Additionally, they create personalized annotating profiles for experts, enhancing and assessing future tasks. Moreover, these methods hold practical value in real-world settings, saving time and resources while overcoming odd-expert-number limitations for accurate ground truth determination.

In conclusion, this research illuminated the shortcomings of transferring methodologies developed from artificial data to real-world applications. However, through this exploration, the value of focusing on uncertain areas and individual expert behaviors was revealed. These insights fostered a more sophisticated construction of the ground truth, highlighting the potential for future research in multi-annotator segmentation.