Analysis and Compensation of Sun Direction Error on Solar Disk Velocity Difference
Abstract
:1. Introduction
2. Solar Disk Velocity Difference
3. The Impact of Sun Direction Error on Integrated Navigation Measurements
3.1. Sun Direction Error
3.2. The Impact of Sun Direction Error on the Solar Disk Velocity Difference
4. Augmented State Sun Direction/Solar Disk Velocity Difference Integrated Navigation
4.1. Augmented State Model
4.2. Measurement Model
4.3. Information Fusion
5. Simulation
5.1. Simulation Conditions
5.2. Simulation Results and Analysis
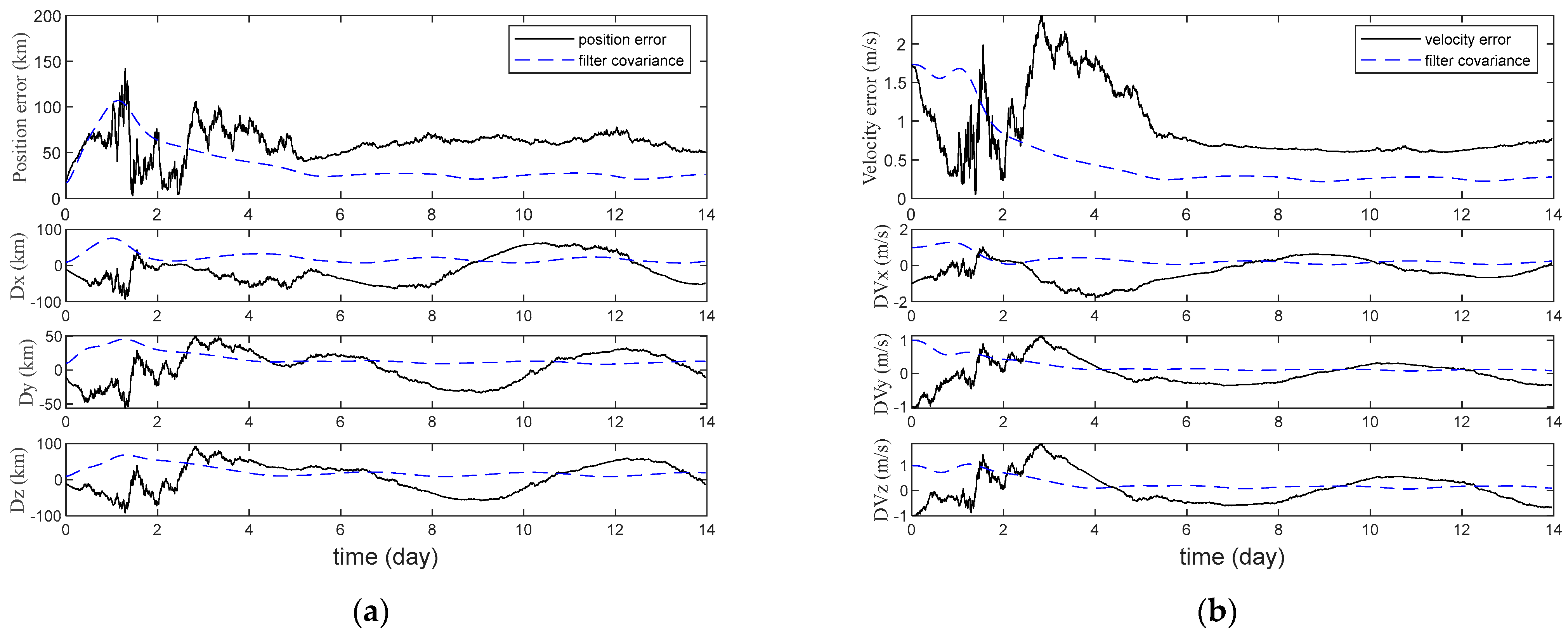
5.2.1. Navigation Results under Different Methods
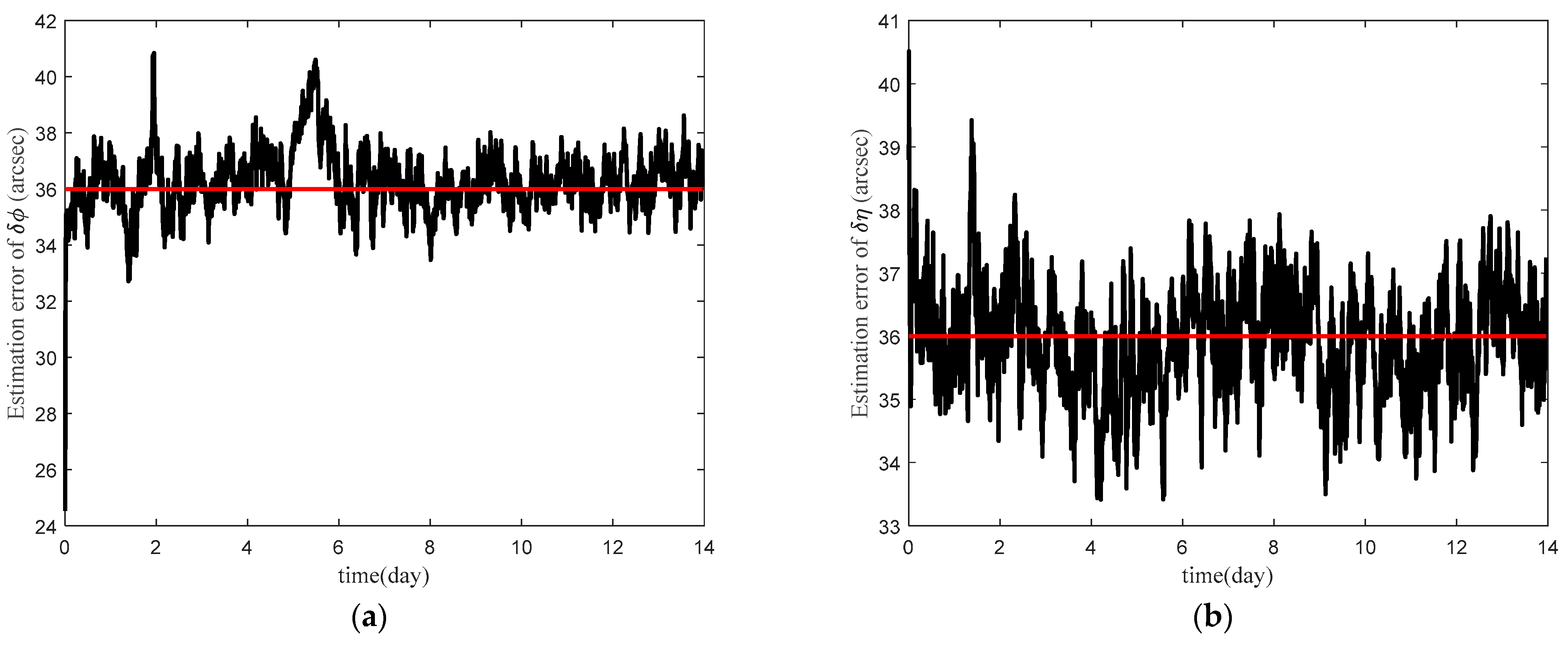
5.2.2. The Estimated Result of Sun Direction Error
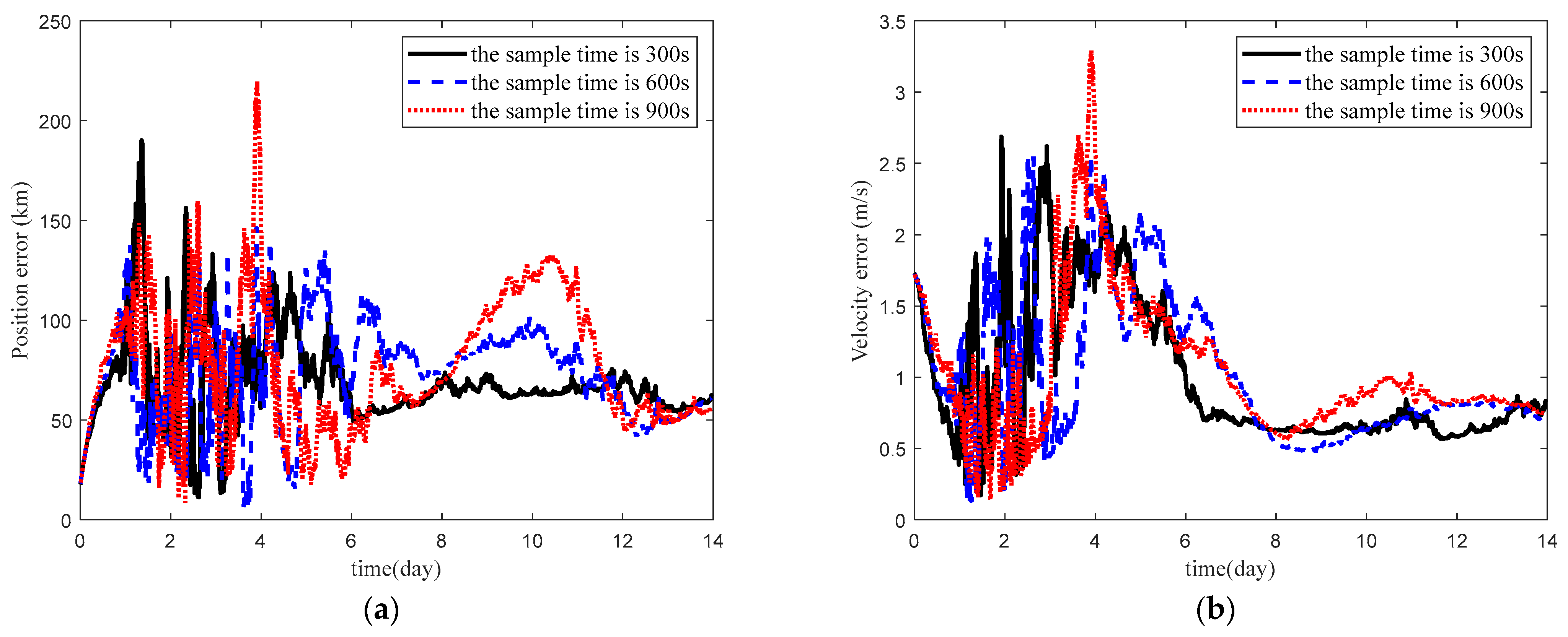
5.2.3. Impact of the Sample Time on Navigation Accuracy
5.2.4. Impact of the Spectrometer Number on Navigation Accuracy
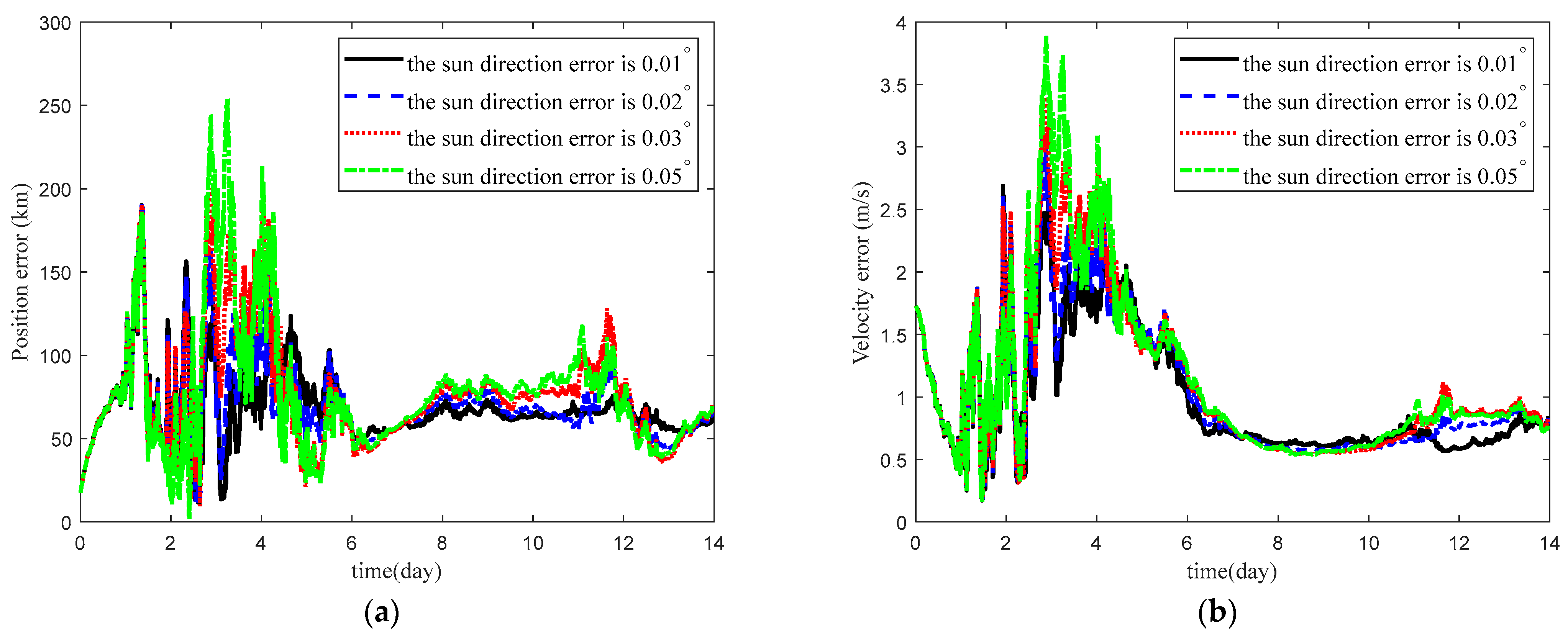
5.2.5. Impact of the Sun Direction Error Value on Navigation Accuracy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, W.; Liu, W.; Qiao, D.; Jie, D. Investigation on the development of deep space exploration. Sci. China-Technol. Sci. 2012, 55, 1086–1091. [Google Scholar] [CrossRef]
- Gao, Y.F.; Cheng, B.; Yu, Y.; Lv, J.; Baoyin, H.X. Stability Analysis on the Moon’s Rotation in a Perturbed Binary Asteroid. Mathematics 2022, 10, 3757. [Google Scholar] [CrossRef]
- Sebastian, A.; Acedo, L.; Morano, J.A. An orbital model for the Parker Solar Probe mission: Classical vs relativistic effects. Adv. Space Res. 2022, 70, 842–853. [Google Scholar] [CrossRef]
- Yang, B.; Jiang, Y.; Li, H.; Jiang, C.; Liu, Y.; Zhan, C.; Jing, H.; Dong, Y. Semi-Analytical Search for Sun-Synchronous and Planet Synchronous Orbits around Jupiter, Saturn, Uranus and Neptune. Mathematics 2022, 10, 2684. [Google Scholar] [CrossRef]
- Yue, X.; Schreiner, W.S.; Kuo, Y.-H.; Zhao, B.; Wan, W.; Ren, Z.; Liu, L.; Wei, Y.; Lei, J.; Solomon, S.; et al. The effect of solar radio bursts on the GNSS radio occultation signals. J. Geophys. Res.-Space Phys. 2013, 118, 5906–5918. [Google Scholar] [CrossRef]
- Pettit, J.; Randall, C.E.; Marsh, D.R. Effects of the september 2005 Solar Flares and Solar Proton Events on the Middle Atmosphere in WACCM. J. Geophys. Res.-Space Phys. 2018, 123, 5747–5763. [Google Scholar] [CrossRef]
- Ahluwalia, H.S. Forecast for sunspot cycle 25 activity. Adv. Space Res. 2022, 69, 794–797. [Google Scholar] [CrossRef]
- Popova, E.; Popov, A.I.; Sagdeev, R. Multimode Representation of the Magnetic Field for the Analysis of the Nonlinear Behavior of Solar Activity as a Driver of Space Weather. Mathematics 2022, 10, 1655. [Google Scholar] [CrossRef]
- Appenzeller, T. Leaving Jupiter, Ulysses Heads for the Sun’s South Pole. Science 1992, 257, 1478–1479. [Google Scholar] [CrossRef]
- Mitchell, J.G.; De Nolfo, G.A.; Hill, M.E. Energetic Electron Observations by Parker Solar Probe/IS circle dot IS during the First Widespread SEP Event of Solar Cycle 25 on 2020 November 29. Astrophys. J. 2021, 919, 119. [Google Scholar] [CrossRef]
- Sakshee, S.; Bandyopadhyay, R.; Banerjee, S. MHD-scale anisotropy in solar wind turbulence near the Sun using Parker solar probe data. Mon. Not. R. Astron. Soc. 2022, 514, 1282–1288. [Google Scholar] [CrossRef]
- Telloni, D.; Scolini, C.; Mostl, C. Study of two interacting interplanetary coronal mass ejections encountered by Solar Orbiter during its first perihelion passage Observations and modeling. Astron. Astrophys. 2021, 656, A5. [Google Scholar] [CrossRef]
- Cesarone, R.J.; Abraham, D.S.; Deutsch, L.J. Prospects for a next-generation deep-space network. Proc. IEEE 2007, 95, 1902–1915. [Google Scholar] [CrossRef]
- Gui, M.; Yang, H.; Ning, X.; Xiong, K.; Liu, J.; Dai, M.-Z. Star angle/double-differenced pulse time of arrival integrated navigation method for Jupiter exploration. Adv. Space Res. 2023, 71, 2669–2678. [Google Scholar] [CrossRef]
- Turan, E.; Speretta, S.; Gill, E. Autonomous navigation for deep space small satellites: Scientific and technological advances. Acta Astronaut. 2022, 193, 56–74. [Google Scholar] [CrossRef]
- Gui, M.; Wei, C.; Wei, Y.; Xiong, K.; Zhang, C.; Dai, M. Parameter-Independent Event-Triggered Implicit UKF for the Celestial Navigation Using Time Delay Measurement. Mathematics 2023, 11, 1952. [Google Scholar] [CrossRef]
- Huang, Y.Q.; Ma, X. Autonomous celestial navigation method for a deep-space probe based on angle-constraint aided celestial angle measurement. Sci. Sin.-Phys. Mech. Astron. 2022, 52, 214512. [Google Scholar] [CrossRef]
- Hong, J.H.; Park, W.; Ryoo, C.K. An Autonomous Space Navigation System Using Image Sensors. Int. J. Control Autom. Syst. 2021, 19, 2122–2133. [Google Scholar] [CrossRef]
- Gui, M.Z.; Zhao, D.J.; Ning, X.L.; Zhang, C.X.; Dai, M.Z. A Time Delay/Star Angle Integrated Navigation Method Based on the Event-Triggered Implicit Unscented Kalman Filter. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Chen, P.-T.; Zhou, B.; Speyer, J.L.; Bayard, D.S.; Majid, W.A.; Wood, L.J. Aspects of Pulsar Navigation for Deep Space Mission Applications. J. Astronaut. Sci. 2020, 67, 704–739. [Google Scholar] [CrossRef]
- Runnels, J.T.; Gebre-Egziabher, D. Estimator for Deep-Space Position and Attitude Using X-ray Pulsars. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2149–2166. [Google Scholar] [CrossRef]
- Liu, J.; Li, Y.Y.; Ning, X.L.; Chen, X.; Kang, Z.W. Modeling and analysis of solar Doppler difference bias with arbitrary rotation axis. Chin. J. Aeronaut. 2020, 33, 3331–3343. [Google Scholar] [CrossRef]
- Ning, X.L.; Gui, M.Z.; Fang, J.C.; Dai, Y.; Liu, G. A Novel Differential Doppler Measurement-Aided Autonomous Celestial Navigation Method for Spacecraft During Approach Phase. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 587–597. [Google Scholar] [CrossRef]
- Howard, R.; Harvey, J. Spectroscopic determinations of solar rotation. Sol. Phys. 1969, 12, 23–51. [Google Scholar] [CrossRef]
- Ning, X.L.; Chao, W.; Huang, Y.L.; Wu, W.R.; Fang, J.C. Spacecraft Autonomous Navigation Using the Doppler Velocity Differences of Different Points on the Solar Disk. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4615–4625. [Google Scholar] [CrossRef]
- Ning, X.L.; Huang, Y.L.; Chao, W. Integrated navigation of solar disk velocity difference and sun direction for spacecraft. Acta Astronaut. Astronaut. Sin. 2020, 41, 271–280. (In Chinese) [Google Scholar]
- Yang, P.; Xie, L.; Liu, J.L. Simultaneous celestial positioning and orientation for the lunar rover. Aerosp. Sci. Technol. 2014, 34, 45–54. [Google Scholar] [CrossRef]
- Hotta, H.; Kusano, K. Solar differential rotation reproduced with high-resolution simulation. Nat. Astron. 2021, 5, 1100–1102. [Google Scholar] [CrossRef]
- Xie, N.; Theuwissen, A.J.P. A Miniaturized Micro-Digital Sun Sensor by Means of Low-Power Low-Noise CMOS Imager. IEEE Sens. J. 2014, 14, 96–103. [Google Scholar] [CrossRef]
- Jing, C.Q.; Liang, T.; Lei, Q.J. A New Kind of Miniature Sun Sensor Design. In Proceedings of the 2016 IEEE International Conference on Electronic Information and Communication Technology, Harbin, China, 20–22 August 2016; pp. 219–222. [Google Scholar]
- Wei, M.S.; Xing, F.; Li, B.; You, Z. Investigation of Digital Sun Sensor Technology with an N-Shaped Slit Mask. Sensors 2011, 11, 9764–9777. [Google Scholar] [CrossRef]
- Xie, R.; Wang, B.; Li, S.; He, Y.; Wu, D.; Sun, S. Method and verification of accuracy improvement of digital sun sensor system. Chin. Space Sci. Technol. 2022, 1–6. (In Chinese) [Google Scholar]
- Rauh, A.; Wirtensohn, S.; Hoher, P.; Reuter, J.; Jaulin, L. Reliability Assessment of an Unscented Kalman Filter by Using Ellipsoidal Enclosure Techniques. Mathematics 2022, 10, 3011. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| Semi-major axis () | |
| Eccentricity () | 0.02 |
| Orbital inclination () | |
| Right ascension of the ascending node () | |
| Argument of perigee () |
| Parameter | Value |
|---|---|
| Initial state error | |
| Initial state covariance | |
| Process noise covariance | |
| Measurement noise covariance | |
| Filter period | 300 s |
| Method | Position Error (km) | Velocity Error (m/s) |
|---|---|---|
| Integrated navigation without sun direction error | 60.14 | 0.90 |
| Integrated navigation with sun direction error | 2750.57 | 32.01 |
| Augmented state integrated navigation | 68.54 | 0.99 |
| Errors | True Error | Mean Estimation Error |
|---|---|---|
| Sample Time (s) | Position Error (km) | Velocity Error (m/s) | Run Time (s) | ||
|---|---|---|---|---|---|
| 300 | 68.54 | 0.99 | 2.33% | 2.03% | 16.796 |
| 600 | 72.65 | 1.01 | 2.38% | 1.94% | 10.437 |
| 900 | 77.13 | 1.03 | 2.54% | 2.31% | 7.670 |
| The Number of Spectrometers | Position Error (km) | Velocity Error (m/s) | ||
|---|---|---|---|---|
| 2 | 95.94 | 1.33 | 3.60% | 3.43% |
| 3 | 70.48 | 0.99 | 2.14% | 1.96% |
| 4 | 68.54 | 0.99 | 2.33% | 2.03% |
| Sun Direction Error Value (Degree) | Position Error (km) | Velocity Error (m/s) | ||
|---|---|---|---|---|
| 0.01 | 68.54 | 0.99 | 2.33% | 2.03% |
| 0.02 | 70.59 | 1.04 | 1.17% | 1.08% |
| 0.03 | 76.15 | 1.11 | 0.87% | 0.85% |
| 0.05 | 78.15 | 1.14 | 0.53% | 0.56% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gui, M.; Yang, H.; Zhao, D.; Dai, M.; Zhang, C. Analysis and Compensation of Sun Direction Error on Solar Disk Velocity Difference. Mathematics 2023, 11, 3716. https://doi.org/10.3390/math11173716
Gui M, Yang H, Zhao D, Dai M, Zhang C. Analysis and Compensation of Sun Direction Error on Solar Disk Velocity Difference. Mathematics. 2023; 11(17):3716. https://doi.org/10.3390/math11173716
Chicago/Turabian StyleGui, Mingzhen, Hua Yang, Dangjun Zhao, Mingzhe Dai, and Chengxi Zhang. 2023. "Analysis and Compensation of Sun Direction Error on Solar Disk Velocity Difference" Mathematics 11, no. 17: 3716. https://doi.org/10.3390/math11173716
APA StyleGui, M., Yang, H., Zhao, D., Dai, M., & Zhang, C. (2023). Analysis and Compensation of Sun Direction Error on Solar Disk Velocity Difference. Mathematics, 11(17), 3716. https://doi.org/10.3390/math11173716








