Free Vibration Analyses of Stiffened Functionally Graded Graphene-Reinforced Composite Multilayer Cylindrical Panel
Abstract
:1. Introduction
2. Deriving the Governing Equations
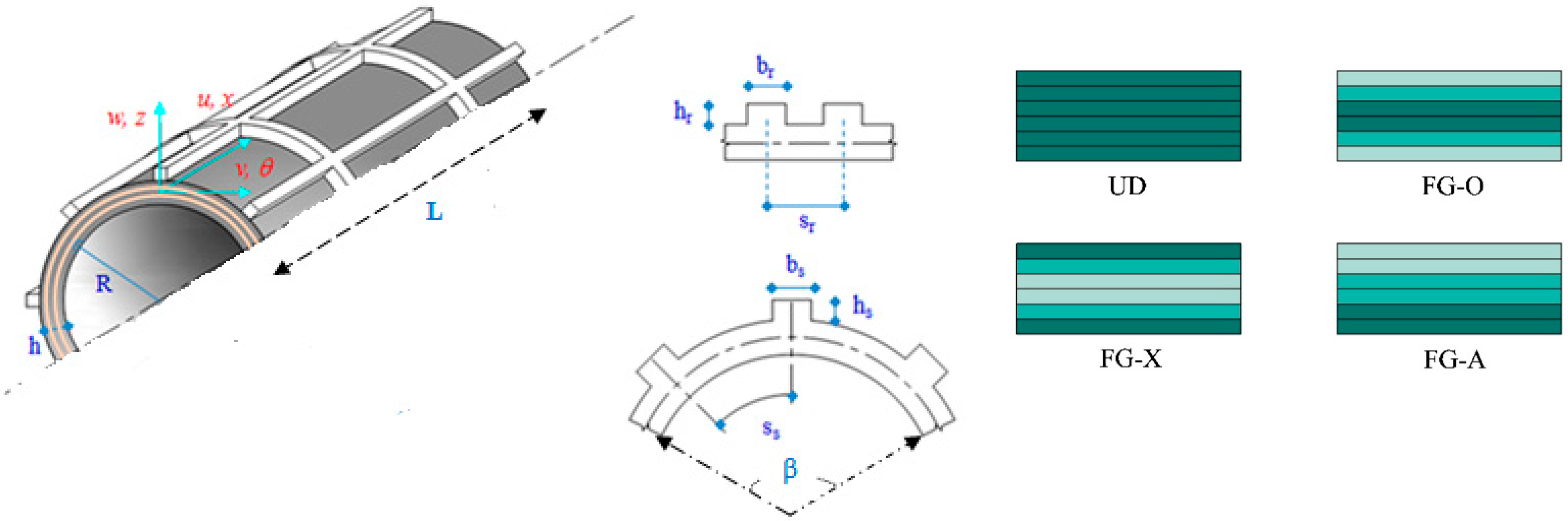
2.1. Definition of the Geometry and Material Properties of the Stiffened Cylindrical Shell Panel
2.2. Governing Equations (FSDT—Virtual Work Principle)
3. Finite Element Modeling
- Calculating the stiffness and mass matrices of each element according to Equation (29);
- Assembling the stiffness and mass matrices of each element to obtain the final stiffness and mass matrices of the shell;
- Applying the Sparse command on the matrices to reduce the size of matrices and also the computation time;
- Applying displacement boundary conditions on the Sparse matrices according to Equation (32);
- Solving the eigenvalue problem (Equation (31)) to obtain the natural frequencies and mode shapes. To solve Equation (31) in Matlab software, the command eigs (, ; number of desired mode shapes, 0) is used. Briefly, 0 means that the lowest natural frequency close to 0 is desired. In this study, number of desired mode shapes = 6.
4. Numerical Results and Discussion
4.1. Verification of Results
4.2. Numerical Results
- (a)
- Geometry of the cylindrical panel: L = 2, R = 0.5,
- (b)
- Geometry of the rings and stringers: hs = 0.02, bs = 0.04, hr = 0.02, br = 0.04
5. Conclusions
- (a)
- Maximum and minimum natural frequencies were related to GPL-X and GPL-UD, respectively;
- (b)
- The effect of reinforcing the shell panel with GPLs on the overall stiffness of the structure was more dominant than that in the case that the rings and stringers were reinforced by GPLs. The maximum influences of the GPL patterns and weight fraction of GPLs on the natural frequencies of the structure were approximately 60% and 118%, respectively;
- (c)
- By increasing the weight fraction of GPLs, the number of natural frequencies of the structure for the GPL-X pattern was increased to more than that of other GPL distributions;
- (d)
- The CCCC boundary condition had higher natural frequencies than did the SSSS boundary condition;
- (e)
- Reinforcement including rings and stringers may decrease or increase the natural frequencies of the structure depending on the boundary condition;
- (f)
- By increasing the number of rings and stringers, the natural frequencies were changed a little;
- (g)
- The influences of strengthening the shell with GPLs was much greater than that of stiffening it with rings and stringers.
- (h)
- In each pattern of reinforcement for the cylindrical shell panel except for GPL-UD, the numbers of natural frequencies of the structure were close to each other when the reinforcement of rings and stringers were considered to be GPL-O and GPL-A. This means that for these cases, they can be used interchangeably.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Crenwelge, O.E., Jr.; Muster, D. Free vibrations of ring-and-stringer-stiffened conical shells. J. Acoust. Soc. Am. 1969, 46, 176–185. [Google Scholar] [CrossRef]
- Nayak, A.N.; Satpathy, L.; Tripathy, P.K. Free vibration characteristics of stiffened plates. Int. J. Adv. Struct. Eng. 2018, 10, 153–167. [Google Scholar] [CrossRef]
- Nayak, A.N.; Bandyopadhyay, J.N. Free Vibration of Laminated Composite Stiffened Shallow Shells. In Toughened Composites; CRC Press: Boca Raton, FL, USA, 2022; pp. 261–276. [Google Scholar]
- Sinha, L.; Mishra, S.S.; Nayak, A.N.; Sahu, S.K. Free vibration characteristics of laminated composite stiffened plates: Experimental and numerical investigation. Compos. Struct. 2020, 233, 111557. [Google Scholar] [CrossRef]
- Nayak, A.N.; Bandyopadhyay, J.N. Free vibration analysis and design aids of stiffened conoidal shells. J. Eng. Mech. 2022, 128, 419–427. [Google Scholar] [CrossRef]
- Naghsh, A.; Saadatpour, M.M.; Azhari, M. Free vibration analysis of stringer stiffened general shells of revolution using a meridional finite strip method. Thin Walled Struct. 2015, 94, 651–662. [Google Scholar] [CrossRef]
- Quoc, T.H.; Van Tham, V.; Tu, T.M. Free Vibration of Stiffened Functionally Graded Porous Cylindrical Shell Under Various Boundary Conditions. In Modern Mechanics and Applications; Springer: Singapore, 2022; pp. 347–361. [Google Scholar]
- Samanta, A.; Mukhopadhyay, M. Free vibration analysis of stiffened shells by the finite element technique. Eur. J. Mech. A Solids 2004, 23, 159–179. [Google Scholar] [CrossRef]
- Mustafa, B.A.J.; Ali, R. An energy method for free vibration analysis of stiffened circular cylindrical shells. Comput. Struct. 1989, 32, 355–363. [Google Scholar] [CrossRef]
- Al-Najafi, A.M.J.; Warburton, G.B. Free vibration of ring-stiffened cylindrical shells. J. Sound Vib. 1970, 13, 9–25. [Google Scholar] [CrossRef]
- Zarei, M.; Rahimi, G.H.; Hemmatnezhad, M. Free vibrational characteristics of grid-stiffened truncated composite conical shells. Aerosp. Sci. Technol. 2020, 99, 105717. [Google Scholar] [CrossRef]
- Zarei, M.; Rahimi, G.H.; Hemmatnezhad, M. On the free vibrations of joined grid-stiffened composite conical-cylindrical shells. Thin Walled Struct. 2021, 161, 107465. [Google Scholar] [CrossRef]
- Aris, H.; Ahmadi, H. Using the higher-order shear deformation theory to analyze the free vibration of stiffened rotating FGM conical shells in a thermal environment. Thin Walled Struct. 2023, 183, 110366. [Google Scholar] [CrossRef]
- Ansari, E.; Hemmatnezhad, M.; Taherkhani, A. Free vibration analysis of grid-stiffened composite truncated spherical shells. Thin Walled Struct. 2023, 182, 110237. [Google Scholar] [CrossRef]
- Tran, M.T.; Nguyen, V.L.; Pham, S.D.; Rungamornrat, J. Free vibration of stiffened functionally graded circular cylindrical shell resting on Winkler–Pasternak foundation with different boundary conditions under thermal environment. Acta Mech. 2020, 231, 2545–2564. [Google Scholar] [CrossRef]
- Tuan, T.A.; Quoc, T.H.; Tu, T.M. Free vibration analysis of laminated stiffened cylindrical panels using finite element method. Vietnam J. Sci. Technol. 2016, 54, 771–784. [Google Scholar] [CrossRef]
- Nguyen, V.L.; Hoang, T.P. Analytical solution for free vibration of stiffened functionally graded cylindrical shell structure resting on elastic foundation. SN Appl. Sci. 2019, 1, 1–12. [Google Scholar] [CrossRef]
- Li, X.-Q.; Zhang, W.; Yang, X.-D.; Song, L.-K. A unified approach of free vibration analysis for stiffened cylindrical shell with general boundary conditions. Math. Probl. Eng. 2019, 2019, 4157930. [Google Scholar] [CrossRef]
- Bich, D.H.; Van Dung, D.; Nam, V.H. Nonlinear dynamical analysis of eccentrically stiffened functionally graded cylindrical panels. Compos. Struct. 2012, 94, 2465–2473. [Google Scholar] [CrossRef]
- Carrera, E.; Zappino, E.; Filippi, M. Free vibration analysis of thin-walled cylinders reinforced with longitudinal and transversal stiffeners. J. Vib. Acoust. 2013, 135, 011019. [Google Scholar] [CrossRef]
- Lugovoi, P.Z.; Prokopenko, N.Y. Influence of reinforcement and elastic foundation on the vibrations of shallow shells with rectangular planform. Int. Appl. Mech. 2011, 47, 714–719. [Google Scholar] [CrossRef]
- Shahani, A.R.; Kiarasi, F. Numerical and Experimental Investigation on Post-buckling Behavior of Stiffened Cylindrical Shells with Cutout subject to Uniform Axial Compression. J. Appl. Comput. Mech. 2023, 9, 25–44. [Google Scholar]
- Rao, M.N.; Schmidt, R.; Schröder, K.U. Forced vibration analysis of FG-graphene platelet reinforced polymer composite shells bonded with piezoelectric layers considering electroelastic nonlinearities. In Smart Materials, Adaptive Structures and Intelligent Systems; Society of Mechanical Engineers: New York, NY, USA, 2018; Volume 51944, p. V001T03A006. [Google Scholar]
- Van Do, V.N.; Lee, C.-H. Bézier extraction based isogeometric analysis for bending and free vibration behavior of multilayered functionally graded composite cylindrical panels reinforced with graphene platelets. Int. J. Mech. Sci. 2020, 183, 105744. [Google Scholar] [CrossRef]
- Amirabadi, H.; Farhatnia, F.; Eftekhari, S.A.; Hosseini-Ara, R. Free vibration analysis of rotating functionally graded GPL-reinforced truncated thick conical shells under different boundary conditions. Mech. Based Des. Struct. Mach. 2020, 50, 3821–3852. [Google Scholar] [CrossRef]
- Jamalabadi, M.Y.A.; Borji, P.; Habibi, M.; Pelalak, R. Nonlinear vibration analysis of functionally graded GPL-RC conical panels resting on elastic medium. Thin Walled Struct. 2021, 160, 107370. [Google Scholar] [CrossRef]
- Salehi, M.; Gholami, R.; Ansari, R. Nonlinear Resonance of Functionally Graded Porous Circular Cylindrical Shells Reinforced by Graphene Platelet with Initial Imperfections Using Higher-Order Shear Deformation Theory. Int. J. Struct. Stab. Dyn. 2022, 22, 2250075. [Google Scholar] [CrossRef]
- Yang, S.; Hao, Y.; Zhang, W.; Yang, L.; Liu, L. Nonlinear vibration of functionally graded graphene platelet-reinforced composite truncated conical shell using first-order shear deformation theory. Appl. Math. Mech. 2021, 42, 981–998. [Google Scholar] [CrossRef]
- Van Do, V.N.; Lee, C.-H. Static bending and free vibration analysis of multilayered composite cylindrical and spherical panels reinforced with graphene platelets by using isogeometric analysis method. Eng. Struct. 2020, 215, 110682. [Google Scholar] [CrossRef]
- Esmaeili, H.R.; Kiani, Y. Vibrations of graphene platelet reinforced composite doubly curved shells subjected to thermal shock. Mech. Based Des. Struct. Mach. 2022, 1–30. [Google Scholar] [CrossRef]
- Baghbadorani, A.A.; Kiani, Y. Free vibration analysis of functionally graded cylindrical shells reinforced with graphene platelets. Compos. Struct. 2021, 276, 114546. [Google Scholar] [CrossRef]
- Dong, Y.; Zhu, B.; Wang, Y.; Li, Y.; Yang, J. Nonlinear free vibration of graded graphene reinforced cylindrical shells: Effects of spinning motion and axial load. J. Sound Vib. 2018, 437, 79–96. [Google Scholar] [CrossRef]
- Dong, Y.; Li, X.; Gao, K.; Li, Y.; Yang, J. Harmonic resonances of graphene-reinforced nonlinear cylindrical shells: Effects of spinning motion and thermal environment. Nonlinear Dyn. 2020, 99, 981–1000. [Google Scholar] [CrossRef]
- Song, J.; Karami, B.; Shahsavari, D.; Civalek, Ö. Wave dispersion characteristics of graphene reinforced nanocomposite curved viscoelastic panels. Compos. Struct. 2021, 277, 114648. [Google Scholar] [CrossRef]
- Sobhani, E.; Masoodi, A.R.; Dimitri, R.; Tornabene, F. Free vibration of porous graphene oxide powder nano-composites assembled paraboloidal-cylindrical shells. Compos. Struct. 2023, 304, 116431. [Google Scholar] [CrossRef]
- Zare, R.; Najaafi, N.; Habibi, M.; Ebrahimi, F.; Safarpour, H. Influence of imperfection on the smart control frequency characteristics of a cylindrical sensor-actuator GPLRC cylindrical shell using a proportional-derivative smart controller. Smart Struct. Syst. Int. J. 2020, 26, 469–480. [Google Scholar]
- Rezaiee Pajand, M.; Sobhan, E.; Masoodi, A. Vibrational behavior of exponentially graded joined conical-conical shells. Steel Compos. Struct. 2022, 43, 603–623. [Google Scholar]
- Sobhani, E.; Avcar, M. The influence of various nanofiller materials (CNTs, GNPs, and GOPs) on the natural frequencies of Nanocomposite Cylindrical Shells: A comparative study. Mater. Today Commun. 2022, 33, 104547. [Google Scholar] [CrossRef]
- Sobhani, E.; Masoodi, A.R.; Ahmadi-Pari, A.R. Free-damped vibration analysis of graphene nano-platelet nanocomposite joined conical-conical-cylindrical shell marine-like structures. Ocean. Eng. 2022, 261, 112163. [Google Scholar] [CrossRef]
- Sobhani, E.; Masoodi, A.R.; Ahmadi-Pari, A.R. Wave frequency responses estimate of the nanocomposite linked hemispherical-conical shell underwater-like bodies with the impacts of two types of graphene-based nanofillers. Ocean Eng. 2022, 262, 112329. [Google Scholar] [CrossRef]
- Sobhani, E.; Masoodi, A.R.; Ahmadi-Pari, A.R. Circumferential vibration analysis of nano-porous-sandwich assembled spherical-cylindrical-conical shells under elastic boundary conditions. Eng. Struct. 2022, 273, 115094. [Google Scholar] [CrossRef]
- Sobhani, E.; Masoodi, A.R.; Civalek, Ö. On vibrational-based numerical simulation of a jet engine cowl shell-like structure. Mech. Adv. Mater. Struct. 2022, 30, 4016–4027. [Google Scholar] [CrossRef]
- Sobhani, E. On the vibrational analysis of combined paraboloidal-conical air vehicle segment shell-type structures. Aerosp. Sci. Technol. 2022, 129, 107823. [Google Scholar] [CrossRef]
- Song, M.; Yang, J.; Kitipornchai, S.; Zhu, W. Buckling and postbuckling of biaxially compressed functionally graded multilayer graphene nanoplatelet-reinforced polymer composite plates. Int. J. Mech. Sci. 2017, 131, 345–355. [Google Scholar] [CrossRef]
- Song, M.; Kitipornchai, S.; Yang, J. Free and forced vibrations of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Struct. 2017, 159, 579–588. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Ye, C.; Zu, J.W. Nonlinear vibration of metal foam cylindrical shells reinforced with graphene platelets. Aerosp. Sci. Technol. 2019, 85, 359–370. [Google Scholar] [CrossRef]
- Chai, Q.; Wang, Y.Q. Traveling wave vibration of graphene platelet reinforced porous joined conical-cylindrical shells in a spinning motion. Eng. Struct. 2022, 252, 113718. [Google Scholar] [CrossRef]
- Ye, C.; Wang, Y.Q. Nonlinear forced vibration of functionally graded graphene platelet-reinforced metal foam cylindrical shells: Internal resonances. Nonlinear Dyn. 2021, 104, 2051–2069. [Google Scholar] [CrossRef]
- Teng, M.W.; Wang, Y.Q. Nonlinear forced vibration of simply supported functionally graded porous nanocomposite thin plates reinforced with graphene platelets. Thin Walled Struct. 2021, 164, 107799. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, H.; Yang, F.; Wang, Q. An efficient method for vibration and stability analysis of rectangular plates axially moving in fluid. Appl. Math. Mech. 2021, 42, 291–308. [Google Scholar] [CrossRef]
- Chai, Q.; Wang, Y.Q. A general approach for free vibration analysis of spinning joined conical–cylindrical shells with arbitrary boundary conditions. Thin Walled Struct. 2021, 168, 108243. [Google Scholar] [CrossRef]
- Safarpour, M.; Rahimi, A.R.; Alibeigloo, A. Static and free vibration analysis of graphene platelets reinforced composite truncated conical shell, cylindrical shell, and annular plate using theory of elasticity and DQM. Mech. Based Des. Struct. Mach. 2020, 48, 496–524. [Google Scholar] [CrossRef]
- Babaei, M.; Kiarasi, F.; Tehrani, M.S.; Hamzei, A.; Mohtarami, E.; Asemi, K. Three dimensional free vibration analysis of functionally graded graphene reinforced composite laminated cylindrical panel. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2022, 236, 1501–1514. [Google Scholar] [CrossRef]
- Kiarasi, F.; Babaei, M.; Mollaei, S.; Mohammadi, M.; Asemi, K. Free vibration analysis of FG porous joined truncated conical-cylindrical shell reinforced by graphene platelets. Adv. Nano Res. 2021, 11, 361–380. [Google Scholar]
- Zhang, D.; Wang, Y.; Li, L. Free Vibration Response of FG Porous Joined Hemispherical–Cylindrical–Hemispherical Shell Vessels Reinforced by Graphene Platelet. Int. J. Struct. Stab. Dyn. 2022, 23, 2350025. [Google Scholar] [CrossRef]
- Zu, X.; Gao, Z.; Zhao, J.; Wang, Q.; Li, H. Vibration Suppression Performance of FRP Spherical-Cylindrical Shells with Porous Graphene Platelet Coating in a Thermal Environment. Int. J. Struct. Stab. Dyn. 2022, 22, 2250081. [Google Scholar] [CrossRef]
- Asgari, G.R.; Arabali, A.; Babaei, M.; Asemi, K. Dynamic instability of sandwich beams made of isotropic core and functionally graded graphene platelets-reinforced composite face sheets. Int. J. Struct. Stab. Dyn. 2022, 22, 2250092. [Google Scholar] [CrossRef]
- Javani, M.; Kiani, Y.; Eslami, M. Thermal buckling of FG graphene platelet reinforced composite annular sector plates. Thin Walled Struct. 2020, 148, 106589. [Google Scholar] [CrossRef]
- Bi, S.; Zhang, E.; Babaei, M.; Tornabene, F.; Dimitri, R. The Influence of GPL Reinforcements on the Post-Buckling Behavior of FG Porous Rings Subjected to an External Pressure. Mathematics 2023, 11, 2421. [Google Scholar] [CrossRef]
- Rostami, H.; Salami, S.J. Large amplitude free vibration of sandwich beams with flexible core and FG Graphene Platelet Reinforced Composite (FG-GPLRC) face sheets based on extended higher-order sandwich panel theory. Thin Walled Struct. 2022, 180, 109999. [Google Scholar] [CrossRef]
- Kiani, Y.; Żur, K.K. Free vibrations of graphene platelet reinforced composite skew plates resting on point supports. Thin Walled Struct. 2022, 176, 109363. [Google Scholar] [CrossRef]
- Kiarasi, F.; Babaei, M.; Sarvi, P.; Asemi, K.; Hosseini, M.; Omidi Bidgoli, O. A review on functionally graded porous structures reinforced by graphene platelets. J. Comput. Appl. Mech. 2021, 52, 731–750. [Google Scholar]
- Wu, H.; Zheng, Z.; Guo, J.; Li, L.; Bao, Y.; Yang, J. Axisymmetric thermal postbuckling of functionally graded graphene nanocomposite annular plates with various geometric imperfections. Thin Walled Struct. 2023, 185, 110594. [Google Scholar] [CrossRef]
- Babaei, M.; Asemi, K.; Kiarasi, F. Static response and free-vibration analysis of a functionally graded annular elliptical sector plate made of saturated porous material based on 3D finite element method. Mech. Based Des. Struct. Mach. 2023, 51, 1272–1296. [Google Scholar] [CrossRef]
- Van Vinh, P. A new first-order mixed beam element for static bending analysis of functionally graded graphene oxide powder-reinforced composite beams. Structures 2022, 36, 463–472. [Google Scholar] [CrossRef]
- Arshid, E.; Amir, S.; Loghman, A. Static and dynamic analyses of FG-GNPs reinforced porous nanocomposite annular micro-plates based on MSGT. Int. J. Mech. Sci. 2020, 180, 105656. [Google Scholar] [CrossRef]
- Babaei, M.; Kiarasi, F.; Asemi, K.; Dimitri, R.; Tornabene, F. Transient Thermal Stresses in FG Porous Rotating Truncated Cones Reinforced by Graphene Platelets. Appl. Sci. 2022, 12, 3932. [Google Scholar] [CrossRef]
- Lam, K.Y.; Qian, W. Free vibration of symmetric angle-ply thick laminated composite cylindrical shells. Compos. Part B Eng. 2000, 31, 345–354. [Google Scholar] [CrossRef]
- Mollaei, S.; Babaei, M.; Asemi, K. Torsional buckling of functionally graded graphene reinforced composite laminated cylindrical panel. Arch. Appl. Mech. 2023, 93, 427–435. [Google Scholar] [CrossRef]
- Nguyen, V.L.; Limkatanyu, S.; Bui, T.Q.; Rungamornrat, J. Free vibration analysis of rotating stiffened functionally graded graphene-platelet-reinforced composite toroidal shell segments with novel four-unknown refined theories. Int. J. Mech. Mater. Des. 2023, 19, 319–350. [Google Scholar] [CrossRef]
- Nazari, H.; Babaei, M.; Kiarasi, F.; Asemi, K. Geometrically nonlinear dynamic analysis of functionally graded material plate excited by a moving load applying first-order shear deformation theory via generalized differential quadrature method. SN Appl. Sci. 2021, 3, 1–32. [Google Scholar] [CrossRef]
- Dong, D.T.; Van Dung, D. A third-order shear deformation theory for nonlinear vibration analysis of stiffened functionally graded material sandwich doubly curved shallow shells with four material models. J. Sandw. Struct. Mater. 2019, 21, 1316–1356. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method: Solid Mechanics; Butterworth-Heinemann: Oxford, UK, 2000. [Google Scholar]
| Natural Frequencies (Hz) | ||||||
|---|---|---|---|---|---|---|
| Samanta and Mukhopadhyay [8] | 144 | 247 | 374 | 559 | 593 | 678 |
| (Present) | 138 | 241 | 369 | 554 | 587 | 669 |
| Number of Elements for Structure () | 30 × 30 | 40 × 30 | 50 × 30 |
|---|---|---|---|
| 326.82 | 312.24 | 310.32 |
| GPL Pattern for Cylindrical Panel Shell | GPL Pattern for Ring and Stringer | ||||||
|---|---|---|---|---|---|---|---|
| GPL-UD | UD | 225.13 | 374.82 | 435.39 | 452.77 | 465.65 | 592.43 |
| X | 258.75 | 433.25 | 504.36 | 578.56 | 593.13 | 769.27 | |
| O | 242.31 | 420.88 | 499.98 | 524.44 | 560.05 | 673.14 | |
| A | 228.54 | 390.43 | 467.24 | 488.34 | 497.22 | 626.46 | |
| GPL-X | UD | 282.76 | 479.21 | 539.81 | 599.99 | 633.12 | 710.47 |
| X | 362.55 | 614.98 | 697.29 | 731.08 | 766.46 | 968.71 | |
| O | 310.32 | 550.74 | 642.12 | 675.84 | 700.48 | 893.65 | |
| A | 299.47 | 494.32 | 566.36 | 620.11 | 658.22 | 760.33 | |
| GPL-O | UD | 240.88 | 390.15 | 470.46 | 506.42 | 525.84 | 631.26 |
| X | 281.65 | 480.67 | 553.57 | 595.72 | 616.71 | 744.64 | |
| O | 276.18 | 466.74 | 549.34 | 588.07 | 600.39 | 730.12 | |
| A | 265.94 | 441.46 | 526.25 | 567.66 | 580.35 | 700.49 | |
| GPL-A | UD | 226.83 | 362.49 | 432.72 | 450.24 | 478.55 | 600.06 |
| X | 273.56 | 471.82 | 520.18 | 590.88 | 601.56 | 716.77 | |
| O | 233.14 | 420.13 | 500.72 | 541.57 | 550.22 | 680.48 | |
| A | 230.13 | 400.78 | 474.30 | 500.94 | 510.74 | 635.33 |
| GPL Pattern for Cylindrical Panel, Ring and Stringer | % | ||||||
|---|---|---|---|---|---|---|---|
| GPL-X | 0 | 166.66 | 277.03 | 322.22 | 347.9 | 355.28 | 438.51 |
| 0.5 | 312.06 | 529.61 | 600.86 | 630.17 | 660.34 | 834.48 | |
| 1 | 362.55 | 614.98 | 697.29 | 731.08 | 766.46 | 968.71 | |
| GPL-A | 0 | 166.66 | 277.03 | 322.22 | 347.9 | 355.28 | 438.51 |
| 0.5 | 203.53 | 357.14 | 423.21 | 446.42 | 455.35 | 566.94 | |
| 1 | 230.13 | 400.78 | 474.30 | 500.94 | 510.74 | 635.33 | |
| GPL-UD | 0 | 166.66 | 277.03 | 322.22 | 347.9 | 355.28 | 438.51 |
| 0.5 | 187.55 | 311.66 | 378.26 | 400.12 | 420.18 | 493.33 | |
| 1 | 225.13 | 374.82 | 435.39 | 452.77 | 465.65 | 592.43 | |
| GPL-O | 0 | 166.66 | 277.03 | 322.22 | 347.9 | 355.28 | 438.51 |
| 0.5 | 230.47 | 391.59 | 473.27 | 498.30 | 500.42 | 634.78 | |
| 1 | 276.18 | 466.74 | 549.34 | 588.07 | 600.39 | 730.12 |
| GPL Pattern for Cylindrical Panel, Ring and Stringer | Boundary Condition | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| GPL-X | cccc | 696.26 | 912.85 | 1057.23 | 1145.3 | 1175.5 | 1289.4 |
| ssss | 362.55 | 614.98 | 697.29 | 731.08 | 766.46 | 968.71 | |
| GPL-UD | cccc | 421.96 | 557.72 | 647.13 | 702.76 | 720.33 | 793.83 |
| ssss | 225.13 | 374.82 | 435.39 | 452.77 | 465.65 | 592.43 | |
| GPL-O | cccc | 524.44 | 884.23 | 1032.75 | 1134.88 | 1140.55 | 1350.62 |
| ssss | 276.18 | 466.74 | 549.34 | 588.07 | 600.39 | 730.12 | |
| GPL-A | cccc | 391.63 | 700.45 | 860.27 | 930.18 | 969.31 | 1235.77 |
| ssss | 230.13 | 400.78 | 474.30 | 500.94 | 510.74 | 635.33 |
| Boundary Condition | Number of Ring and Stringer | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| CCCC | Nr = Ns = 5 | 696.26 | 912.85 | 1057.23 | 1145.3 | 1175.5 | 1289.4 |
| Nr = Ns = 7 | 697.12 | 913.00 | 1053.84 | 1140.72 | 1176.02 | 1284.37 | |
| Nr = Ns = 10 | 698.23 | 913.78 | 1049.6 | 1136.8 | 1177.6 | 1280 | |
| SSSS | Nr = Ns = 5 | 362.55 | 614.98 | 697.29 | 731.08 | 766.46 | 968.71 |
| Nr = Ns = 7 | 360.01 | 613.47 | 690.33 | 727.66 | 767.13 | 969.47 | |
| Nr = Ns = 10 | 359.62 | 613.2 | 685.22 | 719.85 | 770.11 | 971.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Zhang, Y.; Nyasha Chirukam, B.; Li, J.; Lu, C.; Babaei, M.; Asemi, K. Free Vibration Analyses of Stiffened Functionally Graded Graphene-Reinforced Composite Multilayer Cylindrical Panel. Mathematics 2023, 11, 3662. https://doi.org/10.3390/math11173662
Zhou Y, Zhang Y, Nyasha Chirukam B, Li J, Lu C, Babaei M, Asemi K. Free Vibration Analyses of Stiffened Functionally Graded Graphene-Reinforced Composite Multilayer Cylindrical Panel. Mathematics. 2023; 11(17):3662. https://doi.org/10.3390/math11173662
Chicago/Turabian StyleZhou, Yuhua, Yanhu Zhang, Brighton Nyasha Chirukam, Jianwei Li, Congshan Lu, Masoud Babaei, and Kamran Asemi. 2023. "Free Vibration Analyses of Stiffened Functionally Graded Graphene-Reinforced Composite Multilayer Cylindrical Panel" Mathematics 11, no. 17: 3662. https://doi.org/10.3390/math11173662
APA StyleZhou, Y., Zhang, Y., Nyasha Chirukam, B., Li, J., Lu, C., Babaei, M., & Asemi, K. (2023). Free Vibration Analyses of Stiffened Functionally Graded Graphene-Reinforced Composite Multilayer Cylindrical Panel. Mathematics, 11(17), 3662. https://doi.org/10.3390/math11173662







