A Study on the Laney p′ Control Chart with Parameters Estimated from Phase I Data: Performance Evaluation and Applications

Abstract

The Laney p′ control chart is a new type of attribute control chart that can be applied in situations where the process exhibits either overdispersion or underdispersion. While it has gained acceptance in the industry, there is still limited knowledge about its effectiveness in detecting process variation. It is well known that before applying a control chart, understanding its performance is crucial, especially when the parameters of the control chart need to be estimated from historical data. In this study, we used simulations to investigate the ability of the Laney p′ control chart to detect process variations when the parameters are estimated. We designed appropriate experiments to assess the impact of overdispersion on the average run length (ARL) performance. In this study, we assumed that the overdispersion comes from the variation in the mean fraction nonconforming of each sample. The mean value varies according to a uniform distribution. This study evaluated the performance of the Laney $p^{\prime }$ control chart using the average of the ARL (AARL) and the standard deviation of the ARL (SDARL). Additionally, real-world data were utilized to illustrate the practical applications of the Laney $p^{\prime }$ control chart in the PCB and IC substrate industries. The research findings can serve as valuable guidance for practical implementation.

1. Introduction

Control charts are a statistical process control (SPC) tool used to monitor a process over time and determine whether a manufacturing or business process is in control or out of control. An in-control process refers to a process that is stable, predictable, and exhibits only random cause variations [1]. Conversely, an out-of-control process may display various nonrandom patterns on the control chart, indicating the presence of assignable causes that are responsible for variations in process performance [1]. By understanding the underlying causes, organizations can make informed decisions to improve processes, reduce variation, and enhance product or service quality.

Generally, control charts can be divided into two types: variables control charts and attribute control charts [1]. The specific type of control chart used depends on the nature of the data being monitored. A variable control chart is used to monitor and control process variability when the data being measured are quantitative and continuous. On the other hand, an attribute control chart is a tool used to monitor and control process quality characteristics that are discrete or qualitative in nature. In SPC, the $p$ control chart is an attribute control chart used to monitor the fraction of nonconforming items in a sample [1]. The sample fraction nonconforming (also known as nonconforming rate) is defined as the ratio of the number of nonconforming units in a sample (denoted as $X$) to the sample size (denoted as $n$). The $p$ control charts have been widely used in monitoring manufacturing processes. Recently, the use of $p$ control charts is increasing in the healthcare industry [2,3,4,5].

This section provides a brief overview of the $p$ chart. For more details, please refer to Montgomery [1]. The development of the $p$ chart requires estimating the process fraction nonconforming, $p$, from a set of historical data because the value of $p$ is typically unknown. This estimation is carried out by selecting $m$ preliminary samples (also known as subgroups), each with a size of $n$. Denote $\overline{p}$ as the average of these sample fractions nonconforming. The statistic $\overline{p}$ is then used to estimate the unknown fraction nonconforming, $p$. Based on this estimation, the parameters of the $p$ control chart can be expressed as follows:

$$\mathrm{UCL}=\overline{p}+3\sqrt{\frac{\overline{p}\left(1-\overline{p}\right)}{n}}$$

(1)

$$\mathrm{CL}=\overline{p}$$

(2)

$$\mathrm{LCL}=\overline{p}-3\sqrt{\frac{\overline{p}\left(1-\overline{p}\right)}{n}}$$

(3)

If the true fraction nonconforming in the production process is known or is a specified standard value, $p$, then the $\overline{p}$ value in Equations (1)–(3) can be replaced with $p$.

The above description represents the two-phase implementation of control charts. In Phase I, a set of process data is collected and used to estimate the unknown parameters when the process is in control. These estimates are then used to construct the Phase II chart, which monitors the process by plotting the chart statistics and comparing their values to the control limits. It is well known that the more accurate the estimates of the control chart parameters in Phase I, the better the Phase II control chart will perform.

In certain cases where the $p$ control chart is used to monitor the fraction of nonconforming items, the sample consists of a complete inspection of the process output during a specific timeframe. Due to variations in the number of units produced during each period, this leads to variable control limits on the chart.

In the past, numerous studies have been conducted to enhance the traditional $p$ control chart. One area of research involves exploring different control charts, such as MA [6], EWMA [7], and CUSUM [8], to improve the ability to detect changes in the nonconforming rate. Another line of research aims to address the issue of ARL-biased characteristics that emerge when using traditional $p$ control charts to detect changes in the nonconforming rate [9,10,11]. A third category of research focuses on employing supplementary rules to enhance the detection capability of traditional $p$ control charts [9,12,13]. The final research direction aims to modify the traditional $p$ control chart to address the issue of variation in nonconforming rates between samples. This aspect is also the primary focus of our study.

It is important to note that the traditional $p$ control chart assumes that the samples are independent and that the probability of nonconforming is constant over time. If these assumptions are not met, it may be necessary to consider alternative control charts. For instance, in the healthcare application of SPC methods, one issue that raises concern is that of overdispersion. Overdispersion commonly arises in the cases when sample sizes are very large and the parameter $p$ (event probability) is not constant but changes over time.

The Laney $p^{\prime }$ chart [14] is a new type of attribute control chart that is particularly useful in scenarios where there are large sample sizes and the data exhibit overdispersion. Overdispersion can lead to false indications of out-of-control points on a traditional $p$ chart. The Laney $p^{\prime }$ chart incorporates both the variation within samples and the variation between consecutive samples in its definition of common cause variation. When there is overdispersion, the control limits on a Laney $p^{\prime }$ chart are wider in comparison to those of a traditional $p$ chart. The wider control limits mean that only significant deviations in the process are identified as out of control.

The Laney $p^{\prime }$ chart is also useful in the situation when data exhibit underdispersion. Underdispersion, which can occur with samples of any size, is often caused by a lack of randomness. Underdispersion can result in control limits that are too wide for the data. The Laney $p^{\prime }$ chart corrects for underdispersion by calculating narrower control limits.

The calculations for the Laney $p^{\prime }$ chart include ${\sigma }_Z$, which is an adjustment for overdispersion or underdispersion. In order to compute ${\sigma }_Z$, the sample statistic $p_i$ is first standardized using Equation (4):

$$Z_i=\frac{p_i-\overline{p}}{{\sigma }_{p_i}}$$

(4)

where

$${\sigma }_{p_i}=\sqrt{\frac{\overline{p}\left(1-\overline{p}\right)}{n_i}}$$

(5)

The value of ${\sigma }_Z$ can be estimated as

$$\frac{{\overline{MR}}_z}{d_2}$$

(6)

where $d_2=1.128$ if a moving range of two observations is used.

The average of the moving range of $Z_i$ can be obtained by

$${\overline{MR}}_Z=\frac{{{\displaystyle \sum }}_{i=1}^m\left|Z_i-Z_{i-1}\right|}{m-1}$$

(7)

where $m$ is the number of samples. The parameters for the Laney $p^{\prime }$ chart are

$$\mathrm{UCL}=\overline{p}+3{\sigma }_{p_i}\times {\sigma }_z$$

(8)

$$\mathrm{CL}=\overline{p}$$

(9)

$$\mathrm{LCL}=\overline{p}-3{\sigma }_{p_i}\times {\sigma }_z$$

(10)

A ${\sigma }_Z$ value of 1 indicates that no adjustment is necessary and that the Laney $p^{\prime }$ control chart is the same as a traditional $p$ chart.

Equations (8) and (10) reveal that the utilization of a $p^{\prime }$ chart incorporates an extra variance component resulting from the variability in parameter $p$ over time, in addition to the conventional calculation of binomial sampling variance.

After conducting a comprehensive literature review, it is evident that a research gap exists regarding the impact of parameter estimation on the performance of the $p^{\prime }$ control chart. Previous studies have primarily focused on evaluating performance solely based on the average run length (ARL). However, when parameters are estimated, the ARL becomes a random variable, necessitating the consideration of both the average value of the average run length (AARL) and the standard deviation of the average run length (SDARL) for performance evaluation [15,16]. This is crucial because different practitioners may obtain varying estimates of the process parameters, leading to different ARL values. Consequently, practitioner-to-practitioner variability introduces randomness into the ARL.

The main objective of this study is to evaluate the performance of the $p^{\prime }$ chart with estimated parameters based on the AARL and SDARL metrics. We also investigate how the number of samples in Phase I influences the performance of the control chart when the parameters are unknown. Furthermore, we evaluate the performance of the $p^{\prime }$ chart when the values of sample size and nonconforming rate are allowed to vary from sample to sample.

The rest of the paper is organized as follows. Section 2 provides a review of previous studies on the Laney attribute control charts, as well as studies on the performance evaluation of the Laney $p^{\prime }$ control charts, where the parameters are estimated from historical data. Section 3 outlines the experimental setup and simulation procedure employed in this study. Section 4 presents the experimental results. In Section 5, we utilize real data to explain the applications of the Laney $p^{\prime }$ control chart in the PCB and IC substrate industries. Finally, Section 6 summarizes the findings and proposes potential avenues for future research.

2. Related Work

This section presents a literature review on topics that are relevant to this study, which includes the application of Laney control charts, as well as the research on evaluating the performance of the $p^{\prime }$ control chart.

In the past, many researchers have studied the impact of overdispersion or underdispersion on data and proposed solutions. Jones and Govindaraju [17] pointed out that overdispersion refers to the variability in data exceeding the variability assumed by their probability distribution. They proposed a simple graphical method to verify the distributional assumption of attribute control charts. This method can also indicate whether there is excessive dispersion or underdispersion in the data. They also briefly reviewed the literature on handling process attributes that do not follow the binomial or Poisson distribution.

Laney [14] introduced the $p^{\prime }$ control chart as a means to prevent negative outcomes resulting from overdispersion in process data. This new type of attribute control chart can also be utilized in cases where a process exhibits insufficient dispersion. Laney demonstrated the application of the $p^{\prime }$ control chart using examples from Heimann [18] but did not conduct performance testing on this chart. Since its introduction, the Laney $p^{\prime }$ control chart has been widely used in healthcare quality monitoring, particularly in cases with large sample sizes. Mohammed and Laney [19] further applied the $p^{\prime }$ control chart to monitor overdispersion in healthcare performance data, highlighting its relevance in healthcare quality monitoring.

Sellers [20] proposed a generalized statistical control chart that can be used to monitor count data for overdispersion or underdispersion. The distributions considered in this study include the binomial, Poisson, and negative binomial distributions.

Vidmara and Blagus [21] pointed out that the identification of outliers in overdispersed proportion data is crucial for effective healthcare quality monitoring. Their study found that the Laney method produces the lowest rate of false alarms. However, in situations where the sample size is small and the proportion is very low, it is difficult to detect outliers, or when the proportion value is very high, outliers are difficult to detect irrespective of sample size.

Evaluating the microbiological quality of pharmaceutical products is an important criterion for determining whether they can be safely released into the drug market. Eissa [22] stated that since the data of the total viable count (TVC) in pharmaceuticals do not follow any specific distribution type, the Laney $U^{\prime }$ control chart is suitable for application in such cases. Eissa [22] believes that when there is significant overdispersion or underdispersion in the data distribution, the Laney $U^{\prime }$ control chart pattern is highly appropriate for monitoring the microbiological characteristics of pharmaceutical products.

Moon [23] applied the Laney $U^{\prime }$ control chart to schedule performance management. In this study, planned value costs were considered as the sample size, and each dollar was assumed to represent an attribute (inspection) unit. Earned value cost, which represents the value of work completed to date, was treated as a variable. By dividing the earned value cost by the planned value cost, a schedule performance index (SPI) was obtained. The study treated SPI as a sample statistic and monitored its variation using the Laney $U^{\prime }$ control chart.

Arafah [24] utilized the Laney $p^{\prime }$ control chart to monitor the variations in the COVID-19 cases in Jordan. The study defined the infection rate (IR) as the number of confirmed cases divided by the number of polymerase chain reaction (PCR) tests conducted. The objective of the research was to understand the effectiveness of the government’s restrictive measures in controlling the infection rate during the COVID-19 pandemic, which included restrictions on population movement and activities. The study results demonstrated that implementing restrictive measures effectively reduced the infection rate, while relaxing these measures had the opposite effect.

Valdés-Manuel and Cogollo-Flórez [25] pointed out that overdispersion is a phenomenon that frequently occurs in large-sample data analysis. In the analysis of discrete data, it refers to a higher level of variation in the data than what is implied by the reference binomial or Poisson distribution. In clinical laboratories, there is often high variability in the proportion of nonconforming units, leading to the occurrence of overdispersion. Therefore, it is necessary to analyze and identify the most suitable control chart to overcome the limitations of traditional control charts when dealing with overdispersed data.

With the introduction and application of the Laney $p^{\prime }$ control chart, some researchers have recently begun to investigate its performance. Ahsan et al. [26] used simulation to evaluate and compare the in-control and out-of-control average run lengths for the $p$ and Laney $p^{\prime }$ control charts. Their study aimed to determine whether the performance of the Laney $p^{\prime }$ control chart is superior to that of the $p$ control chart.

Hagan and Li [27] evaluated the Phase II performance of the Laney $p^{\prime }$ control chart using a simulation approach. Their study allowed for variation in the sample size ($n$) and process nonconforming rate ($p$) between samples. The study assumed that $n$ and $p$ followed truncated normal distributions with a mean of $\mu$ and a standard deviation of $\mu /5$ (or $\mu /3$). When $p$ was allowed to vary across subgroups, its simulated value of $\mu$ was either 0.1 or 0.5. When $n$ was allowed to vary, its simulated value of μ varied from 10 to 2000. The performance metric was ARL.

The studies of [26,27] assumed that the process parameters are known and evaluated the performance of the control chart in Phase II. In other words, these studies did not take into account the impact of parameter estimation errors on the performance of the control chart. Furthermore, it is worth noting that the study conducted by Ahsan et al. [26] did not consider the variation in the fraction of nonconforming items between samples.

Recently, Goedhart and Woodall [28] proposed a new method for calculating the control limits of the $p$ chart. They demonstrated that the Laney $p^{\prime }$ chart does not perform well when there are significant variations in subgroup sizes. Laney’s method [14] only yields appropriate limits when there is no intersubgroup variation. Additionally, they pointed out that the estimated control limits for the $p^{\prime }$ chart are excessively wide for smaller sample sizes and too narrow for larger sample sizes. They showed that their method is able to handle situations involving varying subgroup sizes and intersubgroup variation.

3. Methods

3.1. Performance Metrics

The detection capability of a control chart is usually evaluated using the average run length (ARL). The run length refers to the number of samples needed until the chart indicates an out-of-control condition. The ARL represents the expected value of the run length. There are two types of ARL: in-control ARL (${\mathrm{ARL}}_0$) and out-of-control ARL (${\mathrm{ARL}}_1$). A control chart with a smaller in-control ARL is more sensitive or responsive to detecting process shifts, but it also has a higher probability of Type I errors. Conversely, a control chart with a larger out-of-control ARL is less sensitive or slower to detect process shifts, resulting in a higher probability of Type II errors. A well-designed control chart should have a small ${\mathrm{ARL}}_1$ when the process undergoes changes, while maintaining a large ${\mathrm{ARL}}_0$ when there are no changes in the process.

When the control chart parameters are known, the ARL is a constant value. For example, in the case of using a 3-sigma control limit for the $\overline{x}$ chart, assuming a normal distribution, the Type I error probability $\alpha$ is 0.0027. In this case, the ${\mathrm{ARL}}_0$ is $1/\alpha$, which is equal to 370.37. This means that, on average, the control chart will signal a false alarm every 370.37 samples when the process is actually in control.

When the parameters of the control chart are estimated from the samples, the ARL becomes a random variable due to the influence of Phase I sampling [15]. When control charts are constructed using estimated parameters, the average of the ARL (AARL) is commonly used as a measure of performance evaluation. However, AARL alone does not capture the other important properties of ARL. Another significant measure is the standard deviation of the ARL (SDARL), which reflects the practitioner-to-practitioner variability [16]. Practitioner-to-practitioner variability refers to the differences in Phase I data collected by different users, resulting in different parameter estimates and consequently affecting the performance of the control chart. Jones and Steiner [29] first proposed the SDARL metric to study the estimation effect on the performance of the risk-adjusted CUSUM chart. Many other authors used it in evaluating control chart performance when the parameters are estimated [30,31,32]. In this study, we employed both the AARL and SDARL metrics when assessing the performance of the $p^{\prime }$ chart with estimated parameters.

When the process parameters are estimated, in order to achieve a stable in-control ARL (${\mathrm{ARL}}_0$), we need a sufficient amount of Phase I sample data so that the in-control AARL value can approach ${\mathrm{ARL}}_0$ and should have a smaller value of SDARL. Zhang et al. [32] suggested that the SDARL value should be within 10% of the expected in-control ARL (${\mathrm{ARL}}_0$). In general, for traditional variable control charts, when the process parameters are known, it is possible to obtain the desired ${\mathrm{ARL}}_0$ by selecting appropriate control chart parameter combinations [15,32]. However, for $p$ and $p^{\prime }$ control charts, where the sample sizes and nonconforming rates may vary across samples, it becomes more challenging to estimate the expected ${\mathrm{ARL}}_0$ accurately. Therefore, the criteria proposed by Zhang et al. [32] may not necessarily be fully applicable to the performance evaluation process of $p$ and $p^{\prime }$ control charts in this study.

3.2. Experimental Setup

To investigate the impact of estimating process parameters, we estimated the unknown parameters based on $m$ Phase I samples of size $n$. The estimated parameters include the in-control process mean $p$ and ${\sigma }_Z$. In our study, we considered values of $m$ ranging from 20 to 10,000. It is important to emphasize that the majority of the nonconforming rates analyzed in this study are below 0.05, aiming to reflect the typical conditions found in the general manufacturing industry. In contrast, Hagan and Li [27] examined nonconforming rates of 0.1 and 0.5, which were considered relatively high for the general manufacturing industry. After Phase I analysis, we constructed the Phase II control chart by substituting the unknown parameters with their estimates derived from the generated Phase I samples. We then evaluated the average run length (ARL) value using a simulation approach, which involves 10,000 simulation runs. Finally, we calculate the average ARL (AARL) and standard deviation of ARL (SDARL) by performing 10,000 simulation iterations, each with a unique set of Phase I samples.

In this study, we assume that the between-sample variation comes from the variation in the mean fraction nonconforming of each sample. The mean varies according to a uniform distribution, denoted as U($a, b$). A value sampled from the interval $a$ to $b$ is then used to simulate the binomial random variates. Assuming that the number of samples collected in Phase I is $m$, the simulation procedure used in this study includes the following steps:

• Define the range of variation for the in-control (process under normal conditions) nonconforming rate $p$ as a uniform distribution $\mathrm{U}\left(p_{min}, p_{max}\right)$ and the range of variation for $n$ as a uniform distribution $\mathrm{U}\left(n_{min}, n_{max}\right)$.
• Using the simulated values of $p_i$ and $n_i$, we generate $m$ independent $X_i$ values from a binomial distribution with parameters $p_i$ and $n_i$. Then, we calculate $p_i=X_i/n_i$.
• Calculate the average of the sample fraction nonconforming:

  $$\overline{p}=\frac{{{\displaystyle \sum }}_{i=1}^m{X}_i}{{{\displaystyle \sum }}_{i=1}^m{n}_i}.$$

  (11)
  The statistic $\overline{p}$ estimates the unknown fraction nonconforming $p$.
• Calculate the control limits for the Laney $p^{\prime }$ control chart using Equations (4)–(10).

The above steps describe how to generate $m$ sets of sample data for Phase I analysis. Next, we generate Phase II data and evaluate the run length based on the control limits mentioned above. Evaluating the ARL performance of the $p$ or $p^{\prime }$ control charts is not a simple task. Both the sample size, $n$, and the process fraction nonconforming, $p$, will affect the characteristics of the ARL. Additionally, the ARL of the $p$ control chart exhibits ARL-biased characteristics [9]. Under this characteristic, the in-control ARL is not the highest point on the entire ARL curve. Figure 1 illustrates the ARL curve for the $p$ control chart with ARL-biased characteristics. The $y$-axis of the ARL curve in Figure 1 is displayed on a logarithmic scale. In this example, the in-control fraction nonconforming is 0.04, and the sample size for each group is $n=400$, with ${\mathrm{ARL}}_0=268.08$. The traditional $\overline{x}$ control chart exhibits ARL-unbiased characteristics. When the process undergoes abnormal changes, its ARL (i.e., out-of-control ${\mathrm{ARL}}_1$) will be lower than the ARL when the process is in a normal state (i.e., in-control ${\mathrm{ARL}}_0$).

Figure 2 illustrates the process for estimating the AARL and SDARL in this study. For each set of Phase I data, this study conducted 10,000 experiments ($j$ = 10,000) to estimate the ARL. We computed a specific set of control limits for each Phase I dataset. This means that throughout the 10,000 simulation runs conducted to obtain an ARL value, the same control limits were applied in each experiment. As the data collected from Phase I may vary, it reflects the variability among practitioners. This study generated 10,000 sets of Phase I data ($i$ = 10,000) to obtain the AARL and SDARL values.

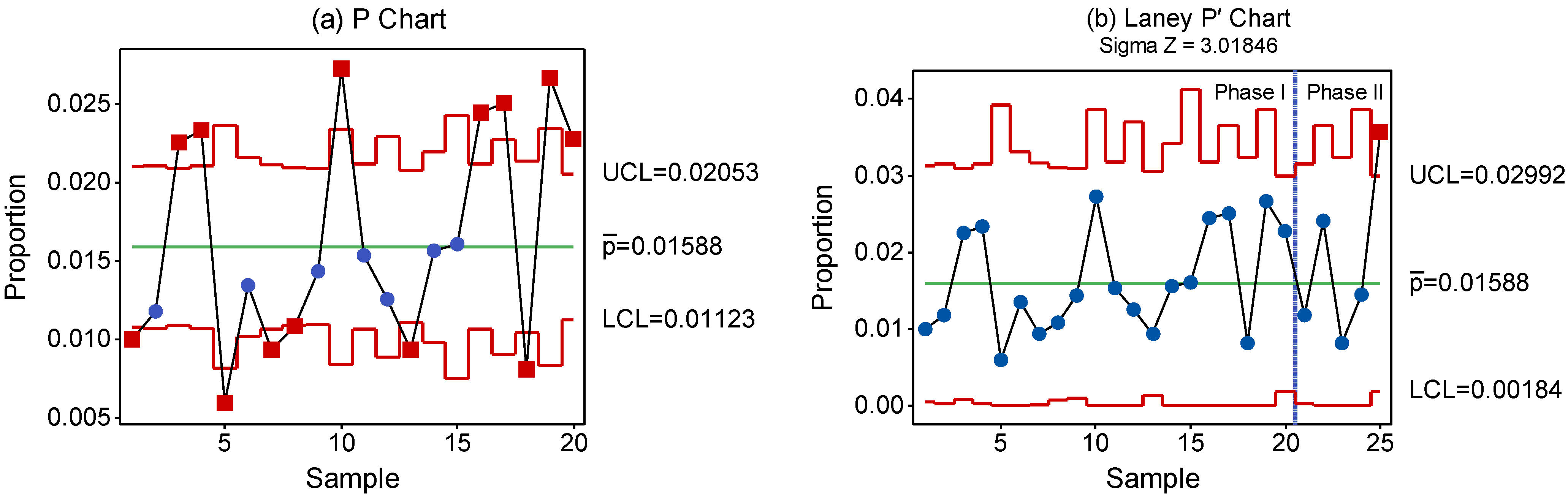
4. Results and Discussion

The aim of this study is to assess the performance of the Laney $p^{\prime }$ control chart through various experiments. In this section, we present the results obtained from the simulation experiments. We investigate the effect of between-sample variation on the ARL performance.

Firstly, we consider the performance of the traditional $p$ control chart and the Laney $p^{\prime }$ control chart under different sample sizes ($n$) when the nonconforming rate varies between samples. In this experiment, we assume $p~\mathrm{U}\left(0.045, 0.055\right)$, which means the average is 0.05. When the sample sizes are 100, 150, 225, 300, and 350, the theoretical ${\mathrm{ARL}}_0$ values of the $p$ chart are 233.96, 277.54, 422.76, 365.86, and 279.28, respectively.

The results of the $p$ chart are presented in

Table 1. The effect of dispersion in $p$ on the in-control AARL of the $p$ chart.

	$\left(\mathbf{a}\right) \mathit{n} =100$ $\mathit{p}~\mathbf{U}\left(0.045, 0.055\right)$		$\left(\mathbf{b}\right) \mathit{n} =150$ $\mathit{p}~\mathbf{U}\left(0.045, 0.055\right)$		$\left(\mathbf{c}\right) \mathit{n} =225$ $\mathit{p}~\mathbf{U}\left(0.045, 0.055\right)$		$\left(\mathbf{d}\right) \mathit{n} =300$ $\mathit{p}~\mathbf{U}\left(0.045, 0.055\right)$		$\left(\mathbf{e}\right) \mathit{n} =350$ $\mathit{p}~\mathbf{U}\left(0.045, 0.055\right)$
$\mathit{m}$	AARL	SDARL	AARL	SDARL	AARL	SDARL	AARL	SDARL	AARL	SDARL
20	327.32	345.69	317.31	225.48	292.50	177.66	273.62	137.39	256.47	121.50
50	273.16	183.91	285.29	163.35	282.15	140.03	266.41	98.79	258.93	97.56
100	237.15	73.63	270.68	124.10	275.80	108.30	261.07	73.98	257.04	81.71
1000	215.75	2.17	246.06	2.47	289.11	83.16	284.55	20.20	225.40	38.15
2000	215.75	2.17	246.06	2.46	299.89	78.63	287.22	7.66	217.59	19.91
3000	215.75	2.17	246.06	2.46	304.11	76.64	287.59	3.64	215.46	4.76
4000	215.75	2.17	246.06	2.46	312.22	71.12	287.61	2.87	215.24	3.77
5000	215.75	2.17	246.06	2.46	315.80	68.64	287.41	2.88	215.00	2.16
6000	215.75	2.17	246.05	2.46	319.47	65.36	287.41	2.88	215.00	2.16
8000	215.75	2.17	246.03	2.45	324.38	60.31	287.41	2.88	215.00	2.16
10,000	215.75	2.17	246.03	2.45	328.23	56.46	287.41	2.87	214.98	2.16

, while

Table 2. The effect of dispersion in $p$ on the in-control AARL of the $p\prime$ chart.

	$\left(\mathbf{a}\right) \mathit{n} =100$ $\mathit{p}~\mathbf{U}\left(0.045, 0.055\right)$		$\left(\mathbf{b}\right) \mathit{n} =150$ $\mathit{p}~\mathbf{U}\left(0.045, 0.055\right)$		$\left(\mathbf{c}\right) \mathit{n} =225$ $\mathit{p}~\mathbf{U}\left(0.045, 0.055\right)$		$\left(\mathbf{d}\right) \mathit{n} =300$ $\mathit{p}~\mathbf{U}\left(0.045, 0.055\right)$		$\left(\mathbf{e}\right) \mathit{n} =350$ $\mathit{p}~\mathbf{U}\left(0.045, 0.055\right)$
$\mathit{m}$	AARL	SDARL	AARL	SDARL	AARL	SDARL	AARL	SDARL	AARL	SDARL
20	557.71	773.40	615.71	817.45	637.49	848.38	633.91	843.58	648.33	856.97
50	378.23	476.36	447.62	547.64	513.17	607.95	521.04	623.57	534.77	641.76
100	298.40	280.70	367.56	363.29	386.91	369.49	420.47	414.75	429.11	422.95
1000	222.77	57.94	262.76	81.59	306.10	93.02	313.45	100.04	327.46	104.59
2000	216.50	16.25	249.34	34.35	314.32	69.83	297.98	58.23	330.56	93.62
3000	215.89	4.83	246.33	12.92	323.63	62.56	293.33	40.41	331.92	93.53
4000	215.91	4.80	246.22	6.43	327.54	57.79	290.84	30.57	334.51	92.04
5000	215.90	4.80	246.06	2.47	334.13	49.20	289.46	22.29	335.87	92.32
6000	215.90	2.17	246.05	2.57	337.44	43.66	288.11	13.28	339.61	91.78
8000	215.89	2.17	246.03	2.52	341.44	35.82	287.65	8.17	346.51	89.92
10,000	215.89	2.17	246.03	2.50	343.85	29.35	287.41	2.87	346.83	90.15

displays the results of the Laney $p^{\prime }$ chart. In general, as the number of Phase I samples increases, the SDARL becomes smaller. The results show that the use of a small number of Phase I samples to estimate the unknown parameters leads to a huge variability in the ARL values, resulting in a very poor chart performance. In this specific case, the variation in the nonconforming rate 𝑝 is not considered significant. It can be observed that the in-control AARL of the 𝑝 control chart and Laney $p^{\prime }$ control chart does not differ significantly when the number of samples 𝑚 is equal to or greater than 1000. However, when the number of samples 𝑚 is small, both the AARL and SDARL of the Laney $p^{\prime }$ control chart will be higher compared to those of the traditional 𝑝 control chart.

When the sample size 𝑛 is large, even if there is not much variation in the nonconforming rate 𝑝, the Laney $p^{\prime }$ control chart will still exhibit higher AARL and SDARL values compared to the traditional 𝑝 control chart. This is evident by comparing column (e) of Table 1 to column (e) of Table 2.

The results from Table 2 also highlight that when the sample size ($n$) is small ($n\le 300$), the AARL of the Laney $p^{\prime }$ control chart does not reach the ${\mathrm{ARL}}_0$ value of the traditional control chart. This observation further illustrates that the Laney $p^{\prime }$ control chart may not adequately widen the control limits when the sample size is relatively small. However, when the sample size ($n$) is increased to 350, the AARL of the Laney $p^{\prime }$ control chart exceeds the theoretical ${\mathrm{ARL}}_0$ value when the number of samples $\left(m\right)$ is 10,000. This indicates that the control limits are excessively widened in this scenario.

Finally, there are some unusual phenomena observed in column (c) of Table 1 and Table 2 that need to be explained. By observing Table 1 and Table 2, it can be seen that under the combination of $n$ and $p$ in column (c) of Table 1, the SDARL is noticeably larger than other combinations. Furthermore, column (c) of Table 2 shows that the SDARL for the Laney $p^{\prime }$ control chart is smaller than the traditional $p$ control chart. After conducting an in-depth investigation, we found that in column (c), under the combination of $n$ and $p$, there may or may not be a lower control limit. This causes an increase in the variability in in-control ARL, resulting in an increase in SDARL. For columns (a) and (b) of Table 1, there are no lower control limits under the combination of $n$ and $p$. Furthermore, for columns (d) and (e) of Table 1, both combinations of $n$ and $p$ have lower control limits. These phenomena result in smaller variations in ARL for columns (a), (b), (d), and (e), indicating smaller values of SDARL.

Next, we consider the impact on the performance of traditional $p$ control charts and Laney $p^{\prime }$ control charts when the sample size $n$ is fixed, and the nonconforming rate varies within different ranges. We consider the case where the true fraction nonconforming $p=0.05$ and sample size $n=300$. In this case, the ${\mathrm{ARL}}_0=365.86$.

Table 3. The effect of dispersion in $p$ on the in-control AARL of the $p$ chart with $n =300$.

	$\left(\mathbf{a}\right) \mathit{n} =300$ $\mathit{p} =0.05$		$\left(\mathbf{b}\right) \mathit{n} =300$ $\mathit{p}~\mathbf{U}\left(0.04, 0.06\right)$		$\left(\mathbf{c}\right) \mathit{n} =300$ $\mathit{p}~\mathbf{U}\left(0.025, 0.075\right)$
$\mathit{m}$	AARL	SDARL	AARL	SDARL	AARL	SDARL
20	344.24	183.03	156.41	74.24	25.58	8.01
50	335.73	128.22	153.87	52.36	26.41	5.98
100	334.79	99.70	153.23	40.21	26.69	4.64
1000	362.66	24.61	164.61	13.35	28.59	2.37
2000	365.15	13.49	166.65	6.52	29.12	1.48
3000	365.85	3.63	166.96	2.84	29.26	1.07
4000	365.86	3.63	167.05	2.30	29.31	0.88
5000	365.85	3.63	167.06	2.29	29.34	0.67
6000	365.85	3.63	167.06	1.68	29.35	0.68
8000	365.85	3.63	167.06	1.68	29.35	0.67
10,000	365.85	3.63	167.06	1.68	29.35	0.67

presents the in-control AARLs and SDARLs of the $p$ control chart when the process parameters are estimated. On the other hand,

Table 4. The effect of dispersion in $p$ on the in-control AARL of the $p\prime$ chart with $n =300$.

	$\left(\mathbf{a}\right) \mathit{n} =300$ $\mathit{p} =0.05$		$\left(\mathbf{b}\right) \mathit{n} =300$ $\mathit{p}~\mathbf{U}\left(0.04, 0.06\right)$		$\left(\mathbf{c}\right) \mathit{n} =300$ $\mathit{p}~\mathbf{U}\left(0.025, 0.075\right)$
$\mathit{m}$	AARL	SDARL	AARL	SDARL	AARL	SDARL
20	437.20	457.00	453.62	430.54	887.39	811.39
50	453.10	410.19	451.46	383.06	877.27	749.50
100	426.80	334.35	382.48	286.55	769.08	605.44
1000	330.55	97.61	310.78	93.00	530.47	154.53
2000	340.78	67.87	309.34	48.73	521.18	107.97
3000	349.09	52.39	310.31	33.40	521.80	88.73
4000	353.97	42.88	312.79	21.22	527.69	70.79
5000	358.30	34.91	312.91	17.90	531.23	62.25
6000	360.37	30.12	313.85	12.83	534.80	56.26
8000	362.85	22.74	314.17	9.28	541.07	46.54
10,000	364.31	17.57	314.51	6.47	546.08	37.61

shows the in-control AARLs and SDARLs for the Laney $p^{\prime }$ chart.

From panel (a) of Table 3, when the number of samples, $m$, exceeds 3000, the AARL of the $p$ control chart approaches the theoretical ${\mathrm{ARL}}_0$ value of 365.86. This demonstrates the high accuracy of the simulation program developed in this study.

Although the Laney $p^{\prime }$ control chart is suitable for situations where the nonconforming rate of the process is excessively dispersed, one may be interested in investigating its performance when there is no variation in sample size $n$ and process $p$. If $m$ is small, one can see from panel (a) of Table 4 that the $p^{\prime }$ chart may tend to overadjust the control limits, leading to the AARLs higher than the ${\mathrm{ARL}}_0$ when the fraction nonconforming remains constant. When $m$ is greater than 2000, the AARL is close to the true ARL value. This can be explained by the fact that the estimate of ${\sigma }_Z$ is more accurate when $m$ increases. When there is neither overdispersion nor underdispersion in the nonconforming rate, and if the number of Phase I samples ($m$) is large, the AARL of the $p^{\prime }$ control chart (panel (a) of Table 4) is close to that of the $p$ control chart (panel (a) of Table 3). However, the $p^{\prime }$ control chart exhibits a higher SDARL. This is because the $p^{\prime }$ control chart requires an additional estimation of ${\sigma }_Z$, leading to greater variability in its performance.

When the control chart parameters are estimated from Phase I samples, it is important to investigate the influence of the number of samples, $m$, on the size of the SDARL. When using control charts, it is generally recommended to have at least 20 or 25 Phase I samples to estimate the unknown parameters [1]. However, in this particular case, even with a significantly larger number of samples exceeding 20, the desired performance is not achieved. For instance, when using 50 samples, the AARL of the $p$ chart is 335.73, which corresponds to approximately 91% of the desired ${\mathrm{ARL}}_0$. Additionally, the SDARL is 128.22, approximately 35% of the ${\mathrm{ARL}}_0$. To attain satisfactory performance, it is necessary to utilize 1000 samples, as this yields an AARL of 362.66 (around 99% of the desired ${\mathrm{ARL}}_0$) and an SDARL of 24.61 (approximately 7% of the desired ${\mathrm{ARL}}_0$). In the case of the Laney $p^{\prime }$ control chart, utilizing 5000 samples is recommended, as it produces an AARL of 358.30 (about 98% of the desired ${\mathrm{ARL}}_0$) and an SDARL of 34.91 (approximately 9.5% of the desired ${\mathrm{ARL}}_0$). It is evident that when using the Laney $p^{\prime }$ control chart, we require a larger number of samples to meet the recommended requirements of Zhang et al. [32].

Next, we investigate the impact of overdispersion in the process fraction nonconforming on the $p$ control chart. Overdispersion refers to the variation in data that exceeds the assumed probability distribution. In this experiment, we assume that the average of the fraction nonconforming is fixed, but the variability in the fraction nonconforming is uniformly distributed.

From the results in Table 3, it can be observed that when the sample size $n$ is fixed, the AARL of the $p$ control chart decreases as the variation in the nonconforming rate increases. From Table 4, it can be seen that the AARL of the $p^{\prime }$ control chart increases as the variability in nonconforming rate increases. The AARL value has exceeded the case when the nonconforming rate follows a binomial distribution (i.e., no overdispersion or underdispersion), indicating that the control limits are excessively widened.

The above results also show that when there is overdispersion in 𝑝, even if the sample size 𝑛 is not very large, it will result in a much lower in-control ARL than the in-control ARL value of the traditional 𝑝 control chart. In other words, using a traditional 𝑝 control chart in this scenario would lead to an elevation in Type I error.

We will now examine situations where the sample sizes differ from those in the previous experiment, while ensuring that the product of sample size and nonconforming rate remains constant.

Table 5. The effect of dispersion in $p$ on the in-control AARL of the $p$ chart with $n =3000$.

	$\left(\mathbf{a}\right) \mathit{n} =3000$ $\mathit{p} =0.005$		$\left(\mathbf{b}\right) \mathit{n} =3000$ $\mathit{p}~\mathbf{U}\left(0.004, 0.006\right)$		$\left(\mathbf{c}\right) \mathit{n} =3000$ $\mathit{p}~\mathbf{U}\left(0.0025, 0.0075\right)$
$\mathit{m}$	AARL	SDARL	AARL	SDARL	AARL	SDARL
20	344.11	182.17	159.46	77.60	27.19	8.93
50	332.13	140.89	157.20	59.37	28.20	7.14
100	326.68	119.57	154.37	49.13	28.46	6.10
1000	292.17	19.08	141.94	11.22	27.69	2.37
2000	290.89	2.89	140.82	1.96	27.38	0.99
3000	290.72	2.89	140.71	1.95	27.28	0.60
4000	290.88	2.91	140.72	1.95	27.25	0.28
5000	290.72	2.91	140.69	1.41	27.25	0.28
6000	290.72	2.91	140.69	1.41	27.25	0.27
8000	290.72	2.89	140.69	1.41	27.25	0.27
10,000	290.72	2.89	140.69	1.41	27.25	0.27

and

Table 6. The effect of dispersion in $p$ on the in-control AARL of the $p\prime$ chart with $n =3000$.

	$\left(\mathbf{a}\right) \mathit{n} =3000$ $\mathit{p} =0.005$		$\left(\mathbf{b}\right) \mathit{n} =3000$ $\mathit{p}~\mathbf{U}\left(0.004, 0.006\right)$		$\left(\mathbf{c}\right) \mathit{n} =3000$ $\mathit{p}~\mathbf{U}\left(0.0025, 0.0075\right)$
$\mathit{m}$	AARL	SDARL	AARL	SDARL	AARL	SDARL
20	434.30	462.21	423.47	416.02	515.65	422.09
50	427.05	403.96	423.08	369.48	583.49	394.31
100	391.80	322.65	372.33	274.48	548.70	344.05
1000	310.44	94.60	294.00	83.64	458.03	128.31
2000	301.02	58.22	279.74	62.55	443.30	89.45
3000	293.33	32.16	271.70	50.38	441.06	72.52
4000	292.97	25.08	267.09	41.90	439.20	54.13
5000	291.58	14.71	263.17	33.06	437.79	43.28
6000	291.11	11.27	260.31	27.67	439.11	35.13
8000	290.79	5.32	258.16	17.17	437.54	21.14
10,000	290.77	4.44	257.58	13.55	436.50	16.86

display the AARLs and SDARLs of the $p$ chart and Laney $p^{\prime }$ chart with a sample size of 3000 and an average fraction nonconforming of 0.005, respectively. In this scenario, the ARL₀ of the $p$ chart is 290.73.

Furthermore,

Table 7. The effect of dispersion in $p$ on the in-control AARL of the $p$ chart with $n =30,000$.

	$\left(\mathbf{a}\right) \mathit{n} =30,000$ $\mathit{p} =0.0005$		$\left(\mathbf{b}\right) \mathit{n} =30,000$ $\mathit{p}~\mathbf{U}\left(0.0004, 0.0006\right)$		$\left(\mathbf{c}\right) \mathit{n} =30,000$ $\mathit{p}~\mathbf{U}\left(0.00025, 0.00075\right)$
$\mathit{m}$	AARL	SDARL	AARL	SDARL	AARL	SDARL
20	341.54	177.11	157.71	77.93	27.61	8.93
50	332.47	141.49	157.10	58.96	28.38	7.19
100	288.50	120.07	154.70	48.73	28.52	6.09
1000	288.06	24.65	140.32	13.35	27.63	2.46
2000	284.85	6.15	138.65	2.23	27.22	1.40
3000	284.63	2.86	138.47	1.39	27.11	0.90
4000	284.62	2.85	138.47	1.38	27.07	0.67
5000	284.63	2.83	138.48	1.39	27.05	0.60
6000	284.63	2.85	138.48	1.38	27.07	0.60
8000	284.59	2.86	138.46	1.40	27.06	0.60
10,000	284.64	2.82	138.48	1.38	27.07	0.59

and

Table 8. The effect of dispersion in $p$ on the in-control AARL of the $p\prime$ chart with $n =30,000$.

	$\left(\mathbf{a}\right) \mathit{n} =30,000$ $\mathit{p} =0.0005$		$\left(\mathbf{b}\right) \mathit{n} =30,000$ $\mathit{p}~\mathbf{U}\left(0.0004, 0.0006\right)$		$\left(\mathbf{c}\right) \mathit{n} =30,000$ $\mathit{p}~\mathbf{U}\left(0.00025, 0.00075\right)$
$\mathit{m}$	AARL	SDARL	AARL	SDARL	AARL	SDARL
20	443.59	472.94	433.71	448.74	523.35	494.67
50	432.40	403.23	407.10	394.53	566.80	458.88
100	398.18	324.28	361.43	301.76	548.09	397.36
1000	313.80	95.58	290.38	88.48	450.77	149.62
2000	297.08	61.10	276.36	68.14	438.84	106.54
3000	290.84	36.12	268.48	55.53	434.34	79.31
4000	288.15	25.19	263.76	48.42	431.65	65.04
5000	285.83	16.01	258.45	36.11	429.31	49.07
6000	285.46	11.96	257.07	32.07	427.98	37.20
8000	284.63	6.60	254.27	23.19	428.17	23.08
10,000	284.54	4.35	253.41	18.89	427.72	18.38

present the AARLs and SDARLs of the $p$ chart and Laney $p^{\prime }$ chart, respectively, with a larger sample size of $n =30,000$ and an average fraction nonconforming of $p =0.0005$. In this case, the ARL₀ of the $p$ chart is 284.51.

Upon comparing Table 3, Table 4, Table 5, Table 6, Table 7 and Table 8, we observe that the conclusions drawn from Table 3 and Table 4 are also applicable to Table 5 and Table 6, as well as Table 7 and Table 8. That is, when the sample size remains constant and the variability in the process nonconforming rate increases, the in-control AARLs of the traditional $p$ control charts decrease. The $p^{\prime }$ chart can address the between-sample variation. The in-control AARLs are close to the advertised values. In some cases, the AARLs may exceed the advertised value.

Next, we consider the scenario where both the sample size, $n$, and the nonconforming rate, $p$, are allowed to vary between samples.

Table 9. The effect of dispersion in $n$ and $p$ on the in-control AARL of the $p$ chart.

	$\left(\mathbf{a}\right) \mathit{n}~\mathbf{U}\left(2400, 3600\right)$ $\mathit{p} =0.005$		$\left(\mathbf{b}\right) \mathit{n}~\mathbf{U}\left(2400, 3600\right)$ $\mathit{p}~\mathbf{U}\left(0.004, 0.006\right)$		$\left(\mathbf{c}\right) \mathit{n}~\mathbf{U}\left(2400, 3600\right)$ $\mathit{p}~\mathbf{U}\left(0.0025, 0.0075\right)$
$\mathit{m}$	AARL	SDARL	AARL	SDARL	AARL	SDARL
20	330.38	167.73	154.36	72.09	26.40	8.17
50	323.90	123.73	151.30	51.96	27.56	6.44
100	312.67	88.46	151.45	40.00	27.68	4.77
1000	303.19	27.92	146.13	12.33	27.88	1.74
2000	302.58	21.15	146.12	9.74	27.88	1.42
3000	302.55	16.79	146.01	7.04	27.86	1.10
4000	302.51	16.64	146.01	6.44	27.88	1.10
5000	302.49	14.32	145.92	5.58	27.89	0.93
6000	302.34	11.55	145.80	5.08	27.92	0.87
8000	302.30	10.53	145.76	4.64	27.92	0.82
10,000	302.27	9.72	145.73	4.43	27.90	0.80

shows the results of the traditional $p$ control chart, while

Table 10. The effect of dispersion in $n$ and $p$ on the in-control AARL of the $p\prime$ chart.

	$\left(\mathbf{a}\right) \mathit{n}~\mathbf{U}\left(2400, 3600\right)$ $\mathit{p} =0.005$		$\left(\mathbf{b}\right) \mathit{n}~\mathbf{U}\left(2400, 3600\right)$ $\mathit{p}~\mathbf{U}\left(0.004, 0.006\right)$		$\left(\mathbf{c}\right) \mathit{n}~\mathbf{U}\left(2400, 3600\right)$ $\mathit{p}~\mathbf{U}\left(0.0025, 0.0075\right)$
$\mathit{m}$	AARL	SDARL	AARL	SDARL	AARL	SDARL
20	471.28	478.12	429.25	455.93	503.63	488.42
50	429.90	400.32	408.95	393.01	568.92	453.98
100	395.38	315.21	373.32	293.14	551.73	402.27
1000	309.67	78.91	291.21	72.93	446.84	127.65
2000	304.46	52.31	285.86	49.15	440.38	89.36
3000	304.04	43.16	284.72	39.19	435.17	71.80
4000	303.23	37.83	283.12	34.93	430.66	61.52
5000	302.45	34.38	282.52	29.67	430.46	57.64
6000	301.03	30.64	282.43	28.04	429.92	51.35
8000	301.02	26.24	281.85	22.92	429.43	44.11
10,000	300.10	24.17	280.99	21.08	430.92	41.88

presents the results of the Laney $p^{\prime }$ control chart. By comparing Table 5 with Table 9 and Table 6 with Table 10, we can observe that the variation in sample size ($n$) does not have a significant impact on the AARL performance of both the traditional $p$ control chart and the Laney $p^{\prime }$ control chart. However, it is worth noting that when both $n$ and $p$ vary, it can lead to an increased variability in parameter estimation, as evidenced by the increase in SDARL.

Next, we set a fixed number of samples for the Phase I dataset and examine the influence of sample size on the in-control AARL and SDARL for the $p$ control chart. In this experiment, we consider a wider range of variations in the sample size. Based on previous experiments, it has been found that when the number of samples is 1000 or more, the AARL and SDARL of the $p$ control chart yield better results. Therefore, we fix the number of samples at 1000 and investigate the impact of sample size on AARL and SDARL when there are variations in the nonconforming rate between samples.

Table 11. The effect of sample size $n$ on the in-control AARL of the $p$ chart.

	$\mathit{p}~\mathbf{U}\left(0.25, 0.75\right)$		$\mathit{p}~\mathbf{U}\left(0.05, 0.15\right)$		$\mathit{p}~\mathbf{U}\left(0.03, 0.09\right)$		$\mathit{p}~\mathbf{U}\left(0.025, 0.075\right)$		$\mathit{p}~\mathbf{U}\left(0.015, 0.045\right)$
$\mathit{n}$	AARL	SDARL	AARL	SDARL	AARL	SDARL	AARL	SDARL	AARL	SDARL
50	4.82	0.24	83.76	2.04	109.63	42.97	127.84	27.85	143.21	31.89
100	2.46	0.02	41.89	6.77	77.85	16.97	70.47	1.16	113.07	26.67
300	1.53	0.01	8.06	0.42	21.37	1.55	28.59	2.37	45.69	10.74
1000	1.23	0.01	2.31	0.03	3.68	0.09	4.60	0.15	9.89	0.70
1500	1.18	0.01	1.87	0.02	2.56	0.04	3.00	0.06	5.40	0.21
3000	1.12	0.00	1.49	0.01	1.76	0.01	1.91	0.02	2.62	0.04
15,000	1.05	0.00	1.17	0.00	1.24	0.01	1.27	0.01	1.39	0.01
30,000	1.03	0.00	1.12	0.00	1.15	0.00	1.18	0.00	1.25	0.01

summarizes the results of the experiment.

From the table, we can observe that the in-control AARL of the traditional $p$ control chart is very small, far below the theoretical values of the 3-sigma $p$ control chart. This is due to the impact of overdispersion. As the sample size increases, the influence of overdispersion on the in-control AARL becomes more significant. In other words, when there is a high degree of variation in the fraction nonconforming between samples, the reduction in AARL for the $p$ control chart becomes more substantial as $n$ increases.

Finally, we compare the out-of-control AARL and SDARL of the $p$ chart and Laney $p^{\prime }$ chart. The magnitude of shift considered is represented by a multiple $k$ of ${\sigma }_p$. If the in-control nonconforming rate varies between U($a, b$), the range of variation for the out-of-control mean is U($a, b$) + $k{\sigma }_p$. After estimating the control limits using a set of Phase I data, the estimation of the out-of-control ARL is performed. The AARL and SDARL performance of the traditional $p$ chart and the Laney $p^{\prime }$ chart are summarized in

Table 12. AARL and SDARL performance of the $p$ chart with m $=$ $1000$.

	(a) $\mathit{p} =0.005$		(b) $\mathit{p}~\mathbf{U}\left(0.004, 0.006\right)$		(c) $\mathit{p}~\mathbf{U}\left(0.0025, 0.0075\right)$		(d) $\mathit{p}~\mathbf{U}\left(0.0005, 0.0015\right)$
Shift	AARL	SDARL	AARL	SDARL	AARL	SDARL	AARL	SDARL
0.0	292.17	19.08	141.94	11.22	27.69	2.37	107.29	13.82
1.0	22.35	1.72	17.40	0.88	8.71	0.61	14.98	1.44
1.5	9.30	0.58	8.15	0.36	5.40	0.31	7.70	0.66
2.0	4.78	0.24	4.51	0.17	3.67	0.18	4.60	0.34
2.5	2.90	0.10	2.86	0.08	2.67	0.10	3.09	0.19
3.0	2.02	0.06	2.04	0.04	2.07	0.07	2.28	0.11

and

Table 13. AARL and SDARL performance of the $p^{\prime }$ chart with m $=$ $3000$.

	(a) $\mathit{p} =0.005$		(b) $\mathit{p}~\mathbf{U}\left(0.004, 0.006\right)$		(c) $\mathit{p}~\mathbf{U}\left(0.0025, 0.0075\right)$		(d) $\mathit{p}~\mathbf{U}\left(0.0005, 0.0015\right)$
Shift	AARL	SDARL	AARL	SDARL	AARL	SDARL	AARL	SDARL
0.0	293.33	32.16	271.70	50.38	441.06	72.52	110.70	9.54
1.0	22.52	1.77	26.54	3.42	56.25	7.48	15.32	0.81
1.5	9.34	0.61	11.55	1.25	25.98	3.02	7.85	0.28
2.0	4.80	0.25	5.97	0.52	13.71	1.34	4.68	0.16
2.5	2.91	0.11	3.58	0.24	8.06	0.67	3.14	0.09
3.0	2.03	0.06	2.42	0.12	5.19	0.36	2.31	0.06

, respectively. In this comparison, the number of Phase I samples ($m$) for the traditional $p$ chart and the Laney $p^{\prime }$ chart is 1000 and 3000, respectively, with a fixed sample size of 3000. The selection of $m$ values for the $p$ chart and the Laney $p^{\prime }$ chart is based on the following rationale. According to Table 5, it is evident that when the value of 𝑚 is 1000 or higher, the SDARL for the 𝑝 control chart stays within 10% of the expected in-control ARL. Similarly, Table 6 shows that the Laney $p^{\prime }$ control chart exhibits a similar behavior when the 𝑚 value is 3000 or above. Table 12 and Table 13 also include the in-control AARL and SDARL values for ease of comparison.

From Table 12 and Table 13, it is observed that both the $p$ chart and Laney $p^{\prime }$ chart exhibit a decrease in AARL as the magnitude of shift increases. When the nonconforming rate is kept fixed among samples, from column (a) of Table 12 and Table 13, we can see that the AARLs of the traditional $p$ control chart and the Laney p′ control chart are very close, but the SDARLs of the Laney $p^{\prime }$ chart are still greater than those of the $p$ chart. As explained earlier, this is because the Laney p′ control chart requires an additional estimation of ${\sigma }_Z$, resulting in an increased variability in ARL. By comparing columns (b) and (c) of Table 12 and Table 13, we can observe significant differences in the in-control and out-of-control performance between the traditional $p$ control chart and the Laney p′ control chart. This is due to variations in the nonconforming rates among different samples, indicating excessive process dispersion. The datasets generated based on the scenarios described in columns (b) and (c) of Table 12 have been checked using Minitab statistical software (Version 19, Minitab LLC, State College, PA, USA) and the diagnostic method described in [17]. This confirms the presence of overdispersion. Additionally, comparing column (d) of Table 12 and Table 13, we can notice that the in-control and out-of-control performance of the two control charts are very similar. The diagnostic method described in [17] confirms that overdispersion does not exist.

Based on the above comparison, this study summarizes the advantages and disadvantages of the 𝑝 control chart and the Laney p′ control chart as follows. While the calculation of the 𝑝 control chart is relatively simple, it tends to have a higher Type I error when the nonconforming rate varies between samples. On the other hand, the Laney p′ control chart has the disadvantage of requiring an estimation of the variation in the nonconforming rate between samples. This typically requires a larger number of samples to achieve an accurate parameter estimation. When the number of samples 𝑚 is small, the SDARL for the Laney p′ control chart is higher compared to the traditional 𝑝 control chart. If there is minimal variation in the nonconforming rate between samples, the control limits of the Laney p′ control chart closely resemble those of the traditional 𝑝 control chart. However, due to the need for estimating between-sample variation, the variability in its performance also increases. Additionally, the Laney p′ control chart addresses the issue of overdispersion by widening the control limits. This study found that the Laney p′ control chart can indeed reduce Type I errors caused by overdispersion. However, in some cases, this approach may result in excessively wide control limits, thereby reducing its ability to detect changes in the nonconforming rate.

5. Applications of the Laney $p^{\prime }$ Chart in Manufacturing Processes

In previous studies [2,3,4,5], researchers have pointed out that the healthcare industry often experiences the phenomenon of overdispersion due to its extremely large sample sizes. However, overdispersion also frequently occurs in the general manufacturing industry, which offers numerous opportunities for the application of Laney $p^{\prime }$ control charts. This section will utilize real cases and data collected from the industry to explain the reasons for having such large sample sizes and demonstrate how to apply Laney $p^{\prime }$ control charts to address the issue of overdispersion and obtain reasonable results. The examples are from the PCB and IC subtractive manufacturing processes. In the process of circuit board and chip substrate manufacturing, a panel can be divided into multiple strips, with each strip containing numerous units. Inspection can be conducted either at the strip level or the unit level in these processes. The size of each sample represents the total number of strips (or units) inspected within a week (or a batch). When calculating the nonconforming rate, a large sample size will be involved.

5.1. Example 1

During the ball placement process of a ball grid array (BGA), the operator first uses an automated optical inspection (AVI) machine to scan the bump area of the BGA. The AVI machine compares the scanned data against an image file or predefined criteria to determine if the bumps meet the required specifications. Any captured images showing abnormal bumps are further examined by operators using the verify and recheck system (VRS) machine. The VRS operator views the magnified images displayed on the VRS screen (at a 32× magnification).

If the bump size of the solder balls within the location marked by the AVI is higher or lower than the adjacent solder balls, they are classified as either large-sized balls or small-sized balls. Considering the nature and severity of the product, if the VRS machine confirms the presence of any large or small balls, regardless of their quantity, the unit is considered nonconforming.

The quality engineer responsible for process improvement decided to set up a control chart in order to improve the fraction of nonconforming units produced by this process. In this application, the 100% inspection approach is adopted. The nonconforming rate is calculated by dividing the number of nonconforming units found per lot by the total number of units inspected in each lot. In this specific case, the sample sizes represent the total number of units inspected in each lot. However, it is important to note that this value is not constant. The number of units in each lots varies depending on the part number, typically ranging from 1800 to 7000 units. In the following presentations, the $p$ chart and Laney $p^{\prime }$ chart were produced using Minitab statistical software.

The quality control engineer gathered data from 20 lots to establish a $p$ control chart. The data are shown in

Table 14. Data for Example 1.

Sample Number	Phase	Sample Size (Number of Inspected Units)	Number of Nonconforming Units	Sample Fraction Nonconforming
1	I	5400	54	0.01000
2	I	5255	62	0.01180
3	I	5675	128	0.02256
4	I	5235	122	0.02330
5	I	2355	14	0.00594
6	I	4315	58	0.01344
7	I	5155	48	0.00931
8	I	5560	60	0.01079
9	I	5720	82	0.01434
10	I	2500	68	0.02720
11	I	5095	78	0.01531
12	I	2870	36	0.01254
13	I	6000	56	0.00933
14	I	3845	60	0.01560
15	I	1995	32	0.01604
16	I	5070	124	0.02446
17	I	2995	75	0.02504
18	I	4705	38	0.00808
19	I	2480	66	0.02661
20	I	6500	148	0.02277
21	II	5255	62	0.01180
22	II	2995	72	0.02404
23	II	4705	38	0.00808
24	II	2480	36	0.01452
25	II	6500	232	0.03569

. Figure 3a presents a traditional $p$ control chart for the 20 lots. The sample fraction nonconforming from each sample is plotted on this chart. The control limits of the 𝑝 control chart vary as a result of employing the 100% inspection method and the variability in daily production output. The data demonstrate a significant amount of overdispersion. The $p$ control chart indicates many points beyond the control limits. However, the analysis of these points does not reveal any reasonable assignable causes for them. The diagnostic method described in [17] confirmed the presence of overdispersion. As a result, the engineer decided to use the Laney $p^{\prime }$ control chart. Figure 3b displays the Laney $p^{\prime }$ control chart, which shows that all points are within the control limits. This suggests a stable process with no assignable causes present. Thus, the engineer has concluded Phase I of the control usage.

Next, the engineer collected Phase II data to monitor the production process. From Figure 3b, it is evident that Sample 25 plots outside the upper control limit, indicating a significant increase in the process nonconforming rate. Subsequently, a process diagnosis must be conducted to identify the assignable causes and initiate improvements. There are several reasons for the generation of large and small balls in this process. The investigation of Sample 25 revealed that the assignable cause is the variation in incoming material. During ball placement, when the substrate magnification matches the steel plate magnification, $\mu$-balls can smoothly fit into the solder mask openings. However, if there is a variation in the magnification of incoming materials (with some substrates being larger or smaller), it can lead to an improper alignment between the steel plate and the substrate. This misalignment causes some balls to fit properly while others do not. As a consequence, the balls cannot accurately land in the solder mask opening, leading to ball misalignment issues.

5.2. Example 2

A PCB lithography process consists of several steps, including preprocessing, lamination, exposure, etching, and finishing. In this process, the nonconforming rate caused by dirt particles is an important quality indicator. The process utilizes a negative-type dry film that polymerizes and hardens when exposed to ultraviolet (UV) light. After lamination is completed, if there are dirt particles adhering to the substrate, the image will be masked during exposure. The unexposed areas will not polymerize or harden, and during development, the dry film is removed (developed), exposing the underlying copper. During the etching stage, the copper layer will be etched away by the etching solution, resulting in nonconformities such as open circuits, nicks, and pinholes.

The quality control engineer collected daily data to create a $p$ control chart with the aim of improving the production process. In this application, the inspection method used is 100% inspection. The current quality control specification states that if any nonconformities are confirmed on a strip, that strip is considered nonconforming. The nonconforming rate is calculated by dividing the number of nonconforming strips found per day by the total number of strips inspected each day. The number of strips in each panel varies depending on the part number, typically ranging from 8 to 12 strips. The production capacity is approximately 28,000 to 35,000 panels per day. To establish a Phase I control chart, preliminary data were collected over a period of 25 days. The data are shown in

Table 15. Data for Example 2.

Sample Number	Phase	Sample Size (Number of Inspected Units)	Number of Nonconforming Units	Sample Fraction Nonconforming
1	I	210,000	1480	0.00705
2	I	268,500	1933	0.00720
3	I	272,500	1934	0.00710
4	I	274,700	2554	0.00930
5	I	364,500	2560	0.00702
6	I	279,000	1841	0.00660
7	I	280,000	2576	0.00920
8	I	276,250	2513	0.00910
9	I	269,750	2778	0.01030
10	I	374,350	2358	0.00630
11	I	264,950	2255	0.00851
12	I	276,800	1651	0.00596
13	I	228,700	1829	0.00800
14	I	277,550	2386	0.00860
15	I	220,000	1475	0.00670
16	I	272,500	1934	0.00710
17	I	274,500	2532	0.00922
18	I	364,500	2625	0.00720
19	I	268,600	2354	0.00876
20	I	364,500	2460	0.00675
21	I	279,000	1841	0.00660
22	I	280,000	2576	0.00920
23	I	268,500	1833	0.00683
24	I	269,750	2581	0.00957
25	I	328,250	2423	0.00738

, and the traditional $p$ control chart is plotted in Figure 4a. The 𝑝 control chart exhibits variable control limits due to the implementation of 100% inspection and the fluctuations in daily production output. In this specific case, the data demonstrate a significant amount of overdispersion due to the large sample size (200,000 to 400,000 strips per day).

An examination of the $p$ control chart reveals that there are many points outside the control limits. Out of the 25 points, 23 points exceed the control limits. This can lead to a misconception that the process is influenced by many assignable causes and is out of control. The occurrence of data points falling outside the control limits can imply the potential existence of assignable causes that warrant investigation and corrective action. However, after conducting a comprehensive analysis of the process, it was determined that the process remains in control, with no identifiable assignable causes present. This phenomenon has been pointed out by Mohammed and Laney [19], who noted that overdispersion caused by large sample sizes may lead to the identification of an inappropriately large number of data points indicating assignable cause variation.

The engineer confirmed the necessity of using the Laney p’ chart by utilizing the diagnostic method described in [17]. The Laney $p^{\prime }$ control chart is shown in Figure 4b, with control limits adjusted for overdispersion. This control chart reveals that all points fall within the control limits, indicating a stable process without any assignable causes. Based on this observation, the engineer adopted the Laney $p^{\prime }$ chart for Phase II usage.

6. Conclusions

In this study, we employed simulation to investigate the performance of the traditional $p$ and Laney $p^{\prime }$ control charts when the parameters are estimated. Both charts were evaluated and compared in terms of AARL and SDARL. Overdispersion was accounted for by allowing for between-sample variation in the nonconforming rate ($p)$. Additionally, variations between samples in both the sample size ($n$) and the nonconforming rate of the process were also considered.

This study found that the Laney $p^{\prime }$ control chart can indeed reduce Type I errors caused by overdispersion, but it may also result in excessively wide control limits and an increased risk of Type II errors. Our results show that the $p^{\prime }$ chart requires a much larger amount of Phase I data than previously recommended in the literature in order to sufficiently reduce the variation in the chart performance. These research findings can serve as a valuable reference for practitioners.

Future research can be conducted in several directions. Firstly, a broader range of combinations of $n$ and $p$ should be investigated to achieve a more comprehensive understanding. Furthermore, the methodology presented in this study can be extended to evaluate the effectiveness of the Laney $U\prime$ control chart. A more comprehensive assessment of its performance will facilitate its practical implementation and promotion in various industries.