A Bimodal Extension of the Log-Normal Distribution on the Real Line with an Application to DNA Microarray Data
Abstract
1. Introduction
- (i)
- The random sign transform (RST) given by
- (ii)
- The random sign mixture transform (RSMT) given by
2. Statistical Properties
2.1. Probability Density Function
2.2. Cumulative Distribution Function
2.3. Hazard Rate Function
2.4. Moments and Associated Measures
2.5. Harmonic Mean
2.6. Entropies
3. Maximum Likelihood Estimation
4. Simulations
- Generate
- Generate
- Generate
- Set
- The bias of the MLEs:
- The mean squared error (MSE) of the MLEs:
- The coverage probability (CP) of the 95% confidence interval of each parameter:
 ), (0.5, 0, 1, 1, 2) ( - - -), , .
), (0.5, 0, 1, 1, 2) ( - - -), , .
 ), (0.5, 0, 1, 1, 2) ( - - -), , .
), (0.5, 0, 1, 1, 2) ( - - -), , .
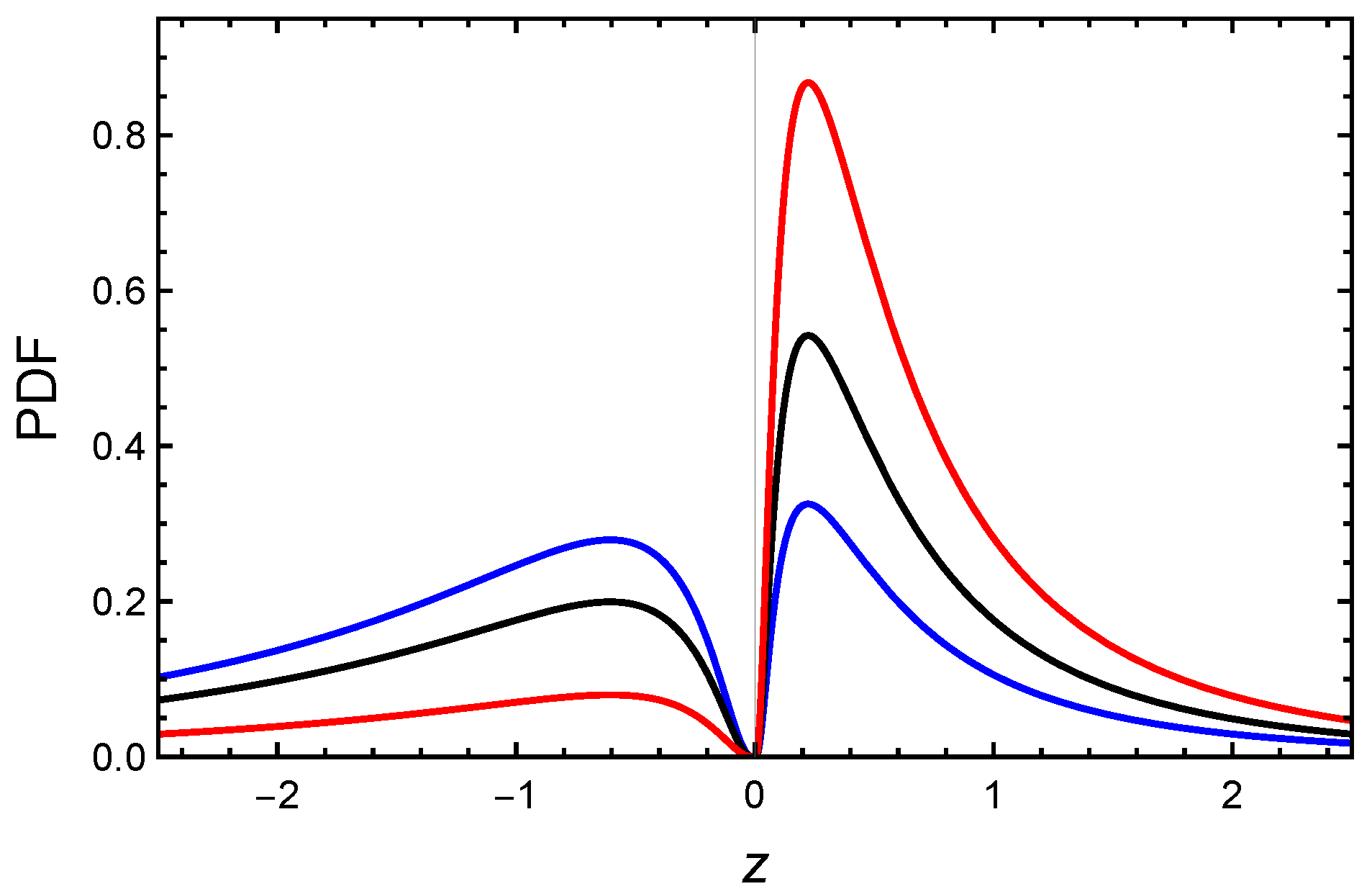
 ), (0.5, 0, 1, 1, 2) ( - - -), (), (0.547, −2.812, 1.016, −2.224, 0.764) ().
), (0.5, 0, 1, 1, 2) ( - - -), (), (0.547, −2.812, 1.016, −2.224, 0.764) ().
 ), (0.5, 0, 1, 1, 2) ( - - -), (), (0.547, −2.812, 1.016, −2.224, 0.764) ().
), (0.5, 0, 1, 1, 2) ( - - -), (), (0.547, −2.812, 1.016, −2.224, 0.764) ().
 ), (0.5, 0, 1, 1, 2) (- - -), (0.8, 2, 1, −1, 2) (), (0.547, −2.812, 1.016, −2.224, 0.764) ().
), (0.5, 0, 1, 1, 2) (- - -), (0.8, 2, 1, −1, 2) (), (0.547, −2.812, 1.016, −2.224, 0.764) ().
 ), (0.5, 0, 1, 1, 2) (- - -), (0.8, 2, 1, −1, 2) (), (0.547, −2.812, 1.016, −2.224, 0.764) ().
), (0.5, 0, 1, 1, 2) (- - -), (0.8, 2, 1, −1, 2) (), (0.547, −2.812, 1.016, −2.224, 0.764) ().
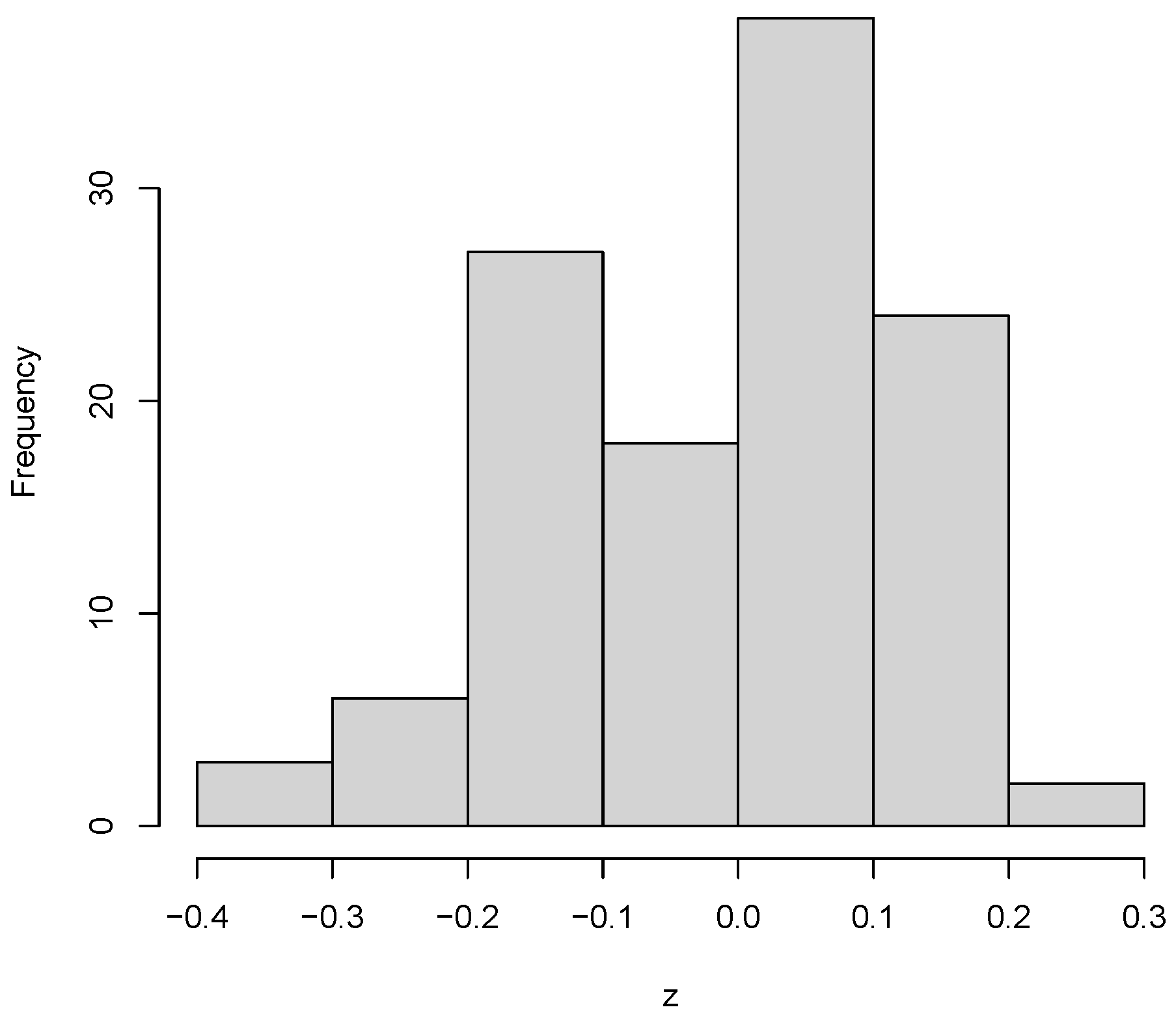
5. Application
6. Conclusions and Comments
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Crow, E.L.; Shimizu, K. Lognormal Distributions: Theory and Applications; Statistics Textbooks and Monographs; Routledge: London, UK, 2018. [Google Scholar]
- Aly, E. A unified approach for developing Laplace-type distributions. J. Indian Soc. Probab. Stat. 2018, 19, 245–269. [Google Scholar] [CrossRef]
- Laplace, P.S. Memoire sur la probabilite des causes par les evenements. Mem. L’Acad. R. Sci. Present. Divers. Savan 1774, 6, 621–656. [Google Scholar]
- Plucinska, A. On a general form of the probability density function and its application to the investigation of the distribution of rheostat resistence. Zastosow. Mat. 1966, 9, 9–19. [Google Scholar]
- Balakrishnan, N.; Kocherlakota, S. On the double Weibull distribution: Order statistics and estimation. Sankhya Indian J. Stat. Ser. B 1985, 47, 161–178. [Google Scholar]
- Kantam, R.R.L.; Narasimham, V.L. Linear estimation in reflected gamma distribution. Sankhya Indian J. Stat. Ser. B 1991, 53, 25–47. [Google Scholar]
- Nadarajah, S.; Afuecheta, E.; Chan, S. A double generalized Pareto distribution. Stat. Probab. Lett. 2013, 83, 2656–2663. [Google Scholar] [CrossRef]
- Bindu, P.; Sangita, K. Double Lomax distribution and its applications. Statistica 2015, 75, 331–342. [Google Scholar]
- Kumar, S.C.; Jose, R. On double Lindley distribution and some of its properties. Am. J. Math. Manag. Sci. 2019, 38, 23–43. [Google Scholar]
- John, S. The three-parameter two-piece normal family of distributions and its fitting. Commun. Stat. Theory Methods 1982, 11, 879–885. [Google Scholar] [CrossRef]
- Kimber, A. Methods for the two-piece normal distribution. Commun. Stat. Theory Methods 1985, 14, 235–245. [Google Scholar] [CrossRef]
- Lingappaiah, G. On two-piece double exponential distribution. J. Korean Stat. Soc. 1988, 17, 46–55. [Google Scholar]
- Abdulah, E.; Elsalloukh, H. Bimodal Class based on the Inverted Symmetrized Gamma Distribution with Applications. J. Stat. Appl. Probab. 2014, 3, 1–7. [Google Scholar] [CrossRef]
- Hoseinzadeh, A.; Maleki, M.; Khodadadi, Z.; Contreras-Reyes, J.E. The skew-reflected-Gompertz distribution for analyzing symmetric and asymmetric data. J. Comput. Appl. Math. 2019, 349, 132–141. [Google Scholar] [CrossRef]
- Halvarsson, D. Maximum likelihood estimation of asymmetric double type II Pareto distributions. J. Stat. Theory Pract. 2020, 14, 22. [Google Scholar] [CrossRef]
- Almutairi, A.; Ghitany, M.; Alothman, A.; Gupta, R.C. Double Inverse-Gaussian Distributions and Associated Inference. J. Indian Soc. Probab. Stat. 2023, 1–32. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Cankaya, M. Asymmetric Bimodal Exponential Power Distribution on the Real Line. Entropy 2018, 20, 23. [Google Scholar] [CrossRef] [PubMed]
- Ratnaparkhi, M.V.; Naik-Nimbalkar, U.V. The Length-biased Lognormal Distribution and its application in the Analysis of data from oil Field Exploration studies. J. Mod. Appl. Stat. Methods 2012, 11, 225–260. [Google Scholar] [CrossRef]
 ), (0.5, −0.5, 1, 0.5, 1) (
), (0.5, −0.5, 1, 0.5, 1) ( ), (
), ( ).
).
 ), (0.5, −0.5, 1, 0.5, 1) (
), (0.5, −0.5, 1, 0.5, 1) ( ), (
), ( ).
).
 ), (0.5, 0.5, 0.9, −0.5, 1) (
), (0.5, 0.5, 0.9, −0.5, 1) ( ), (
), ( ).
).
 ), (0.5, 0.5, 0.9, −0.5, 1) (
), (0.5, 0.5, 0.9, −0.5, 1) ( ), (
), ( ).
).
 ), (
), ( ), (
), ( ).
).
 ), (
), ( ), (
), ( ).
).
 ), (
), ( ), (
), ( ).
).
 ), (3, 1, −3, 1) (
), (3, 1, −3, 1) ( ), (0, 1, 0, 1) (
), (0, 1, 0, 1) ( ).
).
 ), (3, 1, −3, 1) (
), (3, 1, −3, 1) ( ), (0, 1, 0, 1) (
), (0, 1, 0, 1) ( ).
).

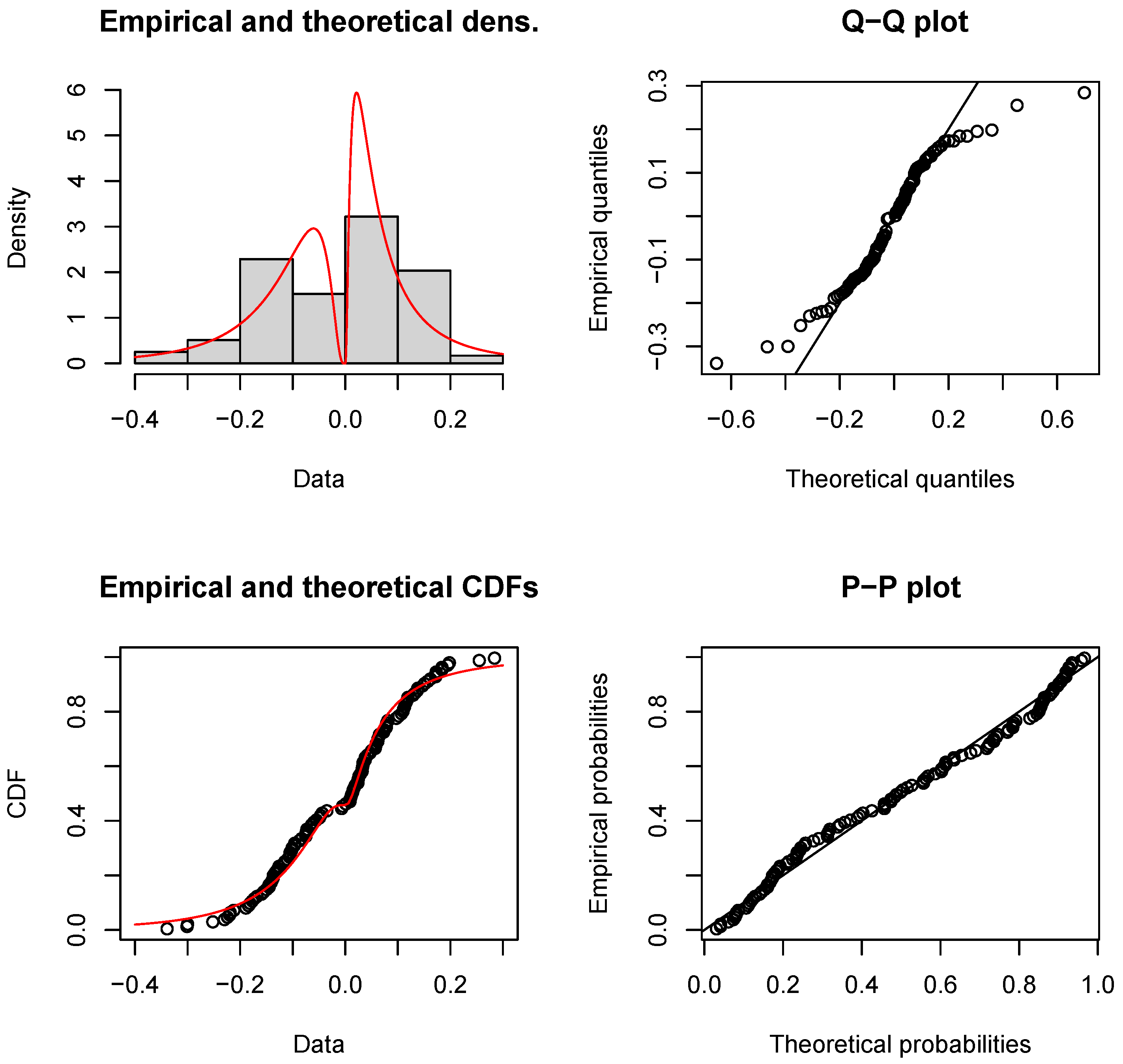
| Model | Parameter | MLE | S.E. | KS (p-Value) | AD (p-Value) | CVM (p-Value) | |
|---|---|---|---|---|---|---|---|
| DIG | 0.542 | 0.046 | 39.249 | 0.126 (0.046) | 3.285 (0.020) | 0.545 (0.030) | |
| 0.087 | 0.017 | ||||||
| 0.036 | 0.006 | ||||||
| 0.132 | 0.018 | ||||||
| 0.126 | 0.024 | ||||||
| DLN | 0.542 | 0.046 | 64.829 | 0.065 (0.709) | 0.851 (0.446) | 0.103 (0.570) | |
| −2.812 | 0.127 | ||||||
| 1.016 | 0.090 | ||||||
| −2.224 | 0.104 | ||||||
| 0.764 | 0.074 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alfahad, M.F.; Ghitany, M.E.; Alothman, A.N.; Nadarajah, S. A Bimodal Extension of the Log-Normal Distribution on the Real Line with an Application to DNA Microarray Data. Mathematics 2023, 11, 3360. https://doi.org/10.3390/math11153360
Alfahad MF, Ghitany ME, Alothman AN, Nadarajah S. A Bimodal Extension of the Log-Normal Distribution on the Real Line with an Application to DNA Microarray Data. Mathematics. 2023; 11(15):3360. https://doi.org/10.3390/math11153360
Chicago/Turabian StyleAlfahad, Mai F., Mohamed E. Ghitany, Ahmad N. Alothman, and Saralees Nadarajah. 2023. "A Bimodal Extension of the Log-Normal Distribution on the Real Line with an Application to DNA Microarray Data" Mathematics 11, no. 15: 3360. https://doi.org/10.3390/math11153360
APA StyleAlfahad, M. F., Ghitany, M. E., Alothman, A. N., & Nadarajah, S. (2023). A Bimodal Extension of the Log-Normal Distribution on the Real Line with an Application to DNA Microarray Data. Mathematics, 11(15), 3360. https://doi.org/10.3390/math11153360







