NISQ-Ready Community Detection Based on Separation-Node Identification
Abstract
1. Introduction
2. Background
- Randomly split the given graph into two equally sized partitions and delete all edges inside the partitions to yield a bipartite graph.
- Find subsets and such that andwhere is the solution to the quadratic program given byHere, denotes the link density of two disjoint sets , given by and represents the number of edges connecting and .
- Identify to be a community and repeat Steps 1 and 2 for the subgraph induced on G by .
3. Proposed Model
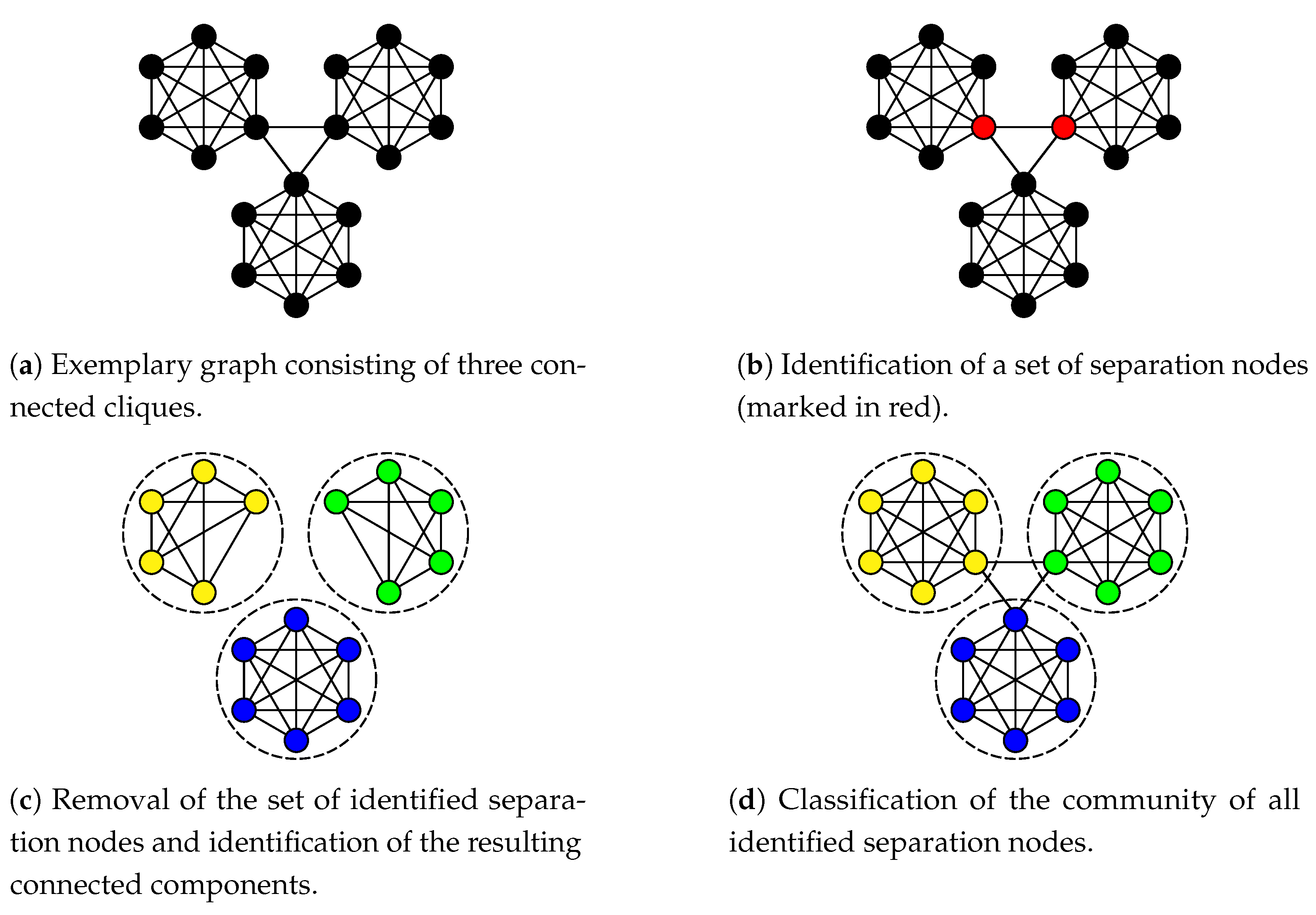
3.1. Separation-Node Sets
- (1)
- Identifying a set of nodes separating communities and thus revealing the fundamental community structure (see Section 3.4 and Section 3.5).
- (2)
- Classifying the community of each separation node to finalize community detection (see Section 3.6).
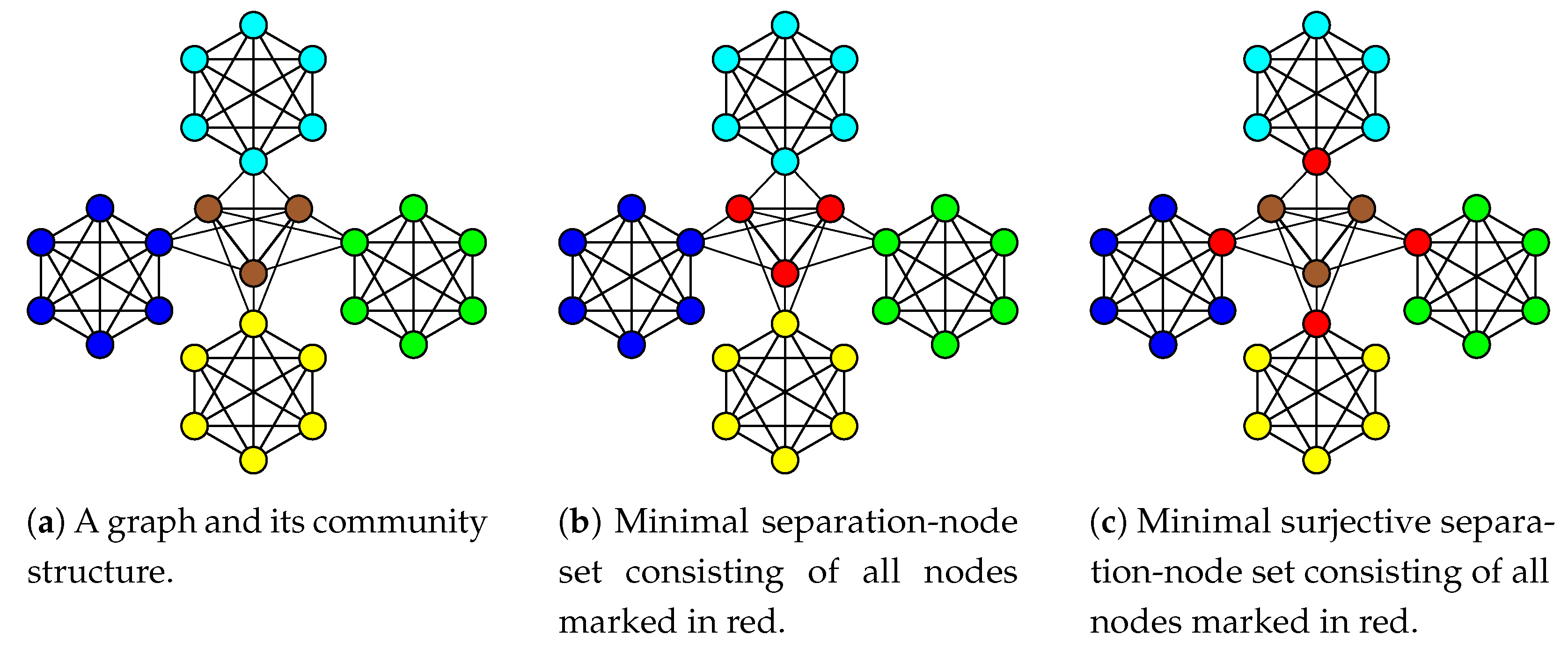
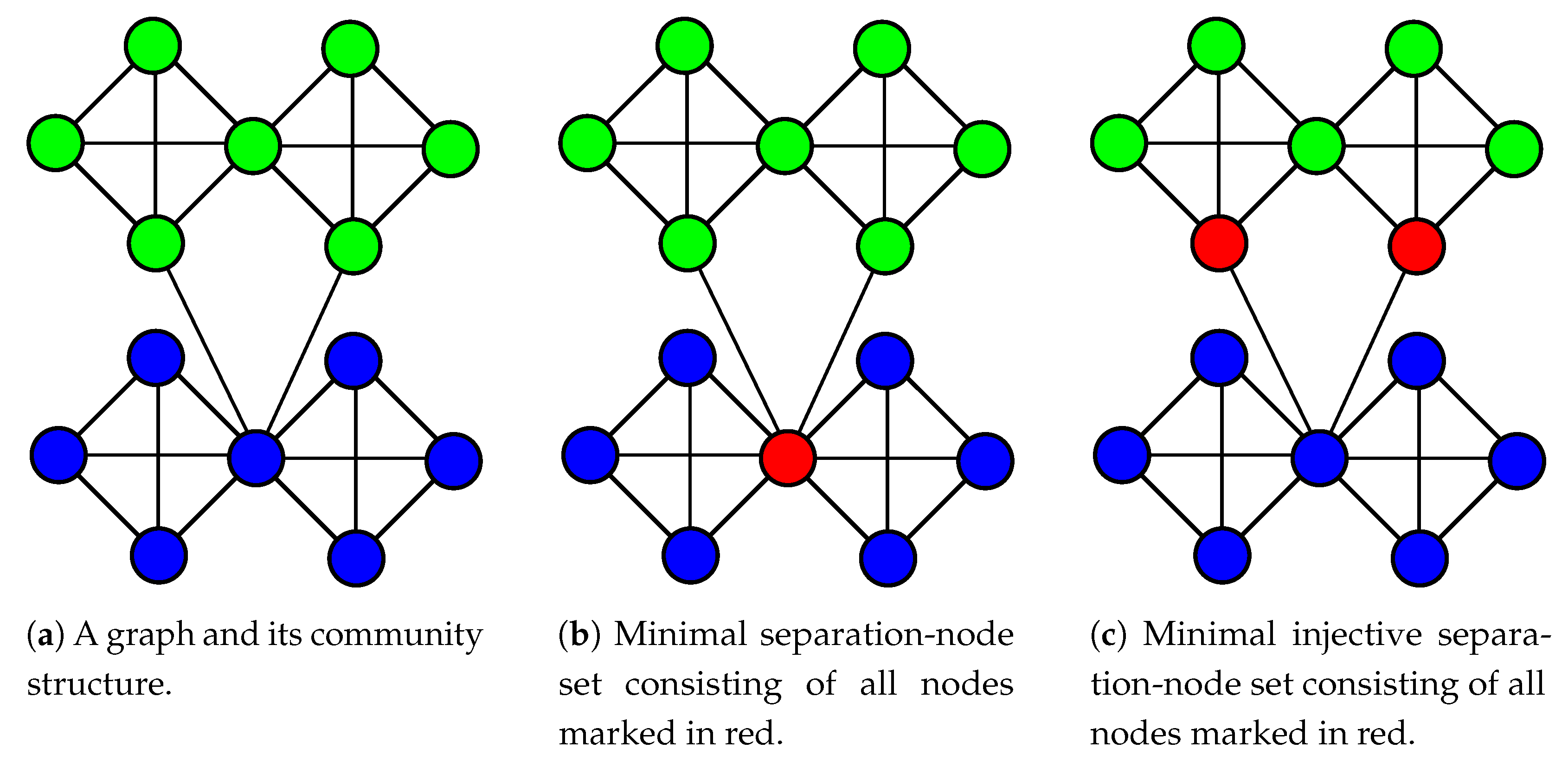
3.2. Proving Theorem 1
- and the separation-node set is smaller than S;
- and the separation-node set is much smaller than S.
- ;
- .
3.3. Constructing Penalty Terms for the In- and Surjectivity Constraints
3.4. Modularity-Based Separation Edge Estimation
- , if less connectivity between and was to be expected, indicating that and likely belong to the same community;
- , if more connectivity between and was to be expected, indicating that and likely belong to different communities.
3.5. Separation Edge Estimation Based on Edge Neighborhood Connectivity
- (1)
- Consider connections between r-neighborhoods with radius ;
- (2)
- Consider paths of length 2.
3.6. Assigning the Separation Nodes to Communities
- (1)
- Count the number of edges to every identified community for each separation node.
- (2)
- Assign the node with the most edges to a single community to that community. In case of a tie, the community that reached the highest number of edges first during the iteration over all adjacent nodes is selected.
- (3)
- Update the counts for every neighboring separation node.
- (4)
- Repeat steps two and three until every separation node is properly assigned to a community.
4. Evaluation
- (1)
- The assignment of separation nodes to their communities is computationally easy given a good enough estimator, i.e., it can be executed accurately in linear runtime with respect to the number of communities for each separation node.
- (2)
- Neighborhood connectivity constitutes a suitable estimator for separation edges, i.e., it can be employed to identify an adequate separation-node set in the here-proposed approach to conduct community detection in practice.
- Modularity. For the comparability between different datasets, we use the approximation ratio based on the best known solution. This yields values between 0 (bad) and 1 (good).
- NMI score. The NMI score is used to compare the community assignments with known ground truth. It yields values between 0 (bad) and 1 (good).
- score. This score is used to estimate predictive performance of the separation edge classification. It yields values between 0 (bad) and 1 (good).
4.1. Evidence That Separation-Node Assignment Is Computationally Cheap
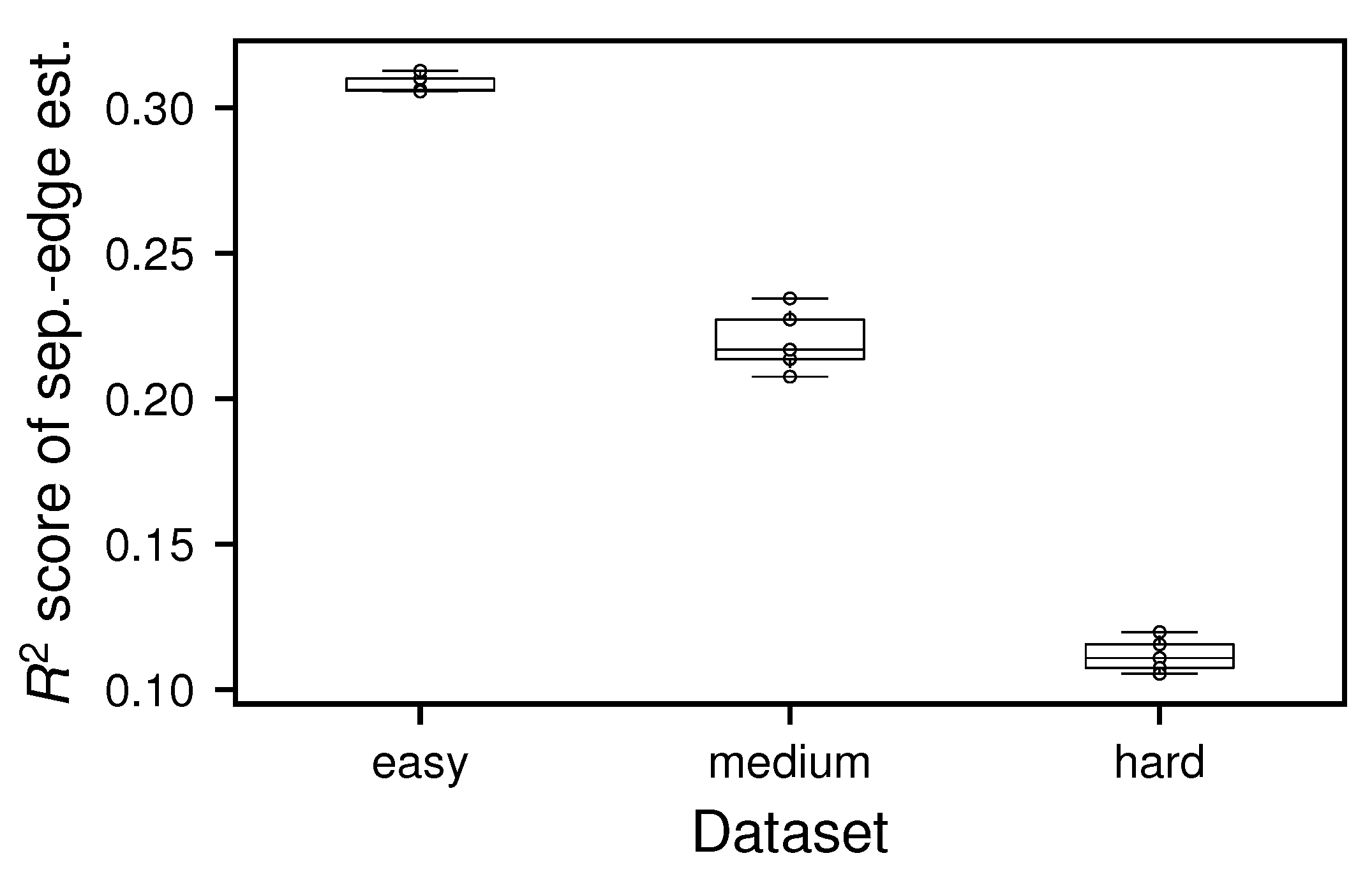
4.2. Neighborhood Connectivity Constitutes a Suitable Estimator for Separation Edges
4.3. Evaluating the Performance of Edge Neighborhood Connectivity

4.4. Evaluating the Separation-Node Assignment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bondy, J.A.; Murty, U.S.R. Graph Theory with Applications; Elsevier: New York, NY, USA, 1976. [Google Scholar]
- Mashaghi, A.R.; Ramezanpour, A.; Karimipour, V. Investigation of a protein complex network. Eur. Phys. J. B Condens. Matter Complex Syst. 2004, 41, 113–121. [Google Scholar] [CrossRef][Green Version]
- Shah, P.; Ashourvan, A.; Mikhail, F.; Pines, A.; Kini, L.; Oechsel, K.; Das, S.R.; Stein, J.M.; Shinohara, R.T.; Bassett, D.S.; et al. Characterizing the role of the structural connectome in seizure dynamics. Brain 2019, 142, 1955–1972. [Google Scholar] [CrossRef] [PubMed]
- Fortunato, S. Community detection in graphs. Phys. Rep. 2010, 486, 75–174. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef]
- Fani, H.; Bagheri, E. Community detection in social networks. Encycl. Semant. Comput. Robot. Intell. 2017, 1, 1630001. [Google Scholar] [CrossRef]
- Vilenchik, D. Simple Statistics Are Sometime Too Simple: A Case Study in Social Media Data. IEEE Trans. Knowl. Data Eng. 2020, 32, 402–408. [Google Scholar] [CrossRef]
- Nadakuditi, R.R.; Newman, M.E.J. Graph Spectra and the Detectability of Community Structure in Networks. Phys. Rev. Lett. 2012, 108, 188701. [Google Scholar] [CrossRef]
- Brandes, U.; Delling, D.; Gaertler, M.; Goerke, R.; Hoefer, M.; Nikoloski, Z.; Wagner, D. Maximizing Modularity is hard. arXiv 2006, arXiv:physics/0608255. [Google Scholar] [CrossRef]
- Decelle, A.; Krzakala, F.; Moore, C.; Zdeborová, L. Inference and Phase Transitions in the Detection of Modules in Sparse Networks. Phys. Rev. Lett. 2011, 107, 065701. [Google Scholar] [CrossRef]
- Newman, M.E.J. Equivalence between modularity optimization and maximum likelihood methods for community detection. Phys. Rev. E 2016, 94, 052315. [Google Scholar] [CrossRef]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.S.L.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef] [PubMed]
- Shaydulin, R.; Ushijima-Mwesigwa, H.; Safro, I.; Mniszewski, S.; Alexeev, Y. Network Community Detection on Small Quantum Computers. Adv. Quantum Technol. 2019, 2, 1900029. [Google Scholar] [CrossRef]
- Denchev, V.S.; Boixo, S.; Isakov, S.V.; Ding, N.; Babbush, R.; Smelyanskiy, V.; Martinis, J.; Neven, H. What is the Computational Value of Finite-Range Tunneling? Phys. Rev. X 2016, 6, 031015. [Google Scholar] [CrossRef]
- Albash, T.; Lidar, D.A. Demonstration of a Scaling Advantage for a Quantum Annealer over Simulated Annealing. Phys. Rev. X 2018, 8, 031016. [Google Scholar] [CrossRef]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing—STOC’96, Association for Computing Machinery, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar] [CrossRef]
- Shor, P.W. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM J. Comput. 1997, 26, 1484–1509. [Google Scholar] [CrossRef]
- Lloyd, S. Universal Quantum Simulators. Science 1996, 273, 1073–1078. [Google Scholar] [CrossRef]
- Ushijima-Mwesigwa, H.; Negre, C.F.A.; Mniszewski, S.M. Graph Partitioning Using Quantum Annealing on the D-Wave System. In Proceedings of the Second International Workshop on Post Moores Era Supercomputing, Denver, CO, USA, 12–17 November 2017; PMES’17, Association for Computing Machinery: New York, NY, USA, 2017; pp. 22–29. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef]
- Kadowaki, T.; Nishimori, H. Quantum annealing in the transverse Ising model. Phys. Rev. E 1998, 58, 5355–5363. [Google Scholar] [CrossRef]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Dalyac, C.; Henriet, L.; Jeandel, E.; Lechner, W.; Perdrix, S.; Porcheron, M.; Veshchezerova, M. Qualifying quantum approaches for hard industrial optimization problems. A case study in the field of smart-charging of electric vehicles. EPJ Quantum Technol. 2021, 8, 12. [Google Scholar] [CrossRef]
- Akbar, S.; Saritha, S.K. Towards quantum computing based community detection. Comput. Sci. Rev. 2020, 38, 100313. [Google Scholar] [CrossRef]
- Zahedinejad, E.; Crawford, D.; Adolphs, C.; Oberoi, J.S. Multiple Global Community Detection in Signed Graphs. In Proceedings of the Future Technologies Conference (FTC) 2019; Arai, K., Bhatia, R., Kapoor, S., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 688–707. [Google Scholar]
- Sedghpour, A.S.; Nikanjam, A. Overlapping Community Detection in Social Networks Using a Quantum-Based Genetic Algorithm. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Denver, CO, USA, 12–17 November 2017; GECCO ’17, Association for Computing Machinery: New York, NY, USA, 2017; pp. 197–198. [Google Scholar] [CrossRef]
- Mukai, K.; Hatano, N. Discrete-time quantum walk on complex networks for community detection. Phys. Rev. Res. 2020, 2, 023378. [Google Scholar] [CrossRef]
- Reittu, H.; Kotovirta, V.; Leskelä, L.; Rummukainen, H.; Räty, T. Towards analyzing large graphs with quantum annealing. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; pp. 2457–2464. [Google Scholar] [CrossRef]
- Chan, E.Y.K.; Yeung, D.Y. A Convex Formulation of Modularity Maximization for Community Detection. In Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence, IJCAI’11, Barcelona, Spain, 16–22 July 2011; AAAI Press: Menlo Park, CA, USA, 2011; Volume 3, pp. 2218–2225. [Google Scholar]
- Chen, Y.; Li, X.; Xu, J. Convexified Modularity Maximization for Degree-Corrected Stochastic Block Models. Ann. Stat. 2018, 46, 1573–1602. [Google Scholar] [CrossRef]
- Abdalla, P.; Bandeira, A.S. Community detection with a subsampled semidefinite program. Sampl. Theory Signal Process. Data Anal. 2022, 20, 6. [Google Scholar] [CrossRef]
- Li, W. Visualizing network communities with a semi-definite programming method. Security and privacy information technologies and applications for wireless pervasive computing environments. Inf. Sci. 2015, 321, 1–13. [Google Scholar] [CrossRef]
- Brandes, U. A faster algorithm for betweenness centrality. J. Math. Sociol. 2001, 25, 163–177. [Google Scholar] [CrossRef]
- Negre, C.F.; Ushijima-Mwesigwa, H.; Mniszewski, S.M. Detecting multiple communities using quantum annealing on the D-Wave system. PLoS ONE 2020, 15, 227538. [Google Scholar] [CrossRef]
- Chapuis, G.; Djidjev, H.; Hahn, G.; Rizk, G. Finding Maximum Cliques on the D-Wave Quantum Annealer. J. Signal Process. Syst. 2019, 91, 363–377. [Google Scholar] [CrossRef]
- Rosenberg, I.G. Reduction of bivalent maximization to the quadratic case. Cah. Cent. D’Etudes Rech. Oper. 1975, 17, 71–74. [Google Scholar]
- Stein, J.; Chamanian, F.; Zorn, M.; Nüßlein, J.; Zielinski, S.; Kölle, M.; Linnhoff-Popien, C. Evidence that PUBO outperforms QUBO when solving continuous optimization problems with the QAOA. arXiv 2023, arXiv:2305.03390. [Google Scholar]
- Thorndike, R.L. Who belongs in the family? Psychometrika 1953, 18, 267–276. [Google Scholar] [CrossRef]
- Sedgewick, R. Algorithms in c, Part 5: Graph Algorithms, 3rd ed.; Addison-Wesley Professional: Hoboken, NJ, USA, 2001. [Google Scholar]
- Van Der Hofstad, R. Random Graphs and Complex Networks; Cambridge University Press: Cambridge, UK, 2009; Volume 11, p. 60. Available online: https://www.win.tue.nl/~rhofstad/NotesRGCN.pdf (accessed on 23 July 2023).
- Amin, M.H.; Andriyash, E.; Rolfe, J.; Kulchytskyy, B.; Melko, R. Quantum Boltzmann Machine. Phys. Rev. X 2018, 8, 021050. [Google Scholar] [CrossRef]
- Holland, P.W.; Laskey, K.B.; Leinhardt, S. Stochastic blockmodels: First steps. Soc. Netw. 1983, 5, 109–137. [Google Scholar] [CrossRef]
- Fred, A.L.N.; Jain, A.K. Robust data clustering. In Proceedings of the 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Madison, WI, USA, 27 June–2 July 2004; Volume 2. [Google Scholar]
- Kuncheva, L.; Hadjitodorov, S. Using diversity in cluster ensembles. In Proceedings of the 2004 IEEE International Conference on Systems, Man and Cybernetics (IEEE Cat. No.04CH37583), Hague, The Netherlands, 10–13 October 2004; Volume 2, pp. 1214–1219. [Google Scholar] [CrossRef]
- Danon, L.; Díaz-Guilera, A.; Duch, J.; Arenas, A. Comparing community structure identification. J. Stat. Mech. Theory Exp. 2005, 2005, P09008. [Google Scholar] [CrossRef]
- Zachary, W.W. An Information Flow Model for Conflict and Fission in Small Groups. J. Anthropol. Res. 1977, 33, 452–473. [Google Scholar] [CrossRef]
- Lusseau, D.; Schneider, K.; Boisseau, O.J.; Haase, P.; Slooten, E.; Dawson, S.M. The bottlenose dolphin community of Doubtful Sound features a large proportion of long-lasting associations. Behav. Ecol. Sociobiol. 2003, 54, 396–405. [Google Scholar] [CrossRef]
- Knuth, D.E. The Stanford GraphBase: A Platform for Combinatorial Algorithms. In Proceedings of the Fourth Annual ACM-SIAM Symposium on Discrete Algorithms, Society for Industrial and Applied Mathematics, SODA ’93, Austin, TX, USA, 25–27 January 1993; pp. 41–43. [Google Scholar]
- Palla, G.; Derényi, I.; Farkas, I.; Vicsek, T. Uncovering the overlapping community structure of complex networks in nature and society. Nature 2005, 435, 814–818. [Google Scholar] [CrossRef]
- Newman, M.E.J. Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef]
- Li, Y.; Li, W.; Tan, Y.; Liu, F.; Cao, Y.; Lee, K.Y. Hierarchical Decomposition for Betweenness Centrality Measure of Complex Networks. Sci. Rep. 2017, 7, 46491. [Google Scholar] [CrossRef]
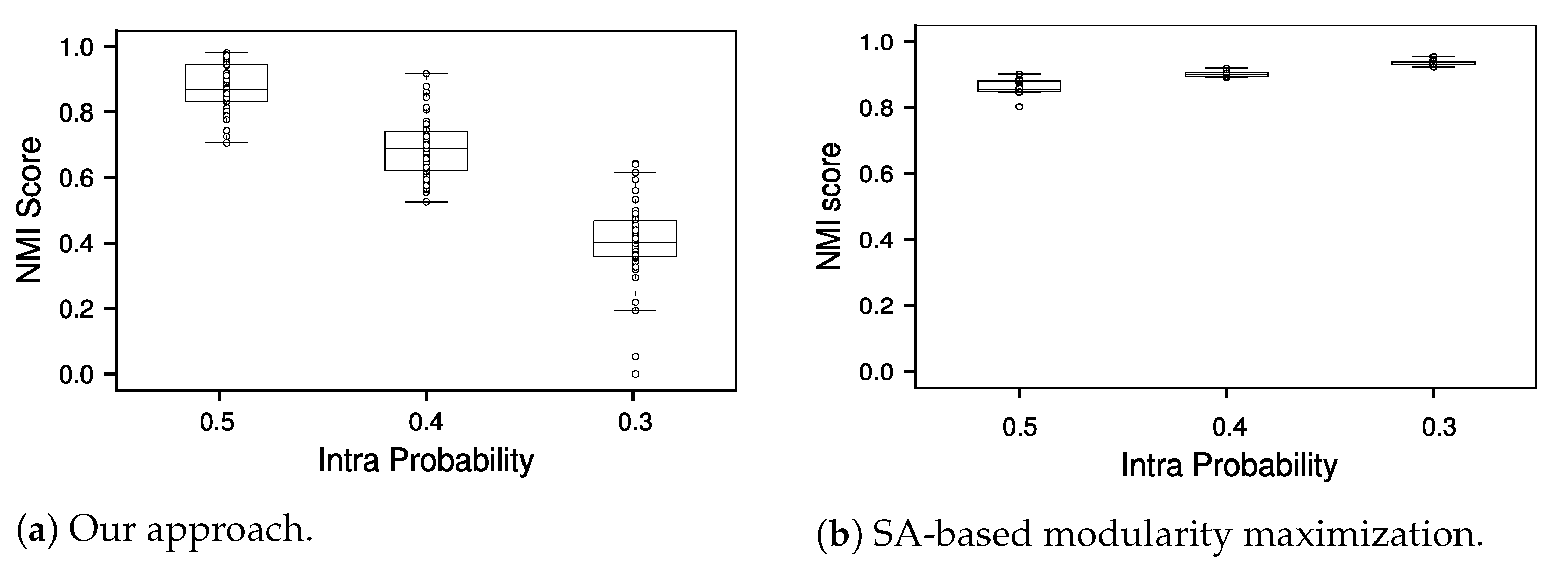


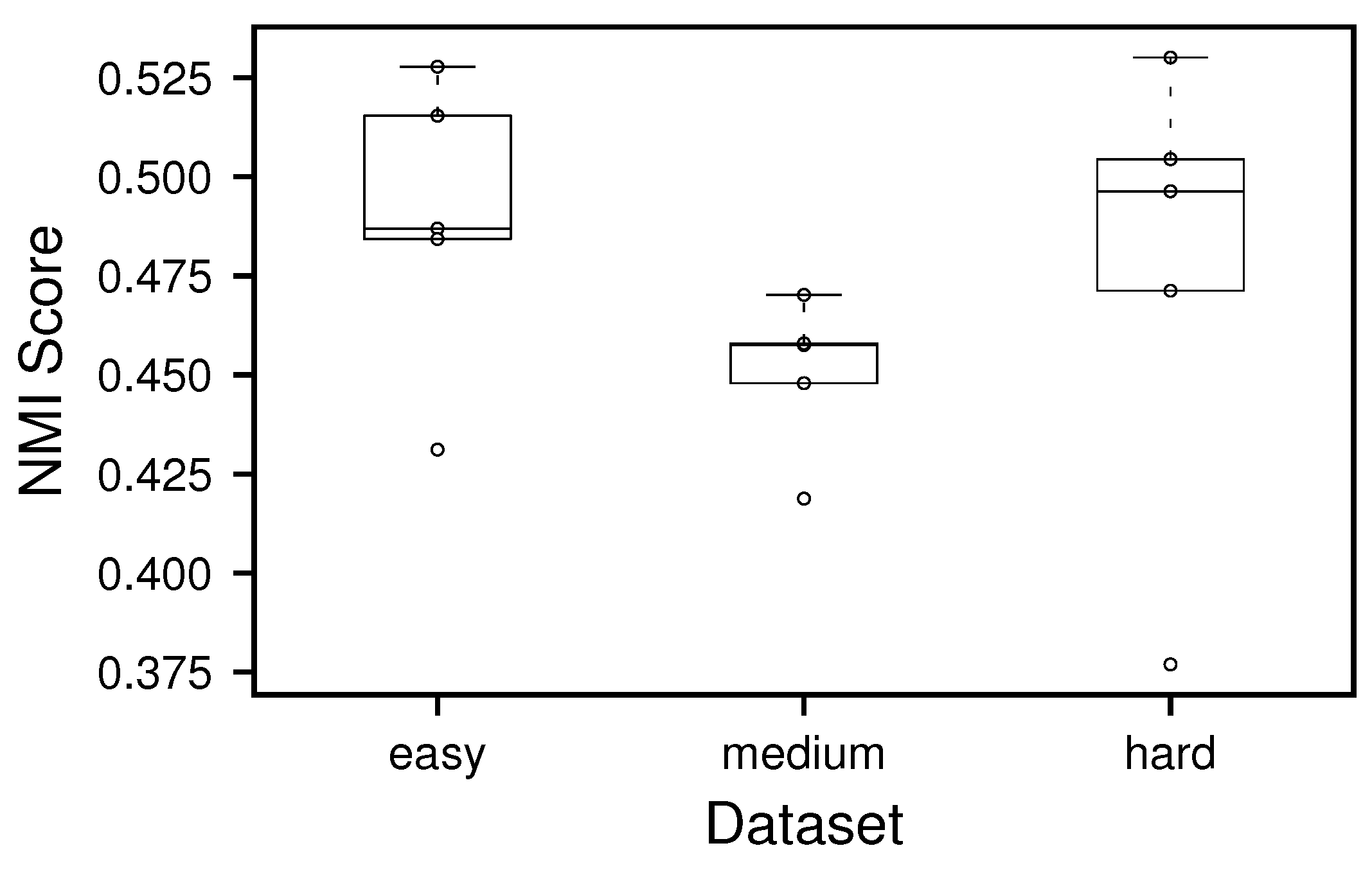
| No. of Nodes | No. of Communities | Intra Prob | |
|---|---|---|---|
| SBM graphs | 250 | 7 | |
| Karate Club | 24 | 2 | cannot be specified |
| Dolphins | 62 | 4 | cannot be specified |
| Miserables | 77 | 5 | cannot be specified |
| Protein | 83 | 9 | cannot be specified |
| Books | 105 | 3 | cannot be specified |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stein, J.; Ott, D.; Nüßlein, J.; Bucher, D.; Schönfeld, M.; Feld, S. NISQ-Ready Community Detection Based on Separation-Node Identification. Mathematics 2023, 11, 3323. https://doi.org/10.3390/math11153323
Stein J, Ott D, Nüßlein J, Bucher D, Schönfeld M, Feld S. NISQ-Ready Community Detection Based on Separation-Node Identification. Mathematics. 2023; 11(15):3323. https://doi.org/10.3390/math11153323
Chicago/Turabian StyleStein, Jonas, Dominik Ott, Jonas Nüßlein, David Bucher, Mirco Schönfeld, and Sebastian Feld. 2023. "NISQ-Ready Community Detection Based on Separation-Node Identification" Mathematics 11, no. 15: 3323. https://doi.org/10.3390/math11153323
APA StyleStein, J., Ott, D., Nüßlein, J., Bucher, D., Schönfeld, M., & Feld, S. (2023). NISQ-Ready Community Detection Based on Separation-Node Identification. Mathematics, 11(15), 3323. https://doi.org/10.3390/math11153323






