High-Order Modeling, Zeroing Dynamics Control, and Perturbations Rejection for Non-Linear Double-Holding Water Tank
Abstract
1. Introduction
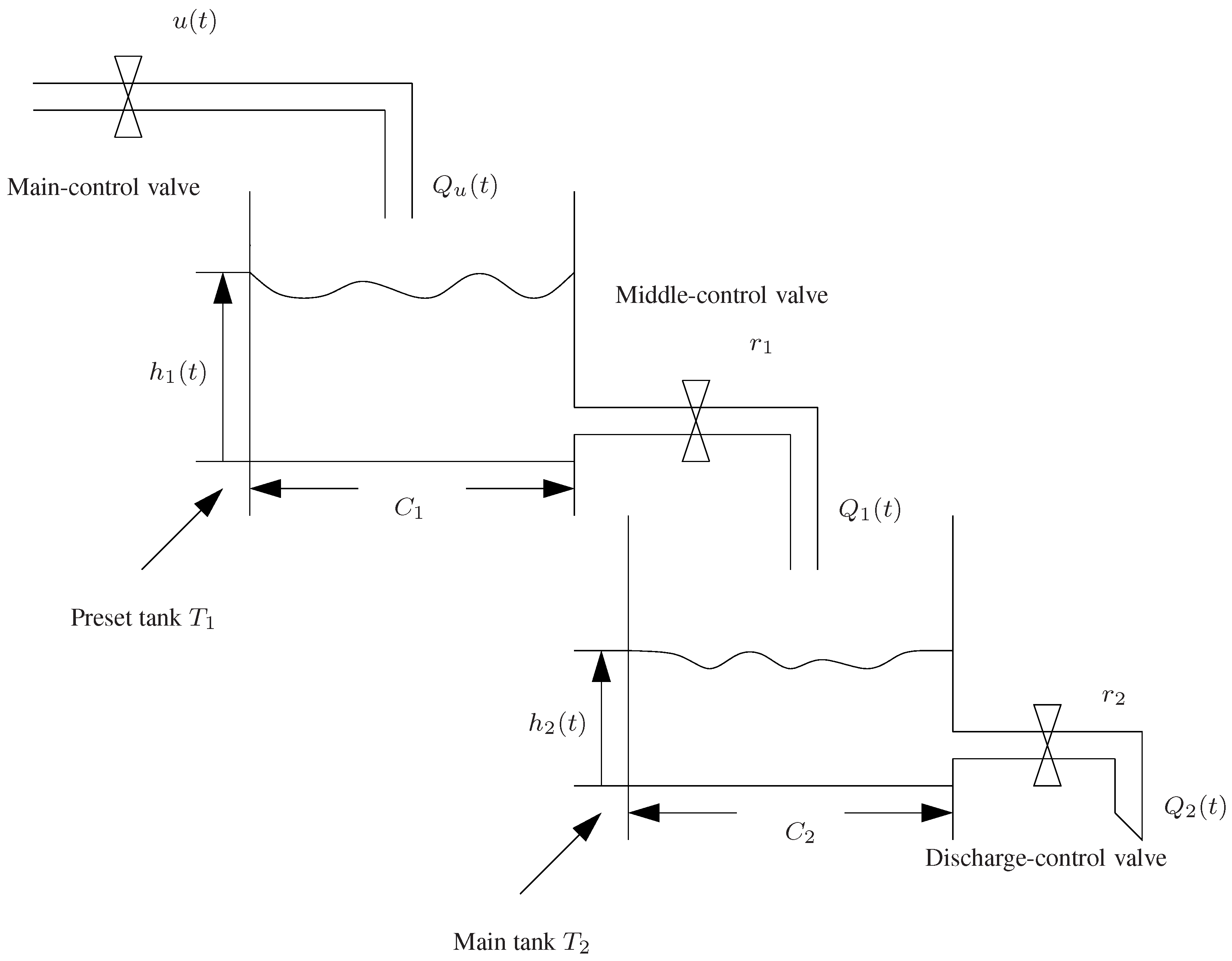
- The fundamental structure of the non-linear double-holding water tank system is given, and a non-linear model is constructed for the double-holding water tank system.
- Based on the ZD method, a design procedure for the ZD controller is detailed; furthermore, the theoretical analysis of the convergence property of the double-holding water tank system equipped with ZD controller is provided.
- The robustness of the double-holding water tank system equipped with the ZD controller in the presence of time-varying perturbations and a theoretical analysis of its bounded property is studied.
- Simulations especially those including perturbations are carried out with four different tracking trajectories. Moreover, for comparison, the tracking control of the double-holding water tank equipped with a backstepping controller is conducted, in order to further illustrate the performance of the ZD method. These simulation results verify the validity of theoretical analyses and the effectiveness of the proposed ZD controller.
2. Non-Linear Modeling and Problem Formulation
2.1. Non-Linear Double-Holding Water Tank System
2.2. Non-Linear Modeling and Problem Formulation
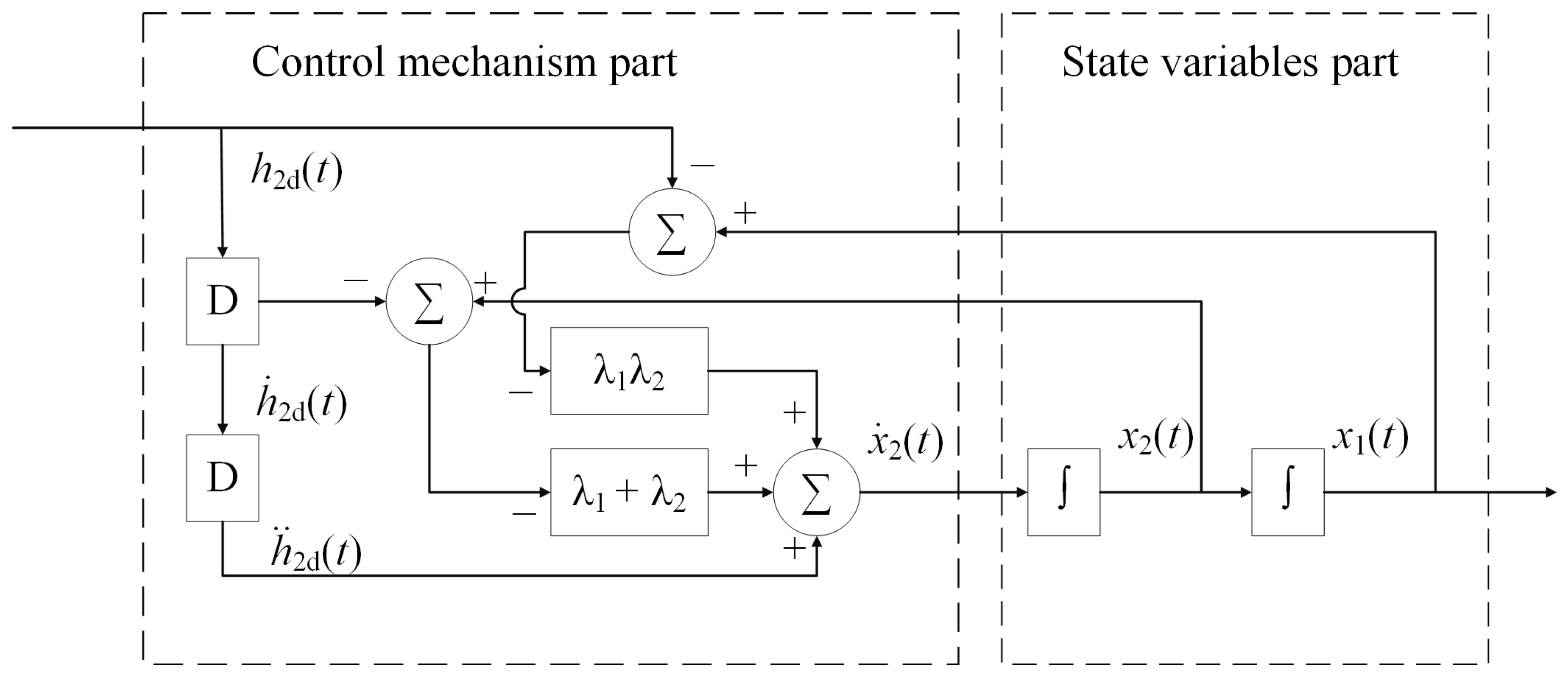
3. ZD Method for Double-Holding Water Tank System
3.1. Controller Design Based on ZD Method
3.2. Theoretical Analysis of Convergence Property
4. Robustness of Double-Holding Water Tank System Based on the ZD Method
5. Simulation, Verification, and Comparison
5.1. Examples without Perturbation
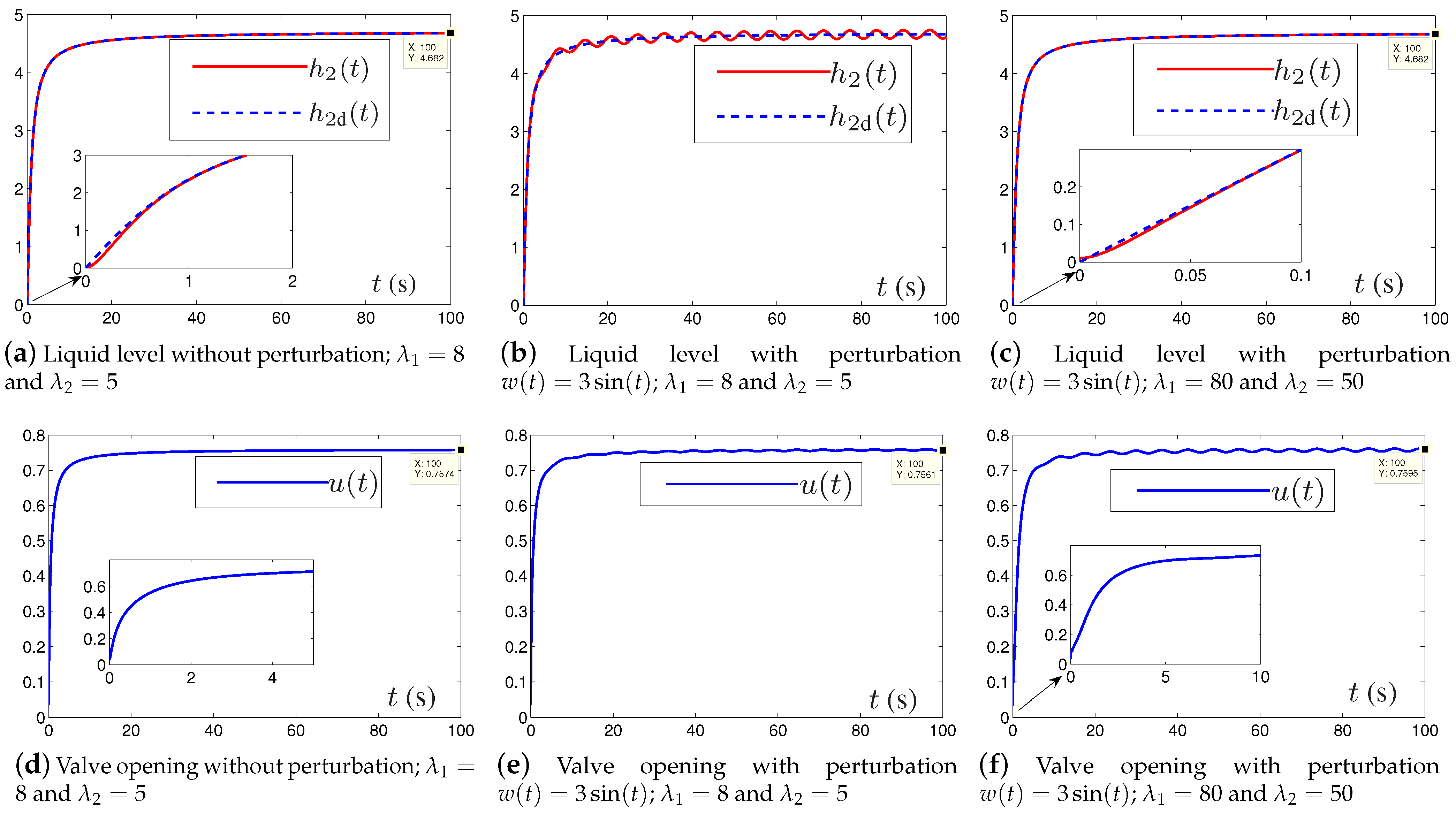
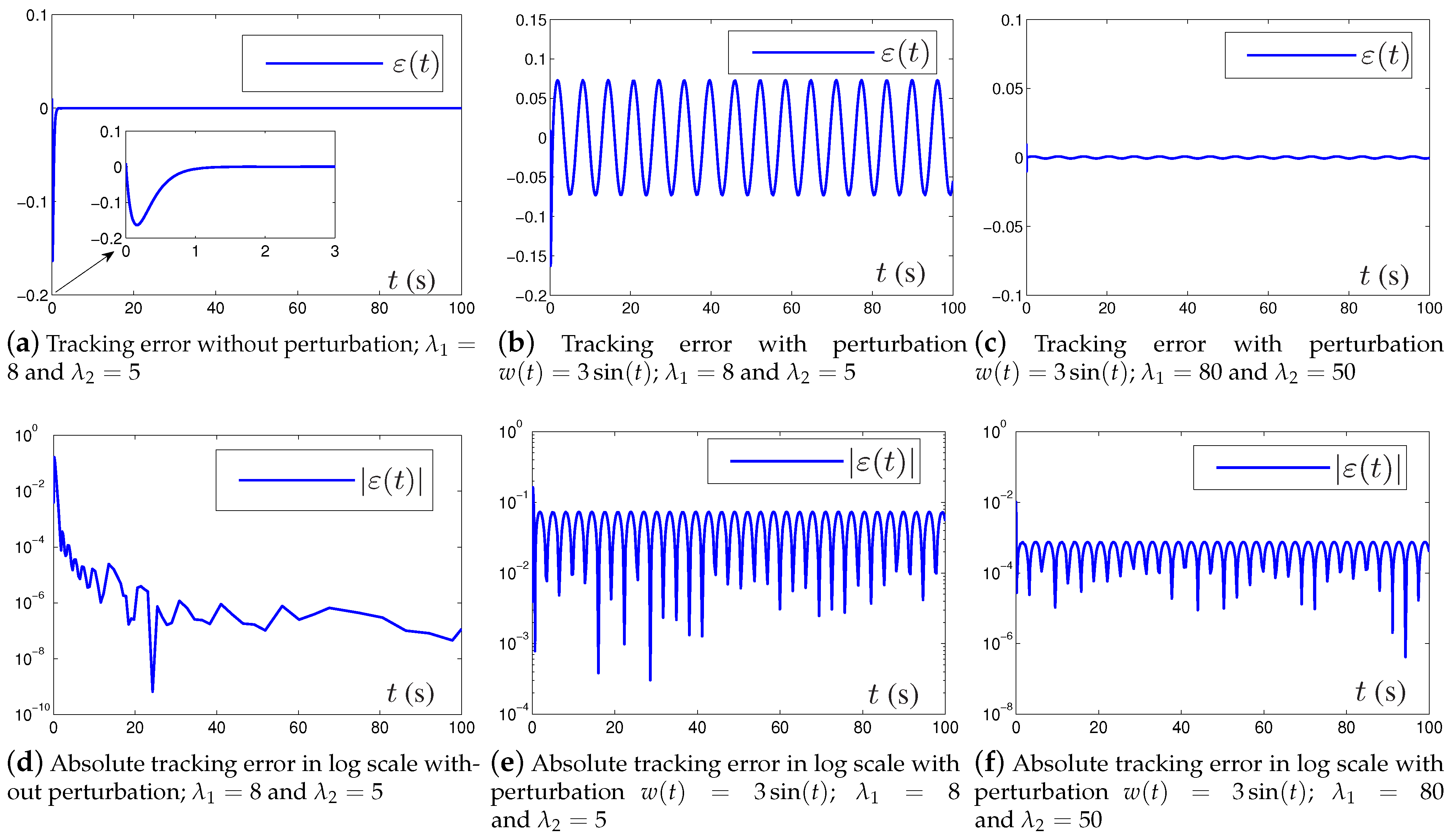
5.2. Examples for Robustness Investigation
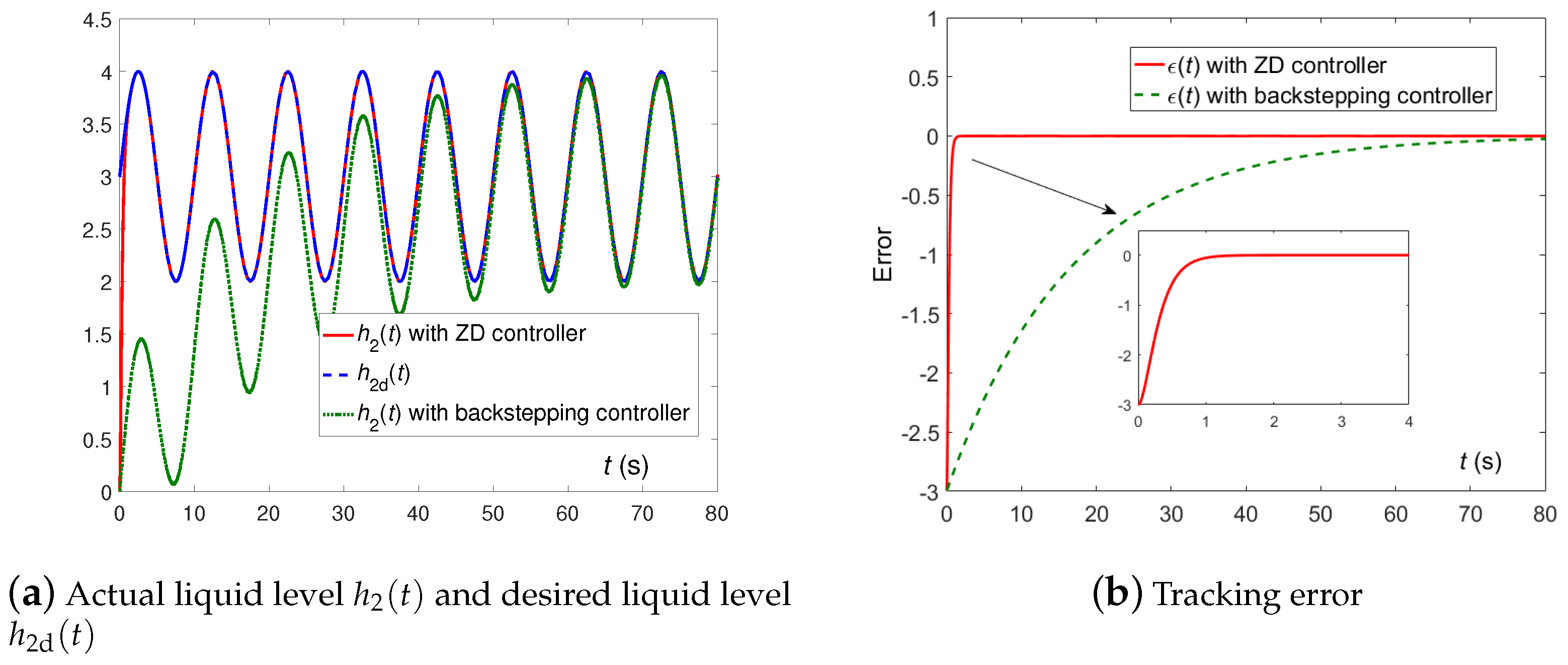
5.3. Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, H.Y.; Zhang, L.X. The simulation on double tank water level control based Matlab. Appl. Mech. Mater. 2012, 217, 1435–1439. [Google Scholar] [CrossRef]
- Yu, M.; Jia, H.L.; Chen, P.J. The research on the system of double-holding water tank liquid level control with the PID control. Adv. Mater. Res. 2014, 945, 2559–2562. [Google Scholar] [CrossRef]
- Auroux, D.; Bonnabel, S. Symmetry-preserving observers for some water tank problems: Theory and application to a shallow water model. Mathematics 2008, 67, 1122. [Google Scholar]
- Lin, Y.; Ye, X.L. Cascade fuzzy self-tuning PID control for the liquid-level control of double water-tank. Adv. Mater. Res. 2011, 383, 207–212. [Google Scholar] [CrossRef]
- Zhou, K.; Yan, B.; Jiang, Y.; Huang, J. Double-tank liquid level control based on genetic algorithm. In Proceedings of the 4nd IEEE International Conference on Intelligent Human-Machine Systems and Cybernetics, Nanchang, China, 26–27 August 2012; pp. 354–357. [Google Scholar]
- Hu, L.; Li, G.; Huang, W. Level control system of double-hold water tank based on inverse system method and PID. In Proceedings of the 2nd IEEE International Conference on Intelligent Human-Machine Systems and Cybernetics, Nanjing, China, 26–28 August 2010; pp. 129–132. [Google Scholar]
- Zhang, R.; Cao, Z.; Lu, R.; Li, P.; Gao, F. State-space predictive-P control for liquid level in an industrial coke fractionation tower. IEEE Trans. Autom. Sci. Eng. 2015, 12, 1516–1524. [Google Scholar] [CrossRef]
- Zhang, Y.; Ding, Y.-Q.; Qiu, B.; Wen, J.; Li, X.-D. ZD method based nonlinear and robust control of agitator tank. Asia J. Contr. 2018, 20, 1464–1479. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, L.; Chen, X.; Zhang, Z.; Nian, H.; Zhao, J.; Deng, R.; Yan, L. Robust active damping control for LCL-type shunt active power filters. IEEE Access 2022, 10, 39456–39470. [Google Scholar] [CrossRef]
- Gillis, N. Robustness analysis of hottopixx, a linear programming model for factoring nonnegative matrices. Mathematics 2012, 34, 1189–1212. [Google Scholar] [CrossRef]
- Bououden, S.; Chadli, M.; Karimi, H.R. A robust predictive control design for nonlinear active suspension systems. Asia J. Contr. 2016, 18, 122–132. [Google Scholar] [CrossRef]
- Jin, L.; Li, S.; Hu, B.; Liu, M.; Yu, J. A noise-suppressing neural algorithm for solving the time-varying system of linear equations:A control-based approach. IEEE Trans. Ind. Inform. 2019, 15, 236–246. [Google Scholar] [CrossRef]
- Sun, Z.; Li, F.; Zhang, B. Different modified zeroing neural dynamics with inherent tolerance to noises for time-varying reciprocal problems: A control-theoretic approach. Neurocomputing 2019, 337, 165–179. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, T.; Wang, M.; Zheng, L. An exponential-type anti-noise varying-gain network for solving disturbed time-varying inversion systems. IEEE Trans. Neural Netw. Learn. Syst. 2021, 31, 3414–3427. [Google Scholar] [CrossRef]
- Li, W.; Xiao, L.; Liao, B. A finite-time convergent and noise rejection recurrent neural network and its discretization for dynamic nonlinear equations solving. IEEE Trans. Cybern. 2020, 50, 3195–3207. [Google Scholar] [CrossRef]
- Yin, C.; Zhao, D.; Zhang, J.; Wang, S.; Xu, X.; Sun, X.; Shi, D. Body height robust control of automotive air suspension system using finite time approach. Asia J. Contr. 2021, 24, 859–871. [Google Scholar] [CrossRef]
- Ding, Y.-Q.; Li, X.-D. A unified adaptive control approach of nonlinear continuous non-parameterized systems with asymmetric control gain for trajectory tracking in different domains. Int. J. Robust Nonlinear Control 2023, 33, 3964–3987. [Google Scholar] [CrossRef]
- Yue, D.; Cao, J.; Li, Q.; Liu, Q. Neural-network-based fully distributed adaptive consensus for a class of uncertain multiagent systems. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 2965–2977. [Google Scholar] [CrossRef]
- Yu, J.; Dong, X.; Li, Q.; Lü, J.; Ren, Z. Fully adaptive practical time-varying output formation tracking for high-order nonlinear stochastic multiagent system with multiple leaders. IEEE Trans. Cybern. 2021, 51, 2265–2277. [Google Scholar] [CrossRef]
- Xu, Q.-Y.; Li, X.-D. HONN-based adaptive ILC for pure-feedback non-affine discrete-time systems with unknown control direction. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 212–224. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Shi, H.; Sun, M. Echo state network-based backstepping adaptive iterative learning control for strict-feedback systems: An error-tracking approach. IEEE Trans. Cybern. 2020, 50, 3009–3022. [Google Scholar] [CrossRef]
- Wang, H.; Liu, S.; Wang, D.; Niu, B.; Chen, M. Adaptive neural tracking control of high-order nonlinear systems with quantized input. Neurocomputing 2021, 456, 156–167. [Google Scholar] [CrossRef]
- Huang, H.; Shirkhani, M.; Tavoosi, J.; Mahmoud, O. A new intelligent dynamic control method for a class of stochastic nonlinear systems. Mathematics 2022, 10, 1406. [Google Scholar] [CrossRef]
- Zhang, H.; Li, B.; Xiao, B.; Yang, Y.; Ling, J. Nonsingular recursive-structure sliding mode control for high-order nonlinear systems and an application in a wheeled mobile robot. ISA Trans. 2022, 130, 553–564. [Google Scholar] [CrossRef]
- Zhang, J.; Meng, W.; Yin, Y.; Li, Z.; Ma, L.; Liang, W. High-order sliding mode control for three-joint rigid manipulators based on an improved particle swarm optimization neural network. Mathematics 2022, 10, 3418. [Google Scholar] [CrossRef]
- Antipov, A.; Krasnova, S.; Utkin, V. Methods of ensuring invariance with respect to external disturbances: Overview and new advances. Mathematics 2021, 9, 3140. [Google Scholar] [CrossRef]
- Drakunov, S.V.; Izosimov, D.B.; Luk’yanov, A.G.; Utkin, V.A. The block control principle I. Autom. Remote Control 1990, 51, 601–609. [Google Scholar]
- Zhang, Y.; Qiu, B.; Li, X.-D. Zhang-Gradient Control; Springer: Singapore, 2020. [Google Scholar]
- Li, J.; Mao, M.; Zhang, Y. Simpler ZD-achieving controller for chaotic systems synchronization with parameter perturbation, model uncertainty and external perturbation as compared with other controllers. Opt.-Int. J. Light Electron Opt. 2016, 131, 364–373. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Chen, D.; Xiao, Z.; Yan, X. From davidenko method to Zhang dynamics for nonlinear equation systems solving. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2817–2830. [Google Scholar] [CrossRef]
- Qiu, B.; Guo, J.; Li, X.; Zhang, Z.; Zhang, Y. Discrete-time advanced zeroing neurodynamic algorithm applied to future equality-constrained nonlinear optimization with various noises. IEEE Trans. Cybern. 2022, 52, 3539–3552. [Google Scholar] [CrossRef] [PubMed]
- Qiu, B.; Zhang, Y. Two new discrete-time neurodynamic algorithms applied to online future matrix inversion with nonsingular or sometimes-singular coefficient. IEEE Trans. Cybern. 2019, 49, 2032–2045. [Google Scholar] [CrossRef] [PubMed]
- Qiu, B.; Zhang, Y.; Yang, Z. New discrete-time ZNN models for least-squares solution of dynamic linear equation system with time-varying rank-deficient coefficient. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5767–5776. [Google Scholar] [CrossRef]
- Guo, P.; Zhang, Y. Tracking control for triple-integrator and quintuple-integrator systems with single input using zhang neural network with time delay caused by backward finite-divided difference formulas for multiple-order derivatives. Mathematics 2022, 10, 1440. [Google Scholar] [CrossRef]
- Liao, S.; Li, S.; Liu, J.; Huang, H.; Xiao, X. A zeroing neural dynamics based acceleration optimization approach for optimizers in deep neural networks. Neural Netw. 2022, 150, 440–461. [Google Scholar] [CrossRef] [PubMed]
- Halliday, D.; Resnick, R.; Wa, J. Fundamentals of Physics; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Zhang, Z.; Zhang, Y. Design and experimentation of acceleration-level drift-free scheme aided by two recurrent neural networks. IET Control Theory Appl. 2013, 7, 25–42. [Google Scholar] [CrossRef]
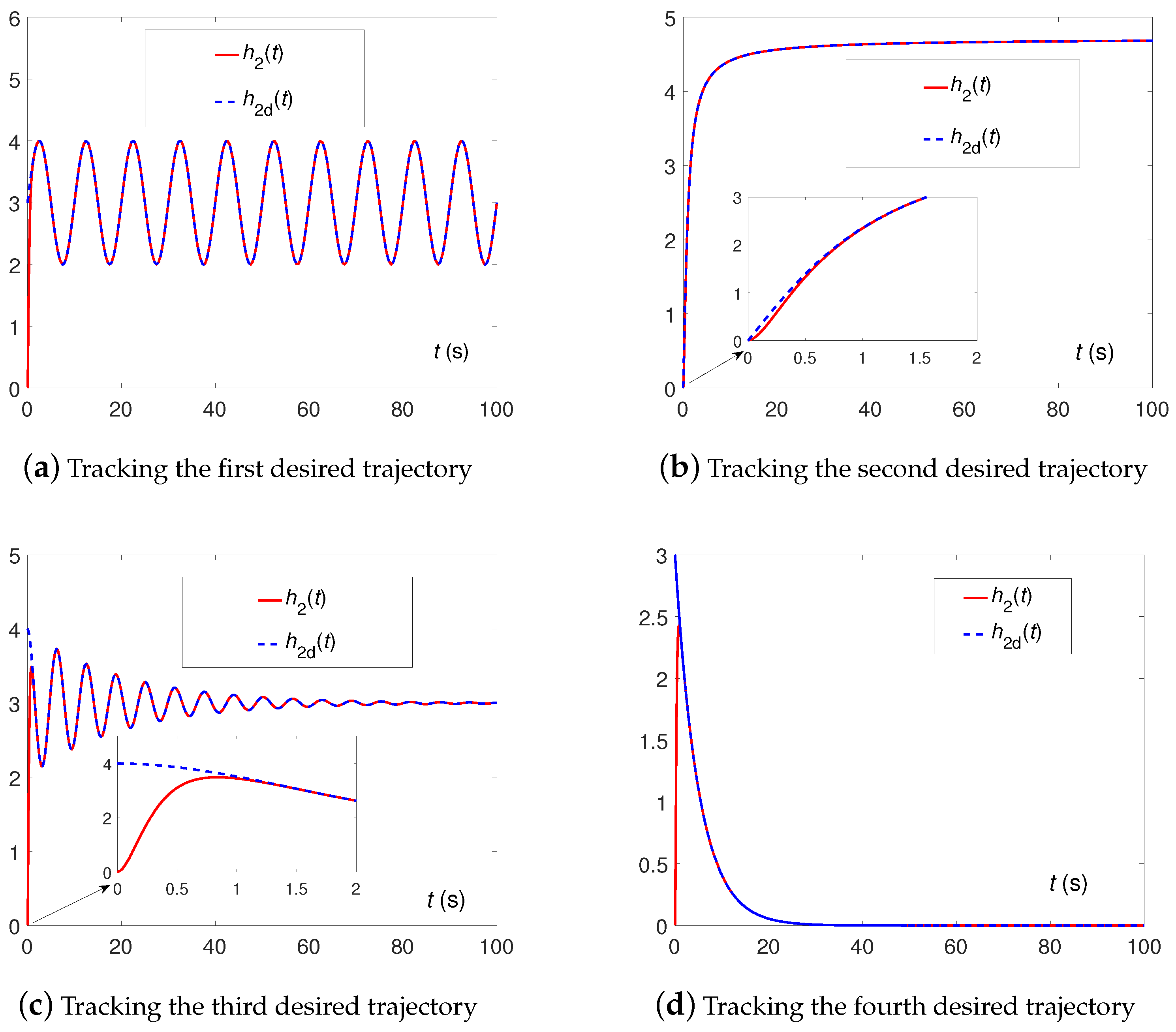
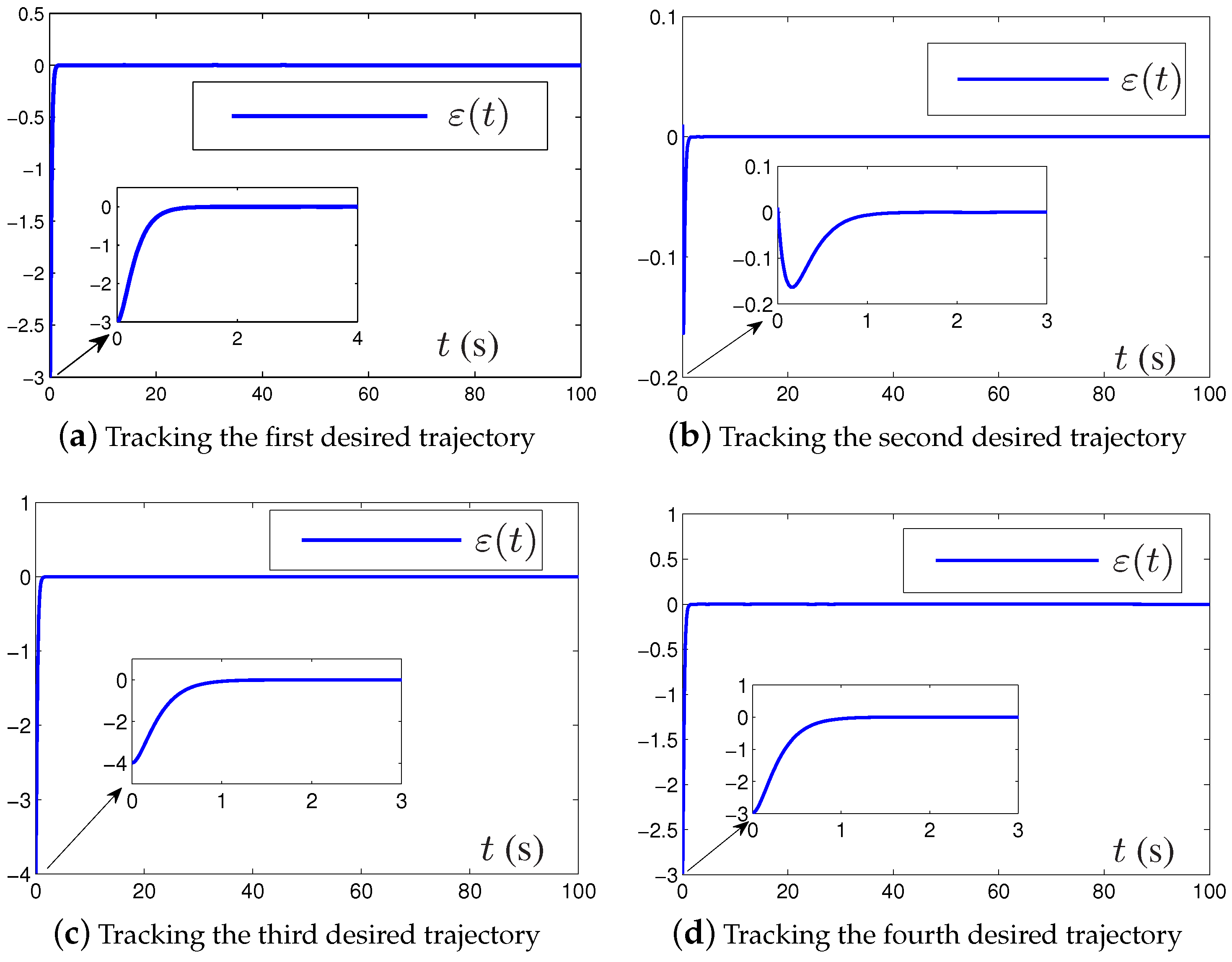
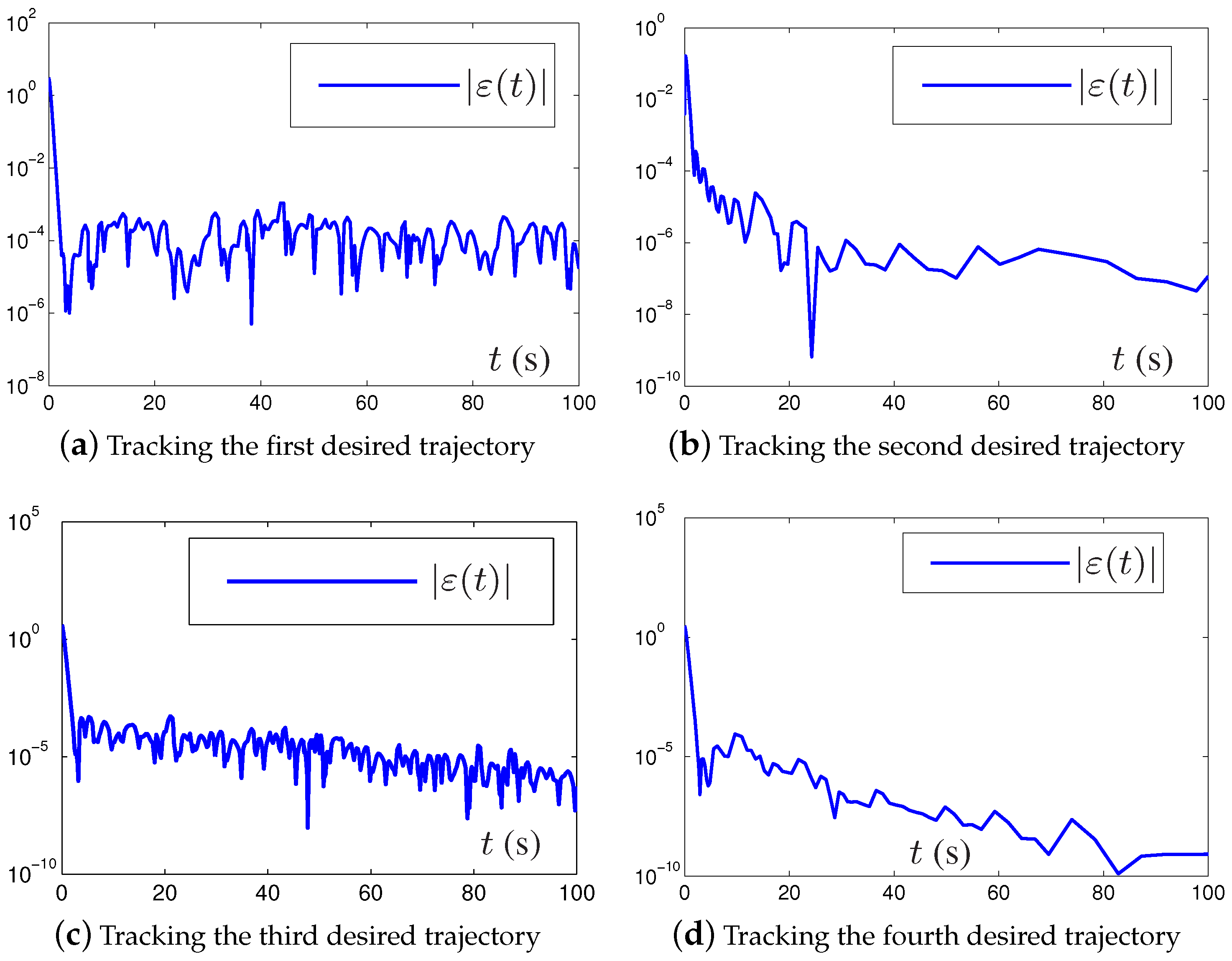

| Tracking Trajectory | |||
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Y.; Jia, H.; Zhang, Y.; Qiu, B. High-Order Modeling, Zeroing Dynamics Control, and Perturbations Rejection for Non-Linear Double-Holding Water Tank. Mathematics 2023, 11, 2989. https://doi.org/10.3390/math11132989
Ding Y, Jia H, Zhang Y, Qiu B. High-Order Modeling, Zeroing Dynamics Control, and Perturbations Rejection for Non-Linear Double-Holding Water Tank. Mathematics. 2023; 11(13):2989. https://doi.org/10.3390/math11132989
Chicago/Turabian StyleDing, Yaqiong, Hanguang Jia, Yunong Zhang, and Binbin Qiu. 2023. "High-Order Modeling, Zeroing Dynamics Control, and Perturbations Rejection for Non-Linear Double-Holding Water Tank" Mathematics 11, no. 13: 2989. https://doi.org/10.3390/math11132989
APA StyleDing, Y., Jia, H., Zhang, Y., & Qiu, B. (2023). High-Order Modeling, Zeroing Dynamics Control, and Perturbations Rejection for Non-Linear Double-Holding Water Tank. Mathematics, 11(13), 2989. https://doi.org/10.3390/math11132989






