Prescribed Fixed-Time Adaptive Neural Control for Manipulators with Uncertain Dynamics and Actuator Failures

Abstract

In this paper, a fixed-time adaptive neural control scheme is proposed to solve the prescribed tracking problem of robot manipulators in the presence of uncertain dynamics, and stuck-type actuator failures which are unknown in time, pattern, and values. Technically, the combination of neural networks and adaptive control is used to handle the uncertainties in system dynamics, an adaptive compensation mechanism is designed to accommodate the failures occurring in actuators, and also a systematic design procedure based on the prescribed performance bounds is presented to establish the conditional inequality for ensuring fixed-time stability. With our scheme, it can be proved rigorously that the tracking errors in joint space can always be kept within the prescribed bounds, and converge to a small region of zero in a bounded settling time, in addition to the closed-loop signal boundedness. The proposed scheme is validated through simulations.

1. Introduction

With the growing demand for robots in various domains of modern society, there is an increasing need for improved robot performance, making the research of robot control technology a significant concern. Existing robot control approaches primarily prioritize achieving accurate position control in the presence of actuator faults, but often overlook transient response and settling time. In practical robotic applications, insufficient transient performance can potentially result in collisions between the robot and its environment, thereby compromising system safety.

Poor transient performance can lead to system safety issues in practical applications by causing the robot to crash with the surroundings. To address this issue and achieve desired transient responses while considering various constraints, several controllers have been proposed for robots, as discussed in previous studies [1,2,3]. In the field of nonlinear control, Barrier Lyapunov Functions (BLFs) have emerged as a novel approach to indirectly enforce state and output constraints. The concept of BLFs was initially introduced in [4,5]. In [4], a BLF-based fuzzy control scheme with an adaptive observer was proposed to address specific challenges in a class of systems. The publication [5] focused on studying the trajectory tracking issue of a particular class of nonlinear dynamic systems that incorporate time-delayed constraints on the entire state.

Uncertain nonlinear elements, such as time-varying parameter values and outside disturbances, frequently affect how robot dynamics systems operate. To tackle these challenges, the utilization of adaptive control techniques in conjunction with neural networks [6,7,8,9,10] and fuzzy logic approaches [11,12,13] has been extensively adopted for the purpose of tracking control in uncertain robot systems. In reference [9], a neural-network-based control method for robots is presented, aiming to accomplish accurate tracking of trajectories while ensuring compliance with output constraints and input saturation limitations. Another approach presented in [10] introduces an adaptive admittance method based on an NN controller, ensuring guaranteed trajectory tracking. Additionally, [14] provides a comprehensive overview of advanced neural network control algorithms suitable for nonlinear systems, including robots. In terms of fuzzy control, [13] suggests an adaptive fuzzy control strategy that meets user-specified performance goals as well as fixed-time convergence. It is worth noting that only a limited number of existing control systems address both convergence time and predicted transient performance simultaneously.

In industrial systems, achieving rapid convergence of system states is crucial for enhancing control performance. Earlier investigations have predominantly centered around the convergence time of system [15,16,17]. As an example, in [15], a fuzzy control strategy is presented, utilizing an adaptive observer to achieve finite-time convergence of a specific category of nonlinear systems characterized by strict feedback. For nonlinear systems with specific matching uncertainties, a flexible finite-time mode control sliding mode strategy is provided in [16]. Moreover, in [18], an appropriate Barrier Lyapunov Function is incorporated into the formulation of a neural network-based control scheme to ensure desired transient performance and prevent deviations in the tracking errors that would violate the output constraints. While the aforementioned research makes substantial contributions to addressing transient behavior and convergence time, they overlook the impact of actuator failure on the overall behavior of the control system. In practical applications, addressing actuator faults has gained considerable attention as a research area to improve the reliability and safety of robots.

Partial loss of effectiveness (PLOE) and total loss of efficacy (TLOE) are the two basic categories into which actuator failures may be divided. In the case of PLOE, the actuator output loses some validity compared to the input. With TLOE, the actuator output becomes unknown regardless of the input. Over the past few decades, several intriguing approaches to fault-tolerant control have been introduced, including multi-model control [19,20], fault detection and diagnostic design [21,22], and sliding mode control [23,24,25,26]. Moreover, adaptive control has emerged as a promising technology [27,28,29,30,31,32,33,34], allowing for the dynamic adaptation of controller settings to effectively estimate and compensate for unknown faults and uncertainties in the system. For nonlinear systems, adaptive fault-tolerant controllers based on reverse iteration have been developed in [32,33,34]. In the context of fault-tolerant robot control, significant progress has been made [35,36,37]. In [35], a novel controller for cooperative robot systems is proposed, combining multiple individual fault compensators with adaptive control techniques. However, it is important to acknowledge that the complete characterization of failure modes can result in rapid growth in the number of estimated parameters, which can significantly affect the dynamic behavior of the system. To tackle this challenge, a dynamic controller structure is introduced in [36] with the aim of minimizing the potential actuator failure modes, thereby enhancing the effectiveness of parameter adaptation. Nevertheless, developing a fixed-time control approach for a robot with malfunctioning actuators that ensures desired transient performance tracking is still a challenging task.

Motivated by the observation above, in this work, we propose a fixed-time adaptive neural control scheme with prescribed tracking performance for robot manipulators with uncertain dynamics, and unknown actuator failures. The strategy of adaptive control, and its combination with neural networks are used to develop techniques to compensate for actuator failures which are unknown in time, pattern, and values, and deal with uncertain structured or unstructured nonlinear dynamics, and then a prescribed performance bounds (PPB)-based design approach is given to construct the control scheme so that the required fixed-time stability condition can be established. In summary, the work of this study has the following novelties and contributions:

• An actuation scheme is constructed for redundant control inputs so that the possible interaction problem in the control gain matrix can be well-circumvented, and then an adaptive compensation mechanism is raised to accommodate the actuator failures, which are unknown in time, pattern, and values.
• Based on the developed adaptive actuator failure compensation strategy, we further propose a PPB-based adaptive neural control algorithm to establish the conditional inequality of fixed-time stability, so that the response plot of tracking error can be kept within some prescribed bounds, and converges to a residual around zero in a bounded settling time (which can be independent of the initial system states).
• For our raised scheme, an optimization strategy is adopted in the design of adaptive laws for handling the unknown weight matrix of neural networks, based on which it is well achieved that the number of adaptive parameters does not increase with the number of neurons. In this sense, the proposed scheme is computationally attractive.

The rest of this paper is organized as follows. In the second part, the formulation and preliminary work of the problems related to control design are presented. The third part makes a technique for separating the control signal from the fault signal that is based on decoupling. The stability study of the system and the construction of a fixed-time neural network control with transient performance are given. The simulation findings are showcased in the fourth segment. The concluding remarks of the thesis are provided in the fifth section.

2. Problem Statement and Preliminaries

This section describes the control problem to be resolved, and presents some basics on fixed-time stability and neural networks.

2.1. Problem Formulation

The dynamics model of a robot manipulator with redundant actuators can be written as follows:

$$D\left(q\right)\ddot{q}+C(q,\dot{q})\dot{q}+G\left(q\right)=\tau ,$$

(1)

where $q,\dot{q},\ddot{q}\in R^n$ are joint variables position, velocity and acceleration vectors; $D\left(q\right)\in R^{n\times n}$ is the inertia matrix, $C(q,\dot{q})\in R^{n\times n}$ is the Coriolis and centrifugal term, $g\left(q\right)\in R^{n\times 1}$ is the gravity term, $\tau \in R^{n\times 1}$ is the joint torque vector and n is the degree of freedom.

In this study, we take into account the robot model with unidentified parameters that is provided in the third portion. The design of the controller with fixed-time convergence aims to enable the joint position q in Equation (1) to follow the intended trajectory $q_d$. The tracking error can simultaneously realize the transitory error specified by the predetermined precision. Figure 1 illustrates the controller design strategy.

2.2. Preliminaries

Property 1

([38]). The matrix $D\left(q\right)$ in Equation (1) possesses the properties of symmetry and positive definiteness. Additionally, the expression $\dot{D}\left(q\right)-2C(q,\dot{q})$ represents a skew-symmetric matrix, which fulfills the condition ${\delta }^T(\dot{D}\left(q\right)-2C(q,\dot{q}))\delta =0$ for any $\delta \in R^n$.

Assumption A1.

The reference trajectory vector $q_d$ and its first-order derivative ${\dot{q}}_d$ are both continuous and bounded, where $q_d\in R^n$ and ${\dot{q}}_d\in R^n$.

Lemma 1

([39]). In the context of a system described by $\dot{x}\left(t\right)=g\left(x\right)$, where x represents the system state, practical fixed-time stability is achieved when the Lyapunov function $V\left(x\right)$ satisfies the following inequality: $\dot{V}\left(x\right)\le -{\mu }_1{V}^{{\eta }_1}\left(x\right)-{\mu }_2{V}^{{\eta }_2}\left(x\right)+\chi$, where, ${\mu }_1$, ${\mu }_2$, and χ represent positive constants, while the parameters ${\eta }_1\in (0,1)$ and ${\eta }_2\in (1,\infty )$. Moreover, the remaining set of the system can be represented as

$$\begin{array}{cc}\hfill {\mathrm{\Omega }}_1=\{x\mid V\le min& \left({\left[\chi /\left({\mu }_1(1-\theta )\right)\right]}^{1/{\eta }_1}\right.\hfill \\ \hfill & \left.\left.{\left[\chi /\left({\mu }_2(1-\theta )\right)\right]}^{1/{\eta }_2}\right)\right\},\hfill \end{array}$$

(2)

given that $\theta \in (0,1)$, we can derive the expression for the time it takes for the system to converge using the following derivation:$T\le T_{max}=\frac{1}{{\mu }_1\theta \left(1-{\eta }_1\right)}+\frac{1}{{\mu }_2\theta \left({\eta }_2-1\right)}$.

Lemma 2

([40]). For every $x_j\in R$ and $d\in R^{+}$, the subsequent inequalities hold true:

$$\begin{array}{c}\hfill \sum _{r=1}^n{\left|x_j\right|}^d\ge {\left(\sum _{j=1}^n\left|x_j\right|\right)}^d,0<d\le 1\end{array}$$

(3)

$$\sum _{j=1}^n{\left|x_j\right|}^d\ge n^{1-d}{\left(\sum _{j=1}^n\left|x_j\right|\right)}^d,d>1.$$

(4)

Lemma 3

([41]). For any $Z\in R$ and $ϵ>0$, the following inequality holds:

$$0\le \left|Z\right|-\frac{Z^2}{\sqrt{Z^2+{ϵ}^2}}\le ϵ.$$

(5)

Remark 1

([42]). For any $\mu \in R$, a new function is defined in the following manner:

$${sig}^b\left(\mu \right)={\left|\mu \right|}^{b}sign\left(\mu \right),$$

(6)

where $b>0$.

Radial Basis Function Neural Network (RBFNN): In this study, the utilization of RBFNN in the controller design aims to tackle an unspecified system function $f\left(Z\right):R^u\to R$:

$$\widehat{f}\left(Z\right)=\sum _{i=1}^{N_0}{\hat{w}}_i{s}_i\left(Z\right)={\widehat{W}}^{T}S\left(Z\right),$$

(7)

where $Z\in {\mathrm{\Omega }}_{Z_0}\subset R^u$, where u represents the size of the NN input vector. The term $\widehat{W}\in R^{N_0}$ denotes the estimation of the optimal constant weight vector $W^{\ast }$, with $N_0$ being the count of chosen NN units. Additionally, $S\left(Z\right)={[s_1\left(Z\right),s_2\left(Z\right),\dots ,s_{N_0}\left(Z\right)]}^T\in R^{N_0}$ represents the regression vector. Each $s_i\left(Z\right)$ is chosen as a typical radial basis function, represented by:

$$s_i\left(Z,v_i\right)=exp\left[\frac{-{\left(Z-v_i\right)}^T\left(Z-v_i\right)}{{\sigma }_i^2}\right],$$

(8)

where $v_i\in R^u$ and ${\sigma }_i\in R$ represent the centroid vector and positive spread value of the ith neural network unit, respectively. By appropriately selecting these parameters, the RBFNN can accurately approximate the continuous function $R^u\to R$ across the bounded region ${\mathrm{\Omega }}_{Z_0}$, assuming a significant number of nodes are employed:

$$f\left(Z\right)=W^{\ast T}S\left(Z\right)+\epsilon \left(Z\right),\forall Z\in {\mathrm{\Omega }}_{Z_0}\in R^u,$$

(9)

where variable $\epsilon \left(Z\right)$ represents the estimation discrepancy of the neural network. The estimation discrepancy $\epsilon \left(Z\right)$ is limited by a non-negative value $\overline{\epsilon }$, satisfying $\left|\epsilon \left(Z\right)\right|\le \overline{\epsilon }$ for all $Z\in {\mathrm{\Omega }}_{Z_0}$. The element that achieves the minimum value of $\epsilon \left(Z\right)$ for every $Z\in {\mathrm{\Omega }}_{Z_0}$ is known as the optimal weight vector:

$$W^{\ast }=arg\underset{W\in R^{N_0}}{min}\left\{\underset{Z\in {\mathrm{\Omega }}_{z_0}}{sup}\left|f\left(Z\right)-{\widehat{W}}^{T}S\left(Z\right)\right|\right\}.$$

(10)

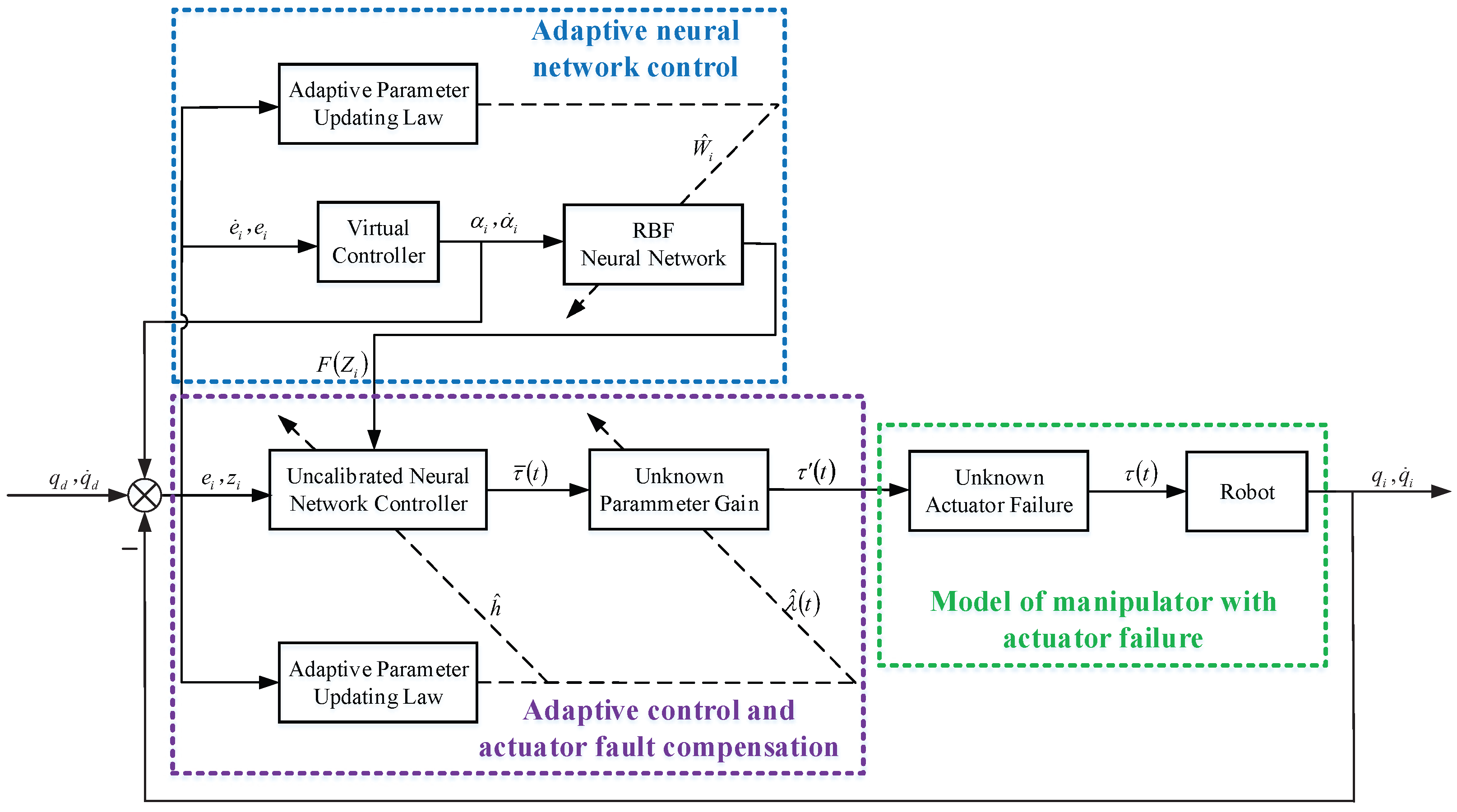
3. Control Design

The dynamics of the manipulator with unknown actuator faults are examined in this part, and a novel adaptive approach is suggested to correct for trapped actuator defects. The robustness of the setup is established by utilizing the Lyapunov stability analysis approach before deploying the controller. Algorithm 1 gives the overall simple design idea.

Algorithm 1: New decoupling algorithm: eliminate actuator faults.

3.1. Dynamics of Manipulator with Unknown Actuator Failure

For the ith joint, denoted by $i\in \{1,2,\cdots ,n\}$, in the scenario of concurrent actuation, there exist $m_i$ interconnected actuators. The motion behavior of the ith joint can be characterized in the following manner:

$$D_i\left(q\right)\ddot{q}+C_i(q,\dot{q})\dot{q}+G_i\left(q\right)={\tau }_i,$$

(11)

The joint torque is defined as follows in order to reflect the redundancy

$${\tau }_i={\tau }_{i1}+{\tau }_{i2}+\cdots +{\tau }_{i{m}_i},$$

(12)

where ${\tau }_{ij}$ represents the torque applied to the ith joint by the jth actuator. The following describes the situation of an actuator with a TLOE-type failure:

$${\sigma }_{ij}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\mathrm{actuator}\mathrm{fails};\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.,$$

(13)

where $j=1,2,\dots ,m_i$ and ${\sigma }_{ij}$ represent the jth actuator associated with the ith joint state, respectively. A common occurrence in actuator malfunction is

$${\overline{\tau }}_{ij}\left(t\right)={\overline{\tau }}_{ij},t\ge t_{ij},$$

(14)

where ${\overline{\tau }}_{ij}$ is the constant torque generated by the fault actuator, and $t_{ij}$ is the unknown instantaneous time when the fault occurs.

The underlying principle of the adaptive compensation technique, which tackles uncertain system dynamics and failure characteristics, is as follows.

• Up to $m_i$−1 actuators can experience instantaneous failure, and even in the absence of knowledge about the specific failure characteristics, the remaining actuators can dynamically adjust their actions to achieve the desired objective.

The torque exerted by the jth actuator on the ith joint of the manipulator can be mathematically represented as follows:

$${\tau }_{ij}=\left(1-{\sigma }_{ij}\right){\tau }_{ij}^{\ast }+{\sigma }_{ij}{\overline{\tau }}_{ij},$$

(15)

where the control input is represented by ${\tau }_{ij}^{\ast }$. All actuators must receive an identical control signal or follow an equivalent actuation scheme to form a meaningful actuation design.

$${\tau }_{i1}^{\ast }\left(t\right)={\tau }_{i2}^{\ast }\left(t\right)=\cdots ={\tau }_{i{m}_i}^{\ast }\left(t\right)={\tau }_i^{\ast }\left(t\right).$$

(16)

By substituting Equation (15) into the joint input of the robot, we acquire

$${\tau }_i=\sum _{j=1}^{m_i}\left(1-{\sigma }_{ij}\right){\tau }_i^{\ast }+\sum _{j=1}^{m_i}{\sigma }_{ij}{\overline{\tau }}_{ij}.$$

(17)

We can express the matrix B and the vector h as follows:

$$\begin{array}{c}\mathbf{B}=diag\left(d_1,d_2,\dots ,d_n\right),d_i={\displaystyle \sum _{j=1}^{m_i}}\left(1-{\sigma }_{ij}\right)\\ \mathbf{h}\left(t\right)={\left(h_1,h_2,\dots ,h_n\right)}^T,h_i={\displaystyle \sum _{j=1}^{m_i}}{\sigma }_{ij}{\overline{\tau }}_{ij}.\end{array}$$

(18)

Based on Equations (17) and (18), we can represent the control signal $\tau \left(t\right)$ as follows:

$$\tau \left(t\right)=\mathbf{B}\left(t\right){\tau }^{\ast }\left(t\right)+\mathbf{h}\left(t\right),$$

(19)

where $\mathbf{B}$ is a positive definite matrix of size $n\times n$. The desired joint input signal to be designed is denoted as ${\tau }^{\ast }$, which is an $n\times 1$ vector. Additionally, $\mathbf{h}\left(t\right)$ represents the constant torque contributed by the failed actuator, forming a constant $n\times 1$ vector.

An unidentified parameter vector was used in the control input design to make it easier. We introduce the parameter $\lambda$, which is defined by the subsequent equation:

$$\begin{array}{cc}\hfill {\lambda }_i& =\frac{1}{d_i}\hfill \\ \hfill {\tau }^{\ast }\left(t\right)& =\widehat{\lambda }\widehat{\tau }\left(t\right),\hfill \end{array}$$

(20)

where $\widehat{\lambda }$ denotes the estimation of $\lambda$, and $\widetilde{{\lambda }_i}$ refers to the difference between the estimated value ${\widehat{\lambda }}_i$ and the actual value ${\lambda }_i$. Mathematically, it can be expressed as $\widetilde{{\lambda }_i}={\widehat{\lambda }}_i-{\lambda }_i$. Additionally, the control input $\widehat{\tau }\left(t\right)$ will be used in place of the designed control input ${\tau }^{\ast }\left(t\right)$. By incorporating Equations (18) and (20) into Equation (19), we can accomplish the task of isolating the control signal $\widehat{\tau }\left(t\right)$, as demonstrated in the following procedure:

$$\begin{array}{cc}\hfill \tau \left(t\right)& =\mathbf{B}\left(t\right){\tau }^{\ast }\left(t\right)+\mathbf{h}\left(t\right)\hfill \\ & =\left[\begin{array}{cccc}{d}_1& & & \\ & d_2& & \\ & & \ddots & \\ & & & d_n\end{array}\right]\left[\begin{array}{c}{\tau }_1^{\ast }\\ {\tau }_2^{\ast }\\ ⋮\\ {\tau }_n^{\ast }\end{array}\right]+\left[\begin{array}{c}{h}_1\\ h_2\\ ⋮\\ h_n\end{array}\right]\hfill \\ & =\left[\begin{array}{cccc}\frac{1}{{\lambda }_1}& & & \\ & & \\ & \frac{1}{{\lambda }_2}& & \\ & & \ddots & \\ & & & \frac{1}{{\lambda }_n}\end{array}\right]\left[\begin{array}{c}\left({\tilde{\lambda }}_1+{\lambda }_1\right){\widehat{\tau }}_1\\ \left({\tilde{\lambda }}_2+{\lambda }_2\right){\widehat{\tau }}_2\\ ⋮\\ \left({\tilde{\lambda }}_n+{\lambda }_n\right){\widehat{\tau }}_n\end{array}\right]+\left[\begin{array}{c}{h}_1\\ h_2\\ ⋮\\ h_n\end{array}\right]\hfill \\ & =\left[\begin{array}{c}{\widehat{\tau }}_1\\ {\widehat{\tau }}_2\\ ⋮\\ {\widehat{\tau }}_n\end{array}\right]+\left[\begin{array}{c}{d}_1{\tilde{\lambda }}_1{\widehat{\tau }}_1\\ d_2{\tilde{\lambda }}_2{\widehat{\tau }}_n\\ ⋮\\ d_n{\tilde{\lambda }}_n{\widehat{\tau }}_n\end{array}\right]+\left[\begin{array}{c}{h}_1\\ h_2\\ ⋮\\ h_n\end{array}\right].\hfill \\ \end{array}$$

Taking this into account, the control input arising from a defective actuator can be redefined as follows:

$$\tau \left(t\right)=\widehat{\tau }\left(t\right)+\mathbf{h}\left(t\right)+\mathbf{r}\left(t\right),$$

(21)

where

$$\mathbf{r}\left(t\right)=\left(\begin{array}{c}{d}_1{\tilde{\lambda }}_1{\widehat{\tau }}_1\\ d_2{\tilde{\lambda }}_2{\widehat{\tau }}_2\\ ⋮\\ d_n{\tilde{\lambda }}_n{\widehat{\tau }}_n\end{array}\right).$$

(22)

By incorporating Equation (21) into Equation (1), we can express the manipulator dynamics:

$$D\left(q\right)\ddot{q}+C(q,\dot{q})\dot{q}+G\left(q\right)=\widehat{\tau }\left(t\right)+\mathbf{h}\left(t\right)+\mathbf{r}\left(t\right).$$

(23)

Remark 2.

Following Equation (23), the control signals for the robotic system under an unforeseen actuator malfunction are denoted by $\widehat{\tau }\left(t\right)$, $\mathbf{h}\left(t\right)$, and $\mathbf{r}\left(t\right)$. The parameter $\mathbf{B}\left(t\right)$ is subject to uncertainty and does not have a predefined range, while the quantity $\mathbf{h}\left(t\right)$ is both limited and of an unspecified nature.

3.2. Fixed-Time Neural Network Controller and Stability Analysis

Prior to proceeding with the controller design, provided below is a description of the tracking error signals:

$$e=q-q_{d}z=\dot{q}-\alpha ,$$

(24)

where $e={\left[e_1,e_2,\dots ,e_n\right]}^T\in R^n$ and $z={\left[z_1,z_2,\dots ,z_n\right]}^T\in R^n$ represent the position tracking error and velocity tracking error vectors of the robot manipulator, respectively. $q\left(t\right)$ and $q_d\left(t\right)\in R^n$ represent the actual and desired trajectories, respectively. Furthermore, $\alpha ={\left[{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right]}^T\in R^n$ represents the virtual controllers, which will be determined later.

To limit the position deviation $e_i$ in various orientations, the boundary functions ${\xi }_{1i}$ and ${\xi }_{2i}$ are devised as follows:

$$\begin{array}{c}{\xi }_{1i}=-\left[\left({\varrho }_{0,1i}-{\varrho }_{\infty ,1i}\right)e^{-k_{1i}t}+{\varrho }_{\infty ,1i}\right]\\ {\xi }_{2i}=\left({\varrho }_{0,2i}-{\varrho }_{\infty ,2i}\right)e^{-k_{2i}t}+{\varrho }_{\infty ,2i}\end{array},$$

(25)

where ${\varrho }_{0,ji},{\varrho }_{\infty ,ji},k_{ji}(j=1,2,i=1,2,\dots ,n)$ are positive constants that are chosen appropriately.

Remark 3.

The functions ${\xi }_{2i}$ and ${\xi }_{1i}$ define the upper and lower limits of the position deviation $e_i$, respectively, with $e_i=q_i-q_{di}$. This means that the tracking error $e_i$ is restricted to the range ${\xi }_{1i}<e_i<{\xi }_{2i}$. By appropriately selecting the variables ${\varrho }_{0,ji}$, ${\varrho }_{\infty ,ji}$, $k_{ji}$, and utilizing the monotonic nature of the exponential function, we can evaluate the tracking performance at a steady state based on Equation (25).

The tracking error vector e undergoes a coordinate transformation as follows:

$${\vartheta }_a={\left[\frac{e_1}{{\xi }_{11}},\frac{e_2}{{\xi }_{12}},\dots ,\frac{e_n}{{\xi }_{1n}}\right]}^T,{\vartheta }_b={\left[\frac{e_1}{{\xi }_{21}},\frac{e_2}{{\xi }_{22}},\dots ,\frac{e_n}{{\xi }_{2n}}\right]}^T.$$

(26)

Then, we define a new vector $\vartheta$ as $\vartheta ={\left[{\vartheta }_1,{\vartheta }_2,\dots ,{\vartheta }_n\right]}^T$, where each element ${\vartheta }_i$ corresponds to

$${\vartheta }_i=H_i\left(e_i\right){\vartheta }_{bi}+\left(1-H_i\left(e_i\right)\right){\vartheta }_{ai},i=1,2,\dots ,n$$

(27)

The elements ${\vartheta }_{ai}$ and ${\vartheta }_{bi}$ in Equation (27) represent the ith components of the vectors ${\vartheta }_a$ and ${\vartheta }_b$, respectively. The function $H_i\left(e_i\right)$ can be expressed by the following definition:

$$H_i\left(e_i\right)=\left\{\begin{array}{cc}1\hfill & e_i\ge 0\hfill \\ 0\hfill & e_i<0\hfill \end{array}.\right.$$

(28)

Then, we consider a Lypunov candidate

$$V_1=\sum _{i=1}^n\left[\frac{H_i}{2}{\vartheta }_{b_i}^2+\frac{\left(1-H_i\right)}{2}{\vartheta }_{a_i}^2\right].$$

(29)

By combining Equations (26) and (28), and their time derivatives, we can obtain the following expression:

$${\dot{V}}_1=\sum _{i=1}^n\left[H_i{\vartheta }_{b_i}{\dot{\vartheta }}_{b_i}+\left(1-H_i\right){\vartheta }_{a_i}{\dot{\vartheta }}_{a_i}\right].$$

(30)

From (24), we have

$${\dot{e}}_i={\dot{q}}_i-{\dot{q}}_{di}=z_i+{\alpha }_i-{\dot{q}}_{di}.$$

(31)

Substituting (26) and (31) into (30), we have

$${\dot{V}}_1=\sum _{i=1}^n\left[\frac{H_i{\vartheta }_{b_i}}{{\xi }_{2i}}\left(z_i+{\alpha }_i-{\dot{q}}_{d_i}-e_i\frac{{\dot{\xi }}_{2i}}{{\xi }_{2i}}\right)\right]+\sum _{i=1}^n\left[\frac{\left(1-H_i\right){\vartheta }_{a_i}}{{\xi }_{1i}}\left(z_i+{\alpha }_i-{\dot{q}}_{d_i}-e_i\frac{{\dot{\xi }}_{1i}}{{\xi }_{1i}}\right)\right].$$

(32)

The formulation of the virtual controller ${\alpha }_i$ is outlined below:

$$\begin{array}{cc}\hfill {\alpha }_i=& {\dot{q}}_{d_i}-k_{1i}{e}_i-H_i{k}_{2i}{\vartheta }_{b_i}^2{e}_i-\left(1-H_i\right)k_{2i}{\vartheta }_{a_i}^2{e}_i-H_i{k}_{3i}{\left(\frac{1}{2}{e}_i^2+\frac{1}{2}{\xi }_{2i}^2\right)}^{\frac{1}{2}}-\hfill \\ & {\delta }_i{e}_i+\left(1-H_i\right)k_{3i}{\left(\frac{1}{2}{e}_i^2+\frac{1}{2}{\xi }_{1i}^2\right)}^{\frac{1}{2}},\hfill \end{array}$$

(33)

where

$${\delta }_i=\sqrt{{\left(\frac{{\dot{\xi }}_{1i}}{{\xi }_{1i}}\right)}^2+{\left(\frac{{\dot{\xi }}_{2i}}{{\xi }_{2i}}\right)}^2+K_{a_i}},$$

(34)

and $k_{1i},k_{2i},k_{3i},k_{ai}$ are all proper positive constants.

By replacing (33) with Equation (32), we obtain the resulting expression:

$$\begin{array}{cc}\hfill {\dot{V}}_1=& \sum _{i=1}^n\left[\left(\frac{H_i{e}_i}{{\xi }_{2i}^2}+\frac{\left(1-H_i\right)e_i}{{\xi }_{1i}^2}\right)z_i\right]-\sum _{i=1}^n\left[\frac{k_{1i}{H}_i{e}_i^2}{{\xi }_{2i}^2}+\frac{k_{1i}\left(1-H_i\right)e_i^2}{{\xi }_{1i}^2}\right]-\hfill \\ & \sum _{i=1}^n\left[k_{2i}{H}_i^2{\vartheta }_{b_i}^4+{\left(1-H_i\right)}^2{k}_{2i}{\vartheta }_{a_i}^4\right]+\sum _{i=1}^n\left[\frac{k_{3i}{H}_i^2{\vartheta }_{bi}\sqrt{\frac{1}{2}{e}_i^2+\frac{1}{2}{\xi }_{2i}^2}}{{\xi }_{2i}}\right]-\hfill \\ & \sum _{i=1}^n\left[\frac{k_{3i}{\left(1-H_i\right)}^2{\vartheta }_{ai}\sqrt{\frac{1}{2}{e}_i^2+\frac{1}{2}{\xi }_{1i}^2}}{{\xi }_{1i}}\right]-\sum _{i=1}^n\left[H_i{\vartheta }_{b_i}^2\left({\delta }_i+\frac{{\dot{\xi }}_{2i}}{{\xi }_{2i}}\right)+\frac{\left(1-H_i\right){\vartheta }_{ai}^2}{1-{\vartheta }_{a_i}^2}\left({\delta }_i+\frac{{\dot{\xi }}_{1i}}{{\xi }_{1i}}\right)\right].\hfill \end{array}$$

(35)

When $e_i\ge 0$, we can derive from Equations (25) and (26):

$$-\sum _{i=1}^n\frac{k_{3i}{H}_i^2{\vartheta }_{bi}\sqrt{\frac{1}{2}{e}_i^2+\frac{1}{2}{\xi }_{2i}^2}}{{\xi }_{2_i}}⩽-\sum _{i=1}^n{K}_{3i}{H}_i^2{\left({\vartheta }_{b_i}^2\right)}^{\frac{3}{4}}.$$

(36)

When $e_i<0$, we can obtain from Equations (25) and (26):

$$\sum _{i=1}^n\frac{k_{3i}{\left(1-H_i\right)}^2{\vartheta }_{a_i}\sqrt{\frac{1}{2}{e}_i^2+\frac{1}{2}{\xi }_{ij}^2}}{{\xi }_{1i}}⩽-\sum _{i=1}^n{k}_{3i}{\left(1-H_i\right)}^2{\left({\vartheta }_{a_i}^2\right)}^{\frac{3}{4}}.$$

(37)

Using Equation (33), we can derive the subsequent inequalities as follows:

$${\delta }_i+\frac{{\dot{\xi }}_{2i}}{{\xi }_{2i}}⩾0{\delta }_i+\frac{{\dot{\xi }}_{1i}}{{\xi }_{1i}}⩾0.$$

(38)

Substituting (36)–(38) into (35), we can find that:

$${\dot{V}}_1\le \sum _{i=1}^n\left[-k_{1i}{\vartheta }_i^2-k_{2i}{\left({\vartheta }_i^2\right)}^2-k_{3i}{\left({\vartheta }_i^2\right)}^{\frac{3}{4}}+{\zeta }_i{e}_i{z}_i\right]$$

(39)

where

$${\zeta }_i=\frac{H_i}{{\xi }_{2i}^2}+\frac{1-H_i}{{\xi }_{1i}^2}.$$

(40)

Subsequently, a potential Lyapunov function can be formulated in the following manner:

$$V_2=V_1+\frac{1}{2}{z}^{T}Dz+\sum _{i=1}^n\frac{d_i}{2c_i}{\tilde{\lambda }}_i^2+\sum _{i=1}^n\frac{1}{2}{\tilde{h}}_i^2,$$

(41)

where $\tilde{h}$ represents the estimation discrepancy of h for the estimated $\widehat{h}$ and actual h.

Consider the derivative of (41), along with (23), (24), and Property 1 to produce

$${\dot{V}}_2={\dot{V}}_1+z^T[\widehat{\tau }+h+r+F\left(z\right)]+\sum _{i=1}^n\frac{d_i}{c_i}{\tilde{\lambda }}_i{\dot{\widehat{\lambda }}}_i+\sum _{i=1}^n{\tilde{h}}_i{\dot{\widehat{h}}}_i.$$

(42)

The vector that will be approximated by the RBFNNs is given by the following definition:

$$F\left(Z\right)=-D\dot{\alpha }-C\alpha -G,$$

(43)

where the symbols D, C, and G are abbreviations for the terms $D\left(q\right)$, $C(q,\dot{q})$, and $G\left(q\right)$, respectively. The input vector, denoted as Z, can be defined as $Z={\left[q^T,{\dot{q}}^T,{\alpha }^T,{\dot{\alpha }}^T\right]}^T\in R^{4n}$. Moreover, the vector $F\left(Z\right)$ represents the concatenation of individual functions $f_i\left(Z\right)$, and is defined as $F\left(Z\right)={\left[f_1\left(Z\right),f_2\left(Z\right),\dots ,f_n\left(Z\right)\right]}^T$.

By utilizing Equation (41), we can deduce the subsequent equalities:

$$\begin{array}{cc}\hfill {\dot{V}}_2& ={\dot{V}}_1+z^T[\widehat{\tau }+F\left(z\right)]+\sum _{i=1}^n{z}_i{r}_i+\sum _{i=1}^n{z}_i{h}_i+\sum _{i=1}^n\frac{d_i}{c_i}{\tilde{\lambda }}_i{\dot{\widehat{\lambda }}}_i+\sum _{i=1}^n{\tilde{h}}_i{\dot{\widehat{h}}}_i\hfill \\ & ={\dot{V}}_1+z^T[\widehat{\tau }+F\left(z\right)]+\sum _{i=1}^n{\tilde{\lambda }}_i\frac{d_i}{c_i}\left({\dot{\widehat{\lambda }}}_i+z_i{c}_i{\widehat{\tau }}_i\right)+\sum _{i=1}^n{h}_i\left(-{\dot{\widehat{h}}}_i+z_i\right)+{\widehat{h}}_i{\dot{\widehat{h}}}_i.\hfill \end{array}$$

(44)

For Equation (44), actuator fault compensation, adaptive rules with unknown parameters $\widehat{\lambda }$ and $\widehat{h}$ can be designed.

$${\dot{\widehat{\lambda }}}_i=-z_i{c}_i{\widehat{\tau }}_i$$

(45)

$${\dot{\widehat{h}}}_i=z_i.$$

(46)

By utilizing Equations (42)–(44), we can deduce the following relationships:

$${\dot{V}}_2={\dot{V}}_1+z^T[\widehat{\tau }+F\left(z\right)]+{\widehat{h}}_i{\dot{\widehat{h}}}_i.$$

(47)

Then, we can employ n radial basis function neural networks (RBFNNs) to approximate the terms $f_i\left(Z\right)$, where $i=1,2,\dots ,n$, in the following manner:

$$\begin{array}{cc}\hfill & {\widehat{f}}_i\left(Z\right)={\widehat{W}}_i^T{S}_i\left(Z\right)\hfill \\ \hfill & f_i\left(Z\right)=W_i^{\ast T}{S}_i\left(Z\right)+{\epsilon }_i.\hfill \end{array}$$

(48)

In this context, $W_i^{\ast T}\in R^{N_i}$ and ${\widehat{W}}_i^T\in R^{N_i}$ indicate the optimal weight vector and the estimated weight vector of the neural network, respectively. $N_i$ denotes the number of nodes in the ith neural network. The vector $S_i\left(Z\right)\in R^{N_i}$ symbolizes the fundamental function vector. The discrepancy ${\epsilon }_i\in R$ corresponds to the estimation error of the ith neural network and is constrained by ${\epsilon }_i<{\overline{\epsilon }}_i$.

The neural network controller can be designed in the following manner:

$$\begin{array}{cc}\hfill {\widehat{\tau }}_i=& -k_{4i}{z}_i-{\widehat{h}}_i-{\zeta }_i{e}_i-\frac{{\widehat{f}}_i^2{z}_i}{\sqrt{{\widehat{f}}_i^2{z}_i^2+{\epsilon }_{1i}^2}}-k_{5i}{z}_i^3-k_{6i}{sig}^{0.5}\left(z_i\right),\hfill \end{array}$$

(49)

where $k_{4i}>\frac{1}{2}$, $k_{5i}>\frac{1}{2}$ and $k_{5i}>0$. The term ${sig}^{0.5}\left(z_i\right)$ carries the significance as described in Remark 1.

The formulation of the adaptive law for updating the neural network weights can be described as

$${\dot{\widehat{W}}}_i=Q_i\left(z_i{S}_i\left(Z\right)-m_i{\widehat{W}}_i\right),$$

(50)

the matrix $Q_i$ is a positive definite diagonal matrix, while the parameter $m_i$ represents a positive constant.

Remark 4.

When analyzing the unknown robot arm described in Equation (23), the tracking error $e_i$ defined in Equation (24) can achieve convergence within a fixed time interval if the error remains within the specified upper and lower bounds as stated in Equation (25). This desirable behavior can be achieved by utilizing the NN controller stated in (49) together with the adaptive law presented in (50).

Theorem 1.

When the controller given by Equation (49) and the adaptive law described in Equation (50) are employed for the unknown manipulator defined in Equation (23), it ensures that the tracking error stated in Equation (24) remains within the specified bounds, namely ${\xi }_{1i}<e_i<{\xi }_{2i}$. Additionally, it can be inferred that all signals within the closed-loop system are bounded.

Proof of Theorem 1.

The Lyapunov function is constructed in the following manner:

$$V=V_2+\frac{1}{2}\sum _{i=1}^n{\tilde{W}}_i^T{Q}_i^{-1}{\tilde{W}}_i,$$

(51)

the term ${\tilde{W}}_i$, which is given by the difference between $W_i^{\ast }$ and ${\widehat{W}}_i$, represents the estimation error of the optimal neural network weight $W_i^{\ast }$.

By differentiating V and combining it with Equations (47) and (50), we can derive the following expression:

$$\dot{V}={\dot{V}}_1+z^T[\widehat{\tau }+F\left(Z\right)]-\sum _{i=1}^n\left[m_i{\tilde{W}}_i^T{\dot{\widehat{W}}}_i-{\widehat{h}}_i{\dot{\widehat{h}}}_i\right].$$

(52)

By substituting Equations (39), (48) and (49) into Equation (52), we can derive the following expression:

$$\begin{array}{cc}\hfill \dot{V}\le & \sum _{i=1}^n\left[-k_{1i}{\vartheta }_i^2-k_{2i}{\left({\vartheta }_i^2\right)}^2-K_{3i}{\left({\vartheta }_i^2\right)}^{\frac{3}{4}}\right]+\sum _{i=1}^n\left[-k_{4i}{z}_i^2--K_{5i}{z}_i^4-k_{6i}{\left(z_i^2\right)}^{\frac{3}{4}}\right]+\hfill \\ & \sum _{i=1}^n\left[z_i{\epsilon }_i+m_i{\tilde{W}}_i^T{\widehat{W}}_i\right]+\sum _{i=1}^n\left[{\widehat{f}}_i{z}_i-\frac{{\widehat{f}}_i^2{z}_i^2}{\sqrt{{\widehat{f}}_i^2{z}_i^2+{ϵ}_i^2}}\right].\hfill \end{array}$$

(53)

Using Lemma 3, we can reach the following conclusion:

$${\widehat{f}}_i{z}_i-\frac{{\widehat{f}}_i^2{z}_i^2}{\sqrt{{\widehat{f}}_i^2{z}_i^2+{ϵ}_i^2}}⩽\left|{\widehat{f}}_i{z}_i\right|-\frac{{\widehat{f}}_i^2{z}_i^2}{\sqrt{{\widehat{f}}_i^2{z}_i^2+{ϵ}_i^2}}⩽{ϵ}_i.$$

(54)

The following results can be obtained for the terms $z_i{\epsilon }_i$ and $m_i{\tilde{W}}_i^T{\widehat{W}}_i$:

$$z_i{\epsilon }_i\le \left|z_i\right|\left|{\epsilon }_i\right|\le \frac{1}{2}\left(z_i^2+{\epsilon }_i^2\right)\le \frac{1}{2}{z}_i^2+\frac{1}{2}{\overline{\epsilon }}_i^2$$

(55)

$$\begin{array}{cc}\hfill m_i{\tilde{W}}_i^T{\widehat{W}}_i& =m_i{\tilde{W}}_i^T\left(W_i^{\ast }-{\tilde{W}}_i\right)=-m_i{∥{\tilde{W}}_i∥}^2+m_i{\tilde{W}}_i^T{W}_i^{\ast }\hfill \\ & \le m_i\left(\frac{{∥W_i^{\ast }∥}^2}{2}-\frac{{∥{\tilde{W}}_i∥}^2}{2}\right).\hfill \end{array}$$

(56)

By substituting Equations (55)–(57) into Equation (53), the following expression is obtained:

$$\begin{array}{cc}\hfill \dot{V}\le & \sum _{i=1}^n\left[-k_{1i}{\vartheta }_i^2-k_{2i}{\left({\vartheta }_i^2\right)}^2-K_{3i}{\left({\vartheta }_i^2\right)}^{\frac{3}{4}}\right]+\hfill \\ & \sum _{i=1}^n\left[-k_{4i}{z}_i^2-K_{5i}{z}_i^4-k_{6i}{\left(z_i^2\right)}^{\frac{3}{4}}\right]+\hfill \\ & \sum _{i=1}^n\left[m_i\left(\frac{{∥W_i^{\ast }∥}^2}{2}-\frac{{∥{\tilde{W}}_i∥}^2}{2}\right)\right]+\hfill \\ & \sum _{i=1}^n\left[\frac{1}{2}{z}_i^2+\frac{1}{2}{\overline{\epsilon }}_i^2+{ϵ}_i\right].\hfill \end{array}$$

(57)

Based on Equation (57), we can obtain the following inequality by deduction:

$$\begin{array}{cc}\hfill \dot{V}\le & \sum _{i=1}^n\left(-2k_{1i}\right)-min\left(\frac{2k_{4i}-1}{{\lambda }_{max}\left(D\right)}\right)\frac{1}{2}{z}^{T}Dz-min\left(\frac{m_i}{{\lambda }_{max}\left(Q_i^{-1}\right)}\right)\sum _{i=1}^n\left(\frac{1}{2}{\tilde{W}}_i^T{Q}_i^{-1}{\tilde{W}}_i\right)\hfill \\ & +{\mathsf{\Lambda }}_1,\hfill \end{array}$$

(58)

where ${\mathsf{\Lambda }}_1={\sum }_{i=1}^n\left[\frac{1}{2}{\overline{\epsilon }}_i^2+\frac{m_i{∥W_i^2∥}^2}{2}+{ϵ}_i\right]$ can be considered a positive constant with an upper bound, where ${\lambda }_{max}(·)$ represents the maximum eigenvalue of the term $(·)$.

Therefore, the desired result can be obtained as follows:

$$\dot{V}\le -{\psi }_{1}V+{\mathsf{\Lambda }}_1,$$

(59)

where ${\psi }_1=min\left(k_{1i},\frac{2k_{4i}-1}{{\lambda }_{max}\left(D\right)},\frac{m_i}{{\lambda }_{max}\left(Q_i^{-1}\right)}\right)$.

By multiplying both sides of Equation (59) by $e^{{\psi }_{1}t}$ and integrating both sides over the interval $[0,t]$, we obtain the following equation:

$$V\le \left[V\left(0\right)-\frac{{\mathsf{\Lambda }}_1}{{\psi }_1}\right]e^{-{\psi }_{1}t}+\frac{{\mathsf{\Lambda }}_1}{{\psi }_1}\le V\left(0\right)+\frac{{\mathsf{\Lambda }}_1}{{\psi }_1}.$$

(60)

The bounded nature of the Lyapunov function $V\left(t\right)$ can be inferred from the aforementioned inequality. By combining the definitions of $V\left(t\right)$ in (29), (53) and (51), we can conclude the boundedness of ${\vartheta }_i^2$, $z_i$, and ${\tilde{W}}_i$, respectively. Thus, it can be guaranteed that $|{\vartheta }_i|<1$. As a result, the tracking constraints specified by ${\xi }_{1i}<e_i<{\xi }_{2i}$ will not be violated, as indicated by Equation (26). Considering Equation (10) and Assumption 1, we can deduce that the variable q remains bounded. Furthermore, taking into account the boundedness of ${\vartheta }_i$, ${\xi }_{1i}$, ${\xi }_{2i}$, ${\dot{\xi }}_{1i}$, and ${\dot{\xi }}_{2i}$, we can conclude that the virtual controller ${\alpha }_i$ is bounded as well. Additionally, considering the finite nature of ${\widehat{W}}_i$ and the vector of Gaussian basis functions $S_i\left(Z\right)$, it can be demonstrated that the controller described in Equation (49) remains bounded. Thus, it can be inferred that all signals within the closed-loop system are limited in amplitude. □

Corollary 1.

Through further investigation, we can not only achieve fast convergence within a predetermined time, but also accurately restrict the tracking deviation $e_i$. Furthermore, we can calculate the exact time needed for the error to converge to a negligible value near zero.

Proof of Corollary 1.

The following inequality may be derived from (57) in a manner similar to the derivation of (58):

$$\begin{array}{cc}\hfill \dot{V}\le & \sum _{i=1}^n\left[-k_{2i}{\left({\vartheta }_i^2\right)}^2-K_{3i}{\left({\vartheta }_i^2\right)}^{\frac{3}{4}}-K_{5i}{z}_i^4-k_{6i}{\left(z_i^2\right)}^{\frac{3}{4}}\right]+\hfill \\ & \sum _{i=1}^n\left[\frac{1}{2}{z}_i^2+\frac{1}{2}{\overline{\epsilon }}_i^2+\frac{m_i{∥W_i^{\ast }∥}^2}{2}+{ϵ}_i\right]\hfill \end{array}.$$

(61)

For the term $\frac{1}{2}{z}_i^2$, we have:

$$\frac{1}{2}{z}_i^2\le \frac{1}{2}{z}_i^4+\frac{1}{8}.$$

(62)

Hence, it can be concluded that the norm of ${\tilde{W}}_i$ is limited by $\parallel {\tilde{W}}_i\parallel \le {\overline{\tilde{W}}}_i$, where ${\overline{\tilde{W}}}_i$ represents an unspecified positive constant. By replacing Equation (62) with Equation (61), we derive:

$$\begin{array}{cc}\hfill \dot{V}\le & \sum _{i=1}^n\left[-k_{2i}{\left({\vartheta }_i^2\right)}^2-K_{3i}{\left({\vartheta }_i^2\right)}^{\frac{3}{4}}-\left(k_{5i}-\frac{1}{2}\right)z_i^4-k_{6i}{\left(z_i^2\right)}^{\frac{3}{4}}\right]-\hfill \\ & \sum _{i=1}^n\left[k_{7i}{\left({∥{\tilde{W}}_i∥}^2\right)}^2+k_{8i}{\left({∥{\tilde{W}}_i∥}^2\right)}^{\frac{3}{4}}\right]+{\mathsf{\Lambda }}_2\hfill \end{array},$$

(63)

where ${\mathsf{\Lambda }}_2={\sum }_{i=1}^n\left[K_{7i}{\overline{\tilde{W}}}_i^4+K_{8i}{\overline{\tilde{W}}}_i^{\frac{3}{2}}+\frac{1}{8}+\frac{1}{2}{\overline{\epsilon }}_i^2+{ϵ}_i+\frac{m_i{∥W_i^{\ast }∥}^2}{2}\right]$.

Remark 5.

To conduct the fixed-time stability analysis, we made the assumption that the norm of ${\tilde{W}}_i$ is limited by $\parallel {\tilde{W}}_i\parallel \le {\overline{\tilde{W}}}_i$. However, the integration of the term $k_{7i}(\parallel {\tilde{W}}_i{\parallel }^2{)}^2+k_{8i}(\parallel {\tilde{W}}_i{{\parallel }^2)}^{\frac{3}{4}}$ to the positive constant ${\mathsf{\Lambda }}_2$ lacks a theoretical basis. In our work, we establish the inequality for the Lyapunov function similar to (46). Therefore, we can ascertain the finite bound of $\parallel {\tilde{W}}_i\parallel$ rather than making assumptions.

By utilizing Equation (63) and applying Lemma 2, we can deduce the following conclusion:

$$\dot{V}\le -{\psi }_2{V}^2-{\psi }_3{V}^{\frac{3}{4}}+{\mathsf{\Lambda }}_2,$$

(64)

where ${\psi }_2=\frac{1}{3n}min\left[4k_{2i},\frac{4k_{5i}-2}{{\lambda }_{max}^2\left(D\right)},\frac{4k_{7i}}{{\lambda }_{max}^2\left(Q_i^{-1}\right)}\right],{\psi }_3=min\left[\frac{k_{3i}}{{\left(\frac{1}{2}\right)}^{\frac{3}{4}}},\frac{k_{6i}}{{\left(\frac{1}{2}\right)}^{\frac{3}{4}}{\lambda }_{max}^{\frac{3}{4}}\left(D\right)},\frac{k_{8i}}{{\left(\frac{1}{2}\right)}^{\frac{3}{4}}{\lambda }_{max}^{\frac{3}{4}}\left(Q_i^{-1}\right)}\right]$.

The inequality form derived in Lemma 1 has been established thus far, demonstrating that the dynamical system achieves fixed-time convergence irrespective of the initial conditions. Furthermore, during the specified time interval, the Lyapunov function V of the system will approach a bounded region defined as follows:

$${\mathrm{\Omega }}_g=\left\{x\mid V\le min\left[{\left(\frac{{\mathsf{\Lambda }}_2}{{\psi }_3\left(1-{\theta }_1\right)}\right)}^{\frac{4}{3}},{\left(\frac{{\mathsf{\Lambda }}_2}{{\psi }_2\left(1-{\theta }_1\right)}\right)}^{\frac{1}{2}}\right]\right\}.$$

(65)

The time required for convergence can be expressed as follows:

$$T_{gmax}=\frac{4}{{\psi }_3{\theta }_1}+\frac{1}{{\psi }_2{\theta }_1},$$

(66)

where ${\theta }_1$ is a positive constant within the range $(0,1)$, we can attain both rapid convergence within a predetermined time and precise restriction of the tracking deviation $e_i$. The constraint is given by ${\xi }_{1i}<e_i<{\xi }_{2i}$, which is a more precise specification compared to the compact set mentioned in Equation (65). It is worth noting that larger values of ${\psi }_1$ and ${\psi }_2$ also contribute to a reduction in the convergence time. □

4. Simulation Study

To assess the effectiveness of the suggested controller, a demonstration involving a robotic system with two degrees of freedom will be employed.

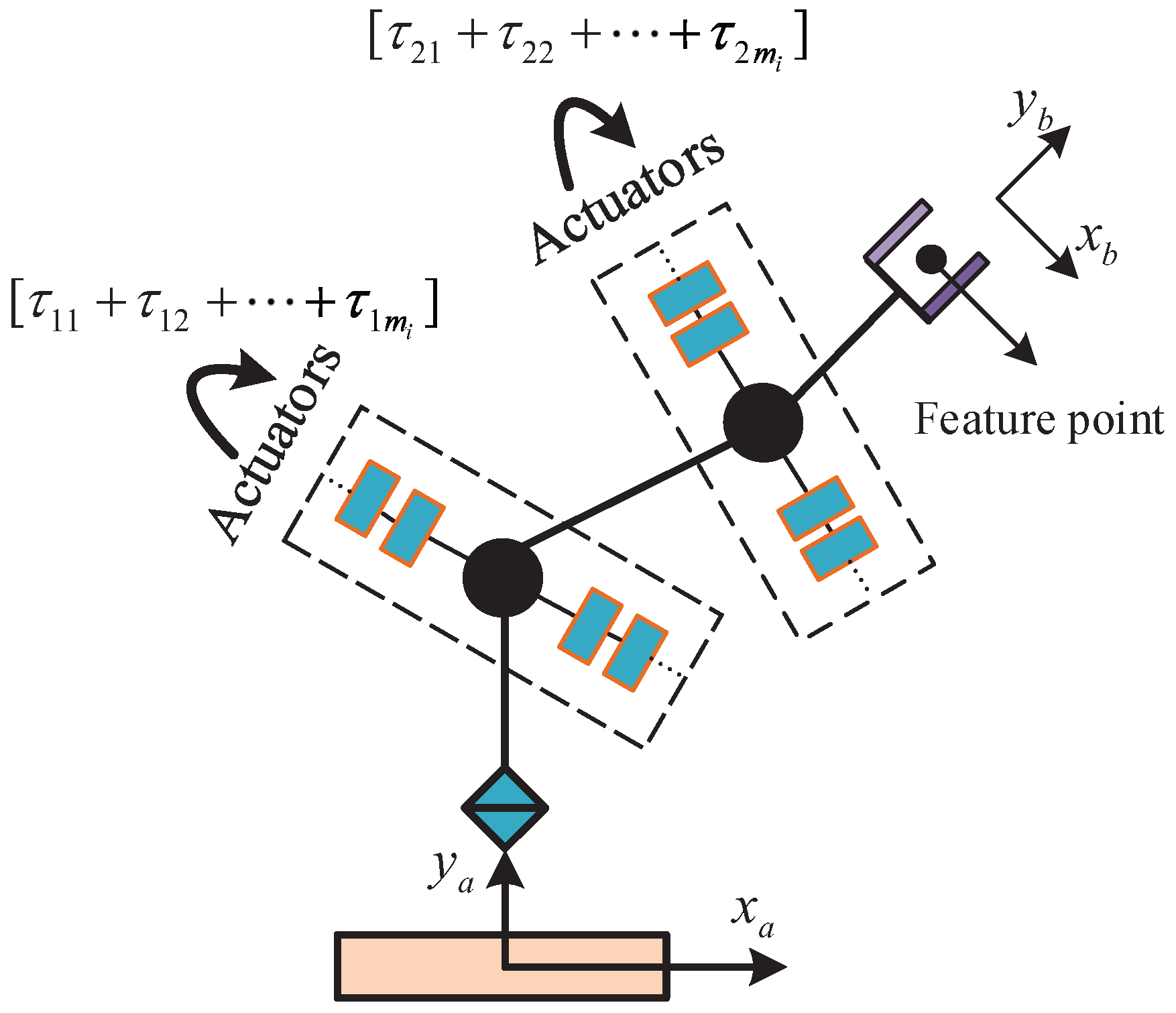
4.1. Robot Kinematics

The system block diagram of the mechanical arm is shown in Figure 2. In the figure, we can see that each joint of the robotic arm is driven by $m_i$ drives. The torque output of each joint of the manipulator is generated by $m_i$ actuators.

However, due to certain constraints and limitations, we only use two actuators per joint when simulating the system. The use of multiple actuators in a robotic system introduces additional complexity to the controller design. It requires the development of appropriate control algorithms to manage and adjust the output of each actuator. This may involve multi-variable control, coordination control and optimization problems, which greatly increases the difficulty of algorithm design and debugging. During the experiment, achieving coordination and synchronization between multiple actuators was also a challenging task. When designing the control algorithm, it is necessary to consider the interaction and mutual influence between each actuator to ensure the coordination and synchronization of the motion of each actuator, so as to achieve the ideal motion trajectory and stability.

Therefore, in our simulation, we chose to use a redundant robotic arm with two degrees of freedom, where each joint is driven by two actuators. In robotic systems, redundancy means having more than the minimum number of actuators needed to complete a particular task. In our example, there are two actuators for each joint, although only one actuator is actually needed to drive that joint. Therefore, we call this robotic arm system a redundant robotic arm.

For the redundant manipulator with two degrees of freedom, each joint is driven by two actuators joint, the joint Angle $q_{1_1}$, $q_{1_2}$, $q_{2_1}$ and $q_{2_2}$. Where $q_{1_1}$, $q_{1_2}$ are the first joint point of view, $q_{2_1}$ and $q_{2_2}$ represent the second joint point of view.

According to the geometric structure of the manipulator and the length of the connecting rod, the forward kinematics equation of the end-effector position is derived. Assuming that the connecting rod lengths of the mechanical arm are $L_1$ and $L_2$, respectively, the coordinates of the end effector position can be represented as

$$\begin{array}{cc}\hfill x& =L_{1}cos\left(q_{1_1}\right)+L_{2}cos(q_{1_1}+q_{2_1})+L_{2}cos(q_{1_1}+q_{2_1}+q_{2_2})\hfill \\ \hfill y& =L_{1}sin\left(q_{1_1}\right)+L_{2}sin(q_{1_1}+q_{2_1})+L_{2}sin(q_{1_1}+q_{2_1}+q_{2_2})\hfill \\ \hfill z& =\mathrm{specific}\mathrm{end}\text{-}\mathrm{effector}\mathrm{height}\mathrm{or}\mathrm{offset}\hfill \end{array}.$$

(67)

The partial derivative of position with respect to the joint angle is obtained by derivation of the forward kinematics equation. According to the chain rule, we calculate the coordinates of the end-effector position:

$$\begin{array}{cc}\hfill \frac{\partial x}{\partial q_{1_1}}& =-L_{1}sin\left(q_{1_1}\right)-L_{2}sin(q_{1_1}+q_{2_1})-L_{2}sin(q_{1_1}+q_{2_1}+q_{2_2})\hfill \\ \hfill \frac{\partial x}{\partial q_{1_2}}& =-L_{2}sin(q_{1_1}+q_{2_1}+q_{2_2})\hfill \\ \hfill \frac{\partial x}{\partial q_{2_1}}& =-L_{2}sin(q_{1_1}+q_{2_1})-L_{2}sin(q_{1_1}+q_{2_1}+q_{2_2})\hfill \\ \hfill \frac{\partial x}{\partial q_{2_2}}& =-L_{2}sin(q_{1_1}+q_{2_1}+q_{2_2})\hfill \\ \hfill \frac{\partial y}{\partial q_{1_1}}& =L_{1}cos\left(q_{1_1}\right)+L_{2}cos(q_{1_1}+q_{2_1})+L_{2}cos(q_{1_1}+q_{2_1}+q_{2_2})\hfill \\ \hfill \frac{\partial y}{\partial q_{1_2}}& =L_{2}cos(q_{1_1}+q_{2_1}+q_{2_2})\hfill \\ \hfill \frac{\partial y}{\partial q_{2_1}}& =L_{2}cos(q_{1_1}+q_{2_1})+L_{2}cos(q_{1_1}+q_{2_1}+q_{2_2})\hfill \\ \hfill \frac{\partial y}{\partial q_{2_2}}& =L_{2}cos(q_{1_1}+q_{2_1}+q_{2_2})\hfill \\ \hfill \frac{\partial z}{\partial q_{1_1}}& =0\hfill \\ \hfill \frac{\partial z}{\partial q_{1_2}}& =0\hfill \\ \hfill \frac{\partial z}{\partial q_{2_1}}& =0\hfill \\ \hfill \frac{\partial z}{\partial q_{2_2}}& =0\hfill \end{array}.$$

(68)

Building Jacobian matrix $J(q_{1_1},q_{1_2},q_{2_1},q_{2_2})$ will obtain the partial derivative and derivative together:

$$J(q_{1_1},q_{1_2},q_{2_1},q_{2_2})=\left[\begin{array}{cccc}\frac{\partial x}{\partial q_{1_1}}& \frac{\partial x}{\partial q_{1_2}}& \frac{\partial x}{\partial q_{2_1}}& \frac{\partial x}{\partial q_{2_2}}\\ \frac{\partial y}{\partial q_{1_1}}& \frac{\partial y}{\partial q_{1_2}}& \frac{\partial y}{\partial q_{2_1}}& \frac{\partial y}{\partial q_{2_2}}\\ \frac{\partial z}{\partial q_{1_1}}& \frac{\partial z}{\partial q_{1_2}}& \frac{\partial z}{\partial q_{2_1}}& \frac{\partial z}{\partial q_{2_2}}\end{array}\right].$$

(69)

According to the Jacobian matrix $J(q_{1_1},q_{1_2},q_{2_1},q_{2_2})$, joint speed ${[\dot{x},\dot{y},\dot{z}]}^T$ and the end executor speed ${[{\dot{q}}_{1_1},{\dot{q}}_{1_2},{\dot{q}}_{2_1},{\dot{q}}_{2_2}]}^T$ can be expressed by the following formula:

$$\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{z}\end{array}\right]=J(q_{1_1},q_{1_2},q_{2_1},q_{2_2})\left[\begin{array}{c}{\dot{q}}_{1_1}\\ {\dot{q}}_{1_2}\\ {\dot{q}}_{2_1}\\ {\dot{q}}_{2_2}\end{array}\right].$$

(70)

The relationship between the joint velocity and the end-effector velocity is obtained by the inverse operation:

$$\left[\begin{array}{c}{\dot{q}}_{1_1}\\ {\dot{q}}_{1_2}\\ {\dot{q}}_{2_1}\\ {\dot{q}}_{2_2}\end{array}\right]=J{(q_{1_1},q_{1_2},q_{2_1},q_{2_2})}^{-1}\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{z}\end{array}\right].$$

(71)

4.2. Simulation Setup

When the value of n is 2 in Equation (23), the expressions for $D\left(q\right)$, $C(q,\dot{q})$, and $G\left(q\right)$ can be formulated in the following manner:

$$\begin{array}{cc}\hfill D\left(q\right)& =\left[\begin{array}{cc}{D}_1\hfill & D_2\hfill \\ D_3\hfill & D_4\hfill \end{array}\right]\hfill \\ \hfill C(q,\dot{q})& =\left[\begin{array}{cc}{C}_1\hfill & C_2\hfill \\ C_3\hfill & C_4\hfill \end{array}\right]\hfill \\ \hfill G\left(q\right)& =\left[\begin{array}{c}{G}_1\hfill \\ G_2\hfill \end{array}\right]\hfill \end{array},$$

(72)

where

$$\begin{array}{cc}\hfill D_1& =m_1{l}_{c1}^2+m_2{l}_1^2+m_2{l}_{c2}^2+m_2{l}_1{l}_{c2}cos{q}_2+J_1+J_2\hfill \\ \hfill D_2& =D_3=m_2{l}_{c2}^2+m_2{l}_1{l}_{c2}cos{q}_2+J_2\hfill \\ \hfill D_4& =m_2{l}_{c2}^2+J_2\hfill \\ \hfill C_1& =-m_2{l}_1{l}_{c2}{\dot{q}}_{2}sin{q}_2\hfill \\ \hfill C_2& =-m_2{l}_1{l}_{c2}{\dot{q}}_{1}sin{q}_2-m_2{l}_1{l}_{c2}{\dot{q}}_{2}sin{q}_2\hfill \\ \hfill C_3& =m_2{l}_1{l}_{c2}{\dot{q}}_{1}sin{q}_2\hfill \\ \hfill C_4& =0\hfill \\ \hfill G_1& =m_1{l}_{c2}gcos{q}_1+m_2{l}_{1}gcos{q}_1+m_2{l}_{c2}gcos\left(q_1+q_2\right)\hfill \\ \hfill G_2& =m_2{l}_{c2}gcos\left(q_1+q_2\right)\hfill \end{array}.$$

(73)

In the given system, the parameters $m_1=m_2=2\mathrm{kg}$ and $l_1=l_2=0.5\mathrm{m}$ represent the mass and length of each link ($i=1,2$), respectively. The term $l_{ci}$$(i=1,2)$ represents the measurement of the separation between the i-1th joint and the center of mass of the ith link. The rotational inertia $J_1=J_2=0.125{\mathrm{kgm}}^2$ is computed for each link.

The reference trajectory is specified as $q_d={[sin\left(0.3t^2\right),2cos\left(0.3t^2\right)]}^T$. To ensure satisfactory transient performance, the output constraints ${\xi }_{1i}$ and ${\xi }_{2i}$ are specified as follows:

$$\begin{array}{c}{\xi }_{11}={\xi }_{12}=-\left(0.92e^{-t}+0.08\right)\hfill \\ {\xi }_{21}={\xi }_{22}=0.92e^{-t}+0.08\hfill \end{array}.$$

(74)

To design the controller, the parameters can be assigned as follows: $k_{1i}=k_{2i}=k_{3i}=2$, $k_{a1}=k_{a2}=0.5$, $k_{4i}=k_{5i}=k_{6i}=2$, and ${ϵ}_i=0.01$. The adaptive laws parameters in Equation (49) are modified to $Q_1=\mathrm{diag}\left\{0.16\right\}$ and $Q_2=\mathrm{diag}\left\{0.3\right\}$.

The simulated fault model can be inferred from Equation (17), where $m_i=i=2$. At the beginning of the normal operation of robot, until the fifth second, a sudden actuator failure occurs in the robot. The duration of the fault is 5 s. Specifically, the first and second joints of the robot experience an actuator failure, while the remaining actuators continue to function normally. This can be expressed as ${\sigma }_{12}={\sigma }_{22}=0$.

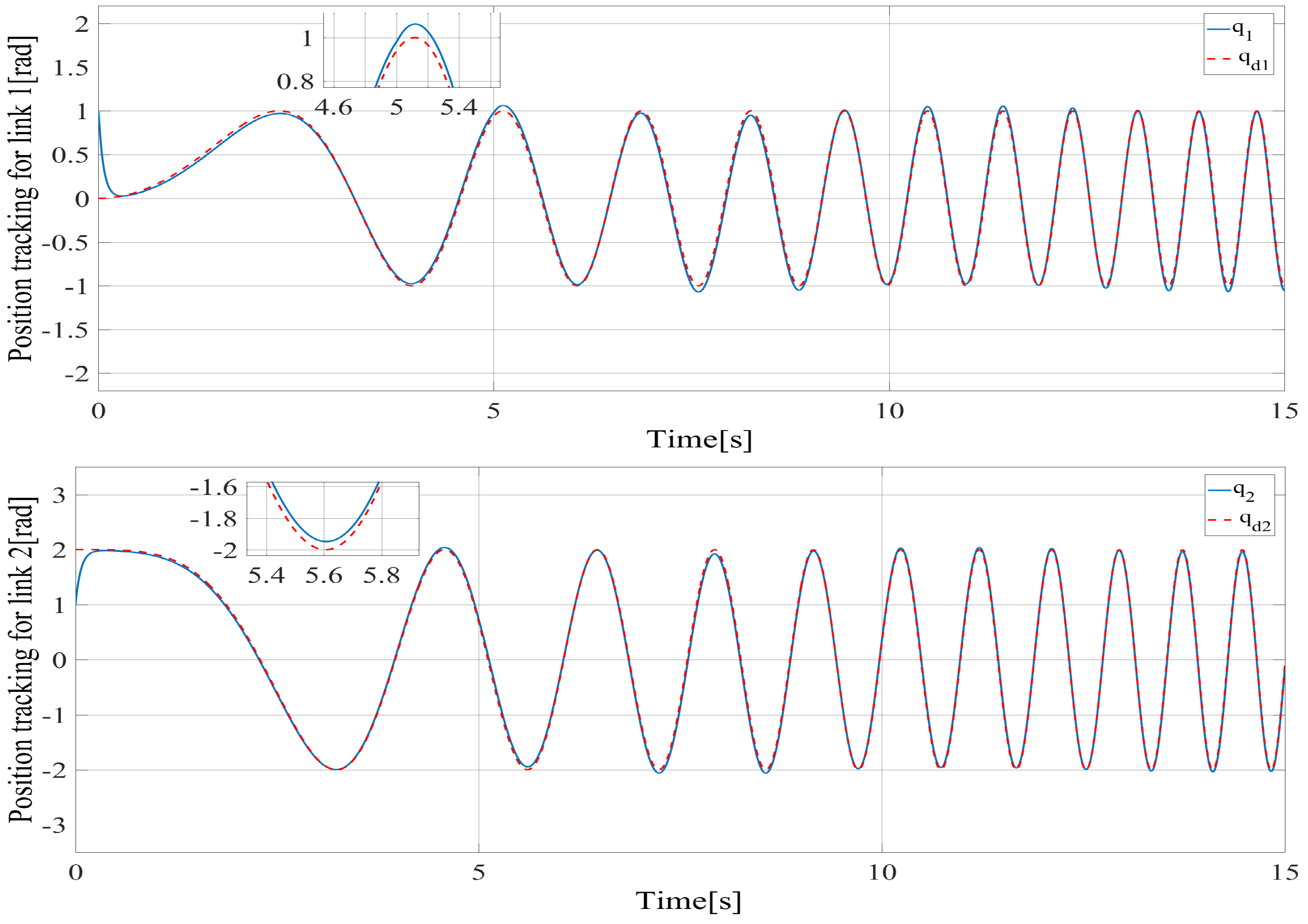
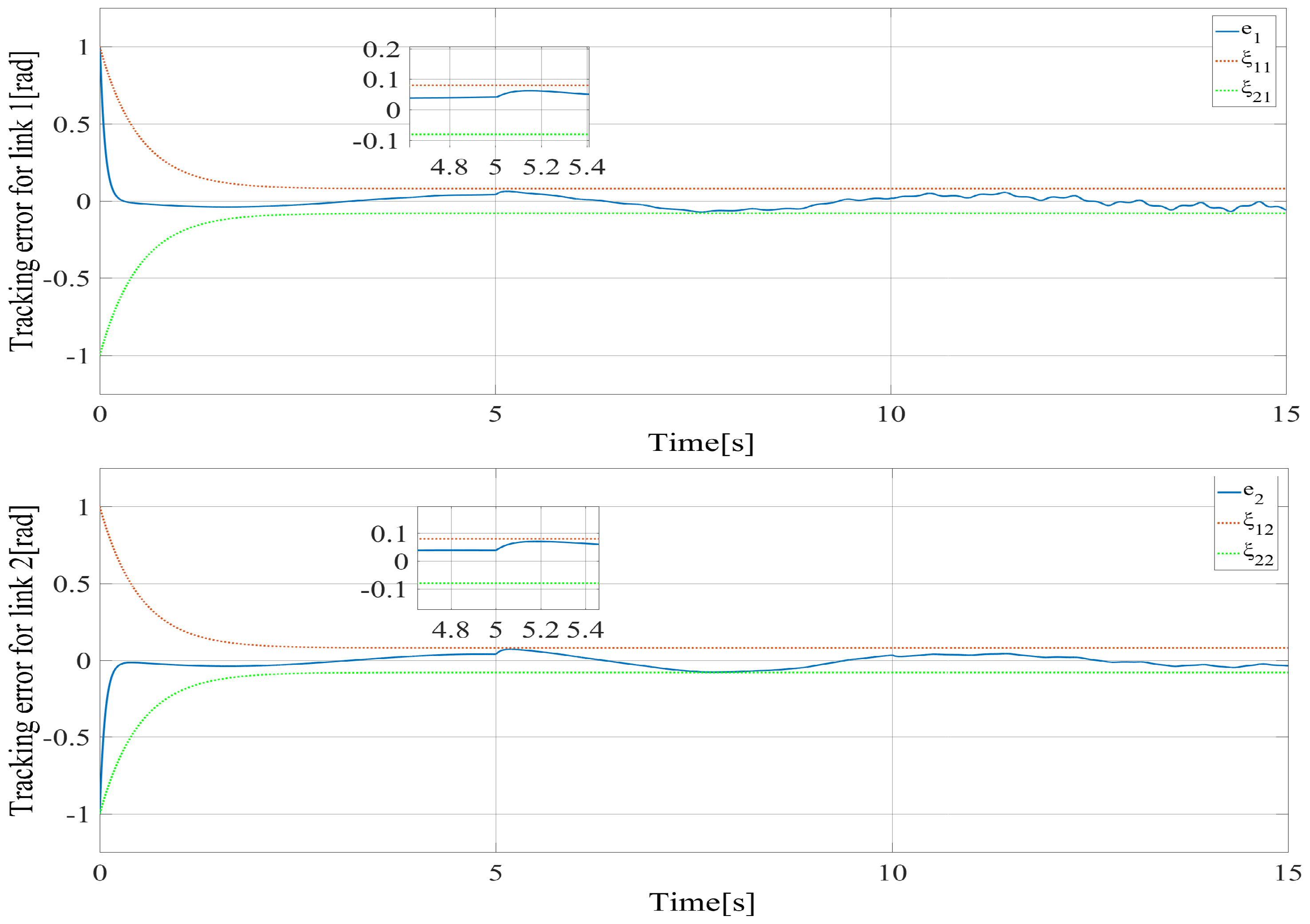
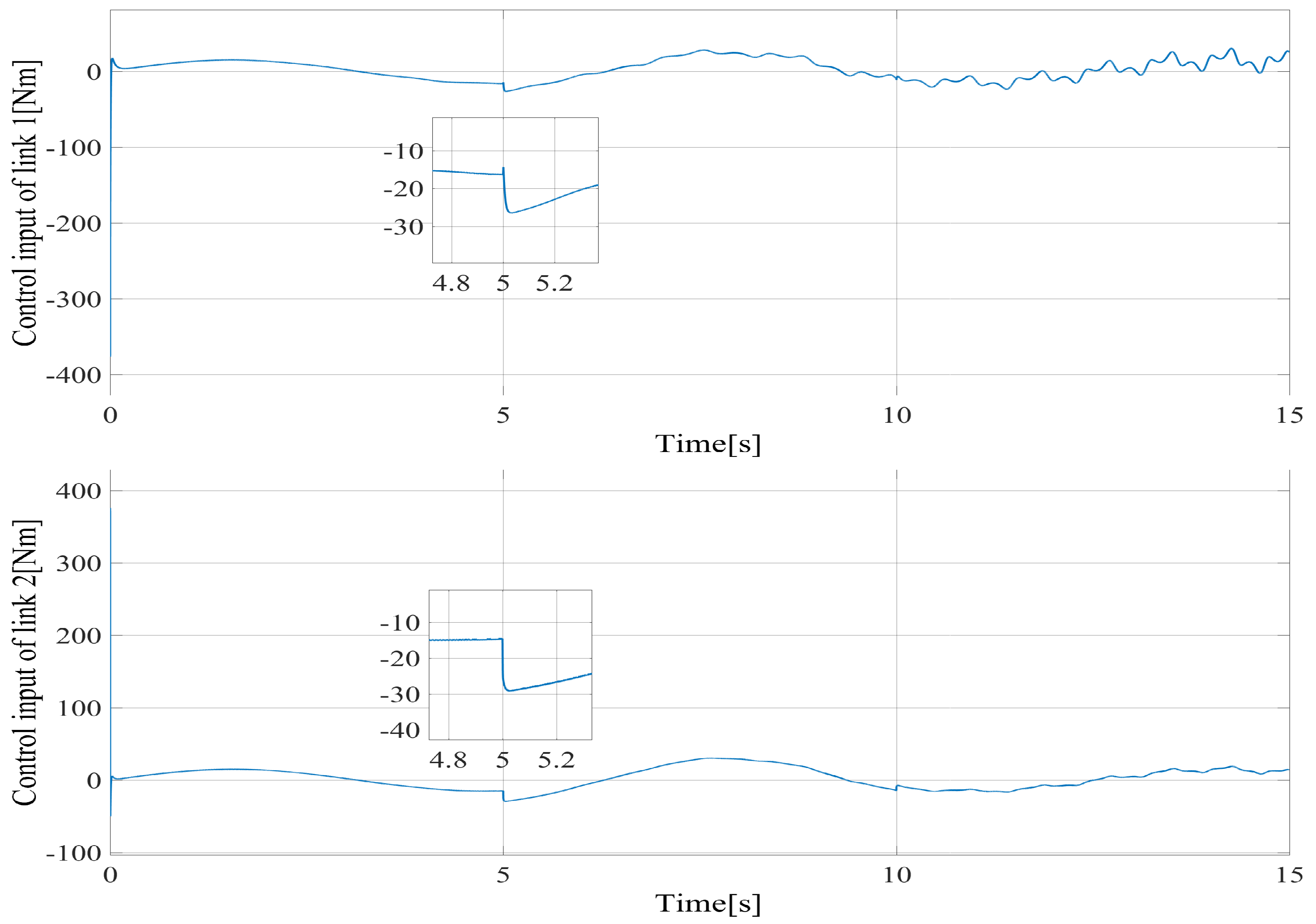
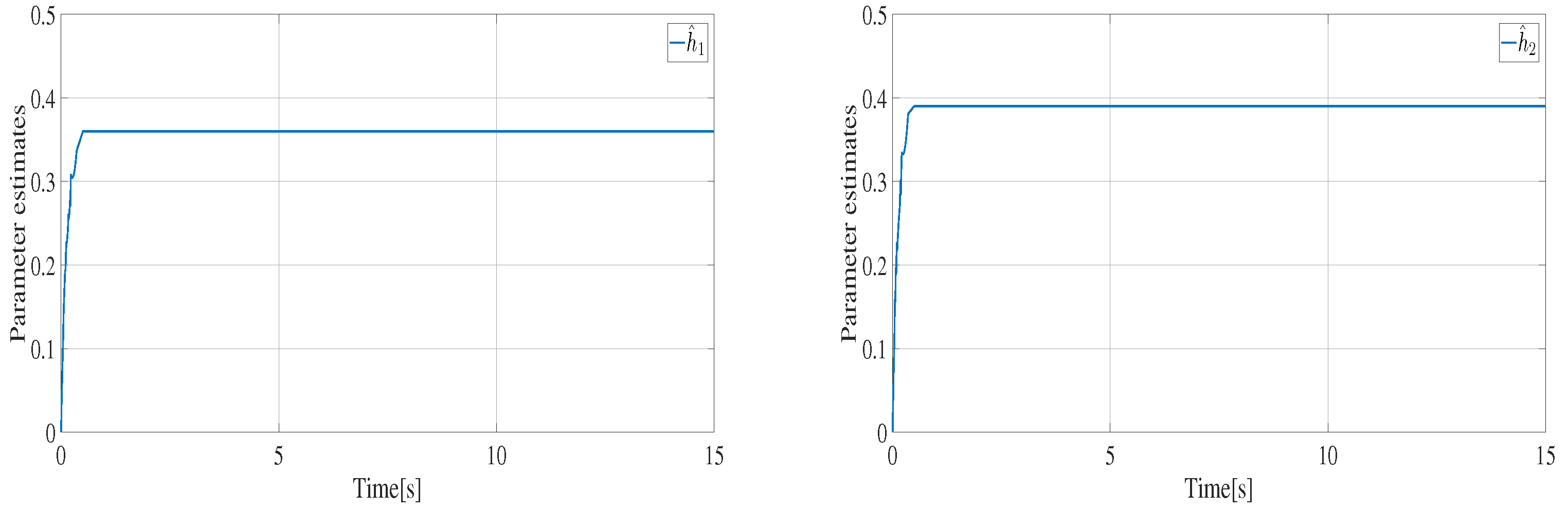
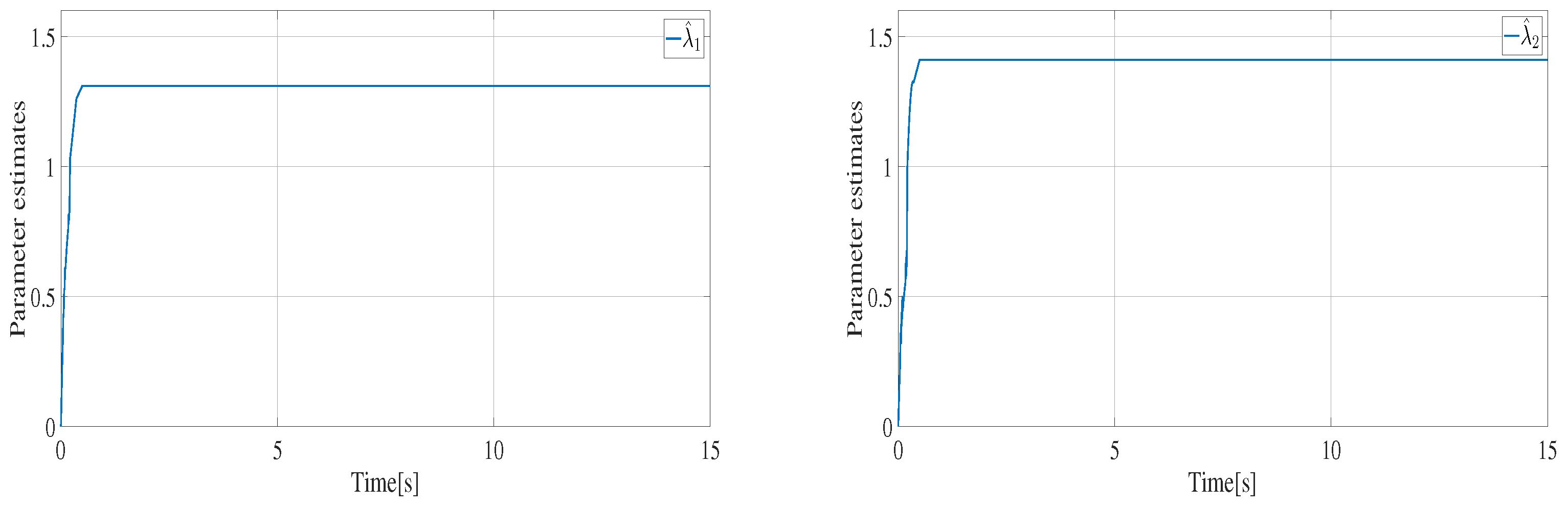
4.3. Simulation Results

By selecting the control design parameters and initial controller parameters, the plots shown in Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 are obtained. From Figure 3, it can be observed that the tracking trajectories of the two joint angles closely follow the desired trajectories during the first five seconds. However, at the fifth second, when the actuator failure occurs, it is evident that the tracking trajectory of the first joint angle deviates significantly from the desired trajectory. Overall, the tracking trajectories show a slightly lower level of fit to the desired trajectories when there is an actuator failure compared to when there is no failure. Figure 4 clearly demonstrates that the tracking error $e_i$ converges to a small value close to zero within 2 s. It can also be observed that there is a noticeable increase in tracking error for both joints when the actuator failure suddenly occurs, and the tracking error with actuator failure is slightly larger than that without failure. During operation, we can ensure that the tracking error $e_i$ remains within the range of ${\xi }_{1i}<e_i<{\xi }_{2i}$, thus guaranteeing the predefined transient performance. The torque ${\tau }_i$ is shown in Figure 5. At the fifth second, both ${\tau }_1$ and ${\tau }_2$ experience a significant jump. The adaptive parameters of the system are illustrated in Figure 6 and Figure 7.

5. Conclusions

This paper presents an adaptive control approach to address the challenge of actuator faults in unknown robots with predefined output constraints. A decoupling-based method is introduced to address actuator faults, and an adaptive rule is proposed to handle system delays resulting from the actuator fault. The unknown system dynamics are approximated using RBFNN, and a neural control scheme is designed to achieve tracking. Unlike conventional fixed-time algorithms, this approach limits tracking errors to predefined ranges instead of uncertain convergence domains.