A Novel Performance Bound for Massive MIMO Enabled HetNets

Abstract

Massive multiple-input and multiple-output (MIMO) networks with higher throughput rates, where a base station (BS) with a large-scale antenna array serves multiple users, have been widely employed in next-generation wireless communication test systems. Massive MIMO-enabled dense heterogeneous networks (HetNets) have also emerged as a promising architecture to increase the system spectrum efficiency and improve the system reliability. Massive MIMO-enabled HetNets have been successfully exploited in sustainable Internet of Thing networks (IoTs). In order to facilitate the testing and performance estimation of IoTs communication systems, this paper studies the achievable rate performance of massive MIMO and HetNets. Differing from the existing literature, we first consider an interference power model for massive MIMO-enabled HetNets. We next obtain an expression for the signal-to-interference-plus-noise ratio (SINR) by introducing an interference power. Furthermore, we derive a new closed-form lower bound expression for the achievable rate. The proposed closedform expression shows that the achievable rate is an explicit expression of the number of transmit antennas. In simulation results, the impact of the number of transmit antennas on the achievable rate performance is investigated.

1. Introduction

Heterogeneous networks (HetNets), where small cells are deployed within a macrocell coverage area, have been widely applied to offload data traffic and reduce network power consumption [1,2]. To further improve performance, massive multiple-input and multiple-output (MIMO)-enabled dense HetNets have emerged as a promising architecture to increase the system spectrum efficiency and improve the system reliability for the next-generation wireless networks [3].

Research works on the achievable rate and resource allocation schemes in massive MIMO-enabled HetNets have been published [4,5,6,7,8,9,10,11]. For example, the authors of [4] analyzed the downlink performance of a cell-free massive MIMO system with finite-capacity fronthaul links between the centralized baseband units and the access point. In [5], the authors investigated the tradeoff between energy efficiency and spectral efficiency in massive MIMO-enabled heterogenous networks, where user association and power coordination are jointly considered. In [6], the authors discussed the joint use of user association and resource allocation to maximize the fairness network utility for massive MIMO-enabled HetNets with backhaul capacity constraints. The authors of [7] studied the joint design of user association and power allocation with load constraint and transmit power constraint for massive MIMO HetNets. The authors of [8] investigated the energy-efficient user-association problem in massive MIMO-enabled HetNets, and formulated the network logarithmic utility maximization problem. The authors in [9] considered the metaheuristic algorithms for the power allocation issue, and a series of state-of-the-art stochastic algorithms are compared with the benchmark algorithm at network scales. The authors in [10] derived the statistical properties of a cellular network equipping a cylindrical array by considering the link blockage and other network parameters. In [11], the authors stuided an optimal solution for energy-efficiency in the downlink operation in the industrial internet based on cell-free massive MIMO systems with distributed operations, and a theoretical analysis of energy efficiency was presented. Additionally, the authors in [12] investigated the per-tier outage probability of multiuser MIMO transmissions in HetNets with joint interference constraint, and derived the closed-form expression of outage probability of downlink multiuser MIMO transmissions. Most of the aforementioned literature neglected the interference power constraint when designing system models. However, to the best of our knoweledge, the interference power constraint has a significant impact on the performance of network system; this is because the harmful transmission of strong interference sources will result in a low achievable rate. This motivated us to derive the performance bound of the achievable rate in massive MIMO-enabled HetNets by establishing an interference power constraint.

In this paper, we first provide an interference power model for a massive MIMO-enabled HetNet. A new expression of lower bound for the achievable rate is also developed. By taking some algebraic manipulations, a closed-form of lower bound, which can be used to assess the achievable rate performance, is derived. The simulation results provide some insights into the effect of the interference power constraint on the massive MIMO-enabled HetNets.

2. System Model

We consider a two-tier downlink massive MIMO HetNet. This network consists of a macro BS (MBS) and multiple pico BSs (PBSs). There are K single-antenna user terminals (UTs) that are uniformly deployed at the same time and bandwidth. This assumption is reasonable from the perspectives of the size and portability of the receiving user. We denote the set of PBSs by ${\mathcal{B}}_p=\{1,\dots ,J\}$ and the set of all BSs by $\mathcal{B}={\mathcal{B}}_p\cup \left\{0\right\}$, where the index 0 is introduced to indicate the MBS. We define $M_j$ as the number of transmit antennas at the jth BS. Let $S_j(1\le S_j\le M_j)$ be the maximum number of downlink data streams that BS j can transmit simultaneously. $k\in \mathcal{U}$ is denoted as the index for each UT, where $\mathcal{U}=\{1,\dots ,K\}$ is the set of UTs.

In our work, the channel vector is ${\mathbf{g}}_{j,k}=\sqrt{{\beta }_{j,k}}{\mathbf{h}}_{j,k}$, where ${\beta }_{j,k}$ and ${\mathbf{h}}_{j,k}\in {\mathbb{C}}^{M_j\times 1}$ represent the large-scale fading and small-scale fading from the jth BS to the kth UT, respectively. We assume that all channels are quasi-static fading channels. This means that ${\beta }_{j,k}$ is assumed to be constant over each resource block but change independently between different resource blocks. ${\mathbf{h}}_{j,k}$ is modeled as a complex Gaussian random vector, and elements of ${\mathbf{h}}_{j,k}$ are independent and identically distributed random variables (RV) with zero mean and unit variance.

The perfect CSI is supposed to be available at all BSs, and the MRT precoding is adopted. Therefore, the received signal of the kth UT associated with the jth BS can be expressed as

$$\begin{array}{cc}\hfill y_{j,k}& =\sqrt{\frac{P_j}{S_j}}{\mathbf{g}}_{j,k}^H{\mathbf{a}}_{j,k}{q}_{j,k}\hfill \\ \hfill & +\sum _{j^{\prime }\in \mathcal{B}\setminus j}\sum _{k^{\prime }\in S_{j^{\prime }}}\sqrt{\frac{P_{j^{\prime }}}{S_{j^{\prime }}}}{\mathbf{g}}_{j^{\prime },k}^H{\mathbf{a}}_{j^{\prime },k^{\prime }}{q}_{j^{\prime },k^{\prime }}+n_{j,k}\hfill \end{array}$$

(1)

where $P_j$ is the transmit power from the jth BS, and $j=0$ denotes the transmit power at the MBS; ${\mathbf{g}}_{j,k}\in {\mathbb{C}}^{M_j\times 1}$ denotes the downlink channel gain between the jth BS and the kth UT; ${\mathbf{a}}_{j,k}=\frac{{\mathbf{g}}_{j,k}}{\parallel {\mathbf{g}}_{j,k}\parallel }\in {\mathbb{C}}^{M_j\times 1}$ denotes the MRT precoding beamforming vector; $q_{j,k}$ is the transmitted information symbol from BS j to UT k with $\mathbb{E}\left\{q_{j,k}\right\}=0$ and $\mathbb{E}\left\{|q_{j,k}{|}^2\right\}=1$; the noise term $n_{j,k}$ is the additive white Gaussian noise (AWGN) with zero-mean and unit variance.

Next, we introduce an interference power to avoid the transmission from harmful interference. In general, the interference power at all UTs inflicted by the jth BS must not exceed the maximal peak interference level $I_p$. Therefore, we can obtain the transmit power at the jth BS, which is given as

$$\begin{array}{c}\hfill P_j=min\left\{{\displaystyle \frac{I_p}{\varpi }},P_{max}\right\}\end{array}$$

(2)

where $\varpi =\underset{k^{\prime }}{\max }\left\{{\left|{\mathbf{g}}_{j,k^{\prime }}\frac{{\mathbf{g}}_{j,k}}{∥{\mathbf{g}}_{j,k}∥}\right|}^2\right\}$; $P_{max}$ is the maximum transmit power at the jth BS. According to (1), the receive signal-to-interference-plus-noise ratio (SINR) of the downlink can be expressed as

$$\begin{array}{cc}\hfill {\gamma }_{j,k}& ={\displaystyle \frac{{\displaystyle \frac{P_j}{S_j}}{∥{\mathbf{g}}_{j,k}∥}^2}{{\displaystyle \sum _{j^{\prime }\in \mathcal{B}\setminus j}}{\displaystyle \sum _{k^{\prime }\in S_{j^{\prime }}}}{\displaystyle \frac{P_{j^{\prime }}}{S_{j^{\prime }}}}{\left|{\displaystyle \frac{{\mathbf{g}}_{j^{\prime },k}^H}{∥{\mathbf{g}}_{j^{\prime },k}^H∥}}{\mathbf{g}}_{j^{\prime },k^{\prime }}\right|}^2+1}}\hfill \\ \hfill & ={\displaystyle \frac{{\displaystyle \frac{min\left\{{\displaystyle \frac{I_p}{\varpi }},P_{max}\right\}}{S_j}}{∥{\mathbf{g}}_{j,k}∥}^2}{{\displaystyle \sum _{j^{\prime }\in \mathcal{B}\setminus j}}{\displaystyle \sum _{k^{\prime }\in S_{j^{\prime }}}}{\displaystyle \frac{P_{j^{\prime }}}{S_{j^{\prime }}}}{\left|{\displaystyle \frac{{\mathbf{g}}_{j^{\prime },k}^H}{∥{\mathbf{g}}_{j^{\prime },k}^H∥}}{\mathbf{g}}_{j^{\prime },k^{\prime }}\right|}^2+1}}\hfill \\ \hfill & ={\displaystyle \frac{{\displaystyle \frac{1}{S_j}}U}{V+1}}\hfill \end{array}$$

(3)

where $U=min\left\{{\displaystyle \frac{I_p}{\varpi }},P_{max}\right\}{X}_j$, with $X_j={∥{\mathbf{g}}_{j,k}∥}^2$; $V={\displaystyle \sum _{j^{\prime }\in \mathcal{B}\setminus j}}{\displaystyle \frac{P_{j^{\prime }}}{S_{j^{\prime }}}}{Y}_{j^{\prime }}$, and where $Y_{j^{\prime }}={\displaystyle \sum _{k^{\prime }\in S_{j^{\prime }}}}{\left|{{\rm Y}}_{k^{\prime }}\right|}^2$, with ${{\rm Y}}_{k^{\prime }}={\displaystyle \frac{{\mathbf{g}}_{j^{\prime },k}^H}{∥{\mathbf{g}}_{j^{\prime },k}^H∥}}{\mathbf{g}}_{j^{\prime },k^{\prime }}$.

3. Performance Bound

In this section, we will show a tight lower bound on the achievable rate and further derive the closed-form of the lower bound. First, the exact achievable rate for the kth UT associated with the jth BS can be written as $R_{j,k}=\mathbb{E}\left\{{\log }_2\left(1+{\gamma }_{j,k}\right)\right\}$. By utilizing Jensen’s inequality [13], the achievable rate can be lower-bounded as

$$\begin{array}{c}\hfill {\overline{R}}_{j,k}={\log }_2\left(1+e^{\Delta }\right)\end{array}$$

(4)

where $\Delta =\mathbb{E}\{ln{\gamma }_{j,k}\}=\mathbb{E}\{lnU\}-\mathbb{E}\{ln(V+1)\}-ln{S}_j$.

Obviously, we can obtain the closed-form expression of the proposed lower bound by deriving the expression of $\Delta$, as shown in Theorem 1.

Theorem 1.

A new closed-form of lower bound on the achievable rate can be expressed as ${\overline{R}}_{j,k}={\log }_2\left(1+e^{\Delta }\right)$, where

$$\begin{array}{cc}\hfill \Delta & =\psi \left(M_j\right)+ln{I}_p{\beta }_{j,k}\hfill \\ \hfill & -\left(1+\sum _{k^{\prime }=1}^{S_{j^{\prime }}}\frac{{(-1)}^{k^{\prime }}}{k^{\prime }!}\underset{|n_1\bigcup \cdots \bigcup n_{k^{\prime }}|=k^{\prime }}{\underbrace{\sum _{n_1=1}^{S_{j^{\prime }}}\cdots \sum _{n_{k^{\prime }}=1}^{S_{j^{\prime }}}}}{e}^{-{\beta }_{j,k^{\prime }}\frac{I_p}{P_{max}}}\right)ln\frac{I_p}{P_{max}}\hfill \\ \hfill & +\sum _{k^{\prime }=1}^{S_{j^{\prime }}}\frac{{(-1)}^{k^{\prime }+1}}{k^{\prime }!}\underset{|n_1\bigcup \cdots \bigcup n_{k^{\prime }}|=k^{\prime }}{\underbrace{\sum _{n_1=1}^{S_{j^{\prime }}}\cdots \sum _{n_{k^{\prime }}=1}^{S_{j^{\prime }}}}}\hfill \\ \hfill & \times \left[\mathrm{Ei}\left(-\frac{{\beta }_{j,k^{\prime }}{I}_p}{P_{max}}\right)-e^{-{\beta }_{j,k^{\prime }}\frac{I_p}{P_{max}}}ln\frac{I_p}{P_{max}}\right]\hfill \\ \hfill & -ln{S}_j-\sum _{h=1}^{\rho \left(\mathcal{A}\right)}\sum _{l=1}^{{\theta }_h\left(\mathcal{A}\right)}{\chi }_{h,l}\left(\mathcal{A}\right){\displaystyle \frac{1}{\left(l-1\right)!}}\Omega \hfill \end{array}$$

(5)

where

$$\begin{array}{cc}\hfill \Omega & =\sum _{\mu =0}^{l-1}{\displaystyle \frac{(l-1)!}{(l-1-\mu )!}}\left[{\displaystyle \frac{{(-1)}^{l-2-\mu }}{{\xi }_h^{l-1-\mu }}}{e}^{\frac{1}{{\xi }_h}}\mathrm{Ei}\left(-\frac{1}{{\xi }_h}\right)\right.\hfill \\ & \left.+\sum _{m=1}^{l-1-\mu }(m-1)!{\left(-\frac{1}{{\xi }_h}\right)}^{l-1-\mu -m}\right]\hfill \end{array}$$

(6)

where $\psi (·)$ is the digamma function; $|n_1\bigcup \cdots \bigcup n_{k^{\prime }}|$ is the cardinality of the union of $k^{\prime }$; $\mathrm{Ei}(·)$ is the exponential integral function; ${\xi }_n=\frac{P_{j^{\prime }}}{S_{j^{\prime }}}{\beta }_{j^{\prime },k^{\prime }}$, with $n=S_{j^{\prime }}(j^{\prime }-1)+k^{\prime }$; $\mathcal{A}=\mathrm{diag}\left({\xi }_1,{\xi }_2,\cdots ,{\xi }_T\right)$, with $T=J{S}_{j^{\prime }}$; $\rho \left(\mathcal{A}\right)$ is the number of distinct diagonal elements of $\mathcal{A}$; ${\xi }_1>{\xi }_2>\cdots >{\xi }_{\rho \left(\mathcal{A}\right)}$ are the distinct diagonal elements in decreasing order; ${\xi }_h\left(\mathcal{A}\right)$ is the multiplicity of ${\xi }_h$; ${\chi }_{h,l}$ is the $(h,l)$th characteristic coefficient of $\mathcal{A}$ [14].

Proof of Theorem 1.

In order to obtain the closed-form, we need to calculate the expectations for $\mathbb{E}\{lnU\}$ and $\mathbb{E}\{ln(V+1\left)\right\}$ separately.

Since ${\mathbf{g}}_{j,k^{\prime }}\frac{{\mathbf{g}}_{j,k}}{∥{\mathbf{g}}_{j,k}∥}$ is a complex Gaussian RV, we can learn the cumulative density function (CDF) of $\varpi$, which is given by

$$\begin{array}{cc}\hfill F_{\varpi }\left(x\right)& =\mathrm{Pr}\left(\underset{k^{\prime }}{max}\left\{{\left|{\mathbf{g}}_{j,k^{\prime }}\frac{{\mathbf{g}}_{j,k}}{∥{\mathbf{g}}_{j,k}∥}\right|}^2\right\}<x\right)\hfill \\ \hfill & =\prod _{k^{\prime }=1}^{S_{j^{\prime }}}\left(1-e^{-\frac{x}{{\beta }_{j,k^{\prime }}}}\right)\hfill \\ \hfill & =1+\sum _{k^{\prime }=1}^{S_{j^{\prime }}}\frac{{(-1)}^{k^{\prime }}}{k^{\prime }!}\underset{|n_1\bigcup \cdots \bigcup n_{k^{\prime }}|=k^{\prime }}{\underbrace{\sum _{n_1=1}^{S_{j^{\prime }}}\cdots \sum _{n_{k^{\prime }}=1}^{S_{j^{\prime }}}}}{e}^{-{\beta }_{j,k^{\prime }}x}.\hfill \end{array}$$

(7)

where $|n_1\bigcup \cdots \bigcup n_{k^{\prime }}|$ is the cardinality of the union of $k^{\prime }$. Therefore, $n_1,\dots ,n_{k^{\prime }}$ denote the $k^{\prime }$ variables, respectively, in the summation calculation.

Furthermore, the probability density function (PDF) of $P_j$ can be expressed as

$$\begin{array}{cc}\hfill f_{\varpi }\left(x\right)& =\sum _{k^{\prime }=1}^{S_{j^{\prime }}}\frac{{(-1)}^{k^{\prime }+1}}{k^{\prime }!}\underset{|n_1\bigcup \cdots \bigcup n_{k^{\prime }}|=k^{\prime }}{\underbrace{\sum _{n_1=1}^{S_{j^{\prime }}}\cdots \sum _{n_{k^{\prime }}=1}^{S_{j^{\prime }}}}}{\beta }_{j,k^{\prime }}{e}^{-{\beta }_{j,k^{\prime }}x}.\hfill \end{array}$$

(8)

Inspired by [15], the PDF of $X_j$ is given by

$$\begin{array}{cc}\hfill f_{X_j}\left(x\right)& ={\displaystyle \frac{x^{M_j-1}}{\left(M_j-1\right)!{\beta }_{j,k}^{M_j}}}{e}^{-\frac{x}{{\beta }_{j,k}}}.\hfill \end{array}$$

(9)

Now, we will compute the CDF of U, which is expressed as

$$\begin{array}{cc}\hfill F_U\left(x\right)& =\mathrm{Pr}\left(min\left\{{\displaystyle \frac{I_p}{\varpi }},P_{max}\right\}{X}_j<x\right)\hfill \\ \hfill & =\mathrm{Pr}\left(X_j<\frac{x}{P_{max}},\varpi <\frac{I_p}{P_{max}}\right)\hfill \\ \hfill & +\mathrm{Pr}\left(\frac{X_j}{\varpi }<\frac{x}{I_p},\varpi >\frac{I_p}{P_{max}}\right)\hfill \\ \hfill & =F_{X_j}\left(\frac{x}{P_{max}}\right)F_{\varpi }\left(\frac{I_p}{P_{max}}\right)\hfill \\ \hfill & +{\int }_{\frac{I_p}{P_{max}}}^{\propto }{F}_{X_j}\left(\frac{xt}{I_p}\right)f_{\varpi }\left(t\right)dt\hfill \end{array}$$

(10)

where $F_{X_j}\left(x\right)$ is the CDF of $X_j$. By taking the derivative of (10), we have

$$\begin{array}{cc}\hfill f_U\left(x\right)& =\frac{1}{P_{max}}{f}_{X_j}\left(\frac{x}{P_{max}}\right)F_{\varpi }\left(\frac{I_p}{P_{max}}\right)\hfill \\ \hfill & +{\int }_{\frac{I_p}{P_{max}}}^{\propto }\frac{t}{I_p}{f}_{X_j}\left(\frac{xt}{I_p}\right)f_{\varpi }\left(t\right)dt\hfill \\ \hfill & ={\displaystyle \frac{x^{M_j-1}}{\left(M_j-1\right)!{\left(P_{max}{\beta }_{j,k}\right)}^{M_j}}}{e}^{-\frac{x}{P_{max}{\beta }_{j,k}}}{F}_{\varpi }\left(\frac{I_p}{P_{max}}\right)\hfill \\ \hfill & +\sum _{k^{\prime }=1}^{S_{j^{\prime }}}\frac{{(-1)}^{k^{\prime }+1}}{k^{\prime }!}\underset{|n_1\bigcup \cdots \bigcup n_{k^{\prime }}|=k^{\prime }}{\underbrace{\sum _{n_1=1}^{S_{j^{\prime }}}\cdots \sum _{n_{k^{\prime }}=1}^{S_{j^{\prime }}}}}{\beta }_{j,k^{\prime }}\hfill \\ \hfill & \times {\displaystyle \frac{x^{M_j-1}}{\left(M_j-1\right)!{\left(I_p{\beta }_{j,k}\right)}^{M_j}}}{\int }_{\frac{I_p}{P_{max}}}^{\propto }{t}^{M_j}{e}^{-\left(\frac{x}{I_p{\beta }_{j,k}}+{\beta }_{j,k^{\prime }}\right)t}dt.\hfill \end{array}$$

(11)

As a result, we can calculate $\mathbb{E}\{lnU\}$ as

$$\begin{array}{cc}\hfill & \mathbb{E}\{lnU\}\hfill \\ \hfill & ={\int }_0^{\propto }{f}_U\left(x\right)lnxdx\hfill \\ & ={\displaystyle \frac{F_{\varpi }\left(\frac{I_p}{P_{max}}\right)}{\left(M_j-1\right)!{\left(P_{max}{\beta }_{j,k}\right)}^{M_j}}}{\int }_0^{\propto }{x}^{M_j-1}{e}^{-\frac{x}{P_{max}{\beta }_{j,k}}}lnxdx\hfill \\ \hfill & +\sum _{k^{\prime }=1}^{S_{j^{\prime }}}\frac{{(-1)}^{k^{\prime }+1}}{k^{\prime }!}\underset{|n_1\bigcup \cdots \bigcup n_{k^{\prime }}|=k^{\prime }}{\underbrace{\sum _{n_1=1}^{S_{j^{\prime }}}\cdots \sum _{n_{k^{\prime }}=1}^{S_{j^{\prime }}}}}{\displaystyle \frac{{\beta }_{j,k^{\prime }}}{\left(M_j-1\right)!{\left(I_p{\beta }_{j,k}\right)}^{M_j}}}\hfill \\ \hfill & \times {\int }_0^{\propto }{x}^{M_j-1}lnxdx{\int }_{\frac{I_p}{P_{max}}}^{\propto }{t}^{M_j}{e}^{-\left(\frac{x}{I_p{\beta }_{j,k}}+{\beta }_{j,k^{\prime }}\right)t}dt\hfill \end{array}$$

(12)

where the first definite integrals of (12) can be simplified as (4.352) in [16]

$$\begin{array}{cc}\hfill & {\int }_0^{\propto }{x}^{M_j-1}{e}^{-\frac{x}{P_{max}{\beta }_{j,k}}}lnxdx\hfill \\ \hfill & ={\left(P_{max}{\beta }_{j,k}\right)}^{M_j}\Gamma \left(M_j\right)\left(\psi \left(M_j\right)+ln{P}_{max}{\beta }_{j,k}\right).\hfill \end{array}$$

(13)

The second definite integrals of (12) can be simplified as

$$\begin{array}{cc}\hfill & {\int }_0^{\propto }{x}^{M_j-1}lnxdx{\int }_{\frac{I_p}{P_{max}}}^{\propto }{t}^{M_j}{e}^{-\left(\frac{x}{I_p{\beta }_{j,k}}+{\beta }_{j,k^{\prime }}\right)t}dt\hfill \\ \hfill & ={\int }_{\frac{I_p}{P_{max}}}^{\propto }{t}^{M_j}{e}^{-{\beta }_{j,k^{\prime }}t}{\int }_0^{\propto }{x}^{M_j-1}{e}^{-\frac{t}{I_p{\beta }_{j,k}}x}lnxdxdt\hfill \\ \hfill & ={\left(I_p{\beta }_{j,k}\right)}^{M_j}\frac{\Gamma \left(M_j\right)}{{\beta }_{j,k^{\prime }}}\left[\left(\psi \left(M_j\right)+ln{I}_p{\beta }_{j,k}\right)e^{-{\beta }_{j,k^{\prime }}\frac{I_p}{P_{max}}}\right.\hfill \\ & \left.-e^{-{\beta }_{j,k^{\prime }}\frac{I_p}{P_{max}}}ln\frac{I_p}{P_{max}}+\mathrm{Ei}\left(-\frac{{\beta }_{j,k^{\prime }}{I}_p}{P_{max}}\right)\right].\hfill \end{array}$$

(14)

Substituting (13) and (14) into (12), we have

$$\begin{array}{cc}\hfill & \mathbb{E}\{lnU\}\hfill \\ \hfill & =\psi \left(M_j\right)+ln{I}_p{\beta }_{j,k}-F_{\varpi }\left(\frac{I_p}{P_{max}}\right)ln\frac{I_p}{P_{max}}\hfill \\ \hfill & +\sum _{k^{\prime }=1}^{S_{j^{\prime }}}\frac{{(-1)}^{k^{\prime }+1}}{k^{\prime }!}\underset{|n_1\bigcup \cdots \bigcup n_{k^{\prime }}|=k^{\prime }}{\underbrace{\sum _{n_1=1}^{S_{j^{\prime }}}\cdots \sum _{n_{k^{\prime }}=1}^{S_{j^{\prime }}}}}\hfill \\ \hfill & \times \left[\mathrm{Ei}\left(-\frac{{\beta }_{j,k^{\prime }}{I}_p}{P_{max}}\right)-e^{-{\beta }_{j,k^{\prime }}\frac{I_p}{P_{max}}}ln\frac{I_p}{P_{max}}\right].\hfill \end{array}$$

(15)

Next, we focus on the expectation $\mathbb{E}\{ln(V+1\left)\right\}$ in (4). The expression of V can be written as a single summation, i.e., $V={\displaystyle \sum _{n=1}^{J{S}_{j^{\prime }}}}{\varphi }_n$, where ${\varphi }_n=\frac{P_{j^{\prime }}}{S_{j^{\prime }}}{\left|{{\rm Y}}_{k^{\prime }}\right|}^2$, and with $n=S_{j^{\prime }}\left(j^{\prime }-1\right)+k^{\prime }$. Thus, we have ${\varphi }_n\sim \mathrm{Exp}\left(\frac{1}{{\xi }_n}\right)$, where $\mathrm{Exp}(·)$ is the exponential distribution; ${\xi }_n=\frac{P_{j^{\prime }}}{S_{j^{\prime }}}{\beta }_{j^{\prime },k^{\prime }}$. Therefore, the PDF of V is given by Theorem 2 in [17]

$$\begin{array}{cc}\hfill & f_V\left(x\right)=\sum _{h=1}^{\rho \left(\mathcal{A}\right)}\sum _{l=1}^{{\theta }_h\left(\mathcal{A}\right)}{\chi }_{h,l}\left(\mathcal{A}\right){\displaystyle \frac{{\xi }_h^{-l}}{\left(l-1\right)!}}{x}^{l-1}{e}^{\frac{-x}{{\xi }_h}}.\hfill \end{array}$$

(16)

As such, we can obtain

$$\begin{array}{cc}\hfill & \mathbb{E}\{ln(V+1\left)\right\}\hfill \\ \hfill & ={\int }_0^{\propto }{f}_V\left(x\right)ln(x+1)dx\hfill \\ & =\sum _{h=1}^{\rho \left(\mathcal{A}\right)}\sum _{l=1}^{{\theta }_h\left(\mathcal{A}\right)}{\chi }_{h,l}\left(\mathcal{A}\right){\displaystyle \frac{{\xi }_h^{-l}}{\left(l-1\right)!}}{\int }_0^{\propto }{x}^{l-1}ln(x+1)e^{\frac{-x}{{\xi }_h}}dx\hfill \\ \hfill & \stackrel{\left(a\right)}{=}\sum _{h=1}^{\rho \left(\mathcal{A}\right)}\sum _{l=1}^{{\theta }_h\left(\mathcal{A}\right)}{\chi }_{h,l}\left(\mathcal{A}\right){\displaystyle \frac{1}{\left(l-1\right)!}}{\int }_0^{\propto }{t}^{l-1}ln({\xi }_{h}t+1)e^{-t}dt\hfill \\ \hfill & \stackrel{\left(b\right)}{=}\sum _{h=1}^{\rho \left(\mathcal{A}\right)}\sum _{l=1}^{{\theta }_h\left(\mathcal{A}\right)}{\chi }_{h,l}\left(\mathcal{A}\right){\displaystyle \frac{1}{\left(l-1\right)!}}\hfill \\ \hfill & \times \sum _{\mu =0}^{l-1}{\displaystyle \frac{(l-1)!}{(l-1-\mu )!}}\left[{\displaystyle \frac{{(-1)}^{l-2-\mu }}{{\xi }_h^{l-1-\mu }}}{e}^{\frac{1}{{\xi }_h}}\mathrm{Ei}\left(-\frac{1}{{\xi }_h}\right)\right.\hfill \\ & \left.+\sum _{m=1}^{l-1-\mu }(m-1)!{\left(-\frac{1}{{\xi }_h}\right)}^{l-1-\mu -m}\right]\hfill \end{array}$$

(17)

where (a) is obtained by replacing x with ${\xi }_{h}t$; (b) is obtained by using Equation (4.337) in [16].

Substituting (15) and (17) into (4), we can obtain the result of Theorem 1. □

With the large number of transmit antennas, we have $\psi \left(M_j\right)\approx ln\left(M_j\right)$. Therefore, the achievable rate of (4) can be approximated as

$$\begin{array}{cc}\hfill {\overline{R}}_{j,k}& \approx {\log }_2\left(1+M_j{e}^{\tilde{\Delta }}\right)\hfill \\ \hfill & ={\log }_2{M}_j+\tilde{\Delta }{\log }_{2}e\hfill \end{array}$$

(18)

where $\tilde{\Delta }=\Delta -\psi \left(M_j\right)$. We can observe from (18) that the achievable rate will increase as ${\log }_2{M}_j$.

4. Simulation Results

In this section, we present the performance and effectiveness of the massive MIMO HetNet system. We consider the number of PBSs as $J=10$, the number of UTs as $K=20$, and the maximum number of downlink data streams is $S_j=4$, $\forall j\in \mathcal{B}$. Moreover, the large-scale fading between BSs and UT is modeled as [18] $-128.1-37.6{log}_{10}d+z_{j,k}$, where d is the distance between each BS and UT in kilometers; $z_{j,k}\sim \mathcal{CN}\left(0,{\sigma }^2\right)$ is a log-normal Gaussian distribution with standard deviation $\sigma =8\mathrm{dB}$. The other parameters are shown in Table 1.

Table 1. Simulation Parameters.

Parameter	Value
Cell radius	1000 m
Bandwidth	1 MHz
Maximum transmit antennas	300
Maximum UTs	100
Maximum transmit powers	25 dB
Maximum peak interference power	10 dB

Figure 1 plots the achievable rate with different maximum transmit power $P_{max}$ versus the number of transmit antennas at MBS, where the closed-form curves of the lower bound on the achievable rate are obtained from (5), and the curves of the lower bound are simulated using the Monte Carlo (MC) method in (4). For a given $P_{max}$, the achievable rate will increase with the number of transmit antennas at MBS. We can also observe from Figure 1 that the proposed closed-form expression of the lower bound is tight in terms of achievable rate. Additionally, for a fixed number of transmit antennas, the growth rate of the achievable rate becomes slower as the maximum transmit power continues to grow. This is because the numerator of the SINR expression in (3) has the interference power constraint. For example, when $M_0=100$, the achievable rate with $P_{max}=15$ dB is about $4.8\%$ more than that with $P_{max}=5$ dB, is about $1.9\%$ more than that with $P_{max}=8$ dB, and is about $0.3\%$ more than that with $P_{max}=10$ dB.

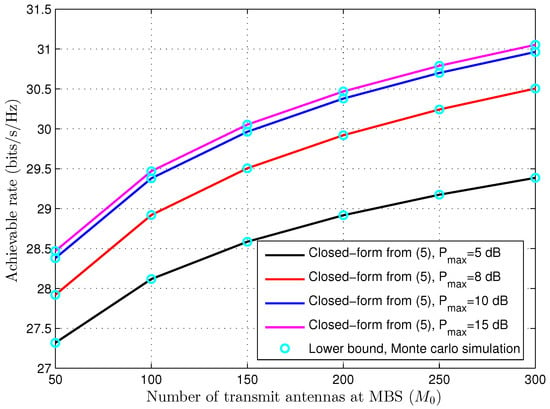
Figure 1. Achievable rate versus the number of transmit antennas at MBS.

In Figure 2, the performance of achievable rate is simulated versus the maximum transmit power $P_{max}$. As expected, the achievable rate first increases when $P_{max}$ increases. However, as the maximum transmit power continues to grow, the achievable rate will reach a certain level due to the interference power constraints. This result is consistent with the conclusion presented in Figure 1.

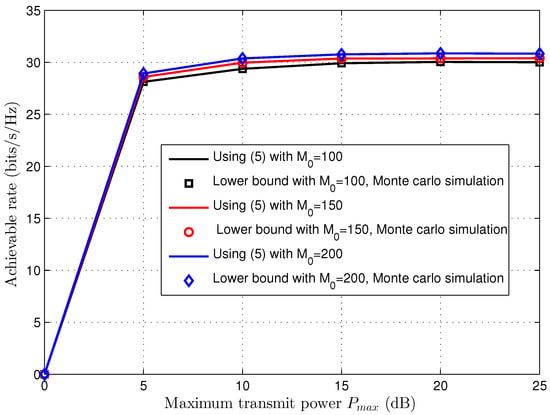
Figure 2. Achievable rate versus the maximum transmit power.

Figure 3 shows the achievable rate using (5) with $M_0=100$ versus the number of UTs, under the case of different maximum transmit power levels. We can see that the achievable rate will decrease with the number of UTs for a fixed transmit power. This is because all UTs are evenly distributed to different BSs, and we can further improve the achievable rate by studying user allocation schemes in future work [19,20]. Moreover, with the maximum transmit power increase, the achievable rate will increase for a fixed number of UTs. For example, when the number of UTs is 60, the achievable rate with $P_{max}=15$ dB is about $5.4\%$ more than that with $P_{max}=5$ dB, is about $2.3\%$ more than that with $P_{max}=8$ dB, and is about $0.8\%$ more than that with $P_{max}=10$ dB.

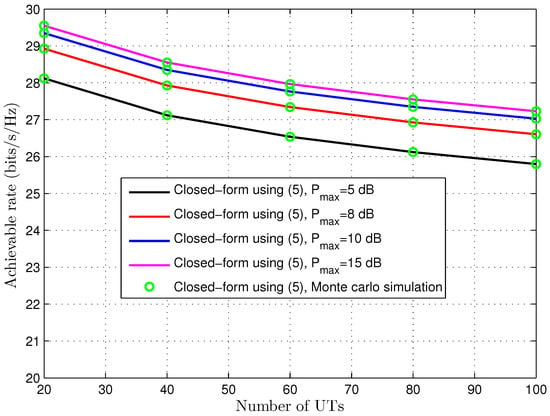
Figure 3. Achievable rate versus the number of UTs.

5. Conclusions

In this paper, we studied the performance bound of the massive MIMO HetNets by introducing an interference power model. A new analytical expression of the lower bound on the achievable rate was derived in closed-form. The proposed closed-form expression shows that the achievable rate is an explicit expression of the number of transmits antennas. In the simulation results, the impacts of the number of transmit antennas on the achievable rate performance were investigated.