Abstract
This paper primarily concerns the Whitham modulation equation of the complex modified Korteweg–de Vries (cmKdV) equation with a step-like initial value. By utilizing the Lax pair, we derive the N-genus Whitham equations via the averaging method. The Whitham equation can be integrated using the hodograph transformation. We investigate Krichever’s algebro-geometric scheme to propose the averaging method for the cmKdV integrable hierarchy and obtain the Whitham velocities of the integrable hierarchy and the hodograph transformation. The connection between the equations of the Euler–Poisson–Darboux type linear overdetermined system, which determines the solutions of the hodograph transformation, is constructed through Riemann integration, which demonstrates that the Whitham equation can be solved. Finally, a step-like initial value problem is solved and an exotic wave pattern is discovered. The results of direct numerical simulation agree well with the Whitham theory solution, which shows the validity of the theory.
MSC:
35Q53
1. Introduction
Nonlinear phenomena play a crucial role in various scientific fields such as fluid mechanics, optical fibers, solid state physics, chemical dynamics and geochemistry, and are modeled using nonlinear partial differential equations. Typical nonlinear dispersion equations include the Korteweg–de Vries (KdV) equation [1,2], the nonlinear Schrödinger (NLS) equation [3,4], the sine-Gordon equation [5,6], the Camassa–Holm equation [7,8], etc. Their precise solutions are of great significance for understanding the mechanisms and dynamic behaviors of complex physical phenomena. Since Gardner et al. [9] proposed the inverse scattering method for solving nonlinear integrable equations, many systematic and effective methods have been developed successively, such as the Hirota bilinear method [10,11], the Darboux transform [12], the Bäcklund transform [13], Painlevé’s analysis [14], the inverse scattering method [9], the Riemann–Hilbert Method [15] and the Whitham method [16,17]. The Whitham method is a powerful tool for solving discontinuous initial value problems [18,19], that was developed by G. B. Whitham [20] in the 1960s. The main idea of the Whitham method is to approximate a nonlinear wave by a slowly varying wave envelope that satisfies a set of differential equations known as the Whitham equations.
In [21], Gurevich and Pitaevskii first applied the Whitham theory to the Korteweg–de Vries (KdV) equation to study the self-similar solutions for dispersive shock waves (DSW), whose evolution can be described by the diagonal Whitham equation. Tian [22,23] connected the Whitham equation with the linear overdetermined equations of the Euler–Poison–Darboux equations of the KdV equation and the NLS equation and obtained the solution of the Whitham equation using Krichever’s algebro-geometric scheme. In recent years, the algebro-geometric scheme has been extensively studied and some significant progress has been made [24,25]. Krichever [26,27] showed that when the fast oscillations of periodic solutions are averaged or smoothed, the Whitham equation appears as a modulation equation of the Riemann surface module; they also parameterized the algebro-geometric periodic solutions and constructed an algebro-geometric n-orthogonal curve coordinate system on the plane space. These results are important for understanding the relationship between integrable systems and algebraic geometry. As we all know, the KdV equation is a classical nonlinear wave equation typically used to describe the propagation of shallow water waves. The complex modified Korteweg–de Vries (cmKdV) adds a complex term, making it even more complex, thereby allowing the equation not only to describe traditional shallow water waves but also simulate the nonlinear evolution of plasma waves [28], the propagation of shear waves in molecular chains [29] and generalized elastic solids [30]. Furthermore, the equation can also be used to describe coherent structures in some physical phenomena, such as solitary waves in disordered media such as plasma and liquid crystals, and simulate shock waves and their interactions in the aforementioned media. Therefore, the cmKdV equation has a wide range of applications in modern physics and engineering. We are interested in the modulation theory and Krichever’s algebro-geometric scheme of the cmKdV equation,
where is the complex wave envelope, is a small modulation scale, and x and t are independent variables. The cmKdV equation has been studied using the Darboux transformation [31], the Hirota method [32], the inverse scattering transformation [33], the Riemann–Hilbert problem [34,35], and so on. As we all know, the zero dispersion limit of the cmKdV equation can be described using the Whitham equation [36,37,38]
with the ordering , where depends on the complete hyperelliptic integral of genus g and will be given later. Equation (2) describes the slow modulation of the parameter on the g-genus solution of integrable nonlinear evolutionary systems. Kodama [36] found that they are neither strictly hyperbolic nor genuinely nonlinear. Wang et al. [37] gave the complete classification of discontinuous initial data. The Whitham Equation (2) in the 1-genus case is transformed into a linear overdetermined system of the Euler–Poisson–Darboux type equations [36],
where a is a constant. The system (3) has a unique solution, which can be expressed explicitly [39]. In this paper, we will connect the g-genus Whitham Equation (2) with a high-dimensional Euler–Poisson–Darboux type linear overdetermined system,
where b is a constant and prove that the solution of Equation (2) can be obtained using Equation (4). The system can provide mathematical models based on the principles of physics to describe the laws of fluid motion. It can be used to study the conservation law, wave propagation, instability and other phenomena in fluid flow, which are of great significance for understanding the properties of fluid mechanics and promoting the scientific progress in related fields.
The organizational structure of this paper is as follows. In Section 2, based on the Lax pair, the Whitham equations are established. In Section 3, Krichever’s algebro-geometric scheme is analyzed to find the solution of a Whitham-type Equation (2). In Section 4, the connection between the Whitham Equation (2) and the Euler–Poisson–Darboux type linear overdetermined system is constructed. In Section 5, we solve a step-like initial value problem. Finally, we provide our conclusions in the last section.
2. The Whitham Modulation Equation
In this section, we use an averaging method to establish the Whitham equation of Equation (1) based on the Lax pair. Equation (1) can be obtained from the compatibility condition of the Lax pair
where
and
For the Bloch function
which satisfies the identity , where is the spectral parameter, p is the quasimomentum and is the quasienergy. From (5)–(7), we have
Consider the Riemann surface of genus :
where is a two-sheet cover of ; the upper (or lower) sheet denotes the points for which .
The averaged equations take the form
where X and T are slowly varying variables and denotes averaging over one period. The system of averaged equations for many-genus solutions of the cmKdV equation can be expressed in Riemann invariants, namely the Whitham Equation (2). Since , , , it follows that . For p and , which are Abelian differentials of the second kind on , we obtain
The cmKdV equation is on one sheet of the Riemann surface and the Abelian differential has this form:
where
and is a polynomial in of degree l, which is related with the number of genera and the asymptotic behavior.
For the multi-gap solution of the cmKdV equation, . Therefore, in order to satisfy the requirements of (14) and (15), we need
Now define two polynomials
with , and uniquely determined by the conditions
where
and the sign is given by .
The motions of are determined by Whitham Equations (2) with velocities
We first consider the case in which a single valued function x represents the evolution curve. In this case, and Equation (18) becomes
where and are determined by (19) and (20). In fact,
According to Equation (21), Equation (2) becomes
where
whose solution satisfies the characteristic equation
where are the initial curves.
The 1-genus case is given by and Equation (18) becomes
where and are
with
and and are complete elliptic integrals of the first and second kind, respectively.
The Whitham system can also be derived using the methods of multiphase averaging [40,41] and multiple scale expansions regardless of the integrability of the systems [42]. Taking the limits and , the velocities of the 1-genus can be reduced to the ones of a 0-genus and the boundaries connecting the 1-genus and 0-genus are continuous. The periodic solution of the cmKdV Equation (1) can be expressed as follows [36],
where is the Jacobian elliptic function, is the traveling transformation, is the traveling velocity and is the phase shift.
Similarly, the velocities of the multi-genus Whitham Equation (2) can be expressed using complete hyperelliptic integrals of genus g. In fact, the Whitham Equation (2) can be integrated using a hodograph transformation and, more precisely, we get the following theorem due to Tsarev [43].
Theorem 1.
If , where denotes solves the overdetermined linear system
where
then the solution of the hodograph transformation
satisfies Equation (2).
It is worth noting that the hodograph method (45) is a generalization of the characteristic method (28). The linear overdetermined system (43) satisfies the compatibility condition and has local solutions. These solutions usually cannot be expanded globally, because in (44) are singular on the phase transition boundaries. Proving the existence of a global solution to the system (43) and using it to construct the solution to the initial value problem of the Whitham Equation (2) are very important problems. In the single-genus case, we will find explicit global solutions to (43) and solve the initial problem of Equation (2).
3. Krichever’s Algebro-Geometric Scheme
In this section, we will analyze Krichever’s scheme to find the solutions of the Whitham Equation (2). According to Jenkins [44], we can define
where the coefficients are uniquely determined by these two conditions
and
It is easy to show that these conditions uniquely determine ’s. Obviously, we have and for the cmKdV Equation (1), where and are given in Equation (18).
We consider a simple initial value with , then the initial curves are
and the initial function , where is a function of x.
Suppose the initial function has the form
where only a finite number of ’s are non-zero.
Construct as
where
The Whitham-type Equation (2) is equivalent to
which can be generalized to the cmKdV hierarchy by the following theorem.
Theorem 2.
If
holds, then if, and only if,
where
Proof.
The proof of the second part is as follows. The time evolution, Equation (60), allows us to rewrite Equation (57) as:
where
is a power series of . By Equation (47) and Equation (51), we get the expansion at
which mean that
Therefore, from Equation (61), we have
which shows that is a polynomial of with a maximum degree of .
Now consider the Riemann surface defined by and cut along interval . We define the cycle as a closed contour, which surrounds the notch on the upper Riemann graph clockwise . The cycle, defined as a closed contour, starts from and goes to , crosses to the lower level and finally returns to .
Integrating (61) along the cycle yields
in which, we used Equation (48) and Equation (51) in the last equation. This is equivalent to
which proves that has at least one zero in the interval , so has at least zeros. This combined with Equation (65) shows that . Equation (54) immediately follows from Equation (61). The proof of Theorem 2 is complete. □
We first state the following classical results about entropy in conservation law theory [45].
Theorem 3.
If Equation (55) implies the existence of an additional conservation law
then we have
The next result shows that the ’s of Equation (56) solve the system (43) of Theorem 1, which can be proved using the method of Levermore [46].
Theorem 4.
W and υ are satisfied for and :
Proof.
By (20), Theorem 2 and Theorem 3, we have
which yields
Finally, we combine Theorem 1 and Theorem 2 to construct the transformation
4. Linear Overdetermined Systems of the Euler–Poisson–Darboux Type
In this section, we show the relation between the Whitham Equation (2) and linear overdetermined systems of the Euler–Poisson–Darboux type (4).
First we define [44]
where the constants are uniquely determined by the normalization conditions
and the cycles ’s are as previously given.
Fixing the point A on the Riemann surface, we define as the standard -edge path, i.e.,
On the other hand, by Equation (76) we have
The integral
has only one singular point at , and the residue can be obtained as follows. Expanding at , we find
which gives
Therefore, we obtain
where we introduce , is the local coordinate and is a constant.
This, together with Equations (79) and (80), yields
which is the Riemann bilinear relation. Rewriting it in the matrix form, we obtain
where
The regularity of matrix follows from Equations (76) and (79), while that of matrix is also easy to check. This, together with (88) and (90), gives
Inverting this, we obtain
where
is the real matrix in view of Equation (20). In particular, by Equations (51), (89) and (91), we get
Next, integrating Equation (54) yields
The first and second terms of Equation (95) are proportional to the wave numbers and frequencies of the modulated multiphase waves for the cmKdV hierarchy, respectively.
Applying Theorem 3 to Equation (95) and using Equations (91) and (94), we get that for ,
which establishes the following theorem.
Theorem 5.
There are fixed real functions , so that the system, Equation (43), has solutions for all polynomial initial data Equations (50)
for , where the ’s are given by Equation (89).
It immediately follows from Equation (20) that
Combined with Equation (82), (98) shows that the ’s satisfy Equation (4). From (89), ’s of (82) obeys
which establishes the following theorem.
Theorem 6.
Each of (89) solves the linear overdetermined system of Euler–Poisson–Darboux Equation (4) with given by
for .
For the special initial value (49), the Whitham Equation (2) has the property that , and are nontrivial functions of . If , we have
In particular, when , we have
Choosing and the other ’s to be zero in Equation (56), we obtain . Therefore we have
5. A Step-like Initial Value Problem
Consider Equation (1) with the initial data
where and are real functions that are independent of . The solution of Equation (1) in the form
where is the density, and is the velocity of the hydrodynamics. Substituting (105) into Equation (1), the conservation form of the cmKdV Equation (1) is obtained. Taking the limit and writing the conservation form in diagonal form, the 0-genus Whitham equation is derived again [36], which is identical to (26).
We consider the step-like initial data
where , , and are constants. Choosing , , and , the distributions of Riemann variables and the structures of density function are shown in Figure 1. Here, we have used a 1-genus Whitham Equation (37). The fundamental wave structures of rarefaction wave (RW) and DSW, along with the relevant mathematical theory, are presented in Ref. [37]. In this case, the Riemann invariants are divided into six regions, which, from left to right, are plateau, DSW, RW, DSW, RW and plateau. We now give the solutions for each region and the boundary velocities.
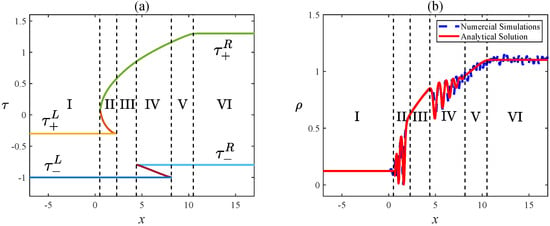
Figure 1.
The self-similar solution with initial condition of , , , with . (a) The distribution of Riemann invariants. (b) The structure diagram of density function .
(I) For ,
where satisfies , is the vertex of the parabola.
(II) For ,
(III) For ,
(IV) For ,
(V) For
(VI) For ,
Direct numerical simulation can effectively test the validity of theoretical solutions [47]. Here, we compare the Whitham theoretical solution with the direct numerical simulation solution obtained from finite differences. It turns out that the two results are in good agreement (see Figure 1). However, it is important to note that in this study, we only considered one specific initial value problem. In fact, using the same method, we can obtain solutions for arbitrary step-like initial data.
6. Conclusions
In conclusion, we have studied the cmKdV Equation (1), which is the second member in the cmKdV hierarchy. We have derived the N-genus Whitham equations based on the Lax pair and provided detailed descriptions of the 0-genus (26) and 1-genus (37) Whitham equations as special cases. In order to solve the Whitham equation, Krichever’s algebro-geometric scheme was established, and the connection between Whitham equation of single-genus and Euler–Poisson–Darboux equations was constructed. With respect to the cmKdV Equation (1), which involves two initial curves, we have employed a simple example where one curve remained constant while the other one varied. Additionally, a step-like initial value problem as an example was solved, and the Whitham modulation solution agreed well with the numerical solution (seen in Figure 1), which proves the validity of the theoretical solution. The results of this paper also provide an effective mathematical method for solving discontinuous initial value problems.
Author Contributions
Conceptualization, S.Z. and Y.L.; methodology, Y.L.; software, S.Z.; validation, S.Z. and Y.L.; formal analysis, S.Z.; investigation, Y.L.; resources, S.Z.; data curation, Y.L.; writing—original draft preparation, S.Z.; writing—review and editing, Y.L.; visualization, S.Z.; supervision, Y.L.; project administration, Y.L.; funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Beijing Natural Science Foundation (No. 1222005), and the Qin Xin Talents Cultivation Program of Beijing Information Science and Technology University (QXTCP C202118).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Korteweg, D.J.; De Vries, G. On the change of form of long waves advancing in a rectangular canal and on a new type of long stationary waves. Phil. Mag. 1895, 39, 422–443. [Google Scholar] [CrossRef]
- Lax, P.; Levermore, C. The small dispersion limit of the Korteweg-De Vries equation. Commun. Pure Appl. Math. 1983, 36, 253–290. [Google Scholar] [CrossRef]
- Tian, F.R.; Ye, J. On the Whitham equations for the semiclassical limit of the defocusing nonlinear Schrödinger equation. Pure Appl. Math. 1999, 52, 655–692. [Google Scholar] [CrossRef]
- Ahmed, I.; Mu, C.; Zheng, P. Exact solution of the (2+1)-dimensional hyperbolic nonlinear Schrödinger equation by Adomian decomposition method. Malaya J. Mat. 2014, 2, 160–164. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, J. Sine-Gordon equation. J. Math. Phys. 1970, 11, 258–266. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Kaup, D.J.; Newell, A.C.; Segur, H. Method for solving the Sine-Gordon equation. Phys. Rev. Lett. 1973, 30, 1262. [Google Scholar] [CrossRef]
- Johnson, R.S. Camassa–Holm, Korteweg–de Vries and related models for water waves. J. Fluid Mech. 2002, 455, 63–82. [Google Scholar] [CrossRef]
- Lenells, J. Traveling wave solutions of the Camassa–Holm equation. J. Differ. Equ. 2005, 217, 393–430. [Google Scholar] [CrossRef]
- Gardner, C.S.; Greene, J.M.; Kruskal, M.D.; Miura, R.M. Method for solving the Korteveg-de Vries equation. Phys. Rev. Lett. 1967, 19, 1095. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory, 1st ed.; Cambridge University Press: Cambridge, UK, 2004; pp. 37–55. [Google Scholar]
- Liu, Y.Q.; Ren, B.; Wang, D.S. Various localised nonlinear wave interactions in the generalised Kadomtsev-Petviashvili equation. East Asian J. Appl. Math. 2021, 11, 301–325. [Google Scholar] [CrossRef]
- Matveev, V.B.; Salle, M.A. Darboux Transformation and Solitons, 1st ed.; Springer-Verlag: Berlin, Germany, 1991; pp. 29–48. [Google Scholar]
- Ohta, Y.; Wang, D.S.; Yang, J. General N-dark-dark solitons in the coupled nonlinear Schrödinger equations. Stud. Appl. Math. 2011, 127, 345–371. [Google Scholar] [CrossRef]
- Weiss, J.; Tabor, M.; Carnevale, G. The Painlevé property for partial differential equations. Math. Phys. 1983, 24, 522–526. [Google Scholar] [CrossRef]
- Deift, P.; Zhou, X. A steepest descent method for oscillatory Riemann-Hilbert problems. Bull. Am. Math. Soc. 1993, 137, 295–368. [Google Scholar] [CrossRef]
- Whitham, G.B. Linear and Nonlinear Waves, 1st ed.; Wiley: New York, NY, USA, 1974; pp. 454–470. [Google Scholar]
- Kamchatnov, A.M. Evolution of initial discontinuities in the DNLS equation theory. J. Phys. Commun. 2018, 2, 025027. [Google Scholar] [CrossRef]
- El, G.A.; Geogjaev, V.V.; Gurevich, A.V.; Krylov, A.L. Decay of an initial discontinuity in the defocusing NLS hydrodynamics. Phys. D 1995, 87, 186–192. [Google Scholar] [CrossRef]
- Ivanov, S.K. Riemann problem for the light pulses in optical fibers for the generalized Chen-Lee-Liu equation. Phys. Rev. A 2020, 101, 053827. [Google Scholar] [CrossRef]
- Whitham, G.B. Nonlinear dispersive waves. Proc. R. Soc. Lond. A 1965, 283, 238–261. [Google Scholar] [CrossRef]
- Gurevich, A.V.; Pitaevskii, L.P. Nonstationary structure of a collisionless shock wave. Sov. Phys. JETP 1974, 2, 291. [Google Scholar]
- Tian, F.R. The Whitham-type equations and linear overdetermined systems of Euler-Poisson-Darboux type. Duke Math J. 1994, 74, 203–221. [Google Scholar] [CrossRef]
- Tian, F.R. The initial value problem for the Whitham averaged system. Commun. Math. Phys. 1994, 166, 79–115. [Google Scholar] [CrossRef]
- Xu, X.X.; Cao, C.W.; Zhang, D.J. Algebro-geometric solutions to the lattice potential modified Kadomtsev-Petviashvili equation. J. Phys. A Math. Theor. 2022, 55, 375201. [Google Scholar] [CrossRef]
- Geng, X.G.; Zeng, X. Algebro-geometric quasi-periodic solutions to the Satsuma-Hirota hierarchy. Physica D 2023, 448, 133738. [Google Scholar] [CrossRef]
- Krichever, I.; Mineev-Weinstein, M.; Wiegmann, P.; Zabrodin, A. Laplacian growth and Whitham equations of soliton theory. Physica D 2004, 198, 1–28. [Google Scholar] [CrossRef]
- Krichever, I. Algebraic-geometrical n-orthogonal curvilinear coordinate systems and solutions of the associativity equations. Funct. Anal. Appl. 1997, 31, 25–39. [Google Scholar] [CrossRef]
- Karney, C.F.F.; Sen, A.; Chu, F.Y.F. Nonlinear evolution of lower hybrid waves. Phys. Fluids 1979, 22, 940–952. [Google Scholar] [CrossRef]
- Gorbacheva, O.B.; Ostrovsky, L.A. Nonlinear vector waves in a mechanical model of a molecular chain. Phys. D 1983, 8, 223–228. [Google Scholar] [CrossRef]
- Erbay, H.A. Nonlinear transverse waves in a generalized elastic solid and the complex modified Korteweg-de Vries equation. Phys. Scrip. 1998, 58, 9–14. [Google Scholar] [CrossRef]
- Xu, T.X.; Qiao, Z.J. Darboux transformation and shocksolitons for complex mKdV equation. Pac. J. Appl. Math. 2010, 3, 1–10. [Google Scholar]
- Zhang, W.X.; Liu, Y.Q. Solitary wave solutions and integrability for generalized nonlocal complex modified Korteweg-de Vries (cmKdV) equations. AIMS Math. 2021, 6, 11046–11075. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, H.H. Robust inverse scattering method to the complex modified Korteweg-de Vries equation with nonzero background condition. Phys. Lett. A 2022, 449, 128359. [Google Scholar] [CrossRef]
- Zhang, Y.S.; Tao, X.X.; Xu, S.W. The bound-state soliton solutions of the complex modified KdV equation. Inverse Prob. 2020, 36, 065003. [Google Scholar] [CrossRef]
- Wang, X.B.; Han, B. Application of the Riemann-Hilbert method to the vector modified Korteweg-de Vries equation. Nonlinear Dyn. 2020, 99, 1363–1377. [Google Scholar] [CrossRef]
- Kodama, Y.; Pierce, V.U.; Tian, F.R. On the Whitham equations for the defocusing complex modified KdV equation. SIAM J. Math. Anal. 2008, 40, 1750–1782. [Google Scholar] [CrossRef]
- Wang, D.S.; Xu, L.; Xuan, Z.X. The complete classification of solutions to the Riemann problem of the defocusing complex modified KdV equation. J. Nonlinear Sci. 2022, 32, 3. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Wang, D.S. Exotic wave patterns in Riemann problem of the high-order Jaulent-Miodek equation: Whitham modulation theory. Stud. Appl. Math. 2022, 149, 588–630. [Google Scholar] [CrossRef]
- Tian, F.R. Oscillations of the zero dispersion limit of the Korteweg-de Vries equation. Commun. Pure. Appl. Math. 1993, 46, 1093–1129. [Google Scholar] [CrossRef]
- Pavlov, M.V. Nonlinear Schrödinger equation and the Bogolyubov-Whitham method of averaging. Theor. Math. Phys. 1987, 71, 584–588. [Google Scholar] [CrossRef]
- Novikov, S. The geometry of conservative systems of hydrodynamic type. The method of averaging for field-theoretical systems. Russ. Math. Surv. 1985, 40, 85–98. [Google Scholar] [CrossRef]
- Ablowitz, M.; Biondini, G.; Wang, Q. Whitham modulation theory for the two-dimensional Benjamin-Ono equation. Phys. Rev. E 2017, 96, 032225. [Google Scholar] [CrossRef]
- Tsarev, S. Poisson brackets and one-dimensional Hamiltonian systems of hydrodynamic type. Sov. Math. Dokl. 1985, 31, 488–491. [Google Scholar]
- Jenkins, R. Regularization of a sharp shock by the defocusing nonlinear Schrödinger equation. Nonlinearity 2014, 28, 2131–2180. [Google Scholar] [CrossRef]
- Lax, P.D. Hyperbolic Systems of Conservation Laws and the Mathematical Theory of Shock Waves; New York University: New York, NY, USA, 1973; pp. 24–33. [Google Scholar]
- Levermore, C.D. The hyperbolic nature of the zero dispersion KdV limit. Commun. Partial. Differ. Equ. 1988, 13, 495–514. [Google Scholar] [CrossRef]
- Esen, A.; Tasbozan, O. Numerical solution of time fractional nonlinear Schrödinger equation arising in quantum mechanics by cubic B-spline finite elements. Malaya J. Mat. 2015, 3, 387–397. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).