A Protocol for Solutions to DP-Complete Problems through Tissue Membrane Systems
Abstract
1. Introduction
2. Methodology
- Cells. The cells of are the cells of and , plus three additional cells.
- Working alphabet. The working alphabet is , where:
- Input alphabet. The input alphabet is , being the input alphabet of , by replacing objects yes and no by objects and , for , respectively.
- Alphabet of the environment. The alphabet of the environment of is , where is the alphabet of the environment of , for .
- Set of labels. The set of labels is , where are different from each other and none of them belong to the set . Specifically, will be the labels associated with the three new cells.
- Initial multisets. The initial multisets of are the following:
- (a)
- For , if h is the label of a cell from whose initial multiset is then the initial multiset associated with h in is , that is, for each object a initially placed in cells of , a primed version is considered instead when is taken as a part of .
- (b)
- , being the union of the initial multisets of .
- (c)
- .
- Set of rules. The set of rules is , where is the set of rules of , for , obtained through the replacement of objects yes and no by objects and , respectively, in each rule. In addition, is the following set of rules:
- 1.
- Rules for simultaneously transporting from cell labeled by to the input cell of , for .
- 1.1.
- , for each .
- 1.2.
- , for each .
- 2.
- Rules to obtain the rules from , for , started in the second transition step.
- 2.1.
- , for each and for each label h of a cell in .
- 3.
- Rules for transporting the pair of answers of the systems , for , from the environment to cell or .
- 3.1.
- .
- 3.2.
- .
- 3.3.
- .
- 3.4.
- .
- 4.
- Rules for the affirmative answer of the system :
- 4.1.
- .
- 4.2.
- .
- 5.
- Rules for the negative answer of the system :
- 5.1.
- .
- 5.2.
- .
- 5.3.
- .
- Input cell. The input cell is the cell labelled by .
An Overview of the Computations of
- Transport stageOnce the input multiset is supplied to the input cell of the system , by applying the rules from 1.1, and 1.2, in the first computation step multisets and enter into the input cell and , respectively. Simultaneously, in this first step, by applying the rules from 2.1, objects initially placed in each cell of is transformed in the corresponding non-primed object a. This stage takes only one transition step.
- Simulation stageStarting at the second transition step, computations of the system with input multiset are simulated by applying the corresponding rules from , for . Then, after at most transition steps, both systems and will send their answers to the environment. Therefore, this stage takes at most steps.
- Output stageThe system with input multiset sends the right answer to the environment according to the results obtained in the previous stage. Bearing in mind that rules 3.1, 3.2, 3.3 and 3.4 are cooperative, they will only be applicable when the environment receive the answers from and . Let us assume that at instant k both answers reach the environment (obviously, k depends on the computations selected in the simulations and ).
- -
- Affirmative answer.In this case, the answers of and will be and , respectively. By applying rule 3.1, objects and are sent to cell , that is . By applying rule 4.1 we will have and . Finally, by applying rule 4.2 the system send out to the object yes and the system halts. It is graphically depicted in Figure 2.
- -
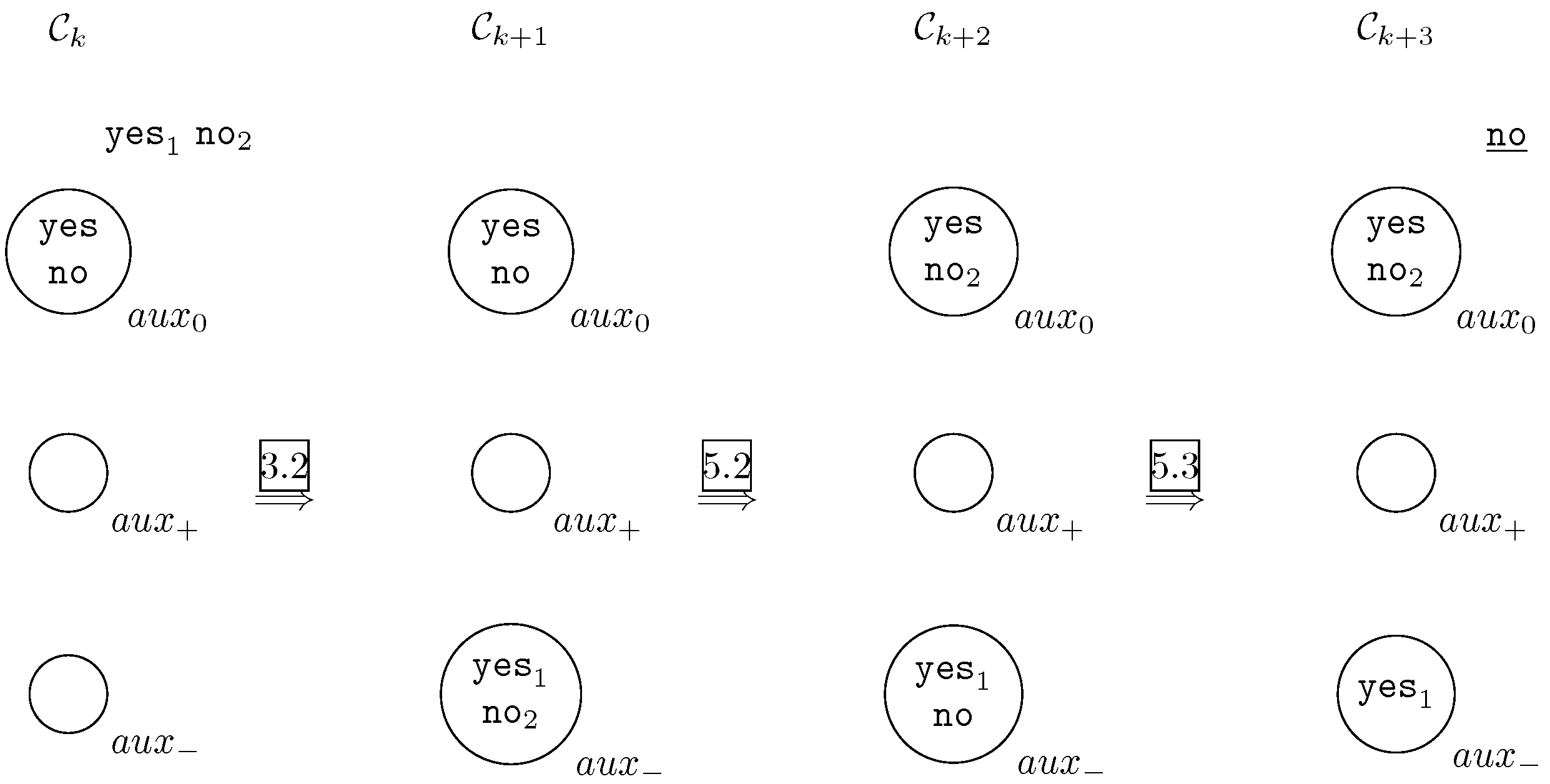
- Negative answer.In this case, at least one answer of or must be negative. By applying rule 3.2 or 3.3 or 3.4, cell from configuration will contain object either object either both of them. By applying rule 5.1 or rule 5.2 (only one of them because cell from configuration only contain one object no) will have . Finally, by applying rule 5.3 the system send out to the object no and the system halts. It is graphically depicted in Figure 3.
- (a)
- Recognizer cooperative tissue-like membrane systems from class are required to allow the use of communication rules with the length of at least 2, and the length of the new rules added is exactly 2.
- (b)
- A explicit solution of the product problem product is provided from two respective solutions of the problems involved in that operation.
3. Solving DP-Complete Problems by Using a New Methodology
- (a)
- (b)
- (c)
- (d)
- for ,
- (e)
- The set of rules is the following:Apart from these, all rules indicated in Section 2 must be added.
- (f)
- and
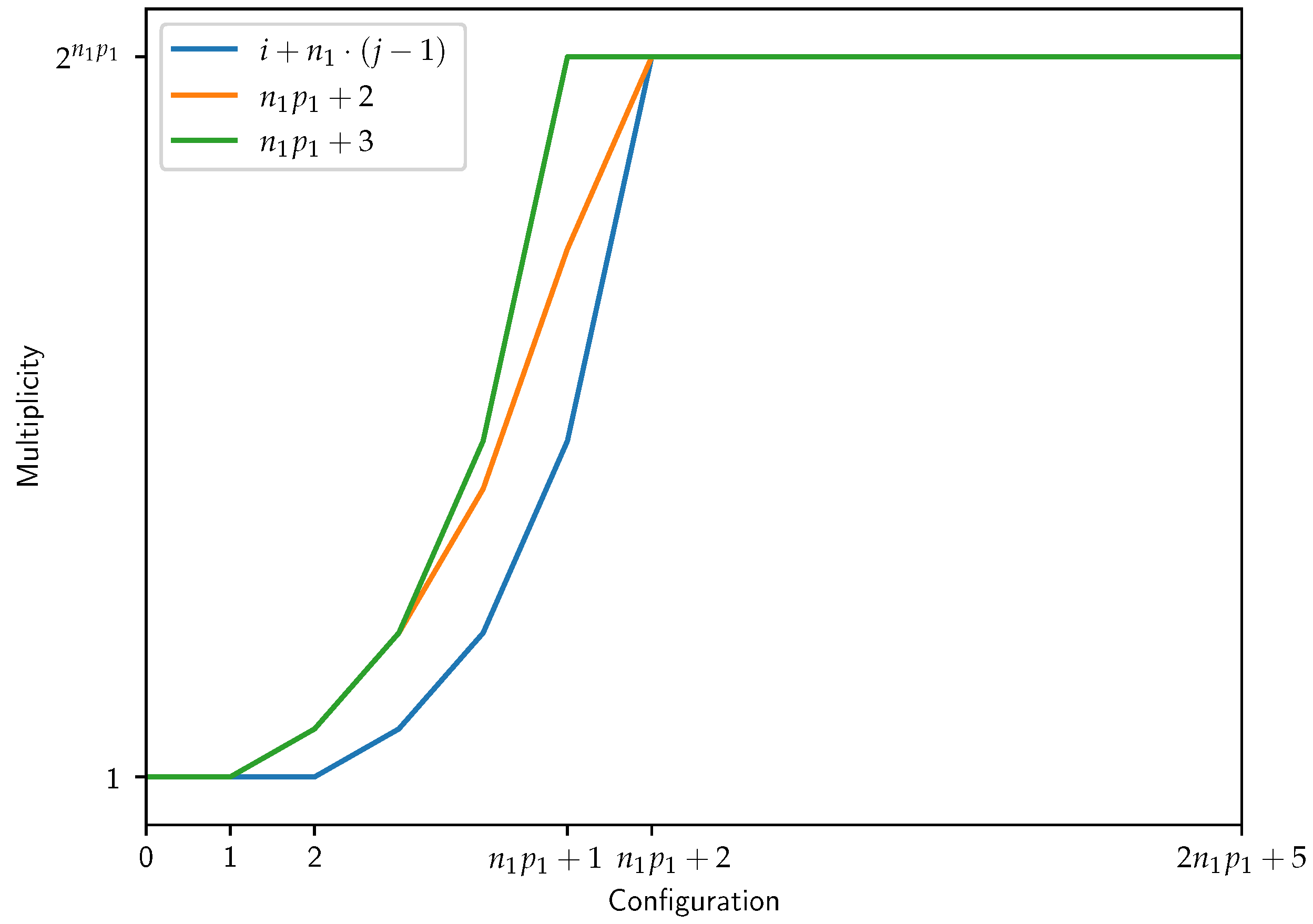
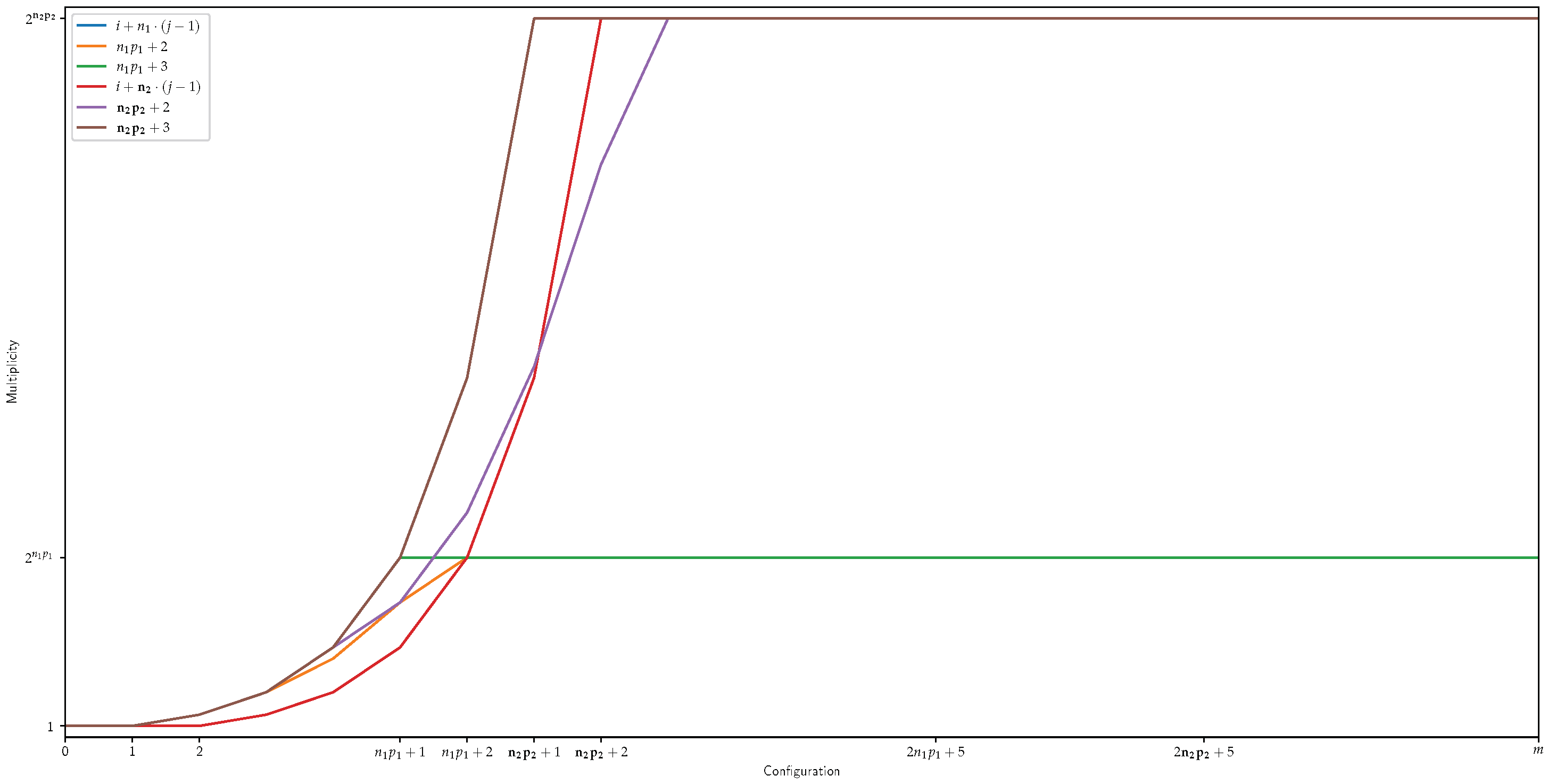
4. Insights from the Evolution of the System
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Păun, G. Computing with membranes. J. Comput. Syst. Sci. 2000, 61, 108–143. [Google Scholar] [CrossRef]
- Păun, A.; Păun, G. The power of communication: P systems with symport/antiport. New Gener. Comput. 2002, 20, 295–305. [Google Scholar] [CrossRef]
- Martín Vide, C.; Pazos, J.; Păun, G.; Rodríguez Patón, A. A New Class of Symbolic Abstract Neural Nets: Tissue P Systems. In Proceedings of the 8th Annual International Conference, COCOON 2002, Singapore, 15–17 August 2002; Volume 2387, pp. 290–299. [Google Scholar]
- Martín Vide, C.; Pazos, J.; Păun, G.; Rodríguez Patón, A. Tissue P systems. Theor. Comput. Sci. 2003, 296, 295–326. [Google Scholar] [CrossRef]
- Alhazov, A.; Freund, R.; Oswald, M. Tissue P Systems with Antiport Rules ans Small Numbers of Symbols and Cells. In Proceedings of the 9th International Conference, DLT, Palermo, Italy, 4–8 July 2005; pp. 100–111. [Google Scholar]
- Bernardini, F.; Gheorghe, M. Cell Communication in Tissue P Systems and Cell Division in Population P Systems. Soft Comput. 2005, 9, 640–649. [Google Scholar] [CrossRef]
- Krishna, S.N.; Lakshmanan, K.; Rama, R. Tissue P Systems with Contextual and Rewriting Rules. In Proceedings of the International Workshop, WMC-CdeA 2002, Curtea de Arges, Romania, 19–23 August 2002; Volume 2597, pp. 339–351. [Google Scholar]
- Pérez-Jiménez, M.J.; Romero-Jiménez, A.; Sancho-Caparrini, F. Decision P systems and the P ≠ NP conjecture. In Proceedings of the International Workshop, WMC-CdeA 2002, Curtea de Arges, Romania, 19–23 August 2002; Volume 2597, pp. 388–399. [Google Scholar]
- Pérez-Jiménez, M.J.; Romero-Jiménez, A.; Sancho-Caparrini, F. Complexity classes in models of cellular computing with membranes. Nat. Comput. 2003, 2, 265–285. [Google Scholar] [CrossRef]
- Valencia-Cabrera, L.; Orellana-Martín, D.; Martínez-del-Amor, M.Á.; Pérez-Hurtado, I.; Pérez-Jiménez, M.J. From NP-completeness to DP-completeness: A Membrane Computing perspective. Complexity 2020, 2020, 6765097. [Google Scholar] [CrossRef]
- Papadimitriou, C.H.; Yannakis, M. The complexity of facets (and some facets of complexity). In Proceedings of the 24th ACM Symposium on the Theory of Computing, San Francisco, CA, USA, 5–7 May 1982; pp. 229–234. [Google Scholar]
- Riscos-Núñez, A.; Valencia-Cabrera, L. From SAT to SAT-UNSAT using P systems with dissolution rules. J. Membr. Comput. 2022, 4, 97–106. [Google Scholar] [CrossRef]
- Macías-Ramos, L.F.; Pérez-Jiménez, M.J.; Riscos-Nú nez, A.; Valencia-Cabrera, L. Membrane fission versus cell division: When membrane proliferation is not enough. Theor. Comput. Sci. 2015, 608, 57–65. [Google Scholar] [CrossRef]
- Leporati, A.; Manzoni, L.; Mauri, G.; Porreca, A.E.; Zandron, C. Tissue P Systems Can be Simulated Efficiently with Counting Oracles. In Membrane Computing. CMC 2015. Lecture Notes in Computer Science; Rozenberg, G., Salomaa, A., Sempere, J., Zandron, C., Eds.; Springer: Cham, Switzerland, 2015; Volume 9504. [Google Scholar]
- Leporati, A.; Manzoni, L.; Mauri, G.; Porreca, A.E.; Zandron, C. Characterising the complexity of tissue P systems with fission rules. J. Comput. Syst. Sci. 2017, 90, 115–128. [Google Scholar] [CrossRef]
- Leporati, A.; Manzoni, L.; Mauri, G.; Porreca, A.E.; Zandron, C. Simulating counting oracles with cooperation. J. Membr. Comput. 2020, 2, 303–310. [Google Scholar] [CrossRef]
- Leporati, A.; Manzoni, L.; Mauri, G.; Porreca, A.E.; Zandron, C. Solving QSAT in sublinear depth. In Proceedings of the 19th International Conference, CMC 2018, Dresden, Germany, 4–7 September 2018. [Google Scholar]
- Leporati, A.; Manzoni, L.; Mauri, G.; Porreca, A.E.; Zandron, C. Membrane Division, Oracles, and the Counting Hierarchy. Fundam. Inform. 2015, 138, 97–111. [Google Scholar] [CrossRef]
- Gutiérrez-Escudero, R.; Pérez-Jiménez, M.J.; Rius-Font, M. Characterizing tractability by tissue-like P systems. In Proceedings of the 10th International Workshop, WMC 2009, Curtea de Arges, Romania, 24–27 August 2009; Volume 5957, pp. 289–300. [Google Scholar]
- Pan, L.; Pérez-Jiménez, M.J.; Riscos-Núñez, A.; Rius, M. New frontiers of the efficiency in tissue P systems. In Proceedings of the Asian Conference on Membrane Computing (ACMC 2012); Pan, L., Paun, G., Song, T., Eds.; Huazhong University of Science and Technology: Wuhan, China, 2012; pp. 61–73. [Google Scholar]
- Porreca, A.E.; Murphy, N.; Pérez-Jiménez, M.J. An optimal frontier of the efficiency of tissue P systems with cell division. In Proceedings of the Tenth Brainstorming Week on Membrane Computing, Seville, Spain, 30 January–3 February 2012; Volume II, pp. 141–166. [Google Scholar]
- Pérez-Jiménez, M.J.; Sosík, P. An Optimal Frontier of the Efficiency of Tissue P Systems with Cell Separation. Fundam. Inform. 2015, 138, 45–60. [Google Scholar] [CrossRef]
- Orellana-Martín, D.; Valencia-Cabrera, L.; Pérez-Jiménez, M.J. An optimal solution to the SAT problem with tissue P systems. In Proceedings of the Eighteenth Brainstorming Week on Membrane Computing, Seville, Spain, 4–7 February 2020; pp. 91–100. [Google Scholar]

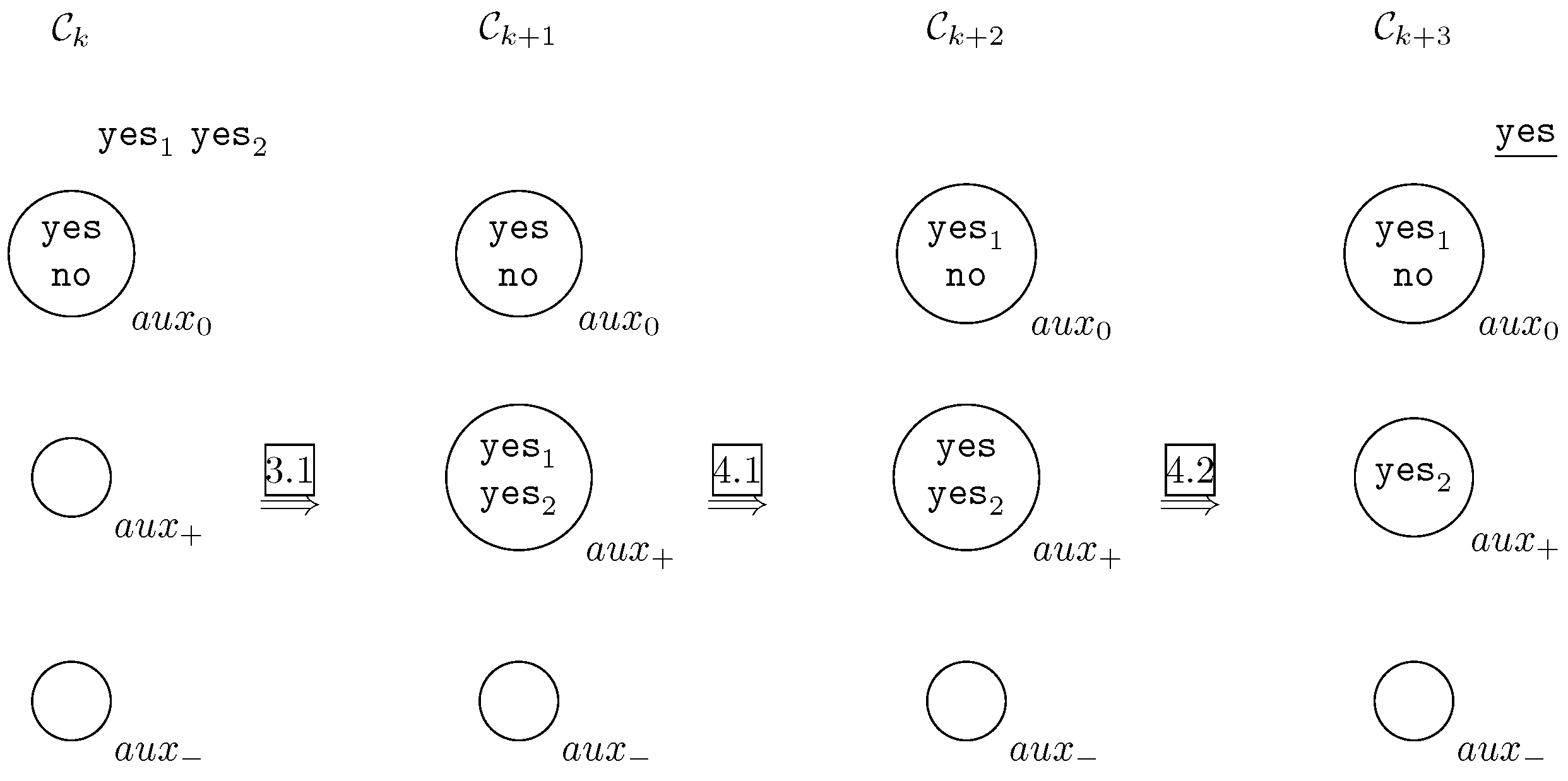

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orellana-Martín, D.; Ramírez-de-Arellano, A.; Andreu-Guzmán, J.A.; Romero-Jiménez, Á.; Pérez-Jiménez, M.J. A Protocol for Solutions to DP-Complete Problems through Tissue Membrane Systems. Mathematics 2023, 11, 2797. https://doi.org/10.3390/math11132797
Orellana-Martín D, Ramírez-de-Arellano A, Andreu-Guzmán JA, Romero-Jiménez Á, Pérez-Jiménez MJ. A Protocol for Solutions to DP-Complete Problems through Tissue Membrane Systems. Mathematics. 2023; 11(13):2797. https://doi.org/10.3390/math11132797
Chicago/Turabian StyleOrellana-Martín, David, Antonio Ramírez-de-Arellano, José Antonio Andreu-Guzmán, Álvaro Romero-Jiménez, and Mario J. Pérez-Jiménez. 2023. "A Protocol for Solutions to DP-Complete Problems through Tissue Membrane Systems" Mathematics 11, no. 13: 2797. https://doi.org/10.3390/math11132797
APA StyleOrellana-Martín, D., Ramírez-de-Arellano, A., Andreu-Guzmán, J. A., Romero-Jiménez, Á., & Pérez-Jiménez, M. J. (2023). A Protocol for Solutions to DP-Complete Problems through Tissue Membrane Systems. Mathematics, 11(13), 2797. https://doi.org/10.3390/math11132797







