Predefined Time Active Disturbance Rejection for Nonholonomic Mobile Robots

Abstract

This article studies the fast path tracking problem for nonholonomic mobile robots with unknown slipping and skidding. Firstly, considering the steering problem, a new mathematical model of nonholonomic mobile robot is derived. Secondly, to estimate the unknown slipping and skidding of a nonholonomic mobile robot quickly and accurately, new predefined time observers, which can attain a predefined settling time, are established. Thirdly, based on the observers and the sliding mode approaches, predefined time active controllers are proposed to achieve high precision control performance of the nonholonomic mobile robot tracking. The method proposed in this article can achieve uniformly global stability within a predefined time, which makes the adjustment of the convergence time of the nonholonomic mobile robot easier and convenient. Finally, the simulation results validated the theoretical results.

1. Introduction

Recently, the path tracking problem for NMRs (nonholonomic mobile robots) has received increasing attention owing to its broad applications in engineering areas, such as space exploration, hospital tasks, search and rescue, etc. [1]. The objective is to design appropriate control laws, such as finite/fixed time sliding mode control [2], adaptive control [3], neural network control, etc., to complete various complex tasks. In addition, NMRs usually need to work in various complex environments, such as curvy roads, slippery roads, forest paths, and roads with small holes. Therefore, designing a control law for an NMR with unknown slipping and skidding is of great significance for improving tracking performance. Wang et al. [4] investigated the problems of modeling and analyzed them for an NMR with unknown slipping and skidding. Yoo et al. [5] proposed an adaptive tracking control method for an NMR with unknown slipping and skidding that considered input saturation. To solve the trajectory tracking problem of NMRs with unmeasurable speeds, a finite time robust composite controller was designed in [6]. To solve the problem of wheeled mobile robots with parametric uncertainties, an efficient controller design method based on active disturbance rejection control was proposed in [7]. The intelligent path following scheme of the wheeled mobile robots can also be realized by estimating the dynamics of robots online and by estimating unpredicted disturbances through a predictive compensator [8]. To solve the unknown slipping and skidding of an NMR, a simple method to deal with disturbance and uncertainty is to compensate them by designing a controller with robust performance.

This idea directly promotes the vigorous development of observer designs, including the design of state observers [9], adaptive observers [10], disturbance observers [11], and finite time observers [12], etc. In theoretical research and practical application, an observer with time constraints is a problem worthy of study and discussion [13]. Among them, the finite time observer is one of the ways to implement the separation principle. In this case, a control algorithm can be individually designed and analyzed. On the other hand, in many practical engineering applications, the conversion process is strongly limited in time. For example, the states of a walking robot must be estimated each time before it touches the ground, i.e., each step length must be calculated [14]. A typical system state estimation method is to use the system mathematical model and additional output terms for the design of dynamic observers [15]. The stability of the error equation between the system and the observer is studied to ensure that the observation error converges to a certain range in finite time or fixed time (which is predefined in advance). To achieve finite time convergence of the error system, HOSM (high-order sliding mode) [16] observers can be used [17]. In order to improve the accuracy and robustness of the system, some finite time observers [18] and finite time controllers [19] are constructed and developed. However, the initial conditions of the system will affect the convergence time, and, as the initial error increases, the initial conditions will become larger. This limits their applications in practice in some cases. Fixed time stability can solve the problem of finite time stability. Aiming at the problem of robust trajectory tracking control of an NMR with unknown slipping and skidding, a generalized extended state observer was designed in [20]. To estimate the skidding and slipping of wheeled mobile robots and to compensate for these factors, a prescribed-time ESO (extended state observer) was designed in [21]. The design of the observer is mainly for the service of the controller. The process of designing the observer to make it converge quickly and track the disturbance quickly is a problem to be solved.

For an NMR, the existence of unknown slipping and skidding makes the controller design of the system more difficult [22]. Notably, finite time stability has better steady-state performance for the system than exponential stability. To solve the problem that the sliding mode control cannot converge and stabilize in finite time, a finite time controller based on a disturbance observer was proposed in [23], which combined with a terminal sliding mode control design. To improve the convergence speed of finite time stability, Zhang et al. [24] designed a global sliding mode finite time tracking controller by adding a linear term to a Lyapunov function that was compared with [6]. As we all know, fixed-time stability has the advantage of not depending on the initial conditions. Huang et al. [25] provided faster fixed time convergence by utilizing higher-order terms and designed a trajectory tracking scheme based on fixed time stability. Defoort et al. [26] proposed a strategy to achieve fixed time stability through local information exchange to address the leader–follower consensus problem and gave an explicit estimation of the convergence time. In addition, in some existing studies of fixed-time stability [27], it is complicated to establish the relationship between the system gain and the upper bound of the convergence time. As a result, it is difficult to easily adjust the system convergence time according to the actual application [28]. Lin et al. [29] proposed a new trajectory tracking predefined time controller combined with a sliding mode method for nonholonomic mobile robots. However, the influence of an NMR with unknown slipping and skidding was not considered. At present, there is a problem in the design of the controller, the convergence of the controller, and the observer considered together. In this case, the parameters of the controller and the observer are coupled together, which makes the adjustment of the parameters very complex and not easy to apply in practice. In order to obtain satisfactory tracking performance, a predefined time tracking control law based on specified performance will be demonstrated for an NMR in this article. The main contributions are as follows:

(1)

We consider the steering problem of an NMR. The mathematical model of an NMR is derived, which is different from that in [30].

(2)

Predefined time stability and backstepping design methods are employed to achieve a fast convergence of the predefined time observers, compared with fixed time observers, which can estimate disturbances with a higher accuracy and adjustable convergence rate.

(3)

Predefined time active controllers based on backstepping design are proposed to achieve high precision tracking performance of an NMR with unknown slipping and skidding.

(4)

To solve the holonomic tracking problem of an NMR, a new tracking trajectory is redesigned to realize the holonomic tracking of the three states of the NMR with unknown slipping and skidding into the three states of the NMR.

2. Preliminaries and Problem Formulation

2.1. Lemmas and Definitions

In this article, we set

$$\begin{array}{c}\hfill sign\left(z\right)=\left\{\begin{array}{c}1,ifz>0\hfill \\ 0,ifz=0\hfill \\ -1,ifz<0\hfill \end{array}\right.\end{array}$$

and

$$\begin{array}{c}\hfill sig{\left(z\right)}^{\eta }=sign\left(z\right){\left|z\right|}^{\eta },\eta >0,\end{array}$$

where $z\in R$, sign(·) represents the sign function, and $\left|z\right|$ represents the absolute of z. Consider the system

$$\dot{x}=g(t,x),x\left(0\right)=x_0,$$

(1)

where $x\in {\mathbb{R}}^n$ denotes the state vector, $g:{\mathbb{R}}_{+}\times {\mathbb{R}}^n\to {\mathbb{R}}^n$ represents a smooth nonlinear function, and $x_0$ is the initial condition.

Definition 1 

([31]). If system (1) is globally finite time stable and the settling time is bounded, i.e., $\exists T_{max}>0$: $\forall x_0\in R^n$, $T\left(x_0\right)\le T_{max}$, then system (1) is globally fixed time stable.

Lemma 1 

([32]). A positive definite and continuously radial function $V\left(x\right):R^n\to R$ for system (1) satisfies $\alpha ,\beta ,\gamma ,\eta >0$, $\gamma \eta >1$ for any $V\left(x\right)>0$ such that

$$\begin{array}{c}\hfill \dot{V}\le -{(\alpha V^{\gamma }+\beta )}^{\eta },x\left(t\right)\in R^n\setminus \left\{0\right\}.\end{array}$$

(2)

Then, system (1) is stable in fixed time, and the settling time is $T_{max}^1$, which is described as

$$\begin{array}{c}\hfill T\left(x_0\right)\le T_{max}^1\triangleq \frac{{\beta }^{\frac{1}{\gamma }-\eta }}{{\alpha }^{\frac{1}{\gamma }}\gamma }B(\frac{1}{\gamma },\eta -\frac{1}{\gamma }),\end{array}$$

(3)

where $B(\frac{1}{\gamma },\eta -\frac{1}{\gamma })$ is the complete beta function.

Definition 2 

([29]). If system (1) is globally fixed time stable and the settling time $T\left(x_0\right)$ is

$$\begin{array}{c}\hfill T\left(x_0\right)\le T_c,\forall x_0\in {\mathbb{R}}^n,\end{array}$$

where $T_c$ is a adjustable parameter called a predefined time, then system (1) is predefined time stable.

Lemma 2 

([32]). A positive definite and continuously radial function $V\left(x\right):R^n\to R$ for system (1) satisfies $\alpha ,\beta ,\gamma ,\eta >0$, $\gamma \eta >1$ for any $V\left(x\right)>0$ such that

$$\begin{array}{c}\hfill \dot{V}\le -\frac{T_{max}^2}{T_c}{(\alpha V^{\gamma }+\beta )}^{\eta },x\left(t\right)\in R^n\setminus \left\{0\right\}\end{array}$$

(4)

with

$$\begin{array}{c}\hfill T_{max}^2=\frac{{\beta }^{\frac{1}{\gamma }-\eta }}{{\alpha }^{\frac{1}{\gamma }}\gamma }B(\frac{1}{\gamma },\eta -\frac{1}{\gamma }).\end{array}$$

(5)

Then, system (1) is stable in predefined time, and the predefined time is $T_c$.

Remark 1. 

The convergence time of fixed time stability depends on the parameters of the control system. It is difficult to find a clear and explicit relationship between the control system parameters and the convergence time, which will lead to difficulty in tuning the convergence time of the system. The predefined time stability converts the complex expression of the convergence time estimation of the fixed time stability into an adjustable parameter $T_c$ in the controller, and the system will achieve uniformly global stability within $T_c$, which makes the adjustment of the convergence time of the system easier and convenient.

2.2. Problem Formulation

Figure 1 shows the model of an NMR. The NMR is driven by two drive wheels at its rear. d is the distance between the center of mass of the two drive wheels and the geometric center P. Choosing $P_d$ as the reference tracking trajectory point, the attitude of an NMR can be defined in the ground coordinates as the following: $p={[x,y,\theta ]}^T$; x and y are the positions, and $\theta$ is the angle between the symmetry axis and the x axis [30]. For an NMR, if we consider the perturbation nonholonomic constraints of slipping and skidding, we can obtain:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \dot{x}=& (v-{\eta }_v)cos\theta -(\mu +d\dot{\theta })sin\theta \hfill \\ \hfill \dot{y}=& (v-{\eta }_v)sin\theta +(\mu +d\dot{\theta })cos\theta \hfill \\ \hfill \dot{\theta }=& w-{\eta }_w\hfill \end{array}\right.,\end{array}$$

(6)

where v is the longitude line velocity, $\mu$ is the lateral line velocity, $\omega$ is the angular speed, ${\eta }_w$ is the yaw rate perturbation due to the slipping of the wheels, and ${\eta }_v$ is the longitudinal slip velocity. We define the pose of the NMR as $p={[x,y,\theta ]}^T$, and we define the reference pose and velocity as $p_d={[x_d,y_d,{\theta }_d]}^T$ and $z_d={[v_d,{\omega }_d]}^T$ respectively. A reference trajectory is designed as shown in the following.

$$\dot{p_d}=\left[\begin{array}{c}\dot{x_d}\\ \dot{y_d}\\ \dot{{\theta }_d}\end{array}\right]=\left[\begin{array}{ccc}& cos{\theta }_d& 0\\ & sin{\theta }_d& 0\\ & 0& 1\end{array}\right]u,$$

(7)

where $u={[v_d,w_d]}^T$ is the control input, $v_d$ represents the the forward velocity, and $w_d$ represents the angular velocity. We define the tracking error as

$$p_e=\left[\begin{array}{c}{x}_e\\ y_e\\ {\theta }_e\end{array}\right]=\left[\begin{array}{cccc}& cos\theta & sin\theta & 0\\ & -sin\theta & cos\theta & 0\\ & 0& 0& 1\end{array}\right]\left[\begin{array}{c}{x}_d-x\\ y_d-y\\ {\theta }_d-\theta \end{array}\right].$$

(8)

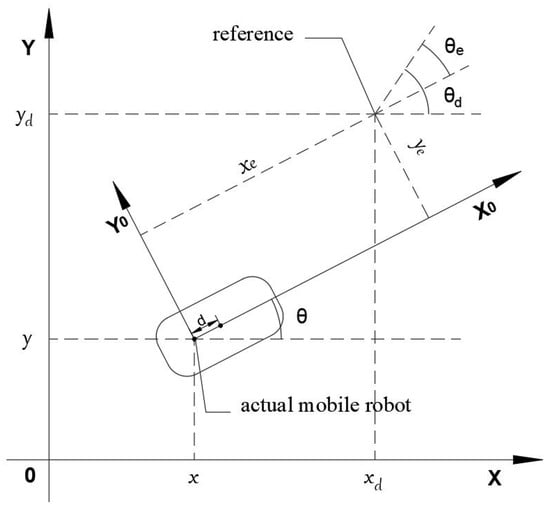
Figure 1. Posture errors of the coordinate for NMR.

Since

$$\begin{array}{c}\hfill x_e=cos\theta (x_d-x)+sin\theta (y_d-y),\end{array}$$

its derivative can be written as

$$\begin{array}{cc}\hfill {\dot{x}}_e=& cos\theta ({\dot{x}}_d-\dot{x})-\dot{\theta }sin\theta (x_d-x)+\dot{\theta }cos\theta (y_d-y)+sin\theta ({\dot{y}}_d-\dot{y})\hfill \\ \hfill =& cos\theta cos{\theta }_d{v}_d-cos\theta ((v-{\eta }_v)cos\theta -(\mu +d\dot{\theta })sin\theta )-\dot{\theta }sin\theta (x_d-x)\hfill \\ \hfill & +\dot{\theta }cos\theta (y_d-y)+sin\theta sin{\theta }_d{v}_d-sin\theta ((v-{\eta }_v)sin\theta +(\mu +d\dot{\theta })cos\theta )\hfill \\ \hfill =& cos\theta cos{\theta }_d{v}_d-co{s}^2\theta (v-{\eta }_v)-cos\theta sin\theta (\mu +d\dot{\theta })-\dot{\theta }sin\theta (x_d-x)\hfill \\ \hfill & +\dot{\theta }cos\theta (y_d-y)+sin\theta sin{\theta }_d{v}_d-si{n}^2\theta (v-{\eta }_v)+sin\theta cos\theta (\mu +d\dot{\theta })\hfill \\ \hfill =& -(v-{\eta }_v)+y_e\dot{\theta }+v_{d}cos(\theta -{\theta }_d)\hfill \\ \hfill =& -v+{\eta }_v+y_{e}w-y_e{\eta }_w+v_{d}cos{\theta }_e.\hfill \end{array}$$

Since

$$\begin{array}{c}\hfill y_e=-sin\theta (x_d-x)+cos\theta (y_d-y),\end{array}$$

its derivative can be written as

$$\begin{array}{cc}\hfill {\dot{y}}_e=& -\dot{\theta }cos\theta (x_d-x)-sin\theta ({\dot{x}}_d-\dot{x})-\dot{\theta }sin\theta (y_d-y)+cos\theta ({\dot{y}}_d-\dot{y})\hfill \\ \hfill =& -\dot{\theta }{x}_e-sin\theta (cos{\theta }_d{v}_d-((v-{\eta }_v)cos\theta -(\mu +d\dot{\theta })sin\theta ))+cos\theta (sin{\theta }_d{v}_d\hfill \\ \hfill & -((v-{\eta }_v)sin\theta +(\mu +d\dot{\theta })cos\theta ))\hfill \\ \hfill =& -\dot{\theta }{x}_e+cos\theta sin\theta (v-{\eta }_v)-cos\theta sin\theta (v-{\eta }_v)+(\mu +d\dot{\theta })-sin\theta cos{\theta }_d{v}_d+cos\theta sin\theta v_d\hfill \\ \hfill =& -\dot{\theta }{x}_e+v_{d}sin{\theta }_e+(\mu +d\dot{\theta }).\hfill \end{array}$$

Since

$$\begin{array}{c}\hfill {\theta }_e={\theta }_d-\theta ,\end{array}$$

its derivative can be written as

$$\begin{array}{c}\hfill {\dot{\theta }}_e={\dot{\theta }}_d-\theta =w_d-w+{\eta }_w.\end{array}$$

Then, the first derivative of $p_e$ can be written as

$$\begin{array}{cc}\hfill \dot{p_e}=& \left[\begin{array}{c}\dot{x_e}\\ \dot{y_e}\\ \dot{{\theta }_e}\end{array}\right]=\left[\begin{array}{c}{v}_{d}cos{\theta }_e+y_{e}w-v\\ v_{d}sin{\theta }_e-x_{e}w+dw\\ w_d-w\end{array}\right]+\left[\begin{array}{ccc}1& -y_e& 0\\ 0& x_e-d& 1\\ 0& 1& 0\end{array}\right]\left[\begin{array}{c}{\eta }_v\\ {\eta }_w\\ \mu \end{array}\right].\hfill \end{array}$$

(9)

In this article, we consider the influence of d, which will affect the steering problem of the NMR. Therefore, Formula (9) is different from that in [30].

3. Main Results

As shown in Figure 2, the detail tracking control can be described in the next three subsections. To solve the problem of unknown slipping and skidding, Section 3.1 proposes predefined time observers to achieve accurate disturbance estimation for ${\eta }_w$, ${\eta }_v$, and $\mu$. Then, Section 3.2 proposes predefined time active controllers to achieve the high-precision tracking performance of the NMR. To solve the holonomic tracking problem of the NMR, the tracking trajectory is redesigned in Section 3.3 to realize the accurate holonomic tracking of the NMR.

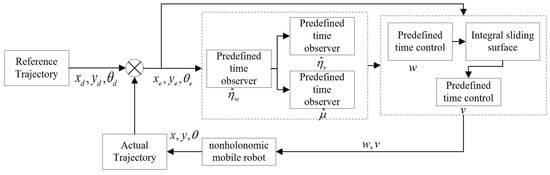
Figure 2. Block diagram of the proposed algorithm.

3.1. Observer Design

To design a control scheme for the disturbance estimation of unknown slipping and skidding, the following assumption is required:

Assumption 1. 

For an NMR, the disturbances ${\eta }_v$,${\eta }_w$, and μ, and their first derivatives are bounded.

$$\begin{array}{cc}\hfill ∥{\eta }_v∥\le {ϵ}_{01},& ∥{\dot{\eta }}_v∥\le {ϵ}_{11}\hfill \\ \hfill ∥{\eta }_w∥\le {ϵ}_{02},& ∥{\dot{\eta }}_w∥\le {ϵ}_{12}\hfill \\ \hfill ∥\mu ∥\le {ϵ}_{03},& ∥{\dot{\mu }}_w∥\le {ϵ}_{13,}\hfill \end{array}$$

where ${ϵ}_{ij}$ with $i=0,1$ and $j=1,2,3$ are the unknown positive constants, which define the upper bound of the disturbance.

Lemma 3. 

Considering the derivation of $p_e$, and supposing that Assumption 1 holds, the disturbance observer of ${\eta }_w$ is desinged as

$$\begin{array}{cc}\hfill {\dot{\widehat{\eta }}}_w=& -{\widehat{\eta }}_w{x}_{12}+\frac{T_{max}^3}{T_{c01}}(k_{01}{x}_{32}^p+k_{02}sign\left(x_{32}\right)+{ϵ}_{02}sign\left(x_{32}\right)|x_{12}|+{ϵ}_{12}sign\left(x_{32}\right)),\hfill \end{array}$$

(10)

where $k_{01}$ and $k_{02}$ are the designed gains. $T_{c01}$ is the parameter predefined in advance, and

$$\begin{array}{c}\hfill T_{max}^3=\frac{k_{02}^{\frac{1}{p}-1}}{k_{01}^{\frac{1}{p}}p}B(\frac{1}{p},1-\frac{1}{p}).\end{array}$$

$x_{32}\in R^3$ is the auxiliary design variable of the predefined time observer, which is designed as

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\dot{\widehat{\theta }}}_e=& w_r-w+{\widehat{\eta }}_w\hfill \\ \hfill x_{12}=& {\theta }_e-\widehat{{\theta }_e}=e_{{\theta }_e}\hfill \\ \hfill \dot{x_{12}}=& {\dot{\theta }}_e-{\dot{\widehat{\theta }}}_e\hfill \\ \hfill =& w_r-w+{\eta }_w-w_r+w-{\widehat{\eta }}_w\hfill \\ \hfill =& {\eta }_w-{\widehat{\eta }}_w\hfill \\ \hfill \ddot{x_{12}}=& {\dot{\eta }}_w-{\dot{\widehat{\eta }}}_w\hfill \\ \hfill x_{32}=& \frac{1}{2}{x}_{12}^2+{\dot{x}}_{12}+k_{03},\hfill \end{array}\right.\end{array}$$

(11)

where $x_{12}$ is the auxiliary design variable of the fixed time observer, and ${\widehat{\theta }}_e$ is the estimation of ${\theta }_e$. Then, the observer (10) can achieve convergence in predefined time $T_{01}$.

Proof. 

For $x_{32}$, we have

$$\begin{array}{cc}\hfill \dot{x_{32}}=& x_{12}\dot{x_{12}}+\ddot{x_{12}}\hfill \\ \hfill =& x_{12}{\eta }_w-x_{12}\widehat{{\eta }_w}+\dot{{\eta }_w}-\dot{\widehat{{\eta }_w}}\hfill \\ \hfill =& x_{12}{\eta }_w+\dot{{\eta }_w}-x_{12}\widehat{{\eta }_w}+x_{12}\widehat{{\eta }_w}+{ϵ}_{02}sign\left(x_{32}\right)|x_{12}|+{ϵ}_{12}sign\left(x_{32}\right))\hfill \\ \hfill & -\frac{T_{max}^3}{T_{c01}}(k_{01}{x}_{32}^p+k_{02}sign\left(x_{32}\right)\hfill \\ \hfill =& x_{12}{\eta }_w+\dot{{\eta }_w}-\frac{T_{max}^3}{T_{c01}}(k_{01}{x}_{32}^p+k_{02}sign\left(x_{32}\right)+{ϵ}_{02}sign\left(x_{32}\right)|x_{12}|+{ϵ}_{12}sign\left(x_{32}\right))\hfill \\ \hfill =& (x_{12}{\eta }_w-{ϵ}_{02}sign(x_{32}|x_{12}\left|\right)+{\dot{\eta }}_w-{ϵ}_{12}sign\left(x_{32}\right))\hfill \\ \hfill & -\frac{T_{max}^3}{T_{c01}}(k_{01}{x}_{32}^p+k_{02}sign\left(x_{32}\right)).\hfill \end{array}$$

(12)

Choose a Lyapunov function candidate as

$$\begin{array}{c}\hfill V_{01}=\left|x_{32}\right|.\end{array}$$

Its derivative along (12) satisfies

$$\begin{array}{cc}\hfill {\dot{V}}_{01}=& sign\left(x_{32}\right)\left(\right(x_{12}{\eta }_w-{ϵ}_{02}sign(x_{32}|x_{12}|)+\dot{{\eta }_w}\hfill \\ \hfill & -{ϵ}_{12}sign\left(x_{32}\right))-\frac{T_{max}^3}{T_{c01}}(k_{01}{x}_{32}^p+k_{02}sign\left(x_{32}\right)))\hfill \\ \hfill =& (sign\left(x_{32}\right){\eta }_w{x}_{12}-{ϵ}_{02}|x_{12}\left|\right)+(sign\left(x_{32}\right){\dot{\eta }}_w-{ϵ}_{12})-\frac{T_{max}^3}{T_{c01}}(k_{01}|x_{32}{|}^p+k_{02})\hfill \\ \hfill \le & -\frac{T_{max}^3}{T_{c01}}(k_{01}|x_{32}{|}^p+k_{02}).\hfill \end{array}$$

According to Lemma 2, it can be concluded that $\underset{t\to T_{c01}}{lim}{x}_{32}=0$; then, we have

$$\begin{array}{c}\hfill \frac{1}{2}{x}_{12}^2+{\dot{x}}_{12}+k_{03}=0.\end{array}$$

Then,

$$\begin{array}{c}\hfill {\dot{x}}_{12}=-\frac{1}{2}{x}_{12}^2-k_{03.}\end{array}$$

According to Lemma 1, it can be concluded that $\underset{t\to T_{fix}}{lim}{x}_{12}=0$, i.e., ${\dot{x}}_{12}\to 0$ and $x_{12}\to 0$ when $t\to T_{01}$, where

$$\begin{array}{c}\hfill T_{01}=T_{c01}+T_{fix}.\end{array}$$

(13)

Based on (11), we have ${\widehat{\theta }}_e={\theta }_e$ and ${\widehat{\eta }}_w={\eta }_w$ when $t\to T_{01}$. The proof is completed. □

Now, based on the results of Lemma 3, we continue to design predefined time observers to estimate the unknown disturbances $\mu$ and ${\eta }_v$ within a predefined time $T_{02}$. Since $\widehat{{\eta }_w}={\eta }_w$ after $T_{01}$, we have

$$\begin{array}{c}\hfill \dot{x_e}=v_{d}cos{\theta }_e+y_{e}w-v+({\eta }_v-y_e{\widehat{\eta }}_w)\end{array}$$

(14)

$$\begin{array}{c}\hfill \dot{y_e}=v_{d}sin{\theta }_e-x_{e}w+dw+x_e{\widehat{\eta }}_w+\mu -d{\eta }_w.\end{array}$$

(15)

It can be seen from the above formulas that disturbance $\mu$ only affects Formula (15), and disturbance ${\eta }_v$ only affects Formula (14), so they can be estimated separately.

Lemma 4. 

Considering (15), supposing that Assumption 1 and Theorem 3 hold; the disturbance observer of μ is then designed as

$$\begin{array}{cc}\hfill \dot{\widehat{\mu }}=& -\widehat{\mu }{x}_{13}+\frac{T_{max}^3}{T_{c02}}(k_{01}{x}_{33}^p+k_{02}sign\left(x_{33}\right))+{ϵ}_{03}sign\left(x_{33}\right)\left|x_{13}\right|+{ϵ}_{13}sign\left(x_{33}\right),\hfill \end{array}$$

(16)

where $T_{c02}$ is the parameter predefined in advance. $x_{33}$ is the auxiliary design variable of the predefined time observer, which is designed as

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\dot{\widehat{y}}}_e=& v_{d}sin{\theta }_e-x_{e}w+dw-d{\widehat{\eta }}_w+x_e{\widehat{\eta }}_w+\widehat{\mu }\hfill \\ \hfill x_{13}=& y_e-{\widehat{y}}_e=e_{y_e}\hfill \\ \hfill {\dot{x}}_{13}=& {\dot{y}}_e-{\dot{\widehat{y}}}_e\hfill \\ \hfill =& v_{r}sin{\theta }_e-x_{e}w+dw-d{\widehat{\eta }}_w+x_e{\widehat{\eta }}_w+\mu \hfill \\ \hfill & -(v_{r}sin{\theta }_e-x_{e}w+dw-d{\widehat{\eta }}_w+x_e{\widehat{\eta }}_w+\widehat{\mu })\hfill \\ \hfill =& \mu -\widehat{\mu }\hfill \\ \hfill {\ddot{x}}_{13}=& \dot{\mu }-\dot{\widehat{\mu }}\hfill \\ \hfill x_{33}=& \frac{1}{2}{x}_{13}^2+{\dot{x}}_{13}+k_{03,}\hfill \end{array}\right.\end{array}$$

(17)

where $x_{12}$ is the auxiliary design variable of the fixed time observer, and ${\widehat{y}}_e$ is the estimation of $y_e$. Then, the observer (16) can achieve convergence in predefined time $T_{02}$.

Proof. 

For $x_{33}$, we have

$$\begin{array}{cc}\hfill lll{\dot{x}}_{33}=& x_{13}\dot{x_{13}}+{\ddot{x}}_{13}\hfill \\ \hfill =& x_{13}\mu -x_{13}\widehat{\mu }+\dot{\mu }-\dot{\widehat{\mu }}\hfill \\ \hfill =& x_{13}\mu +\dot{\mu }-\frac{T_{max}^3}{T_{c02}}(k_{01}{x}_{33}^p+k_{02}sign\left(x_{33}\right))-{ϵ}_{03}sign\left(x_{33}\right)\left|x_{13}\right|-{ϵ}_{13}sign\left(x_{33}\right).\hfill \end{array}$$

(18)

Choose a Lyapunov function candidate as

$$\begin{array}{c}\hfill V_{02}=\left|x_{33}\right|.\end{array}$$

Its derivative along (18) satisfies

$$\begin{array}{cc}\hfill {\dot{V}}_{02}=& sign\left(x_{33}\right)(x_{13}\mu +\dot{\mu }-\frac{T_{max}^3}{T_{c02}}(k_{01}{x}_{33}^p+k_{02}sign\left(x_{33}\right))\hfill \\ \hfill & -{ϵ}_{03}sign\left(x_{33}\right)|x_{13}|-{ϵ}_{13}sign\left(x_{33}\right))\hfill \\ \hfill =& (sign\left(x_{33}\right)x_{13}\mu -{ϵ}_{03}|x_{13}\left|\right)+(sign\left(x_{33}\right)\dot{\mu }-{ϵ}_{13})-\frac{T_{max}^3}{T_{c02}}(k_{01}|x_{33}{|}^p+k_{02})\hfill \\ \hfill \le & -\frac{T_{max}^3}{T_{c02}}(k_{01}|x_{33}{|}^p+k_{02}).\hfill \end{array}$$

According to Lemma 2, it can be concluded that $\underset{t\to T_{c02}}{lim}{x}_{33}=0$; then, we have

$$\begin{array}{c}\hfill \frac{1}{2}{x}_{13}^2+{\dot{x}}_{13}+k_{03}=0.\end{array}$$

Then,

$$\begin{array}{c}\hfill {\dot{x}}_{13}=-\frac{1}{2}{x}_{13}^2-k_{03.}\end{array}$$

According to Lemma 1, it can be concluded that $\underset{t\to T_{fix}}{lim}{x}_{13}=0$, i.e., ${\dot{x}}_{13}\to 0$ and $x_{13}\to 0$ when $t\to T_{02}$, where

$$\begin{array}{c}\hfill T_{02}=T_{01}+T_{c02}+T_{fix}=T_{c01}+T_{c02}+2T_{fix}.\end{array}$$

(19)

Based on (17), we have $\widehat{y_e}=y_e$ and $\widehat{\mu }=\mu$ when $t\to T_{02}$. The proof is completed. □

Next, we continue to design a predefined time observer to estimate ${\eta }_v$.

Lemma 5. 

Considering (14), supposing that Assumption 1 and Lemma 3 hold, the disturbance observer of ${\eta }_v$ is designed as

$$\begin{array}{cc}\hfill {\dot{\widehat{\eta }}}_v=& -x_{11}{\widehat{\eta }}_v+\frac{T_{max}^3}{T_{c02}}(k_{01}{x}_{31}^p+k_{02}sign\left(x_{31}\right)+{ϵ}_{01}sign\left(x_{31}\right)|x_{11}|+{ϵ}_{11}sign\left(x_{31}\right)),\hfill \end{array}$$

(20)

where $x_{31}$ is the auxiliary design variable of the predefined time observer, which is designed as

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\dot{\widehat{x}}}_e=& v_{r}cos{\theta }_e+y_{e}w-v+(\widehat{{\eta }_v}-y_e{\widehat{\eta }}_w)\hfill \\ \hfill x_{11}=& x_e-{\widehat{x}}_e=e_{x_e}\hfill \\ \hfill {\dot{x}}_{11}=& (v_{r}cos{\theta }_e+y_{e}w-v+({\eta }_v-y_e{\widehat{\eta }}_w))-(v_{r}cos{\theta }_e+y_{e}w-v+(\widehat{{\eta }_v}-y_e{\widehat{\eta }}_w))\hfill \\ \hfill =& {\eta }_v-\widehat{{\eta }_v}\hfill \\ \hfill {\ddot{x}}_{11}=& {\dot{\eta }}_v-{\dot{\eta }}_v\hfill \\ \hfill x_{31}=& x_{11}+{\dot{x}}_{11,}\hfill \end{array}\right.\end{array}$$

(21)

where $x_{11}$ is the auxiliary design variable of the fixed time observer, and ${\widehat{x}}_e$ is the estimation of $x_e$. Then, the observer (20) can achieve convergence in predefined time $T_{02}$.

Proof. 

For $x_{31}$, we have

$$\begin{array}{cc}\hfill llll{\dot{x}}_{31}=& x_{11}\dot{x_{11}}+{\ddot{x}}_{11}\hfill \\ \hfill =& x_{11}{\eta }_v-x_{11}{\widehat{\eta }}_v+{\dot{\eta }}_v-{\dot{\widehat{\eta }}}_v\hfill \\ \hfill =& x_{11}{\eta }_v+{\dot{\eta }}_v-x_{11}{\widehat{\eta }}_v+x_{11}{\widehat{\eta }}_v-\frac{T_{max}^3}{T_{c02}}(k_{01}{x}_{31}^p+k_{02}sign\left(x_{31}\right))\hfill \\ \hfill & +{ϵ}_{01}sign\left(x_{31}\right)\left|x_{11}\right|+{ϵ}_{11}sign\left(x_{31}\right).\hfill \end{array}$$

(22)

Choose a Lyapunov function candidate as

$$\begin{array}{c}\hfill V_{03}=\left|x_{31}\right|.\end{array}$$

Its derivative along (22) satisfies

$$\begin{array}{cc}\hfill {\dot{V}}_{03}=& sign\left(x_{31}\right)\left(\right(x_{11}{\eta }_v-{ϵ}_{01}sign\left(x_{31}\right)|x_{11}|+{\dot{\eta }}_v-{ϵ}_{11}sign\left(x_{31}\right))\hfill \\ \hfill & -\frac{T_{max}^3}{T_{c02}}(k_{01}{x}_{31}^p+k_{02}sign\left(x_{31}\right)))\hfill \\ \hfill =& (sign\left(x_{31}\right){\eta }_v{x}_{11}-{ϵ}_{01}|x_{11}\left|\right)+(sign\left(x_{31}\right){\dot{\eta }}_v-{ϵ}_{11})-\frac{T_{max}^3}{T_{c02}}(k_{01}|x_{31}{|}^p+k_{02})\hfill \\ \hfill \le & -\frac{T_{max}^3}{T_{c02}}(k_{01}|x_{31}{|}^p+k_{02}).\hfill \end{array}$$

According to Lemma 2, it can be concluded that $\underset{t\to T_{c02}}{lim}{x}_{31}=0$; then, we have

$$\begin{array}{c}\hfill \frac{1}{2}{x}_{11}^2+{\dot{x}}_{11}+k_{03}=0.\end{array}$$

Then,

$$\begin{array}{c}\hfill {\dot{x}}_{11}=-\frac{1}{2}{x}_{11}^2-k_{03}.\end{array}$$

According to Lemma 1, it can be concluded that $\underset{t\to T_{fix}}{lim}{x}_{11}=0$, i.e., ${\dot{x}}_{11}\to 0$ and $x_{11}\to 0$ when $t\to T_{02}$. Based on (21), we have $\widehat{x_e}=x_e$ and $\widehat{{\eta }_v}={\eta }_v$ when $t\to T_{02}$. The proof is completed. □

Remark 2. 

From Lemma 3, the disturbance ${\eta }_w$ can be accurately estimated by ${\widehat{\eta }}_w$ within the predefined time $T_{01}$. From the observation formula of disturbance ${\eta }_v$ and the observation formula of disturbance μ, they both depend on disturbance ${\eta }_w$, and they are independent of each other, which can be estimated simultaneously. From Lemma 4 and 5, both disturbances ${\eta }_v$ and μ can be accurately estimated within the predefined time of $T_{02}$.

Remark 3. 

Mario et al. [33] solved the robust synchronization problem of a class of differential-drive mobile robots in distance and orientation by designing an active disturbance rejection controller (ADRC). In this article, the predefined time observers were used to track unknown slipping and skidding in real time, and the following controllers were designed on this basis, which could effectively avoid the impact of system disturbances on the robustness of the controllers.

3.2. Control Law Design

By relying on the estimation of the disturbances ${\eta }_w$ by observer (10), $\mu$ by observer (16), and ${\eta }_v$ by observer (20), the unknown slipping and skidding problem of system (9) was resolved. Then, the tracking problem of the system (6) needed to be solved, where the objective is for the NMR to track the tracking trajectory $p_d$. Considering an NMR (6) with unknown slipping and skidding, the robust controller is designed as

$$\begin{array}{c}\hfill w=w_d+{\widehat{\eta }}_w+\frac{T_{max}^3}{T_{c03}}(k_{01}{\theta }_e^p+k_{02}sign\left({\theta }_e\right)),\end{array}$$

(23)

where $T_{c03}$ is the parameter predefined in advance. Then, the tracking error (8) has predefined time stability under the developed disturbance observers. Based on the design idea of backstepping, we consider the following subsystem

$$\begin{array}{c}\hfill {\dot{\theta }}_e=w_d-w+\widehat{{\eta }_w}.\end{array}$$

(24)

Theorem 1. 

The tracking error ${\theta }_e$ can achieve convergence in predefined time $T_{03}$ under the angular velocity controller designed as (23), where the predefined time $T_{03}$ is described as

$$\begin{array}{c}\hfill T_{03}=T_{c03}+T_{02}.\end{array}$$

(25)

Proof. 

Invoking (24) and (23) yields

$$\begin{array}{c}\hfill {\dot{\theta }}_e=-\frac{T_{max}^3}{T_{c03}}(k_{01}{\theta }_e^p+k_{02}sign\left({\theta }_e\right)).\end{array}$$

(26)

Choose a Lyapunov function candidate as

$$\begin{array}{c}\hfill V_{04}=\left|{\theta }_e\right|.\end{array}$$

Its derivative along (26) satisfies

$$\begin{array}{cc}\hfill {\dot{V}}_{04}=& sign\left({\theta }_e\right){\dot{\theta }}_e\hfill \\ \hfill =& -sign\left({\theta }_e\right)\frac{T_{max}^3}{T_{c03}}(k_{01}{\theta }_e^p+k_{02}sign\left({\theta }_e\right))\hfill \\ \hfill =& -\frac{T_{max}^3}{T_{c03}}(k_{01}|{\theta }_e{|}^p+k_{02}).\hfill \end{array}$$

According to Lemma 2, it can be concluded that $\underset{t\to T_{03}}{lim}{\theta }_e=0$, i.e., ${\theta }_e\to 0$ when $t\to T_{03}$, where

$$\begin{array}{c}\hfill T_{03}=T_{c03}+T_{02}.\end{array}$$

This proof is completed. □

Since ${\theta }_e\equiv 0$ after $T_{03}$, then we have

$$\begin{array}{c}\hfill w_d-w+{\widehat{\eta }}_w=0,\end{array}$$

and

$$\begin{array}{c}\hfill w=w_d+{\widehat{\eta }}_w.\end{array}$$

(27)

By invoking (27) and the second-order subsystems (14) and (15), we have

$$\begin{array}{cc}\hfill \dot{x_e}=& v_d+y_{e}w-v+({\widehat{\eta }}_v-y_e{\widehat{\eta }}_w)\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill \dot{y_e}=& -x_{e}w+x_e{\widehat{\eta }}_w+\widehat{\mu }+dw-d{\widehat{\eta }}_w\hfill \\ \hfill =& -x_e(w_d+{\widehat{\eta }}_w)+x_e{\widehat{\eta }}_w+\widehat{\mu }+d(w_d+{\widehat{\eta }}_w)-d{\widehat{\eta }}_w\hfill \\ \hfill =& -x_e{w}_d+\widehat{\mu }+d{w}_d.\hfill \end{array}$$

(29)

Theorem 2. 

There exists

$$\begin{array}{c}\hfill x_e=\frac{T_{max}^3}{T_{c04}{w}_d}(k_{01}{y}_e^p+k_{02}sign\left(y_e\right)+\frac{T_{c04}}{T_{max}^3}\widehat{\mu })+d.\end{array}$$

(30)

Thus, system (29) is stable in predefined time, and the settling time is $T_{04}$, which is described as

$$\begin{array}{c}\hfill T_{04}=T_{c04}+T_{03}.\end{array}$$

Proof. 

Invoking (30) and (29), we have

$$\begin{array}{cc}\hfill {\dot{y}}_e=& -(\frac{T_{max}^3}{T_{c04}{w}_d}(k_{01}{y}_e^p+k_{02}sign\left(y_e\right)+\frac{T_{c04}}{T_{max}^3}\widehat{\mu })+d)w_d+\widehat{\mu }+d{w}_d\hfill \\ \hfill =& -\frac{T_{max}^3}{T_{c04}}(k_{01}{y}_e^p+k_{02}sign\left(y_e\right))+\widehat{\mu }-\widehat{\mu }\hfill \\ \hfill =& -\frac{T_{max}^3}{T_{c04}}(k_{01}{y}_e^p+k_{02}sign\left(y_e\right)).\hfill \end{array}$$

(31)

We choose a Lyapunov function candidate as

$$\begin{array}{c}\hfill V_{05}=\left|y_e\right|.\end{array}$$

Its derivative satisfies

$$\begin{array}{cc}\hfill {\dot{V}}_{05}=& sign\left(y_e\right)(-\frac{T_{max}^3}{T_{c04}}(k_{01}{y}_e^p+k_{02}sign\left(y_e\right)))\hfill \\ \hfill =& -\frac{T_{max}^3}{T_{c04}}(k_{01}|y_e{|}^p+k_{02}).\hfill \end{array}$$

According to Lemma 2, it can be concluded that $\underset{t\to T_{04}}{lim}{y}_e=0$, i.e., $y_e\to 0$ when $t\to T_{04}$, where

$$\begin{array}{c}\hfill T_{04}=T_{c04}+T_{03}.\end{array}$$

This proof is completed. □

To achieve the predefined time stability of $y_e$, the sliding manifold method is adopted in this article. The sliding manifold is defined by

$$\begin{array}{c}\hfill s=x_e-\frac{T_{max}^3}{T_{c04}{w}_d}(k_{01}{y}_e^p+k_{02}sign\left(y_e\right))-\frac{\widehat{\mu }}{w_d}-d.\end{array}$$

Its derivative can be written as

$$\begin{array}{cc}\hfill \dot{s}=& {\dot{x}}_e-\frac{T_{max}^3}{T_{c04}{w}_d}{k}_{01}p{y}_e^{p-1}(-(x_e-d)w_d+\widehat{\mu })-\frac{\dot{\widehat{\mu }}}{w_d}\hfill \\ \hfill =& {\dot{x}}_e+\frac{T_{max}^3}{T_{c04}}{k}_{01}p{y}_e^{p-1}(x_e-d)-\frac{T_{max}^3}{T_{c04}{w}_d}{k}_{01}p{y}_e^{p-1}\widehat{\mu }-\frac{\dot{\widehat{\mu }}}{w_d}.\hfill \end{array}$$

(32)

Theorem 3. 

The tracking errors $x_e$ and $y_e$ can achieve convergence in predefined time $T_{05}$ using the velocity controller of a nonholonomic mobile robot designed as

$$\begin{array}{cc}\hfill v=& v_d+y_{e}w+{\widehat{\eta }}_v-y_e{\widehat{\eta }}_w+\frac{T_{max}^3}{T_{c04}}{k}_{01}p{y}_e^{p-1}{x}_e-\frac{T_{max}^3}{T_{c04}{w}_d}{k}_{01}p{y}_e^{p-1}\widehat{\mu }\hfill \\ \hfill & -\frac{T_{max}^3}{T_{c04}}{k}_{01}p{y}_e^{p-1}d-\frac{\dot{\widehat{\mu }}}{w_d}+\frac{T_{max}^3}{T_{c05}}(k_{01}{s}^p+k_{02}sign\left(s\right)).\hfill \end{array}$$

(33)

Thus, subsystems (28) and (29) are global predefined time stable, and the predefined time $T_{05}$ is described as

$$\begin{array}{c}\hfill T_{05}=T_{c05}+T_{04}.\end{array}$$

Proof. 

Choose a Lyapunov function candidate as

$$\begin{array}{c}\hfill V_{06}=\left|s\right|.\end{array}$$

Its derivative along (32) satisfies

$$\begin{array}{cc}\hfill {\dot{V}}_{06}=& sign\left(s\right)\dot{s}\hfill \\ \hfill =& sign\left(s\right)(v_d+y_{e}w-v+({\widehat{\eta }}_v-y_e{\widehat{\eta }}_w)-\frac{T_{max}^3}{T_{c04}{w}_d}{k}_{01}p{y}_e^{p-1}(-(x_e-d)w_d+\widehat{\mu })-\frac{\dot{\widehat{\mu }}}{w_d})\hfill \\ \hfill =& sign\left(s\right)(v_d+y_{e}w-(v_d+y_{e}w+{\widehat{\eta }}_v-y_e{\widehat{\eta }}_w\hfill \\ \hfill & +\frac{T_{max}^3}{T_{c04}}{k}_{01}p{y}_e^{p-1}{x}_e-\frac{T_{max}^3}{T_{c04}{w}_d}{k}_{01}p{y}_e^{p-1}\widehat{\mu }-\frac{T_{max}^3}{T_{c04}}{k}_{01}p{y}_e^{p-1}d-\frac{\dot{\widehat{\mu }}}{w_d})\hfill \\ \hfill & +\frac{T_{max}^3}{T_{c05}}(k_{01}{s}^p+k_{02}sign\left(s\right))\hfill \\ \hfill & +({\widehat{\eta }}_v-y_e{\widehat{\eta }}_w)+\frac{T_{max}^3}{T_{c04}}{k}_{01}p{y}_e^{p-1}(x_e-d)-\frac{T_{max}^3}{T_{c04}{w}_d}{k}_{01}p{y}_e^{p-1}\widehat{\mu }-\frac{\dot{\widehat{\mu }}}{w_d})\hfill \\ \hfill =& \frac{T_{max}^3}{T_{c05}}(k_{01}{\left|s\right|}^p+k_{02}).\hfill \end{array}$$

According to Lemma 2, it can be concluded that $\underset{t\to T_{05}}{lim}s=0$, i.e., $s\to 0$ when $t\to T_{05}$, where

$$\begin{array}{c}\hfill T_{05}=T_{c05}+T_{04}.\end{array}$$

This proof is completed. □

Remark 4. 

A new type of ESO was established in [34] to estimate the states and the total disturbance of wheeled mobile robots. Then, a fixed time controller based on the above ESO was developed to achieve high-precision control performance. Compared with [34], the complex relationship between the system parameters and the settling time was transformed into a one-to-one correspondence between the settling time and the parameter $T_{05}$ (where $T_{05}=T_{c05}+T_{c04}+T_{c03}+T_{c02}+T_{c01}+2T_{fix}$) in this article. By tuning $T_{05}$, system (9) can be stabilized at different predefined time, which is simpler and more effective than the fixed time stability.

3.3. The Holonomic Tracking Problem of NMR

If $y_e=0$, according to Theorem 2, it can be obtained that

$$\begin{array}{c}\hfill x_e=\frac{\widehat{\mu }}{w_d}+d.\end{array}$$

Then,

$$\left[\begin{array}{c}\frac{\widehat{\mu }}{w_d}+d\\ 0\\ 0\end{array}\right]=\left[\begin{array}{cccc}& cos\theta & sin\theta & 0\\ & -sin\theta & cos\theta & 0\\ & 0& 0& 1\end{array}\right]\left[\begin{array}{c}{x}_d-x\\ y_d-y\\ {\theta }_d-\theta \end{array}\right].$$

(34)

One can obtain that

$$\begin{array}{c}\hfill \frac{\widehat{\mu }}{w_d}+d=cos\theta (x_d-x)+sin\theta (y_d-y)\\ \hfill 0=-sin\theta (x_d-x)+cos\theta (y_d-y).\end{array}$$

Then we have

$$\begin{array}{c}\hfill x_d-x=(\frac{\widehat{\mu }}{w_d}+d)cos\theta \\ \hfill y_d-y=(\frac{\widehat{\mu }}{w_d}+d)sin\theta .\end{array}$$

If $\widehat{\mu }\ne 0$ or $d\ne 0$, then $x\ne x_d$ and $y\ne y_d$. In order to realize holonomic tracking of the NMR, we assume that $x=x_d$ and $y=y_d$; the new tracking trajectory is designed as follows:

$$\begin{array}{c}\hfill {\widehat{x}}_d=x_d-(\frac{\widehat{\mu }}{w_d}+d)cos\theta \\ \hfill {\widehat{y}}_d=y_d-(\frac{\widehat{\mu }}{w_d}+d)sin\theta .\end{array}$$

Then,

$$\begin{array}{cc}\hfill {\widehat{x}}_e=& cos\theta ({\widehat{x}}_d-x)+sin\theta ({\widehat{y}}_d-y)\hfill \\ \hfill =& cos\theta (-(\frac{\widehat{\mu }}{w_d}+d)cos\theta +x_d-x)+sin\theta (-(\frac{\widehat{\mu }}{w_d}+d)sin\theta +y_d-y)\hfill \\ \hfill =& -(\frac{\widehat{\mu }}{w_d}+d)+cos\theta (x_d-x)+sin\theta (y_d-y)\hfill \\ \hfill =& -(\frac{\widehat{\mu }}{w_d}+d)+(\frac{\widehat{\mu }}{w_d}+d)\hfill \\ \hfill =& 0.\hfill \end{array}$$

In this article, modifying $x_d$ and $y_d$ to ${\widehat{x}}_d$ and ${\widehat{y}}_d$ can realize holonomic tracking of $x_d$ and $y_d$.

Remark 5. 

By redesigning the new tracking trajectory, this article changes the original situation that it is impossible to realize the holonomic tracking of the three states of an NMR with unknown slipping and skidding into the three states of an NMR.

4. Simulation

We applied the proposed predefined time observers and active predefined time controllers to an NMR. The simulation environment was MATLAB 2021B SIMULINK, and the step size was set to 0.001. Independent of the initial conditions, the desired tracking posture $p_d={[x_d,y_d,{\theta }_d]}^T$ of the NMR is specified as

$$\begin{array}{cc}\hfill x_d\left(t\right)=& rcos{w}_{d}t\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill y_d\left(t\right)=& rsin{w}_{d}t\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill {\theta }_d\left(t\right)=& w_{d}t.\hfill \end{array}$$

(37)

The desired posture was a circle with the radius of the circular trajectory $r=v_d/w_d$. Then, the NMR could make a uniform circular motion. The desired forward velocity was given by $v_d=5.0$. The desired angular velocity was given by $w_d=1.0$.

According to Lemma 3, we can design the predefined time observer for ${\eta }_w$ as (10). The parameters of the observer were chosen as $\alpha =5$, $\beta =2$, $\eta =1$, $\gamma =1$, and ${ϵ}_{01}={ϵ}_{11}=0.4$. Similarly, we can design the observer for $\mu$ as in (16), and we can design the observer ${\eta }_v$ as in (20), where the parameters were chosen as ${ϵ}_{02}={ϵ}_{12}=0.7$ and ${ϵ}_{03}={ϵ}_{13}=2$. The disturbances were set as ${\eta }_w=0.7sin\left(t\right)$, ${\eta }_v=0.4cos\left(10t\right)$, and $\mu =2$. The simulation results are given in Figure 3, Figure 4, Figure 5 and Figure 6. In Figure 3, under the conditions that the initial conditions were unknown, the disturbance estimation ${\widehat{\eta }}_w$ could achieve an accurate estimation of the disturbance ${\eta }_w$ before the different predefined time $T_{01}$. Similarly, it can be seen from Figure 4 and Figure 5 that, even if the disturbance was not constant, the disturbance ${\eta }_v$ and $\mu$ could also be accurately estimated within the predefined time $T_{02}$. It was proven that Lemmas 4 and 5 are effective.

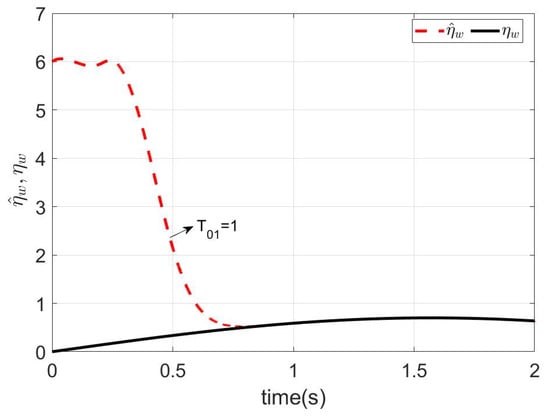
Figure 3. Estimations of ${\eta }_w$.

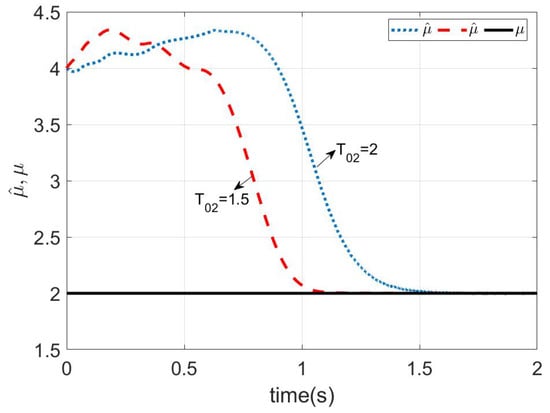
Figure 4. Estimations of $\mu$.

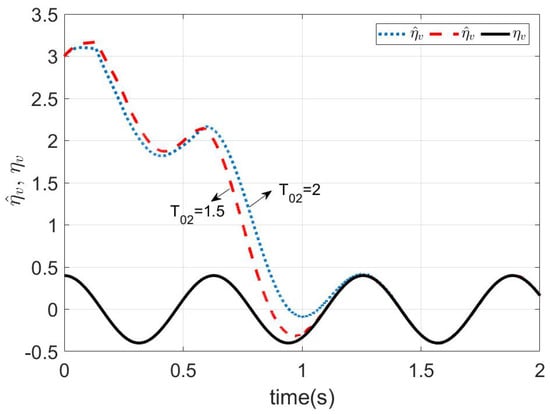
Figure 5. Estimations of ${\eta }_v$.

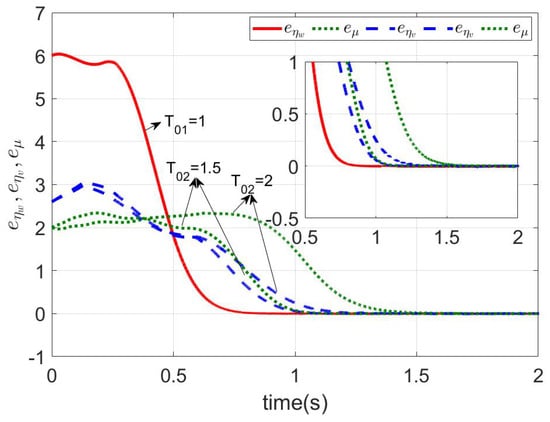
Figure 6. Estimation errors of ${\eta }_w$, $\mu$, and ${\eta }_v$.

Figure 6 shows the observer tracking error curves, namely, $e_{{\eta }_w}$, $e_{{\eta }_v}$, and $e_{\mu }$. The disturbance of $e_{{\eta }_w}$, $e_{{\eta }_v}$, and $e_{\mu }$ all converged before the different predefined time. Next, the predefined time active controller was designed for the NMR. The parameters of the controllers (23) and (33) were chosen as $T_{c03}=1$, $T_{c04}=2$, and $T_{c05}=3$. Then, we could get the whole predefined time, which is shown as

$$\begin{array}{c}\hfill T_{05}=T_{c03}+T_{c04}+T_{c04}+T_{02}=6.5.\end{array}$$

The simulation results are shown in Figure 7 and Figure 8. As shown in Figure 7, it is worth noting that the angle error of tracking posture (37) converged to zero in $5<T_{05}$. Similarly, the y-axis error of tracking posture (36) converged to zero. However, the x-axis error did not to converge to zero. The reason is that the mobile robot is nonholonomic. It is consistent with the results described in Remark 1. For the actual tracking trajectory shown in Figure 8, the NMR could not fully track the given tracking trajectory. For the predefined time $T_{05}=0.4$, the simulation results are shown in Figure 9. It can be seen that the results are the same as in Figure 7, except that the convergence time was changed. The method proposed in this article could simply achieve a change in the system convergence time by changing the predefined time parameter $T_{05}$. In order to realize holonomic tracking, we design the tracking trajectory as

$$\begin{array}{cc}\hfill x_d\left(t\right)=& rcos{w}_{d}t-(\frac{\widehat{\mu }}{w_d}+d)cos\theta \hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill y_d\left(t\right)=& rsin{w}_{d}t-(\frac{\widehat{\mu }}{w_d}+d)sin\theta \hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill {\theta }_d\left(t\right)=& w_{d}t.\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \end{array}$$

(40)

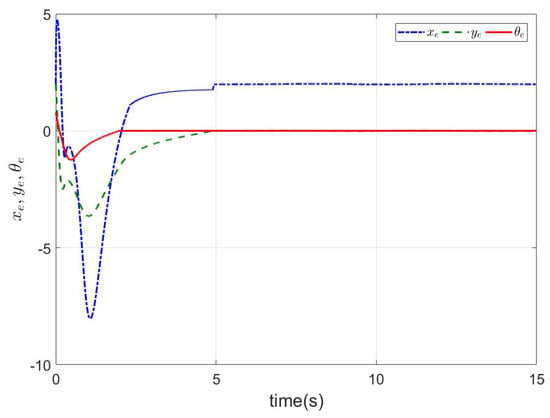
Figure 7. The tracking errors of (35)–(37) with $T_{05}=0.5$.

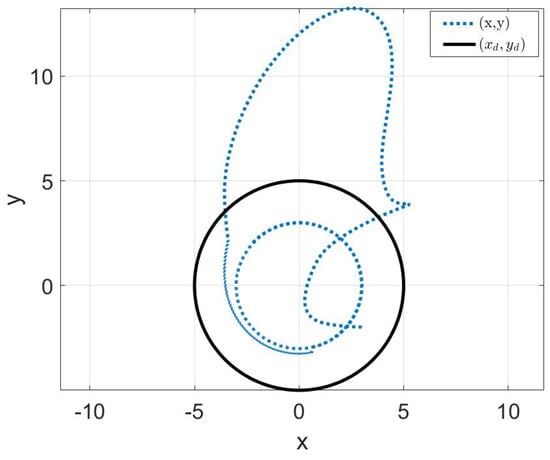
Figure 8. The tracking trajectories of (35)–(37).

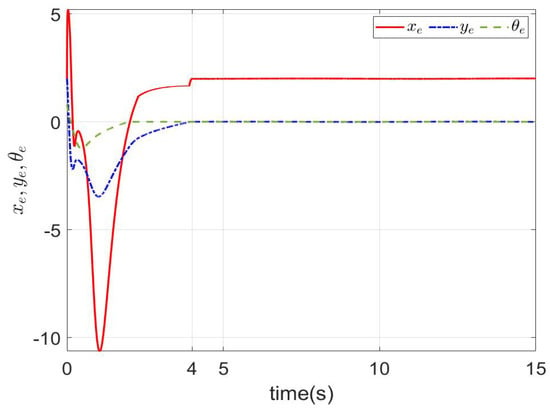
Figure 9. The tracking errors of (35)–(37) with $T_{05}=0.4$.

The simulation results are shown in Figure 10 and Figure 11. The tracking error is shown in Figure 10. As shown in Figure 10, it is worth noting that the angle error of tracking trajectory (40) converged to zero in $5<T_{05}$. Similarly, the x-axis and y-axis errors of tracking postures (38) and (39) converged to zero in $T_{05}$, respectively. It shows that, by modifying the tracking trajectory, the pseudo-full drive control of the nonholonomic system can be realized. The tracking curve is shown in Figure 11. The NMR could fully track the given signal. For the predefined time $T_{05}=0.4$, the simulation results are shown in Figure 12. It can be seen that the results are the same as Figure 10, except that the convergence time was changed. Similarly, the method proposed in this article could simply achieve a change in the system convergence time by changing the predefined time parameter $T_{05}$.

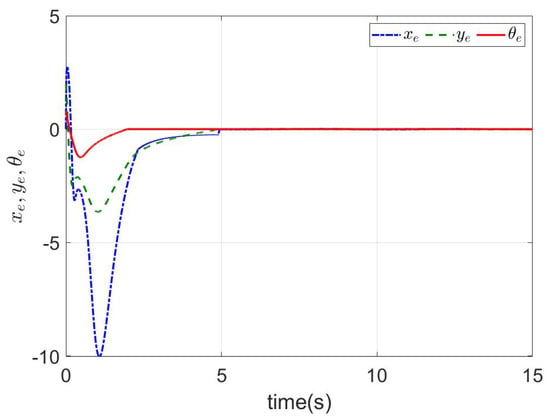
Figure 10. The tracking errors of (38)–(40) with $T_{05}=0.5$.

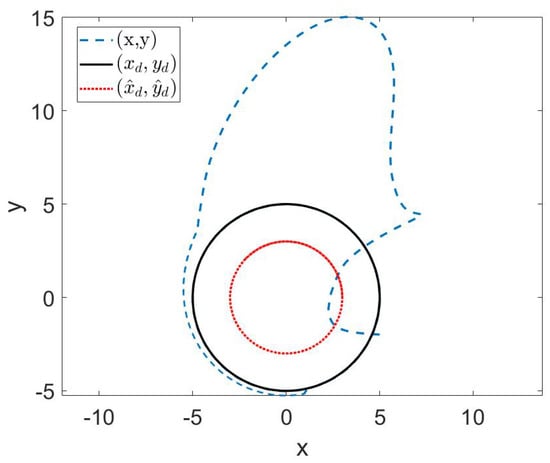
Figure 11. The tracking trajectories of (38)–(40).

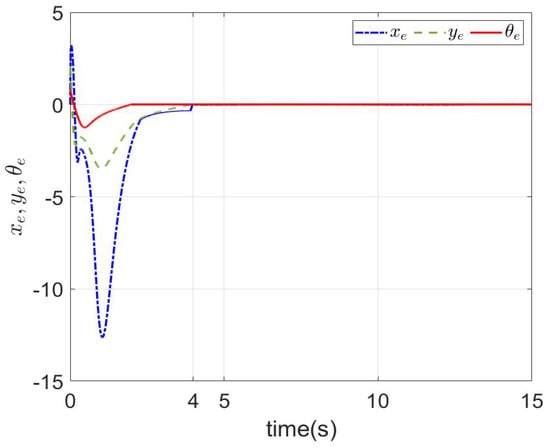
Figure 12. The tracking errors of (38)–(40) with $T_{05}=0.4$.

Remark 6. 

The simulation results show that the proposed method is effective and feasible. The predefined time controllers designed in this article for an NMR did not consider the input saturation, so it could be stable within predefined time, and its convergence time was adjustable. Because of the input saturation of the actual NMR, the process of designing the predefined time controller under the condition of input saturation is the future work to do. This article assumes that the measurement data is accurate, but the sensor data of the actual NMR is uncertain, so it is necessary to consider the accuracy of the measurement data when the proposed method is applied to the actual environment.

Remark 7. 

As shown in Figure 10, $x_e$, $y_e$, and ${\theta }_e$ all tended to zero within predefined time, thus indicating that the redesigned tracking trajectory could realize fast and accurate tracking of all the states of x, y, and θ of the NMR. Thus, the distance error ($\sqrt{x^2+y^2}$) and the orientation error (${\theta }_e$) also tended to zero in predefined time.

5. Conclusions

This article proposed a framework to solve the fast path tracking problem for an NMR with unknown slipping and skidding. Based on predefined time stability, predefined time observers were designed to accurately estimate the unknown slipping and skidding. Then, the trajectory tracking problem of NMR was solved by predefined time active controllers via backstepping design. Based on the simulation results, the designed predefined time observers could not only accurately estimate ${\eta }_w$, ${\eta }_v$, and $\mu$, but also the settling time of the observer could be adjusted according to the actual situation. The designed predefined time controllers could realize fast and accurate tracking of the given trajectory. The redesigned new tracking trajectory could achieve full tracking of all states of the NMR. The proposed solution can be easily expanded for other types of tracking systems. In the upcoming research, we will focus on the following directions.

(1)

The model parameters used in this article are ideal without practical errors, while the parameters involve uncertainty in the actual NMR. In future work, the uncertainty of model parameters will be considered, and it is hoped that other schemes can be combined to achieve accurate estimation of the model of an NMR.

(2)

We will continue to apply the method of predefined time observer and predefined time controller in this article to an actual NMR for verification.

(3)

Compared with classical controllers such as the PID controller, the proposed scheme is more complex, theoretically requires more computation, and occupies more CPU resources. In practical applications, algorithm improvements should be made to adapt to the configuration of the actual hardware environment of an actual NMR, thus reducing the complexity and computational complexity of the algorithm and improving its computing speed.