Hopf Bifurcation, Periodic Solutions, and Control of a New 4D Hyperchaotic System

Abstract

In this paper, a new four-dimensional (4D) hyperchaotic biplane system is designed and presented. The dynamical properties of this new system are studied by means of tools such as bifurcation diagrams, Lyapunov exponents and phase diagrams. The Hopf bifurcation and periodic solutions of this hyperchaotic system are solved analytically. In addition, a new hyperchaotic control strategy is applied, and a comparative analysis of the controlled system is performed.

1. Introduction

In 1979, Rössler discovered and studied the first hyperchaotic system—the Rössler system [1]. It is known that the minimum dimension of the phase space in which the hyperchaotic attractor is embedded should exceed three. It means that hyperchaos is a more complex dynamical phenomenon than chaos. Later, many four-dimensional hyperchaotic systems were discovered and studied [2,3], specifically four-dimensional hyperchaotic Lorenz-type systems [4,5]. Jia [6] constructed a hyperchaotic Lorenz-type system using state feedback control and studied its associated dynamics using Lyapunov exponents and bifurcation diagrams. Wang et al. [7] characterized a-new-uniform-four-dimensional-uniform-hyperchaotic-Lorenz-type system, employing a bifurcation method and Lyapunov stability theory. Compared to ordinary chaotic systems, hyperchaotic systems have more potential applications in information security [8,9,10,11,12], finance [13,14], lasers [15,16,17], and circuits [18,19,20,21]. Due to their higher dimensionality, hyperchaotic systems are accompanied by a vast amount of randomness and unpredictability. To the best of our knowledge, the complexity of the dynamics of hyperchaotic systems is yet to be fully grasped. There are only a few studies on the dynamics of hyperchaotic systems.

More effective methods must be used to analyze and study the complex dynamics of high-dimensional hyperchaotic systems. Moreover, it is necessary to study new high-dimensional hyperchaotic systems and investigate their hyperchaotic properties. Pecora [22] proposed that high-dimensional hyperchaotic systems are safer than chaotic systems because of their increased randomness and higher unpredictability. From a practical application and engineering point of view, hyperchaotic systems should have a higher level of complexity [23]. Although analytical tools and techniques are available in the literature for bifurcation and stability analysis [24,25], no such analytical tools are available for attractors, so we must rely on some graphical tools. Mahmoud et al. [26] constructed a new hyperchaotic complex Lorentz system by extending the idea of adding state feedback control and introducing complex periodic forces.

Similarly, a new 4D four-wing memristor hyperchaotic system was presented by incorporating a magnetron memristor with a linear memristor in the four-wing Chen system [27]. Moreover, a hyperchaotic system of a 4D generalized Lorenz first state equation was proposed by introducing a linear state feedback control [28]. Mezatio et al. proposed hyperchaos and the coexistence of infinite hidden attractors in a six-dimensional system [29]. In one study, the dynamical richness of the hyperchaotic systems and their increased complexity were recognized with the addition of nonlinear controllers [30]. Furthermore, some scholars succeeded in constructing hyperchaotic systems [31,32]. These systems have significantly broadened the study of hyperchaos and provided some control strategies and research methods.

It is difficult for mathematicians and engineers to fully understand the behavior of hyperchaotic systems because the associated dynamics of hyperchaotic systems exist in higher dimensions simultaneously. The main components of the hyperchaotic system are two positive Lyapunov exponents, Hopf bifurcation and the attractor. Hopf bifurcation and chaotic attractors are both richly developed on the basis of chaos theory [33,34,35]. Hopf bifurcation is critical in analyzing the stability of equilibrium points of the hyperchaotic system in high dimensions, and it is used to study the dynamical behavior of hyperchaotic systems [36,37,38] and to control hyperchaos [39,40,41] for various applications.

This paper is structured as follows. The first part of this work describes the numerical simulation results of the proposed new system. Then, the output of MATLAB codes is presented that graphically represents the system. In this study, the Runge–Kutta algorithm was mainly utilized for the numerical simulations. Moreover, the analysis of the system characteristics, such as chaos and hyperchaos, is numerically verified using a bifurcation diagram, Phase diagram, Lyapunov exponents spectrum, and Poincaré maps. The conditions for the Hopf bifurcation of the new chaotic system are obtained in the second part of this work. In the third part, the stability of the bifurcation period solution and the Hopf bifurcation direction formula of the system are calculated using the normal form theory [42]. In addition, two examples were used to test and verify the theoretical results. In the fourth part, hyperchaotic control is investigated [43]. The results show that the linear feedback control method can control the system reasonably if appropriate feedback coefficients are chosen. In Section 6, the outcomes of the study are summarized.

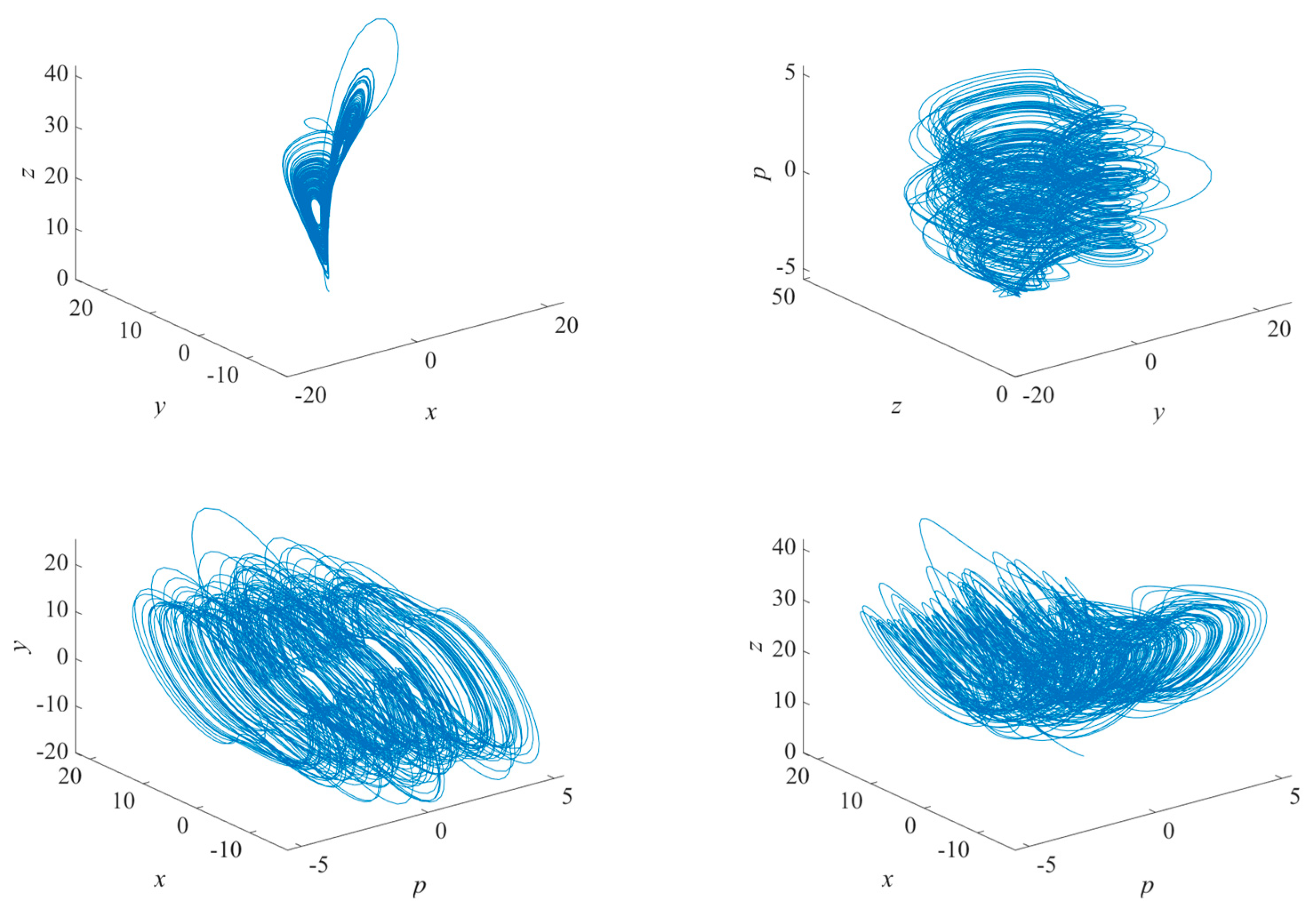
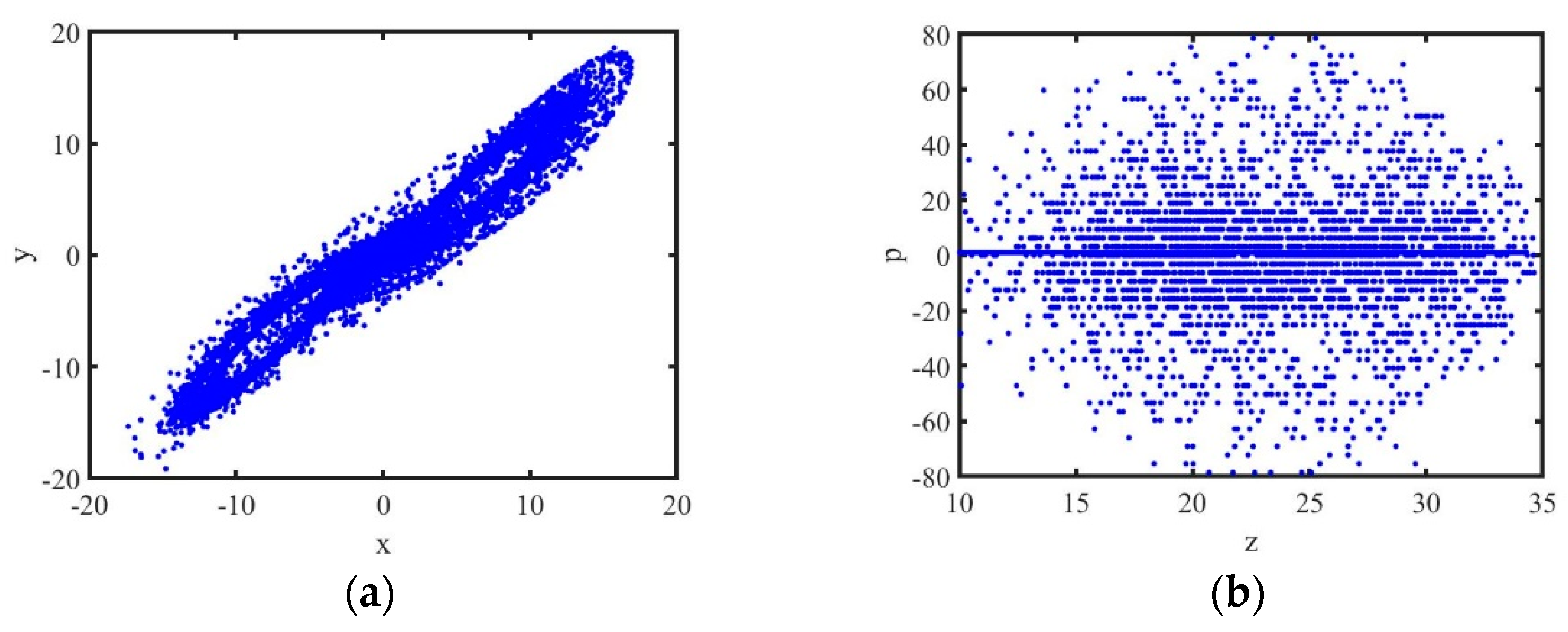
2. Description of the Model

In 1994, Sprott obtained 19 third-order quadratic systems that exhibit chaotic behavior via a computational search method [44]. This assumption is of great theoretical and practical significance for studying some systems. In 2010, Wei [45] obtained a new generalized Sprott C system and proposed methods to improve a similar system proposed by Zhang et al. [46] and Jafari et al. [47,48]. The new chaotic system proposed in this study is as follows:

$$\{\begin{array}{l}\dot{x}=a(y-x),\\ \dot{y}=cy-xz,\\ \dot{z}=-bz+y^2.\end{array}$$

(1)

The following new four-dimensional hyperchaotic system is introduced by adding a linear controller to the system of equations given in (1):

$$\{\begin{array}{l}\dot{x}=a(y-x),\\ \dot{y}=cy-xz+p,\\ \dot{z}=-bz+y^2,\\ \dot{p}=-e(x+y).\end{array}$$

(2)

where $x$, $y$, $z$ and $p$ are state variables, $a$, $b$, $c$ and $e$ are system parameters, and also $e$ is the main control parameter of System (2).

In this subsection, some characteristics of System (2) are discussed, and more simulation results are present from the numerical methods. The dynamics of System (2) can be characterized by its Lyapunov exponents using the real constants $a=40$, $b=2$, $c=22$. The corresponding bifurcation diagram is given in Figure 1. We apply the Jacobi method to calculate the Lyapunov exponent. The Lyapunov exponent spectrum of System (2) is shown in Figure 2.

According to the correspondence of Figure 1 and Figure 2, when the parameter $e=0.5$, the Lyapunov exponent of the new 4D System (2) is $L_1=16.9402$, $L_2=-3.4133$, $L_3=0$, and $L_4=6.9890$. It can be seen that $L_1>0$, $L_4>0$ and $L_3=0$. Thus, System (2) is hyperchaotic at parameters $a=40$, $b=2$, $c=22$ and $e=0.5$. In this case, System (2) has a hyperchaotic attractor, as shown in Figure 3. Moreover, the Poincaré maps in the $x-y$ and $z-p$ planes are given in Figure 4.

In general, the above results show that System (2) has complex and interesting dynamical behavior, including hyperchaos and chaos.

3. Stability Analysis and the Existence of Hopf Bifurcation

3.1. Equilibrium Stability

The equilibria of System (2) can be found by solving the following equations simultaneously:

$$\{\begin{array}{l}a(y-x)=0,\\ cy-xz+p=0,\\ -bz+y^2=0,\\ -e(x+y)=0.\end{array}$$

(3)

A simple analysis makes it easy to obtain the unique equilibrium at $E_0(0,0,0,0)$ for System (2).

The Jacobian matrix of System (2) at $E_0(0,0,0,0)$ is given by the following matrix:

$$J\left(E_0\right)=\left(\begin{array}{cccc}-a& a& 0& 0\\ 0& c& 0& 1\\ 0& 0& -b& 0\\ -e& -e& 0& 0\end{array}\right),$$

(4)

The following determinant can be obtained from the Jacobian matrix:

$$\left|\lambda E-J\left(E_0\right)\right|=\left|\begin{array}{cccc}\lambda +a& -a& 0& 0\\ 0& \lambda -c& 0& -1\\ 0& 0& \lambda +b& 0\\ e& e& 0& \lambda \end{array}\right|.$$

(5)

The characteristic equation is therefore given below:

$$\begin{array}{l}\hspace{1em}\hspace{1em}f\left(\lambda \right)=(\lambda +b)({\lambda }^3+\left(a-c\right){\lambda }^2+(e-ac)\lambda +2ae)\\ ={\lambda }^4+\left(a+b-c\right){\lambda }^3+\left(e-ac-bc+ab\right){\lambda }^2+(2ae+be-abc)\lambda +2abe=0.\end{array}$$

(6)

The following relation can be obtained using the Routh–Hurwitz discriminant condition [49]:

$$f\left(\lambda \right)=P_0{\lambda }^4+P_1{\lambda }^3+P_2{\lambda }^2+P_3\lambda +P_4=0.$$

(7)

A one-to-one correspondence between Equations (6) and (7) can be obtained by considering the following coefficients:

$$P_0=1, P_1=a+b-c, P_2=e-ac-bc+ab, P_3=2ae+be-abc, P_4=2abe.$$

The following determinant is obtained by substituting the $P_0$, $P_1$, $P_2$, $P_3$ and $P_4$.

$$D=\left|\begin{array}{cccc}{P}_1& P_3& 0& 0\\ P_0& P_2& P_4& 0\\ 0& P_1& P_3& 0\\ 0& P_0& P_2& P_4\end{array}\right|.$$

(8)

It can be seen that the necessary and sufficient conditions for the real parts to be negative for all eigenvalues of the system are given in the following inequalities:

$$D_1=P_1=a+b-c>0,$$

(9)

$$D_2=\left|\begin{array}{cc}{P}_1& P_3\\ P_0& P_2\end{array}\right|=P_1{P}_2-P_{{}_0}{P}_3>0,$$

(10)

$$D_3=P_3{D}_2-P_4{P}_1^2>0,$$

(11)

$$D_4=D=P_4{D}_3>0.$$

(12)

From Equations (9)–(12), we have the following conditions.

$$b>0,e>ac,a>c,ae>0,a{c}^2-a^{2}c+ae-ce>0$$

Therefore, the system will bifurcate when $e=\frac{ac(c - a)}{a + c}$. So, $e$ is a critical value and is referred to as $e=e_0$.

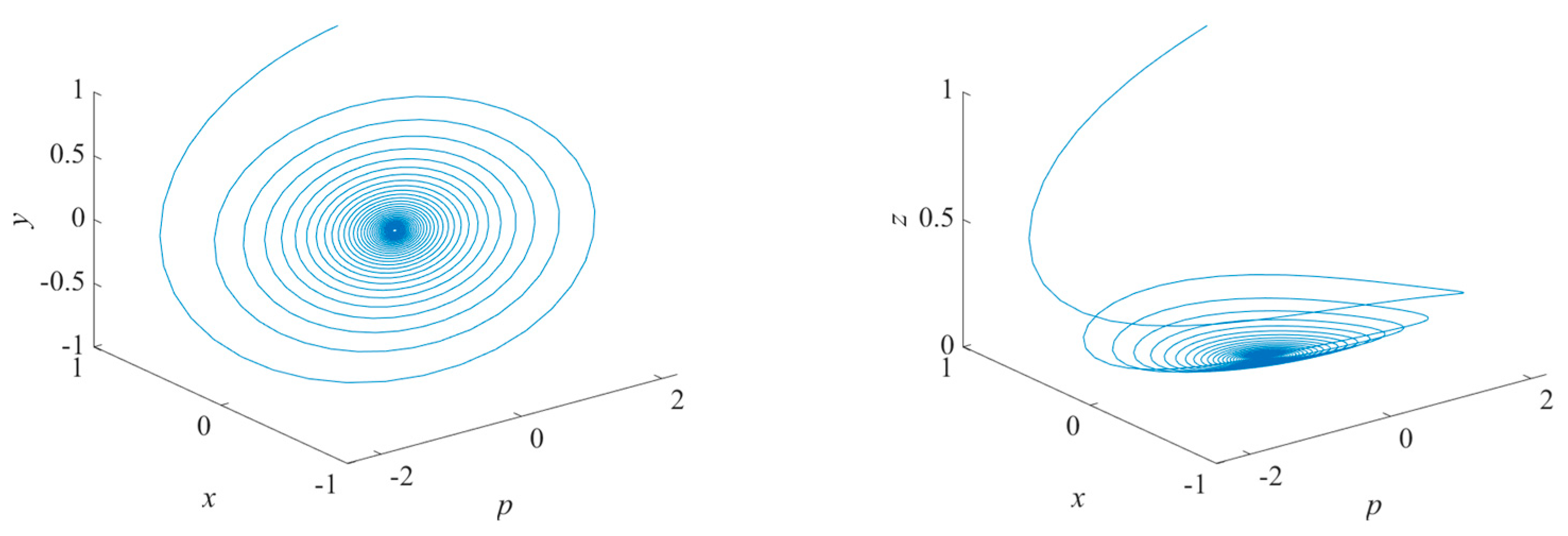
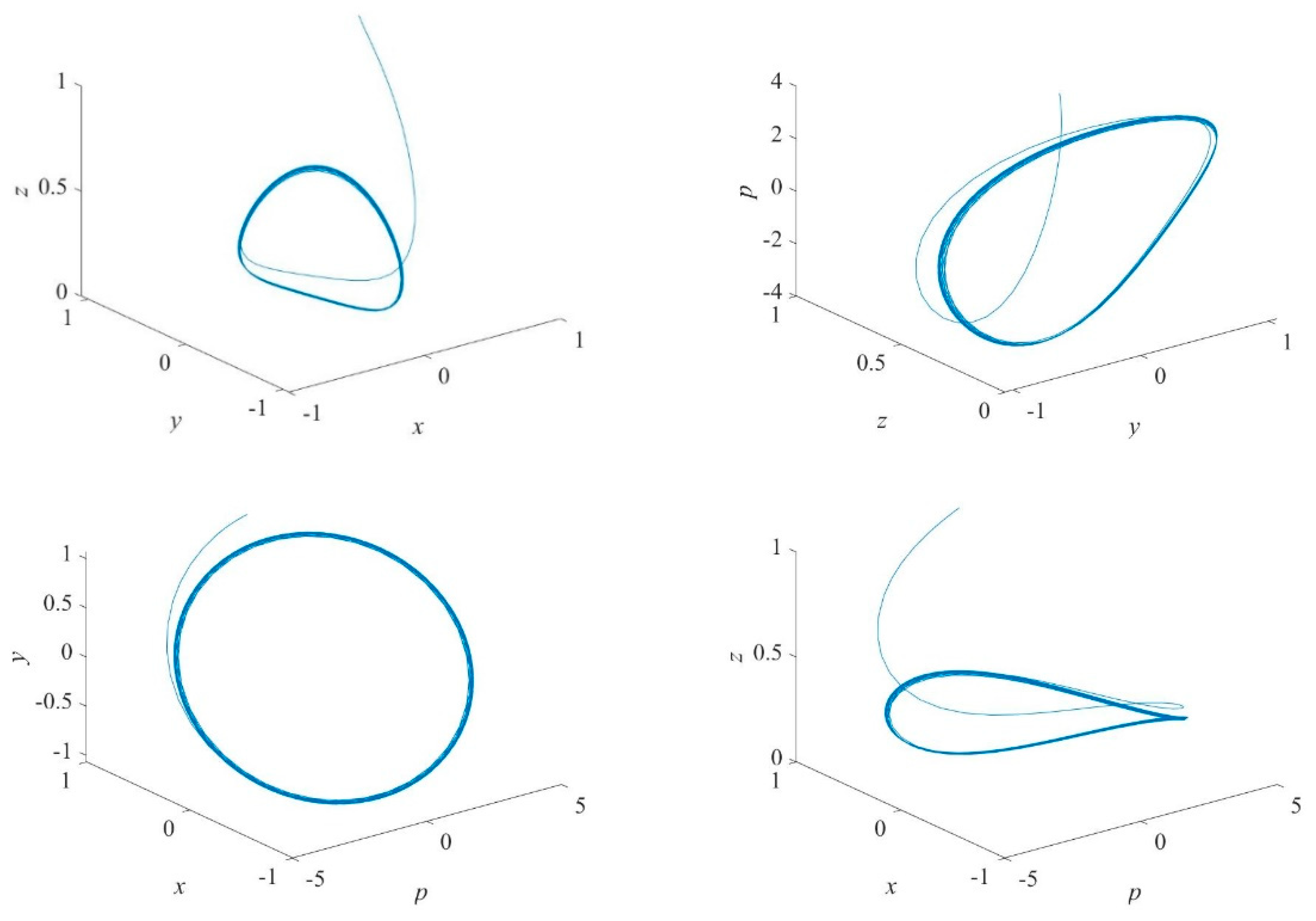
3.2. Existence of a Hopf Bifurcation

Assume that System (2) of equations has a pure imaginary root $\lambda =\omega i$ ($\omega \in R^{+}$). From Equation (6), the following relation can be obtained:

$$\omega ={\omega }_0=\sqrt{e-ac},e=e_0=\frac{ac(c-a)}{a+c}.$$

Substituting $e=e_0$ into Equation (6), the following relationships are derived:

$${\lambda }_1=-b,{\lambda }_2=c-a,{\lambda }_3=i{\omega }_0,{\lambda }_4=-i{\omega }_0.$$

Hence, System (2) satisfies the first condition of the Hopf bifurcation theorem. By differentiating the characteristic equations of the equilibrium point $E_0$ with respect to $e$, the following differential equation is acquired:

$$3{\lambda }^2\frac{d\lambda }{de}+2(a-c)\lambda \frac{d\lambda }{de}+(e-ac)\frac{d\lambda }{de}+2a+\lambda =0,$$

(13)

and

$${\lambda }^{\prime }(e)=\frac{d\lambda }{de}=-\frac{2a+\lambda }{3{\lambda }^2+2(a-c)\lambda +e-ac}.$$

(14)

Substituting the bifurcation value and eigenvalues into the above equation gives the following results:

$${\alpha }^{\prime }(0)={\mathrm{Re}({\lambda }^{\prime }(e_0))|}_{\lambda =\sqrt{e-ac}i}=\frac{{(a+c)}^2}{4a{c}^2+2{(a-c)}^2(a+c)}>0,$$

(15)

$${\omega }^{\prime }(0)={\mathrm{Im}({\lambda }^{\prime }(e_0))|}_{\lambda =\sqrt{e-ac}i}=\frac{2a^2-ac-c^2}{8a{c}^3+4c(a+c){(a-c)}^2}\sqrt{2a(a+c)}\ne 0.$$

(16)

Hence, the second condition of the Hopf bifurcation theorem is satisfied.

The proposed chaotic system thus satisfies both conditions of the Hopf bifurcation theorem [50]. When $e=e_0$, the system shows Hopf bifurcations at the equilibrium point $E_0$.

4. Direction and Stability of Bifurcating Periodic Solutions

The primary purpose of this section is to find the direction and stability of the periodic solutions of the Hopf bifurcations in System (2). An approach based on the normal form theory and center manifold theorem is used [42].

First, the eigenvectors of the matrix are solved by setting the following solution equations:

$$\{\begin{array}{r}(\lambda +a)u_1-a{u}_2=0,\\ (\lambda -c)u_2-u_4=0,\\ (\lambda +b)u_3=0,\\ e{u}_1+e{u}_2+\lambda u_3=0.\end{array}$$

(17)

Let $v_1$, $v_2$ and $v_3$ represent the eigenvectors that correspond to the eigenvalues ${\lambda }_1=-b$, ${\lambda }_2=c-a$ and ${\lambda }_3=i{\omega }_0$, respectively. It can be shown that the following relations hold:

$$v_1=\left(\begin{array}{c}0\\ 0\\ 1\\ 0\end{array}\right),v_2=\left(\begin{array}{c}\frac{a}{c}\\ 1\\ 0\\ -a\end{array}\right),v_3=\left(\begin{array}{c}-\frac{ac}{e}+\frac{c}{e}\sqrt{e-ac}i\\ 1\\ 0\\ -c+\sqrt{e-ac}i\end{array}\right).$$

A matrix Q can then be defined using the acquired expressions for the eigenvectors as follows:

$$Q=(\mathrm{Re}{v}_3,-\mathrm{Im}{v}_3,v_1,v_2)=\left(\begin{array}{cccc}-\frac{ac}{e}& -\frac{c}{e}\sqrt{e-ac}& 0& \frac{a}{c}\\ 1& 0& 0& 1\\ 0& 0& 1& 0\\ -c& -\sqrt{e-ac}& 0& -a\end{array}\right).$$

(18)

Considering the following transformation,

$$\left(\begin{array}{c}x\\ y\\ z\\ p\end{array}\right)=Q\left(\begin{array}{c}{x}_1\\ y_1\\ z_1\\ p_1\end{array}\right),$$

(19)

a relationship between $x,y,z,p$ and $x_1,y_1,z_1,p_1$ can be obtained in the following manner:

$$\left(\begin{array}{c}x\\ y\\ z\\ p\end{array}\right)=\left(\begin{array}{c}-\frac{ac}{e}{x}_1-\frac{c}{e}\sqrt{e-ac}{y}_1+\frac{a}{c}{p}_1\\ x_1+p_1\\ z_1\\ -c{x}_1-\sqrt{e-ac}{y}_1-a{p}_1\end{array}\right).$$

(20)

By taking the derivative of Equation (20) and substituting the results into System (2), a new system expression is obtained, which is given below:

$$\{\begin{array}{l}{\dot{x}}_1=-\sqrt{e-ac}{y}_1+F_1(x_1,y_1,z_1,p_1),\\ {\dot{y}}_1=\sqrt{e-ac}{x}_1+F_2(x_1,y_1,z_1,p_1),\\ {\dot{z}}_1=-b{z}_1+F_3(x_1,y_1,z_1,p_1),\\ {\dot{p}}_1=(c-a)p_1+F_4(x_1,y_1,z_1,p_1).\end{array}$$

(21)

where,

$$\begin{array}{l}{F}_1(x_1,y_1,z_1,p_1)=-k(\frac{ac}{e}{x}_1{z}_1+\frac{c}{e}\sqrt{e-ac}{y}_1{z}_1-\frac{a}{c}{z}_1{p}_1),\\ F_2(x_1,y_1,z_1,p_1)=[(c-a)k-a](\frac{ac}{e}{x}_1{z}_1+\frac{c}{e}\sqrt{e-ac}{y}_1{z}_1-\frac{a}{c}{z}_1{p}_1),\\ F_3(x_1,y_1,z_1,p_1)=x_1{}^2+p_1{}^2+2x_1{p}_1,\\ F_4(x_1,y_1,z_1,p_1)=(k+1)(\frac{ac}{e}{x}_1{z}_1+\frac{c}{e}\sqrt{e-ac}{y}_1{z}_1-\frac{a}{c}{z}_1{p}_1),\\ k=\frac{ae+a{c}^2}{c^3-ae-2a{c}^2}.\end{array}$$

Then, using formulas reported in the literature [42], the following expressions related to the bifurcation at $e=e_0$ and $(x_1,y_1,z_1,p_1)=(0,0,0,0)$ can be obtained:

$$\begin{array}{l}{g}_{11}=\frac{1}{4}[\frac{{\partial }^2{F}_1}{\partial x_1^2}+\frac{{\partial }^2{F}_1}{\partial y_1^2}+i(\frac{{\partial }^2{F}_2}{\partial x_1^2}+\frac{{\partial }^2{F}_2}{\partial y_1^2})]=0,\\ g_{02}=\frac{1}{4}[\frac{{\partial }^2{F}_1}{\partial x_1^2}-\frac{{\partial }^2{F}_1}{\partial y_1^2}-2\frac{{\partial }^2{F}_2}{\partial x_1\partial y_1}+i(\frac{{\partial }^2{F}_2}{\partial x_1^2}-\frac{{\partial }^2{F}_2}{\partial y_1^2}+2\frac{{\partial }^2{F}_1}{\partial x_1\partial y_1})]=0,\\ g_{20}=\frac{1}{4}[\frac{{\partial }^2{F}_1}{{\partial }^2{x}_1^2}-\frac{{\partial }^2{F}_1}{{\partial }^2{y}_1^2}+2\frac{{\partial }^2{F}_2}{\partial x_1\partial y_1}+i(\frac{{\partial }^2{F}_2}{{\partial }^2{x}_1^2}-\frac{{\partial }^2{F}_2}{{\partial }^2{y}_1^2}-2\frac{{\partial }^2{F}_1}{\partial x_1\partial y_1})]=0,\\ G_{21}=\frac{1}{8}[\frac{{\partial }^3{F}_1}{\partial x_1^3}+\frac{{\partial }^3{F}_1}{\partial x_1\partial y_1^2}+\frac{{\partial }^3{F}_2}{\partial x_1^2\partial y_1}+\frac{{\partial }^3{F}_2}{\partial y_1^3}+i(\frac{{\partial }^3{F}_2}{\partial x_1^3}+\frac{{\partial }^3{F}_2}{\partial x_1\partial y_1^2}-\frac{{\partial }^3{F}_1}{\partial x_1^2\partial y_1}-\frac{{\partial }^3{F}_1}{\partial y_1^3})]=0.\end{array}$$

From the dimension $n=4>2$, we calculate the following variables:

$$\begin{array}{l}{h}_{11}^1=\frac{1}{4}(\frac{{\partial }^2{F}_3}{\partial x_1^2}+\frac{{\partial }^2{F}_3}{\partial y_1^2})=\frac{1}{4},h_{11}^2=\frac{1}{4}(\frac{{\partial }^2{F}_4}{\partial x_1^2}+\frac{{\partial }^2{F}_4}{\partial y_1^2})=0,\\ h_{20}^1=\frac{1}{4}(\frac{{\partial }^2{F}_3}{\partial x_1^2}-\frac{{\partial }^2{F}_3}{\partial y_1^2}-2i\frac{{\partial }^2{F}_3}{\partial x_1\partial y_1})=\frac{1}{4},h_{20}^2=\frac{1}{4}(\frac{{\partial }^2{F}_4}{\partial x_1^2}-\frac{{\partial }^2{F}_4}{\partial y_1^2}-2i\frac{{\partial }^2{F}_4}{\partial x_1\partial y_1})=0.\end{array}$$

By solving the following equations,

$$D{w}_{11}=-h_{11},(D-2i{\omega }_{0}I)w_{20}=-h_{20},$$

where

$$h_{11}=\left(\begin{array}{c}{h}_{11}^1\\ h_{11}^2\end{array}\right),h_{20}=\left(\begin{array}{c}{h}_{20}^1\\ h_{20}^2\end{array}\right),$$

We obtain the following relations:

$$w_{11}=\left(\begin{array}{c}{w}_{11}^1\\ w_{11}^2\end{array}\right)=\left(\begin{array}{c}\frac{b}{4}\\ 0\end{array}\right),w_{20}=\left(\begin{array}{c}{w}_{20}^1\\ w_{20}^2\end{array}\right)=\left(\begin{array}{c}\frac{c-a}{4}-\frac{\sqrt{e-ac}}{2}i\\ 0\end{array}\right).$$

Furthermore,

$$\begin{array}{ll}{G}_{110}^1& =\frac{1}{2}[\frac{{\partial }^2{F}_1}{\partial x_1\partial z_1}+\frac{{\partial }^2{F}_2}{\partial y_1\partial z_1}+i(\frac{{\partial }^2{F}_2}{\partial x_1\partial z_1}-\frac{{\partial }^2{F}_1}{\partial y_1\partial z_1})]\hfill \\ & =\frac{ack}{2e}(i-1)+\frac{c\sqrt{e-ac}}{2e}[k(c-a)-a](i+1),\hfill \\ G_{110}^2& =0,\\ G_{101}^2& =0,\\ G_{101}^1& =\frac{1}{2}[\frac{{\partial }^2{F}_1}{\partial x_1\partial z_1}-\frac{{\partial }^2{F}_2}{\partial y_1\partial z_1}+i(\frac{{\partial }^2{F}_2}{\partial x_1\partial z_1}+\frac{{\partial }^2{F}_1}{\partial y_1\partial z_1})]\hfill \\ & =\frac{ack}{2e}(-i-1)+\frac{c\sqrt{e-ac}}{2e}[k(c-a)-a](i-1),\hfill \\ g_{21}\hfill & =G_{21}+{\displaystyle \sum _{n=1}^2(2G_{110}^n{w}_{11}^n+G_{101}^n{w}_{20}^n)}\hfill \\ & =-\frac{2abc+ac(c-a)+2ac\sqrt{e-ac}}{8e}k+\frac{2bc-c^2+ac+2c}{8e}\sqrt{e-ac}[k(c-a)-a]\hfill \\ & +\frac{(2bc+c^2-ac)\sqrt{e-ac}+2c(e-ac)}{8e}[k(c-a)-a]i\hfill \\ & +\frac{2abc-ac(c-a)+2ac\sqrt{e-ac}}{8e}ki.\hfill \end{array}$$

Based on these calculations and analyses, we obtain the following results:

$$C_1(0)=\frac{i}{2{\omega }_0}[g_{20}{g}_{11}-2{\left|g_{11}\right|}^2-\frac{1}{3}{\left|g_{02}\right|}^2]+\frac{1}{2}{g}_{21}=\frac{1}{2}{g}_{21}$$

(22)

$${\mu }_2=-\frac{\mathrm{Re}{C}_1(0)}{{\alpha }^{\prime }(0)},$$

(23)

$${\beta }_2=2\mathrm{Re}{C}_1(0),$$

(24)

$${\tau }_2=-\frac{\mathrm{Im}{C}_1(0)+{\mu }_2{\omega }^{\prime }(0)}{{\omega }_0}.$$

(25)

The following conclusions can also be drawn:

(i)

If ${\mu }_2>0(<0)$, the Hopf bifurcation is supercritical (subcritical), and for $e>e_0(<e_0)$, the bifurcation has a periodic solution;

(ii)

If ${\beta }_2<0(>0)$, the bifurcating periodic solutions are stable (unstable) on their orbits;

(iii)

If ${\tau }_2>0(<0)$, the period of bifurcating periodic solutions increases or decreases.

For the verification of the above theoretical analysis, it is assumed that

$$a=3,b=2,c=-1$$

Then, $e_0=6$, and the following values are calculated:

$${\mu }_2=5.13,{\beta }_2=-0.54,{\tau }_2\approx 0.35147$$

Therefore, when the parameter $e$ is at its critical value, the Hopf bifurcation of the system at the equilibrium point $E_0(0,0,0,0)$ is supercritical. Moreover, the bifurcation direction is $e<e_0=6$. The bifurcation period solution of the system is stable, as shown in Figure 5. $e>e_0=6$ as shown in Figure 6.

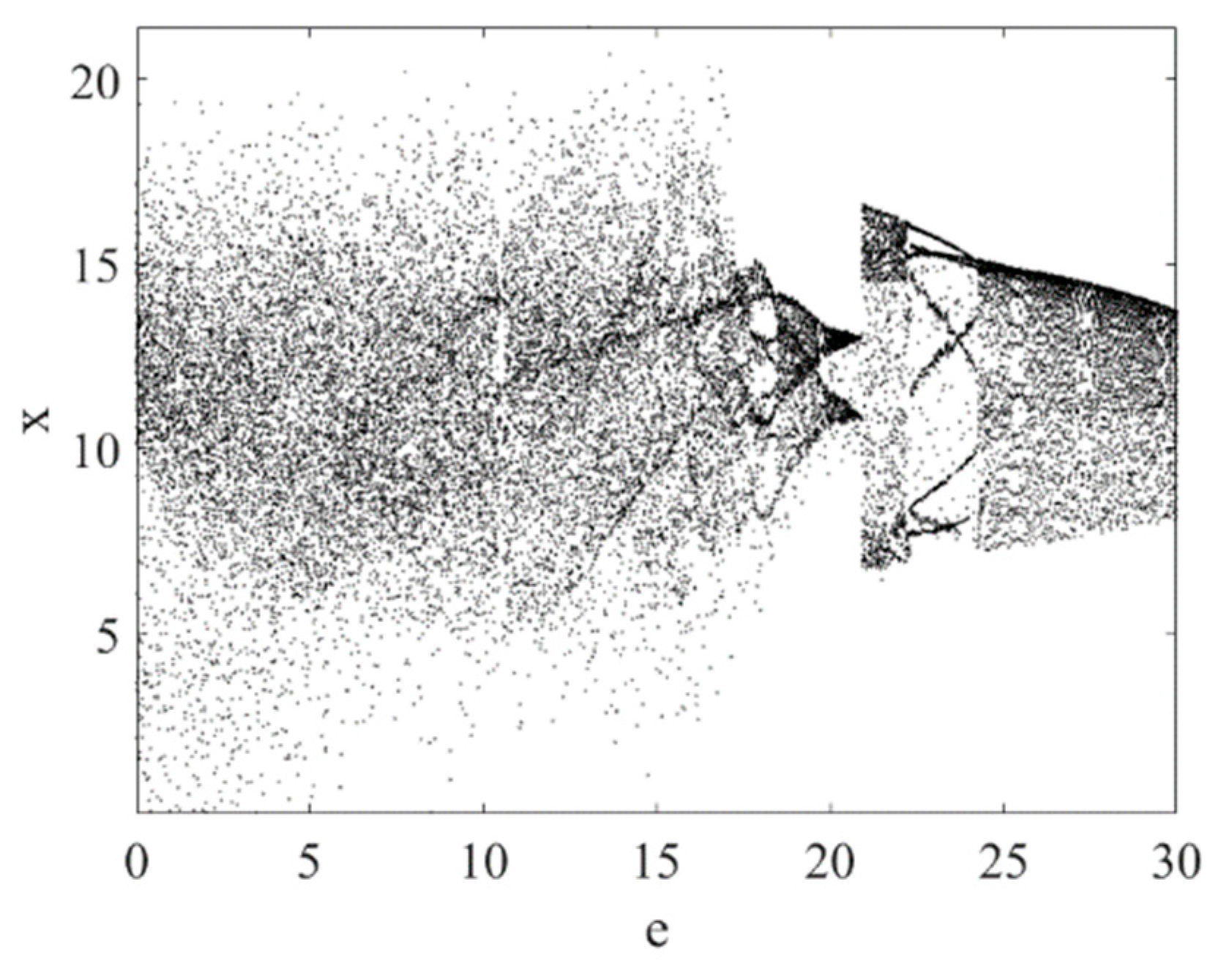
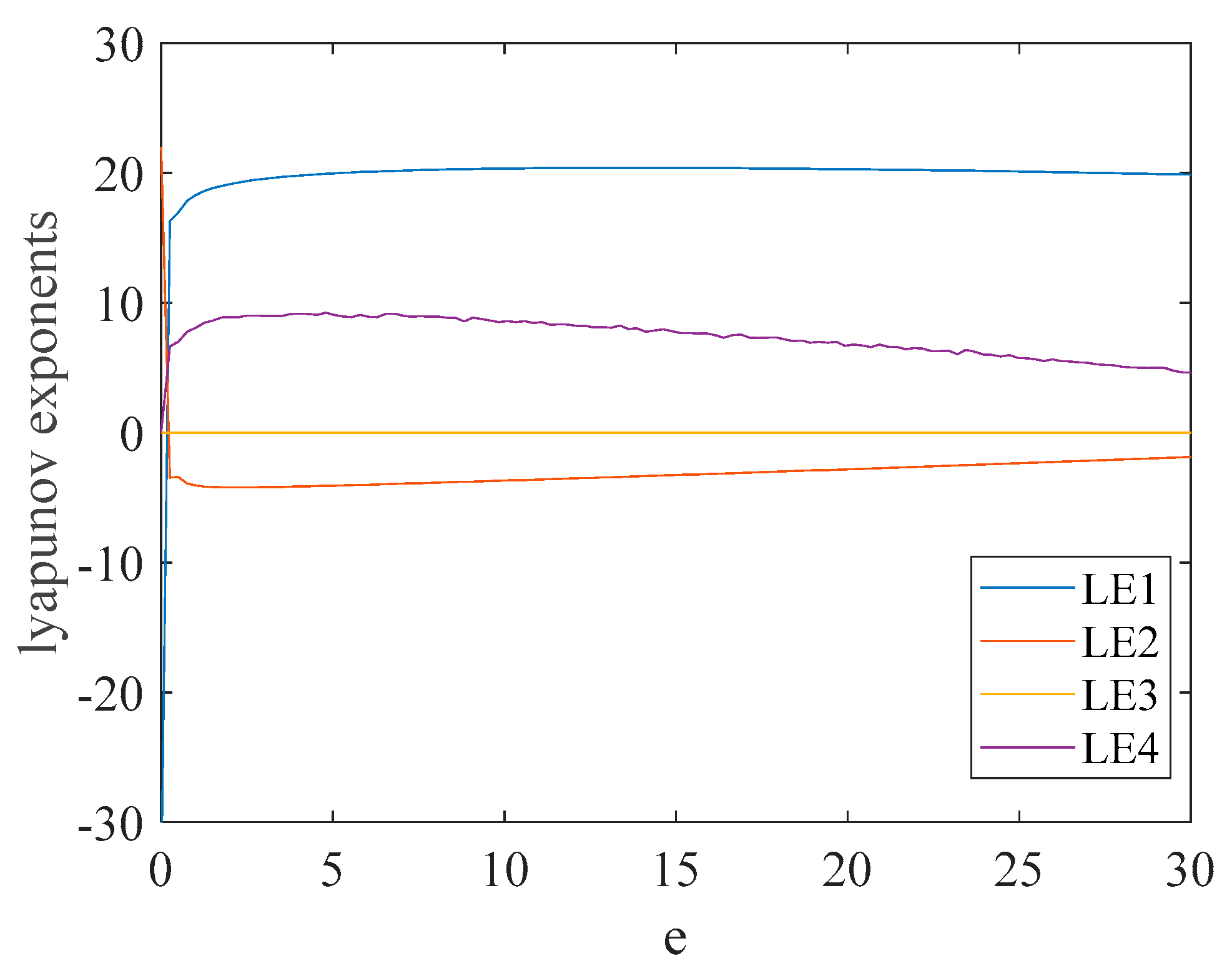
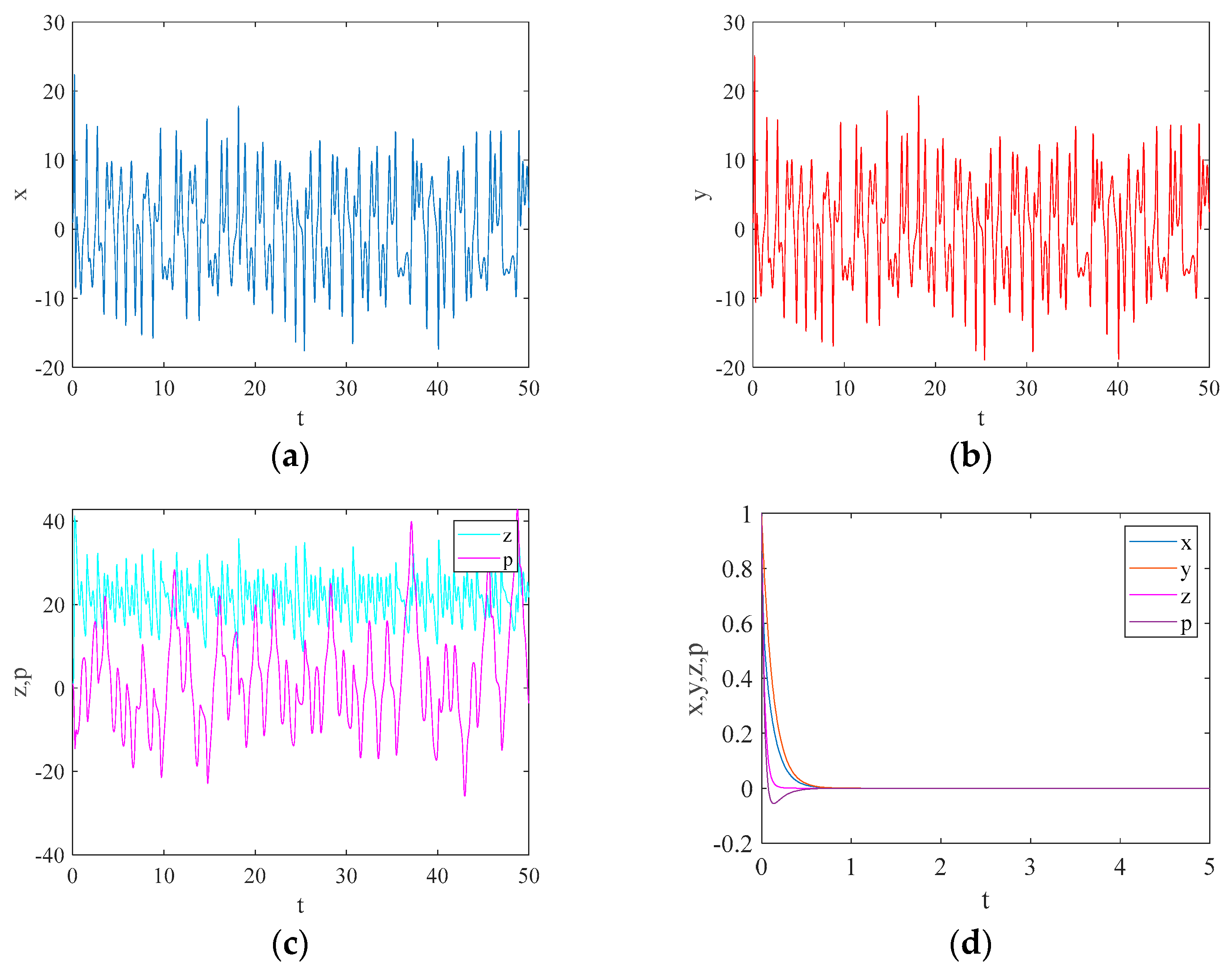
5. Hyperchaos Control

In many cases, chaos is generally harmful and needs to be suppressed. Therefore, scholars have paid extensive attention to controlling it. Scholars have developed many valuable methods for chaos control, such as the hybrid control c-strategy [51] and the ultimate boundedness [52]. The equation of the controlled system is as follows:

$$\{\begin{array}{l}\dot{x}=a(y-x)+r_{1}x,\\ \dot{y}=cy-xz+p+r_{2}y,\\ \dot{z}=-bz+y^2+r_{3}z,\\ \dot{p}=-e(x+y)+r_{4}p,\end{array}$$

(26)

where $r_1$, $r_2$, $r_3$ and $r_4$ are feedback coefficients. The Jacobian matrix of System (26) at the zero-equilibrium point is the following:

$$J_r=\left|\begin{array}{cccc}-a+r_1& a& 0& 0\\ 0& c+r_2& 0& 1\\ 0& 0& -b+r_3& 0\\ -e& -e& 0& r_4\end{array}\right|,$$

(27)

The following determinant can be obtained from the Jacobian matrix:

$$\left|\lambda E-J_r\right|=\left|\begin{array}{cccc}\lambda +a-r_1& -a& 0& 0\\ 0& \lambda -c-r_2& 0& -1\\ 0& 0& \lambda +b-r_3& 0\\ e& e& 0& \lambda -r_4\end{array}\right|.$$

(28)

The characteristic equation can be found in the following:

$$f_r\left(\lambda \right)=R_4{\lambda }^4+R_3{\lambda }^3+R_2{\lambda }^2+R_1\lambda +R_0,$$

(29)

where,

$$\begin{array}{cc}\hfill R_0& =2abe+ac{r}_4-2ae{r}_3-be{r}_1+e{r}_1{r}_3+ab{r}_2{r}_4-bc{r}_1{r}_4-ac{r}_3{r}_4\hfill \\ & -a{r}_2{r}_3{r}_4+b{r}_1{r}_2{r}_4+c{r}_1{r}_3{r}_4-r_1{r}_2{r}_3{r}_4,\hfill \\ \hfill R_1& =2ae-be-abc-e{r}_1+e{r}_3+bc{r}_1+bc{r}_4-ab{r}_2-ab{r}_4+ac{r}_3+ac{r}_4+a{r}_2{r}_4+a{r}_2{r}_3\hfill \\ & +a{r}_3{r}_4+b{r}_1{r}_2++b{r}_1{r}_4-c{r}_1{r}_3-c{r}_1{r}_4-c{r}_3{r}_4+r_1{r}_2{r}_4++r_1{r}_2{r}_3-r_1{r}_3{r}_4-r_2{r}_3{r}_4,\hfill \\ \hfill R_2& =ab-ac-bc-e-a{r}_2-a{r}_3-a{r}_4-b{r}_1-b{r}_2-b{r}_4\hfill \\ & +c{r}_1+c{r}_3+c{r}_4+r_1{r}_2+r_1{r}_3+r_1{r}_4+r_2{r}_3+r_2{r}_4+r_3{r}_4,\hfill \\ \hfill R_3& =a+b-c-r_1-r_2-r_3-r_4,\hfill \\ \hfill R_4& =1.\hfill \end{array}$$

According to the Routh–Hurwitz discriminant condition [49], the real parts of eigenvalues are negative if and only if,

$$R_3{R}_2-R_1>0,R_3(R_1{R}_2-R_3{R}_0)-R_1^2>0, R_3>0, R_0>0.$$

Case 1:

When $a=40$, $b=2$, $c=22$ and $e=1$, we assume $r_{1,2,3,4}=-25$. The corresponding Lyapunov exponents for System (2) are as follows:

$$L_1=18.2980, L_2=-4.0706, L_3=0, L_4=8.0878.$$

Then, the corresponding Lyapunov exponents for System (26) are as follows:

$$L_1=-3.2103,L_2=-13.5230,L_3=-23.3526,L_4=-22.5437.$$

So, the zero-equilibrium point is asymptotically stable.

Case 2:

When $a=40$, $b=2$, $c=22$ and $e=3$, we assume $r_{1,2,3,4}=-30$. The corresponding Lyapunov exponents for System (2) are as follows:

$$L_1=19.5457,L_2=-4.1972,L_3=0,L_4=8.9684.$$

Then, the corresponding Lyapunov exponents for System (26) are the following:

$$L_1=-8.3379,L_2=-16.6337,L_3=-29.2114,L_4=-27.8364.$$

Hence, the zero-equilibrium point is asymptotically stable.

For the two cases above, the time-domain waveforms of the hyperchaotic System (2) and the controlled System (26) are shown in Figure 7 and Figure 8. By choosing appropriate feedback coefficients, the controlled System (26) is asymptotically stable at the zero-equilibrium point.

6. Conclusions

This paper obtains a novel four-dimensional hyperchaotic system based on the generalized Sprott C system. This system has two nonlinear terms and seven linear terms. The system has Hopf bifurcation and can be solved to obtain explicit formulas for the direction and stability of the bifurcation periodic solutions. Additionally, we show the phase diagram of the bifurcation periodic solutions stability versus direction in Figure 5 and Figure 6. We mainly use the Runge–Kutta algorithm for the numerical simulations in this paper. The results show that the new 4D hyperchaotic system has complex dynamical behavior.

In addition, we also performed linear feedback control on the new 4D hyperchaotic system. This new control strategy is novel and effective regarding hyperchaotic phenomena in control systems, as shown in Figure 7 and Figure 8.

In the future, we will study more complex high-dimensional hyperchaotic systems and apply different methods. Five- and even six-dimensional hyperchaotic systems have rich and exciting properties and should be studied in depth.