Optimizing Vehicle Repairs Scheduling Using Mixed Integer Linear Programming: A Case Study in the Portuguese Automobile Sector

Abstract

This study investigates the scheduling of mechanical repairs performed at a Portuguese firm in the automobile sector. The aim is to reduce the amount of time that vehicles spend inactive between interventions by developing a mathematical model that takes into account the available resources and mechanics, the necessary interventions, and the time required for each repair. To accomplish this, a mixed-integer linear programming (MILP) model was employed, incorporating various variables to schedule interventions, allocate resources, and determine start times for each vehicle. The problem was formulated using the AMPL modeling language, and real-world instances of the problem, derived from data provided by the company, were solved using the Gurobi solver. Results show that the developed model significantly improves the scheduling of the vehicles’ repairs at the firm, leading to a reduction of 67% on average in the downtime of the vehicles and allowing an automatic correct schedule of the mechanical interventions. Moreover, the comparison of the scheduling obtained from the developed model and the firm’s procedure shows that interventions on vehicles arriving at the repair shop are mostly repaired on the day of entry, allowing for quicker delivery to the customer.

1. Introduction

In the automobile sector, the downtime of vehicles between interventions can lead to significant economic losses for firms. To tackle this issue, scheduling repairs in an efficient and timely manner is crucial. The scheduling of repairs is a complex problem that requires taking into account multiple factors, such as available resources, mechanics, necessary interventions, and the time required for each repair.

Scheduling holds significance across various disciplines as it involves decision-making processes and represents a classic combinatorial problem much studied by researchers in operational research (OR) [1,2]. Since the early 1950s, this subject has received much attention from OR practitioners, management scientists, production and operations research workers, as well as mathematicians [3]. It represents a very important activity of many firms and can be defined as the allocation of resources to perform a set of tasks over a period of time, to optimize some or several performance measures [1,4]. These resources and tasks differ, depending on the type of organization in question: resources may be, for example, machines in a repair shop, runways at an airport, while tasks may be, for example, operations in a production process, airport takeoffs and landings [5]. A general problem, often used in the literature, to describe scheduling problems is the Job Shop Problem (JSP), which can be described as a set of jobs to be processed in a set of machines, and each job can consist of a set of operations and its processing order. An extension of this problem, which fits the environment of the problem addressed in this project is the Flexible job shop problem (FJSP), where an operation can be processed on any machine, in a set of available machines [4].

To solve the scheduling problems, several types of models were developed to describe the systems in which they are uncertain. Lin et al. [6] clarifies that most scheduling models are developed using mathematical methods.

Baker and Trietsch ([7], pp. 3, 4) state that scheduling theory mainly deals with creating mathematical models that relate to scheduling processes. The development of effective models is an ongoing interaction between theory and practice, leading to practical insights and solution techniques. The authors also highlighted that this theoretical perspective involves a quantitative approach, which aims to represent the problem structure in mathematical form. This approach starts by describing resources, tasks, and translating decision-making goals into an objective function.

The empirical work addressed in this study focuses on a challenge presented by a Portuguese company operating in the automobile sector, engaging in vehicle sales and maintenance. Of the various branches that it owns, scattered throughout the country, the one that is portrayed in this project is the branch located in Porto, particularly in its repair shop. There are different areas in the repair shop, namely repair, administration, and quality control. These areas also have specific subareas, through which the workers of the firm are distributed, and depending on the area, the workers will have different functions to perform. The area that will be analyzed in this project will be the mechanical area. The firm provided data on eight mechanics and on the mechanical repairs carried out over a time horizon period of one year—August 2016–July 2017.

The main objective of the firm is that the vehicles that arrive at the repair shop stay the least possible amount of time without any intervention being performed until all repairs have been completed. To achieve this objective, a mathematical model was created to efficiently schedule the necessary interventions for a specific group of vehicles, ensuring they are prepared for delivery to customers with minimal downtime. The model takes inspiration from previous works such as [8,9].

This study serves as an expansion of the research conducted in [10]. It introduces a mixed-integer linear programming (MILP) model that incorporates linear ordering variables to sequence interventions for individual vehicles. Additionally, assignment variables and linear variables for the start time are integrated into the model’s framework.

Numerous studies in the literature, as highlighted by Melo et al. [11], often lack the utilization of real data. This can be attributed to various factors, including obstacles imposed by companies regarding data sharing, the challenge of data collection, or the absence of readily available data that necessitate time-consuming preparation and aggregation. Sarker et al. [12] proposed that, due to the inherent complexity of real-world problems, researchers and practitioners frequently resort to simplifications or assumptions when employing mathematical approaches to address the problem’s intricacy.

Hence, the significance of this study lies in the opportunity to tackle a genuine problem using actual data provided by the company. Working with such authentic data enhances the value and credibility of this research.

In a study by [13], it was found that only 9% of the works surveyed addressed issues specific to the automotive industry, while only 2% were related to the transportation industry. Similarly, Chaudhry and Khan [14] noted that a mere 7% of the studies related to FJSP used mathematical programming, such as integer/linear programming (IP/LP). These findings suggest that there is a lack of literature on FJSP problems in the context of the automotive industry, making it an area of great interest.

Decision makers have recognized the potential benefits of applying OR approaches to problem-solving, such as cost savings. In the context of this project, optimizing the scheduling of repairs can lead to decreased unproductive time in the repair shop, which can ultimately maximize the firm’s costs and customer satisfaction. Satisfied customers are likely to return, making customer satisfaction a crucial factor [12].

In this manuscript, we present a comprehensive analysis of the scheduling problem faced by the company. We start by providing a concise overview of the relevant literature on scheduling, quantitative models, and their applications (Section 2). This literature review establishes the theoretical foundation and highlights the gaps that our research aims to address.

Section 3 provides an in-depth description of the company and the specific problem we are addressing. By understanding the company’s operations, constraints, and objectives, we can develop a tailored solution that aligns with their requirements.

Next, in Section 4, we explain the methodology and model that we developed to solve the scheduling problem. This model takes into account various factors such as resource availability, task dependencies, and operational constraints to generate efficient schedules.

The results obtained from real instances provided by the company are presented in Section 5. These results demonstrate the effectiveness of our approach and provide insights into the challenges faced in scheduling tasks within the repair shop environment.

Finally, in Section 6, we summarize the findings of our study and discuss their implications. We also identify potential areas for future research and improvement to further enhance the scheduling process and optimize repair shop operations.

2. Literature Review

Scheduling is a classic combinatorial problem which has been extensively studied by researchers in OR [2]. Scheduling problems occur in all economic domains, from computer engineering to manufacturing [15]. The field of scheduling is driven by the challenges encountered in diverse domains such as production planning, telecommunications, logistics, and computer control, as noted by Unlu et al. [16]. The significance of scheduling has been recognized by OR practitioners, management scientists, production and operations researchers, and mathematicians since the early 1950s [3]. It has garnered substantial attention and interest from these professionals, reflecting its importance and relevance in various disciplines. A significant variety of works have been published since then (see for, e.g., [17,18,19,20,21,22,23,24,25,26]).

However, despite being an area that has been widely studied, and after several decades of work, only a limited set of scheduling problems ensure optimization [27]. This is also due to the fact that most scheduling problems are complex combinatorial optimization problems, and are therefore difficult to solve [15]. The first developments in scheduling were motivated by problems in manufacturing. For this reason, the manufacturing vocabulary has been employed when specifying scheduling problems, and although it currently has considerable significance in many non-manufacturing areas, the terminology associated with manufacturing is still widely used [7].

The literature encompasses various classifications of scheduling. These classifications consider factors such as the number of machines, jobs, and operations involved, as well as the rules dictating the scheduling of operations, scheduling can be classified as [28]:

• Single-machine shop (SMS): there is only a single machine in the shop, and each job has a single operation to be performed on that machine. Therefore, the scheduling task is to find the ideal sequence for all jobs to be processed;
• Parallel machine shop (PMS): there are m machines that work in parallel, and each job has a single operation to be processed, where one job can be processed on several or any of the machines;
• Flow-shop (FSP): there are m machines, and each job consists of a strictly ordered sequence of operations, where the order of the machines for all jobs is identical;
• Job shop (JSP): there are m machines and n jobs, where each job has its own processing order through the machines, and may have no resemblance to that of any other job;
• Open shop (OSP): an extension of the JSP, and here there is no restriction of order within each job.

A basic example that has been extensively studied is the that of the JSP [28], where resources are usually called machines and tasks are called jobs. Furthermore, sometimes jobs can contain several elementary tasks called operations [7]. This problem is very important in the field of production scheduling [29] and is acknowledged to be one of the hardest combinatorial optimization problems [12]. Furthermore, its wide applicability in real-world manufacturing systems makes it one of the most popular scheduling problems [30]. The general JSP is strongly NP-hard [31], since no efficient polynomial algorithms are known for its resolution [32].

An extension of the classic JSP is the flexible job shop problem (FJSP), where an operation is allowed to be processed by any machine from a given set of available alternative machines [14]. The FJSP comprises two main sub-problems. Firstly, the routing sub-problem involves the assignment of each operation to a suitable machine from a given set of capable machines. Secondly, the scheduling sub-problem focuses on sequencing the assigned operations on all the machines to generate an optimal schedule that minimizes a specified objective function [29]. The pioneering work by Brucker et al. [33] introduced the resolution of such problems by developing a polynomial algorithm specifically designed for solving the FJSP with two jobs. This breakthrough was further supported by the works of Shen et al. [30] and Xia et al. [29].

As defined by Ozguven et al. [19], the FJSP can be described as follows: Given a set of n independent jobs denoted as j, each with its own unique processing order across a set of available k machines, a series of $l_j$ ordered operations ($O_{j1},\cdots ,O_{j{l}_{\left(j\right)}}$) must be executed to complete job j. Each operation $O_{ji}$ of job j can be processed by any machine belonging to a given set $M_i\in M$, with a corresponding processing time of $p_{ik}$.

The difference to the FJSP is that instead of having to be processed in a predefined machine $m_g\in M$ as in the JSP, each operation can be processed by any machine on a set $M_g\in M$. [19] pointed out that FJSP can be considered to consist of many unique JSPs due to the flexibility of routing. While the JSP is only a sequencing problem because the assignment of operations to the machines is given in advance, the FJSP becomes a routing and sequencing problem. Having already observed that the JSP is NP-hard and given that FJSP adds the need to determine the assignment of operations to machines, it can be concluded that FJSP is also a strongly NP-hard [15].

In terms of scheduling environment, when making assumptions about the availability of information on future requirements, it is necessary to make a distinction between static and dynamic environments [26]. In a static environment, the scheduling problem is defined in relation to a finite set of fully specified requirements, where no additional requirements will be added to this set, and none of the specifications made will be changed. In contrast, if the scheduling problem is defined not only for known requirements but also for additional requirements and specifications, the environment is dynamic [26]. For example, if the set of jobs available for scheduling does not change over time, the system is called static, otherwise, if new jobs appear over time, it is called dynamic [7]. As stated by Baker and Triersch ([7], p. 4), static models have been more extensively studied and are easier to handle compared to dynamic models because all the model parameters are predetermined. Nonetheless, Baker acknowledges that dynamic models are more relevant in real-world applications since unforeseen events may occur. Despite this, static models can still provide insights into dynamic systems, and analyzing static problems can reveal useful principles and insights for dynamic situations.

As noted earlier, the efficient utilization of resources, rapid responses to demands, and close conformance to prescribed deadlines are decision-making goals that must prevail in scheduling [34]. Scheduling objectives, also known as performance measures, are criteria by which the performance of a particular solution method can be measured [35].

After the parameters (such as processing time, tasks to be made or set of available machines) and the variables of the model are set, the objective function to be minimized or maximized is defined, according to the objectives that are intended to be achieved. According to [34], there are numerous criteria that have been used in theoretical scheduling studies, and, in varied circumstances, these criteria assume different degrees of relevance. In [22], the author claims that it is not easy to state the objectives in scheduling because these are numerous, complex, and often conflicting. Hence, the author defines performance measures grouped into three different categories: (a) criteria based upon complete times: Maximum flowtime ($F_{max}=max{F}_j$), maximum complete time or makespan ($C_{max}=max{C}_j$), mean flowtime ($\overline{F}=\frac{1}{n}{\sum }_{j=1}^n{F}_j$) and mean complete time ($\overline{C}=\frac{1}{n}{\sum }_{j=1}^n{C}_j$). (b) Criteria based upon due dates: Maximum lateness ($L_{max}=max{L}_j$), maximum tardiness ($Tmax=max{T}_j$), mean lateness ($\overline{L}=\frac{1}{n}{\sum }_{j=1}^n{L}_j$), and mean tardiness ($\overline{T}=\frac{1}{n}{\sum }_{j=1}^n{T}_j$). (c) Criteria based upon the inventory and utilization cost: Mean number of jobs waiting for machines ($\overline{N_w}$), mean number of unfinished jobs ($\overline{N_u}$), mean number of complete jobs ($\overline{N_c}$), mean number of jobs actually being processed at any time ($\overline{N_p}$), mean machine idle time ($\overline{I}$), and maximum machine idle time ($I_{max}$).

According to the explanation in [36], OR analysis involves the use of quantitative techniques such as applied statistics to develop mathematical and statistical models that represent real-life scenarios. These models are then utilized to find solutions and interpret the outcomes.

In [37], the authors reviewed the literature on various methods for solving scheduling problems in a hybrid flow shop (HFS), which involves scheduling flow shops with multiple parallel machines. Different variants of the problem are discussed, each with distinct constraints, assumptions, and objective functions.

Meanwhile, [16] evaluated four different formulations of MIP models for parallel machine scheduling problems, each based on different types of decision variables.

For the specific case of a Canadian transportation firm and their truck scheduling, ref. [38] proposed an MIP formulation that considers both customer visits and required rest periods for truck drivers in compliance with Canadian commercial vehicle drivers’ hours of service regulations. Additionally, an iterative dynamic scheduling approach is suggested to minimize the duration of the truck schedules that follow the regulations.

In [39], a decomposition heuristic is proposed for various job shop scheduling problems that have LP formulations. The objective functions in these problems are based on both the job completion time and the intermediate operation completion times.

In response to the analysis conducted in two previously published articles on scheduling problems involving setup times/costs, namely the first review covering approximately 200 articles published from 1960 to 1988 [40] and the second survey encompassing around 300 articles published between 1998 and 2006 [41], Allahverdi et al. [42] presented a third survey on scheduling issues. This third survey encompassed approximately 500 articles published from 2006 to 2014, which explore scheduling problems in various environments, including static, dynamic, deterministic, and stochastic contexts.

The article by [42] introduced a classification framework for scheduling problems based on the shop environments. These environments included single- machine shop, parallel-machine shop, flow shop, job shop, and open shop settings. Furthermore, this article categorizes the problems based on the presence of family or non-family setups, as well as sequence-dependent or sequence-independent setup times/costs. This comprehensive survey provides valuable insights into the diverse aspects of scheduling problems, considering installation times/costs, and consolidating the research contributions made in the field during the specified time frame.

The article in [43] described the application of an MILP model to an ice-cream processing facility in a multi-week context, with the goal of minimizing the makespan. Similarly, the article [44] presented an MILP model to address a problem in the petroleum industry, with the objective of minimizing the total investment and satisfying the constraints of the submarine terrain and production process.

In [19], the authors discussed two types of FJSP problems, namely FJSP covering sub-problems of routing and sequencing, and FJSP with the process plan flexibility which includes the process plan selection sub-problem. This article presents an MILP model for each context and compares them with alternative models in the literature, assessing computational efficiency. In [45], the relevance of modeling workshop scheduling problems in the context of FJSP is investigated, using the discrete event system (DES) approach based on timed automata (TA). The authors compared this approach with the classic MILP approach, taking into account the generation and measurement systems based on three criteria and associated metrics.

The article [30] tackles a scheduling problem in the context of FJSP with sequence-dependent setup times, with the objective of minimizing the makespan. The authors presented an MILP model to solve small instances optimally and also develop a tabu search algorithm with novel neighborhood functions and a specific diversification structure. Computational experiments compare the MILP model and the tabu search algorithm with other approaches found in the literature.

Furthermore, ref. [46] addresses a scheduling problem in the context of military aircraft maintenance, aiming to meet the aircraft’s requirements for a number of missions in the presence of failures. The authors employ multiple approaches for resolution, including MIP, logic-based Benders decomposition (LBBD), a dispatching heuristic, and two hybrid approaches. In [47], the authors developed a novel integrated iterative approach using MIP and simulation–optimization to solve an integrated demand-responsive scheduling problem in a military supply chain.

Additionally, ref. [48] presents an MILP model for scheduling the repairment of aircraft engines in a context of a flexible job shop problem, with the objective of minimizing total tardiness and makespan. In [49], the authors studied the case of scheduling preventive maintenance tasks in a large-scale Viennese electrical network within a planning horizon of three decades. They formulate the problem as an MIP model and also develop a metaheuristic based on a large neighborhood search.

In [50], the authors studied an aircraft maintenance company using real-life data, focusing on line maintenance with a three-stage MIP approach to optimize the skill mix and training schedule for aircraft maintenance workers. Finally, the article in [51] addresses a problem of scheduling the maintenance of edges in a transport and telecommunications network to minimize network outages, using exact and approximation algorithms. The authors considered preemptive and non-preemptive maintenance jobs for MINCONNEXTIVITY and MAXCONNECTIVITY problems.

For a recent review of FJSP scheduling, with real-world applications and detailed future research trends and opportunities see [52].

More recently, the study in [53] presents solutions to the distributed flexible job shop scheduling problem (DFJSP) with the objective of minimizing the maximum completion time (makespan). The authors proposed four MILP models and a constraint programming (CP) model. While MILP models are effective for small-scaled problems, the DFJSP is NP-hard, so the authors also propose an efficient CP model based on interval decision variables and domain-filtering algorithms.

3. Firm and Challenge Description

This empirical study is concerned with a Portuguese firm in the automobile sector, and its vehicle sales and maintenance activities, that has branches scattered throughout the country. In this analysis, the focus will be on the Filinto Mota branch located in Porto, particularly in their repair shop.

The company has a total workforce of 28 employees who are assigned to various departments, namely repair, administration, and quality control. The repair department encompasses different areas, including mechanics, collision, service station, preparation of new vehicles (PNV), diagnosis, and electronics. The mechanics area comprises eight workers, including two senior mechanic specialists who possess expertise in various tasks, including diagnostics. The remaining six workers in the mechanics area are senior mechanics who specialize in specific tasks but do not perform diagnostics. The collision area consists of seven workers, comprising three sheet metal workers, three painters, and one chief of collision. Additionally, the service station employs two washers, while the PNV area is managed by a single employee responsible for preparing new vehicles before delivery to customers. The administrative department comprises eight workers, including three receptionists, one repair shop manager, one quality control officer, one guarantees operator, and two staff members responsible for billing. The receptionists are responsible for receiving the vehicle, filling in the opening repair order (RO) forms, indicating the expected interventions to perform, and setting an expected delivery date with the customer. They are also responsible for performing the visual inspection of the state of the vehicle when entering the repair shop, such as checking for scratches or dents, fuel and kilometers, among others. The repair shop manager is responsible for distributing the vehicles, which have already completed the RO form and are waiting to be repaired by the available mechanics in the repair shop and the work they are already performing, as well as the type of interventions that the vehicle needs to perform. As previously verified, not all mechanics perform the same tasks.

The working hours of the repair shop are governed by Portuguese labor law, regulated by number 1 of Article 203 of the Código de trabalho (Labor Code), which states that “the normal working hours may not exceed eight hours a day and forty hours a week” [54]. As such, the repair shop works eight hours a day, during working days, and its opening hours are from 8:30 a.m. to 12:30 a.m. and from 1:30 p.m. to 5:30 p.m. During the morning and afternoon work periods, workers take a 10 min break.

It is possible that the vehicles are received or delivered to the customers by the security guarding the repair shop, outside of working hours of the repair shop. In these cases, the security guard signals the necessary repairs to be performed so that the receptionist may fill the RO form the next working day. Thus, in the database, there are vehicles that have an entry (or exit) hour before the opening hours (and after the closing hours) of the repair shop. For the purposes of this analysis, it was established that, for vehicles arriving before the opening hour of the repair shop, the registered starting hour would be the opening hour of that day (i.e., 8:30 a.m.). For those vehicles arriving after the closing hour, the registered starting hour would be the opening of the following working day.

The focus of this empirical work will be on the mechanical area and on the interventions performed. The firm provided a database with information regarding one year (from August 2016 to July 2017) of the repairs that were performed at the repair shop. According to the firm, most repairs are pre-scheduled (75%) one or two days in advance, and only a small percentage are scheduled on the same day (25%). The repair shop has two time clocking stations, where the mechanics perform a time clock registration when starting and finishing a certain mechanical intervention. This time-clocking system provides information for a computer system, from which it is possible to project real-time information on the state of repair of a particular vehicle. This information is projected on a screen, such that the receptionist can control whether the vehicle will be ready on the expected delivery date initially agreed upon the customer.

From the moment it enters the repair shop, until the moment it is delivered, the vehicles go through different processes. The first step consists of filling the RO form with the repairs required by the customer. After completing the RO form, the vehicle is parked, waiting for the moment when the mechanic who will start repairing is available. The repair shop management represents the “bridge” between reception and mechanics, since, as previously mentioned, it is they who distribute the vehicles awaiting repair by the available mechanics. As soon as a vehicle begins to be operated, the mechanic starts a time clock, referring to the first intervention performed, and when this repair is finished, they perform another time clock. This time clock process is repeated, depending on the number of interventions that need to be performed. The same intervention may have more than one time clock if the mechanic needs to make a stop. After all repairs are completed, the vehicle goes through quality control to ensure that they have been performed correctly. It is the firm’s policy that all repaired vehicles should be washed at the service station in the end. After these steps, the vehicle moves back into the parking lot, waiting for the customer to pick it up. When the customer comes to pick up the vehicle, the billing of the services performed is carried out, thus ending the vehicle’s permanence in the repair shop.

As previously mentioned, this work is focused on the mechanical area, and consequently, on the eight mechanics that belong to this section, along with the interventions that they perform.

4. Methodology

The problem in this case study consists of a FJSP, which arises due to the presence of multiple machines working simultaneously and several mechanics capable of performing the same mechanical tasks. FJSP can be broken down into two sub-problems: routing and scheduling. In the routing sub-problem, each operation is assigned to a machine from a set of available machines. In the scheduling sub-problem, operations are assigned to all machines in a way that yields a valid schedule that optimizes a particular objective function, as described in [29].

The firm’s specificities are the following:

• The sequence of interventions assigned to each vehicle is determined based on the actual repair order established at the repair shop, and this sequence is assumed to be known. Additionally, the order of interventions is fixed and cannot be altered.
• The time required by each mechanic to perform a particular intervention remains consistent across all mechanics. These time durations are specified using standardized barème times defined by each car brand. It should be noted that, for the purpose of this analysis, the barème times associated with the same intervention were adjusted to ensure consistency.
• The interventions can be interrupted and resumed at any point in time, allowing for flexibility in the execution process.
• The interventions performed in the repair shop, are different from the interventions considered in this analysis, since for the firm, the repairs are composed of a set of lines, which will be considered in this analysis as the interventions actually performed, since it is on them that the barème times are associated.
• Each vehicle can only have one mechanic working on it at any given time.
• Only one intervention can be carried out at a time on each vehicle.
• The firm employs mechanics with two levels of qualification. As a result, multiple mechanics possess the necessary skills to perform the same interventions. However, not all mechanics are capable of executing all interventions due to variations in their qualifications. The qualifications are: (i) senior specialized mechanics, who can perform any intervention, including diagnosis; and (ii) senior mechanics, who can perform any intervention, with the exception of diagnostics;
• There are vehicles that present interventions that are not executed in the mechanical area, but these are interventions that have to be considered in this analysis since they are interventions that actually happened in the repair shop, and it required time for the vehicle to be in the repair shop.
• In most cases, when the vehicle arrives at the repair shop, the delivery date is negotiated between the receptionist and the customer. However, this delivery date is not negotiated for all vehicles.
• The working day is divided into two periods: a 4 h duration in the morning and another 4 h duration in the afternoon. There is a designated lunch break lasting for 1 h. Additionally, two flexible breaks of 10 min each are provided, with one break scheduled in the morning and another in the afternoon. In the developed model, time will be treated as a continuous variable, allowing for more precise analysis and scheduling.

The mathematical model presented herein for scheduling the repairs of the vehicles that arrive at the firm is an MILP model. This model was initially introduced in the work presented by [10]. It draws inspiration from the model proposed in [48] and incorporates elements from the models presented in [4]. The combination of these references serves as the foundation for the development and formulation of the model under consideration.

The sets and indexes of the MILP model are defined in

Table 1. Sets and indexes of the MILP model.

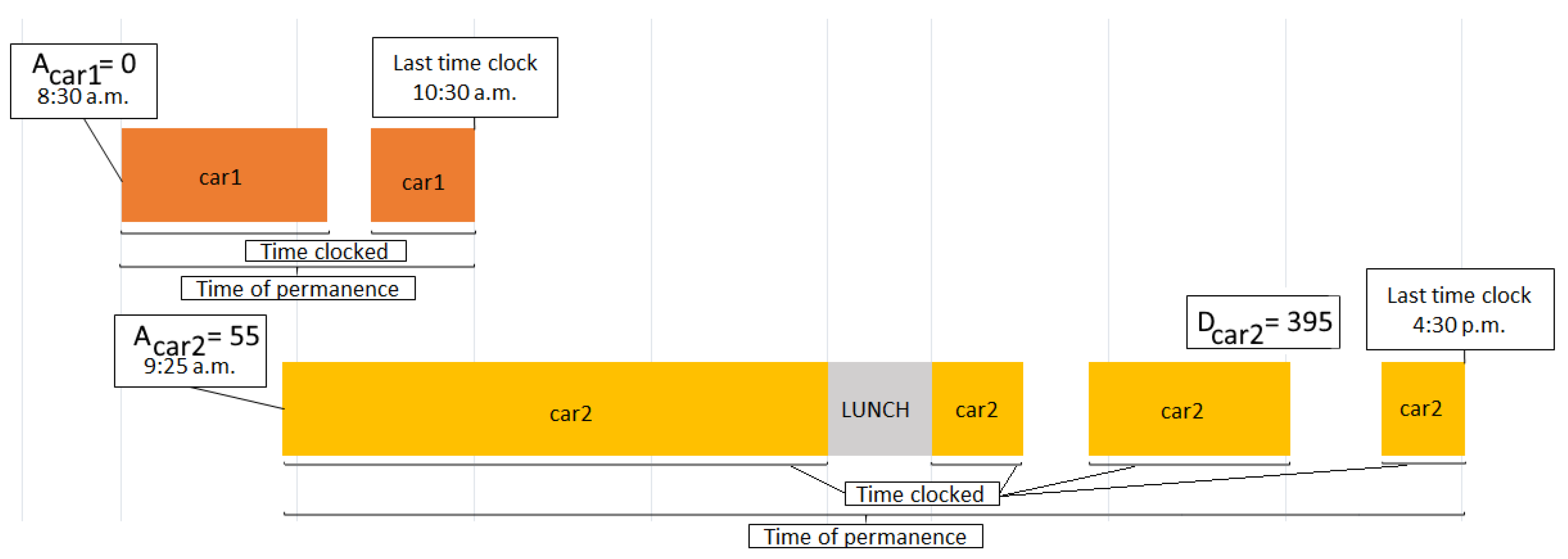
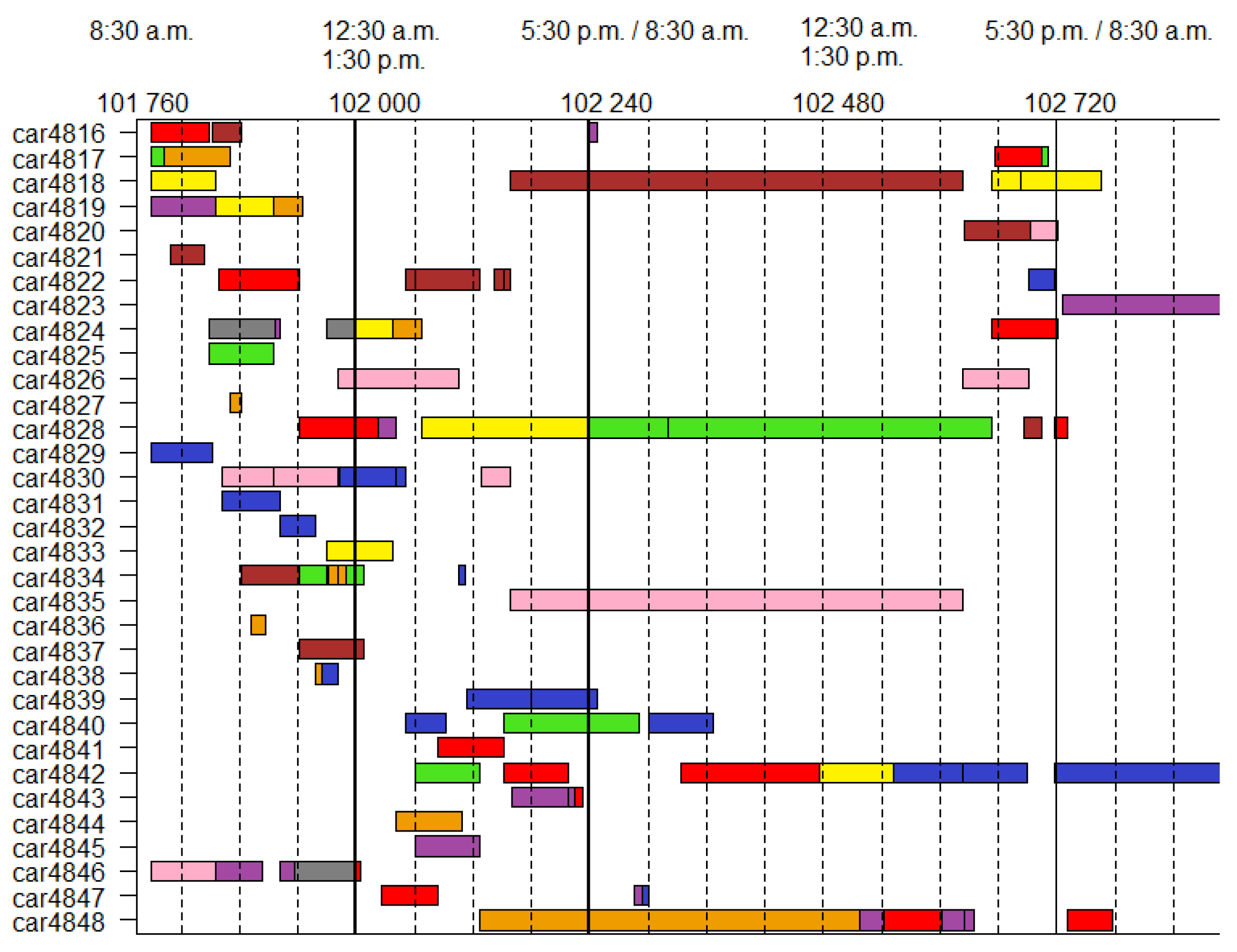
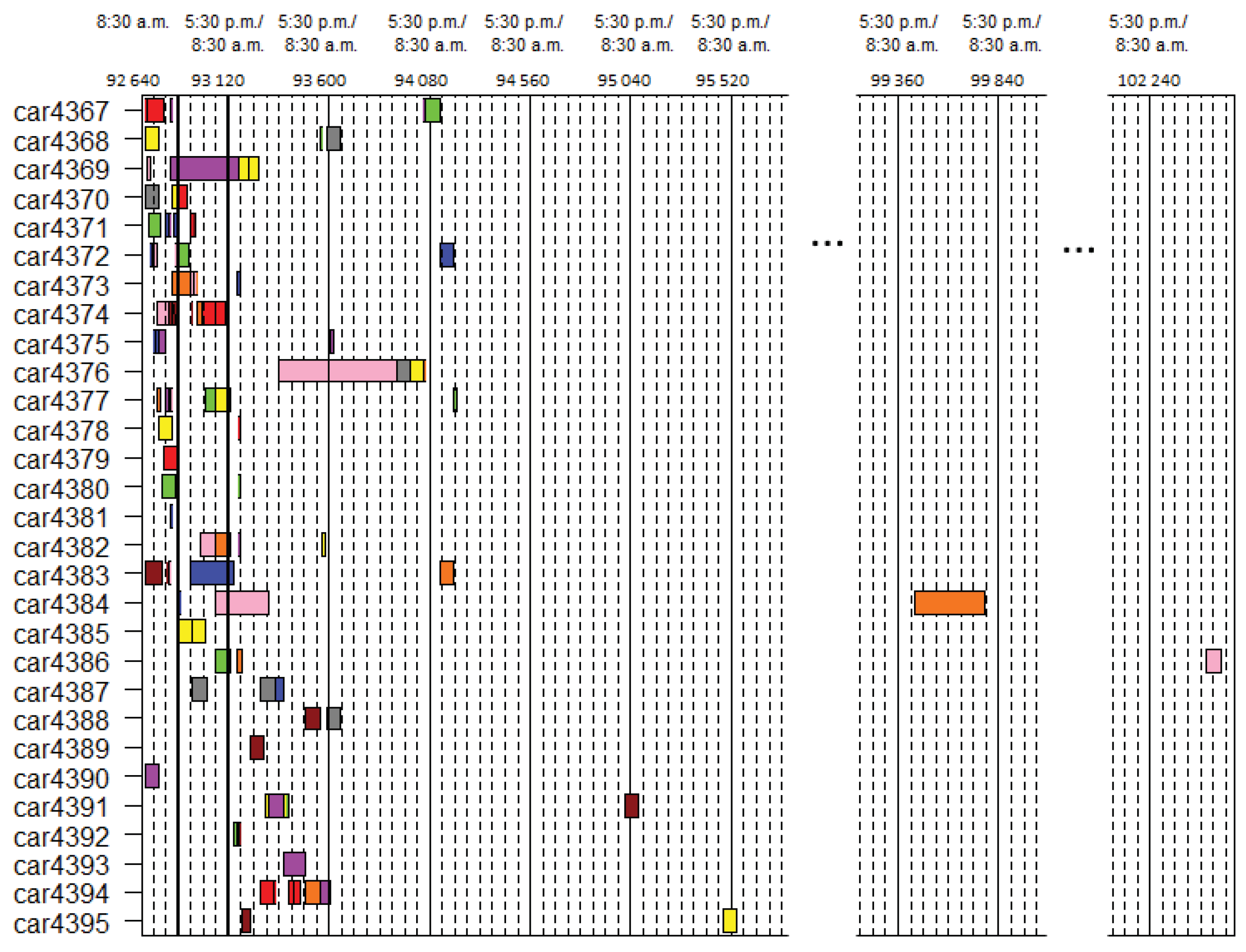
Name	Description
$o\in O$	ROs (i.e., vehicles to be repaired).
$m\in M$	Mechanics employed.
$i\in I_{all}$	All possible mechanical interventions.
$I_o$	Predetermined and ordered interventions to be performed on a specific $o\in O$ vehicle.
$(i,o)\in (I_{all}\times O)$	Specific pair of interventions that are to be performed in a predetermined sequence on a particular vehicle $o\in O$.
$M_{(i,o)}$	Mechanics that are qualified to perform the required interventions on vehicle o, i.e., $(i,o)\in I_o$.

, while the parameters are defined in

Table 2. Parameters of the MILP model.

Name	Description
$t_{(i,o)}$	Processing time of intervention $(i,o)\in I_o$, in minutes.
$D_o$	Deadline or delivery time of vehicle $o\in O$, defined as the time from the moment that vehicle o arrives at the repair shop until the expected delivery date, in minutes.
$A_o$	Release date of vehicle $o\in O$, defined as the time of arrival of vehicle o into the repair shop, in minutes.
$c_o$	Describes whether vehicle $o\in O$ has an established expected delivery date, such that $c_o=1$ if vehicle $o\in O$ has an expected delivery time $D_o$ and 0 otherwise.
L	A sufficiently large positive number.

and the decision variables are defined in

Table 3. Decision variables of the MILP model.

Name	Description
$x_{(i,o),(j,o^{\prime })}$	Binary variables that define the precedence relations between interventions $(i,o)$ and $(j,o^{\prime })$, with $M_{(i,o)}\cap M_{(j,o^{\prime })}\ne \varnothing$ and $i\ne j$ or $o\ne o^{\prime }$. It is equal to 1 if intervention $(i,o)$ is performed before intervention $(j,o^{\prime })$. Otherwise, it is equal to 0.
$a_{(i,o)}^m$	Binary variables that define the assigning of each mechanical intervention i on vehicle o to a mechanic m. It is equal to 1 if intervention $(i,o)$ is assigned to mechanic m. Otherwise, it is equal to 0.
$S_{(i,o)}$	Non-negative variables that define the starting time of intervention i on vehicle o, in minutes.
$T_o$	Non-negative variables that define the tardiness of vehicle o.

.

Parameter $t_{(i,o)}$ (see Table 2) represents the processing time of intervention i in vehicle o, considering the barème time defined for each type of intervention. It is associated with the combination of the intervention performed and the vehicle. The parameter $D_o$ was determined by taking into account the total working minutes of the repair shop, starting from the moment when vehicle o enters the repair shop until the expected delivery time agreed-upon with the customer; Figure 1 presents an illustrative example of these parameters. The parameter $A_o$ is calculated as the duration in minutes from the reference day and hour (specifically, 1 August 2016, 8:30 a.m.) until the arrival time of vehicle o at the repair shop. For instance, in the case of vehicle $car1$ entering the repair shop at 8:30 a.m. on 1 August 2016, the value of $A_{car1}$ is 0. Similarly, for vehicle $car2$ entering the repair shop at 9:25 a.m., $A_{car2}$ is calculated as 55 min. Additionally, the parameter $D_{car2}$ denotes a repair duration of 395 min for a vehicle $car2$, representing the total time from its entry into the repair shop until completion.

The parameter $c_o$ serves as an indicator of whether an expected delivery date has been established with the client for vehicle o. When an expected delivery date is set, $c_o$ takes the value of 1, indicating that an agreement has been made. On the other hand, when no expected delivery date has been established, $c_o$ is set to 0, indicating the absence of such an agreement. For the example presented in Figure 1, $c_{car1}=0$ and $c_{car2}=1$.

The MILP for scheduling the mechanical interventions at the repair shop is the following:

$$\begin{array}{ccc}\hfill min& & \sum _{o\in O}{T}_o{c}_o+\sum _{o\in O}\sum _{i\in I_o}{S}_{(i,o)}(1-c_o)\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& & \hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill & & \sum _{m\in M_{(i,o)}}{a}_{(i,o)}^m=1,\forall (i,o)\in I_o\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill & & S_{(j,o)}\ge S_{(i,o)}+t_{(i,o)},\forall o\in O,\forall i,j\in I_o:j=\mathrm{next}\left(i\right)\hfill \\ & & S_{(j,o^{\prime })}\ge S_{(i,o)}+t_{(i,o)}-L\left(1-x_{(i,o),(j,o^{\prime })}\right),\hfill \end{array}$$

(3)

$$\begin{array}{ccc}& & \forall (i,o),(j,o^{\prime })\in I_o:M_{(i,o)}\cap M_{(j,o^{\prime })}\ne \varnothing \wedge (i,o)\ne (j,o^{\prime })\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill & & T_o\ge S_{(i,o)}+t_{(i,o)}-(A_o+D_o),\forall o\in O,\forall i\in I_o\hfill \\ \hfill & & x_{(i,o),(j,o^{\prime })}+x_{(j,o^{\prime }),(i,o)}\le 1,\hfill \end{array}$$

(5)

$$\begin{array}{ccc}& & \forall (i,o),(j,o^{\prime })\in I:M_{(i,o)}\cap M_{(j,o^{\prime })}\ne \varnothing \wedge (i,o)\ne (j,o^{\prime })\hfill \\ & & x_{(i,o),(j,o^{\prime })}+x_{(j,o^{\prime }),(i,o)}\ge a_{(i,o)}^m+a_{(j,o^{\prime })}^m-1,\hfill \end{array}$$

(6)

$$\begin{array}{ccc}& & \forall (i,o),(j,o^{\prime })\in I,(i,o)\ne (j,o^{\prime }),m\in M_{(i,o)}\cap M_{(j,o^{\prime })}\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill & & x_{(i,o),(j,o)}=1,\forall o\in O,\forall i\in I_o,i\ne \mathrm{last}\left(I_o\right),j=\mathrm{next}\left(i\right)\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill & & x_{(j,o),(i,o)}=0,\forall o\in O,\forall i\in I_o,i\ne \mathrm{last}\left(I_o\right),j=\mathrm{next}\left(i\right)\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill & & S_{(i,o)}\ge A_o+15,\forall o\in O,\forall i\in I_o\hfill \end{array}$$

(10)

$$\begin{array}{ccc}& & T_o\ge 0,\forall o\in O\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill & & S_{(i,o)}\ge 0,\forall o\in O,\forall i\in I_o\hfill \end{array}$$

(12)

The objective function, denoted as Equation (1), aims to minimize the total tardiness of vehicles for which an expected delivery date has been established ($c_o=1$). Additionally, it includes the sum of the start times of interventions for vehicles without an established expected delivery date ($c_o=0$). The constraint, represented by Equation (2), ensure that each intervention $(i,o)$ is assigned to exactly one mechanic $m\in M_{(i,o)}$. Furthermore, constraint (3) guarantee that the start of intervention $(j,o^{\prime })$ can only occur after the completion of intervention $(i,o)$ if the mechanical intervention $(i,o)$ is performed prior to the intervention $(j,o^{\prime })$.

The disjunctive constraint (4) guarantee that there is no overlapping of interventions for the same mechanic. These are only activated if intervention $(i,o)$ precedes the intervention $(j,o^{\prime })$ whenever they are performed by the same mechanic. The lower bound for the tardiness of each vehicle $o\in O$ is defined in constraint (5). The linear ordering of the interventions is established by constraints (6) and (7). The introduced constraints, denoted by Equation (6), serve to ensure the following possibilities: either intervention $(i,o)$ precedes intervention $(j,o^{\prime })$, or intervention $(j,o^{\prime })$ precedes intervention $(i,o)$, or interventions $(i,o)$ and $(j,o^{\prime })$ are not performed by the same mechanic. Additionally, constraint (7) is only active when interventions $(i,o)$ and $(j,o^{\prime })$ are executed by the same mechanic, guaranteeing that either $(i,o)$ precedes $(j,o^{\prime })$ or $(j,o^{\prime })$ precedes $(i,o)$.

To establish the precedence relationship between the interventions performed on the same vehicle, constraints (8) and (9) set $x_{(i,o),(j,o)}=1$ if intervention $(i,o)$ precedes $(j,o)$ and otherwise zero.

Finally, constraint (10) stipulates that each vehicle o must undergo repairs at least 15 min after its arrival at the repair shop, which corresponds to the time required for filling out the repair order (RO) form.

5. Results

This section presents the results obtained from 12 instances derived from real data provided by the firm, which represent vehicles that arrived at the repair shop during a one-year period. These 12 instances are used to test the models (1)–(12) presented in Section 4. Furthermore, the results obtained using the MILP model are compared with the firm’s procedure. A total of 251 working days and 5848 ROs, that occurred in the repair shop from August 2016 to July 2017, were considered. Figure 2 presents the number of vehicles (or RO) and respective interventions carried out during this period.

For each instance, first, its full characterization is presented and next the firm’s solution, obtained using the information provided by the firm, more precisely, the time clocked interventions registered by the firm, is depicted. Then, the scheduling obtained using models (1)–(12) is presented per vehicle and per mechanic. Finally, in order to perceive the improvements obtained with the developed model, this scheduling is compared to the firm’s scheduling.

The MILP model was implemented using the AMPL modeling language [55,56]. This is one of the most used [57] modeling languages for mathematical programming due to the generality of its syntax and the similarity of its expressions with algebraic notations, which enables one to easily specify and understand the objective function, the constraints, as well as the logical relations between variables [55,56]. The real instances were solved using Gurobi with the AMPL interface [58].

All results were obtained using an Intel Core i7-4510U@2.0 GHz 4 GB RAM running Windows 10 64-bits.

5.1. Selection of the Real Instances

The selected instances from the real data provided by the firm represent the most challenging scenarios encountered in the daily operations of the repair shop. By evaluating the results, we aim to determine whether the proposed model ensures minimal downtime for vehicles in the repair shop, and whether it is at the beginning, end, or between interventions. Achieving this goal will lead to a more efficient utilization of the available resources at the repair shop.

Based on Figure 2 and

Table 4. Total number of opened and time-clocked ROs, and the total downtime, that occurred at the repair shop each month from August 2016 until July 2017.

Year	Month	Total # of Opened ROs	Total # of Time Clocked ROs	Total Downtime (in min.)
2016	August	441	540	387,709.2
	September	455	646	354,881.2
	October	498	687	392,858.0
	November	473	664	306,310.0
	December	454	620	253,616.0
2017	January	516	707	278,735.8
	February	430	592	368,473.4
	March	519	748	369,077.0
	April	450	596	192,531.4
	May	547	754	255,557.8
	June	532	737	257,939.0
	July	533	713	264,060.6

, it is evident that the months with the highest number of repair order (RO) entries, including May, July, June, March, and January, do not necessarily align with the months having the highest number of time-clocked ROs, which are May, March, June, July, and January. Conversely, the months with the lowest downtime are April, December, May, June, and July, as shown in Figure 3 and Table 4.

Considering these observations, the three most challenging months, namely May, June, and July, were selected to construct the problem instances. Specifically, the days with the highest workload, indicated by the highest number of RO entries, were chosen within each of these months. Two distinct scenarios were tested: one with the lowest downtimes (19 and 26 May, 2 and 30 June, 14 and 27 July), and the other with the highest downtimes (9 and 16 May, 5 and 23 June, 11 and 4 July).

Additionally, it is noteworthy that the number of time-clocked ROs exceeds the number of RO entries for all months (Table 4), suggesting the existence of ROs opened in previous months that are only attended to at a later date.

5.2. Results of the 12 Real Instances

For all instances, the optimal solution to the optimization problems was found in a competitive computational time.

Table 5. Results of the MILP models (1)–(12) for 12 instances.

Instance	#O	#${\mathit{I}}_{\mathit{o}}$	#var	#constr	Objective	Downtime	%
9 May	29	71	9360	84,892	70	30,655.5	98.8%
16 May	28	95	13,410	123,592	2275.2	9877.8	46.4%
19 May	18	53	3181	27,071	26.7	271.6	8.9%
26 May	21	53	4174	36,099	0	2204.6	43.4%
2 June	13	31	1186	9056	51.9	103.9	4.9%
5 June	33	112	12,244	112,567	0	13,355.9	46.5%
23 June	27	63	4322	36,846	31.5	3301.5	12.4%
30 June	20	63	4060	34,972	167	599.4	21.0%
4 July	29	84	8821	79,648	0	10,955.6	34.2%
11 July	29	47	4391	37,734	114,174	3471.8	10.4%
14 July	19	56	3535	3286	0	1251.4	29.9%
27 July	26	45	4558	39,802	2,634,170	1656.0	39.1%
Mean	23.8	64.4	6103.5	54,380.4	252,952.2	6475.4	33.0%
StDev	6.0	23.7	3943.1	37,175.7	78,178.5	9072.7	25.8%

presents the results of the MILP model for the 12 instances. For each instance, the number of vehicles, #O; the total number of interventions on all vehicles, #$I_o$; the dimensions of the optimization problems (i.e., the number of variables, # var, and the number of constraints, # constr); the value of the objective function; the downtime of all the vehicles, in minutes; and the percentage of the downtime obtained using the model compare to the one observed in the firm, are all shown.

The smallest optimization problem occurs for the 2 June, with 1186 decision variables and 9056 constraints, which corresponds, as expected, to the day with the minor number of vehicles and required mechanical interventions (i.e., 13 vehicles and 31 interventions).

The largest optimization problem corresponds to the 5 June instances with 13,244 decision variables and 112,567 constraints, relative to the schedule of 112 mechanical interventions on 33 vehicles. On average, the problems have approximately 6100 decision variables and 54,000 constraints (Table 5). These are small-scale optimization problems that are solved in a competitive computational time.

It is possible to observe in Table 5 that there is a large variability in the downtime of the vehicles for the 12 instances. In fact, the downtime of the vehicles was on average 6475.4 min, with a standard deviation of 9072.7 min. The minimum was of 103.9 min for 2 June, and the maximum was of 30,655.5 min for 9 May.

For all instances, the downtime of the scheduling using the (1)–(12) model resulted in a reduction in the one obtained at the firm. On average, the downtime of the vehicles using the optimization model was 33% of the one observed at the firm. However, a standard deviation of 25.8% was observed, showing a large variability in the results, which occurs due to the large variety of instances that were tested, reflecting the everyday operation of the repair shop. Furthermore, in 11 of the 12 instances, the downtime of the vehicles is less than 50% of that observed on the firm. Furthermore, in six of the instances, it was less than 33%. This shows the quality of the scheduling obtained using the MILP model.

The average downtime of the firm was 16,221.3 min; while using the model, it was 6455.4 min, which corresponds to a 67% reduction. Furthermore, for 2 June, the total downtime of the vehicles using the scheduling yield by solving the (1)–(12) model represents only approximately 4.9% of the downtime of the firm. However, it is important to note that, on that day, the firm also conducted mechanical repairs on other vehicles, which were not included in this particular instance. Additionally, there were instances where vehicles could not be repaired due to the unavailability of certain mechanical parts at the repair shop. The second highest reduction in downtimes was of 91.1%, observed on 19 May, for which the downtime of the vehicle using the optimization model corresponds to only 8.9% of the downtime observed at the firm that day.

The opposite situation was observed for the 9 May instance. For this day, the downtimes of the firm and model are almost the same. In fact, the downtime using the model corresponded to 98.8% of the downtime observed at the company. The instance that presented the second lowest reduction in the downtimes of the vehicles was 5 June, with the model yielding 46.5% of the downtime observed at the firm.

The day for which the firm presented the largest number of vehicles and corresponding mechanical interventions was 5 June. Therefore, a more detailed analysis of the results for this instance will be presented.

The 33 vehicles that arrived at the repair shop on 5 June were repaired by the firm on 10 different days (see Figure 4, Figure 5 and Figure 6). Eighteen of the vehicles (namely car4816, car4819, car4821, car4825, car4827, car4829, car4830, car4831, car4832, car4833, car4836, car4837, car4838, car4839, car4843, car4844, car4845, and car4846) were repaired by the firm on the day of arrival (Figure 4) while the mechanical interventions on the remaining vehicles (i.e., car4817, car4818, car4820, car4822, car4823, car4824, car4826, car4828, car4834, car4835, car4840, car4841, car4842, car4847, and car4848) were only completed after (see Figure 5 and Figure 6). Large periods during which the vehicles are at the repair shop without being repaired can be observed for several vehicles.

Using the scheduling obtained using the MILP model, the repairs on all vehicles that arrived at the firm on 5 June would take place on only five different days (Figure 7 and Figure 8). Furthermore, the majority of the mechanical interventions were scheduled for 5 June.

In Figure 7, it can be seen that 5 of the 33 vehicles started to be intervened with immediately after completing the RO form. Furthermore, 17 of the 33 vehicles completed all the necessary mechanical repairs on the day of arrival (i.e., 5 June). Therefore, approximately 51.5% of the vehicles would be available to be delivered to the customers on the same day. The exceptions were the vehicles car4817, car4818, car4820, car4822, car4823, car4824, car4826, car4828, car4834, car4835, car4840, car4841, car4842, car4847, and car4848 (see Figure 8), for which the repairs continue beyond 5 June.

It is possible to observe that there are periods of time for which some vehicles are waiting to be repaired (Figure 7 and Figure 8). However, these are considerably less than those observed at the firm (Figure 4, Figure 5 and Figure 6). In fact, the downtimes of the vehicles arrived on 5 June, for the scheduling with the MILP model represents less than half (46.5%) of the downtime observed at the firm (see Table 4).

On 9 May as well as on 4 and 11 July, 29 vehicles arrived at the repair shop to be repaired. On those days, 71, 84, and 47 interventions had to be performed on the vehicles. As can be seen in Table 4 for July 11, the downtime using the schedule proposed by the MILP model would only be 10.4% of that observed in the firm, and for July 4, it would be 34.2%. These present a significant reduction in the downtime. However, for 9 May, the downtime of the vehicles using the schedule proposed by the MILP model would almost be the same as the one observed in the firm. Next, a close look at this case will be performed.

The 29 vehicles that arrived on 9 May were repaired by the firm on nine different days (Figure 9 and Figure 10). Furthermore, long periods of inactivity were observed for several vehicles.

Using the scheduling given by the MILP model, the repairs would also be scheduled on nine different days; however, the majority were scheduled on 9 May (Figure 11). Furthermore, only 8 of the 71 mechanical interventions were performed after 12 May (corresponding to 94,080 min).

As depicted in Figure 9 and Figure 10, almost 38% (11 in 29) of the vehicles were repaired on 9 May. The remaining ones (i.e., car4367, car4368, car4369, car4372, car4375, car4376, car4377, car4382, car4383, car4384, car4386, car4387, car4388, car4389, car4391, car4393, car4394, and car4395) were intervened with in the subsequent days.

Using the schedule obtained using the MILP model, 12 of the 29 vehicles started to be intervened with immediately after completing the RO form (see Figure 11). Among the 29 vehicles, 11 would be ready to be delivered to the customer on the same day of arrival (i.e., May 9). However, the remaining ones (namely the vehicles car4367, car4368, car4369, car4372, car4375, car4376, car4377, car4382, car4383, car4384, car4386, car4387, car4388, car4389, car4391, car4393, car4394, and car4395) would be ready for delivery after 9 May. It is also possible to observe that the interventions on each vehicle are performed with some breaks. In fact, the total downtime of the vehicles would be almost the same (98.8%) as the one obtained at the firm.

However, for 19 May and 2 June, using the MILP model, the total downtime of the vehicles would be only 4.9% and 8.9%, respectively, of those observed at the firm (see Table 5). A detailed description of the results found for these two instances can be found at [10].

Table 6. Comparison of the downtime of the vehicles that were observed at the firm with the ones using the scheduling given by the MILP model.

Day		Min	Mean	Median	Max	Total
May 9	Model	0.0	1057.1	328.7	9604.2	30,655.5
	Firm	3.0	1069.7	300.6	11,622.8	31,021.0
May 19	Model	0.0	15.1	2.8	92.9	271.6
	Firm	2.8	168.9	107.3	1011.0	3040.2
June 2	Model	0.0	8.0	0.0	60.0	103.9
	Firm	0.0	162.4	72.4	938.6	2111.6
June 5	Model	0.0	404.7	195.7	1669.8	13,355.9
	Firm	0.0	870.8	299.0	5674.0	28,735.8

shows the statistics on the downtime of the vehicles for the 9 and 19 of May and the 2 and 5 June, as observed at the firm and proposed by the MILP model.

On 9 and 19 May, the lowest downtimes registered at the firm in a vehicle were 3.0 and 2.8 min, respectively. For 2 and 5 June, there was no downtime. In contrast, for 9 and 19 May, the highest downtime registered at the firm was 11,622.8 min and 1011 min, while for 2 and 5 June, the maximum downtime of a vehicle was 938.6 min and 5674 min.

Regarding the downtime of the vehicles, the schedule proposed by the MILP model saw that vehicles started being repaired as soon as they arrived at the repair shop, for 9 and 19 May and 2 and 5 June, and their repairs were performed without any inactivity (see Table 6). The vehicles with the highest downtime, would be of 9604.2, 92.9, 60, and 1669.8 min, for 9 and 19 May, and 2 and 5 June, respectively. These downtimes are considerably smaller than those observed at the firm.

For 9 and 19 May and 2 and 5 June, on average, the firm registered a downtime per vehicle of 1069.7, 168.9, 162.4, and 870.8 min, respectively. Whereas the schedule proposed by the MILP model would present a downtime per vehicle of only 1057.1, 15.1, 8, and 404.7 min.

Furthermore, for half of the vehicles, the downtime was at most 107.3 min at the firm and only 2.8 min using the MILP model for 19 May. For 2 June, half of the vehicles in the firm presented downtimes of at most 72.4 min, while there would be no downtime if the MILP model was used. Furthermore, for 5 June, a comparison of the downtime for half of the vehicles observed on the firm and proposed by the model shows a large reduction (from 299.0 min for the firm vs. 195.7 min for the model). In contrast, for 9 May, the median downtime would be larger if the MILP model was used.

6. Conclusions and Future Work

Scheduling theory has been the subject of significant interest among OR practitioners, management scientists, production and operations research workers, as well as mathematicians since the early 1950s [3]. The allocation of resources to perform a set of tasks during a specific time period, known as scheduling, poses varying levels of complexity depending on the problem’s environment, process constraints, and desired performance measures [4,5].

The empirical work, based on real data addressed in this paper, falls within the context of the FJSP, which is an extension of the JSP. In the FJSP, operations can be processed on any machine from a set of alternative machines, adding a routing sub-problem that involves assigning machines to process each operation, in addition to the scheduling sub-problem of sequencing the assigned operations [14]. This extension makes the FJSP more complex than the JSP, requiring a comprehensive approach to tackle the routing and scheduling aspects simultaneously.

In the present study, the results on 12 real instances are presented and discussed. An MILP model, initially proposed in [10], is used to schedule each of the mechanical repairs of the vehicles.

The primary objective of this study was to minimize the downtime between interventions performed on vehicles and reduce the overall time that vehicles remain without any ongoing intervention. The focus was on optimizing the scheduling process to ensure the efficient utilization of resources and minimize idle time for vehicles, thus improving the overall productivity of the repair shop.

For all 12 real instances, it was possible to obtain the optimal solution to the corresponding problems. The downtime of the vehicles would decrease on average by 67% if the schedule proposed by the MILP model would be used. Furthermore, in 11 of the 12 instances, the reduction would be of more than 50% in comparison to that observed at the firm.

The results of the case study in the Portuguese automobile sector demonstrate the potential benefits of using MILP to optimize repair schedules. The method was able to significantly reduce the time that vehicles spend in the shop, which can lead to the higher satisfaction of the customers and to increased profitability for the repair shop.

One important consideration when using MILP for vehicle repair scheduling is the need to balance conflicting objectives, such as minimizing vehicle downtime and maximizing mechanic utilization. This requires the careful consideration of factors such as the number of available mechanics, the skill levels of each mechanic, and the availability of repair bays.

Another important factor to consider when using MILP is the need to constantly update the model with new data. This can include information about the number of vehicles currently in the shop, the availability of mechanics, and the estimated repair times for each vehicle. By keeping the model up-to-date, repair shops can ensure that they are making the most informed decisions possible.

In future work, the developed model can be further refined to minimize the downtimes of the mechanics and maximize their work by considering factors such as the mechanic breaks and interventions of vehicles that arrived in the repair shop on previous days. Additionally, exploring the integration of deep learning techniques with the optimization model could enhance the modeling ability and improve the overall scheduling performance.

Deep learning has emerged as a highly promising method in various fields, including data mining, computer vision, natural language processing, and demand prediction. It has demonstrated the potential to complement optimization models and enhance their effectiveness. For instance, studies such as [59,60] have showcased the successful combination of deep learning and optimization techniques.

Therefore, future research in this area could explore the integration of deep learning methods, such as neural networks, with the developed optimization model. This approach could potentially improve the accuracy and efficiency of scheduling decisions by leveraging the power of deep learning in analyzing complex data patterns and making informed predictions.

Moreover, expanding the scope of the optimization model to consider additional factors can lead to more comprehensive and realistic scheduling solutions. Factors such as the availability of spare parts, the scheduling of routine maintenance tasks, and the influence of weather and traffic conditions on repair times should be incorporated into the model. By accounting for these factors, repair shops can further enhance their efficiency and effectiveness in managing their operations.

In summary, future research efforts should aim to refine the developed model by integrating deep learning techniques and considering a broader range of factors. This approach will contribute to the continuous improvement of repair shop scheduling, enabling better resource allocation, reduced downtimes, and enhanced overall performance. By leveraging the potential of advanced modeling approaches, repair shops can strive for higher levels of efficiency, customer satisfaction, and operational excellence.