Optical Solitons and Modulation Instability Analysis with Lakshmanan–Porsezian–Daniel Model Having Parabolic Law of Self-Phase Modulation
Abstract
1. Introduction
2. Governing Model
3. Optical Soliton Solutions
3.1. Auxiliary Equation Method
- Set 1From (26), one can retrieve the general form of the Jacobi elliptic function (JEF) solutions of Equation (20) asprovided that and . Hence, the relations (3) and (19) lead to the general solution of Equation (2) aswhere provided that and .Making use of some of Jacobi elliptic functions, we can obtain the following types of solutions:Case 1. If , then . Subsequently, we extract JEF solutions of Equation (2) in the formwhere . As , solution (29) degenerates to soliton solutions given bywhere .Case 2. If , then . Accordingly, the JEF solutions of Equation (2) are written aswhere . As , solution (31) gives rise to soliton solutions given bywhere .Case 3. If , then . Thus, we end up with JEF solutions of Equation (2) in the formwhere . As , solution (33) reduces to soliton solutions given bywhere .Case 4. If , then . In consequence, we obtain JEF solutions of Equation (2) aswhere . As , solution (35) is converted into singular soliton solutions given bywhere .
- Set 2From (41), the general form of JEF solutions of Equation (20) can be expressed asprovided that and . By virtue of relations (3) and (19), the general solution of Equation (2) is written aswhere provided that and . Thus, implementing some of the Jacobi elliptic functions generates distinct types of solutions displayed as follows.Case 1. If , then . Hence, we secure JEF solutions of Equation (2) aswhere . As , solution (44) degenerates to soliton solutions aswhere .Case 2. If , then . Therefore, we arrive at JEF solutions of Equation (2) given bywhere provided that . As , solution (46) is converted to soliton solutions in the formwhere .Case 3. If , then . As a consequence, we obtain JEF solutions of Equation (2) as followswhere provided that . As , solution (48) reduces to the soliton solutions aswhere .Case 4. If , then . Subsequently, we obtain JEF solutions of Equation (2) with the formwhere . As , solution (50) gives rise to singular soliton solutions aswhere .
3.2. Bernoulli Sub-ODE Method
- Set 1
- Set 2
- Set 3
- Set 4
- Set 5
- Set 6
- Set 7
4. Modulation Instability Analysis
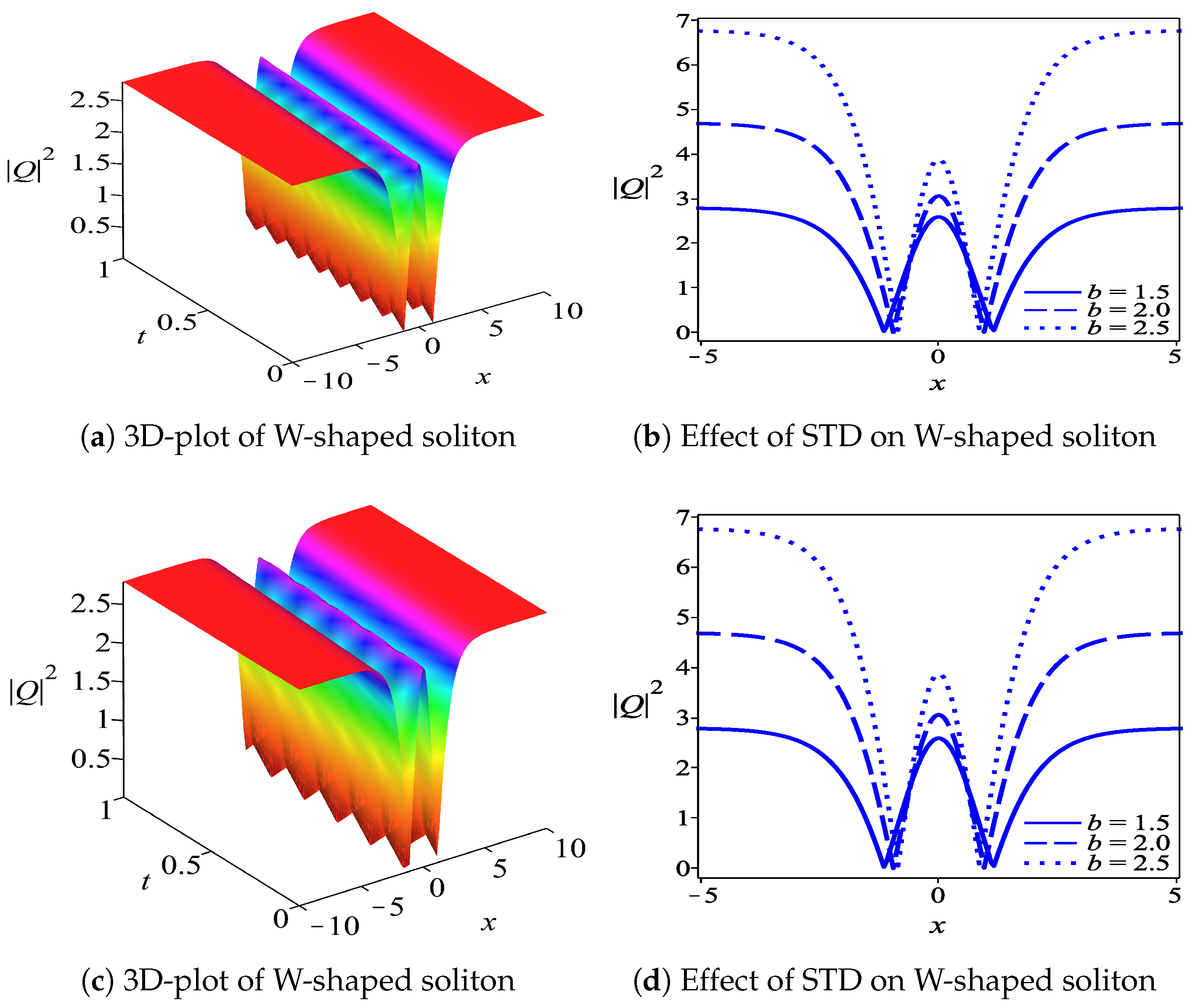
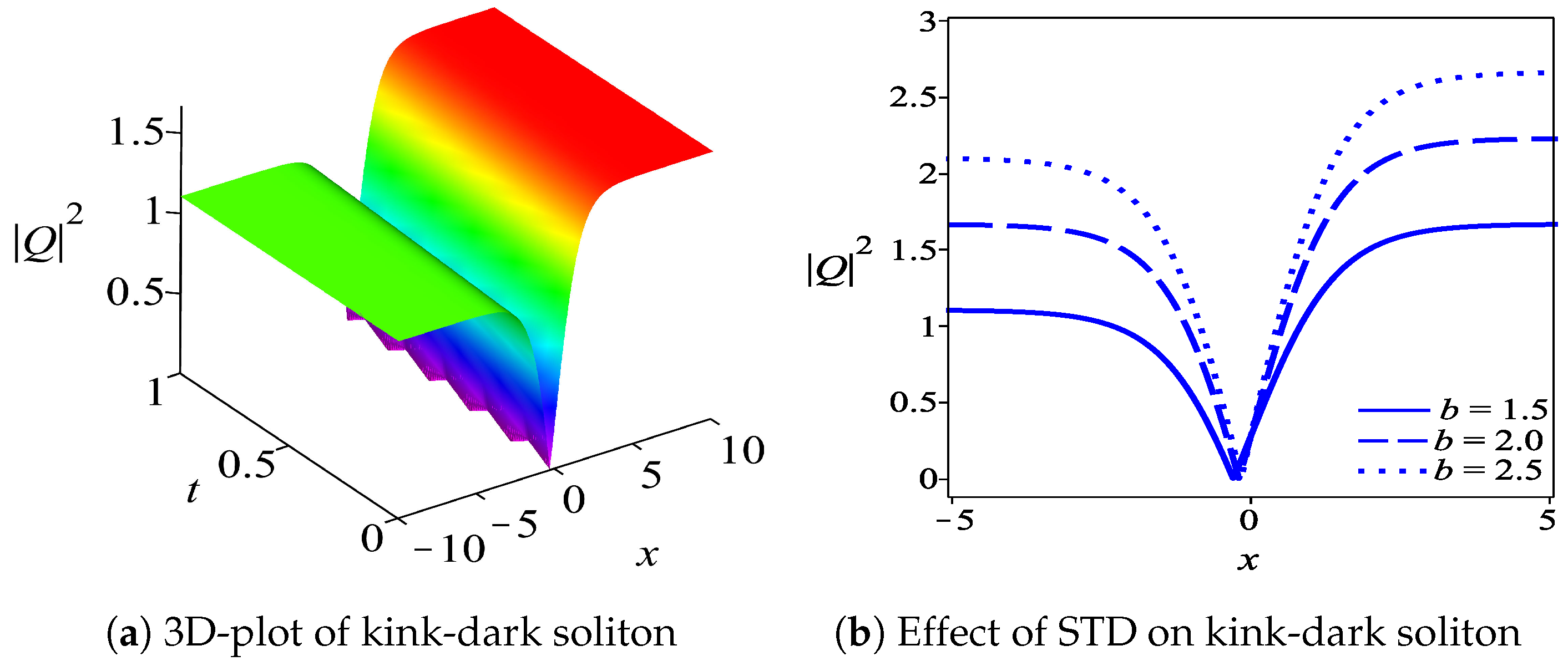
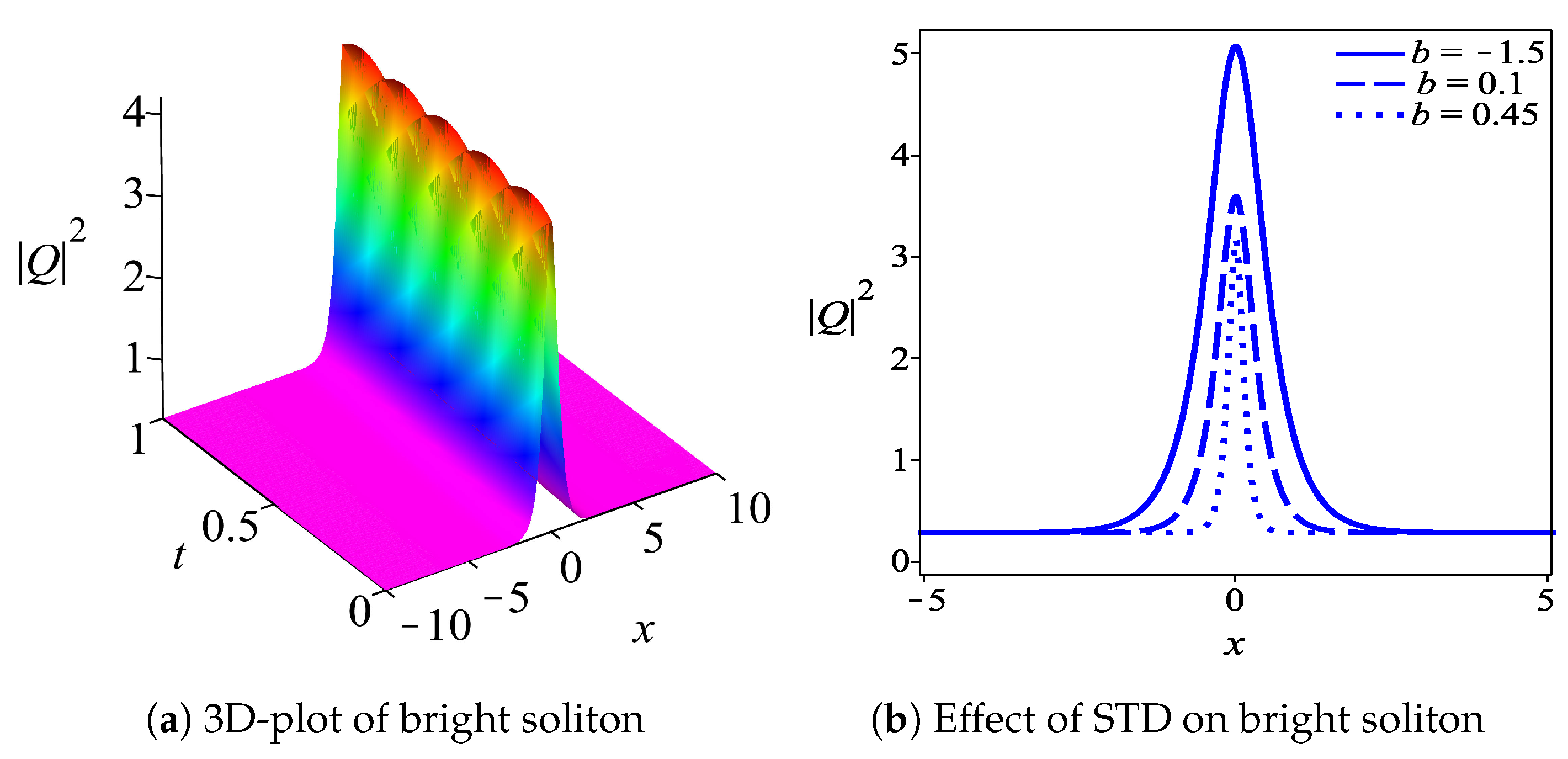
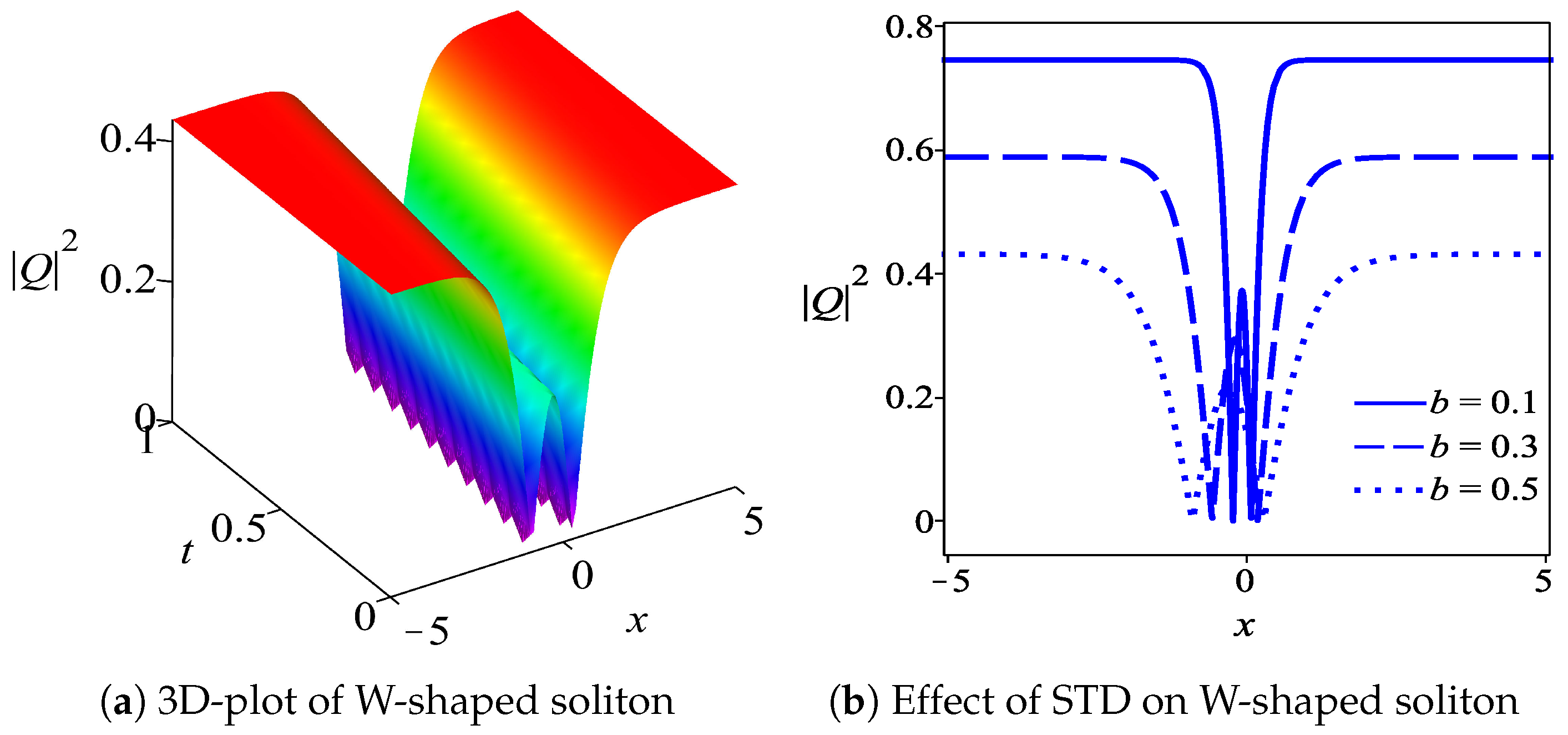
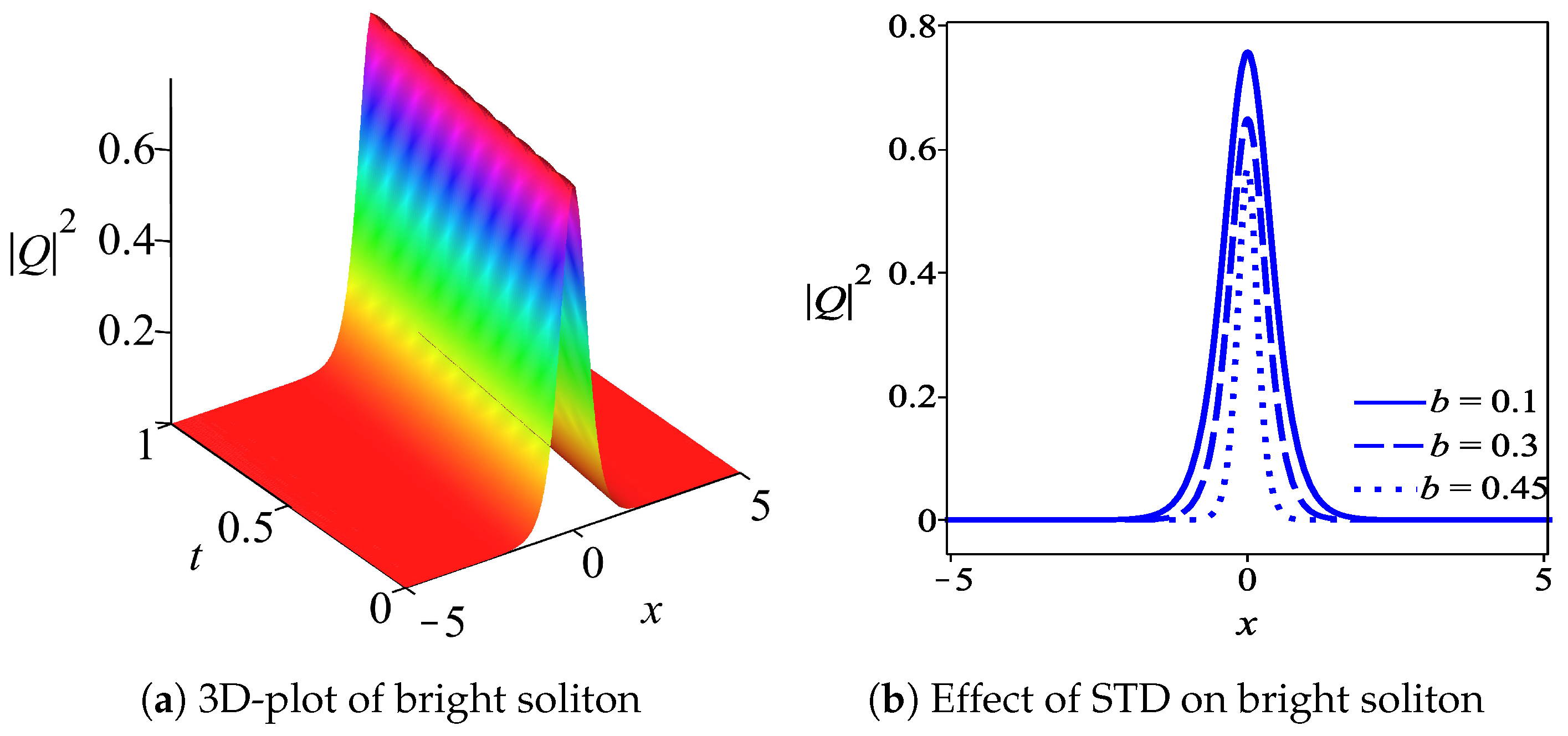
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hasegawa, A. Massive WDM and TDM Soliton Transmission Systems: A ROSC Symposium; Kluwer Academic: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Smith, F.G.; King, T.A.; Wilkins, D. Optics and Photonics: An Introduction; John Wiley & Sons: Chichester, UK, 2007. [Google Scholar]
- Sadegh Amiri, I.; Alavi, S.E.; Mahdaliza Idrus, S. Introduction of fiber waveguide and soliton signals used to enhance the communication security. In Soliton Coding for Secured Optical Communication Link; Springer: Singapore, 2015; pp. 1–16. [Google Scholar]
- Bhadra, S.; Ghatak, A. Guided Wave Optics and Photonic Devices; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Triki, H.; Wazwaz, A.M. New types of chirped soliton solutions for the Fokas–Lenells equation. Int. J. Number Method Heat Fluid Flow 2017, 27, 1596–1601. [Google Scholar] [CrossRef]
- Zayed, E.M.; Alngar, M.E.; Biswas, A.; Yıldırım, Y.; Khan, S.; Alzahrani, A.K.; Belic, M.R. Cubic–quartic optical soliton perturbation in polarization-preserving fibers with Fokas–Lenells equation. Optik 2021, 234, 166543. [Google Scholar] [CrossRef]
- Al-Ghafri, K.S.; Krishnan, E.V.; Biswas, A. Cubic–quartic optical soliton perturbation and modulation instability analysis in polarization-controlled fibers for Fokas–Lenells equation. J. Eur. Opt. Soc. 2022, 18, 9. [Google Scholar] [CrossRef]
- Arshed, S. Two reliable techniques for the soliton solutions of perturbed Gerdjikov–Ivanov equation. Optik 2018, 164, 93–99. [Google Scholar] [CrossRef]
- Yaşar, E.; Yıldırım, Y.; Yaşar, E. New optical solitons of space-time conformable fractional perturbed Gerdjikov-Ivanov equation by sine-Gordon equation method. Results Phys. 2018, 9, 1666–1672. [Google Scholar] [CrossRef]
- Al-Kalbani, K.K.; Al-Ghafri, K.; Krishnan, E.; Biswas, A. Solitons and modulation instability of the perturbed Gerdjikov–Ivanov equation with spatiotemporal dispersion. Chaos Solitons Fractals 2021, 153, 111523. [Google Scholar] [CrossRef]
- Biswas, A.; Jawad, A.J.M.; Manrakhan, W.N.; Sarma, A.K.; Khan, K.R. Optical solitons and complexitons of the Schrödinger–Hirota equation. Opt. Laser Technol. 2012, 44, 2265–2269. [Google Scholar] [CrossRef]
- Arnous, A.H.; Ullah, M.Z.; Asma, M.; Moshokoa, S.P.; Zhou, Q.; Mirzazadeh, M.; Biswas, A.; Belic, M. Dark and singular dispersive optical solitons of Schrödinger–Hirota equation by modified simple equation method. Optik 2017, 136, 445–450. [Google Scholar] [CrossRef]
- Kilic, B.; Inc, M. Optical solitons for the Schrödinger–Hirota equation with power law nonlinearity by the Bäcklund transformation. Optik 2017, 138, 64–67. [Google Scholar] [CrossRef]
- Kaur, L.; Wazwaz, A.M. Bright–dark optical solitons for Schrödinger-Hirota equation with variable coefficients. Optik 2019, 179, 479–484. [Google Scholar] [CrossRef]
- Liang, G.; Liu, J.; Hu, W.; Guo, Q. Unique features of nonlocally nonlinear systems with oscillatory responses. Appl. Sci. 2022, 12, 2386. [Google Scholar] [CrossRef]
- Shen, S.; Yang, Z.J.; Pang, Z.G.; Ge, Y.R. The complex-valued astigmatic cosine-Gaussian soliton solution of the nonlocal nonlinear Schrödinger equation and its transmission characteristics. Appl. Math. Lett. 2022, 125, 107755. [Google Scholar] [CrossRef]
- Lu, Z.; Tu, J.; Zhen, W.; He, S.; Wang, J.; Yan, J.; Zhang, Y.; Deng, D. Propagation properties of the superimposed chirped Bessel–Gaussian vortex beams in strongly nonlocal nonlinear medium. Opt. Commun. 2022, 516, 128238. [Google Scholar] [CrossRef]
- Justin, M.; David, V.; Shahen, N.H.M.; Sylvere, A.S.; Rezazadeh, H.; Inc, M.; Betchewe, G.; Doka, S.Y. Sundry optical solitons and modulational instability in Sasa-Satsuma model. Opt. Quantum. Electron. 2022, 54, 81. [Google Scholar] [CrossRef]
- Shahen, N.H.M.; Ali, M.S.; Rahman, M. Interaction among lump, periodic, and kink solutions with dynamical analysis to the conformable time-fractional Phi-four equation. Part. Diff. Equ. Appl. Math. 2021, 4, 100038. [Google Scholar] [CrossRef]
- Shahen, N.H.M.; Bashar, M.H.; Tahseen, T.; Hossain, S. Solitary and rogue wave solutions to the conformable time fractional modified kawahara equation in mathematical physics. Adv. Math. Phys. 2021, 2021, 6668092. [Google Scholar] [CrossRef]
- An, T.; Shahen, N.H.M.; Ananna, S.N.; Hossain, M.F.; Muazu, T. Exact and explicit travelling-wave solutions to the family of new 3D fractional WBBM equations in mathematical physics. Results Phys. 2020, 19, 103517. [Google Scholar] [CrossRef]
- Shahen, N.H.M.; Rahman, M. Dispersive solitary wave structures with MI Analysis to the unidirectional DGH equation via the unified method. Part. Diff. Equ. Appl. Math. 2022, 6, 100444. [Google Scholar] [CrossRef]
- Lakshmanan, M.; Porsezian, K.; Daniel, M. Effect of discreteness on the continuum limit of the Heisenberg spin chain. Phys. Lett. A 1988, 133, 483–488. [Google Scholar] [CrossRef]
- Biswas, A.; Yildirim, Y.; Yasar, E.; Zhou, Q.; Moshokoa, S.P.; Belic, M. Optical solitons for Lakshmanan–Porsezian–Daniel model by modified simple equation method. Optik 2018, 160, 24–32. [Google Scholar] [CrossRef]
- Akram, G.; Sadaf, M.; Dawood, M.; Baleanu, D. Optical solitons for Lakshmanan–Porsezian–Daniel equation with Kerr law non-linearity using improved tanψ (η) 2-expansion technique. Results Phys. 2021, 29, 104758. [Google Scholar] [CrossRef]
- Vega-Guzman, J.; Alqahtani, R.T.; Zhou, Q.; Mahmood, M.F.; Moshokoa, S.P.; Ullah, M.Z.; Biswas, A.; Belic, M. Optical solitons for Lakshmanan–Porsezian–Daniel model with spatiotemporal dispersion using the method of undetermined coefficients. Optik 2017, 144, 115–123. [Google Scholar] [CrossRef]
- Alqahtani, R.T.; Babatin, M.; Biswas, A. Bright optical solitons for Lakshmanan-Porsezian-Daniel model by semi-inverse variational principle. Optik 2018, 154, 109–114. [Google Scholar] [CrossRef]
- Biswas, A.; Ekici, M.; Sonmezoglu, A.; Triki, H.; Majid, F.B.; Zhou, Q.; Moshokoa, S.P.; Mirzazadeh, M.; Belic, M. Optical solitons with Lakshmanan–Porsezian–Daniel model using a couple of integration schemes. Optik 2018, 158, 705–711. [Google Scholar] [CrossRef]
- Javid, A.; Raza, N. Singular and dark optical solitons to the well posed Lakshmanan–Porsezian–Daniel model. Optik 2018, 171, 120–129. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Mirzazadeh, M.; Mirhosseini-Alizamini, S.M.; Neirameh, A.; Eslami, M.; Zhou, Q. Optical solitons of Lakshmanan–Porsezian–Daniel model with a couple of nonlinearities. Optik 2018, 164, 414–423. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Kumar, D.; Neirameh, A.; Eslami, M.; Mirzazadeh, M. Applications of three methods for obtaining optical soliton solutions for the Lakshmanan–Porsezian–Daniel model with Kerr law nonlinearity. Pramana 2020, 94, 39. [Google Scholar] [CrossRef]
- Manafian, J.; Foroutan, M.; Guzali, A. Applications of the ETEM for obtaining optical soliton solutions for the Lakshmanan-Porsezian-Daniel model. Eur. Phys. J. Plus 2017, 132, 494. [Google Scholar] [CrossRef]
- Arshed, S.; Biswas, A.; Majid, F.B.; Zhou, Q.; Moshokoa, S.P.; Belic, M. Optical solitons in birefringent fibers for Lakshmanan–Porsezian–Daniel model using exp (-ϕ (ξ))-expansion method. Optik 2018, 170, 555–560. [Google Scholar] [CrossRef]
- El-Sheikh, M.; Ahmed, H.M.; Arnous, A.H.; Rabie, W.B.; Biswas, A.; Alshomrani, A.S.; Ekici, M.; Zhou, Q.; Belic, M.R. Optical solitons in birefringent fibers with Lakshmanan–Porsezian–Daniel model by modified simple equation. Optik 2019, 192, 162899. [Google Scholar] [CrossRef]
- AlQarni, A.; Ebaid, A.; Alshaery, A.; Bakodah, H.; Biswas, A.; Khan, S.; Ekici, M.; Zhou, Q.; Moshokoa, S.P.; Belic, M.R. Optical solitons for Lakshmanan–Porsezian–Daniel model by Riccati equation approach. Optik 2019, 182, 922–929. [Google Scholar] [CrossRef]
- Rizvi, S.T.R.; Ali, K.; Akram, U.; Younis, M. Analytical study of solitons for Lakshmanan–Porsezian–Daniel model with parabolic law nonlinearity. Optik 2018, 168, 27–33. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Kalbani, K.K.; Al-Ghafri, K.S.; Krishnan, E.V.; Biswas, A. Optical Solitons and Modulation Instability Analysis with Lakshmanan–Porsezian–Daniel Model Having Parabolic Law of Self-Phase Modulation. Mathematics 2023, 11, 2471. https://doi.org/10.3390/math11112471
Al-Kalbani KK, Al-Ghafri KS, Krishnan EV, Biswas A. Optical Solitons and Modulation Instability Analysis with Lakshmanan–Porsezian–Daniel Model Having Parabolic Law of Self-Phase Modulation. Mathematics. 2023; 11(11):2471. https://doi.org/10.3390/math11112471
Chicago/Turabian StyleAl-Kalbani, Kaltham K., Khalil S. Al-Ghafri, Edamana V. Krishnan, and Anjan Biswas. 2023. "Optical Solitons and Modulation Instability Analysis with Lakshmanan–Porsezian–Daniel Model Having Parabolic Law of Self-Phase Modulation" Mathematics 11, no. 11: 2471. https://doi.org/10.3390/math11112471
APA StyleAl-Kalbani, K. K., Al-Ghafri, K. S., Krishnan, E. V., & Biswas, A. (2023). Optical Solitons and Modulation Instability Analysis with Lakshmanan–Porsezian–Daniel Model Having Parabolic Law of Self-Phase Modulation. Mathematics, 11(11), 2471. https://doi.org/10.3390/math11112471