An Epidemiological Model for Tuberculosis Considering Environmental Transmission and Reinfection
Abstract
:1. Introduction
2. Model Building
3. Mathematical Model Analysis
3.1. Positivity of Solutions
3.2. Boundedness
4. Disease-Free Equilibrium Point and Basic Regeneration Number [32,33]
4.1. Existence of Disease-Free Equilibrium Points
4.2. Basic Regeneration Number
4.3. Stability of Disease-Free Equilibrium Points
4.3.1. Local Asymptotic Stability of Disease-Free Equilibrium Points
4.3.2. Global Stability of Disease-Free Equilibrium Points
5. Existence and Global Stability of Endemic Equilibrium Points
5.1. Existence of Local Equilibrium Points
- 1.
- A particular endemic equilibrium when cases 1–3 and are met;
- 2.
- One endemic equilibrium or many endemic equilibriums when and instances 5–7 are met;
- 3.
- No endemic equilibrium when and case 8 shows that all coefficients are positive.
5.2. Global Stability of Local Equilibrium Points
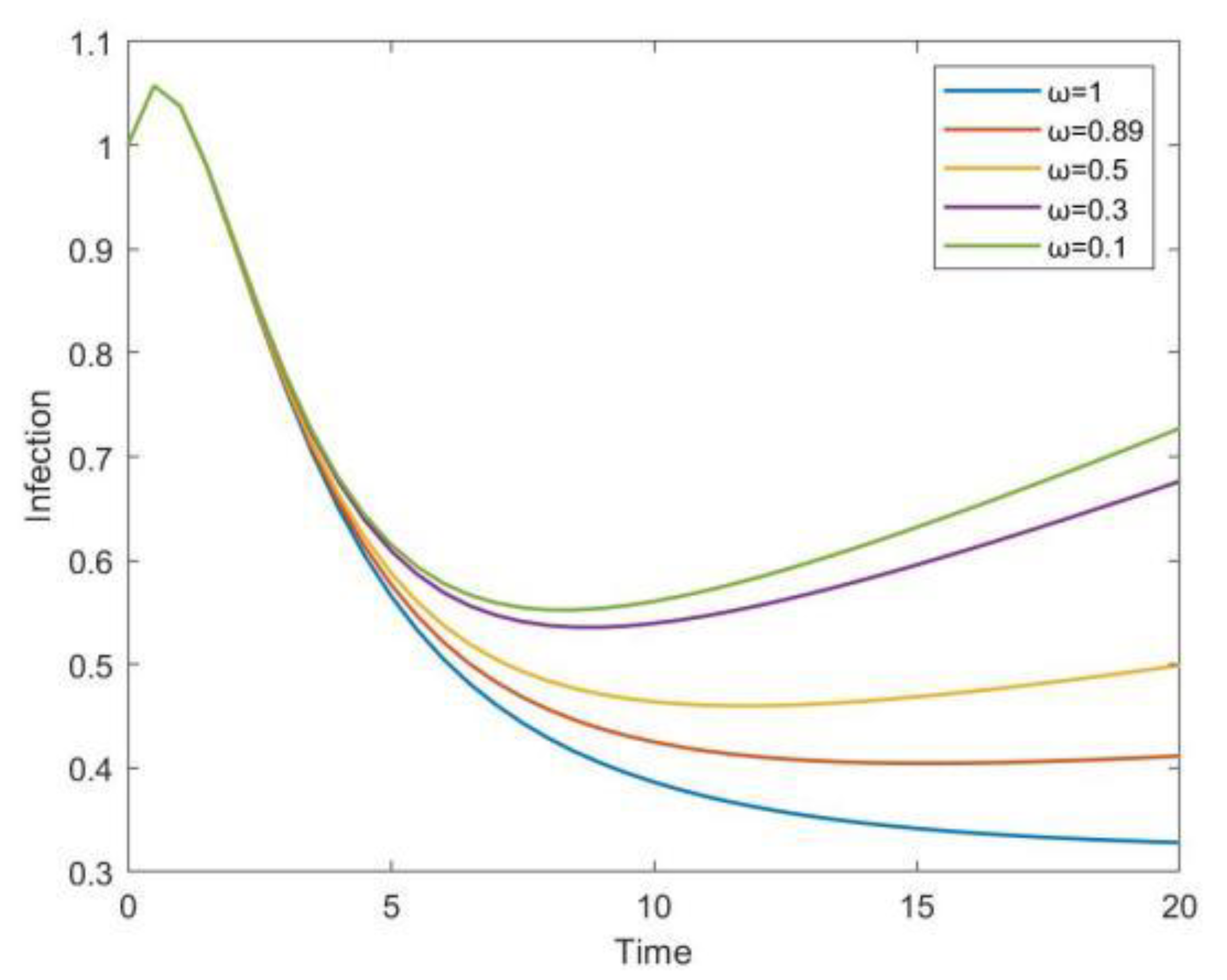
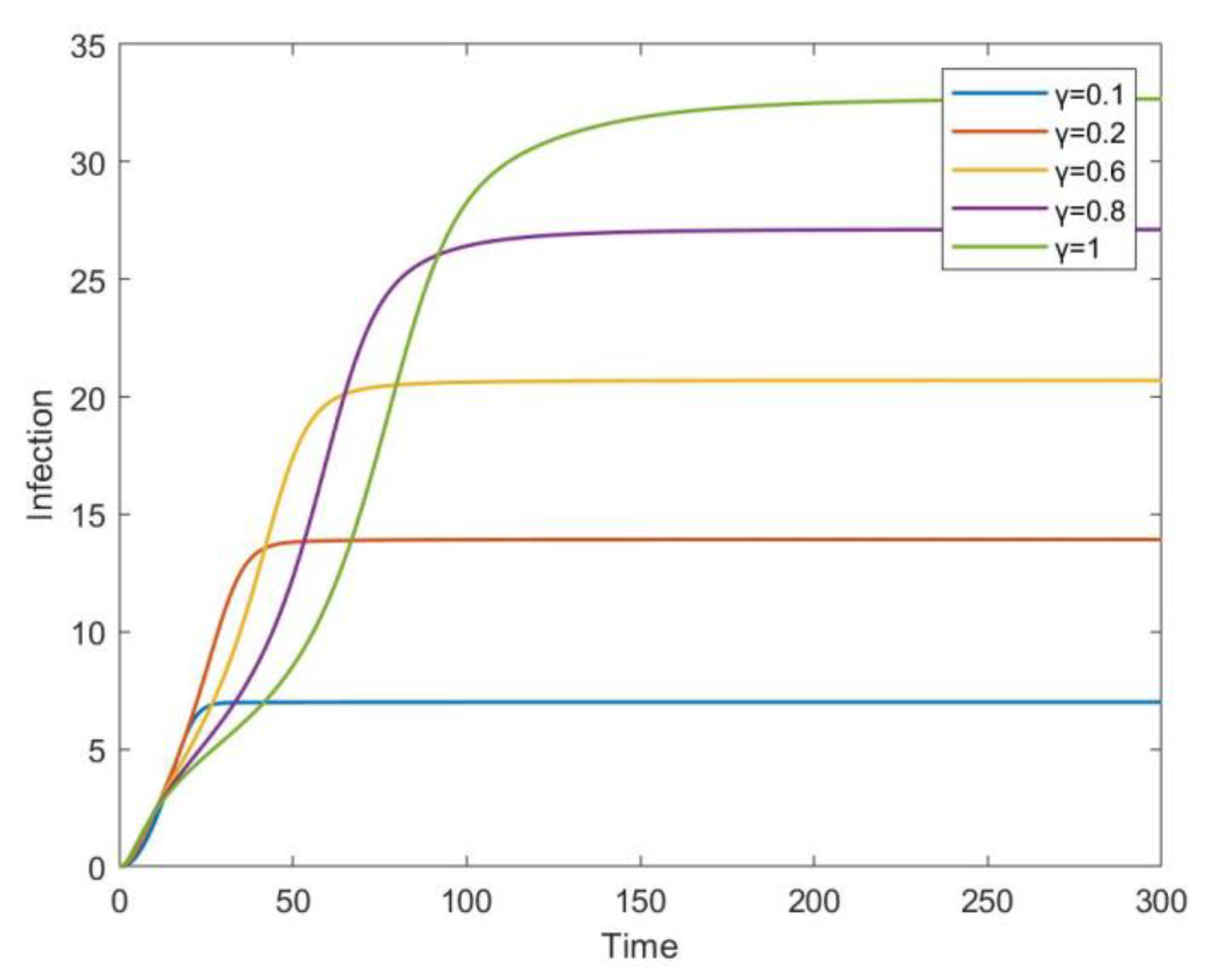
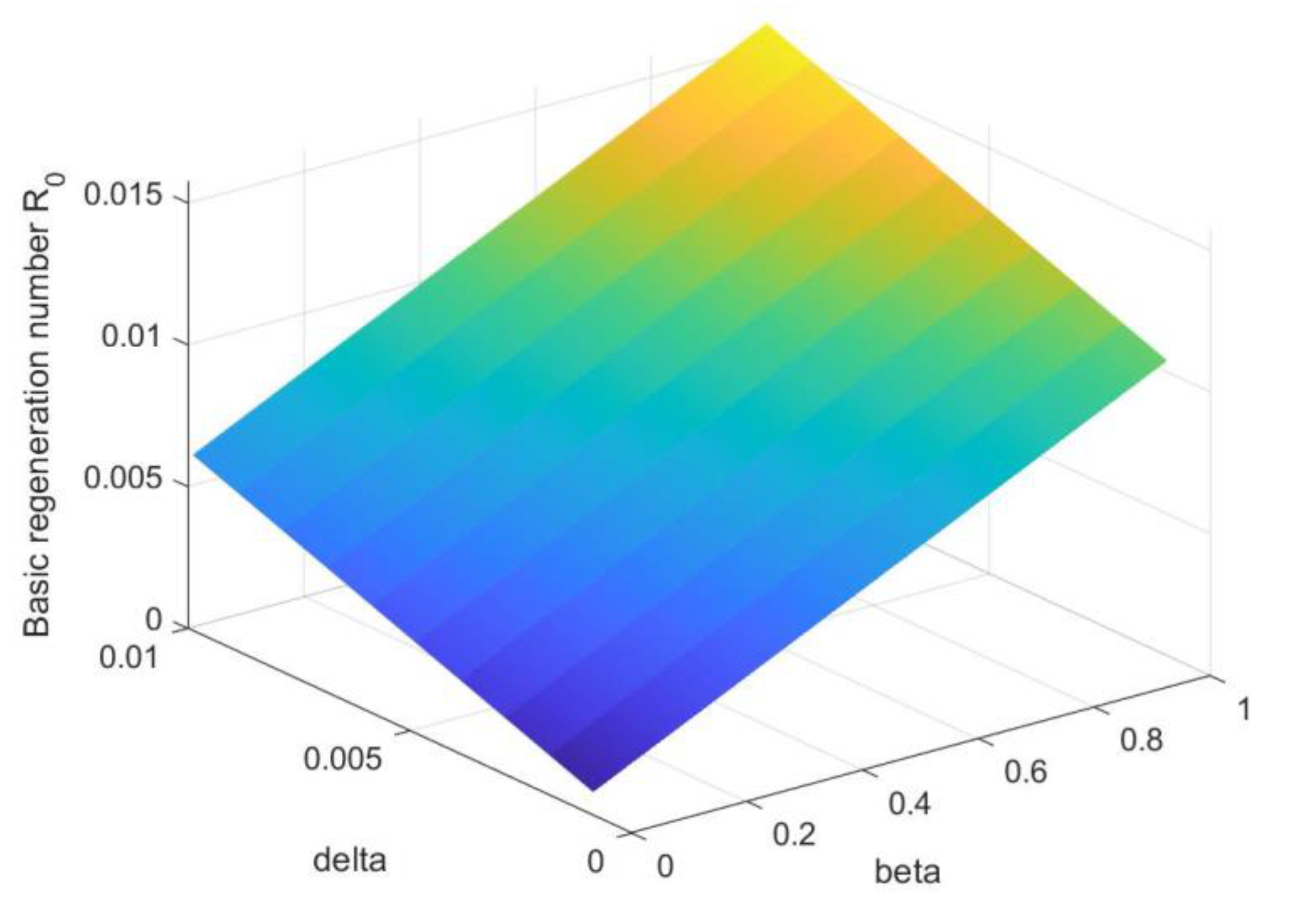
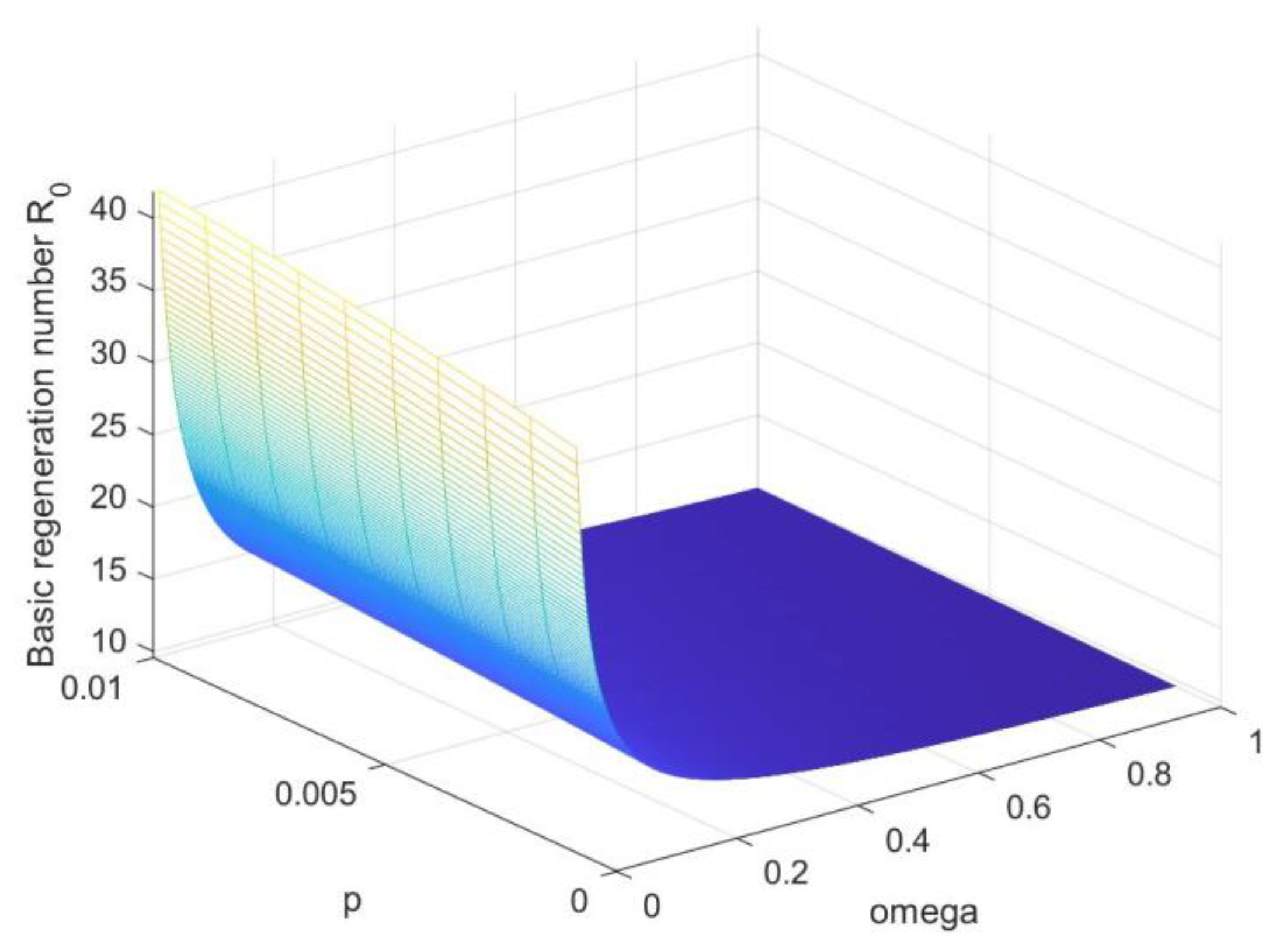
6. Numerical Simulation and Discussion
7. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Castillo-Chavez, C.; Feng, Z. To Treat or Not to Treat: The Case of Tuberculosis. J. Math. Biol. 1997, 35, 629–656. [Google Scholar] [CrossRef]
- Global Tuberculosis Report 2022. Available online: https://www.who.int/teams/global-tuberculosis-programme/tb-reports/global-tuberculosis-report-2022 (accessed on 13 March 2023).
- Adewale, S.O.; Podder, C.N.; Gumel, A.B. Mathematical Analysis of a TB Transmission Model with DOTS. Can. Appl. Math. Q. 2009, 17, 1–36. [Google Scholar]
- Behr, M.A.; Kaufmann, E.; Duffin, J.; Edelstein, P.H.; Ramakrishnan, L. Latent Tuberculosis: Two Centuries of Confusion. Am. J. Respir. Crit. Care Med. 2021, 204, 142–148. [Google Scholar] [CrossRef]
- Shen, G.; Xue, Z.; Shen, X.; Sun, B.; Gui, X.; Shen, M.; Mei, J.; Gao, Q. Recurrent Tuberculosis and Exogenous Reinfection, Shanghai, China. Emerg. Infect. Dis. 2006, 12, 1776. [Google Scholar] [CrossRef]
- Chiang, C.-Y.; Riley, L.W. Exogenous Reinfection in Tuberculosis. Lancet Infect. Dis. 2005, 5, 629–636. [Google Scholar] [CrossRef]
- Shen, X.; Yang, C.; Wu, J.; Lin, S.; Gao, X.; Wu, Z.; Tian, J.; Gan, M.; Luo, T.; Wang, L.; et al. Recurrent Tuberculosis in an Urban Area in China: Relapse or Exogenous Reinfection? Tuberculosis 2017, 103, 97–104. [Google Scholar] [CrossRef] [PubMed]
- Feng, Z.; Castillo-Chavez, C.; Capurro, A.F. A Model for Tuberculosis with Exogenous Reinfection. Theor. Popul. Biol. 2000, 57, 235–247. [Google Scholar] [CrossRef]
- Khajanchi, S.; Das, D.K.; Kar, T.K. Dynamics of Tuberculosis Transmission with Exogenous Reinfections and Endogenous Reactivation. Phys. A Stat. Mech. Its Appl. 2018, 497, 52–71. [Google Scholar] [CrossRef]
- Adebimpe, O.; Bashiru, K.A.; Ojurongbe, T.A. Stability Analysis of an SIR Epidemic Model with Non-Linear Incidence Rate and Treatment. Open J. Model. Simul. 2015, 3, 104–110. [Google Scholar] [CrossRef]
- Schrager, L.K.; Vekemens, J.; Drager, N.; Lewinsohn, D.M.; Olesen, O.F. The Status of Tuberculosis Vaccine Development. Lancet Infect. Dis. 2020, 20, e28–e37. [Google Scholar] [CrossRef] [PubMed]
- Xu, R. Global Dynamics of a Delayed Epidemic Model with Latency and Relapse. NAMC 2013, 18, 250–263. [Google Scholar] [CrossRef]
- Bowong, S.; Tewa, J.J. Global Analysis of a Dynamical Model for Transmission of Tuberculosis with a General Contact Rate. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 3621–3631. [Google Scholar] [CrossRef]
- Feng, Z.; Velasco-Hernandez, J.; Tapia-Santos, B. A Mathematical Model for Coupling Within-Host and between-Host Dynamics in an Environmentally-Driven Infectious Disease. Math. Biosci. 2013, 241, 49–55. [Google Scholar] [CrossRef] [PubMed]
- Dushoff, J. Incorporating Immunological Ideas in Epidemiological Models. J. Theor. Biol. 1996, 180, 181–187. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.-D.; Huo, H.-F.; Xiang, H.; Zhang, Y.-D.; Huo, H.-F.; Xiang, H. Dynamics of Tuberculosis with Fast and Slow Progression and Media Coverage. MBE 2019, 16, 1150–1170. [Google Scholar] [CrossRef] [PubMed]
- Hadeler, K.P.; Van den Driessche, P. Backward Bifurcation in Epidemic Control. Math. Biosci. 1997, 146, 15–35. [Google Scholar] [CrossRef]
- Gumel, A.B. Causes of Backward Bifurcations in Some Epidemiological Models. J. Math. Anal. Appl. 2012, 395, 355–365. [Google Scholar] [CrossRef]
- Greenhalgh, D.; Diekmann, O.; de Jong, M.C.M. Subcritical Endemic Steady States in Mathematical Models for Animal Infections with Incomplete Immunity. Math. Biosci. 2000, 165, 1–25. [Google Scholar] [CrossRef]
- Chekroun, A.; Frioui, M.N.; Kuniya, T.; Touaoula, T. Global Stability of an Age-Structured Epidemic Model with General Lyapunov Functional. Math. Biosci. Eng. 2019, 16, 1525–1553. [Google Scholar] [CrossRef]
- Omame, A.; Okuonghae, D.; Umana, R.A.; Inyama, S.C. Analysis of a Co-Infection Model for HPV-TB. Appl. Math. Model. 2020, 77, 881–901. [Google Scholar] [CrossRef]
- Roeger, L.-I.W.; Feng, Z.; Castillo-Chavez, C. Modeling TB and HIV Co-Infections. Math. Biosci. Eng. 2009, 6, 815–837. [Google Scholar]
- Gumel, A.B.; Song, B. Existence of Multiple-Stable Equilibria for a Multi-Drug-Resistant Model of Mycobacterium Tuberculosis. Math. Biosci. Eng. 2008, 5, 437–455. [Google Scholar] [PubMed]
- Sulayman, F.; Abdullah, F.A.; Mohd, M.H. An SVEIRE Model of Tuberculosis to Assess the Effect of an Imperfect Vaccine and Other Exogenous Factors. Mathematics 2021, 9, 327. [Google Scholar] [CrossRef]
- Ding, Z.; Li, Y.; Wang, X.; Li, H.; Cai, Y.; Wang, B.; Wang, K.; Wang, W.; Ding, Z.; Li, Y.; et al. The Impact of Air Pollution on the Transmission of Pulmonary Tuberculosis. MBE 2020, 17, 4317–4327. [Google Scholar] [CrossRef]
- Li, M.; Ma, J.; van den Driessche, P. Model for Disease Dynamics of a Waterborne Pathogen on a Random Network. J. Math. Biol. 2015, 71, 961–977. [Google Scholar] [CrossRef]
- Frontiers. The Transmission Dynamics of the Monkeypox Virus in the Presence of Environmental Transmission. Available online: https://www.frontiersin.org/articles/10.3389/fams.2022.1061546/full (accessed on 11 May 2023).
- Kumari, P.; Singh, S.; Singh, H.P. Dynamical Analysis of COVID-19 Model Incorporating Environmental Factors. Iran. J. Sci. Technol. Trans. A Sci. 2022, 46, 1651–1666. [Google Scholar] [CrossRef]
- Addai, E.; Ngungu, M.; Omoloye, M.A.; Marinda, E.; Addai, E.; Ngungu, M.; Omoloye, M.A.; Marinda, E. Modelling the Impact of Vaccination and Environmental Transmission on the Dynamics of Monkeypox Virus under Caputo Operator. MBE 2023, 20, 10174–10199. [Google Scholar] [CrossRef]
- Nyerere, N.; Luboobi, L.S.; Nkansah-Gyekye, Y. Bifurcation and Stability Analysis of the Dynamics of Tuberculosis Model Incorporating, Vaccination, Screening and Treatment. Commun. Math. Biol. Neurosci. 2014, 2014, 3. [Google Scholar] [CrossRef]
- Kelemu Mengistu, A.; Witbooi, P.J. Modeling the Effects of Vaccination and Treatment on Tuberculosis Transmission Dynamics. J. Appl. Math. 2019, 2019, e7463167. [Google Scholar] [CrossRef]
- Song, B. Basic Reinfection Number and Backward Bifurcation. MBE 2021, 18, 8064–8083. [Google Scholar] [CrossRef]
- van den Driessche, P. Reproduction Numbers of Infectious Disease Models. Infect. Dis. Model. 2017, 2, 288–303. [Google Scholar] [CrossRef] [PubMed]
- Yuan, X.; Xue, Y.; Liu, M. Global Stability of a SIR Model with Two Susceptible Groups on Complex Networks. Chaos Solitons Fractals 2014, 59, 42–50. [Google Scholar] [CrossRef]
- Shevitz, D.; Paden, B. Lyapunov Stability Theory of Nonsmooth Systems. IEEE Trans. Autom. Control 1994, 39, 1910–1914. [Google Scholar] [CrossRef]
- Zhou, X.; Guo, Z. Analysis of an Influenza A (H1N1) Epidemic Model with Vaccination. Arab. J. Math. 2012, 1, 267–282. [Google Scholar] [CrossRef]
- Cohen, T.; Colijn, C.; Finklea, B.; Murray, M. Exogenous Re-Infection and the Dynamics of Tuberculosis Epidemics: Local Effects in a Network Model of Transmission. J. R. Soc. Interface 2006, 4, 523–531. [Google Scholar] [CrossRef]
- Sharomi, O.Y.; Safi, M.A.; Gumel, A.B.; Gerberry, D.J. Exogenous Re-Infection Does Not Always Cause Backward Bifurcation in TB Transmission Dynamics. Appl. Math. Comput. 2017, 298, 322–335. [Google Scholar] [CrossRef]
- Liu, J.; Chen, L.; Wei, F. The Persistence and Extinction of a Stochastic SIS Epidemic Model with Logistic Growth. Adv. Differ. Equ. 2018, 2018, 68. [Google Scholar] [CrossRef]
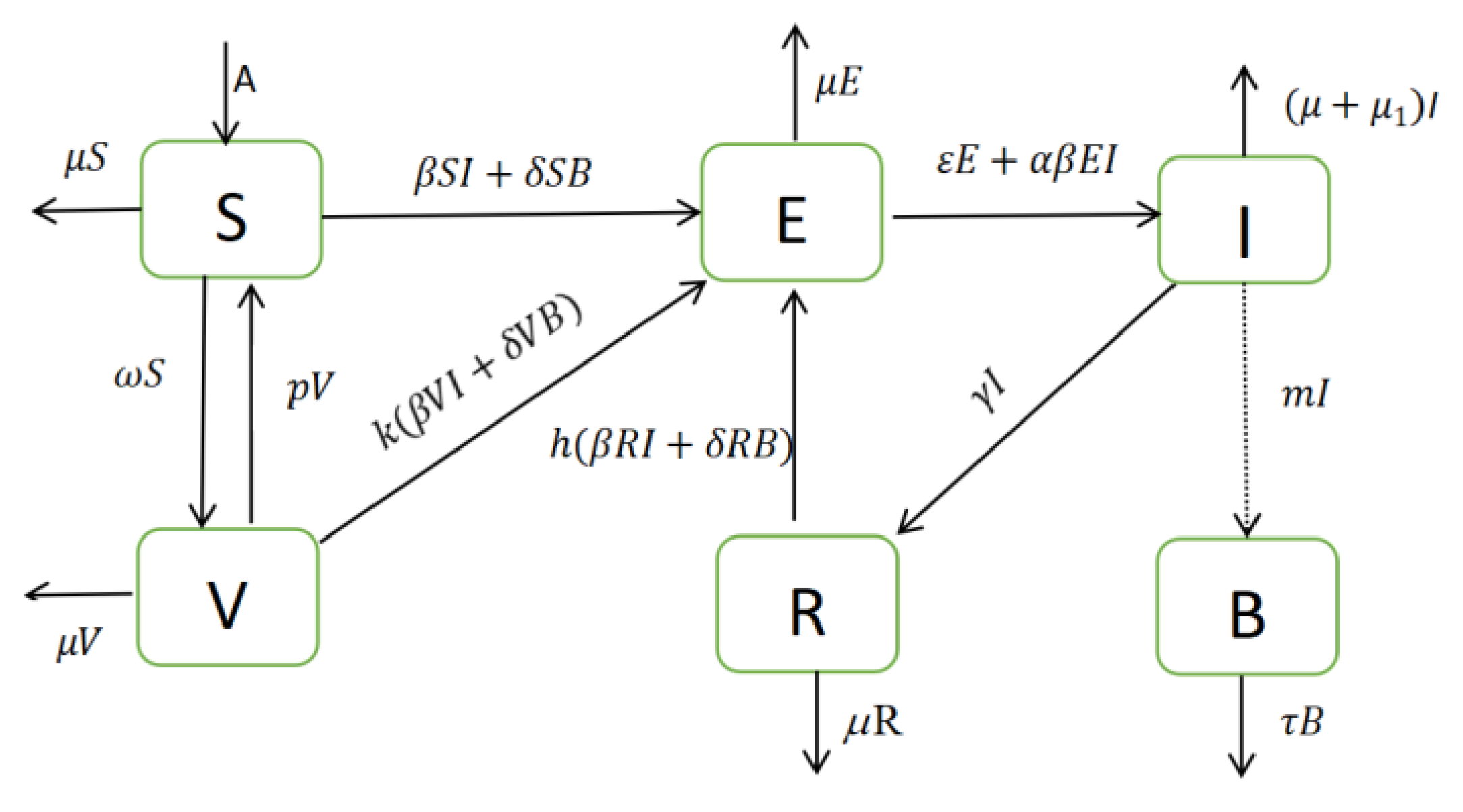

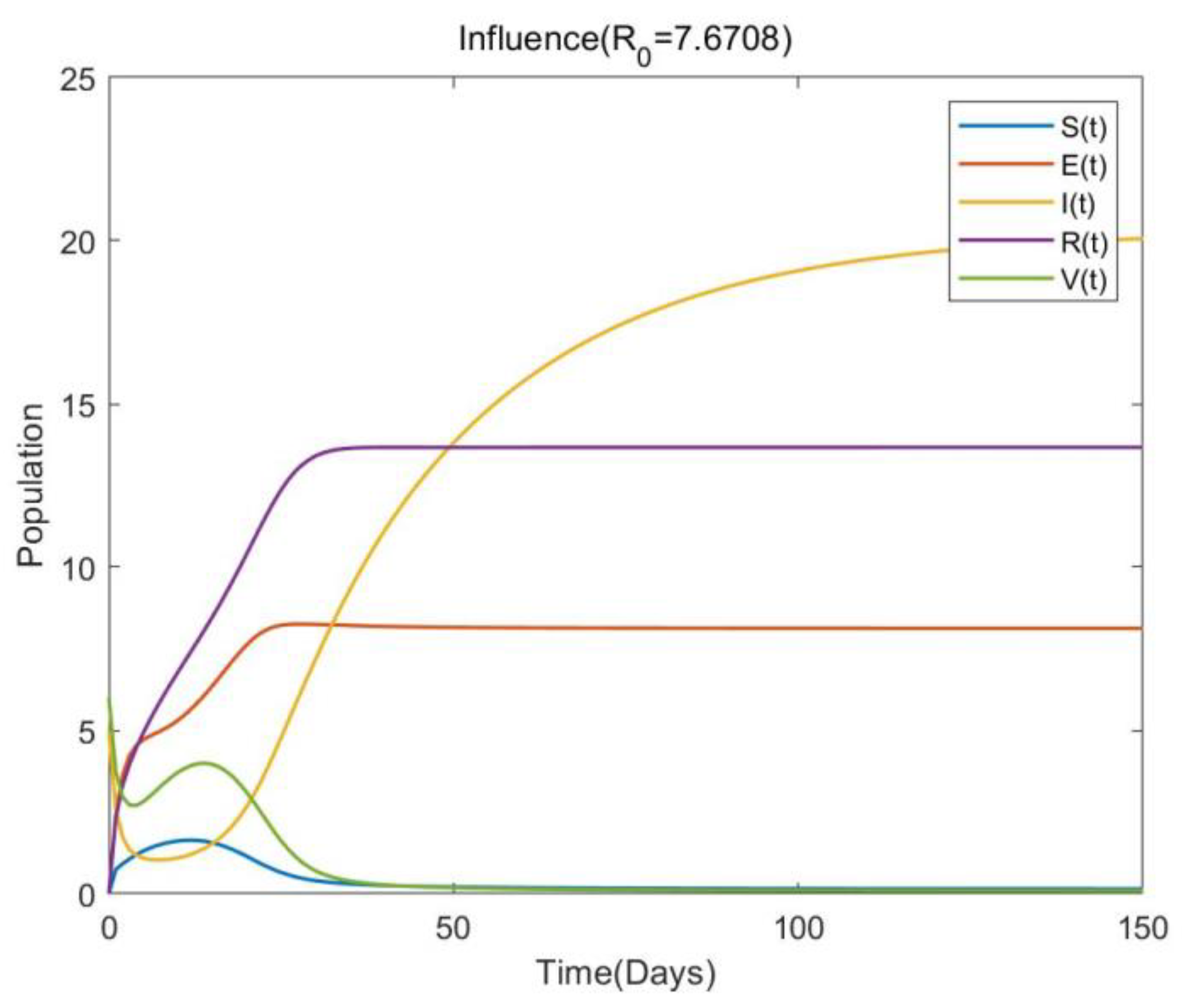
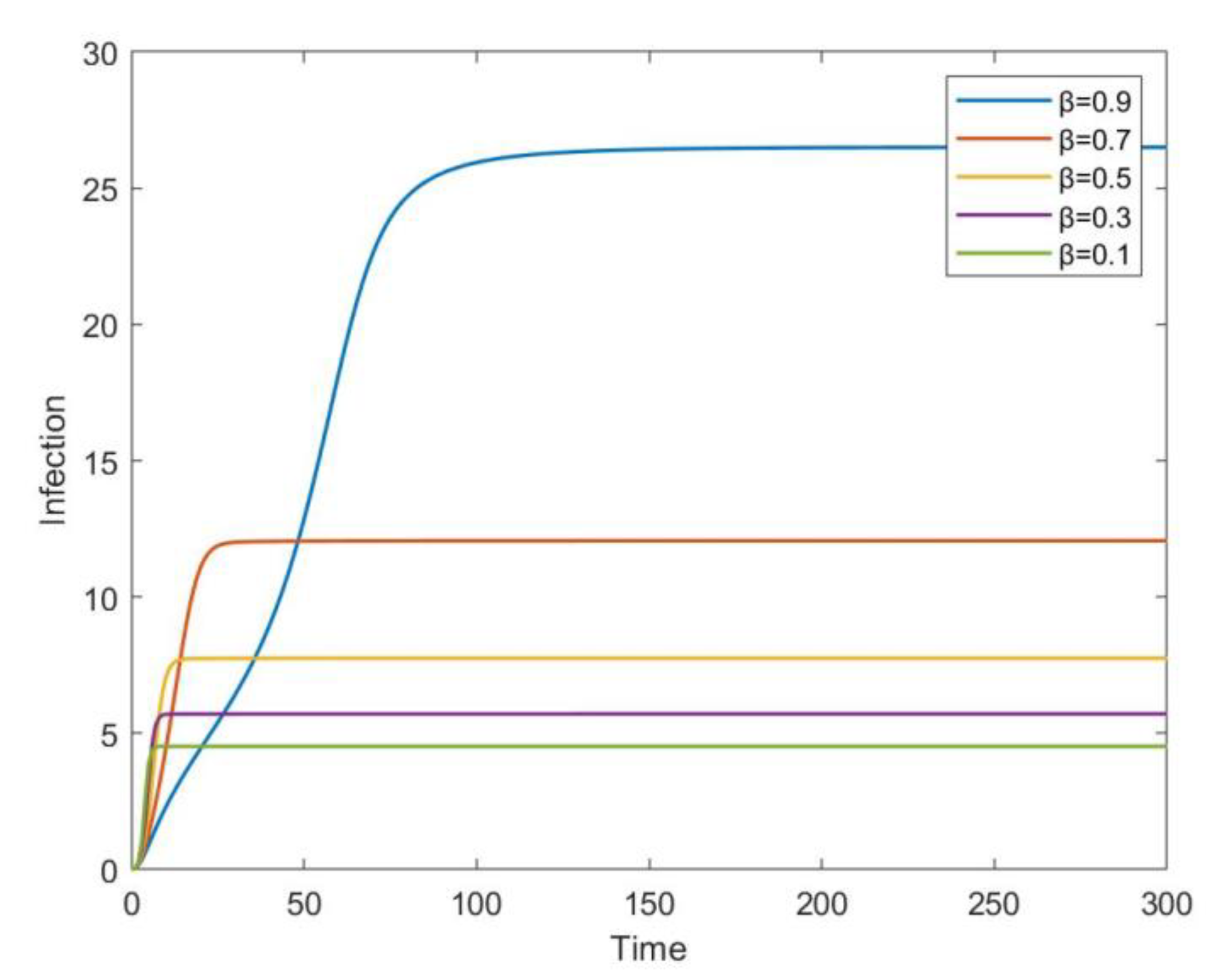
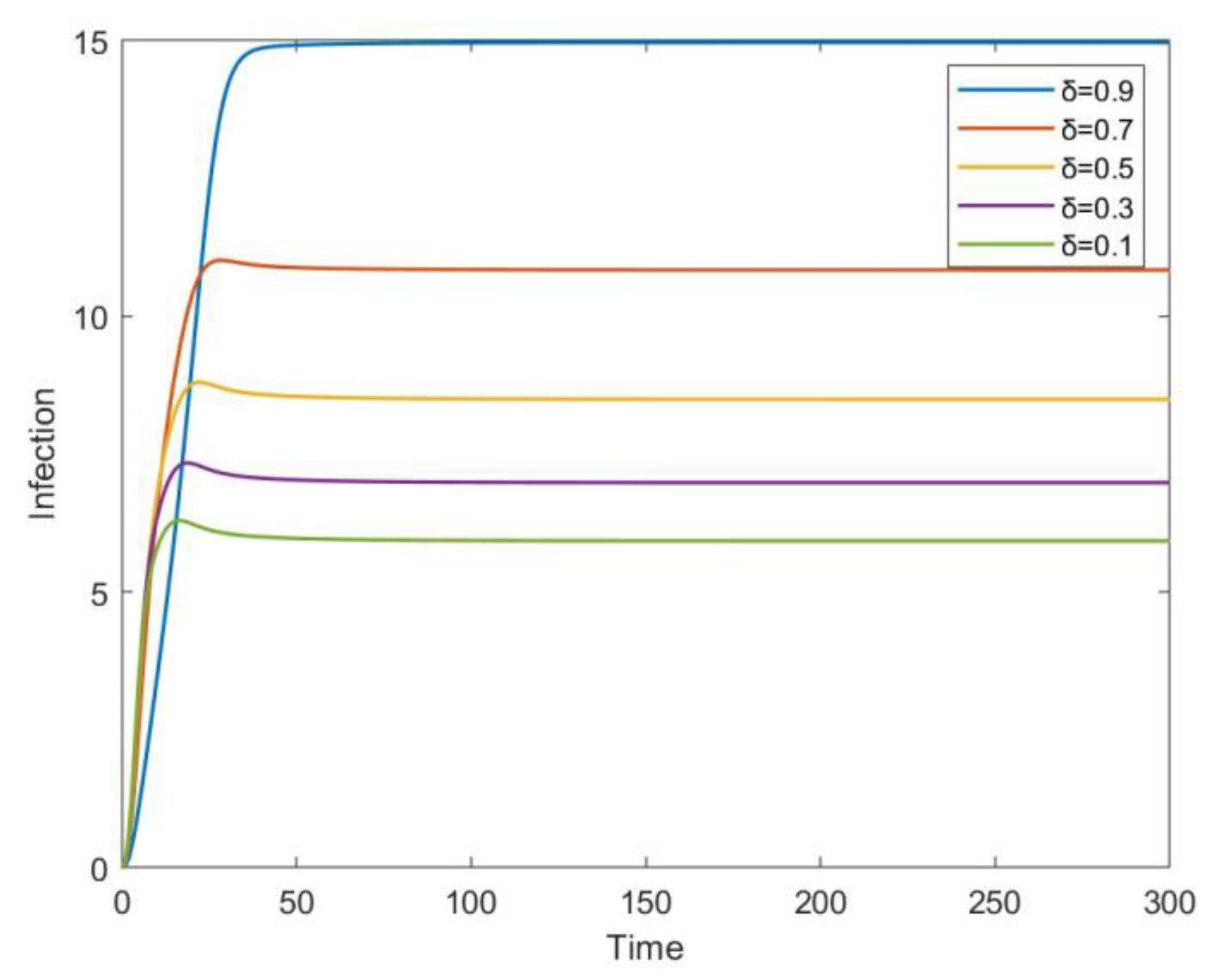
| Cases | Changes in Sign | Total Possible Positive Roots | |||||
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | |||||
| 2 | 1 | 1 | |||||
| 3 | 1 | 1 | |||||
| 4 | 3 | 1, 3 | |||||
| 5 | 2 | 0, 2 | |||||
| 6 | 2 | 0, 2 | |||||
| 7 | 2 | 0, 2 | |||||
| 8 | 0 | 0 |
| Description | Parameters | Value | Unit | B |
|---|---|---|---|---|
| Recruitment of person through birth or immigration | 1 | year−1 | - | |
| Natural death rate | 0.027 | year−1 | - | |
| The virus lapse rate in the environment | 0.6 | days−1 | - | |
| Rate of virus release into the environment by infected individuals | 0.45 | - | - | |
| Transmission rates between people and the environment | 0–1, 0.36, 0.1 | year−1 | - | |
| Transmission rate | 0–1 | - | [3,8,11] | |
| Exogenous reinfection | 0.3 | - | [6] | |
| Reinfection among the treated individuals | 0–1, 0.26 | year−1 | [28] | |
| Probability of endogenous morbidity | 0.002 | year−1 | [5,18] | |
| Recovery rate | 0.78 | year−1 | [12] | |
| Vaccine viability | 0.63 | - | - | |
| The rate of vaccine waning | 0.23 | - | - | |
| The rate of vaccination of those who are vulnerable | 0–1, 0.79 | year−1 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Wang, F. An Epidemiological Model for Tuberculosis Considering Environmental Transmission and Reinfection. Mathematics 2023, 11, 2423. https://doi.org/10.3390/math11112423
Li Q, Wang F. An Epidemiological Model for Tuberculosis Considering Environmental Transmission and Reinfection. Mathematics. 2023; 11(11):2423. https://doi.org/10.3390/math11112423
Chicago/Turabian StyleLi, Qiuyun, and Fengna Wang. 2023. "An Epidemiological Model for Tuberculosis Considering Environmental Transmission and Reinfection" Mathematics 11, no. 11: 2423. https://doi.org/10.3390/math11112423
APA StyleLi, Q., & Wang, F. (2023). An Epidemiological Model for Tuberculosis Considering Environmental Transmission and Reinfection. Mathematics, 11(11), 2423. https://doi.org/10.3390/math11112423





