Abstract
The class of H-matrices, also known as Generalized Diagonally Dominant (GDD) matrices, plays an important role in many areas of applied linear algebra, as well as in a wide range of applications, such as in dynamical analysis of complex networks that arise in ecology, epidemiology, infectology, neurology, engineering, economy, opinion dynamics, and many other fields. To conclude that the particular dynamical system is (locally) stable, it is sufficient to prove that the corresponding (Jacobian) matrix is an H-matrix with negative diagonal entries. In practice, however, it is very difficult to determine whether a matrix is a non-singular H-matrix or not, so it is valuable to investigate subclasses of H-matrices which are defined by relatively simple and practical criteria. Many subclasses of H-matrices have recently been discussed in detail demonstrating the many benefits they can provide, though one particular subclass has not been fully exploited until now. The aim of this paper is to attract attention to this class and discuss its relation with other more investigated classes, while showing its main advantage, based on its simplicity and elegance. This new approach, which we are presenting in this paper, will be compared with the existing ones, in three possible areas of applications, spectrum localization; maximum norm estimation of the inverse matrix in the point, as well as the block case; and error estimation for LCP problems. The main conclusion is that the importance of our approach grows with the matrix dimension.
Keywords:
H-matrices; block H-matrices; eigenvalue localization; inverse matrix norm estimation; error estimation for LCP MSC:
15A09; 15A18; 15B99
1. Introduction
The class of generalized diagonally dominant (GDD), also known as the H-matrix class, as well as its various subclasses, attract significant scientific attention due to its central subclass, the strictly diagonally dominant (SDD) class, which appears to be very important and productive in many fields of applied linear algebra, for example:
- The famous Geršgorin theorem [1] is, in fact, equivalent to non-singularity result for SDD matrices [2];
- For a given SDD matrix, an infinity norm estimation for its inverse can be easily found by Varah’s theorem [3];
- For an arbitrary matrix, its pseudospectrum can be easily localized by pseudo Geršgorin set [4];
- If the (Jacobian) matrix off a particular (non-linear) dynamical system is an SDD matrix with negative diagonal entries, then this dynamical system is (locally) stable;
- The error bound for linear complementarity problems can be easily calculated for the class of SDD matrices [5];
- The Schur complement of an SDD matrix is SDD itself [6].
All of these applications are simple and elegant as they only require simple operations with matrix entries. In comparison, even if we manage to find an analogue application for GDD-matrices (such as Minimal Geršgorin set [2] for the first item), it is neither simple nor elegant. For this reason, something between SDD and GDD classes, i.e., various H-matrix subclasses, became relevant. Many such subclasses have been discovered over the years, such as doubly strictly diagonally dominant (DSDD), also known under the name Ostrowski matrices [7,8,9], Dashnic–Zusmanovich matrices [10], Dashnic–Zusmanovich type matrices [11], S-SDD or CKV matrices [12,13], CKV type matrices [14], Nekrasov matrices [15,16,17], SDD matrices [18,19], etc. Various problems related to these classes have been studied, including eigenvalue localizations [2,7], pseudospectra localizations [4], infinity norm estimations of the inverse [18,20,21,22,23,24,25,26,27], Schur complement problems [28,29,30,31], error bound for linear complementarity problems [32,33,34,35,36], etc. Furthermore, introducing new H-matrix subclasses can provide more benefits for SDD class itself. For example, infinity norm estimation for the inverse of Nekrasov matrices, see [17,21], can be used for SDD matrices as well (since SDD class is a subset of Nekrasov class), and produce better estimation than Varah’s one. This idea has been specifically essential to estimate the infinity norm of the iterative matrix of a parallel-in-time iterative algorithm for Volterra partial integro-differential problems [37], and to analyze the preconditioning technique for an all-at-once system from Volterra subdiffusion equations [38]. Of course, as a matrix class under consideration becomes wider, the more computational effort has to be performed to obtain a corresponding result.
On the other hand, in many applications, such as in ecology for example, a matrix under consideration is almost an SDD matrix, meaning that in only one row is strictly diagonally not dominant. Such matrices might belong to Ostrowski or Dashnic–Zusmanovich classes, which are widely investigated in the recent years [8,23,29,31,39,40]. However, if we focus on matrices with only one non-SDD row, which are not Ostrowski matrices, we can find a simpler condition than Dashnic–Zusmanovich one, providing an H-matrix property. This condition can be derived from a non-singular class of matrices from [41], which, to author’s knowledge, has not been fully exploited up to now. In this paper, we will present a new approach to this class, show how many benefits we can achieve in the case of matrices with only one non-SDD row, and compare our results with the existing ones in three possible areas of applications, which are eigenvalue localization; maximum norm estimation of the inverse matrix in the point, as well as the block case; and error estimation for LCP problems.
Throughout this paper, the usual notations shall be used:
In [41], the following non-singularity result was proved.
Theorem 1.
If a matrix , , satisfies the conditions
and
then A is non-singular.
The matrix class described by conditions (1) and (2) we will call Nearly-SDD class. To authors’ knowledge, the relationship with some other known non-singular classes has not been established yet. Hence, first of all, we will discuss these relationships, and then present some advantages of using the Nearly-SDD class in applications.
A closer look at conditions (1) and (2), leads to the conclusion that all matrices from the Nearly-SDD class have at most one non-SDD row, i.e., the matrix is either an SDD (strictly diagonally dominant) matrix, meaning that
or there is only one index , such that
and
Hence, Theorem 1 has the following Corollary:
Corollary 1.
If for a matrix , , there exists an index k, such that
and for all
then A is non-singular.
This particular situation, when a given matrix has at most one non-SDD row, happens also with two well-known subclasses of H-matrices, Ostrowski (or Doubly Diagonally Dominant), [9], defined by the condition
and Dashnic–Zusmanovich (DZ) [10], defined by the condition that there exists an index , such that
So, the natural question that immediately arises is what is the relation between these classes?
Recently, in [18,19], another H-matrix subclass which treats differently SDD and non-SDD rows, has been proposed. Let be the subset of indices that correspond to non-SDD rows, i.e.,
and
We say that a matrix A is SDD matrix if
Among SDD matrices, obviously, one can find matrices with only one non-SDD row (for such matrices is a singleton), so we will compare the Nearly-SDD class with the SDD class, too. By convention, we will assume that SDD matrices (the case ) does belong to SDD class.
2. The Relation between Classes
Figure 1 illustrates the relationship between Nearly-SDD, Ostrowski, Dashnic–Zusmanovich, and SDD classes.
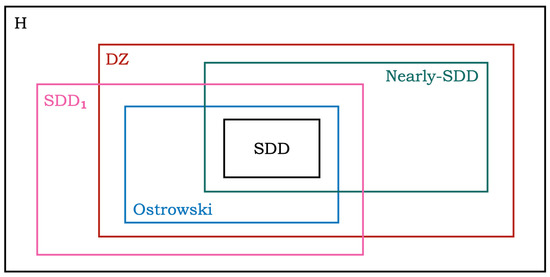
Figure 1.
The relationship between classes.
In order to confirm this, we will present the following:
- 1*
- An example—matrix —belonging to Nearly-SDD, but not to Ostrowski,
- 2*
- An example—matrix —belonging to Ostrowski, but not to Nearly-SDD,
- 3*
- An example—matrix —belonging to DZ, but neither to Ostrowski, nor to Nearly-SDD,
- 4*
- An example—matrix —belonging to Nearly-SDD, but not to SDD,
- 5*
- The proof that every Nearly-SDD matrix is a DZ, too.
Other relations presented in the picture are obvious.
The following examples arise in ecological modelling, more precisely in the generalized Lotka–Volterra equations, representing energy flow in complex food webs. Matrices , , , and are community matrices of such models.
- 1*
- The matrixis a Nearly-SDD matrix (for ), but it is not an Ostrowski matrix, for
- 2*
- The matrixis an Ostrowski matrix, but it is not a Nearly-SDD matrix, for the only non-SDD row is , and
- 3*
- The matrixis a DZ matrix, but it is neither an Ostrowski matrix, because ofnor a Nearly-SDD matrix, for the only non-SDD row is , and
- 4*
- The matrixis a Nearly-SDD matrix (for ), but it is not an SDD matrix, for
- 5*
- Proof.Assume that A belongs to Nearly-SDD class. If A is an SDD matrix, the conclusion follows immediately. Hence, suppose that there exists an index k, such thatand for all other indices it holds thatThen,or, equivalently,holds for all , which means that A belongs to DZ class. □
3. Scaling Technique for Nearly-SDD Class
It is well known that every H-matrix can be diagonally scaled, from the right-hand side, to an SDD matrix, i.e., that there exists a positive diagonal matrix W, such that is an SDD matrix. The class we are dealing with in this paper, the Nearly-SDD class, is a subclass of H-matrices, which we confirm by constructing a scaling matrix W.
First of all, if A is an SDD matrix itself, then there is nothing to prove, since the role of the scaling matrix is played by the identity matrix.
Consequently, assume that A belongs to Nearly-SDD class, and that k is the index of the only non-SDD row:
Note that for all other indices it holds that
We choose the scaling matrix W to have the following form:
In order to ensure that is an SDD matrix, we have to choose , such that:
and
Since (9) is fulfilled for all j, for which , and due to the fact that , it means that has to be chosen from the following interval
This interval is not empty, because from (6) and (7), we have
or, equivalently,
Note that we can always choose from interval
where
which is a bit smaller than (10), but very easy to calculate. It is also non-empty, because of (6) and (7), rewritten as
so that
Remark 1.
The form of a scaling matrix also proves that the Nearly-SDD class is contained in DZ class (which is fully characterized with the scaling matrices of this form, see [42]).
Remark 2.
Although Nearly-SDD class is a subset of DZ class, it is worth discussing its applications, since its definition, in the form of (6) and (7) (which covers all Nearly-SDD matrices except SDD ones) suggests that we can expect computationally more efficient eigenvalue localizations, upper bound for the inverse, etc., compared to those obtained for wider classes of matrices.
Remark 3.
Obviously, Nearly-SDD class is a subclass of non-singular H-matrices.
4. Possible Applications
4.1. A New Eigenvalue Localization Set
It is well-known that every subclass of H-matrices can lead to an eigenvalue localization set, see [2,7]. For example, the condition defining SDD matrices leads to the well-known Geršgorin set [1], and the condition defining DZ matrices leads to the DZ eigenvalue localization set, a special case of the eigenvalue localization set in [12]. Here, we will reformulate Theorem 6 from [12] for the case , which corresponds to DZ class. As usual, by we denote the spectrum of A.
Theorem 2
([12], Corrolary of Theorem 6). Let be an arbitrary index, and . For a given matrix , and all , define sets
Then
Furthermore
Analogously, here, by the use of Theorem 1, we obtain the following eigenvalue localization result.
Theorem 3.
For a given matrix , , for , define the Geršgorin- type disks
and for all , the ellipses
Then
Proof.
Suppose, on the contrary, that there exists an eigenvalue of A, such that . Then, for all , , and for all , , i.e.,
which means that is a Nearly-SDD matrix, hence non-singular. This is an obvious contradiction, so the proof is concluded. □
Obviously, for every , where denotes the th Geršgorin disk:
More precisely:
- If , then ,
- If , then is an ellipse with foci and .
As an immediate consequence, we have the following statement.
Corollary 2.
If for a given matrix , ,
This Corollary says that if we have a matrix for which all Geršgorin circles are isolated, then it is possible to reduce their radius. Here, we give an illustrative example.
Example 1.
In stability theory of continuous time-independent dynamical systems, the position of the spectrum of a considered matrix is crucial. In order to ensure that the whole spectrum lies in the open left-half plane, it is sufficient to find agoodspectrum of localization, which lies in the open left-half plane itself. This is the main reason for finding as many as possible elegant, meaning computationally cheap, eigenvalue localizations. This particular example shows how Corollary 2 can help to achieve this goal.
Consider a matrix
In Figure 2, Geršgorin circles are marked by full line, exact eigenvalues by red crosses, and localization area obtained by Corollary 2 (smaller circles) is shaded. Obviously, the original Geršgorin set goes to the right-half plane, so it can not provide conclusion about stability, while the localization set is completely in the left-half plane, hence, we now have an answer, the corresponding dynamical system is stable.
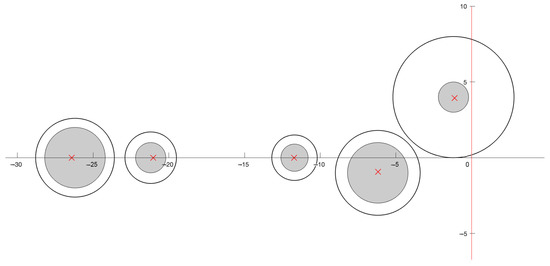
Figure 2.
Comparison between the Geršgorin set (black line) and from Corollary 2 (shaded). Exact eigenvalues are marked by red crosses.
Remark 4.
Similar observations can be found in [41], but the proof given there is based on the structure of the corresponding eigenvector, hence it required more technicalities, comparing to the approach presented here, which is based on the Equivalence Principle between subclasses of H-matrices and corresponding Geršgorin-type localizations.
4.2. Upper Bounds for the Norm of the Inverse of Matrices from Nearly-SDD Class
In order to give an upper bound for the maximum norm of the matrix inverse to a Nearly-SDD matrix A, we will use the facts from the previous section.
Theorem 4.
Let be a Nearly-SDD matrix, for which there exists an index k, such that
Then,
where
Proof.
Let W be a scaling matrix, such that is an SDD matrix. Then
Choose from the admissible interval (11), i.e.,
Since we immediately have
On the other hand, according to Varah’s well-known result, for the inverse of SDD matrix we have
Denoting by
for an arbitrary from the interval given in (14), we have
Obviously, function is a decreasing function by , while
is an increasing function by . Since
the minimum over will be attained for satisfying
if such a belongs to the admissible interval (14). This is the case, because, due to (12)
and
Finally,
and (13) is proved. □
Remark 5.
Since the Nearly-SDD class is a subset of DZ class, which is a special case of SDD class for S being a singleton, it is worthwhile to compare our inverse norm bound with the known ones from [22,27]. However, in [39], all these known bounds were discussed in more details, and the best one for DZ matrices is given in the following form (see Theorem 4.2 in [39]):
Theorem 5.
Let , , be a DZ matrix, such that
Then
where
In our case, when matrix A has only one non-SDD row, and the index of this row is k, we have
so there are no indices satisfying condition in the definition of . Hence,
Obviously, the bound (15) is an increasing function by , while the equivalent expression
suggests that it is a decreasing function over . Hence, our bound (13) can not be better than (15), but it requires less computations. Namely, for a given matrix with only one non-SDD row, we know index k of that row, so for the bound given by (13), we have to find , and then calculate expression only once, while for the bound given by (15), we have to calculate expressions , and then find their maximum.
4.3. Linear Complementarity Problem
Given and , the linear complementarity problem (LCP()) is to find a vector , such that
or to show that such vector does not exist. It is well known that LCP() has a unique solution for any if, and only if, the matrix A is a matrix, a real square matrix with all its principal minors positive, see [43]. Here, we will consider the Nearly-SDD matrices with positive diagonal entries. Such matrices are -matrices (i.e., H-matrices with positive diagonal entries), so they are P-matrices.
In defining an upper error bound for LCP, the following fact can be a starting point, see [44],
where , and .
In the same paper, for A being an -matrix, it has been shown that
where is the comparison matrix to matrix A, defined with
and is the diagonal part of A. Here, we have used the max operator in the following sense:
Obviously, if A is a Nearly-SDD matrix, then its comparison matrix is an M-matrix, and (13) can be treated as an upper bound of its inverse, as well. Hence
On the other hand,
so that
However, when we are considering a subclass of -matrices, for which we know a form of the scaling matrix, then we can use the approach presented in [33]. In fact, we can apply Proposition 3.1 from this paper, since our class belongs to the SDD class (the class for which there exists a non-empty subset S, such that matrix A is an SDD matrix). From this Proposition, because of our scaling parameter is greater than 1, we conclude that
where
while W denotes a scaling matrix
Obviously,
so that
Hence, we have proved the following proposition.
Proposition 1.
Let us assume that is a Nearly-SDD matrix, which is not SDD, i.e., there exist an index k, such that
Let defined by (14). Then
Let us consider the same example as in [33], and compare the corresponding bounds.
Example 2
([33]). Let
It is a Nearly-SDD matrix, which is not SDD, and satisfies conditions of Proposition 1 for , so we can conclude that for all it holds that
We will choose γ, such that
Obviously
Finally,
In [33], the obtained bound for this matrix is which is greater than 2.
| estimation from [33] | estimation (17) |
4.4. Block Case
It is well-known that in real applications, particularly in ecology, matrices might have zeros on diagonal places and this restriction can not be avoided due to some physical explanations. However, this fact immediately makes such a matrix outside of the non-singular H-matrix class. This is one of the reasons why block generalizations become important. The other important reason is that partitioning a given matrix into blocks reduces the dimension of the problem.
Block generalizations of the class of H-matrices were considered in [45].
For a matrix and a partition of the index set N, one can present A in the block form as Here, we will consider only one possible way of introducing the comparison matrix for a given A and a partition of the index set. The comparison matrix will be denoted by where
For a given and a given partition of the index set we say that:
- A is a block H-matrix if is an H-matrix,
- A is a block SDD matrix if is an SDD matrix,
- A is a block Nearly-SDD matrix if is a Nearly-SDD matrix,
- Etc.
In [46] the following results has been proved.
Theorem 6
([46]). If is a block π H-matrix, then
Due to this theorem, we are able to estimate the norm of the inverse of matrices which are not H-matrices. The following example illustrates how this works:
This is a matrix with zeros on its diagonal, so it can not be a non-singular H-matrix, meaning that we can not apply any of known point-wise estimations for subclasses of H-matrices. However, if we consider this matrix in its block form, with respect to partition , we obtain the comparison matrix
This matrix is, obviously from Nearly-SDD class for , hence (13) gives us an upper bound for the inverse of comparison matrix, as well as for the original matrix , due to Theorem 6:
It is a good estimation, since the exact values are
Note that comparison matrix is not the Ostrowski matrix, while, as we have already pointed out, it is a DZ matrix. However, this information is not providing a better bound, it is the same as (18), while, at the same time, required computational work is more demanding. Of course, the above example is just an illustrative one, the importance of such approach grows with the matrix dimension.
5. Conclusions
While the H-matrix class itself is very important from the application point of view, checking if a matrix is an H-matrix is a computationally very demanding job. Instead, it is much more efficient to check if a matrix belongs to an H-matrix subclass. In the case of a positive answer, there are lots of benefits from this fact. Let us recall just a few:
- If all diagonal entries are negative, then we immediately conclude that the corresponding continuous linear (non-linear) dynamical system is asymptotically (locally) stable, without calculating exact eigenvalues.
- Moreover, if a particular feature in mathematical model depends only on the position of eigenvalues, we have a new localization area for eigenvalues, easily constructed from a given H-matrix subclass by equivalence principle, which might help.
- We are able to estimate max-norm of the inverse matrix, which is important in the perturbation theory of ill-conditioned matrices in engineering, etc.
- We can apply this new max norm estimation for the inverse to SDD matrices, potentially beneficial in the analysis of a parallel-in-time iterative algorithm for Volterra partial integro-differential problems and the preconditioning technique for an all-at-once system from Volterra subdiffusion equations.
A subclass of H-matrices, called in this paper the Nearly-SDD class, has not been exploited in the above sense, yet.In order to reveal the place and significance of this subclass of H-matrices. let us conclude the following:
- If all rows of the matrix are SDD, the technique is already known and developed.
- If the matrix has only one non-SDD row, the known technique offers to check if the matrix is double SDD (satisfy condition (3)). If not, the known technique offers to check the condition (4), i.e., whether the matrix is DZ or not. However, for that check, it is necessary to go through all the indices, and for each of them check conditions.
Obviously, as the matrix dimension grows, savings become more important.
Author Contributions
Both authors have equally contributed to preparation of all parts of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research paper has been supported by the Ministry of Science, Technological Development and Innovation through project no. 451-03-47/2023-01/200156 “Innovative scientific and artistic research from the FTS (activity) domain”.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Geršgorin, S. Über die Abgrenzung der Eigenwerte einer Matrix (German) (About the delimitation of the eigenvalues of a matrix). Izv. Akad. Nauk. Sssr, Seriya Mat. 1931, 7, 749–754. [Google Scholar]
- Varga, R.S. Geršgorin and His Circles; Springer: New York, NY, USA, 2004. [Google Scholar]
- Varah, M. A lower bound for the smallest singular value of a matrix. Linear Algebra Appl. 1975, 11, 3–5. [Google Scholar] [CrossRef]
- Kostić, V.R.; Cvetković, L.; Cvetković, D.L. Pseudospectra localizations and their applications. Numer. Linear Algebra Appl. 2016, 23, 55–75. [Google Scholar] [CrossRef]
- Garcia-Esnaola, M.; Pena, J.M. A comparison of error bounds for linear complementarity problems of H-matrices. Linear Algebra Appl. 2010, 433, 956–964. [Google Scholar] [CrossRef]
- Carlson, D.; Markham, T. Schur complements of diagonally dominant matrices. Czech. Math. J. 1979, 29, 246–251. [Google Scholar] [CrossRef]
- Cvetković, L. H-matrix theory vs. eigenvalue localization. Numer. Algor. 2006, 42, 229–245. [Google Scholar] [CrossRef]
- Li, B.S.; Tsatsomeros, M.J. Doubly diagonally dominant matrices. Linear Algebra Appl. 1997, 261, 221–235. [Google Scholar] [CrossRef]
- Ostrowski, A.M. Über die Determinanten mit Überwiegender Hauptdiagonale (German) (About the determinants with predominant main diagonal). Comment. Math. Helv. 1937, 10, 69–96. [Google Scholar] [CrossRef]
- Dashnic, L.S.; Zusmanovich, M.S. O nekotoryh kriteriyah regulyarnosti matric i lokalizacii ih spectra (In Russian) (On some criteria for the nonsingularity of matrices and the localization of their spectrum). Zh. Vychisl. Matem. Matem. Fiz. 1970, 5, 1092–1097. [Google Scholar]
- Zhao, J.X.; Liu, Q.L.; Li, C.Q.; Li, Y.T. Dashnic-Zusmanovich type matrices: A new subclass of nonsingular H-matrices. Linear Algebra Appl. 2018, 552, 277–287. [Google Scholar] [CrossRef]
- Cvetković, L.; Kostić, V.; Varga, R.S. A new Geršgorin-type eigenvalue inclusion set. Electron. Trans. Numer. Anal. 2004, 18, 73–80. [Google Scholar]
- Gao, Y.M.; Wang, X.H. Criteria for generalized diagonally dominant matrices and M-matrices. Linear Algebra Appl. 1992, 169, 257–268. [Google Scholar] [CrossRef]
- Cvetković, D.L.; Cvetković, L.; Li, C.Q. CKV-type matrices with applications. Linear Algebra Appl. 2021, 608, 158–184. [Google Scholar] [CrossRef]
- Gudkov, V.V. On a certain test for nonsingularity of matrices. Latvian Math. Yearbook 1966, 1965, 385–390. [Google Scholar]
- Li, W. On Nekrasov matrices. Linear Algebra Appl. 1998, 281, 87–96. [Google Scholar] [CrossRef]
- Szulc, T. Some remarks on a theorem of Gudkov. Linear Algebra Appl. 1995, 225, 221–235. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.; Liu, L.; Wang, Y. Infinity norm upper bounds for the inverse of SDD1 matrices. AIMS Math. 2022, 7, 8847–8860. [Google Scholar] [CrossRef]
- Pena, J.M. Diagonal dominance, Schur complements and some classes of H-matrices and P-matrices. Adv. Comput. Math. 2011, 35, 357–373. [Google Scholar] [CrossRef]
- Cvetković, L.; Kostić, V.; Doroslovački, K. Max-norm bounds for the inverse of S-Nekrasov matrices. Appl. Math. Comput. 2012, 218, 9498–9503. [Google Scholar] [CrossRef]
- Cvetković, L.; Dai, P.F.; Doroslovački, K.; Li, Y.T. Infinity norm bounds for the inverse of Nekrasov matrices. Appl. Math. Comput. 2013, 219, 5020–5024. [Google Scholar] [CrossRef]
- Kolotilina, L.Y. New subclasses of the class of H-matrices and related bounds for the inverses. J. Math. Sci. 2017, 224, 911–925. [Google Scholar] [CrossRef]
- Li, C.Q.; Cvetković, L.; Wei, Y.; Zhao, J.X. An infinity norm bound for the inverse of Dashnic-Zusmanovich type matrices with applications. Linear Algebra Appl. 2019, 565, 99–122. [Google Scholar] [CrossRef]
- Kolotilina, L.Y. Bounds for the infinity norm of the inverse for certain M- and H-matrices. Linear Algebra Appl. 2009, 430, 692–702. [Google Scholar] [CrossRef]
- Kolotilina, L.Y. On bounding inverse to Nekrasov matrices in the infinity norm. J. Math. Sci. 2014, 199, 432–437. [Google Scholar] [CrossRef]
- Li, W. The infinity norm bound for the inverse of nonsingular diagonal dominant matrices. Appl. Math. Lett. 2008, 21, 258–263. [Google Scholar] [CrossRef]
- Morača, N. Upper bounds for the infinity norm of the inverse of SDD and S-SDD matrices. J. Comput. Appl. Math. 2007, 206, 666–678. [Google Scholar] [CrossRef]
- Cvetković, L.; Nedović, M. Eigenvalue localization refinements for the Schur complement. Appl. Math. Comput. 2012, 218, 8341–8346. [Google Scholar] [CrossRef]
- Li, C.Q.; Huang, Z.Y.; Zhao, J.X. On Schur complements of Dashnic-Zusmanovich type matrices. Linear Multilinear Algebra 2022, 70, 4071–4096. [Google Scholar] [CrossRef]
- Liu, J.Z.; Zhang, F.Z. Disc separation of the Schur complement of diagonally dominant matrices and determinantal bounds. SIAM J. Matrix Anal. Appl. 2005, 27, 665–674. [Google Scholar] [CrossRef]
- Liu, J.Z.; Zhang, J.; Liu, Y. The Schur complement of strictly doubly diagonally dominant matrices and its application. Linear Algebra Appl. 2012, 437, 168–183. [Google Scholar] [CrossRef]
- Gao, L.; Wang, Y.; Li, C.Q.; Li, Y. Error bounds for linear complementarity problems of S-Nekrasov matrices and B-S-Nekrasov matrices. J. Comput. Appl. Math. 2019, 336, 147–159. [Google Scholar] [CrossRef]
- Garcia-Esnaola, M.; Pena, J.M. Error bounds for the linear complementarity problem with a Σ-SDD matrix. Linear Algebra Appl. 2013, 438, 1339–1346. [Google Scholar] [CrossRef]
- Garcia-Esnaola, M.; Pena, J.M. Error bounds for linear complementarity problems of Nekrasov matrices. Numer. Algor. 2014, 67, 655–667. [Google Scholar] [CrossRef]
- Li, C.Q.; Dai, P.F.; Li, Y.T. New error bounds for linear complementarity problems of Nekrasov matrices and B-Nekrasov matrices. Numer. Algor. 2017, 74, 997–1009. [Google Scholar] [CrossRef]
- Li, C.Q.; Yang, S.; Huang, H.; Li, Y.; Wei, Y. Note on error bounds for linear complementarity problems of Nekrasov matrices. Numer. Algor. 2020, 83, 355–372. [Google Scholar] [CrossRef]
- Gu, X.M.; Wu, S.L. A parallel-in-time iterative algorithm for Volterra partial integral-differential problems with weakly singular kernel. J. Comput. Phys. 2020, 417, 109576. [Google Scholar] [CrossRef]
- Zhao, J.L.; Gu, X.M.; Ostermann, A. A Preconditioning Technique for an All-at-once System from Volterra Subdiffusion Equations with Graded Time Steps. J. Sci. Comput. 2021, 88, 11. [Google Scholar] [CrossRef]
- Kolotilina, L.Y. On Dashnic-Zusmanovich (DZ) and Dashnic-Zusmanovich type (DZT) matrices and their inverses. J. Math. Sci. 2019, 240, 799–812. [Google Scholar] [CrossRef]
- Min, Y.U.; Hongmin, M.O. Error Bound of Linear Complementarity Problem for Dashnic-Zusmanovich Matrix. J. Jishou Univ. (Natural Sci. Ed.) Math. 2019, 40, 4–9. [Google Scholar]
- Pupkov, V.A. Ob izolirovannom sobstvennom znachenii matricy i strukture ego sobstvennogo vektora (in Russian) (On the isolated eigenvalue of a matrix and the structure of its eigenvector). Zh. Vychisl. Matem. Matem. Fiz. 1983, 23, 1304–1313. [Google Scholar]
- Cvetković, L.; Kostić, V. Between Geršgorin and minimal Geršgorin sets. J. Comput. Appl. Math. 2006, 196, 452–458. [Google Scholar] [CrossRef]
- Cottle, R.W.; Pang, J.S.; Stone, R.E. The Linear Complementarity Problem; Academic Press: San Diego, CA, USA, 1992. [Google Scholar]
- Chen, X.J.; Xiang, S.H. Computation of error bounds for P-matrix linear complementarity problems. Math. Program. Ser. A 2006, 106, 513–525. [Google Scholar] [CrossRef]
- Robert, F. Blocs-H-matrices et convergence des methodes iteratives classiques par blocks (French) (Block-H-matrices and convergence of classical iterative methods by blocks). Linear Algebra Appl. 1969, 2, 223–265. [Google Scholar] [CrossRef]
- Cvetković, L.; Doroslovački, K. Max norm estimation for the inverse of block matrices. Appl. Math. Comput. 2014, 242, 694–706. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).