Intrusion Detection in Networks by Wasserstein Enabled Many-Objective Evolutionary Algorithms
Abstract
1. Introduction
1.1. Motivations
1.2. Contributions
- The contributions of this paper are listed below.
- A risk-aware optimal sensor placement model.
- A many-objective optimization formalization of the optimal sensor placement problem, where the objectives are the mean and the standard deviation of the detection time over a set of simulated contamination events along with the amount of contaminated water consumed before detection and its variance.
- The representation of the weights in the decomposition as discrete probability distributions whose distance is computed by the Wasserstein distance.
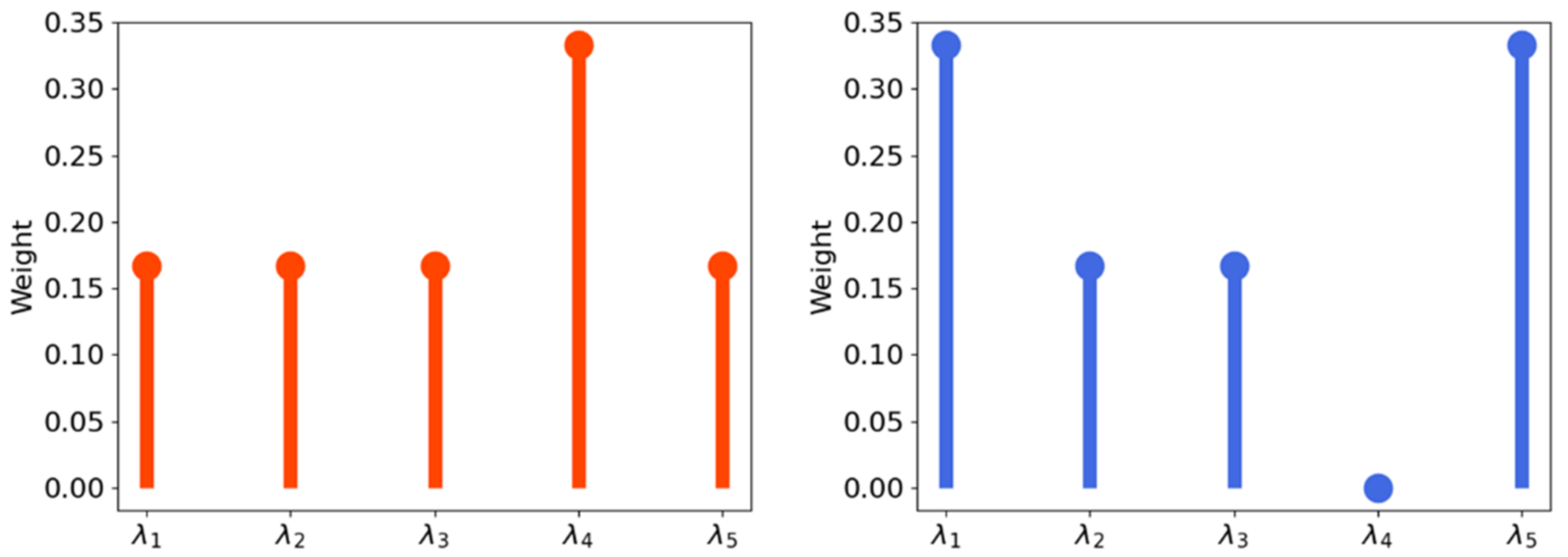
- The formulation of a Wasserstein enabled selection of the weight parameters in the scalarization.
- A set of computational results, for standard benchmark problems and a real-world application, which demonstrates that MOEA/D/W has a significant performance improvement over MOEA/D.
1.3. Organization of the Paper
2. Related Works
- The number of objectives has been augmented from 2 (mean detection time and its standard deviation) to 4, including the mean amount of water consumed and its standard deviation.
- While the paper [16] was focused on the Pareto sampling strategy of non-dominated sorting, the current paper is based on decomposition, which is usually held to be higher performing for many-objective problems.
- This has required a new strategy to map the MOEA/D algorithm into the Wasserstein base MOEA/D/W.
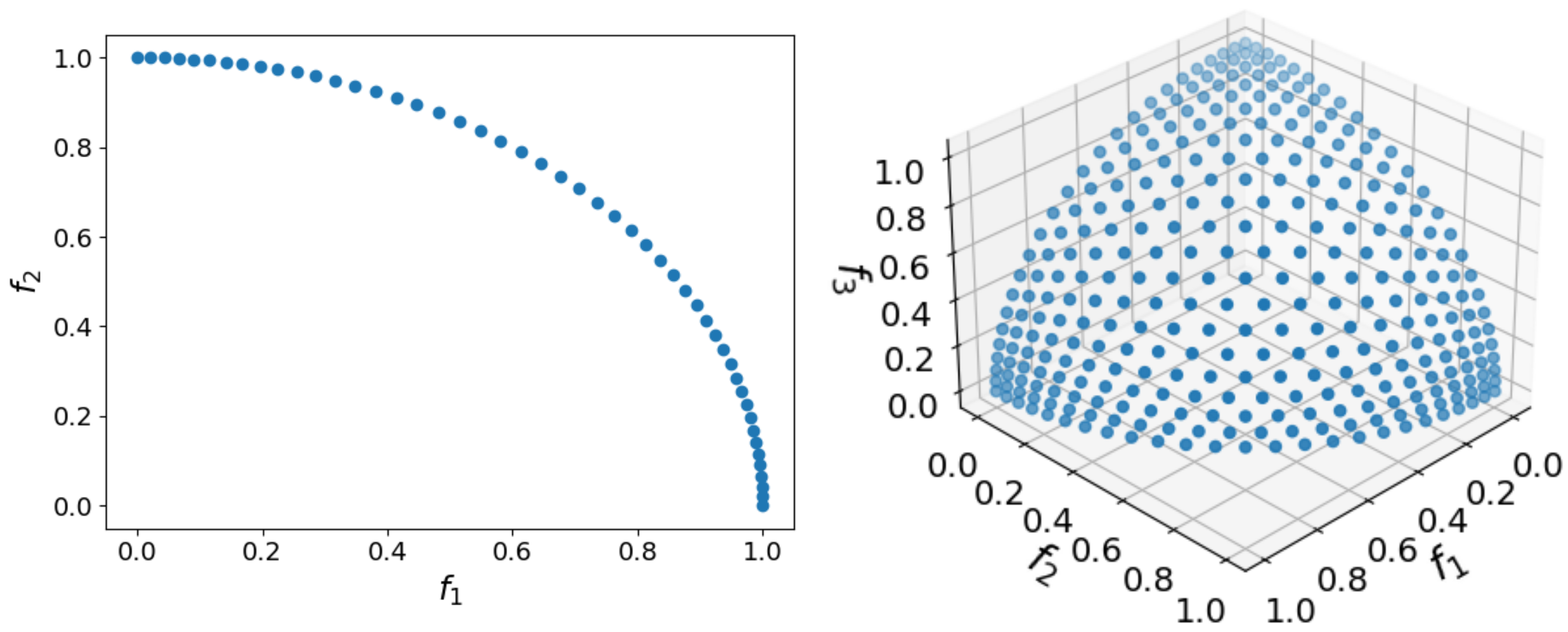
- The set of test functions has been substantially augmented including DTLZ2.
3. The Probability Simplex and the Wasserstein Space
4. Problem Formulation
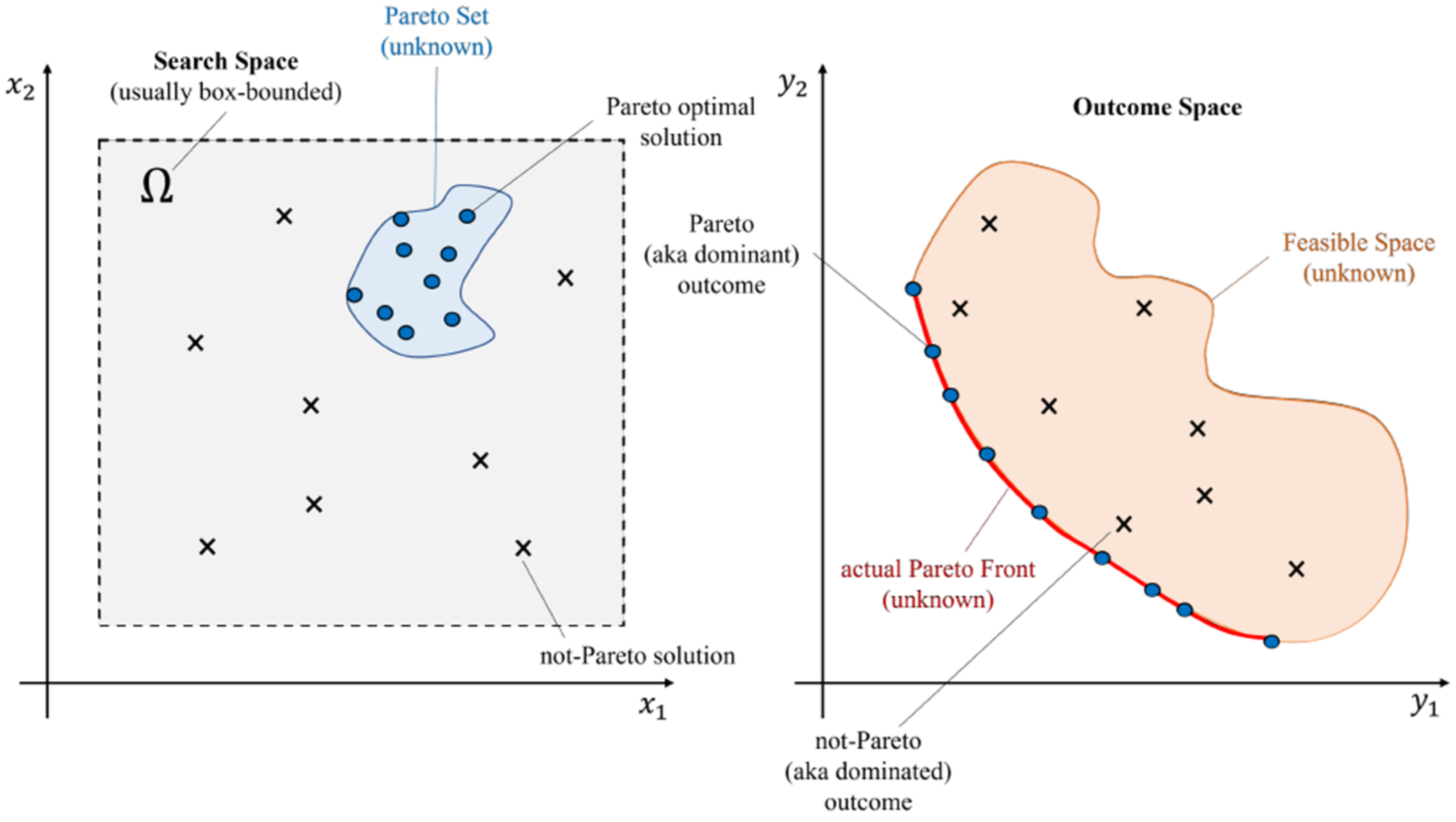
4.1. Multi-Objective Optimization
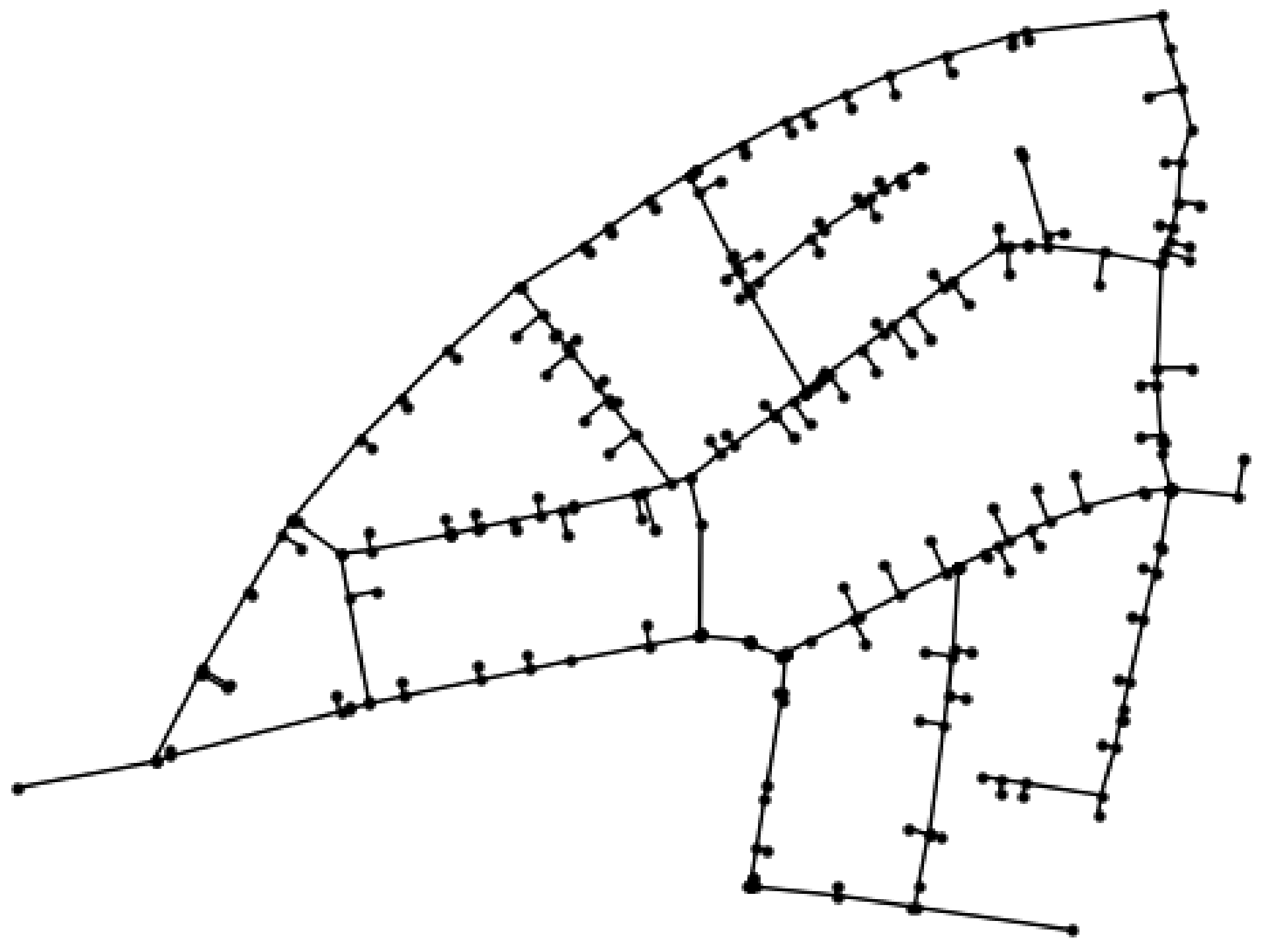
4.2. Optimal Sensor Placement
4.3. Simulation and Event Data Description
5. Wasserstein-Enabled Multi-Objective Evolutionary Algorithm
6. Computational Results
6.1. Experimental Setting
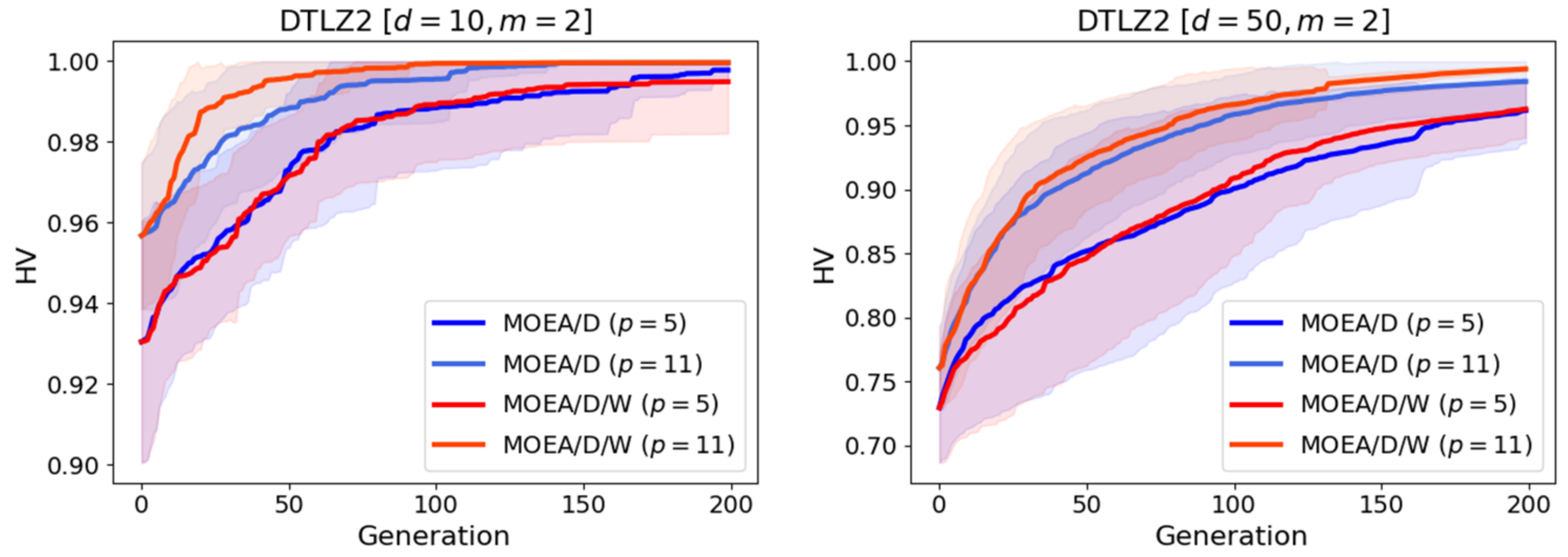
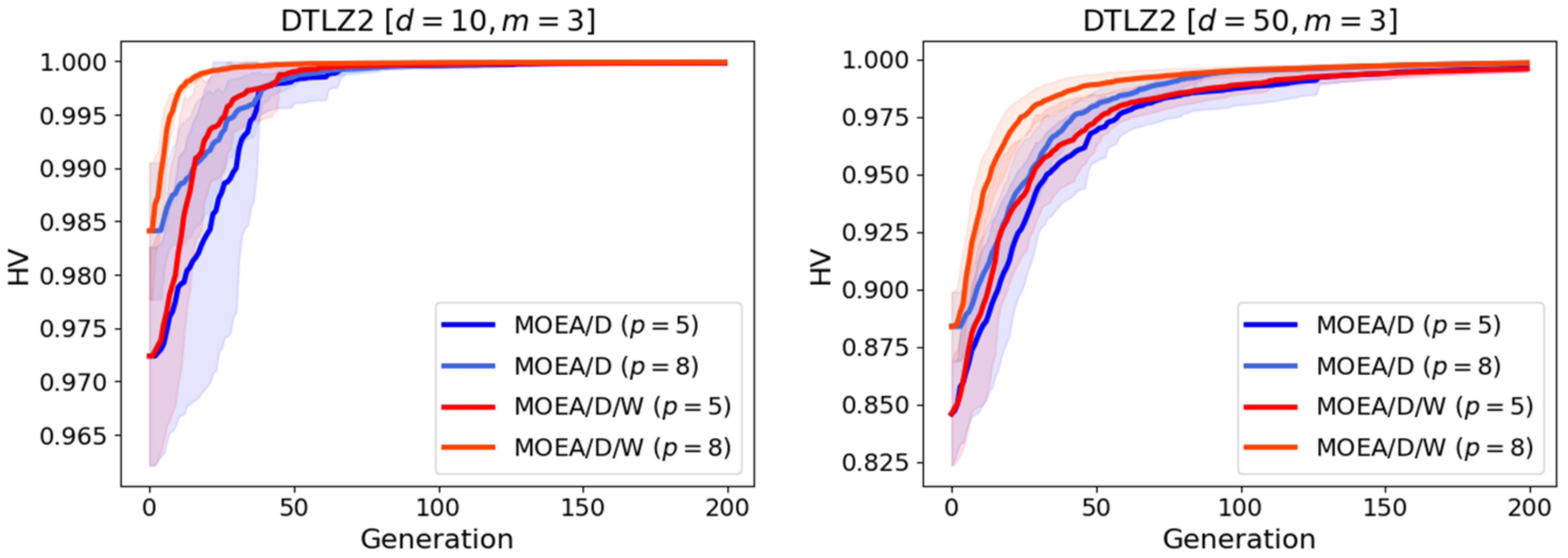
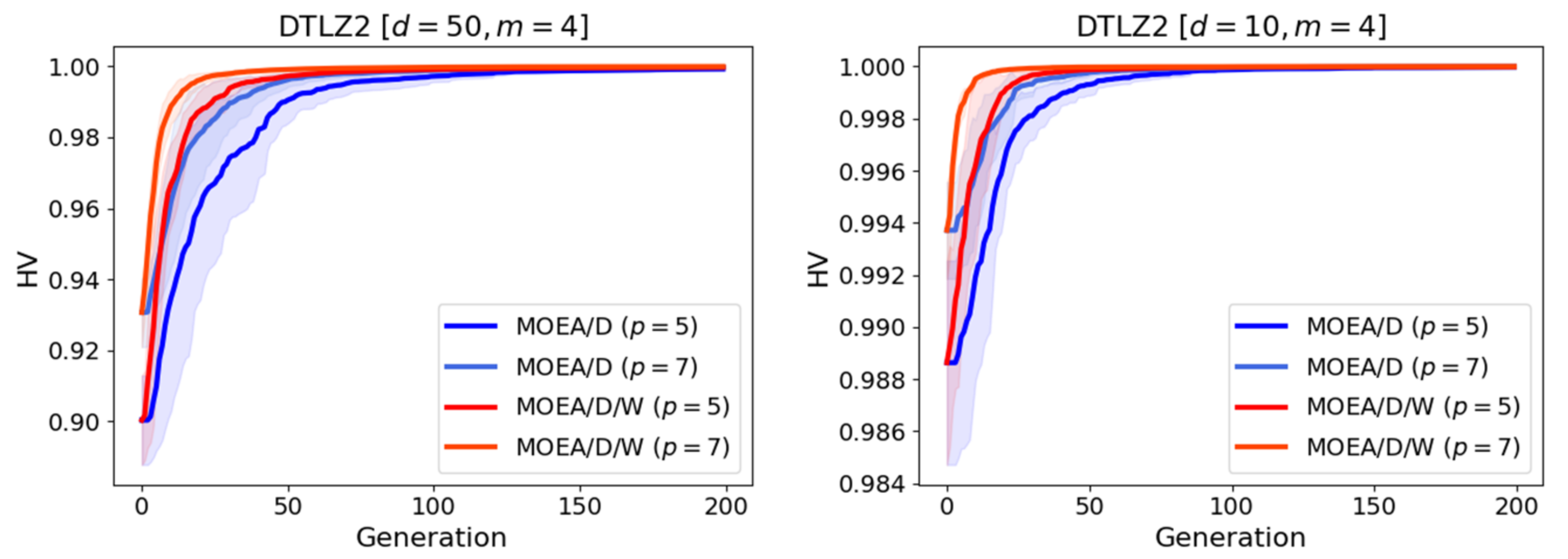
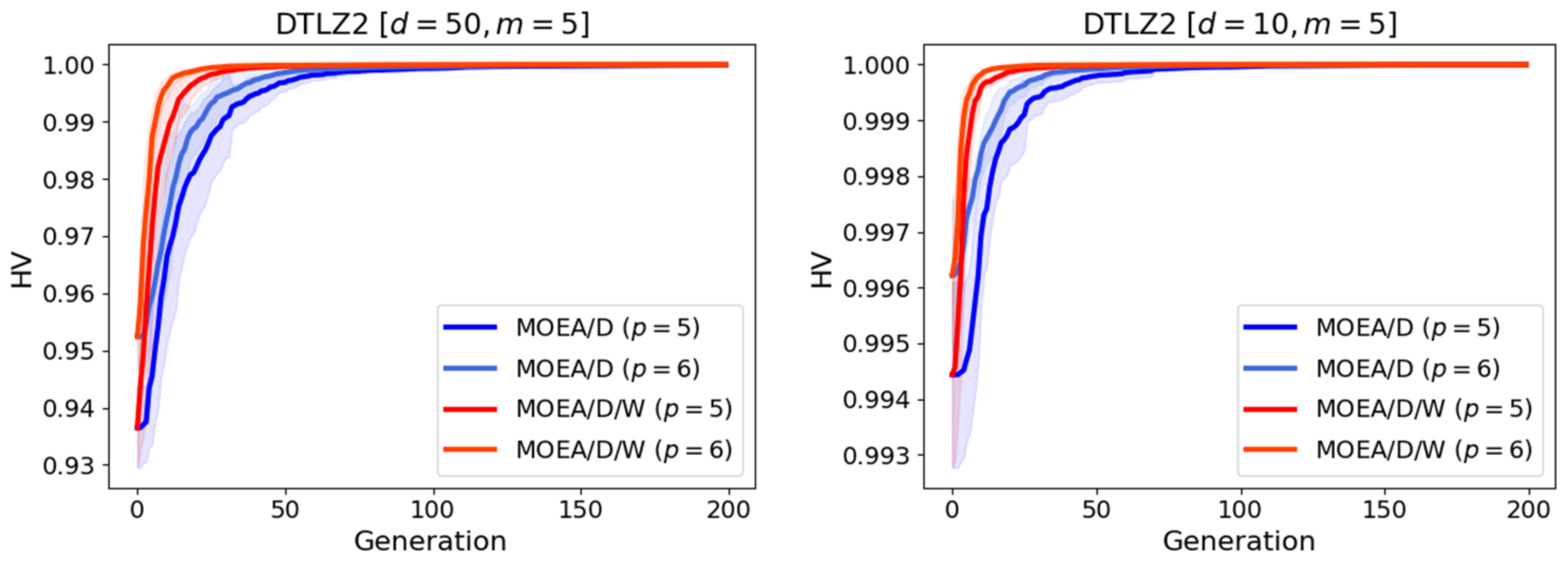
6.2. Results on Test Functions
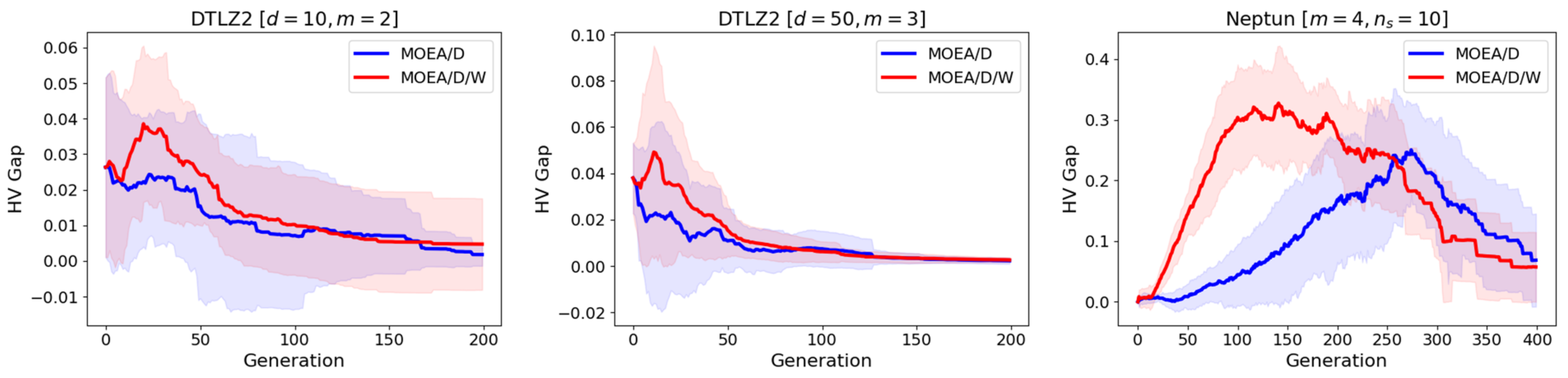
6.3. Results of Optimal Sensor Placement
6.4. Discussion of the Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cori, A.; Nouvellet, P.; Garske, T.; Bourhy, H.; Nakouné, E.; Jombart, T. A Graph-Based Evidence Synthesis Approach to Detecting Outbreak Clusters: An Application to Dog Rabies. PLoS Comput. Biol. 2018, 14, e1006554. [Google Scholar] [CrossRef]
- Yu, P.-D.; Tan, C.W.; Fu, H.-L. Epidemic Source Detection in Contact Tracing Networks: Epidemic Centrality in Graphs and Message-Passing Algorithms. IEEE J. Sel. Top. Signal Process. 2022, 16, 234–249. [Google Scholar] [CrossRef]
- Gangireddy, S.C.R.; Long, C.; Chakraborty, T. Unsupervised Fake News Detection: A Graph-Based Approach. In Proceedings of the 31st ACM Conference on Hypertext and Social Media, Online, 13–15 July 2020; pp. 75–83. [Google Scholar]
- Xu, W.; Wu, J.; Liu, Q.; Wu, S.; Wang, L. Evidence-Aware Fake News Detection with Graph Neural Networks. In Proceedings of the ACM Web Conference 2022, Online, 25–29 April 2022; pp. 2501–2510. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Monge, G. Mémoire sur la Théorie des Déblais et des Remblais. In Histoire de l’Académie Royale des Sciences de Paris; Imprimerie Royale: Louvre, France, 1781. [Google Scholar]
- Kantorovich, L. On the Transfer of Masses (in Russian). Proc. Dokl. Akad.Nauk. 1942, 37, 227–229. [Google Scholar]
- Villani, C. Optimal Transport: Old and New; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Volume 338. [Google Scholar]
- Peyré, G.; Cuturi, M. Computational Optimal Transport. arXiv 2020, arXiv:1803.00567. [Google Scholar]
- Redko, I.; Vayer, T.; Flamary, R.; Courty, N. CO-Optimal Transport. arXiv 2020, arXiv:2002.03731. [Google Scholar]
- Öcal, K.; Grima, R.; Sanguinetti, G. Parameter Estimation for Biochemical Reaction Networks Using Wasserstein Distances. J. Phys. A Math. Theor. 2019, 53, 034002. [Google Scholar] [CrossRef]
- Vayer, T.; Chapel, L.; Flamary, R.; Tavenard, R.; Courty, N. Optimal Transport for Structured Data with Application on Graphs. arXiv 2018, arXiv:1805.09114. [Google Scholar]
- Frogner, C.; Mirzazadeh, F.; Solomon, J. Learning Embeddings into Entropic Wasserstein Spaces. arXiv 2019, arXiv:1905.03329. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein Generative Adversarial Networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 214–223. [Google Scholar]
- Ponti, A.; Candelieri, A.; Archetti, F. A New Evolutionary Approach to Optimal Sensor Placement in Water Distribution Networks. Water 2021, 13, 1625. [Google Scholar] [CrossRef]
- Margarida, D.; Antunes, C.H. Multi-Objective Optimization of Sensor Placement to Detect Contamination in Water Distribution Networks. In Proceedings of the Companion Publication of the 2015 Annual Conference on Genetic and Evolutionary Computation, Madrid, Spain, 11–15 July 2015; pp. 1423–1424. [Google Scholar]
- Candelieri, A.; Soldi, D.; Archetti, F. Cost-Effective Sensors Placement and Leak Localization–the Neptun Pilot of the ICeWater Project. J. Water Supply Res. Technol.—AQUA 2015, 64, 567–582. [Google Scholar] [CrossRef]
- Naserizade, S.S.; Nikoo, M.R.; Montaseri, H. A Risk-Based Multi-Objective Model for Optimal Placement of Sensors in Water Distribution System. J. Hydrol. 2018, 557, 147–159. [Google Scholar] [CrossRef]
- Beume, N.; Naujoks, B.; Emmerich, M.T.M. SMS-EMOA: Multiobjective Selection Based on Dominated Hypervolume. Eur. J. Oper. Res. 2007, 181, 1653–1669. [Google Scholar] [CrossRef]
- Weickgenannt, M.; Kapelan, Z.; Blokker, M.; Savic, D.A. Risk-Based Sensor Placement for Contaminant Detection in Water Distribution Systems. J. Water Resour. Plan. Manag. 2010, 136, 629–636. [Google Scholar] [CrossRef]
- Deb, K.; Myburgh, C. A Population-Based Fast Algorithm for a Billion-Dimensional Resource Allocation Problem with Integer Variables. Eur. J. Oper. Res. 2017, 261, 460–474. [Google Scholar] [CrossRef]
- Wang, Y.; van Stein, B.; Bäck, T.; Emmerich, M. A Tailored NSGA-III for Multi-Objective Flexible Job Shop Scheduling. In Proceedings of the 2020 IEEE Symposium Series on Computational Intelligence (SSCI), Canberra, Australia, 1–4 December 2020; pp. 2746–2753. [Google Scholar]
- Shi, J.; Sun, J.; Zhang, Q. Multi-Objectivization Inspired Metaheuristics for the Sum-of-the-Parts Combinatorial Optimization Problems. Appl. Soft Comput. 2021, 103, 107157. [Google Scholar] [CrossRef]
- Li, M.; Yao, X. Quality Evaluation of Solution Sets in Multiobjective Optimisation: A Survey. ACM Comput. Surv. (CSUR) 2019, 52, 1–38. [Google Scholar] [CrossRef]
- Knowles, J.D. ParEGO: A Hybrid Algorithm with on-Line Landscape Approximation for Expensive Multiobjective Optimization Problems. IEEE Trans. Evol. Comput. 2006, 10, 50–66. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, W.; Tsang, E.; Virginas, B. Expensive Multiobjective Optimization by MOEA/D with Gaussian Process Model. IEEE Trans. Evol. Comput. 2009, 14, 456–474. [Google Scholar] [CrossRef]
- Akimoto, Y.; Hansen, N. Projection-Based Restricted Covariance Matrix Adaptation for High Dimension. In Proceedings of the Genetic and Evolutionary Computation Conference 2016, Denver, CO, USA, 20–24 July 2016; pp. 197–204. [Google Scholar]
- Berry, J.; Hart, W.E.; Phillips, C.A.; Uber, J.G.; Watson, J.-P. Sensor Placement in Municipal Water Networks with Temporal Integer Programming Models. J. Water Resour. Plan. Manag. 2006, 132, 218–224. [Google Scholar] [CrossRef]
- Zhao, Y.; Schwartz, R.; Salomons, E.; Ostfeld, A.; Poor, H.V. New Formulation and Optimization Methods for Water Sensor Placement. Environ. Model. Softw. 2016, 76, 128–136. [Google Scholar] [CrossRef]
- Chowdhury, S.; Mémoli, F. The Gromov–Wasserstein Distance between Networks and Stable Network Invariants. Inf. Inference A J. IMA 2019, 8, 757–787. [Google Scholar] [CrossRef]
- Xu, H.; Luo, D.; Carin, L. Scalable Gromov-Wasserstein Learning for Graph Partitioning and Matching. Adv. Neural Inf. Process. Syst. 2019, 3046–3056, 1742. [Google Scholar]
- Xu, H. Gromov-Wasserstein Factorization Models for Graph Clustering. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 6478–6485. [Google Scholar]
- Solomon, J.; Rustamov, R.M.; Guibas, L.J.; Butscher, A. Wasserstein Propagation for Semi-Supervised Learning. In Proceedings of the 31th International Conference on Machine Learning, ICML 2014, Beijing, China, 21–26 June 2014; Volume 32, pp. 306–314. [Google Scholar]
- Xu, H.; Luo, D.; Carin, L.; Zha, H. Learning Graphons via Structured Gromov-Wasserstein Barycenters. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 10505–10513. [Google Scholar]
- Klise, K.A.; Murray, R.; Haxton, T. An Overview of the Water Network Tool for Resilience (WNTR). Available online: https://www.osti.gov/servlets/purl/1569415 (accessed on 29 March 2023).
- Ponti, A.; Candelieri, A.; Archetti, F. A Wasserstein Distance Based Multiobjective Evolutionary Algorithm for the Risk Aware Optimization of Sensor Placement. Intell. Syst. Appl. 2021, 10, 200047. [Google Scholar] [CrossRef]
- Das, I.; Dennis, J.E. Normal-Boundary Intersection: A New Method for Generating the Pareto Surface in Nonlinear Multicriteria Optimization Problems. SIAM J. Optim. 1998, 8, 631–657. [Google Scholar] [CrossRef]

| Function Evaluations | |||
|---|---|---|---|
| 2 | 5 | 6 | 1200 |
| 11 | 12 | 2400 | |
| 3 | 5 | 21 | 4200 |
| 8 | 45 | 9000 | |
| 4 | 5 | 56 | 11,200 |
| 7 | 120 | 24,000 | |
| 5 | 5 | 126 | 25,200 |
| 6 | 210 | 42,000 |
| Function Evaluations | |||
|---|---|---|---|
| 2 | 6 | 7 | 2800 |
| 13 | 14 | 5600 | |
| 4 | 6 | 84 | 33,600 |
| 8 | 165 | 66,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ponti, A.; Candelieri, A.; Giordani, I.; Archetti, F. Intrusion Detection in Networks by Wasserstein Enabled Many-Objective Evolutionary Algorithms. Mathematics 2023, 11, 2342. https://doi.org/10.3390/math11102342
Ponti A, Candelieri A, Giordani I, Archetti F. Intrusion Detection in Networks by Wasserstein Enabled Many-Objective Evolutionary Algorithms. Mathematics. 2023; 11(10):2342. https://doi.org/10.3390/math11102342
Chicago/Turabian StylePonti, Andrea, Antonio Candelieri, Ilaria Giordani, and Francesco Archetti. 2023. "Intrusion Detection in Networks by Wasserstein Enabled Many-Objective Evolutionary Algorithms" Mathematics 11, no. 10: 2342. https://doi.org/10.3390/math11102342
APA StylePonti, A., Candelieri, A., Giordani, I., & Archetti, F. (2023). Intrusion Detection in Networks by Wasserstein Enabled Many-Objective Evolutionary Algorithms. Mathematics, 11(10), 2342. https://doi.org/10.3390/math11102342






