Magnetic Field Dynamical Regimes in a Large-Scale Low-Mode αΩ-Dynamo Model with Hereditary α-Quenching by Field Energy

Abstract

The article considers a large-scale model of an $\alpha \Omega$-dynamo in the low-mode approximation. The intensity of the $\alpha$-effect is regulated by a process that depends on the energy of the magnetic field and has hereditarity properties (finite “memory”). The regulation process is included in the MHD-system in the form of an additive correction. The action character of the process is defined by the alternating kernel with variable parameters: the damping frequency and the damping coefficient. The Reynolds number and the $\alpha$-effect measure are the control parameters of the system. Information about the action of a large-scale generator is contained in the Reynolds number, and that about the action of a turbulent one is contained in the measure of the $\alpha$-effect. The stability of the solution of the MHD-system is studied depending on the values of the control parameters and the parameters of the alternating kernel. Based on the results of numerical simulation of the dynamical regimes, limitations are determined for the values of the model parameters at which the regimes are reproduced against the background of small oscillations of the viscous liquid velocity field. The results of the study of the stability of solutions and numerical simulations of the dynamical regimes are represented on the phase plane of the control parameters. The paper investigates the question of changing the pattern on the phase plane depending on the values of the damping coefficient, the damping frequency, and the waiting time. A comparison is made with the results obtained earlier, when the $\alpha$-effect intensity is a constant or is regulated by a process with an exponential kernel and the same values of the damping coefficient.

1. Introduction

This article generalizes research in one of the directions of the cycle of papers of the IKIR FEB RAS on the study of a low-mode model of Earth’s dynamo [1,2,3,4,5,6,7,8]. Despite the progress made in geomagnetism theory, the problem of the origin of the Earth’s magnetic field and that of space objects has not been fully resolved. Therefore, the task of investigating varied approximations that reproduce the geomagnetic field close to the observed one is relevant [9,10,11,12]. Three classical mechanisms are used to describe the dynamo systems of astrophysical objects: ${\alpha }^2$, ${\alpha }^2\Omega$ and $\alpha \Omega$ [13,14,15,16]. Other mechanisms can also be considered [12,17]. It should be noted that the scope of application of the finite element method [17] in the study of magnetic systems goes beyond the limits of magnetohydrodynamics [18,19,20]. In this paper, a study is carried out for Earth-type objects. The dynamos of such objects assume a strong differential rotation of the object and turbulence in the nature of the conductive medium motion [3,5,13,14,15,21], and the presence of chaotic reversals without significant restructuring of the conducting medium motion [22]. The $\alpha \Omega$-dynamo model is the most suitable for describing such properties [13]. The mechanisms of the ${\alpha }^2\Omega$- and ${\alpha }^2$-dynamos are used under the condition of weak or non-existent differential rotation of the conductive medium.

To investigate the nature of the magnetic field occurrence, its structure and possible changes, various approximate solutions of the geodynamo equations are used, because their exact solutions are unknown. The study is carried out using both direct number simulation [23,24], and based on simplified models [5,7,16]. Model studies of the MHD-system behavior are limited by computational capabilities. Direct simulation of MHD-equations makes it possible to construct MHD-flows, but only on small timescales, and to reproduce numerous reversal regimes. However, it is difficult to determine the cause of the reversals, since the complete equations include a large set of parameters. In addition, the estimates of these parameters either differ by many orders of magnitude, or do not exist. Therefore, to explain the physical cause of reversals and to understand the most important properties of the polarity change phenomenon, it is preferable to use simple low-dimensional dynamical systems. This approach makes it possible to reproduce the evolution of large-scale spatial structures on large timescales and to reduce the number of variable parameters. The choice of parameters included in the system is specified by the information about the magnetic field and the velocity field contained in them. Thus, changes in the values of the corresponding parameters give an understanding of the nature of the changes in the considered fields [9,14,21,22].

In the framework of this study, the $\alpha \Omega$-dynamo model is considered in a low-mode approximation. The generation of the magnetic and the velocity fields is defined by the action of $\Omega$- and $\alpha$-generators. The intensity of the generators’ action changes in time under the action of the Lorentz force. In the deterministic dynamic model of $\alpha \Omega$-dynamo, a process with a finite “memory” is used as an additive regulator of the $\alpha$-effect intensity (the quenching process of the $\alpha$-effect, i.e., $\alpha$-quenching). The process is defined by a functional, the kernel of which is an alternating function $J\left(t\right)=e^{-bt}cosat$ with a coefficient b and a frequency a of the damped oscillations [8,25,26]. It should be noted that a rescaled and dimensionless MHD-system is used in the paper. The timeline unit is equal to the damping time of the magnetic field [7].

The purpose of this study is to determine the values of the parameters in the model at which various dynamical regimes of the magnetic field can be obtained, including a chaotic regime on the background of the insignificantly varying velocity field, and to conduct a comparative analysis of the results of numerical simulation with previously obtained results at a constant intensity of the $\alpha$-effect and using $\alpha$-quenching with the kernel $J\left(t\right)=e^{-bt}$ [7].

2. Statement of a Problem

The study uses the $\alpha \Omega$-dynamo model and assumes the conditions of axial symmetry of both the magnetic field $\mathbf{B}$ and the velocity field $\mathbf{v}$ in a spherical shell of a viscous incompressible fluid rotating at a constant angular velocity $\Omega$ around the Earth’s axis. In the framework of the model, the following conditions for the core are accepted: the physical parameters of the viscous fluid are unchanged, the turbulence is isotropic and the velocity field of the fluid satisfies the adhesion conditions at the boundaries of the spherical shell, i.e., it is equal to zero. It is believed that the permeability in the core is the same, and the vacuum boundary conditions at the outer boundary of the core and boundedness conditions at the center of the Earth are satisfied. It is also assumed that the turbulent $\alpha$-effect is antisymmetric about the equator. Therefore, the scalar parametrization can be given by a function $\tilde{\alpha }(r,\theta )={\alpha }_{0}a\left(r\right)cos\theta ={\alpha }_0\alpha (r,\theta )$, where the coefficient ${\alpha }_0$ is positive and determines the highest intensity of the $\alpha$-effect, $\alpha (r,\theta )$ is a dimensionless quantity that satisfies the condition $max\left|\alpha \right(r,\theta \left)\right|=1$ and the radial component $a\left(r\right)=r$. In accordance with the considered dynamo model, it is assumed that the action of the Archimedean (buoyancy) force with a mass density ${\mathbf{f}}_{out}$ determines the differential rotation of the averaged flow $\overline{\mathbf{v}}$ [14,15,21]. Thus, the MHD-equations, including the equations of the Navier–Stokes and the magnetic field induction $\mathbf{B}$, taking into account the turbulent $\alpha$-effect, the continuity condition of the velocity field $\mathbf{v}$, the solenoidality condition of the magnetic field $\mathbf{B}$ and boundary conditions of adhesion, take the form [8]:

$${\displaystyle \begin{array}{c}{\displaystyle \frac{\partial \mathbf{v}}{\partial t}+(\mathbf{v}\nabla )\mathbf{v}+{\mathbf{f}}_c=\nu \Delta \mathbf{v}-\frac{1}{{\rho }_0}\nabla P-{\mathbf{f}}_K+{\mathbf{f}}_{out}+{\mathbf{f}}_L,}\hfill \\ \frac{\partial \mathbf{B}}{\partial t}=\nabla \times (\mathbf{v}\times \mathbf{B})+\nabla \times \left(\tilde{\alpha }(r,\theta )\mathbf{B}\right)+{\nu }_m\Delta \mathbf{B},\hfill \\ \Delta \mathbf{v}=0,\hfill \\ \Delta \mathbf{B}=0,\hfill \\ \mathbf{v}\left({\mathbf{r}}_1\right)=\mathbf{v}\left({\mathbf{r}}_2\right)=0,\hfill \end{array}}$$

(1)

where ${\mathbf{f}}_c$ is centrifugal force acceleration, $\nu$ is kinematic viscosity, ${\rho }_0$ is density, P is pressure, ${\mathbf{f}}_K$ is Coriolis force mass density, ${\mathbf{f}}_L$ is Lorentz force mass density, ${\nu }_m$ is magnetic viscosity and ${\mathbf{r}}_{i,(i=1,2)}$ is the radius-vector of the (inner, outer) boundary of the spherical shell.

If the $\alpha$-effect intensity ${\alpha }_0$ is assumed to be constant, then the MHD-system admits three types of solutions [7] for a magnetic field in the range of changes of the control parameters, namely, damped (with or without oscillations), infinitely increasing (with or without oscillations) and steady oscillations. The intensity ${\alpha }_0$ changes in time under the action of the Lorentz force. Assuming that such action depends on the prehistory and on the changes in the magnetic field, we define it by the process $Z\left(t\right)$, which is given by the functional

$$Z\left(t\right)=\underset{0}{\overset{t}{\int }}J(t-\tau )Q\left(\mathbf{B}\left(\tau \right),\mathbf{B}\left(\tau \right)\right)\mathrm{d}\tau$$

(2)

with the velocity dimension [m/s], as well as the function $\tilde{\alpha }(r,\theta )$. The dimensionless kernel $J(t-\tau )$ defines the character of the action of the process, and the quadratic form $Q\left(\mathbf{B}\right(\tau ),\mathbf{B}(\tau \left)\right)$ determines its strength. Thus, process Z at time t depends on the previous values of field $\mathbf{B}$, i.e., it has memory (hereditarity), which is implemented through the kernel function $J(t-\tau )$. The use of such a kind of kernel provides time invariance of the quenching functional.

Taking into account the $\alpha$-quenching in the form of the functional (2), the MHD-system (1) can be written as follows [8]

$${\displaystyle \begin{array}{c}{\displaystyle \frac{\partial \mathbf{v}}{\partial t}+(\mathbf{v}\nabla )\mathbf{v}+{\mathbf{f}}_c=\nu \Delta \mathbf{v}-\frac{1}{{\rho }_0}\nabla P-{\mathbf{f}}_K+{\mathbf{f}}_{out}+{\mathbf{f}}_L,}\hfill \\ \frac{\partial \mathbf{B}}{\partial t}=\nabla \times (\mathbf{v}\times \mathbf{B})+\nabla \times ({\alpha }_0-Z\left(t\right))\alpha (r,\theta )\mathbf{B}+{\nu }_m\Delta \mathbf{B},\hfill \\ \Delta \mathbf{v}=0,\hfill \\ \Delta \mathbf{B}=0,\hfill \\ \mathbf{v}\left({\mathbf{r}}_1\right)=\mathbf{v}\left({\mathbf{r}}_2\right)=0\hfill \end{array}}$$

(3)

.

A detailed description of the rescaling and the dimensionlessness of MHD-system (3) is carried out in the article [7]; therefore, within the framework of this paper, we use the already transformed system of MHD-equations with the $\alpha$-quenching [8]

$${\displaystyle \begin{array}{c}{\displaystyle \frac{\partial {\mathbf{v}}^{\prime }}{\partial t^{\prime }}=P_m\Delta {\mathbf{v}}^{\prime }-\nabla P^{\prime }-E^{-1}{P}_m({\mathbf{e}}_z\times {\mathbf{v}}^{\prime })+{\mathbf{f}}_{out}^{\prime }+(\nabla \times {\mathbf{B}}^{\prime })\times {\mathbf{B}}^{\prime },}\hfill \\ \frac{\partial {\mathbf{B}}^{\prime }}{\partial t^{\prime }}=R{e}_m[\nabla \times ({\mathbf{v}}^{\prime }\times {\mathbf{B}}^{\prime })]+(R_{\alpha }-Z^{\prime }\left(t^{\prime }\right))[\nabla \times \alpha (r,\theta ){\mathbf{B}}^{\prime })]+\Delta {\mathbf{B}}^{\prime },\hfill \\ \Delta {\mathbf{v}}^{\prime }=0,\hfill \\ \Delta {\mathbf{B}}^{\prime }=0,\hfill \\ {\mathbf{v}}^{\prime }\left(\frac{{\mathbf{r}}_1}{L}\right)={\mathbf{v}}^{\prime }\left({\mathbf{e}}_2\right)=0,\hfill \end{array}}$$

(4)

where $L=r_2$ [m] is characteristic linear size, ${\mathbf{e}}_z$ is the unit vector, directed along the axis of rotation, $R{e}_m$ is the magnetic Reynolds number, $R_{\alpha }$ is the measure of the $\alpha$-effect, $P_m$ is the magnetic Prandtl number and E is the Ekman number. The unit of dimensionless time $t^{\prime }$ corresponds to the damping time of the magnetic field whithout external influence. This is the dissipation time of the magnetic field, equal to $L^2/{\nu }_m$ [s], the order of which is ${10}^4$ years. The magnetic Reynolds number $R{e}_m$ and the measure of the $\alpha$-effect $R_{\alpha }$ are the control parameters of the system. Further in the article, to simplify the writing of the system (4), the primes will not be written.

3. Mathematical Model

Based on the statement of a problem, the velocity of the average flow $\overline{\mathbf{v}}$ of a viscous liquid has the character of differential rotation. The model considers one layer of differential rotation. The source of large-scale differential rotation is turbulence [27]. When a large-scale toroidal field appears, Coriolis drift leads to the appearance of a large-scale poloidal field, which also gives large-scale convection. Continuing the process further, we obtain a family of toroidal and poloidal modes. To represent the velocity $\mathbf{v}(t,\mathbf{r})$, a single-mode approximation by the eigenmode ${\mathbf{v}}_0\left(\mathbf{r}\right)$ of free small oscillations of a viscous rotating liquid (Poincare problem solution) is used, proposed in papers [1,2,5]. This choice is explained by the property of Poincare modes to preserve information about rotation, because the Galerkin procedure removes the Coriolis term from the MHD-system in the case of a single-mode approximation. However, the exact solutions of the Poincare problem in the case of a viscous liquid for a spherical shell are unknown [28]. Therefore, the Poincare mode can be approximated by a linear combination of toroidal ${\mathbf{v}}_{k,n,m}^T(r,\theta ,\varphi )$ and poloidal ${\mathbf{v}}_{k,n,m}^P(r,\theta ,\varphi )$ eigenmodes of free oscillations of a non-rotating liquid, because these modes form a complete system. Indices $k,n,m$ correspond to discretization of the oscillation spectrum in the radial, latitudinal and longitudinal directions, respectively [1,2]. Index k is equal to the number of convection layers in the radial direction, and index $m=0$ in the axisymmetric case. The choice of ${\mathbf{v}}_{k,n,m}^T$ and ${\mathbf{v}}_{k,n,m}^P$ modes satisfies the following conditions: firstly, such modes generate an invariant subspace of the operator of the Poincare problem, and secondly, this subspace contains the ${\mathbf{v}}_{k,1,0}^T$ mode responsible for the differential rotation. Thus, in this model, it is assumed that, in the first approximation, the differential rotation is described by the component ${\mathbf{v}}_{0,1,0}^T$. Its Coriolis drift leads to the appearance of the nearest poloidal component ${\mathbf{v}}_{0,2,0}^P$ from the invariant subspace

$$H_0^T=\{{\mathbf{v}}_{k_1,1,0}^T,{\mathbf{v}}_{k_2,2,0}^P,{\mathbf{v}}_{k_3,3,0}^T,{\mathbf{v}}_{k_4,4,0}^P,\cdots \},k_i=0,1,2,\dots .$$

Then we increase the index values by one more to surround the poloidal mode on both sides. Accordingly, three more nearest toroidal modes ${\mathbf{v}}_{1,1,0}^T$, ${\mathbf{v}}_{0,3,0}^T$, ${\mathbf{v}}_{1,3,0}^T$ are obtained from the same subspace. The combination of the obtained modes gives a rough approximation of the Poincare mode ${\mathbf{v}}_0\left(\mathbf{r}\right)$ [7]:

$$\begin{array}{c}\mathbf{v}(t,\mathbf{r})=u\left(t\right){\mathbf{v}}_0\left(\mathbf{r}\right)=\\ =u\left(t\right)({\alpha }_1{\mathbf{v}}_{0,1,0}^T\left(\mathbf{r}\right)+{\alpha }_2{\mathbf{v}}_{0,2,0}^P\left(\mathbf{r}\right)+{\alpha }_3{\mathbf{v}}_{0,3,0}^T\left(\mathbf{r}\right)+{\alpha }_{11}{\mathbf{v}}_{1,1,0}^T\left(\mathbf{r}\right)+{\alpha }_{13}{\mathbf{v}}_{1,3,0}^T\left(\mathbf{r}\right)),\end{array}$$

(5)

where time independence of the velocity field components is assumed, $\mid {\mathbf{v}}_0\left(\mathbf{r}\right)\mid =1$, the value $u\left(t\right)$ is the amplitude of the velocity field and the values ${\alpha }_i$ are the coefficients of vector decomposition in the selected basis. Further, only significant subscripts will be used when writing the modes. The coefficients ${\alpha }_i$ are calculated when solving the Poincare problem for the dimensionless Navier–Stokes equation from the MHD-system (4), where it is assumed ${\mathbf{v}}^{\prime }=e^{-\lambda t}{\mathbf{v}}_0\left(\mathbf{r}\right)$ and $P^{\prime }=e^{-\lambda t}p\left(\mathbf{r}\right)$:

$${\displaystyle -\lambda {\mathbf{v}}_0\left(\mathbf{r}\right)=P_m\Delta {\mathbf{v}}_0\left(\mathbf{r}\right)-\nabla p\left(\mathbf{r}\right)-E^{-1}{P}_m({\mathbf{e}}_z\times {\mathbf{v}}_0\left(\mathbf{r}\right)).}$$

(6)

By substituting the decomposition of the velocity mode ${\mathbf{v}}_0\left(\mathbf{r}\right)$ from the expression (5) into the Equation (6) and applying the Galerkin method, a system of equations was obtained

$$(\lambda -P_m{\lambda }_s){\alpha }_s-E^{-1}{P}_m\sum _j{\alpha }_j{P}_{sj}=0,$$

(7)

where the coefficients $P_{sj}=\langle {\mathbf{e}}_z\times {\mathbf{v}}_j\left(\mathbf{r}\right),{\mathbf{v}}_s\left(\mathbf{r}\right)\rangle$ (

Table 1. Values of the coefficients $P_{sj}$.

s	j	$P_{sj}$
2	1	−0.1929
1	2	0.1929
3	2	−0.3648
11	2	0.402
13	2	0.2993
2	3	0.3648
2	11	−0.402
2	13	−0.2993

) and ${\lambda }_s=-\langle \Delta {\mathbf{v}}_s\left(\mathbf{r}\right),{\mathbf{v}}_s\left(\mathbf{r}\right)\rangle$ (

Table 2. Values of the coefficients ${\lambda }_s$ and ${\alpha }_s$.

s	${\mathit{\lambda }}_{\mathit{s}}$	${\mathit{\alpha }}_{\mathit{s}}$
1	28.1592	−0.9353
2	86.5734	$1.7497\times {10}^{-6}$
3	50.9094	−0.33353
11	98.8577	0.1048
13	125.9759	0.0556

) are volume integrals calculated by the program [29,30], the subscripts s and j take the values of significant subscripts from the expression (5) and the values $E^{-1}={10}^{-7}$ and $P_m=5$ correspond to the Earth’s core [5,22]. The values of the coefficients that are not specified in the tables are equal to zero. In addition, all the values required for calculations are attached in Supplementary Materials. The characteristic equation of the system (7) gives non-trivial solutions $\lambda$. For each real solution $\lambda$, the value ${\alpha }_2$ is calculated based on the condition ${\displaystyle \sum _j}{\alpha }_j^2=1$ (because the vector ${\mathbf{v}}_0$ is a unit vector in a given basis). Further, the solutions obtained with the smallest real value of the eigenvalue $\lambda$ are used. It was noted in the paper [6], that with an increase in the eigenvalue $\lambda$, the frequency of oscillations increases without changing the dynamical regimes of the magnetic field as a whole.

To represent the magnetic field, some of the ohmic dissipation modes ${\mathbf{B}}_{k,n,m}^T$ and ${\mathbf{B}}_{k,n,m}^P$, i.e., eigenmodes of the free damped oscillation [1,31], are used. The required number of modes for the occurrence of reversals in the $\alpha \Omega$-dynamo model was defined in the papers [1,5,31] according to the scheme proposed by the authors of the study [16]. In the presence of a dipole component ${\mathbf{B}}_{0,1,0}^P\left(\mathbf{r}\right)$ of the magnetic field, differential rotation generates other components of the magnetic field. Depending on the method of specifying the radial type of the $\alpha$-effect and on the choice of the variant of the Poincare mode composition, the appearance of oscillatory-type changes in the magnetic field turned out to be possible in the presence of three components of the magnetic field: dipole poloidal ${\mathbf{B}}_{0,1,0}^P\left(\mathbf{r}\right)$, toroidal ${\mathbf{B}}_{0,2,0}^T\left(\mathbf{r}\right)$ and poloidal ${\mathbf{B}}_{0,3,0}^P\left(\mathbf{r}\right)$ [5,6]. If the decomposition of the magnetic field includes a smaller number of modes, then either there are no reversals, or the magnetic field decays quickly. Thus, to describe the magnetic field with reversals in the $\alpha \Omega$-dynamo model, it is sufficient to use three eigenmodes ${\mathbf{B}}_{0,1,0}^P,{\mathbf{B}}_{0,2,0}^T,{\mathbf{B}}_{0,3,0}^P$ that correspond to the smallest eigenvalues, i.e., the longest damping times. These modes provide an oscillating dynamo [5],

$$\begin{array}{c}\mathbf{B}=B_2^T\left(t\right){\mathbf{B}}_{0,2,0}^T\left(\mathbf{r}\right)+B_1^P\left(t\right){\mathbf{B}}_{0,1,0}^P\left(\mathbf{r}\right)+B_3^P\left(t\right){\mathbf{B}}_{0,3,0}^P\left(\mathbf{r}\right),\hfill \end{array}$$

(8)

where the magnetic field components are assumed to be independent of time. Further, only significant subscripts will be used in the notation of the components.

In the context of this study it is believed that the nature of the quenching process Z(t) is determined by the prehistory on the interval $[0,t]$, the influence of which decreases with distance from the instant of time t. The alternating function specifying damped oscillations with b coefficient and a frequency satisfies this condition and the previously indicated conditions for the kernel $J\left(t\right)$ of the functional (2). The strength of the effect of the process $Z\left(t\right)$ depends on the energy of the magnetic field. Then the process $Z\left(t\right)$ is given by the functional (2) written in the following form:

$$Z\left(t\right)=\underset{0}{\overset{t}{\int }}\left[e^{-b(t-\tau )}cos\left(a(t-\tau )\right)\right]{\mathbf{B}}^2\left(\tau \right)\mathrm{d}\tau .$$

(9)

4. Numerical Method and Model Parameters

The substitution of decompositions (5) and (8) and functional (9) into the MHD-system (4) and the application of the Galerkin method [9] made it possible to obtain the equations of the model that are used for numerical simulation by the Predictor–Corrector Method:

$$\begin{array}{c}{\displaystyle \frac{\mathrm{d}u\left(t\right)}{\mathrm{d}t}}=-P_{m}u\left(t\right){\displaystyle \sum _s}{\alpha }_s^2{\lambda }_s+f_{out}+{\displaystyle \sum _{s,i,j}}{\alpha }_s{L}_{sij}{B}_i\left(t\right)B_j\left(t\right),\hfill \\ {\displaystyle \frac{\mathrm{d}{B}_i\left(t\right)}{\mathrm{d}t}}=R{e}_{m}u\left(t\right){\displaystyle \sum _{s,j}}{\alpha }_s{W}_{isj}{B}_j\left(t\right)-{\mu }_i{B}_i\left(t\right)+(R_{\alpha }-Z){\displaystyle \sum _j}{W}_{ij}^{\alpha }{B}_j\left(t\right),\hfill \\ {\displaystyle \frac{\mathrm{d}Z\left(t\right)}{\mathrm{d}t}}={\displaystyle \sum _j}{B}_j^2\left(t\right)-bZ\left(t\right)-a{Z}_s\left(t\right),{\displaystyle \frac{\mathrm{d}{Z}_s\left(t\right)}{\mathrm{d}t}}=aZ\left(t\right)-b{Z}_s\left(t\right),\hfill \\ i,j=\{1,2,3\},s=\{1,2,3,11,13\},\hfill \end{array}$$

(10)

where ${\lambda }_s=-\langle \Delta {\mathbf{v}}_s,{\mathbf{v}}_s\rangle$ is the eigenvalue of the Poincare mode [29,30] (Table 2), ${\mu }_i=-\langle \Delta {\mathbf{B}}_i,{\mathbf{B}}_i\rangle$ is the viscous dissipation coefficient [29,30], coefficients $L_{sij}=\langle (\nabla \times {\mathbf{B}}_i)\times {\mathbf{B}}_j,{\mathbf{v}}_s\rangle$ (

Table 3. Values of the coefficient $L_{sij}$.

s	i	j	$L_{sij}$
2	1	1	−0.1697
2	1	3	0.1459
1	2	1	0.4873
3	2	1	−0.7552
11	2	1	1.2321
13	2	1	0.1692
2	2	2	0.2108
1	2	3	−0.5719
3	2	3	−0.4535
11	2	3	−1.0872
13	2	3	−0.0769
2	3	1	0.6108
2	3	3	0.3764

), $W_{isj}=\langle \nabla \times ({\mathbf{v}}_s\times {\mathbf{B}}_j),{\mathbf{B}}_i\rangle$ (

Table 4. Values of the coefficient $W_{isj}$.

i	s	j	$W_{isj}$
2	1	1	−0.4873
2	1	3	0.5719
1	2	1	0.1697
3	2	1	−0.6108
2	2	2	−0.2108
1	2	3	−0.1459
3	2	3	−0.3764
2	3	1	0.7552
2	3	3	0.4535
2	11	1	−1.2321
2	11	3	1.0872
2	13	1	−0.1692
2	13	3	0.0769

), $W_{ij}^{\alpha }=\langle \nabla \times \alpha (r,\theta ){\mathbf{B}}_j),{\mathbf{B}}_i\rangle$ (

Table 5. Values of the coefficients $W_{ij}^{\alpha }$.

i	j	${\mathit{W}}_{ij}^{\mathit{\alpha }}$
2	1	0.7883
3	1	1.6361
1	2	1.0728
1	3	1.2005

) are volume integrals of the fields under consideration [29,30], dimensionless quantities: $u\left(t\right)$ is the amplitude of the velocity field, $B_i\left(t\right)$ is the amplitude of the i-th component of the magnetic field induction, $f_{out}$ is the mass density of the Archimedean force, i.e., buoyancy force, $Z_s\left(t\right)=\underset{0}{\overset{t}{\int }}{e}^{-b(t-\tau )}sin\left(a(t-\tau )\right){\mathbf{B}}^2\left(\tau \right)\mathrm{d}\tau$.

The following values of the coefficients were used in the experiment: the Ekman number $E={10}^7$ and the Prandtl number $P_m=5$ which corresponds to the Earth’s core, the viscous dissipation coefficients ${\mu }_1=9.8696$, ${\mu }_2={\mu }_3=33.2175$, the a and b parameters from the set $\{0.1,0.5,1,5,10\}$. The values of the remaining coefficients of the system are given in the Table 2, Table 3, Table 4 and Table 5. The values of the coefficients that are not specified in the tables are equal to zero. In addition, all the values required for calculations are attached in Supplementary Materials.

In the numerical simulation [32] of the model (10), the step value h is two orders of magnitude less than the smallest of the values $(1/{\lambda }_s)$ and $(1/{\mu }_i)$, i.e., of the damping times of the velocity field and magnetic field, respectively. The initial conditions are chosen in the vicinity of the rest point of the system (10) so that the mutual reproduction of the considered fields is ensured

$$u\left(0\right)=1,B_2^T\left(0\right)=0,B_1^P\left(0\right)=1,B_3^P\left(0\right)=0,Z\left(0\right)=0,Z_s\left(0\right)=0.$$

In the model, it is assumed that the external effect of the buoyancy force maintains the undamped velocity field. Therefore, in a numerical experiment, the value of the mass density $f_{out}$ is taken to be equal to the value of the coefficient at the amplitude $u\left(t\right)$ of the velocity field [7]. The control parameters of the system take values from the intervals $R{e}_m\in [{10}^{-1},{10}^3]$ and $R_{\alpha }\in [{10}^{-1},{10}^2]$.

5. Study of the Field Generation Conditions in the Linear Approximation

The system of differential Equation (10) in linearized form is written as follows

$$\begin{array}{c}{\displaystyle \frac{\mathrm{d}{B}_i\left(t\right)}{\mathrm{d}t}}=R{e}_{m}u\left(t\right){\displaystyle \sum _{s,j}}{\alpha }_s{W}_{isj}{B}_j\left(t\right)-{\mu }_i{B}_i\left(t\right)+R_{\alpha }\sum _j{W}_{ij}^{\alpha }{B}_j\left(t\right),\hfill \\ i,j=\{1,2,3\},s=\{1,2,3,11,13\}.\hfill \end{array}$$

(11)

The dynamics of system solutions (11) is determined by the location of the eigenvalues of its matrix on the complex plane [33,34]. Let $\Lambda$ be the rightmost eigenvalue of the matrix. If the value $Re\Lambda <0$, then the zero rest point is asymptotically stable. From the dynamo’s point of view, the magnetic field is not generated. If the value $Re\Lambda >0$, then the rest point is unstable. This means that the small initial value of the magnetic field will increase due to the action of the dynamo mechanism. When the eigenvalue $\Lambda$ satisfies the condition $Jm\Lambda \ne 0$, there are oscillations in the magnetic field. Otherwise, there are no oscillations. The research of the solution stability of system (11) by Lyapunov [33] is carried out with a constancy of the velocity field and without the $\alpha$-quenching.

For the numerical solution of the system (11), the Predictor–Corrector Method is used. The parameters of the method are specified in the previous section. The value of the velocity amplitude $u\left(t\right)$ is taken to be equal to one. Lyapunov eigenvalues [33,34] for a system of linear differential Equation (11) were calculated for fixed values of control parameters taken from the intervals $R{e}_m\in [{10}^{-1},{10}^3]$ and $R_{\alpha }\in [{10}^{-1},{10}^2]$, with a logarithmic step equal to $0.05$. 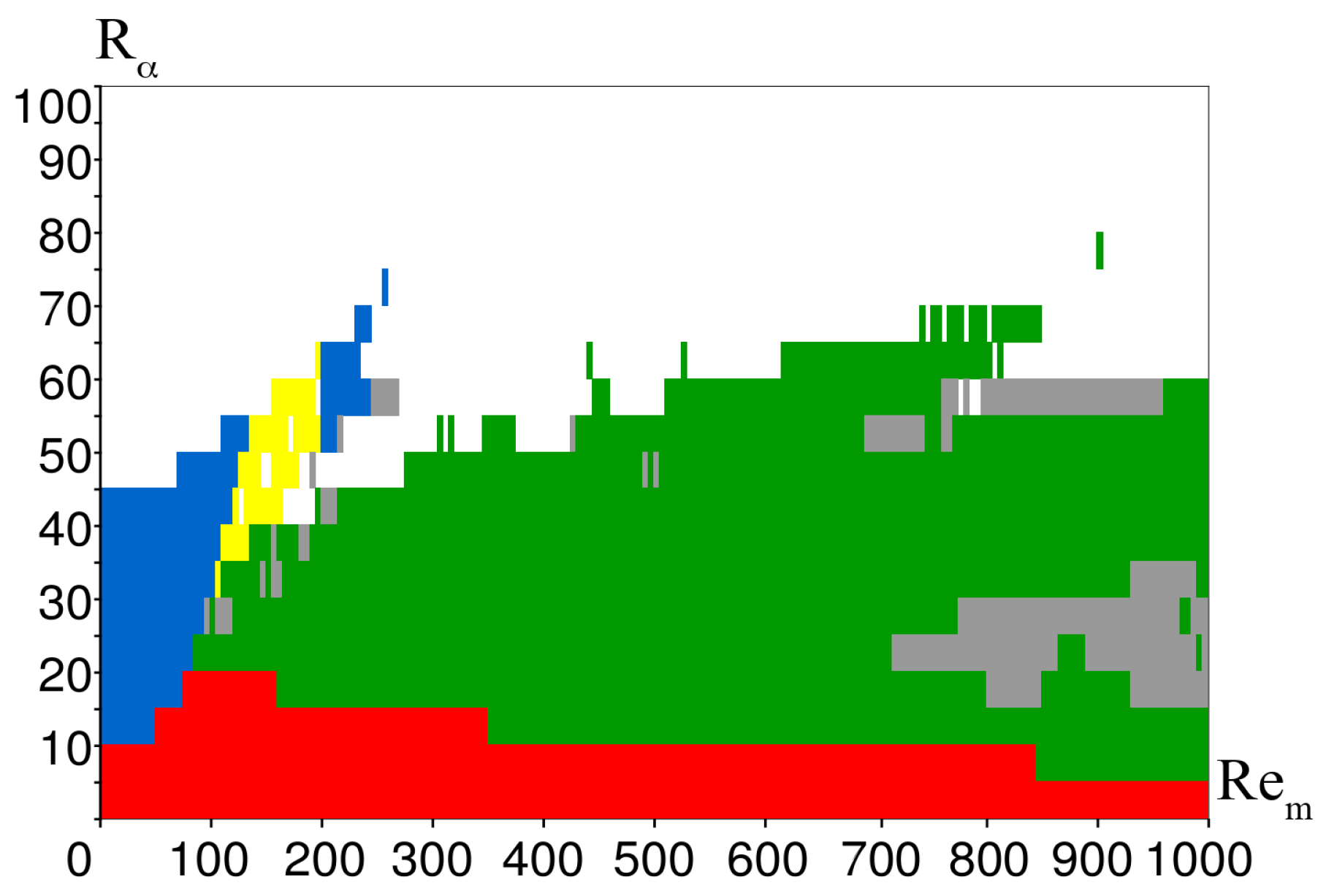The result of the numerical simulation is four regions, shown on the phase plane of the control parameters (Figure 1a): the red region corresponds to the stable system solution without oscillations, the stable solution with oscillations is formed in the green region and the white region corresponds to the unstable solution without oscillations and the unstable solution with oscillations is formed in the gray region.

In this case, with a fixed intensity of the $\alpha$-effect from the interval $R_{\alpha }\in [10,{10}^{1.2}]$ it is possible to transit from the region of unstable solutions without oscillations (white) through the regions of stable solutions (red, green) to the region of unstable oscillating solutions (gray) under the action of a large-scale generator, which in this model is defined by the Reynolds number—an analogue of the root mean square (rms) value of the velocity. If the value of the Reynolds number from the interval $R{e}_m\in [{10}^{-1},{10}^3]$ is fixed, then the action of the turbulent generator makes it possible to transit only from the region of stable solutions to the region of unstable ones (from the red region to the white one, from the green one to the gray region). The exception is a small neighborhood of the value $R{e}_m\approx {10}^{1.8}$, where there is a transition from the region of stable solutions without oscillations to the region of stable solutions with oscillations and back.

Further, the changes in the obtained distribution (Figure 1a) on the phase plane will be investigated when the numerical simulation are carried out for the initial system (10). For each pair of fixed values of control parameters $R{e}_m$ and $R_{\alpha }$ at each step of the numerical scheme, the values of $u\left(t\right)$ and $Z\left(t\right)$ were calculated. For these constant values, the solution stability of the system was studied. The process $Z\left(t\right)$ is included to quench the divergence of the magnetic field, therefore the changes appeared in the regions where the solution is unstable. Then, for the resulting sample (the sample size is 1,584,620 values), the relative frequency of obtaining a stable system was found. This frequency is considered as a probabilistic characteristic of the system stability. The value $0.5$ was chosen as the threshold one. If the relative frequency exceeds the threshold value, then the solution of system (10) is considered stable. Figure 1 shows the results of a study of the solution stability by Lyapunov of a differential equations system (10) for some values of the parameters a and b of the kernel $J\left(t\right)$ of the functional (9). The $\alpha$-quenching leads to the changes in the configurations of the regions shown in Figure 1a. Namely, if the frequency a of damped oscillations takes values close to zero, then the region of stable solution increases with an increase in the values of the control parameter $R_{\alpha }$ (Figure 1b,c), and an increase in the parameter a leads to the reduction of the region of stable solution (Figure 1d). Thus, the action of the process $Z\left(t\right)$ on the $\alpha$-effect intensity leads to quench of the divergence of the magnetic field, but this action is attenuating with an increase in the values of the parameter a. Note, that an increase in the values of parameter a leads to the reduction the region of unstable solution with oscillations because the region of unstable solution without oscillations expands with an increase in the action of a large-scale generator (with an increase in the parameter $R{e}_m$). If the value of the damping coefficient b increases, when a frequency a is constant, then the region of stable solution expands, and to a greater extent the region with oscillations (the green region) (Figure 1c,e,f).

Therefore, using a function of the form $J\left(t\right)=e^{-bt}cos\left(at\right)$ as the kernel of the quenching process $Z\left(t\right)$ of the turbulent effrct leads to an increase in the region, where solution of the dynamo-system (10) is stable, in comparison with the results obtained for the linearized system (11) without such an action. If the measure of the $\alpha$-effect is fixed in the system (10), then a transition under the action of a large-scale generator from the region of unstable solution to the region of stable ones and back is possible (Figure 1b–f). A similar situation is obtained if the value of the Reynolds number is fixed constant and the turbulence generator acts.

6. Results of Simulation and Discussion

Four regions of the dynamical regimes of the magnetic field were obtained earlier as a result of solving the system (10) without $\alpha$-quenching and were presented in paper [7]: damping (corresponds to stable solutions without oscillations and with oscillations), steady (corresponds to stable solutions with oscillations), and infinitely increasing (corresponds to unstable solutions) regimes.

The $\alpha$-quenching, defined by the process $Z\left(t\right)$ (9) with an alternating kernel $J\left(t\right)=e^{-bt}cos\left(at\right)$, allowed us to obtain regions with the chaotic reversals regime, compared to the results for the exponential kernel [7], and led to an increase in the variety of magnetic field dynamical regimes. In particular, in addition to the abovementioned, steady, steady-state, vacillation regimes (Figure 2) were obtained in the region of stable solution (Figure 1b–f, red and green regions) and dynamo-burst and chaotic regimes (Figure 2) were obtained in the region of unstable solution with oscillations on the border with the region of stable solutions (Figure 1b–f, gray region)[8,25,26]. Usually, regions with the regime of the chaotic reversals arise either on the border with the region of unlimited growing of the magnetic field [25,26], or on transition from the region of the one regime to another (Figure 2). The classification of the regime as chaotic one was carried out on the basis of the Benettin algorithm [35,36], where the criterion of chaos is the positive sign of the calculated values of Lyapunov Characteristic Exponents (LCEs).

In the described model, the variation of the parameter values allows us to reproduce a chaotic regime with reversals at small changes of the velocity field in the magnetic field (Figure 3a). It should be noted, that initially chaotic behavior in some cases was replaced by steady regime after a certain period of time (Figure 3c), but with a further increase in the action of a large-scale generator (an increase in the control parameter $R{e}_m$), the regime passes into a chaotic regime, and then passes into the regime of an infinitely increasing magnetic field.

The stability study showed that the pattern on the phase plane of control parameters $R{e}_m$ and $R_{\alpha }$ changes depending on the values of damping frequency a and damping coefficient b of the kernel $J\left(t\right)$. These parameters a and b define the final waiting time $t_0$ (memory) of the process $Z\left(t\right)$ in the model under consideration. The formula for calculating waiting time $t_0$ is given in the article [26]. Earlier in the papers [7,25] it was pointed out that an increase in the values of the damping coefficient b leads to a decrease in the waiting time $t_0$ and to a significant reduction in the region of unlimited growing of the magnetic field (the region, where the solution is unstable) as a result of the region extension of the steady regime of magnetic field. This indicates that the quenching action of the process $Z\left(t\right)$ on the $\alpha$-effect is defined to a large extent by the instant of time t and in the vicinity of it, and to a lesser extent by the prehistory. An increase in the values of the parameter b ($b>1$) is characterized by a decrease in the variety of magnetic field regimes and also the appearance of large-amplitude oscillations in the velocity field for both stable and unstable solutions of the system (10) at values of the Reynolds number $R{e}_m\ge 200$ (Figure 3b,d). Thus, this model has a limitation on the values of the control parameter $R{e}_m<200$ to reproduce both chaotic and any other regimes with small changes in the velocity field.

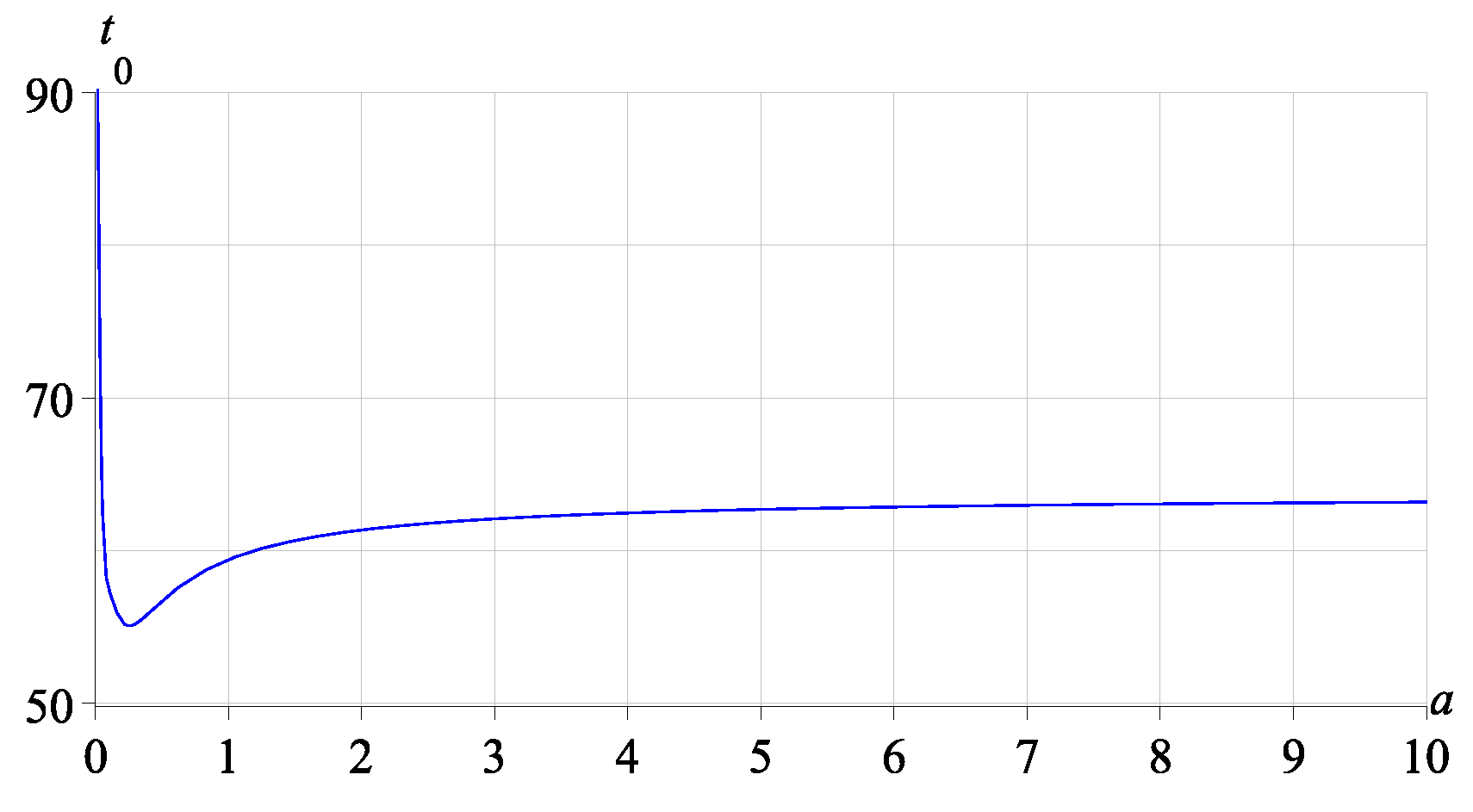
The dependence of the waiting time $t_0$ of the process $Z\left(t\right)$ on the frequency a of damped oscillations at a fixed coefficient b is more complex (Figure 4). If the values of the frequency a is in the region of monotone decrease of the waiting time $t_0$, then the total accumulated effect for the oscillating function $J\left(t\right)$ decreases, but differs little from the exponential one, because the oscillation frequency is low [26]. Therefore, a decrease in the quenching action of the process $Z\left(t\right)$ is mapped only in a slight change in the pattern on the phase plane.

An increase in the values of the frequency a in the interval of waiting time $t_0$ increase is accompanied by comparable amplitudes of damped oscillations of the kernel function $J\left(t\right)$ (this is typical for values of the damping coefficient $b\le 1$), that leads to a significant decrease in the total accumulated effect and, as a consequence, to a decrease in $\alpha$-quenching and an increase in the region of divergence of the magnetic field. Generalizing, it can be concluded that an increase in the frequency values leads to a decrease in the waiting time $t_0$ and in the total accumulated effect compared to the results for the exponential kernel $J\left(t\right)$ and to an attenuation of the quenching action of the process $Z\left(t\right)$ to the turbulent generator.

It is necessary to note, that an increase in the a parameter value determines an increase in the oscillation amplitude in the magnetic field and the velocity field (in the article [26] a study was conducted for the value of the damping coefficient $b=0.1$). Consequently, despite the appearance of regions with a chaotic regime of magnetic field, such regimes are usually accompanied by large-amplitude oscillations in the velocity field (Figure 3b,d), which is not typical for an Earth’s dynamo. In accordance with the purpose of this study, the appearance of chaotic regimes of magnetic field with minor changes in the velocity field in the model under consideration is limited by the values of the control parameter $R_{\alpha }\le 40$.

Thus, it can be concluded that, under certain limitations of the model parameters, the inclusion of the $\alpha$-quenching in the MHD-system in the form of a process $Z\left(t\right)$ (9) defined by a functional with an alternating kernel $J\left(t\right)$ leads to the appearance of regions with a chaotic regime against the background of an insignificant change in the velocity field. Such regimes arise in the regions of unstable solution of the system (10), namely, on the border with the region of unlimited growing of the magnetic field or in the region of transition from one regime of magnetic field to another. There is no change in the sign of the amplitude $u\left(t\right)$ during oscillations in the velocity field. Consequently, the reversals regime is implemented in the model without rearranging the convection structure.

Generalizing, it can be said that in the model under consideration, large-amplitude oscillations in the velocity field appear for values of the kernel parameters more than 1. An increase in the damping coefficient b reduces the variety of the dynamical regimes of magnetic field, but increases the range of regular regimes. Therefore, the applicability of the model has limitations both on the parameters of the kernel $J\left(t\right)$, that defines the character of the action of the process $Z\left(t\right)$, and on the control parameters, containing information about the action of the large-scale generator and of the turbulent generator.

7. Conclusions

The use of the $\alpha$-effect intensity regulator $Z\left(t\right)$ in the large-scale $\alpha \Omega$-dynamo model led to an increase in both the regions of regular magnetic field regimes and their variety compared to the results obtained without the $\alpha$-quenching.

The inclusion of $\alpha$-quenching into the MHD-system, where the character of the action is defined by the alternating kernel $J\left(t\right)=e^{-bt}cosat$, made it possible to obtain not only regular magnetic field regimes that are reproducible when using an exponential kernel $J\left(t\right)=e^{-bt}$, such as steady regime, steady-state one, vacillation, dynamo-burst, but also a chaotic regime with reversals.

An increase in the value of the damping coefficient b increases the region of stable solutions of the MHD-system, and an increase in the value of the frequency a decreases on the contrary. The presence of such a dependence leads to an increase in the region of an infinitely growing magnetic field with an increase in the parameter a compared with the results for an exponential kernel with the same value of the damping coefficient b.

The proposed model made it possible to obtain a chaotic regime of magnetic field on the background of the insignificantly varying velocity field with limitations on the values of the control parameters $R{e}_m\le 200$ and $R_{\alpha }\le 40$. The limitations are associated with an increase in the oscillations amplitude in the velocity field both with an increase in the control parameters values and in the values of the parameters of the kernel $J\left(t\right)$ of the functional defining the quenching process $Z\left(t\right)$.