Abstract
KLFCM is a clustering algorithm proposed by introducing K-L divergence into FCM, which has been widely used in the field of fuzzy clustering. Although many studies have focused on improving its accuracy and efficiency, little attention has been paid to its convergence properties and parameter selection. Like other fuzzy clustering algorithms, the output of the KLFCM algorithm is also affected by fuzzy parameters. Furthermore, some researchers have noted that the KLFCM algorithm is equivalent to the EM algorithm for Gaussian mixture models when the fuzzifier is equal to 2. In practical applications, the KLFCM algorithm may also exhibit self-annealing properties similar to the EM algorithm. To address these issues, this paper uses Jacobian matrix analysis to investigate the KLFCM algorithm’s parameter selection and convergence properties. We first derive a formula for calculating the Jacobian matrix of the KLFCM with respect to the membership function. Then, we demonstrate the self-annealing behavior of this algorithm through theoretical analysis based on the Jacobian matrix. We also provide a reference strategy for determining the appropriate values of fuzzy parameters in the KLFCM algorithm. Finally, we use Jacobian matrix analysis to investigate the relationships between the convergence rate and different parameter values of the KLFCM algorithm. Our experimental results validate our theoretical findings, demonstrating that when selecting appropriate lambda parameter values, the KLFCM clustering algorithm exhibits self-annealing properties that reduce the impact of initial clustering centers on clustering results. Moreover, using our proposed strategy for selecting the fuzzy parameter lambda of the KLFCM algorithm effectively prevents coincident clustering results from being produced by the algorithm.
Keywords:
KLFCM clustering algorithm; Jacobian matrix; convergence properties analysis; self-annealing MSC:
68T10
1. Introduction
Clustering and fuzzy-based clustering have become popular techniques in data mining and machine learning due to their ability to identify patterns and group similar data points without the need for training data [1,2]. Clustering algorithms are a type of unsupervised approach where data are partitioned into subgroups based on their similarities or distances from each other [3]. The partition matrix represents the degree of membership of each data point in each cluster [4]. Since Zadeh [5] introduced the fuzzy set theory, the hard clustering algorithm was extended to the FCM (Fuzzy C-means) clustering algorithm in [6]. Clustering algorithms can be applied to a wide range of applications, such as image segmentation, customer segmentation, and anomaly detection.
In the literature, there are numerous improvements to the FCM algorithm that aim to address various clustering problems or enhance clustering performance [7,8,9,10,11]. The KLFCM (FCM with K-L information term) algorithm is one of the more well-known methods. Honda and Ichihashi proposed a modified objective function for Fuzzy c-Means (FCM) clustering that includes a regularizer based on K-L information [7]. In KLFCM, a regularization term based on the K-L divergence metric is added to the objective function to encourage cluster centers to be spaced further apart. The K-L divergence is used to measure the difference between two probability distributions, however, it can be used to measure the degree of separation between two cluster centers in this case. By including the regularization term, the algorithm ensures that the distance between cluster centers is maximized, which can help prevent the formation of overlapping clusters and ensure the resulting clusters are well separated. This algorithm has such unique characteristics that it has inspired the development of many clustering algorithms based on its principles, which have been proposed in the research literature. Honda applied probabilistic principal component analysis (PCA) mixture models to linear clustering and proposed a constrained model KLFCV [12]. Gharieb and Gendy [13] modified the regularization term of the original KLFCM algorithm using the Kullback–Leibler (KL) divergence, which measures the proximity between a pixel membership and the local average of this membership in the immediate neighborhood. Zhang et al. [14] combined the benefits of KLFCM and Student’s t-distribution to propose a new algorithm for image segmentation. A novel image segmentation algorithm based on KLFCM is proposed in [15] to increase the ability to overcome noise and describe the segmentation uncertainty. Amira et al. [16] incorporated conditional probability distributions and the probabilistic dissimilarity functional into the conventional KLFCM algorithm and proposed a new model called CKLFCM.
While numerous clustering methods based on the KLFCM algorithm have been proposed in the literature, few provide clear explanations for how and why this algorithm works. Furthermore, there is a lack of theoretical research into its convergence properties and optimal parameter selection. Similar to the FCM clustering algorithm, the degree of fuzziness in KLFCM’s membership values is regulated by the fuzzifier parameter. Larger values lead to fuzzier memberships [17], which can result in coincident clustering when fuzziness approaches infinity. In our research, “coincident clustering result” refers to a specific type of coincident clustering where all cluster centers coincide with the dataset’s mass center and merge into a single center, resulting in a loss of clustering information and decreased accuracy in data partitioning. Hence, selecting the proper fuzzifier value is crucial for obtaining accurate clustering results. Nevertheless, the use of KL divergence as a penalty term in the algorithm helps prevent the overlapping of the cluster centers by spreading them throughout the data space. Consequently, theoretically, the algorithm can eliminate overlap between the dataset’s mass center and all cluster centers. We have addressed the parameter selection of the clustering algorithm by using Jacobian matrix analysis in previous papers [18,19,20,21]. In these papers, we revealed the relationship between the stable fixed points of the clustering algorithm and the datasets using Jacobian matrix analysis. In [18], we provided an explanation of the self-annealing behavior observed in the EM algorithm for Gaussian mixtures, along with the initialization lower bound of the temperature parameter in the DA-EM algorithm. In addition, Ref. [21] demonstrated that coincident clustering results are not stable fixed points of the GG clustering algorithm and discussed the correlation between the clustering algorithm’s convergence rate and the fuzziness index. In this paper, we further analyze the parameter selection and convergence properties of the KLFCM clustering algorithm through Jacobian matrix analysis, building on our previous work.
The primary contributions of this paper can be summarized as follows:
- Firstly, we constructed the Jacobian matrix of the KLFCM algorithm regarding the membership function. Then, we provided theoretical proof for the self-annealing property of the KLFCM algorithm.
- We discussed the reference methods for selecting fuzzy parameters in practical applications of the KLFCM algorithm. Specifically, we talked about how to choose appropriate values for the parameters’ lambda to ensure poor clustering results are avoided.
- Additionally, similar to the Hessian matrix, the Jacobian matrix can be utilized to estimate the convergence rate of an algorithm. Since computing the Jacobian matrix is simpler than computing the Hessian matrix, the third contribution of this paper is to estimate the convergence rate of the KLFCM algorithm under different parameter conditions using the Jacobian matrix.
- Finally, we conducted experiments to verify the accuracy and effectiveness of the theoretical derivation.
The experimental results indicate that the fuzzy parameter lambda has a significant impact on the clustering outcome of the algorithm, and inappropriate parameter selection can result in poor clustering performance. The research also demonstrates that the coincident clustering solution is not a stable fixed point of the KLFCM algorithm. Therefore, under certain parameter conditions (i.e., where the chosen results in the spectral radius of the Jacobian matrix at the coincident clustering center being greater than 1), even if the initial clustering center selection is suboptimal, the algorithm may still produce good clustering results. Meanwhile, we used the spectral radius of the Jacobian matrix to estimate the convergence rate of the KLFCM algorithm under different parameter conditions in the experiment and further explained the relationship between the parameters and convergence rate.
In this research, we provide an introduction to the KLFCM clustering algorithm with a brief overview in Section 2. We then analyze the Jacobian matrix and discuss the theoretical behavior of the KLFCM algorithm in Section 3. To validate our theoretical findings, we present various experimental results in Section 4. Additionally, we include a discussion on the experimental outcomes in Section 5. Finally, we summarize our research in Section 6.
2. The KLFCM Clustering Algorithm
This section provides a concise overview of the KLFCM clustering algorithm.
Firstly, we focus on the original FCM clustering algorithm. Let be a dataset from an s-dimensional Euclidean space. The aim of clustering is to find structure in data and cluster n data points to c clusters. The assignment of all items to the clusters is determined by their membership values, indicating the degree to which each item belongs to each cluster. The membership matrix represents these values, where denotes the membership value of the ith data sample for the jth cluster. It should be noted that all membership values must adhere to the following constraints:
We denote the set of fuzzy partition matrices as
The objective function of the FCM algorithm [6] is formulated as follows:
where and is the Euclidian distance from the kth object to the ith cluster center . m is the weighting exponent which determines the degree of fuzziness and . The necessary conditions for optimality of (1) are derived as follows: and
Miyamoto et al. [22] proposed the introduction of an entropy term and a positive parameter , resulting in the minimization of a new objective function instead of . This approach is commonly known as entropy regularization.
The objective function of the FCM clustering method with regularization by K-L information (KLFCM) is obtained by substituting the entropy term in Equation (4) with K-L information. The objective function is given by the following equation:
where represents the proportion of samples belonging to the ith cluster. In the KLFCM algorithm, the Mahalanobis distance is utilized to quantify the dissimilarity between each data point and the cluster centers during the clustering process. The Mahalanobis distance takes into account the covariance structure of the data, which makes it a more precise distance measure than Euclidean distance. By considering the distribution of the data and the correlation between variables, it can provide better estimates of similarity or dissimilarity between data points. The formula for the Mahalanobis distance is as follows:
The objective funciton of KLFCM (5) is minimized under the condition that , , respectively. Then, the updating rules in the KLFCM clustering algorithm are as follows:
where . The KLFCM clustering algorithm is equivalent to the Expectation-Maximization (EM) algorithm with Gaussian Mixture Models (GMMs) only when the value of is equal to 2. This relationship between the two algorithms is well established in the literature.
The KLFCM Algorithm is summarized in Algorithm 1:
| Algorithm 1: KLFCM algorithm. |
|
For a better understanding of the impact of the fuzzy parameter on the output results of the KLFCM algorithm, we conducted experiments using the Iris dataset as the experimental object to observe the clustering results obtained by selecting different fuzzy parameters. In the clustering results, we used * (green asterisks), Δ (red triangles), and ⋆ (blue pentagrams) to represent sample points that belong to different clusters. The sample cluster centers were represented by black circles ●. In the use of the KLFCM clustering algorithm, it is generally necessary to initialize the cluster centers and membership matrix of the algorithm. To accomplish this task, we utilize the K-means clustering algorithm for initialization. Specifically, we use the K-means clustering algorithm to divide the sample data into k clusters and use each cluster’s centroid as the initial cluster center in the KLFCM algorithm. Additionally, based on the K-means clustering results, we calculate the distance between each sample point and the various cluster centers, which allows us to establish the initial membership matrix in the KLFCM algorithm.
The simulation shown in Figure 1 highlights the importance of choosing an appropriate value for the parameter in the KLFCM clustering algorithm. The results demonstrate that different values of can lead to significantly different clustering outcomes, and a poor choice of can result in an invalid or uninformative clustering solution. When is set to 2 or 4, reasonable clustering outcomes are obtained with low error counts of 5 and 44, respectively. This indicates that the algorithm was able to produce meaningful clusters with acceptable levels of misclassification. However, when is improperly initialized to 8 or 36, as illustrated in Figure 1e,f, the clustering algorithm fails to produce informative results. Specifically, the algorithm outputs a single cluster, which indicates that the clustering solution is invalid and uninformative.
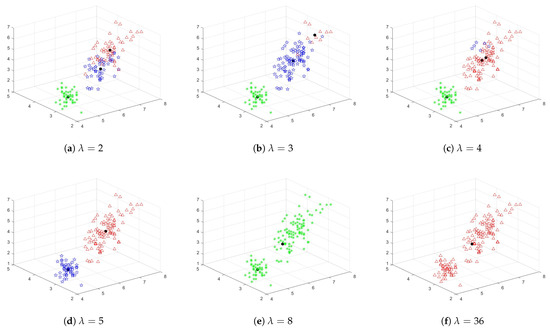
Figure 1.
KLFCM Clustering Results with Different for Iris Dataset.
Following that, we manually designate the initial class center of the KLFCM algorithm under identical conditions regarding the fuzzy parameter. The initial cluster centers are closely situated to each other, but there is no complete overlap. Then we will apply the KLFCM algorithm to cluster the Itis dataset and display the clustering results in Figure 2. We use ○ (magenta circles) to represent the initial cluster centers.
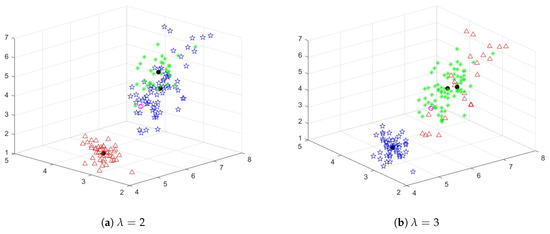
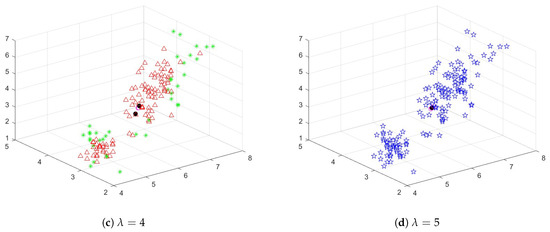
Figure 2.
KLFCM Clustering Results with Inappropriate Cluster Center Initialization for Iris Dataset.
The initial cluster centers are already tightly close to each other (however, it is not completely overlapping). Even with poor initial clustering center selection, the algorithm can still prevent convergence towards overlapping clustering centers as long as the fuzzy parameter is appropriately chosen. That means the KLFCM clustering algorithm possesses the capability of evading these kinds of erroneous clustering outcomes, which highlights its potential self-annealing properties. When the fuzzy parameter is set to 2, the KLFCM clustering algorithm delivers satisfactory clustering results despite the less-than-ideal initial clustering center. However, when the fuzzy parameter is set to 5, the KLFCM clustering algorithm fails to prevent producing clustering results in which all samples are assigned to a single class. The self-annealing property refers to the ability of an algorithm to adapt and improve its performance without explicit external intervention. In the context of the KLFCM clustering algorithm, it means that the algorithm has the ability to adjust its parameters during the iterative process to achieve better clustering results. The algorithm seems to “self-anneal” toward a more meaningful clustering outcome, even when the initial parameter selection may be inappropriate.
In the upcoming section, we will perform a theoretical analysis of the KLFCM clustering algorithm using Jacobian matrix analysis.
3. Convergence and Parameter Analysis Based on Jacobian Matrix
It is a well-known fact that when partitioning a dataset into clusters, each cluster should have distinct centers from the others. Otherwise, if all degrees of membership between samples and any clustering center are equal, it would imply that we cannot meaningfully divide the dataset into subsets based on the membership matrix. Similarly, in the case of the KLFCM algorithm, we would expect it to circumvent this potential drawback; otherwise, it cannot be considered successful as a clustering algorithm.
As we mentioned in Section 2, the KLFCM cluster centers and membership values of the data points with them are updated through the following iterations.
where . and are the ith cluster center and membership value of kth sample for the ith cluster obtaind in the tth iteration, and so on.
We considering the KLFCM clustering algorithm as a map , where the mapping function and satisty and . Then is called the iteration sequence or convergent sequence of the KLFCM algorithm. If the iteration sequence converges to a point , this point should be a fixed point of the algorithm which satisfies . Set the convergence domain of the KLFCM clustering algorithm as
Clearly, if the iteration process is starting from a point , then the iteration process will terminate at a point in the convergence domain, or there is a subsequence converges to a point in .
If the initial membership matrix is , then the KLFCM clustering centers are equal to the mass center of the dataset . In next iteration, we still get and . That is, is actually the fixed point of the KLFCM algorihtm. If the KLFCM algorithm converges to this point, the algorithm will fail to produce meaningful clusters. Moreover, if is a stable fixed point of KLFCM clustering algorithm, this clustering algorithm will not escape from this point. Of course, this kind of situation should be avoided.
The KLFCM clustering result may be heavily influenced by the parameter value of , such as shown in Figure 1. However, the KLFCM clustering algorithm can avoid outputting the coincident clustering result in , which means it is not a stable fixed point of the algorithm. Next, we address the convergence and parameter analysis of the KLFCM clustering algorithm using the Jacobian matrix. Our theoretical analysis is based on Olver’s Corollary [23]. According to Olver ([23], p. 143), for Jacobian matrix , if the spectral radius (i.e., the maximum of absolute eigenvalues of the matrix) is less than one, then the fixed point is asymptotically stable. That is, for KLFCM, if spectral radius of the Jacobian matrix at point is not less than 1, then is not a stable fixed point of the clustering algorithm.
Next, we construct the formula for the element of the Jacobian matrix. The element of Jacobian matrix is obtained by taking the derivations of with respect to .
Theorem 1.
For , and , , each element of Jacobian matrix is
where and is the Kronecker delta function.
Proof.
Each element of the Jacobian matrix is obtained as follows:
Recall that the membership matrix of the KLFCM clustering algorithm satisfies , thus, we have:
For each element in Equation (16), we can get following result by simple computation:
We have that , so
Finally, we substitute the above equations into Equation (16). Then the element of the KLFCM Jacobian matrix can be rewritten as
We further simplify the formula and get
Set . Then each element in the Jacobian matrix is:
The proof is completed. □
Now, we get a general form for the Jacobian matrix. To discuss the theoretical behavior of the KLFCM clustering algorithm, we should consider the Jacobian matrix at the special point . We define a notation as follows: For any matrix , .
Theorem 2.
Each element of Jacobian matrix at the special point is
where
and , , is the Kronecker delta function.
Proof.
If , then , and . Thus, the Jacobian matrix at this special point becomes
Consider that where a and b are column vectos, also we have for matrices A, B, and C, the following equations can be obtianed by simple computation:
Equation (18) can be further simplified as
The trace of the matrix can be interpreted as , where and denote the element of row i and column j in and respectively. Moreover, we have that and . It implies that , where and . Finally, we have
Let
We have that
Then the element in the Jacobian matrix at the special point is
The proof is completed. □
We have mentioned that the spectral radius of the Jacobian matrix can reflect the theoretical behavior of the algorithm. For KLFCM algorithm, if the spectral radius of the Jacobian matrix at point is not less than 1, then it is not a stable fixed point of the algorithm. Next, we focus on the spectral radius of the Jacobian matrix calculated by Equation (17).
Theorem 3.
Let denote the spectral radius of Jacobian matrix , then we have that .
Proof.
Because of the eigenvalues of matrix are equal to the eigenvalues of matrix , the spectral radius of matrix is the same as that of . That is, the spectral radius of Jacobian matrix is equal to the spectral radius of symmetric matrix computed by Equation (19).
where
It is true that for the symmetric matrix , the following statement holds.
where the symbol represents the maximum eigenvalue of the matrix. Let is a vector in which the ith element is one and other elements are zero. Obviously, we have the following inequality holds:
Based on the above analysis, we can conclude that . □
The study reveals that the coincident clustering results are not stable fixed points of the KLFCM algorithm. As an example, when analyzing the Iris dataset, inappropriate selection of the fuzziness parameter may lead to all data points being assigned to a single cluster in the clustering result, as shown in Figure 1. Despite this clustering outcome being incorrect, the KLFCM algorithm avoids outputting the coincident clustering result, where all cluster centers are equal to the sample mean.
4. Experimental Results
In this section, we validate our theoretical results through experimental examples. We use both artificial and real datasets to demonstrate that the KLFCM clustering algorithm may exhibit self-annealing properties when selecting a suitable fuzzy parameter . We calculate the spectral radius of the Jacobian matrix at the coincident clustering result for the KLFCM algorithm under different lambda parameter conditions. A spectral radius greater than 1 indicates that the coincident clustering result is not a stable fixed point of the clustering algorithm. In addition, we found that the spectral radius of the Jacobian matrix can be applied in analyzing the convergence rate of the KLFCM algorithm. In all examples, the results of the K-means algorithm are used as the initialization for the KLFCM clustering algorithm. Let denote the spectral radius of Jacobian matrix at point . Subsequently, we conducted this experiment through a MATLAB model running on Windows 11 with the version of MATLAB being R2022a.
Example 1.

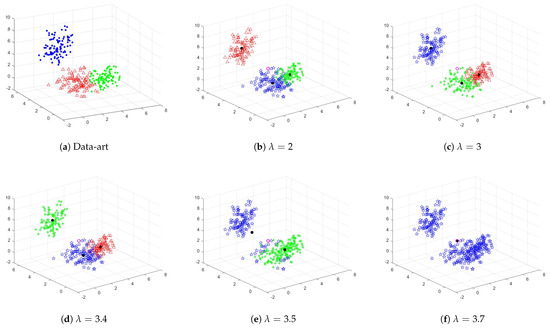
First, we synthesized GMM data with three clusters. The mixing proportions, mean values, and variances are listed in Table 1. The total number of data points is 300. The artificial dataset named Data-art is shown in Figure 3a. Data points generated from different models are denoted by different shapes, such as * (green), Δ (red) and ⋆ (blue).

Table 1.
Mixing Proportions, Means Values and Variances of Gaussian Mixture Models to Generate Data-art.

Figure 3.
Clustering Results of the Data-art Dataset with Different .
After initializing the KLFCM clustering algorithm with manually given cluster centers, we choose different values to observe their influence on the clustering result. The clustering results corresponding to different values are listed in Figure 3b–f.
To illustrate the clustering outcome, we use different colors and shapes to signify data points that belong to different clusters. Furthermore, we represent the initial cluster centers with ○ (magenta circles). It can be seen from Figure 3 that, although the three clustering centers are very close during initialization, as long as we choose appropriate fuzzy parameters, the KLFCM algorithm can still produce relatively good clustering results through iteration. This is demonstrated in Figure 3b–d. We observed that as the value of the fuzzy parameter increases, the KLFCM algorithm may produce clustering results where all samples belong to the same cluster. For example, when lambda = 3.7. We further calculated that when lambda = 3.7, the spectral radius of the Jacobian matrix at coincident clustering result is equal to 1, . In other words, since the KLFCM algorithm inherently exhibits self-annealing properties, choosing appropriate parameters that satisfy will ensure that the algorithm produces interpretable and acceptable clustering results with any initial cluster centers, except for the case where all initial cluster centers are set equal to the sample mean. This finding is particularly intriguing. Next, we present more experimental results on real datasets.
Example 2.

We conduct experiments on six datasets from UCI Machine Learning Repository. The datasets we used in our experiments are described in Table 2.

Table 2.
Experiments on Real Datasets from UCI Databases.
We have theoretically proved the spectral radius of Jacobian matrix at the special point is not less than 1, . That is, is not a stable fixed point of the KLFCM clustering algorithm. Our previous analysis reveals that for the KLFCM algorithm, the spectral radius of its Jacobian matrix at is solely dependent on the fuzziness parameter and the data, while it remains unaffected by the initial clustering center of the algorithm. If the lambda value we choose ensures , then the clustering algorithm is likely to output good clustering results despite poorly choosing initial clustering centers, thanks to its self-annealing property.
By employing Equation (19), we have computed the spectral radius for different values, and the corresponding results are showcased in Table 3.

Table 3.
Spectral Radius of the Jacobian Matrix Corresponding to Different .
It can be seen from Table 3 that the spectral radius of Jacobian matrix at the special point is not smaller than 1 for any fuzziness index value, which is consistent with the result of our theoretical analysis. We select parameter values that satisfy , such as or , and employ the K-means clustering algorithm and manual initialization to set the initial cluster centers of the KLFCM algorithm. Next, we apply the KLFCM clustering algorithm with different initialization methods to cluster the Iris dataset.
The clustering results are depicted in Figure 4. The ● (magenta circles) and ● (black circles), respectively, represent the initial cluster centers and the cluster centers obtained after clustering.
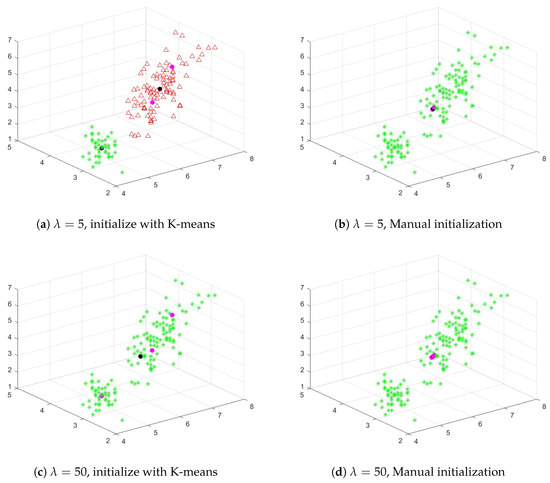
Figure 4.
The Clustering Results of KLFCM Algorithm with Different Initialization Methods on the Iris Dataset.
We have observed that when the spectral radius is equal to 1, several clusters are merged into a new cluster. However, different results can be obtained using different initialization methods. For instance, when and we use the K-means algorithm to initialize KLFCM, two clusters are obtained in the clustering results, which also preserve some structural information of the original data. On the other hand, if we initialize the KLFCM algorithm manually, all the samples in the clustering results will belong to the same cluster. If the value of the lambda parameter is large enough, for example, , regardless of the initialization method used, the KLFCM algorithm may output clustering results where all samples belong to the same cluster. Interestingly enough, the KLFCM algorithm is not suitable for the Balance Scale clustering issue because under any parameter condition.
Therefore, for the case where the spectral radius is equal to 1, as shown in Table 3, does the clustering algorithm avoid outputting overlapping clustering results? Next, we borrow the non-fuzzy index (NFI) to make a more advanced analysis. The NFI index is proposed by Roubens [24].
These NFIs can be used to compare the performances of the clustering results. It is obvious that if the membership values are close to 0 or 1, then the NFI index will be close to 1. Otherwise, if , the NFI index will then be close to 0. In other words, indicates that the algorithm outputs the coincident clustering result That is,
We initialized the KLFCM clustering algorithm with the K-means clustering algorithm and calculated the NFI value of the resulting clustering. The results are shown in Table 4.

Table 4.
NFI Values Corresponding to Different for Different Real Datasets.
Table 4 shows that under the parameter conditions listed, the NFI value of the KLFCM clustering results is almost always greater than 0. We further find that as the values of increase, the KLFCM clustering result has the NFI values with a decreasing trend. For the Iris dataset, if , then the spectral radius will be equal to 1 (see Table 3). We found that all data points are assigned to one cluster in this situation (see Figure 1). However, the NFI value is greater than 0, which means that the KLFCM clustering algorithm did not output the coincident clustering results in . In fact, the KLFCM algorithm may output two cluster centers.
The above results indicate that even if the fuzzy parameters we choose are not optimal enough, the KLFCM algorithm has self-annealing property, which enables the algorithm to avoid producing coincident clustering centers at convergence. Even in some cases where the spectral radius is equal to 1, the KLFCM clustering results can still capture aspects of the underlying data structure because K-means initialization allows initial clustering centers to be distributed across different regions of the data. However, when the value of parameter used in the KLFCM clustering algorithm is too large, for example, , when clustering the Iris dataset, the algorithm may fail to distinguish between overlapping clusters and produce inaccurate clustering results.
Example 3.
In this example, we further discuss the impact of parameter λ on the convergence rate of the KLFCM clustering algorithm. We have previously regarded the KK algorithm as a mapping . If we assume that converges to and that the mapping is differentiable in a neighborhood of , then we can use a simple Taylor expansion to derive an expression.
where is the usual Euclidean norm. Within a certain neighborhood of , the behavior of the KLFCM algorithm can be well approximated by a linear iteration using the Jacobian matrix .
Our focus now is on investigating the convergence rate of linear iterations in the KLFCM algorithm. Specifically, we define the global rate of convergence for this algorithm as . Furthermore, a higher value of corresponds to a slower rate of convergence. To estimate the convergence rate of KLFCM, we calculate the spectral radius of at the point of convergence, . This is because the convergence rate of KLFCM is determined by the spectral radius of , as indicated by Equation (20). By evaluating the spectral radius, we can approximate how quickly the algorithm will converge to its solution.
We varied the parameter in the KLFCM clustering algorithm, and for each value, we computed the spectral radius of the Jacobian matrix at the convergence point. This was done to explore how different parameter values influence the convergence rate of the algorithm. At the point of convergence, we can use Equation (14) to calculate the spectral radius of the Jacobian matrix for KLFCM and denote it as . The results are shown in Table 5.

Table 5.
Spectral radius of the Jacobian matrix corresponding to different values of .
We know that the larger the value of , the slower the convergence rate. Table 5 demonstrates that as the values of increase, the KLFCM algorithm exhibits a decreasing trend in convergence rates due to an increasing trend in the spectral radius. In the case of the Iris dataset, setting results in . However, if we increase the value of to 3, we get a spectral radius of 0.9221. Clearly, the convergence rate is observed to decrease in response to higher parameter values. This trend aligns with most experimental findings of the KLFCM algorithm. Specifically, setting a large value for the parameter in the KLFCM clustering algorithm can result in a fuzzier output, potentially causing slower convergence. Our demonstration shows that the Jacobian matrix can also be utilized to estimate the convergence rate.
5. Discussion
5.1. Main Results
Our experimental results indicate the following facts:
(1) The fuzzy parameter is a critical factor in the KLFCM algorithm. If the value is excessively large, it could lead to clustering failure.
(2) The KLFCM algorithm will exhibit self-annealing properties. Let denote the spectral radius of Jacobian matrix . If we choose a parameter that satisfies the condition of , even with suboptimal initial clustering center selection, the algorithm can still produce satisfactory clustering results through its self-regulating nature.
(3) This study suggests that selecting parameter values leading to greater than 1 is optimal due to the possibility of some clusters merging or overlapping when .
(4) The convergence rate of the KLFCM clustering algorithm can be estimated using the spectral radius of the Jacobian matrix at the convergence point.
5.2. Discussion of
As with other clustering algorithms, the KLFCM algorithm’s outcomes can be influenced by parameter values. When the value is too large, clustering results may exhibit partial cluster overlap. In cases where the parameter values are exceedingly large, the algorithm may produce outputs where all samples belong to one cluster due to its inability to differentiate significant overlapping clusters. This issue arises regardless of the initial class center selection of the KLFCM algorithm. Hence, discussing the algorithm’s self-annealing behavior becomes irrelevant when the parameter values are excessively large, (see Figure 1 and Figure 2).
5.3. Discussion of Self-Annealing Property
Based on the experimental results, it was observed that selecting parameters leading to greater than 1 allows the KLFCM algorithm to produce satisfactory clustering outcomes, even with suboptimal initial center selection or cases where the cluster centers are very close to each other. For instance, in Example 1, when is less than 3.4, all values satisfy the condition of . As a result, in these scenarios, the data were perfectly partitioned into different clusters. The experimental results suggest that the KLFCM clustering algorithm can exhibit self-annealing properties when certain conditions are met in parameter selection, (see Figure 2 and Figure 3).
5.4. Discussion of Parameter Selection
It is evident that when the chosen parameter values meet the condition of , the clustering algorithm’s output results exhibit strong interpretability and acceptability. When the selected parameter leads to , the initial cluster center selection can impact the algorithm’s clustering results. For example, in the case of the Iris dataset, we employed two different cluster center initialization methods under the same parameter conditions (e.g., ). Initializing the clustering centers using the K-means algorithm ensured that they were uniformly distributed across various data regions, resulting in more reliable clustering outcomes. Therefore, when investigating parameter selection issues, we used the K-means algorithm output as initialization for the KLFCM algorithm. From the findings presented in Table 4, we discovered that even in some cases where , we could still identify partial underlying data features through the clustering results, (see Figure 4, Table 3 and Table 4).
It should be emphasized that for datasets from UCI databases in Table 2, the majority of them meet the condition of when . In previous literature, it has been suggested that when , the KLFCM algorithm is equivalent to the EM algorithm for Gaussian mixtures. Our prior work has illustrated the self-annealing property of the EM algorithm, which aligns with the research outcomes presented in this paper.
5.5. Discussion of Convergence Rate
The degree of fuzziness in KLFCM algorithm clusters can be managed by adjusting the value of lambda. When increases, the fuzziness of the clusters also increases, leading to less distinct and more blurred cluster results that are harder to interpret. Furthermore, as lambda increases, the algorithm takes longer to converge due to the greater complexity of the optimization problem. Our experimental findings align with this phenomenon, (see Table 5).
6. Conclusions
Since its inception by Ichihashi and Honda, the KLFCM algorithm has become one of the most widely used clustering models. In this article, we perform convergence and parameter analysis of the KLFCM clustering algorithm using the Jacobian matrix. Our findings suggest that the coincident clustering result is not a stable fixed point of KLFCM clustering. Additionally, we discovered an interesting pattern in most datasets where results in . While our research includes theoretical analysis, it also has practical implications for the application of the KLFCM algorithm. Not only did we provide a theoretical basis for the self-annealing behavior of the KLFCM algorithm, but we also proposed an initialization selection strategy for algorithm parameters. The ideal parameter value should avoid .
The primary advantage of our proposed analysis method is that we can use Jacobian matrix-based analysis to evaluate any clustering algorithm with an iterative update formula. However, this method has its limitations. For example, we only considered consistent clustering results, but when the parameters are not appropriately selected, there may be some clusters merging in the output. Clearly, while the KLFCM algorithm has self-annealing properties, it may not always produce good results, especially when the parameters are not initialized properly. Therefore, future research must focus on developing better parameter selection strategies to ensure that clustering results accurately reflect the underlying structure of the data.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 62006257).
Data Availability Statement
The dataset used for this work is sourced from the UCI database. It can be found at https://archive.ics.uci.edu/ml/index.php (accessed on 12 January 2023).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sathiyasek, K.; Karthick, S.; Kanniya, P.R. The survey on various clustering technique for image segmentation. Int. J. Adv. Res. Electron. Comm. Eng. 2014, 3, 1. [Google Scholar]
- Ghosal, A.; Nandy, A.; Das, A.K.; Goswami, S.; Panday, M. A short review on different clustering techniques and their applications. Emerg. Technol. Model. Graph. 2018, 2020, 69–83. [Google Scholar]
- Ghosh, S.; Dubey, S.K. Comparative analysis of K-means and fuzzy C-means algorithms. Int. J. Adv. Comput. Sci. Appl. 2013, 4, 35–39. [Google Scholar] [CrossRef]
- Everitt, B.S. Cluster Analysis; Halstead Press: London, UK, 1974. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1954, 8, 338–356. [Google Scholar] [CrossRef]
- Dunn, J.C. A fuzzy relative of the ISODATA process and its use in detecting compact well separated clusters. J. Cybern. 1974, 3, 32–57. [Google Scholar] [CrossRef]
- Ichihashi, H.; Miyagishi, K.; Honda, K. Fuzzy c-means clustering with regularization by KL information. In Proceedings of the 10th IEEE International Conference on Fuzzy Systems (Cat. No. 01CH37297), Melbourne, VIC, Australia, 2–5 December 2001; Volume 2, pp. 924–927. [Google Scholar]
- Karlekar, A.; Seal, A.; Krejcar, O.; Gonzalo-Martin, C. Fuzzy k-means using non-linear s-distance. IEEE Access 2019, 7, 55121–55131. [Google Scholar] [CrossRef]
- Zhao, X.; Nie, F.; Wang, R.; Li, X. Improving projected fuzzy K-means clustering via robust learning. Neurocomputing 2022, 491, 34–43. [Google Scholar] [CrossRef]
- Yang, X.; Zhu, M.; Sun, B.; Wang, Z.; Nie, F. Fuzzy C-Multiple-Means Clustering for Hyperspectral Image. IEEE Geosci. Remote Sens. Lett. 2023, 20, 5503205. [Google Scholar] [CrossRef]
- Seal, A.; Karlekar, A.; Krejcar, O.; Gonzalo-Martin, C. Fuzzy c-means clustering using Jeffreys-divergence based similarity measure. Appl. Soft Comput. 2020, 88, 106016. [Google Scholar] [CrossRef]
- Honda, K.; Ichihashi, H. Regularized linear fuzzy clustering and probabilistic PCA mixture models. IEEE Trans. Fuzzy Syst. 2005, 13, 508–516. [Google Scholar] [CrossRef]
- Gharieb, R.R.; Gendy, G. Fuzzy C-means with a local membership KL distance for medical image segmentation. In Proceedings of the Cairo International Biomedical Engineering Conference (CIBEC), Giza, Egypt, 11–13 December 2014; pp. 47–50. [Google Scholar]
- Zhang, H.; Wu, Q.M.J.; Nguyen, T.M. A robust fuzzy algorithm based on student’s t-distribution and mean template for image segmentation application. IEEE Signal Process. Lett. 2012, 20, 117–120. [Google Scholar] [CrossRef]
- Li, X.L.; Chen, J.S. Region-Based Fuzzy Clustering Image Segmentation Algorithm with Kullback-Leibler Distance. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 4, 27–31. [Google Scholar] [CrossRef]
- Amira, O.; Zhang, J.S.; Liu, J. Fuzzy c-means clustering with conditional probability based K–L information regularization. J. Stat. Comput. Simul. 2021, 91, 2699–2716. [Google Scholar] [CrossRef]
- Yun, S.; Zanetti, R. Clustering Methods for Particle Filters with Gaussian Mixture Models. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 1109–1118. [Google Scholar] [CrossRef]
- Yu, J.; Chaomurilige, C.; Yang, M.S. On convergence and parameter selection of the EM and DA-EM algorithms for Gaussian mixtures. Pattern Recognit. 2018, 77, 188–203. [Google Scholar] [CrossRef]
- Chaomurilige; Yu, J.; Yang, M.S. Analysis of parameter selection for Gustafson–Kessel fuzzy clustering using Jacobian matrix. IEEE Trans. Fuzzy Syst. 2015, 23, 2329–2342. [Google Scholar] [CrossRef]
- Chaomurilige; Yu, J.; Yang, M.S. Deterministic annealing Gustafson-Kessel fuzzy clustering algorithm. Inf. Sci. 2017, 417, 435–453. [Google Scholar] [CrossRef]
- Chaomurilige, C.; Yu, J.; Zhu, J. Analysis of Convergence Properties for Gath-Geva Clustering Using Jacobian Matrix. In Proceedings of the Chinese Conference on Pattern Recognition, Chengdu, China, 5–7 November 2016. [Google Scholar]
- Sadaaki, M.; Masao, M. Fuzzy c-means as a regularization and maximum entropy approach. In Proceedings of the 7th International Fuzzy Systems Association World Congress (IFSA’97), Prague, Czech Republic, 25–29 June 1997; Volume 2, pp. 86–92. [Google Scholar]
- Olver, P.J. Lecture Notes on Numerical Analysis. Available online: http://www.math.umn.edu/~olver/num.html (accessed on 1 March 2023).
- Roubens, M. Pattern classification problems and fuzzy sets. Fuzzy Sets Syst. 1978, 1, 239–253. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).