Application of Fuzzy Network Using Efficient Domination

Abstract

Let H_eff (V_eff, E_eff) be a finite simple connected graph of order m with vertex set V_eff and edge set E_eff. A dominating set $S_{ds}\subseteq V_{eff}$ is called an efficiently dominating set if, for every vertex $u_a\in V_G,\hspace{0.33em}\left|N_G\left[u_a\right]\cap S_{ds}\right|=1$—where NG [u_a] denotes the closed neighborhood of the vertex u_a. Using efficient domination techniques and labelling, we constructed the fuzzy network. An algorithm has been framed to encrypt and decrypt the secret information present in the network, and furthermore, the algorithm has been given in pseudocode. The mathematical modelling of a strong fuzzy network is defined and constructed to elude the burgeoning intruder. Using the study of the efficient domination of fuzzy graphs, this domination parameter plays a nuanced role in encrypting and decrypting the framed network. One of the main purposes of fuzzy networks is encryption, so one of our contributions to this research is to build a novel combinatorial technique to encrypt and decode the built-in fuzzy network with a secret number utilizing effective domination. An illustration with an appropriate secret message is provided along with the encryption and decryption algorithms. Furthermore, we continued this study in intuitionistic fuzzy networks.

1. Introduction

The link between lines and points is described by a graph, which is a mathematical representation of a network. A graph is composed of some points and their connecting lines. Labelling is a tool for counting the people (nodes) and the relationships (links) that exist between any two members. This helps to identify the set of significant individuals who play a vital role in the given network. The secret information will be developed in the network using the encryption technique and decoded using the decryption process. In order to prevent unwanted parties from reading a communication, it must first be transformed from a readable form into an unreadable one through the process of encryption. Decryption is the process of returning an encrypted message to its original (readable) format. To develop this role in the network graphs, network graphs are used to depict and study the relationships between entities. An entity may be a person, an event, a transaction, a vehicle, or anything else. The relationships between entities are shown as lines called links, while the entities themselves are shown as nodes. As we have network graphs, the domination concept is used to identify the effective node to monitor the network.

Hence, domination plays a vital role in the decision making, monitoring, an minimizing the cost of the network, etc. Let ‘O’ denote the set of monitoring members (a set of nodes) of the given network. Every member in the given network except the monitoring members should be the neighbor of at least one monitoring member of the given network. The minimum number of monitoring members of this network is the domination number of the given network. Every member in the given network except the monitoring members should be a neighbor of exactly one monitoring member of the given network. The minimum number of monitoring members of this network is the efficient domination number of the given network. Even though the given secret information is a non-zero integer, while using fuzzy graphs, it has been converted to a non-integer by some combinatorial technique.

Zadeh proposed a mathematical framework to characterize the phenomenon of uncertainty in real-world situations in 1965 [1]. The idea of fuzzy graphs and various fuzzy analogues of graph theory ideas with connectedness were first introduced. Bondy and U.S.R. Murthy [2] introduced graph theory and its applications. Ore [3] and Berge started researching graphs’ domination sets. Paired domination studies were initiated by Teresa W. Haynes and Slater P. J. [4]. Biggs [5] and Kulli [6] wrote the theory of domination in graphs. Kulli and Janakiram [7] were the first to investigate split domination in graphs, and Kulli et al. [8] studied the total efficient domination in graphs. The independent domination number was first used in graphs by Cockayne and Hedetniemi [9]. Equitable domination was introduced by Swaminathan and Dharmalingam [10]. Paired equitable domination was introduced and studied by Meenakshi and Baskar Babujee [11], and it continued in an inflated graph and its complement of a graph [12]. Kwon et al. [13] studied the classification of efficiently dominating sets of circulant graphs of a degree of 5.

Somasundram and Somasundram [14] initiated the studies of domination and total domination in fuzzy graphs. Nagoorgani and Chandrasekaran [15] instigated the domination in fuzzy graphs using strong arcs. Domination in fuzzy directed graphs was proposed by Enrico Enriquez [16]. Intuitionistic fuzzy relations and intuitionistic fuzzy graphs (IFGs) were developed by Atanassov [17]. IFG was defined by Karunambigai et. al. [18], which is a special case of IFGs defined by Shannon and Atanassov of [19]. The terms “order,” “degree,” and “size” of IFG were defined by Nagoor Gani and Shajitha Begum [20]. Split domination in intuitionistic fuzzy graphs was introduced by Nagoor Gani and Anu Priya [21]. Split domination in the neutrosophic graph was studied by Mullai et al. [22]. Meenakshi and Baskar Babujee [23] studied encryption through labeling using efficient domination, and it has been generalized in [24]. The research work presented in [23,24] is extended to fuzzy graphs and intuitionistic fuzzy graphs.

Our contributions in this research work seek to establish the new combinatorial technique to encrypt and decrypt the constructed fuzzy network with a secret number using efficient domination, which is one of the main applications of fuzzy networks. Furthermore, we constructed a strong intuitionistic fuzzy network using the same concept defined in a strong fuzzy network. Along with the encryption and decryption algorithms, an illustration has been given for both cases with a suitable secret message.

2. Preliminaries

Definition 1.

A fuzzy graph (FG) is of the form $H_{FG}=(V_F,E_F)$ which is a pair of functions ${\sigma }_{V_F}:V_F\to [0,1]$; ${\mu }_{V_F}:V_F\times V_F\to [0,1]$ where ${\mu }_{V_F}(a_1,a_2)\le \mathit{min}\{{\sigma }_{V_F}\left(a_1\right),{\sigma }_{V_F}\left(a_2\right)\}$ for $a_1,a_2\in V_F.$

Definition 2.

The underlying graph of a fuzzy graph (FG) is of the form HFG * = (VF, EF) where VF = $\{a_1\in V_F:{\sigma }_{V_F}(a_1)>0\}$ and EF = $\left\{\left(a_1,a_2\right)\in V_F\times V_F:{\mu }_{V_F}\left(a_1,a_2\right)>0\right\}.$

Definition 3.

A subset T_F of V_F is said to be the dominating set of a fuzzy graph if, for every vertex in V_F − T_F, is dominated by at least one vertex of V_F. The dominating set T_F is said to be minimal if no proper subset of T_F is a dominating set.

Definition 4.

An arc $a_1{a}_2$ is said to be a strong arc if its degree of edge membership value is equal to the strength of connectedness between u and v.

Definition 5.

Let e = ($a_1,a_2$) be an edge of a fuzzy graph. We say that $a_1$ dominates $a_2$ if there exists a strong arc between them.

Definition 6.

Let HG (VG, EG) be a finite simple connected graph of order m with vertex set VG and edge set EG. A dominating set $S_{ds}\subseteq V_G\left(G\right)$ is called an efficiently dominating set if for every vertex $u_a\in V_G,\hspace{0.33em}\left|N_G\left[u_a\right]\cap S_{ds}\right|=1$—where NG [u_a] denotes the closed neighborhood of the vertex u_a.

3. Efficient Domination in Fuzzy Graph

Definition 7.

Fuzzy network (FN) is defined as a group of the same category peoples (a set of nodes) which interact with each other and work together (the link is a relation which represents the sharing work or sharing information) such that every node (person) has a degree membership of value. The relation (information, knowledge sharing, etc.) between any two persons is represented by link. The link also has a degree of membership value.

Definition 8.

A network is said to be a fuzzy network if it satisfies ${\mu }_{V_F}(a_1,a_2)\le \mathit{min}\{{\sigma }_{V_F}\left(a_1\right),{\sigma }_{V_F}\left(a_2\right)\}$ for every $a_1,a_2\in V_F.$

Definition 9.

A fuzzy network is said to be strong if it satisfies ${\mu }_{V_F}(a_1,a_2)=\mathit{min}\{{\sigma }_{V_F}\left(a_1\right),{\sigma }_{V_F}\left(a_2\right)\}$ for every $a_1,a_2\in V_F.$

Definition 10.

A dominating set T_F of V_F is said to be an efficiently dominating set of a fuzzy graph if $\left|T_F\cap N\left[v_F\right]\right|=1$ for every vertex $v_F$ in V_F − T_F, where N[$v_F$] represents the closed neighborhood of $v_F$. The dominating set T_F is said to be minimally efficiently dominating if no proper subset of T_F is efficiently dominating. The following fuzzy network FN is strong.

Example

Every edge in the fuzzy graph in Figure 1 is strong, and the only efficiently dominating set is TF = {a, d} since every vertex in VF − TF is dominated by exactly one vertex and this dominating set is unique.

4. Encryption and Decryption of Fuzzy Network Using Efficient Domination

This main framework of this paper consists of:

(a)

The construction of SFN from sub-SFN, where SFN is a strong fuzzy network;

(b)

Secret key generation;

(c)

An encryption algorithm;

(d)

A decryption algorithm.

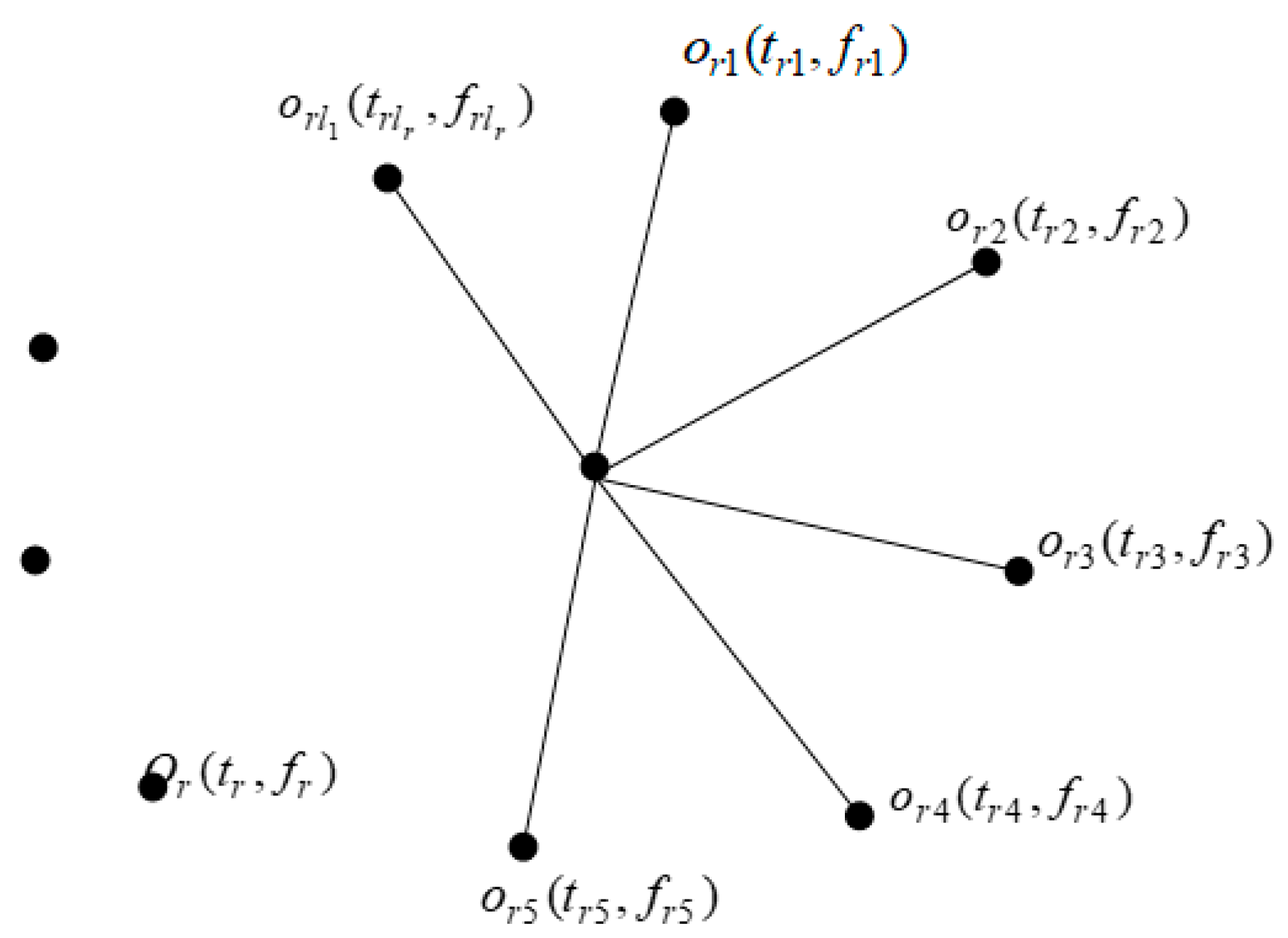
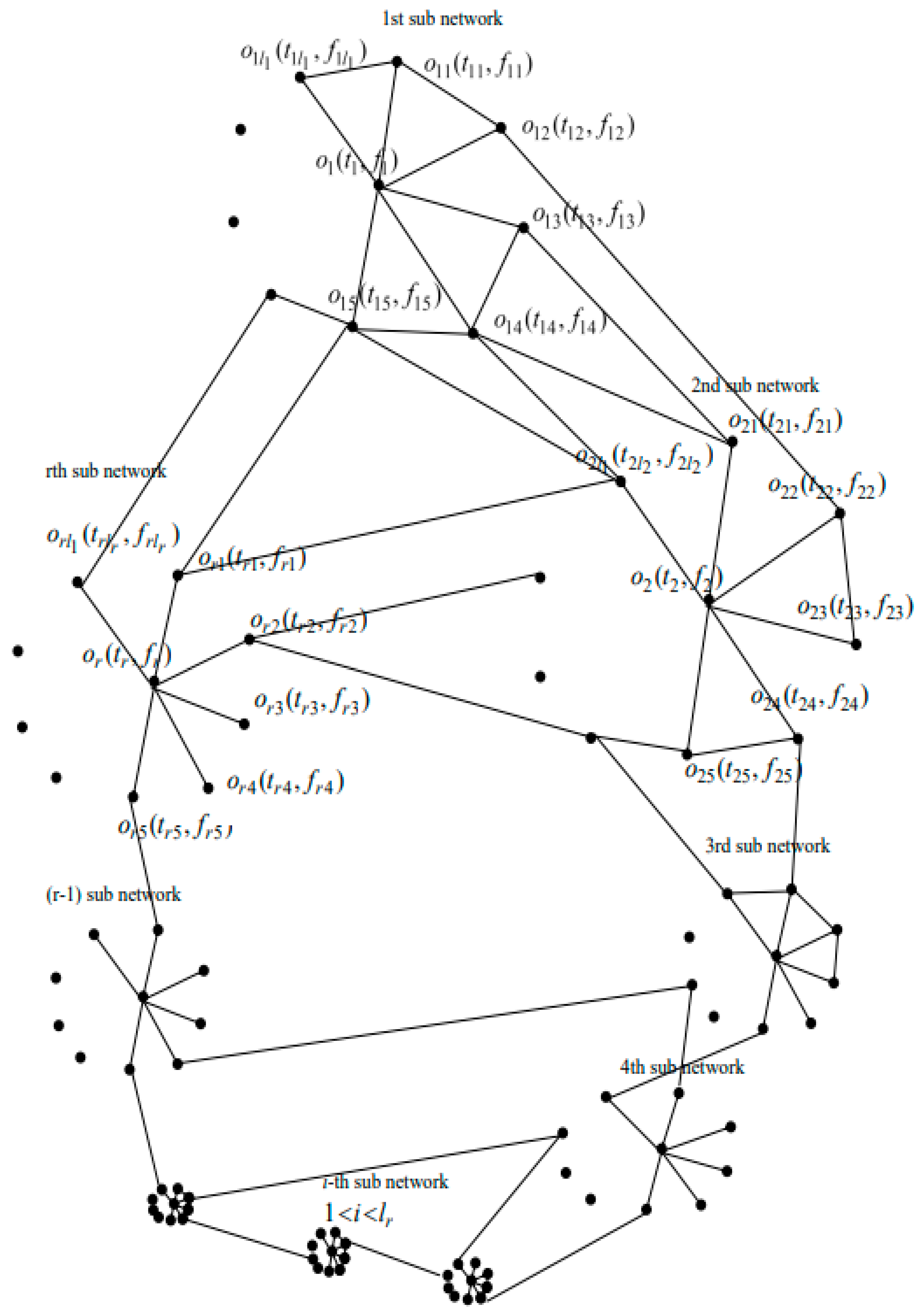
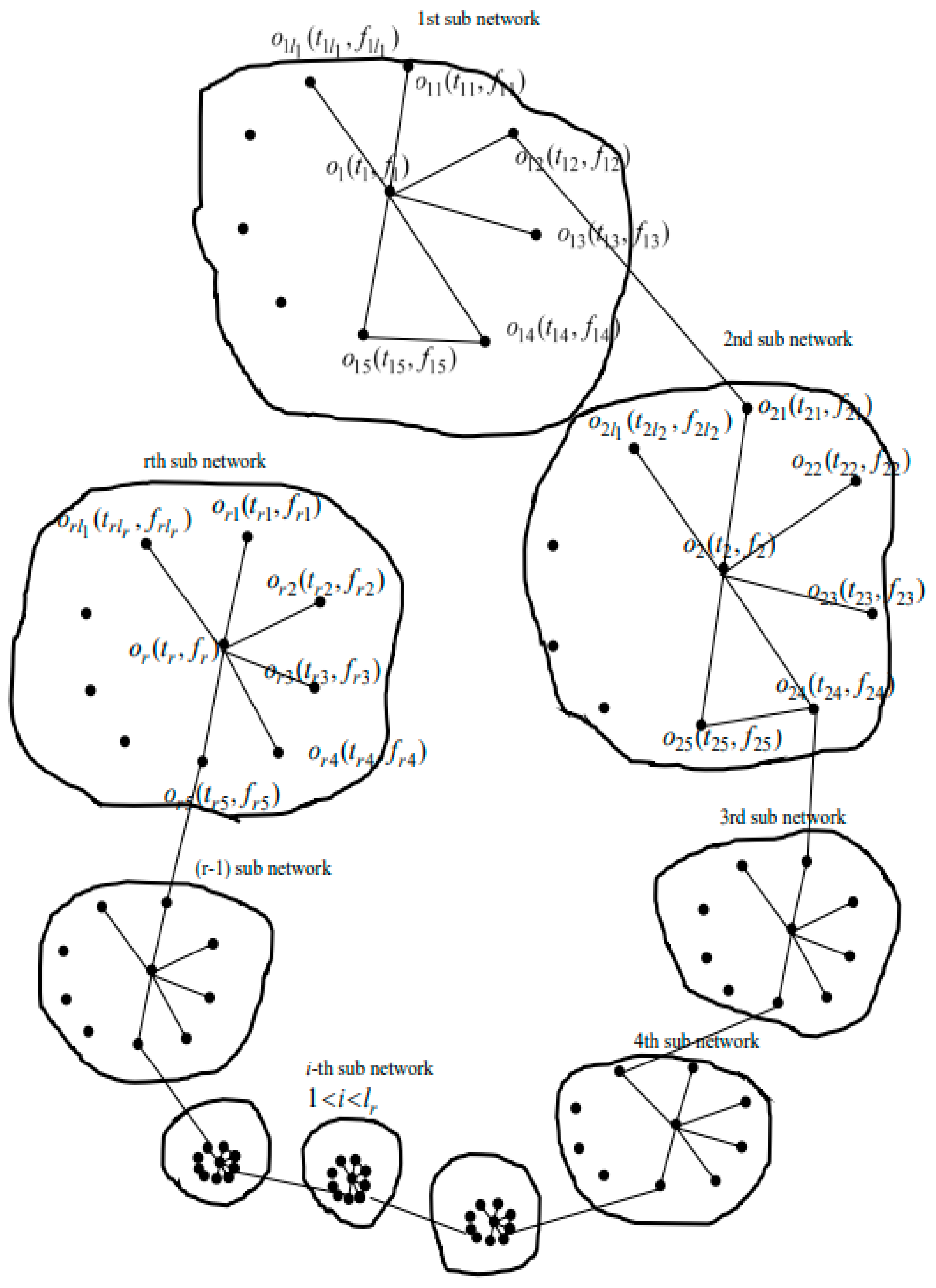
4.1. Construction of SFN from Sub-SFN

The secret number (numerical value) to be encrypted is a positive integer which is not zero. Select the suitable numerical value $N_u{V}_a\ne 0$. Now, N_uV_a is subdivided into ‘r’ values, say $N_u{V}_{a_1}$, $N_u{V}_{a_2}$, …, $N_u{V}_{a_r}$ such that $N_u{V}_{a_1}\equiv R_1\left(\mathit{mod}{r}_m\right)$ (where R₁ = 0), $N_u{V}_{a_2}\equiv R_2\left(\mathit{mod}{r}_m\right)$ (where R₂ = 1), $N_u{V}_{a_3}\equiv R_3\left(\mathit{mod}{r}_m\right)$ (where R₃ = 2), …, $N_u{V}_{a_r}\equiv R_r\left(\mathit{mod}{r}_m\right)$ (where R_r = r_m⁻¹). Since we have ‘r’ subdivision values, we have to frame the ‘r’ subnetwork and plan to assign ‘r’ efficient domination nodes in the constructed network. Let the efficiently dominating nodes (EDNs) be o₁, o₂, o₃, …, o_r. These nodes are the center of the subnetworks, say SFN₁, SFN₂, SFN₃, …, SFN_r, respectively. Let the neighbors of o₁, o₂, o₃, …, o_r be $o_{11},o_{12},\dots ,o_{1l_1}$; $o_{21},o_{22},\dots ,o_{2l_2}$;$o_{31},o_{32},\dots ,o_{3l_3}$,….,$o_{r1},o_{r2},\dots ,o_{r{l}_r,}$ respectively.

The first SFN subnetwork is SFN_1, whose center is o₁ and its neighbors are $o_{11},o_{12},\dots ,o_{1l_1}$.$o_{11},o_{12},\dots ,o_{1l_1}$. The first subdivision value $N_u{V}_{a_1}\equiv R_1\left(mod{r}_m\right)$. Set $V_1=\frac{N_u{V}_{a_1}}{r_m}$ and $D_1=D_{v_{12}}/V_1$ (where $D_{v_1}$ is the numerical value 1 followed by the number of 0 digits of the integral part of V₁) partitioned into the sum of l₁ values, say $d_{11},d_{12},\dots d_{1_{l_1}}$, respectively, and assign these values a minimum value of either o₁ or $o_{11},o_{12},\dots ,o_{1l_1}$, and a degree of edge membership value, which is shown in Figure 2.

The second SFN subnetwork is SFN₂ (Figure 3), whose center is o₂ and its neighbors are $o_{21},o_{22},\dots ,o_{2l_2}.$ The first subdivision value $N_u{V}_{a_2}\equiv R_2\left(\mathit{mod}{r}_m\right)$. Set $V_2=\frac{N_u{V}_{a_{21}}}{r_m}$ and $D_2=D_{v_2}/V_2$ (where $D_{v_2}$ is the numerical value 1 followed by the number of 0 digits of integral part of V₂) partitioned into the sum of l₂ values, say $d_{21},d_{22},\dots ,d_{2_{l_2}}$, and assign these values a minimum value of either o₂ or $o_{21},o_{22},\dots ,o_{2l_2}$, as a degree of truth membership value. Repeat the process until the subnetwork SFN_r is framed (Figure 4).

By the definition of SFN, the degree of membership values of the edges $o_1{o}_{11},o_1{o}_{12},\dots ,o_1{o}_{1l_1}$ are min{$o_1\left(t_1\right),o_{11}\left(t_{11}\right)\}$, min{$o_1\left(t_1\right),o_{12}\left(t_{12}\right)\}$, …, min {$o_1\left(t_1\right),o_{1l_1}\left(t_{1l_1}\right)\}$, respectively.

By the definition of SFN, the degree of membership values of the edges $o_2{o}_{21},o_2{o}_{22},\dots ,o_2{o}_{2l_2}$ are the min${\{o}_2\left(t_2\right),o_{21}\left(t_{21}\right)\}$, min{$o_2\left(t_2\right),o_{22}\left(t_{22}\right)\}$, …, min{$o_2\left(t_2\right),o_{2l_1}\left(t_{2l_2}\right)\},$ respectively. Repeat the process until framing the subnetwork SFN_r and by the definition of FSN, the rest of the edge’s degree membership values will be defined.

By the definition of SFN, the degree of membership values of the edges $o_r{o}_{r1},o_r{o}_{r2},\dots ,o_r{o}_{r{l}_r}$ are min{$o_r\left(t_r\right),o_{r1}\left(t_{r1}\right)\}$, min{$o_r\left(t_r\right),o_{r2}\left(t_{r2}\right)\}$, …, min{$o_r\left(t_r\right),o_{r{l}_r}\left(t_{r{l}_r}\right)\}$, respectively.

4.2. Secret Key

The key is to break the encrypted SFN into the efficiently dominating set of the SFN encrypted network. Once we find the efficiently dominating set of this SFN network, we can decrypt it.

4.3. Encryption Algorithm

Input: $N_u{V}_a\ge r_m$, $r_m\ne 0$ as the secret number;

Output: encrypted SFN network;

Step 1.

Subdivide the secret number $N_u{V}_a$ into “r” values $N_u{V}_{a_1}$, $N_u{V}_{a_2}$, …, $N_u{V}_{a_r}$ such that $N_u{V}_{a_1}\equiv R_1\left(mod{r}_m\right)$ (where R₁ = 0), $N_u{V}_{a_2}\equiv R_2\left(\mathit{mod}{r}_m\right)$ (where R₂ = 1), $N_u{V}_{a_3}\equiv R_3\left(\mathit{mod}{r}_m\right)$ (where R₃ = 2), …, $N_u{V}_{a_r}\equiv R_r\left(\mathit{mod}{r}_m\right)$ (where R_r = r_m − 1).

Step 2.

Frame the ‘r’ subnetwork and assign the ‘r’ efficient domination nodes in the constructed network. The efficiently dominating nodes (EDN) are o₁, o₂, o₃, …, o_r. These nodes are the centers of the subnetworks say SFN₁, SFN₂, SFN₃, …, SFN_r, respectively. The neighbors of o₁, o₂, o₃,…, o_r are $o_{11},o_{12},I,o_{1l_1}$; $o_{21},I\dots ,o_{2l_2}$; $o_{31},I,\dots ,o_{3l_3}$,…., $o_{r1},I,\dots ,o_{r{l}_r},$ respectively (conveniently choose the number of neighboring vertices $I,l_2,\dots ,l_r$ of o₁, o₂,o₃,…, o_r, respectively, where $l_1,l_2,\dots ,l_r\ge 1)$.

Step 3.

The number of nodes present in the SFN network is $rI+l_2+\dots +l_r$. Define Min E (minimum no. of edges present in the constructed network denoted by Min E) $=\left\{o_1{o}_{1j_1},I{o}_{2j_2},\dots ,o_r{o}_{r{j}_r}/1\le j_1\le I,1\le j_2\le l_2,\dots ,1\le j_r\le l_r\right\}\cup \{o_{1j_1}{o}_{2j_2},I{o}_{3j_3},\dots ,o_{(r-1)j_{r-1}}{o}_{r{j}_r}\}$ I only one $j_1,j_2,\dots ,j_r$ where $1\le I\le l_1,1\le j_2\le l_2,\dots ,1\le j_r\le l_r.$ Hence, the minimum number of edges present in the network is $\left(r-1\right)+l_1+l_2+\dots +l_r.$

Step 4.

Define (maximum no. of edges present in the constructed network is denoted by Max E)MaI $=\left\{(a,b);1\le a,b\le l_1+l_2+\dots +l_r+r;a\ne b\right\}-\left\{\begin{array}{c}{o}_1{o}_{k_1}where2\le k_1\le r,o_2{o}_{k_2}where3\le k_2\le rI{o}_{k_3}where4\le k_3\le r,\dots ,o_{r-1}I\\ o_1{o}_{2j_2},o_1{o}_{3j_3}\dots ,o_1{o}_{rI};o_2{o_{3j}}_3,o_2{o_{4j}}_4,\dots o_2{o_I}_r;o_3{o_I}_4,o_3{o_{5j}}_5,\dots o_3{o_{rj}}_r;\dots ;o_{r-1}{I}_r\\ where1\le j_2\le l_2,1\le j_3\le l_3\dots ,1\le j_r\le l_r.\end{array}\right.,$

Step 5.

Set $V_1=\frac{N_u{V}_{a_1}}{r_m}$, $V_2=\frac{N_u{V}_{a_2}}{r_m}$, …, $V_r=\frac{N_u{V}_{a_r}}{r_m}$

$D_1=D_{v_1}/V_1$ (where $D_{v_1}$ denotes the numerical value 1 followed by the number of 0 digits of integral part of V₁);

$D_2=D_{v_2}/V_2$ (where $D_{v_2}$ denotes the numerical value 1 followed by the number of 0 digits of integral part V₂)_, …, $D_r=D_{v_r}/V_r$;

(where $D_{v_r}$ denotes the numerical value 1 followed by the number of 0 digits of integral part of V_r).

Step 6.

Split $I{d}_{11}+d_{12}+\dots +d_{1l_1}$; $D_{2}I+d_{22}+\dots +d_{2l_2}$;….; $D_r=d_{r1}+d_{r2}+\dots +d_{r{l}_r}$;

Assign $\mathit{min}\{o_1\left(t_1\right),o_{11}\left(t_{11}\right)\}=d_{11}$, $\mathit{min}\{o_1\left(t_1\right),o_{12}\left(t_{12}\right)\}=d_{12}$, …, $\mathit{min}\{o_1\left(t_1\right),o_{1l_1}\left(t_{1l_1}\right)\}=d_{1l_1}$ in the first subnetwork.

Assign $\mathit{min}\{o_2\left(t_1\right),o_{21}\left(t_{21}\right)\}=d_{21}$, $\mathit{min}\{o_2\left(t_1\right),o_{22}\left(t_{22}\right)\}=d_{22}$, …, $\mathit{min}\{o_2\left(t_1\right),o_{2l_2}\left(t_{2l_2}\right)\}=d_{2l_2}$ in the second subnetwork, continuing the process until assigning $\mathit{min}\{o_r\left(t_1\right),o_{r1}\left(t_{r1}\right)\}=d_{r1}$, $\mathit{min}\{o_r\left(t_1\right),o_{r2}\left(t_{r2}\right)\}=d_{r2}$, …, $\mathit{min}\{o_r\left(t_1\right),o_{r{l}_r}\left(t_{r{l}_r}\right)\}=d_{r{l}_r}$, in the r-th subnetwork.

Step 7.

Rest of the edge’s membership values will be followed by the definition of FSN

The pseudocode for the encryption algorithm is listed below as Algorithm 1.

Algorithm 1: Encryption Algorithm
function subdivide_secret_number (NuVa, rm):
	NuVa_sub = [] for i in range(rm):
		NuVa_sub.append(NuVa % (i + 1))
	return NuVa_sub
function construcI_networkI efficient_dominating_nodes):
	sub_networks = [] for i in range(r):
		sub_networks.append(SubNetwork(efficient_dominating_nodes[i]))
	return sub_networks
function min_edges(sub_networks):
	min_e = set() for i in range(len(sub_networks)):
		for j in range(1, len(sub_networks[i].neighbors) + 1):
			min_e.add((sub_networks[i].center,sub_networks[i].neighbors[j − 1]))
	return min_e
function max_edges(sub_networks):
	max_e = set() for a in range(1, total_nodes + 1):
		for b in range(1, total_nodes + 1):
			if a! = b and not aIy([a = sub_networks[i].center and b = sub_networks[i + 1].center for i in range(len(sub_networks) − 1)]):
				max_e.add((a, b))
	return max_e
function split_D_values(NuVa_sub):
	D_values = [] for i in range(len(NuVa_sub)):
		D_values.append(calculate_D(NuVa_sub[i]))
	return D_vaIues
function assign_membership_values(sub_networks, D_values):
	for i in range(len(sub_networks)):
		for j in range(len(sub_networks[i].neighbors)):
			membership_value = min(sub_networks[i].center, sub_networks[i].neighbors[j]) sub_networks[i].neighbors[j].membership_value = D_values[i][j]
# Main function NuVa_sub = subdivide_secret_number(NuVa, rm) sub_networks = construct_network(r, efficient_dominating_nodes) min_e = min_edges(sub_networks) max_e = max_edges(sub_networks) D_values = split_D_values(NuVa_sub) assign_membership_values(sub_networks, D_values)

4.4. Decryption Algorithm

Input: encrypted SFN

Output: $N_u{V}_a$, the secret number

Step 1:

Find the efficiently dominating memIs of SFN o₁, o₂, o₃, …, o_r, such that $N_e\left[o_1\right]\cap N_e\left[o_2\right]\cap \dots N_e\left[o_r\right]=\phi$ where $N_e\left[o_i\right]$ represent the neighbours of the vertex o_i.

Step 2.

$V_1=D_{v_1}\left({\sum }_{j_1=1}^{l_1}{d}_{1j_1}\right);V_2=D_{v_2}\left({\sum }_{j_2=1}^{l_2}{d}_{1j_2}\right)$, …, $V_r=D_{v_r}\left({\sum }_{j_r=1}^{l_r}{d}_{1j_r}\right)$

Step 3.

$N_u{V}_a=r_m\left({\sum }_{i=1}^r{V}_i\right)$

The pseudocode for the decryption algorithm is listed below as Algorithm 2.

Algorithm 2: Decryption Algorithm
function efficient_dominating_members(FSN, r):
	# Find r verticIs with nIommon neighbors dominating_members = empty array of size r for i in range(r):
		# Find efficiently dominating member oioi = find_efficient_member(FSN, dominating_members)# Add oi to the list of dominating membersdominating_members[i] = oi
	return dominating_members
function find_efficient_member(FSN, dominating_members):
	# Find an efficiently dominating member that has no common neighbors with other members for vertex in FSN.vertices:
		if vertex not in dominating_members:
			is_efficient = check_efficiency(FSN, vertex, dominating_members)if is_efficient:
				return vertex
	return None
function check_efficiency(FSN, vertex, dominating_members):
	# Check if the vertex is an efficiently dominating member that has no common neighbors with other members neighbors = FSN.get_neighbors(vertex) for member in dominating_members:
		member_neighbors = FSN.get_neighbors(member)common_neighbors = neighbors.intersection(member_neighbors)if len(common_neighbors) > 0:
			return False
	return FSN.is_efficient(vertex)
function compute_values(FSN, dominating_members):
	# CompuIe the vaIs Vi for each dominating member values = empty array of size r for i in range(r):
		vertex = dominating_members[i]D_vi = compute_D(FSN.secret_number, FSN.rm, FSN.Rm[vertex])dj_values = compute_dj_values(FSN, vertex)Vi = D_vi * np.sum(dj_values)values[i] = Vi
	return values
function compute_NuVa(rm, values):
	# Compute NuVa as rm times the sum of the Vi values NuVa = rm * np.sum(values) return NuVa
# Main FSN = create_FSN() # create a FSN object with a secret number and network structure r = random_number dominating_members = efficient_dominating_members(FSN, r) values = compute_values(FSN, dominating_members) NuVa = compute_NuVa(FSN.rm, values) print(NuVa)

5. Illustration

The secret number is $N_u{V}_a=\mathrm{10,810}$

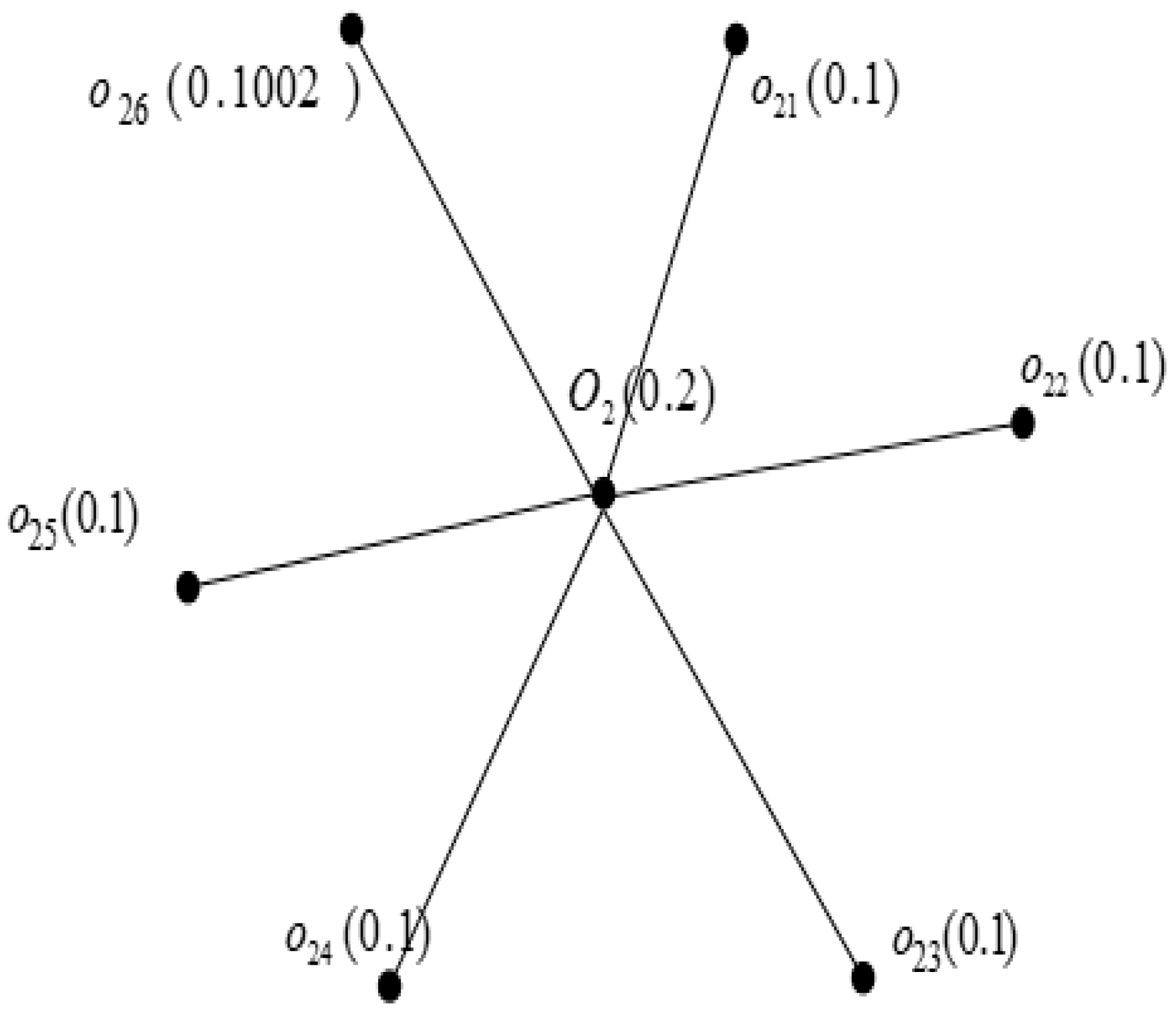
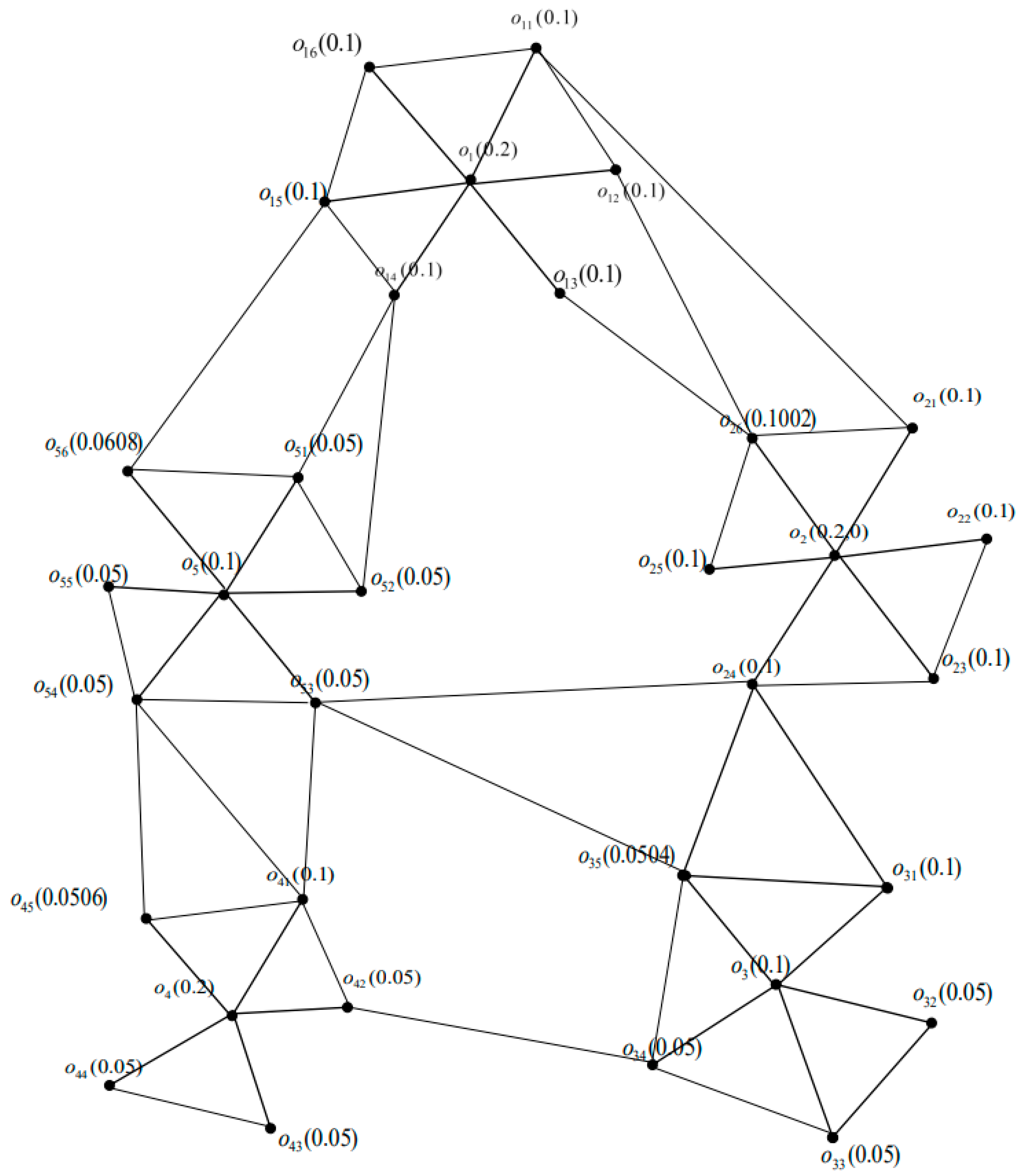
5.1. Construction of SFN from Sub-SFN

We have to split this suitable numerical value $N_u{V}_a$ under modulo r_m = 5. Now, $N_u{V}_a$ is subdivided into ‘five’ values, namely $N_u{V}_{a_1}$, $N_u{V}_{a_2}$, $N_u{V}_{a_3}$, $N_u{V}_{a_4}$, and $N_u{V}_{a_5}$, such that $N_u{V}_{a_1}=3000\equiv 0\left(mod{r}_m\right)$ (where R₁ = 0), $N_u{V}_{a_2}=3001\equiv 1\left(mod{r}_m\right)$ (where R₂ = 1), $N_u{V}_{a_3}=1502\equiv 2\left(mod{r}_m\right)$ (where R₃ = 2), $N_u{V}_{a_4}=1503\equiv 3\left(mod{r}_m\right)$ (where R₃ = 3) $N_u{V}_{a_5}=1804\equiv 4\left(mod{r}_m\right)$ (where R₄ = 4). Since we have ‘five’ subdivision values, we have to frame five subnetworks and plan to assign ‘five’ efficient domination nodes in the constructed network. Let the efficiently dominating nodes (EDN) be o₁, o₂, o₃, o₄, o₅. These nodes are the center of the subnetworks SFN₁, SFN₂, SFN₃, SFN₄, SFN₅, respectively. Let the neighbors of o₁, o₂, o₃, and o₄, o₅ be $o_{11},o_{12},o_{13},o_{14},o_{15},o_{16}$ ; $o_{21},o_{22},o_{23},o_{24}$; $o_{31},o_{32},o_{33},o_{34}$;$o_{41},o_{42},o_{43},o_{44}$; and $o_{51},o_{52},o_{53},o_{54},o_{55},o_{56}$, respectively.

The first subnetwork is SFN₁ (Figure 5), whose center is o₁ and its neighbors are $o_{11},o_{12},o_{13},o_{14},o_{15},o_{16}$. The first subdivision value $N_u{V}_{a_1}=3000\equiv 0\left(mod{r}_m\right)$. Set $V_1=\frac{N_u{V}_{a_1}}{r_m}=\frac{3000}{5}=600 and D_1=D_{v_1}/V_1=1000/600=0.600$ (where $D_{v_1}$ is the numerical value 1 followed by the number of 0 digits of an integral part of V₁), which is partitioned into the sum of six values, say $d_{11},d_{12},\dots d_{1_6}$, which are assigned minimum values of either o₁ or $o_{11},o_{12},o_{13},o_{14},o_{15},o_{16}$, respectively.

The second subnetwork is SFN₂ (Figure 6) whose center is $o_2$ and its neighbors are $o_{21},o_{22},o_{23},o_{24},o_{25}.o_{26}$. The second subdivision value $N_u{V}_{a_2}=3001\equiv 1\left(\mathit{mod}{r}_m\right)$. Set $V_2=\frac{N_u{V}_{a_2}}{r_m}=\frac{3001}{5}=600.2and$ $D_2=D_{v_2}/V_2=1000/600.2=0.6002$ (where $D_{v_2}$ is the numerical value 1 followed by the number of 0s of integral part of V₂) is partitioned into the sum of six values, namely $d_{21},d_{22},\dots d_{26}$, which are assigned minimum values of either o₂ or $o_{21},o_{22},\dots ,o_{26}$ as truth degree membership values.

By the definition of SFN, the degree of membership values of the edges are min {$o_1,o_{11}\}$, min$\{o_1,o_{12}\}$, …, min$\{o_1,o_{16}\}$, respectively.

By the definition of SFN, the degree of membership values of the edges $o_2{o}_{21},o_2{o}_{22},\dots ,o_2{o}_{2l_2}$ are min{$o_2,o_{21}\}$, min{$o_2,o_{22}\}$, …, min{$o_2,o_{26}\}$ r, respectively.

The third subnetwork is FSN_3, whose center is o₃ and its neighbors are $o_{31},o_{32},o_{33},o_{34},o_{35}$. The third subdivision value $N_u{V}_{a_3}=1502\equiv 2\left(mod{r}_m\right)$. Set $V_3=\frac{N_u{V}_{a_3}}{r_m}=\frac{1502}{5}=300.4$ and $D_3=D_{v_3}/V_3=1000/300.4=0.3004$ (where $D_{v_3}$ is the numerical value 1 followed by the number of 0s of an integral part of V₃) is partitioned into the sum of five values, say $d_{31},d_{32},\dots d_{35}$ and assign these values minimum values of either o₃ or $o_{31},o_{32},o_{33},o_{34},o_{35}$ as degree membership values. Construct the FSN₃ subnetwork-3, similarly to the construction of subnetwork-2 in Figure 6.

Fourth subnetwork is SFN_4, whose center is o₄ and its neighbors are $o_{41},o_{42},o_{43},o_{44},o_{45}$. The fourth subdivision value $N_u{V}_{a_4}=1503\equiv 3\left(\mathit{mod}{r}_m\right)$. Set $V_4=\frac{N_u{V}_{a_4}}{r_m}=\frac{1503}{5}=300.6$ and $D_4=D_{v_4}/V_4=1000/300.6=0.3006$ (where $D_{v_4}$ is the numerical value 1 followed by the number of 0s of an integral part of V₄) is partitioned into the sum of five values, namely $d_{41},d_{42},\dots d_{45},$ and assign these values minimum values of either o₄ or $o_{41},o_{42},o_{43},o_{44},o_{45}$ as truth degree membership values. Construct FSN₄ subnetwork-4, similarly to the construction of subnetwork-2 Figure 6.

The fifth subnetwork is SFN_5, whose center is o₅ and its neighbors are $o_{51},o_{52},o_{53},o_{54},o_{55},o_{56}$. The fifth subdivision value $N_u{V}_{a_5}=1804\equiv 4\left(\mathit{mod}{r}_m\right)$. Set $V_5=\frac{N_u{V}_{a_5}}{r_m}=\frac{1804}{5}=360.8$ and $D_5=D_{v_5}/V_5=1000/360.8=0.3608$ (where $D_{v_5}$ is the numerical value 1 followed by the number of 0s of the integral part of V₅) is partitioned into the sum of six values, say $d_{41},d_{42},\dots d_{45}$, and assign these values minimum values of either o₅ or $o_{51},o_{52},o_{53},o_{54},o_{55},o_{56}$, an a truth degree membership value. Construct the SFN₅ subnetwork-5, similarly to in Figure 6. From all the fuzzy strong subnetworks, frame the fuzzy strong network which is shown in Figure 7.

5.2. Secret Key

The key is breaking the encrypted SFN is the efficiently dominating members of the SFN encrypted network, which are shown in Figure 7. Once we find the efficiently dominating set of this network, we can decrypt it. The efficiently dominating members of this SFN are o₁, o₂, o₃, o₄, and o₅.

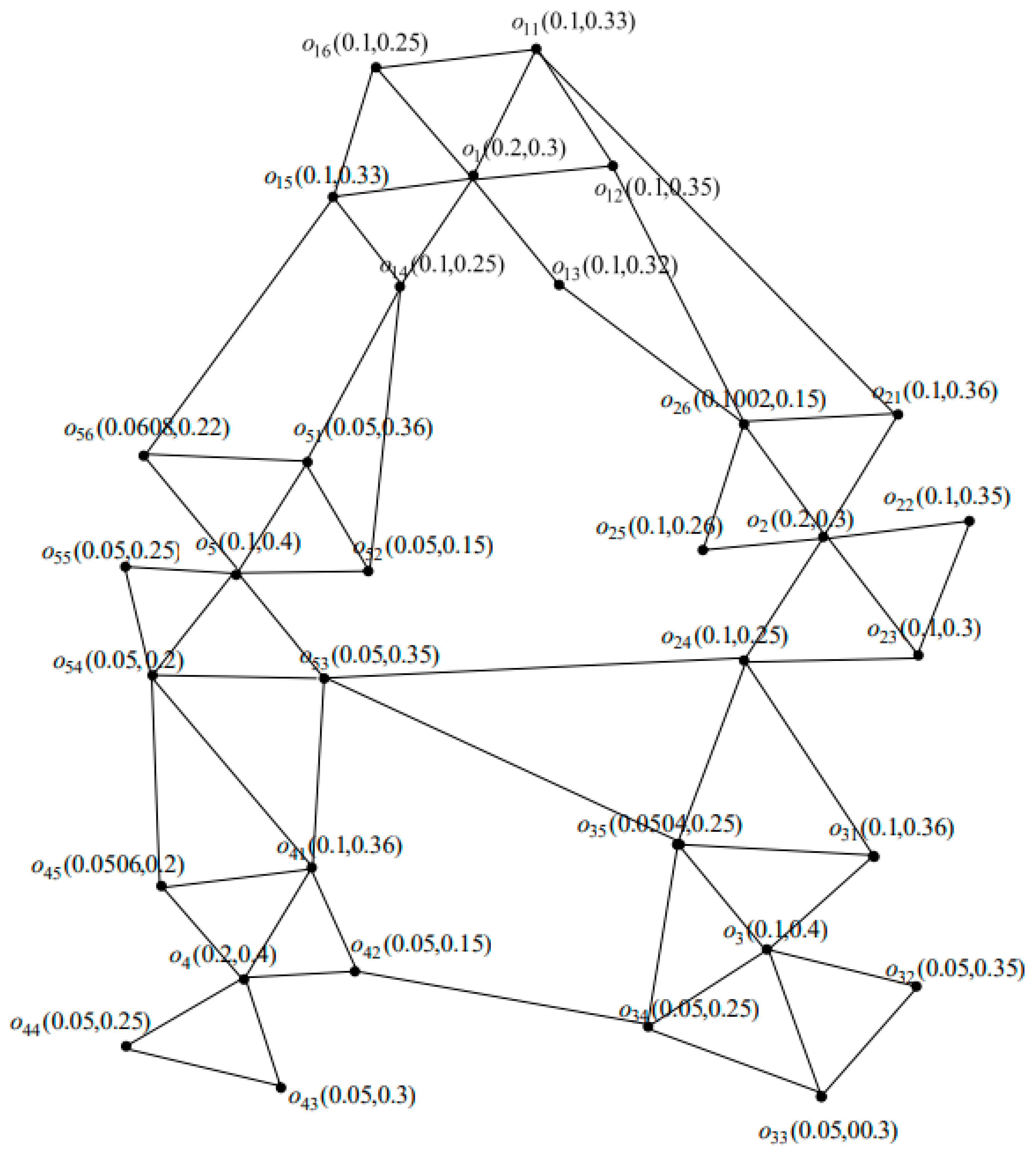
5.3. Encryption Algorithm

Input: $N_u{V}_a=\mathrm{10,810}$ is the secret number.

Output: encrypted FSN network (Figure 7).

Begin

Step 1.

Subdivide the secret number $N_u{V}_a$ into ‘five’ values $N_u{V}_{a_1}$, $N_u{V}_{a_2}$, $N_u{V}_{a_3}$, $N_u{V}_{a_4}$, $N_u{V}_{a_5}$ such that $N_u{V}_{a_1}=3000\equiv 0\left(mod{r}_m\right)$, $N_u{V}_{a_2}=3001\equiv 1\left(mod{r}_m\right)$, $N_u{V}_{a_3}=1502\equiv 2\left(mod{r}_m\right),N_u{V}_{a_4}=1503\equiv 3\left(mod{r}_m\right)$ and $N_u{V}_{a_5}=1804\equiv 4\left(mod{r}_m\right)$.

Step 2.

Frame ‘five’ subnetworks and plan to assign ‘five’ efficient domination nodes in the constructed network. The efficiently dominating nodes (EDNs) are o₁, o₂, o₃, o₄, and o₅. These nodes are the centers of the subnetworks, say SFN ₁, SFN ₂, SFN _3, SFN ₄, and SFN _5, respectively. Let the neighbors of o₁, o₂, o₃, o₄, and o₅ be $o_{11},o_{12},o_{13},o_{14},o_{15},o_{16}$; $o_{21},o_{22},o_{23},o_{24},o_{25},o_{26}$; $o_{31},o_{32},o_{33},o_{34}$; $o_{41},o_{42},o_{43},o_{44}$; $o_{51},o_{52},o_{53},o_{54},o_{55},o_{56}$, respectively.

Step 3.

The number of nodes present in the SFN network is 33.

Minimum no. of edges present in the constructed network is denoted by Min E =$\left\{o_1{o}_{1j_1},o_2{o}_{2j_2},\dots ,o_5{o}_{5j5}/1\le j_1\le \mathrm{6,1}\le j_2\le \mathrm{6,1}\le j_3\le \mathrm{5,1}\le j_4\le \mathrm{5,1}\le j_5\le 6\right\}\cup \{o_{1j_1}{o}_{2j_2},o_{2j_2}{o}_{3j_3},o_{4j_4}{o}_{5j_5}\}$ for only one $j_1,j_2,\dots ,j_5$ where $1\le j_1\le \mathrm{6,1}\le j_2\le \mathrm{6,1}\le j_3\le \mathrm{5,1}\le j_4\le \mathrm{5,1}\le j_5\le 6$

Hence, the minimum number of edges present in the network is 32.

Step 4.

Maximum number of edges present in the constructed network is denoted by Max E $\left\{(a,b);1\le a,b\le 33;a\ne b\right\}-\left\{\begin{array}{c}{o}_1{o}_{k_1}where2\le k_1\le 6,o_2{o}_{k_2}where3\le k_2\le 6,o_3{o}_{k_3}where4\le k_3\le 5,.o_4{o}_5,\\ o_1{o}_{2j_2},o_1{o}_{3j_3}\dots ,o_1{o}_{5j_5};o_2{o_{3j}}_3,o_2{o_{4j}}_4,\dots o_2{o_{5rj}}_5;o_3{o_{4j}}_4,o_3{o_{o5j}}_5;o_4{o_{5j}}_5\\ where1\le j_2\le \mathrm{6,1}\le j_3\le \mathrm{5,1}\le j_4\le \mathrm{5,1}\le j_5\le 6.\end{array}\right.,$

Step 5.

$V_1=\frac{N_u{V}_{a_1}}{r_m}=\frac{3000}{5},$$V_2=\frac{3001}{5},$$V_3=\frac{1502}{5},$$V_4=\frac{1503}{5}$, $V_5=\frac{1804}{5}$

$D_1=D_{v_1}/V_1=1000/600=0.600$; $D_1=D_{v_1}/V_1$ (where $D_{v_1}$ denotes the numerical value 1 followed by the number of 0 digits of integral part of V₁). The remaining values of D₂, D₃, D₄, D₅ are calculated the same way that D₁ was.

$D_2=1000/600.2=0.6002$; $D_3=1000/300.4=0.3004$; $D_4=1000/300.6=0.3006$.

Step 6.

Split $D_1=d_{11}+d_{12}+d_{13}+d_{14}+d_{15}$ = 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1; $D_2=d_{21}+d_{22}+d_{23}+d_{24}+d_{25}=0.1+0.1+0.1+0.1+0.1+0.1002$: $D_3=d_{31}+d_{32}+d_{33}+d_{34}+d_{35}=0.05+0.05+0.05+0.1+0.0504$.

$D_4=d_{41}+d_{42}+d_{43}+d_{44}+d_{45}=0.05+0.05+0.05+0.1+0.0506$ $D_5=d_{51}+d_{52}+d_{53}+d_{54}+d_{55}+d_{56}=0.05+0.05+0.05+0.05+0.05+0.0608$

Assign $\mathit{min}\{o_1\left(t_1\right),o_{11}\left(t_{11}\right)\}=d_{11}$, $\mathit{min}\{o_1\left(t_1\right),o_{12}\left(t_{12}\right)\}=d_{12}$,…, $\mathit{min}\{o_1\left(t_1\right),o_{16}\left(t_{16_1}\right)\}=d_{16}$ in the first subnetwork

Assign $\mathit{min}\{o_2\left(t_1\right),o_{21}\left(t_{21}\right)\}=d_{21}$, $\mathit{min}\{o_2\left(t_1\right),o_{22}\left(t_{22}\right)\}=d_{22}$,…, $\mathit{min}\{o_2\left(t_1\right),o_{26}\left(t_{26}\right)\}=d_{26}$ in the second subnetwork, continuing the process until to assign $\mathit{min}\{o_5\left(t_1\right),o_{51}\left(t_{51}\right)\}=d_{51}$, $\mathit{min}\{o_5\left(t_1\right),o_{52}\left(t_{52}\right)\}=d_{52}$,…, $\mathit{min}\{o_5\left(t_1\right),o_{56}\left(t_{56}\right)\}=d_{56}$, in the fifth subnetwork.

Step 7.

Rest of the edge’s membership values will be followed by the definition of SFN.

end

5.4. Decryption Algorithm

Input: encrypted SFN

Output: $N_{u}V$, the secret number

Begin

Step 1.

Find the efficiently dominating members of FSN o₁, o₂, o₃, o₄, o₅ such that

$N_e\left[o_1\right]\cap N_e\left[o_2\right]\cap N_e\left[o_3\right]\cap N_e\left[o_4\right]\cap N_e\left[o_5\right]=\phi$.

Step 2.

$V_1=D_{v_1}\left({\sum }_{j_1=1}^6{d}_{1j_1}\right)=1000(0.1+0.1+0.1+0.1+0.1+0.1)=600$

$V_2=D_{v_2}\left({\sum }_{j_2=1}^6{d}_{1j_2}\right)=1000\left(0.6004\right)=600.4$,

$V_3=D_{v_3}\left({\sum }_{j_2=1}^5{d}_{1j_2}\right)=1000\left(0.3004\right)=300.4$,

$V_4=D_{v_4}\left({\sum }_{j_2=1}^5{d}_{1j_2}\right)=1000\left(0.3006\right)=300.6$,

$V_5=D_{v_5}\left({\sum }_{j_2=1}^6{d}_{1j_2}\right)=1000\left(0.3608\right)=360.8$.

Step 3.

$N_u{V}_a=r_m\left({\sum }_{i=1}^5{V}_i\right)=5\left(2162\right)=10810$.

end

5.5. Encryption and Decryption of Intuitionistic Fuzzy Network (IFN) Using Efficient Domination

Definition  11:

An intuitionistic fuzzy graph (IFG) is of the form H_NG = (V_s, E_s) where:

(i)

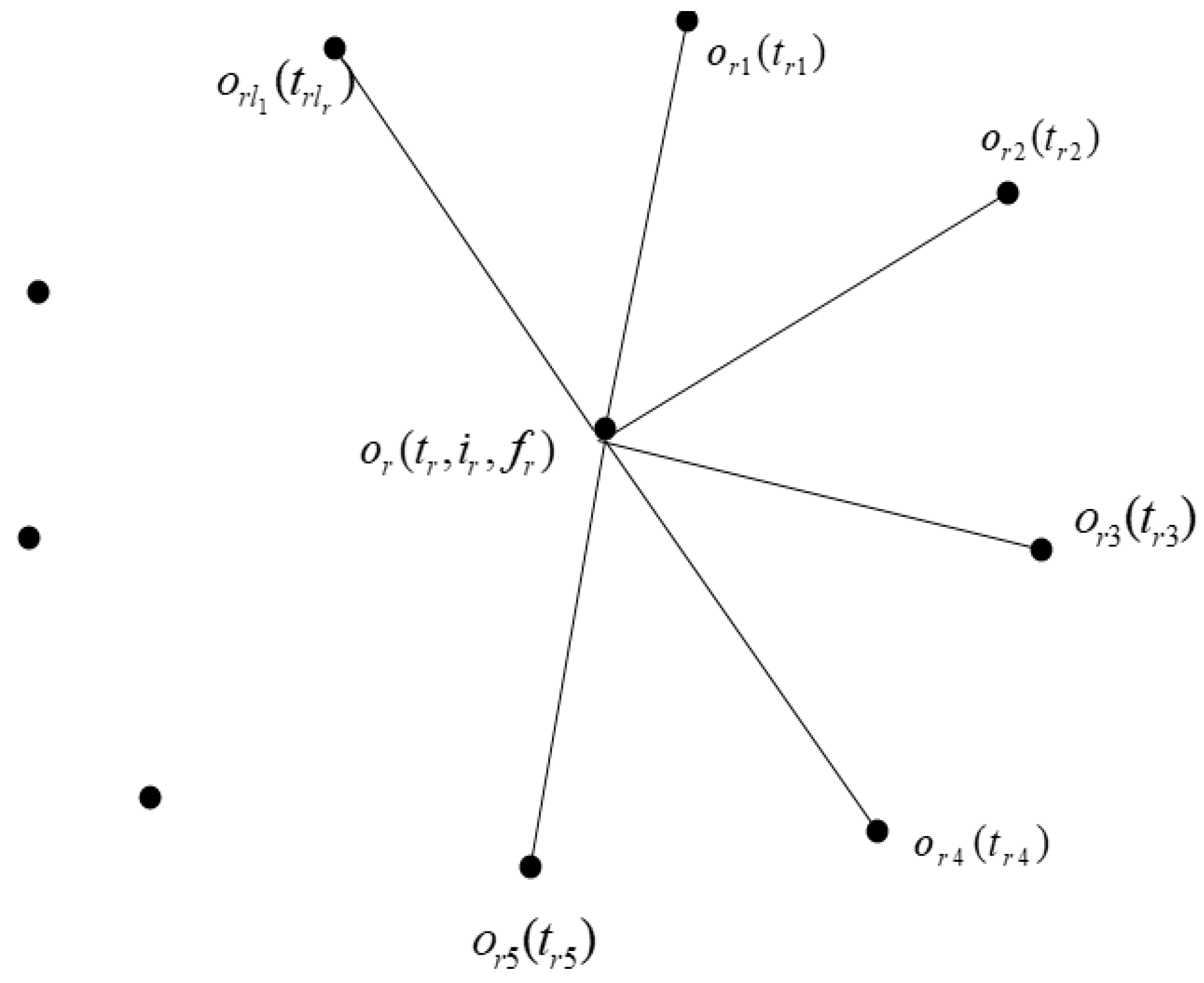
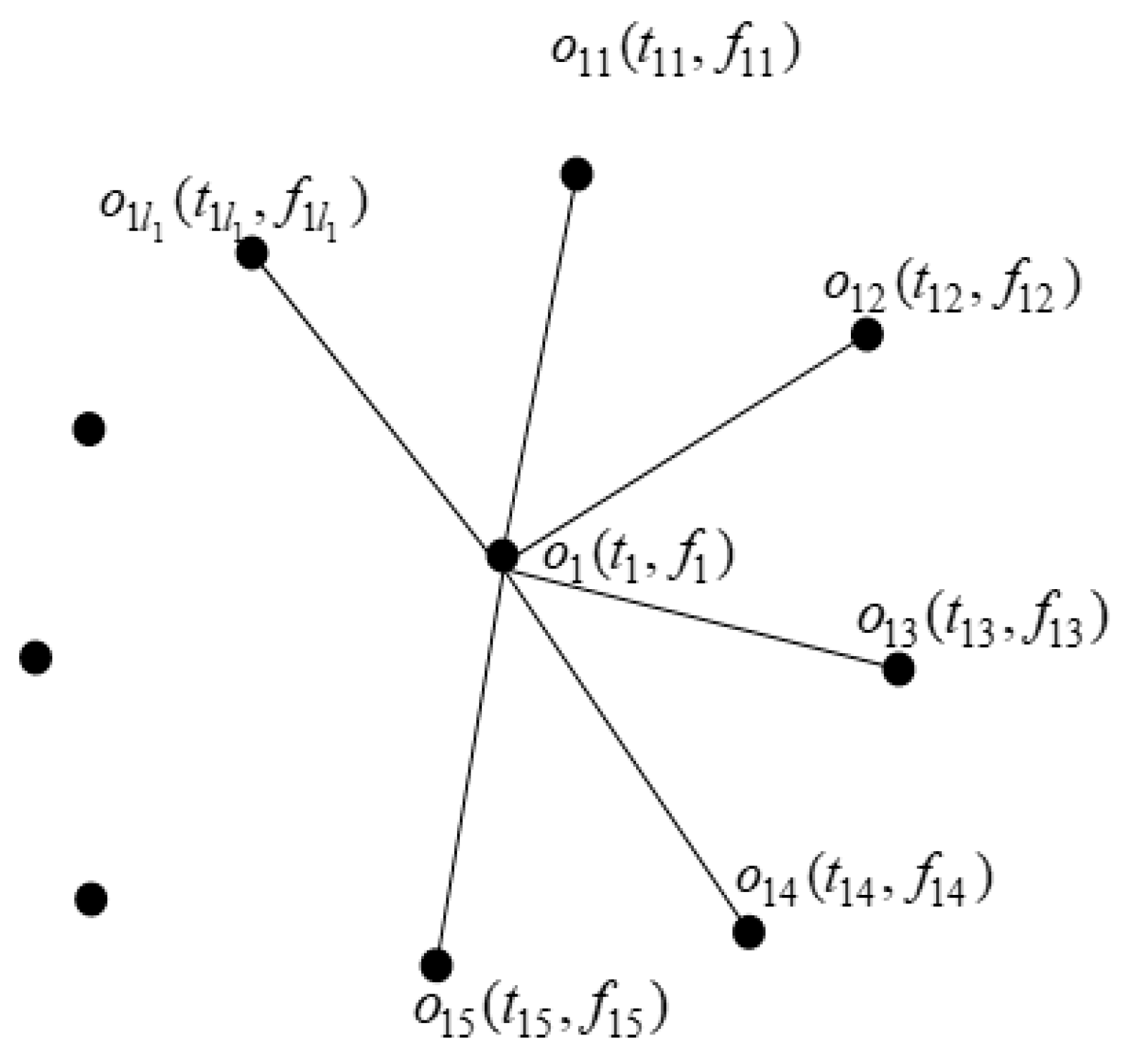
V_s = {o₁,o₂,…,o_n} such that $T_{V_s}:V_s\to [0,1]$; and $F_{V_s}:V_s\to [0,1]$ denote the degree of truth membership value, degree of indeterminacy membership value, and degree of falsity membership value, respectively, and $0\le T_{V_s}(v_s)+F_{V_s}(v_s)\le 2$ for every $v_s\in V.$

(ii)

$E\subseteq V\times Vwhere{T}_{E_s}:V\times V\to [0,1]$; $F_{E_s}:V\times V\to [0,1]$ are defined by $T_{E_s}\{(a_i,a_j)\}$ $\le \min \{T_{V_s}(a_i),T_{V_s{}_{}}(a_j)\}$; $F_{E_s}\{(a_i,a_j)\}\ge \max \{F_{V_s}(a_i),F_{V_s}(a_j)\}$ denote the degree of truth membership value and degree of falsity membership value of the edge $(a_i,a_j)\in E_s$, respectively, where $0\le T_{E_s}\{(a_i,a_j)\}+F_{E_s}\{(a_i,a_j)\}\le 2$$\forall (a_i,a_j)\in E_s$.

Definition  12:

A subset T of V¹ is said to be the dominating set of a single valued IFG if every vertex in V¹ − T is dominated by at least one vertex of V¹. The dominating set T is said to be minimal if no proper subset of T is a dominating set.

Definition  13:

An arc (u − v) is said to be a strong arc if its degree of edge membership value is equal to the strength of connectedness between u and v.

Definition  14:

Let e = (a, b) be the edge of an IFG. We say that a dominates b if there exists a strong arc between them.

Definition  15:

Intuitionistic fuzzy network (IFN) is defined as a group of the same category peoples (a set of nodes) that they interact with each other and work together (the link is a relation which represents the sharing work or sharing information) such that every node (person) has true a degree membership value (T), an indeterminacy degree membership value of (I), and a falsity degree membership (F). The relation (information, knowledge sharing, etc.) between any two persons is represented by the link. The link also has a true degree membership value (T) and falsity degree membership (F).

Definition  16:

An IFG is said to be strong if it satisfies the following:

$T_{E_s}\{(a_i,a_j)\}$$=\min \{T_{V_s}(a_i),T_{V_s{}_{}}(a_j)\}$; $F_{E_s}\{(a_i,a_j)\}=\max \{F_{V_s}(a_i),F_{V_s}(a_j)\}$ $\forall (a_i,a_j)\in E_{s}and{a}_i\&a_j\in V_s.$

Definition  17:

A strong intuitionistic fuzzy network (SIFN) is an IFN, which satisfies the following

$T_{E_s}\{(a_i,a_j)\}$$=\min \{T_{V_s}(a_i),T_{V_s{}_{}}(a_j)\}$; $F_{E_s}\{(a_i,a_j)\}=\max \{F_{V_s}(a_i),F_{V_s}(a_j)\}$ $\forall (a_i,a_j)\in E_{s}and{a}_i\&a_j\in V_s.$

Definition 18:

A dominating set T of V_s is said to be the efficiently dominating set of an IFG if $\left|T\cap N[v]\right|=1$, for every vertex v in V_s − T, where N[v] represents the closed neighborhood of v. The dominating set T is said to be minimally efficiently dominating if no proper subset of T is efficiently dominating. The following IFG is strong.

The vertex and edge degree membership values of the SIFG in Figure 8 and

Table 1. Vertex degree and edge degree membership values.

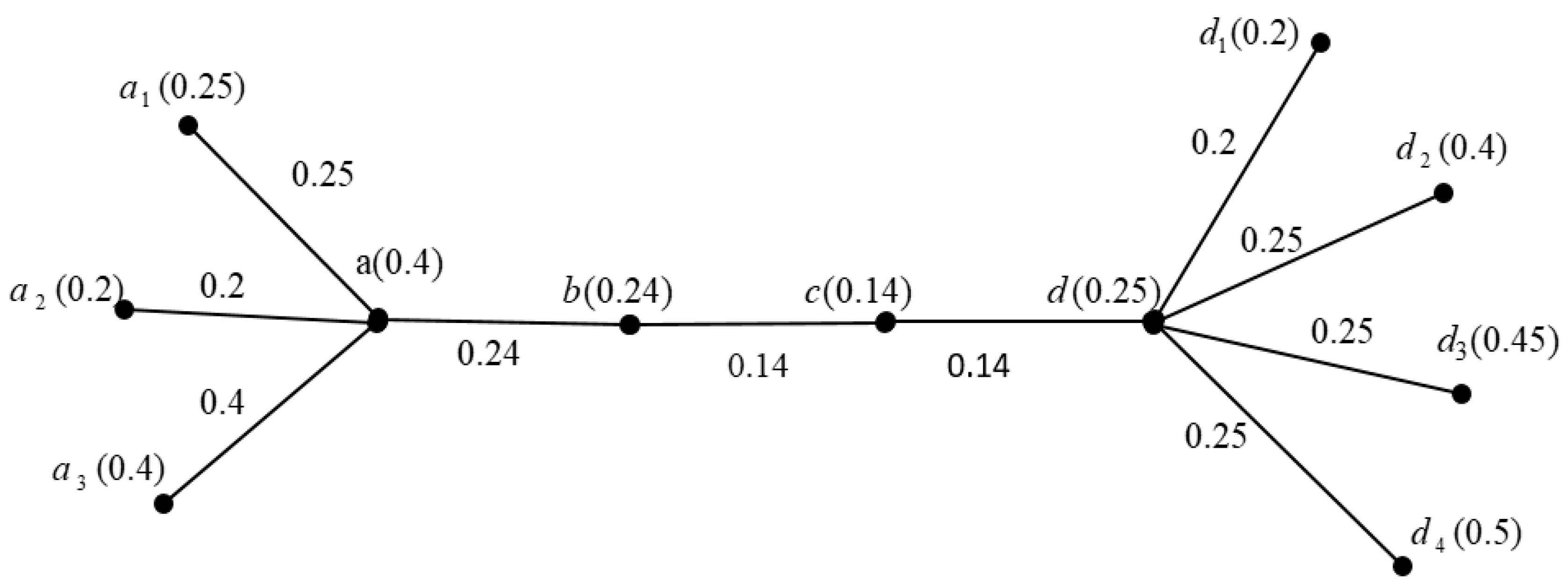
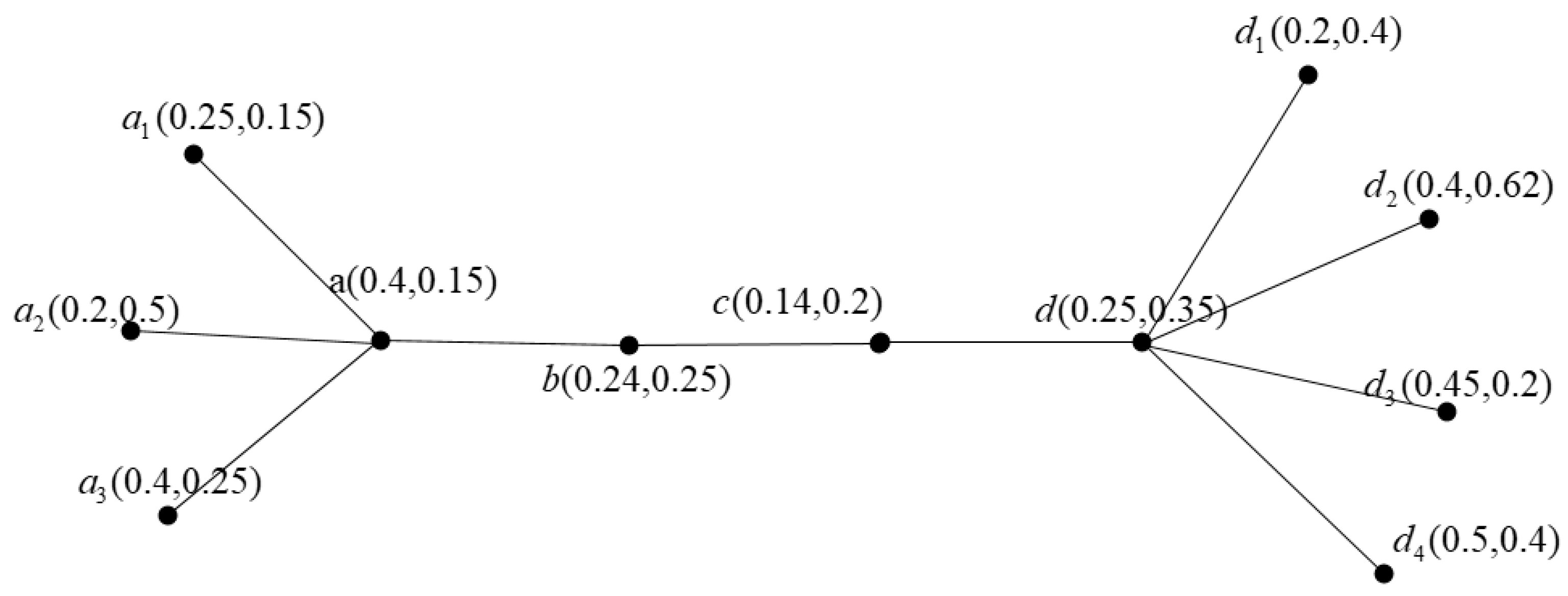
Vertex Degree Membership Values	Edge Degree Membership Values
a (0.4, 0.15)	ab (0.24, 0.25)
b (0.24, 0.25)	bc (0.14, 0.25)
c (0.14, 0.2)	cd (0.14, 0.35)
d (0.25, 0.35)	ab (0.24, 0.25)
a1 (0.25, 0.15)	aa1 (0.25, 0.15)
a2 (0.2, 0.5)	aa2 (0.2, 0.5)
a3 (0.4, 0.25)	cc3 (0.4, 0.25)
d1 (0.2, 0.4)	dd1 (0.2, 0.4)
d2 (0.4, 0.62)	dd2 (0.25, 0.62)
d3 (0.45, 0.2)	dd3 (0.25, 0.35)
d4 (0.5, 0.4)	dd4 (0.25, 0.4)

is as follows.

Every edge in the IFG (Figure 8) is strong, and the only efficiently dominating set is T = {a, d} since every vertex in V − T is dominated by exactly one vertex and this dominating set is unique. The construction of the sub-SIFN is different from the construction of SFN. As the intuitionistic fuzzy network for every node and edge has membership values, let the efficiently dominating nodes (EDNs) be o₁, o₂, o₃, o₄, …, o_r. These nodes are the center of the subnetworks, namely say SIFN₁, SIFN₂, SIFN_3, SIFN₄, …, and SIFN₅, respectively. Let the neighbors of o₁, o₂, o₃, o₄, …, o_r be $o_{11},o_{12},o_{13},,\dots ,o_{1l_1}$; $o_{21},o_{22},o_{23},\dots ,o_{2l_r}$; $o_{31},o_{32},o_{33},\dots ,o_{3l_r}$, …, $o_{51},o_{52},o_{53},\dots ,o_{r{l}_r}$, respectively. First, the SIF subnetwork is SIFN_1, whose center is o₁ and its neighbors are $o_{11},o_{12},\dots ,o_{1l_1}$. The first subdivision value $N{V}_1\equiv R_1(\mathrm{mod}r)$. Set $V_1=\frac{N{V}_1}{r}and$$D_1=D_{v1}/V_1$ (where $D_{v1}$ is the numerical value 1 followed by the number of 0 digits of an integral part of V₁) partitioned into the sum of l₁ values, say $d_{11},d_{12},\dots d_{1_{l_1}}$, respectively, and assign these values minimum values of either o₁ or $o_{11},o_{12},\dots ,o_{1l_1}$, as degree of truth membership values. Likewise, the frame of the r th subnetwork continues, which is SIFN_r. The SIF subnetwork 1 and the rth networks are shown in Figure 9 and Figure 10, respectively.

The encrypted SIFN with a minimum number of edges and a moderate number of edges is shown in Figure 11 and Figure 12, respectively. The rest of the framework of SIFN is similar to SFN. One of the illustrations is given as follows.

5.6. Illustration

The secret number is $NV=10,810$. The encrypted SIFN with the secret number is shown in Figure 13. The edge membership values are given in the following

Table 2. Degree of edge membership values in Figure 13.

Edges	Degree of Membership Values	Edges	Degree of Membership Values
o1o11	(0.1, 0.33)	o33o34	(0.05, 0.3)
o1o12	(0.1, 0.35)	o34o35	(0.05, 0.25)
o1o13	(0.1, 0.32)	o4o41	(0.1, 0.4)
o1o14	(0.1, 0.3)	o4o42	(0.05, 0.4)
o1o15	(0.1, 0.33)	o4o43	(0.05, 0.4)
o1o16	(0.1, 0.3)	o4o44	(0.05, 0.4)
o11o21	(0.1, 0.36)	o4o45	(0.0506, 0.4)
o12o26	(0.1, 0.35)	o41o45	(0.0506, 0.36)
o13o26	(0.1, 0.32)	o41o42	(0.05, 0.36)
o11o16	(0.1, 0.33)	o43o44	(0.05, 0.3)
o11o12	(0.1, 0.36)	o41o53	(0.05, 0.36)
o14o15	(0.1, 0.25)	o45o54	(0.05, 0.2)
o15o16	(0.1, 0.33)	o41o54	(0.05, 0.2)
o2o21	(0.1, 0.36)	o5o51	(0.05, 0.4)
o2o22	(0.1, 0.3)	o5o52	(0.05, 0.36)
o2o23	(0.1, 0.3)	o5o53	(0.05, 0.4)
o2o24	(0.1, 0.3)	o5o54	(0.05, 0.4)
o2o25	(0.1, 0.3)	o5o55	(0.05, 0.4)
o2o26	(0.1002, 0.3)	o5o56	(0.0608, 0.4)
o21o26	(0.1, 0.36)	o14o52	(0.05, 0.25)
o25o26	(0.1, 0.2)	o14o51	(0.05, 0.36)
o23o24	(0.1, 0.3)	o15o56	(0.0608, 0.33)
o22o23	(0.1, 0.35)	o51o56	(0.05, 0.36)
o3o31	(0.05, 0.36)	o51o52	(0.05, 0.361)
o3o32	(0.05, 0.4)	o53o54	(0.05, 0.35)
o3o33	(0.05, 0.4)	o54o55	(0.05, 0.25)
o3o34	(0.05, 0.4)	o24o53	(0.05, 0.35)
o3o35	(0.0504, 0.4)	o34o53	(0.05, 0.35)
o31o35	(0.0504, 0.36)	o45o42	(0.05, 0.25)
o32o33	(0.05, 0.35)

.

6. Real-Time Applications

In this section, we present several real-world scenarios where the application of our fuzzy network using efficient domination can be beneficial. By illustrating the practical relevance of our proposed system, we aim to demonstrate its value and applicability in various domains.

6.1. Telecommunications Networks

The proposed system can be employed to optimize the structure of telecommunication networks, minimize latency and reduce the costs associated with infrastructure deployment and maintenance [25]. By identifying the efficiently dominating nodes within the network, our approach can help design networks with improved connectivity, fault tolerance, and resource allocation [26]. For instance, the placement of cell towers or routers can be optimized to ensure the maximum coverage with the minimum number of links. This will reduce the overall cost of establishing and maintaining the network [27,28].

6.2. Transportation Systems

Our approach can be applied to optimize transportation networks, such as road networks or public transit systems. By efficiently connecting critical points (e.g., hubs, stations), using the minimum number of links, our proposed system can result in reduced travel times, lower infrastructure costs, and enhanced traffic flow. In the context of public transit systems, efficient domination can be used to determine the optimal location and connections of stations, minimizing the number of transfers required for passengers and improving the overall efficiency of the system [29,30].

6.3. Social Network Analysis

The proposed system can be applied to analyze social networks to identify influential nodes, optimize information dissemination, and improve community detection. By employing efficient domination, our approach can help in understanding the structure and dynamics of social networks, enabling researchers and practitioners to develop more effective strategies for information diffusion, marketing, or public health interventions [31,32].

7. Conclusions

We delivered the combinatorial technique to find the secret number, which has been presented in the constructed strong fuzzy network. Constructing the strong fuzzy network plays an important role in the network due to the concept of efficient domination. The efficiently dominating members are certain nodes of the dominating set such that every vertex that is not in the dominating set is adjacent to exactly one vertex of the dominating member. The secret key is to identify the most efficient and dominant set of SFN. The network becomes more complicated to decrypt as we assign the repeated values of d_ij and the maximum number of edges present in the constructed SFN. Furthermore, the efficiently dominating set of the constructed network is unique. Moreover, we developed the intuitionistic fuzzy network, and an illustration was given that provides a better understanding of encryption and decryption using efficient domination.