Network Structure Identification Based on Measured Output Data Using Koopman Operators

Abstract

This paper considers the identification problem of network structures of interconnected dynamical systems using measured output data. In particular, we propose an identification method based on the measured output data of each node in the network whose dynamic is unknown. The proposed identification method consists of three steps: we first consider the outputs of the nodes to be all the states of the dynamics of the nodes, and the unmeasurable hidden states to be dynamical inputs with unknown dynamics. In the second step, we define the dynamical inputs as new variables and identify the dynamics of the network system with measured output data using Koopman operators. Finally, we extract the network structure from the identified dynamics as the information transmitted via the network. We show that the identified coupling functions, which represent the network structures, are actually projections of the dynamical inputs onto the space spanned by some observable functions. Numerical examples illustrate the validity of the obtained results.

1. Introduction

Nowadays, network theory shows great importance in various fields such as engineering [1,2,3,4], finance [5] and bioscience [6]. Particularly, the problem of inferring structures of networks from measured data becomes an important task, and many practical issues can be categorized as such problems, e.g., modeling human brains [7] or detecting sources of rumor propagation [8]. The network identification problem has been studied in many perspectives, and various methods have been developed. Data correlation [9,10,11,12,13,14,15,16] plays an important role in network identification problems: in the presence of noises [9,14,15] or unmeasured hidden signals [16,17], the time derivative of the dynamical correlation matrix among the nodes reveals the relationship between the adjacency matrix of the network and the covariance matrix of the noise. With the help of basis functions, nonlinearity is identified with a higher order data correlation [13,18]. Furthermore, sparse identification (compressive sensing) [19,20] techniques are employed to identify the structure of networks [21,22]: linear evolution of data is identified by finding the sparsest matrix that maps the data to the next step. Taylor expansion or trigonometric basis functions also make the method applicable to networks with nonlinear couplings [13,23,24]. In [25], the Koopman operator theory and sparse identification techniques are combined to achieve accurate identification of nonlinear coupling functions. Moreover, adaptive master–slave synchronization-based methods [26,27], statistic-based methods [28] and variable (or phase) resetting-based methods [15,29] also achieve success.

Although most of the above-mentioned methods assume that all the states of the nodes are measurable, in practical cases there may exist states that cannot be measured, which are known as hidden variables. In [10,11,17], the hidden variables are considered colored noises, and the identification is performed in the subspace spanned by the measurable states. In [16], networks with hidden nodes are identified by reconstructing the adjacency matrix corresponding to the network and calculating the covariance of the obtained results, basing on the principle that unknown input signals from hidden nodes would enlarge the covariance. In [30], such a method is extended to networks with transmission time delays. In this paper, we consider networks of interconnected dynamical systems and model the network structures as coupling functions that describe the inputs to the nodes via the network. Specifically, we focus on the case where only the output data of the nodes are measurable. The goal of this paper is then reduced to identifying the coupling functions from measured output data.

Generally speaking, the statistic-based [28] and correlation-based methods [9,22] detect whether transmission between nodes exists; therefore, these methods could only obtain results about the topology of networks. Nonlinearity in network structures, modeled as nonlinear coupling functions, is commonly identified by approximating the dynamics that govern the nonlinear evolution of measured data with the help of basis functions [13,21,23,25,31]. In this paper, compared to the widely studied case where all the states of the nodes can be measured, a major difficulty of obtaining the possibly nonlinear coupling function is that the coupling function may be dependent on the unmeasurable states, so the dynamics cannot be fully revealed from measured data. On the other hand, in the case where neither the dynamics of the nodes without inputs is unknown, nor data of unforced nodes can be measured, it is also a challenging task to distinguish the coupling function from the identified dynamics of all the nodes. Towards solving these problems, we propose an identification method that makes it possible to obtain the possibly nonlinear coupling functions from solely measured output data. The proposed method consists of the following three steps. First, we reformulate the dynamical model of the network. We consider the outputs of each node as the full states and the dynamics of the output signals as the dynamics of the node. In the second step, the unmeasurable hidden states are then modeled as unknown dynamical inputs. Defining such dynamical inputs as new variables, time series data of the new variables can be calculated and the dynamics of such variables can be identified with the help of Koopman operators. In the third step, the network dynamics are then identified in terms of the outputs and the new variables using measured data, and the network structure is extracted as the data transmission in the network. If the dimension of the output is so low that the dynamics of the network cannot be embedded into the space spanned by the outputs and the new variables, then additional variables are introduced based on past data [32]. We show that the obtained coupling function is a projection of the future values of the dynamical inputs onto the space spanned by some pre-defined observable functions, and discuss the causes of identification errors. Compared to previous efforts, the contribution of this paper is two-fold:

• The proposed method is applicable to networks whose nodes have unknown dynamics and only the outputs can be measured;
• The proposed method is applicable to the case where data transmission in the network is represented by nonlinear functions.

With these advantages, the proposed method is expected to be applicable to practical problems such as analyzing electronic circuits with limited measurements and modeling nervous systems.

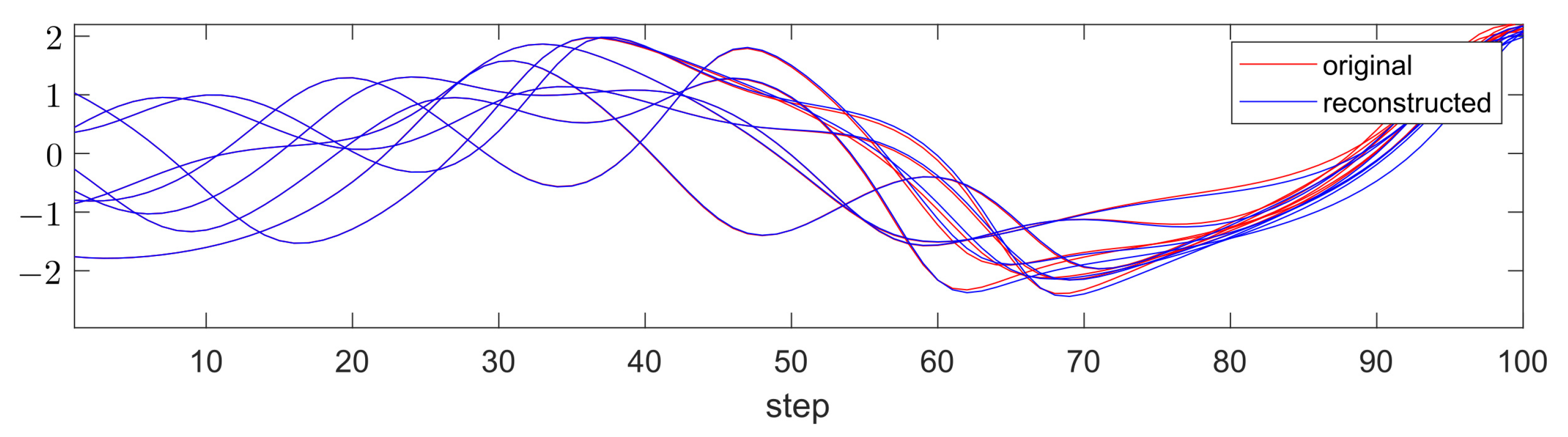
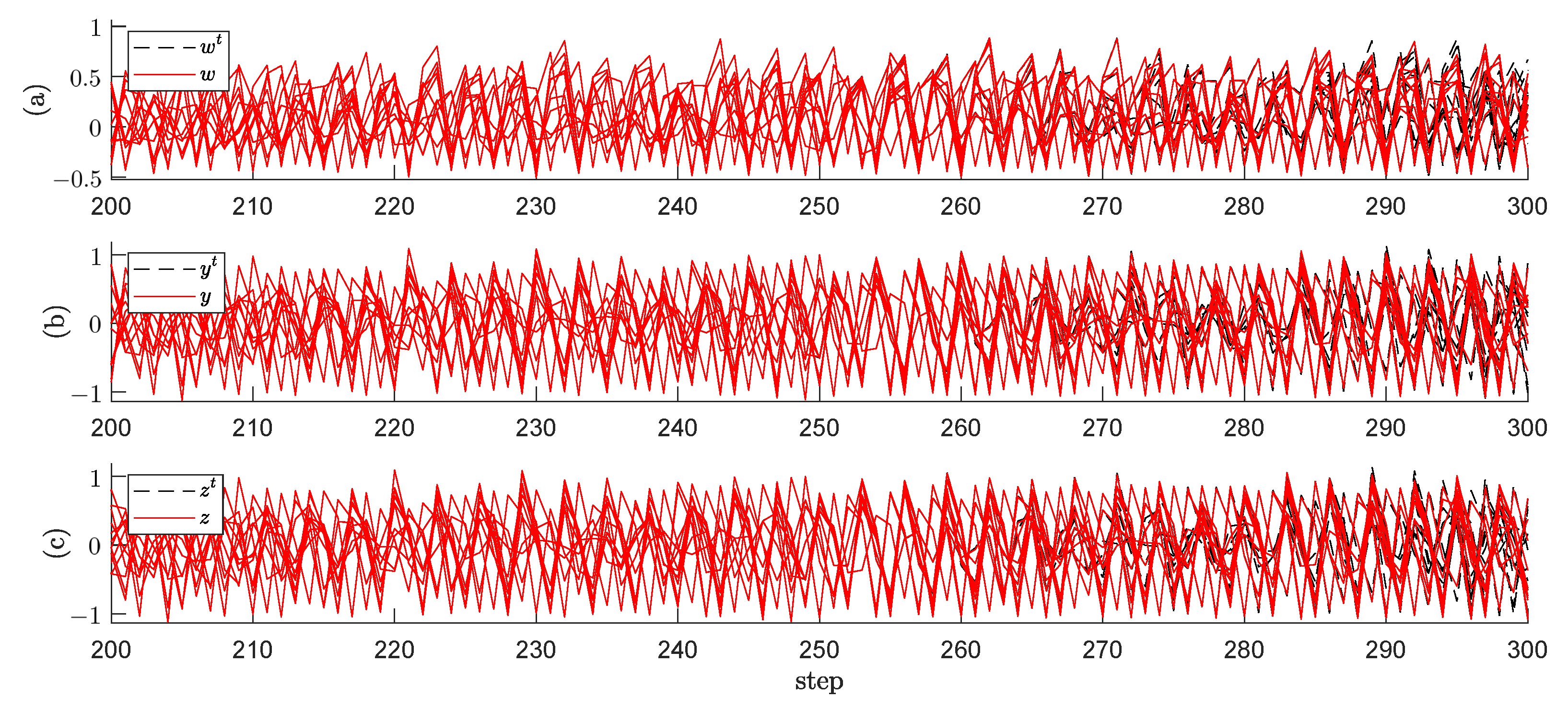
This paper is organized as follows. In Section 2, we provide brief introductions to the Koopman operator and Koopman mode decomposition. Section 3 describes the proposed identification method, and Section 4 presents numerical identification examples to show the validity and usefulness of the obtained results. In Section 5, we summarize the paper and conclude with some remarks and discussions.

Throughout this paper, $\mathbb{N}$, $\mathbb{R}$ and $\mathbb{C}$ denote the sets of all the natural numbers, all the real numbers and all the complex numbers, respectively. ${\parallel x\parallel }_p$ denotes the p norm of an n-dimensional vector x defined by ${\parallel x\parallel }_p={\sum }_{i=1}^n{\left|x_i\right|}^p$, where $p=1,2,\cdots ,\infty$ and ${\parallel A\parallel }_F$ denote the Frobenius norm of matrix $A\in {\mathbb{C}}^{n\times m}$ defined by ${\parallel A\parallel }_F=\sqrt{{\sum }_{i=1}^n{\sum }_{j=1}^m{\left|a_{ij}\right|}^2}$. For constants, vectors, matrices or functions $v_1,\cdots ,v_n$, ${\mathrm{col}}_{i=1}^n\left(v_i\right)$ or $\mathrm{col}(v_1,\cdots ,v_n)$ denote the composed vector (or matrix) ${(v_1^{*},\cdots ,v_n^{*})}^{*}$, where $v_i^{*}$ is the Hermitian transpose of $v_i$. For a vector $a=\mathrm{col}(v_1,\cdots ,v_n)$, $\mathrm{span}\left\{a\right\}$ denotes the space spanned by all its entries, i.e., $\mathrm{span}\left\{a\right\}=\left\{f\right|f={\sum }_{i=1}^n{c}_i{a}_i,\forall c_i\in \mathbb{C}\}$, and $\mathrm{span}{\left\{a\right\}}^n$ denotes the space of n-dimensional vectors whose entries are contained in $\mathrm{span}\left\{a\right\}$. For a functional space $\mathcal{G}$ and its subspace $\mathcal{F}$, ${\mathbb{P}}_{\mathcal{F}}\phi$ denotes the projection operator defined by ${\mathbb{P}}_{\mathcal{F}}\phi ={\mathrm{argmin}}_{\varphi \in \mathcal{F}\subset \mathcal{G}}\parallel \varphi -\phi \parallel$, where $\phi \in \mathcal{G}$ and $\parallel ·\parallel$ is a norm defined on $\mathcal{G}$. ${\mathit{e}}_i$ denotes the ith standard basis vector of appropriate dimension such that the ith entry of ${\mathit{e}}_i$ is 1 and other entries are 0. $x^{i+}$ denotes the evolution of variable x, i.e., $x^{i+}\left[k\right]=x[k+i]$ where $k\in \mathbb{N}$, and specially, $x^{+}=x^{1+}$.

2. Preliminary: The Koopman Operator

In this paper, we consider Koopman operators in discrete-time settings [33,34]. For the discrete-time system described by

$$\begin{array}{c}\hfill x^{+}=f\left(x\right),\end{array}$$

(1)

where $x\in {\mathbb{R}}^n$ and $f:{\mathbb{R}}^n\to {\mathbb{R}}^n$ is a nonlinear vector field, define $\psi :{\mathbb{R}}^n\to \mathbb{C}$ to be an observable (function), and denote the space of all the observables by $\mathcal{F}$. Define the operator space of all the operators that map $\mathcal{F}$ to $\mathcal{F}$ by $\mathcal{B}$, i.e., $\mathcal{B}=\mathcal{L}(\mathcal{F},\mathcal{F})$. Then, the evolution of the states of system (1) can be described by the evolution of the observable functions governed by the Koopman Operator K defined on $\mathcal{B}$ by

$$\begin{array}{c}\hfill K\psi \left(x\right)=\psi \left(f\right(x\left)\right).\end{array}$$

(2)

The Koopman operator is an infinite-dimensional operator that preserves all the nonlinear characteristics of vector field $f(·)$, and is linear in the sense that $K(a{\psi }_1+b{\psi }_2)=aK{\psi }_1+bK{\psi }_2$ for any $a,b\in \mathbb{C}$ and ${\psi }_1,{\psi }_2\in \mathcal{F}$. Define ${\varphi }_1,{\varphi }_2,\cdots$ and ${\lambda }_1,{\lambda }_2,\cdots$ to be eigenfunctions and the corresponding eigenvalues of Koopman operator K such that $K{\varphi }_i={\lambda }_i{\varphi }_i$. If the eigenfunctions span $\mathcal{F}$, then for any $\xi \in \mathcal{F}$, there exist $c_i$ for $i=1,2,\cdots$ such that $\xi ={\sum }_{i=1}^{\infty }{c}_i{\varphi }_i$ and

$$\begin{array}{c}\hfill K\xi =\sum _{i=1}^{\infty }{c}_{i}K{\varphi }_i=\sum _{i=1}^{\infty }{c}_i{\lambda }_i{\varphi }_i.\end{array}$$

(3)

Equation (3) is called the Koopman mode decomposition of $K\xi \left(x\right)=\xi \left(f\right(x\left)\right)$, and $c_i$ is called the eigenmode of $\xi \left(f\right(x\left)\right)$ with respect to $\mathrm{span}\left\{{\varphi }_i\right\}$.

To obtain a q-dimensional approximation of K, we consider the first q dominant pairs of eigenvalues and eigenfunctions of Koopman operators K, denoted by $(({\lambda }_1,{\varphi }_1),\cdots ,({\lambda }_q,{\varphi }_q))$. Define the space spanned by the q eigenfunctions by ${\mathcal{F}}_q$, i.e., ${\mathcal{F}}_q=\mathrm{span}\{{\varphi }_1,\cdots ,{\varphi }_q\}$. For any $\phi \in {\mathcal{F}}_q$, there exists a $c_{\phi }\in {\mathbb{C}}^q$ such that $\phi =c_{\phi }^{*}\mathsf{\Phi }$ and

$$\begin{array}{c}\hfill K\phi =c_{\phi }^{*}\mathsf{\Lambda }\mathsf{\Phi },\end{array}$$

where $\mathsf{\Lambda }=\mathrm{diag}({\lambda }_1,\cdots ,{\lambda }_q)$ and $\mathsf{\Phi }=\mathrm{col}({\varphi }_1,\cdots ,{\varphi }_q)$. If the set of eigenfunctions $\{{\varphi }_1,\cdots ,{\varphi }_q\}$ is sufficiently rich, then the spanned space can be considered to contain all the observable functions, i.e., ${\mathcal{F}}_q\approx \mathcal{F}$. Furthermore, consider an observable function set $\{{\psi }_1,\cdots ,{\psi }_q\}$ of q linearly independent elements, and define $\mathsf{\Psi }=\mathrm{col}({\psi }_1,\cdots ,{\psi }_q)$. Suppose that $\{{\psi }_1,\cdots ,{\psi }_q\}$ also forms a set of linearly independent basis of ${\mathcal{F}}_q$, then there exists an invertible linear map P that maps $\mathsf{\Psi }$ to $\mathsf{\Phi }$, i.e., $\mathsf{\Phi }=P\mathsf{\Psi }$, and

$$\begin{array}{cc}\hfill K\mathsf{\Psi }=& K{P}^{-1}\mathsf{\Phi }=P^{-1}\mathsf{\Lambda }\mathsf{\Phi }\hfill \\ \hfill =& P^{-1}\mathsf{\Lambda }P\mathsf{\Psi }.\hfill \end{array}$$

Setting $A=P^{-1}\mathsf{\Lambda }P$, A is a q-dimensional approximation of Koopman operator K, such that $A\mathsf{\Psi }\left(x\right)=\mathsf{\Psi }\left(f\right(x\left)\right)$. For any $\phi \in \mathcal{F}$ that has an approximation $\phi \approx c^{*}\mathsf{\Psi }\in {\mathcal{F}}_q$, a q-dimensional approximation of $K\phi$ can be obtained as

$$\begin{array}{c}\hfill K\phi \approx c^{*}A\mathsf{\Psi }.\end{array}$$

(4)

In this paper, a Koopman operator acts on a vector in an entry-wise manner, i.e., $Kv={\mathrm{col}}_{i=1}^N\left(K{v}_i\right)$ for $v={\mathrm{col}}_{i=1}^N\left(v_i\right)$, where $v_i\in \mathcal{F}$.

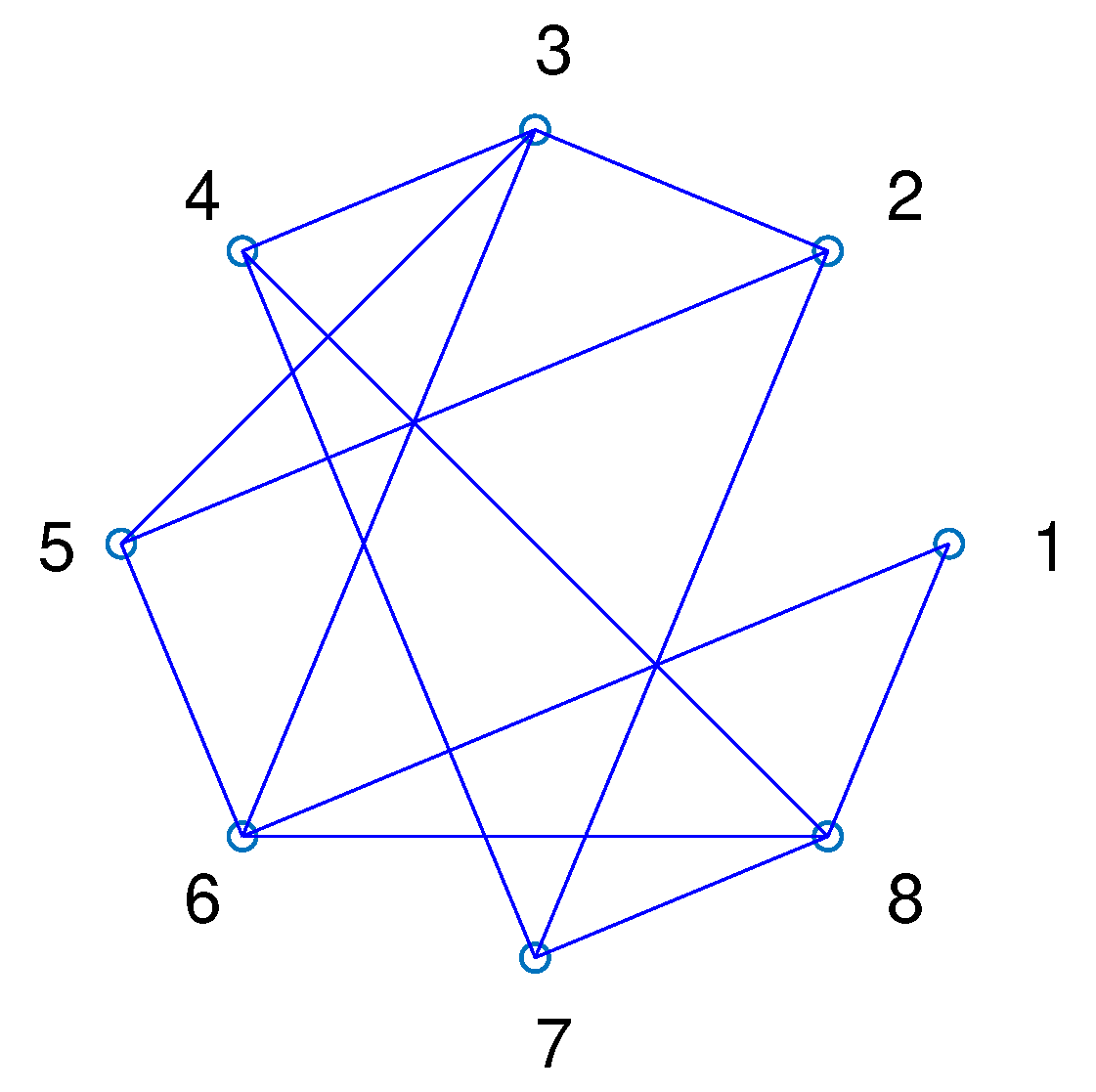
3. Network Structure Identification Based on Output Data

Consider the network system of N nodes described by

$$\begin{array}{cc}\hfill x_i^{+}=& f\left(x_i\right)+B{u}_i\left(x\right),\hfill \\ \hfill w_i=& C{x}_i,\hfill \\ \hfill u_i\left(x\right)=& \sum _{j=1}^N{a}_{ij}g(x_i,x_j),\hfill \end{array}$$

(5)

where $x_i\in {\mathbb{R}}^n$, $x={\mathrm{col}}_{i=1}^N\left(x_i\right)\in {\mathbb{R}}^{Nn}$ denotes the states, $f:{\mathbb{R}}^n\to {\mathbb{R}}^n$ is locally Lipschitz continuous, $w_i\in {\mathbb{R}}^m$ is the output of node i, and $u_i\left(x\right):{\mathbb{R}}^{Nn}\to {\mathbb{R}}^m$ denotes the transmission sent to node i via the network where $a_{ij}$ is the $(i,j)$ entry of the adjacency matrix associated with the network topology. Define $w={\mathrm{col}}_{i=1}^N\left(w_i\right)$ and rewrite the dynamics of the network into

$$\begin{array}{cc}\hfill x^{+}=& \mathit{f}\left(x\right)+\mathit{Bg}\left(x\right),\hfill \\ \hfill w=& \mathit{C}x,\hfill \end{array}$$

(6)

where $\mathit{f}\left(x\right)={\mathrm{col}}_{i=1}^N\left(f\left(x_i\right)\right)$, $\mathit{g}\left(x\right)={\mathrm{col}}_{i=1}^N\left(u_i\right)$, $\mathit{B}=I_N\otimes B$, $\mathit{C}=I_N\otimes C$, and ⊗ denotes the Kronecker product. Here, the network structure is fully contained in $\mathit{g}\left(x\right)$, so the network structure identification problem is reduced to identifying $\mathit{g}\left(x\right)$. Specifically, we consider the case where a linear approximation of the dynamical model is known, and attempt to identify the network structure from measured output data. We first reformulate the dynamical model of the nodes such that the data of the new variables used to describe the dynamics can be calculated from the output, and then describe a numerical method to obtain the coupling function. The identification method is also considered in two cases where the dimension of the output is sufficiently high or not, respectively.

We first construct the dynamical model of the nodes such that the outputs $w_i$ correspond to the full states, and the unmeasurable states as unknown dynamical inputs. Let $Fx$ be a linear approximation of $f\left(x\right)$ where $F\in {\mathbb{R}}^{n\times n}$, $f\left(x\right)\equiv Fx+\tau \left(x\right)$ and $\tau \left(x\right)$ denote the modeling error. Let $T\in {\mathbb{R}}^{(n-m)\times n}$ be such that $\mathrm{col}(C,T)$ has full rank, and rewrite (5) into

$$\begin{array}{cc}\hfill w_i^{+}=C{x}_i^{+}=& CF{x}_i+C\tau \left(x_i\right)+CB{u}_i\left(x\right),\hfill \end{array}$$

(7a)

$$\begin{array}{cc}\hfill T{x}_i^{+}=& TF{x}_i+T\tau \left(x_i\right)+TB{u}_i\left(x\right).\hfill \end{array}$$

(7b)

Since only data of the outputs $w_i$ of the nodes can be measured, we rewrite $CF{x}_i$ into $CF{x}_i\equiv F_1{w}_i+F_2{x}_i$, where $F_1\in {\mathbb{R}}^{m\times m}$ consists of the first m columns of $CF{\left[\begin{array}{c}C\\ T\end{array}\right]}^{-1}$ and $F_2\in {\mathbb{R}}^{m\times n}$. Define $y_i=F_2{x}_i+C\tau \left(x_i\right)+CB{u}_i\left(x\right)$ for $i=1,\cdots ,N$. Substituting $y_i$ into (7a), $y_i$ is considered a dynamical input to $w_i$, i.e., $w_i^{+}=F_1{w}_i+y_i$, where the dynamics of $y_i$ are unknown. The merits of defining the variables $y_i$ are two-fold: the dynamics of $w_i$ becomes fully known and $y_i\left[k\right]$ can be obtained as $w_i[k+1]-F_1{w}_i\left[k\right]$. We consider two cases where the dimension of $\mathrm{col}(w_i,y_i)$ is smaller than the dimensional of $x_i$ or not, respectively. Note that though $y_i$ is unknown, data for $y_i$ can be calculated from $w_i$ and the dimension of $y_i$ can be inferred by checking the linear dependency of the data series.

We first consider the case where $\dim \left(y_i\right)+m\ge n$. In this case, no additional variables are required to span the dynamics of $x_i$, so let the dynamics of $y_i$ be described by $y_i^{+}=h_i(w,y)$, where $y={\mathrm{col}}_{i=1}^N\left(y_i\right)\in {\mathbb{R}}^{Nm}$ and $h_i:{\mathbb{R}}^{Nm}\times {\mathbb{R}}^{Nm}\to {\mathbb{R}}^m$. Reformulate the dynamical models of the nodes as

$$\begin{array}{cc}\hfill w_i^{+}=& F_1{w}_i+y_i,\hfill \end{array}$$

(8a)

$$\begin{array}{cc}\hfill y_i^{+}=& h_i(w,y),\hfill \end{array}$$

(8b)

for $i=1,\cdots ,N$, and rewrite the dynamics of the network into

$$\begin{array}{cc}\hfill w^{+}=& {\mathit{F}}_{1}w+y,\hfill \end{array}$$

(9a)

$$\begin{array}{cc}\hfill y^{+}=& \mathit{h}(w,y),\hfill \end{array}$$

(9b)

where $\mathit{h}(w,y)={\mathrm{col}}_{i=1}^N\left(h_i(w,y)\right)$, ${\mathit{F}}_1=I_N\otimes F_1$ and ⊗ denotes the Kronecker product.

Next, we attempt to extract the dynamics of y, i.e., $\mathit{h}(w,y)$, from measured data $w\left[k\right]$ and $y\left[k\right]$ using the Koopman operator theory. Define ${\psi }_i(w,y)\in \mathcal{F}$ to be observable for $i=1,\cdots ,q$ where $\mathcal{F}$ is the space of all the complex-valued scalar functions, i.e., $\mathcal{F}=\left\{f\right|f:{\mathbb{R}}^{Nm}\times {\mathbb{R}}^{Nm}\to \mathbb{C}\}$. Let K denote the Koopman operator associated with dynamics (9), which governs the evolution of the observables, i.e.,

$$\begin{array}{c}\hfill K{\psi }_i(w,y)={\psi }_i(w^{+},y^{+})={\psi }_i({\mathit{F}}_{1}w+y,\mathit{h}(w,y)),\end{array}$$

(10)

for $i=1,\cdots ,q$. Define $\mathsf{\Psi }(w,y)=\mathrm{col}({\psi }_1,\cdots ,{\psi }_q):{\mathbb{R}}^{Nm}\times {\mathbb{R}}^{Nm}\to {\mathbb{C}}^q$ to be an observable set. Then, for any observable $\phi \in \mathcal{F}$, which can be approximated as $\phi \approx c_{\phi }\mathsf{\Psi }$, $c_{\phi }\in {\mathbb{C}}^{1\times q}$, it follows from (4) that a q-dimensional approximation of $K\phi$ can be obtained as

$$\begin{array}{c}\hfill K\phi \approx c_{\phi }A\mathsf{\Psi },\end{array}$$

where $A\in {\mathbb{C}}^{q\times q}$ is such that $K\mathsf{\Psi }\approx A\mathsf{\Psi }$. Here, $c_{\phi }$ and A numerically satisfy $c_{\phi }={\mathrm{argmin}}_c{\parallel f-c\mathsf{\Psi }\parallel }_{L_2}$ and $A={\mathrm{argmin}}_H{\parallel \mathsf{\Psi }({\mathit{F}}_{1}w+y,\mathit{h}(w,y))-H\mathsf{\Psi }\parallel }_{L_2}$, respectively. As a result, by considering the states y as variables, the right-hand side of (9b) can be approximated as

$$\begin{array}{c}\hfill \mathit{h}(w,y)=Ky\approx C_{y}A\mathsf{\Psi }(w,y),\end{array}$$

where $C_y$ is such that $y\equiv C_y\mathsf{\Psi }(w,y)$. Note that the existence of the expansion matrix $C_y$ can always be ensured by including the states w and y as observables in $\mathsf{\Psi }(w,y)$. The identification problem is then reduced to obtaining A, which is a matrix approximation of K.

To obtain A from data, suppose that $M+2$ steps of data, indexed by $w\left[0\right],w\left[1\right],\cdots ,w\left[M\right],w[M+1]$, are measured. Then, data for $y\left[k\right]$ can be obtained as $y\left[k\right]=w[k+1]-{\mathit{F}}_{1}w\left[k\right]$ for $k=0,\cdots ,M$. Define data matrices $X,Y\in {\mathbb{C}}^{q\times M}$ as

$$\begin{array}{cc}\hfill X=& \left[\begin{array}{ccc}\mathsf{\Psi }\left(w\right[0],y[0\left]\right)& \cdots & \mathsf{\Psi }\left(w\right[M-1],y[M-1\left]\right)\end{array}\right],\hfill \end{array}$$

(11a)

$$\begin{array}{cc}\hfill Y=& \left[\begin{array}{ccc}\mathsf{\Psi }\left(w\right[1],y[1\left]\right)& \cdots & \mathsf{\Psi }\left(w\right[M],y[M\left]\right)\end{array}\right].\hfill \end{array}$$

(11b)

According to the definition of K, i.e., (10), entries in Y contain the evolution of the observations in X so $KX=Y$ holds, and the desired A can be obtained as the transition matrix that maps X to Y, i.e.,

$$\begin{array}{c}\hfill A=\underset{H}{\mathrm{argmin}}{\parallel HX-Y\parallel }_F^2,\end{array}$$

(12)

where ${\parallel ·\parallel }_F$ denotes the Frobenius norm. Denote the optimality of optimization problem (12) by $A^{opt}$, and an approximation of dynamics (9b) is obtained as

$$\begin{array}{c}\hfill y^{+,id}={\mathit{h}}^{id}(w,y)=C_y{A}^{opt}\mathsf{\Psi }(w,y).\end{array}$$

(13)

Next, we obtain information about the network structure from the identified dynamics of y, i.e., ${\mathit{h}}^{id}(w,y)$. Specifically, we extract the information sent to the nodes from other nodes via the network [31]. If all the connections in the network were cut, then $\mathit{g}\left(x\right)=0$ and $y_i^{+}$ should depend only on $y_i$ and $w_i$. This fact indicates that the transmission from node j to node i can be identified as the terms in the dynamical model of node i that depends on $w_j$ or $y_j$. It follows (13) that for the ith node,

$$\begin{array}{c}\hfill y_i^{+}=C_i{C}_y{A}^{opt}\mathsf{\Psi }(w,y),\end{array}$$

(14)

where $C_i\in {\mathbb{R}}^{m\times Nm}$ is such that $y_i\equiv C_{i}y$. Define ${\mathsf{\Psi }}_i(w_i,y_i)\in {\mathbb{R}}^q$ to be the observable vector such that all the entries, which are dependent on $w_j$ or $y_j$ for any $j\ne i$, in $\mathsf{\Psi }(w,y)$ are set to 0, and define ${\mathsf{\Psi }}_i^{\prime }(w,y)=\mathsf{\Psi }(w,y)-{\mathsf{\Psi }}_i(w_i,y_i)$. Note that ${\mathsf{\Psi }}_i(w_i,y_i)$ now contains observables that only depend on the states of node i. Then, (14) can be rewritten as

$$\begin{array}{c}\hfill y_i^{+}=C_i{C}_y{A}^{opt}{\mathsf{\Psi }}_i(w_i,y_i)+C_i{C}_y{A}^{opt}{\mathsf{\Psi }}_i^{\prime }(w,y).\end{array}$$

(15)

Here, $C_i{C}_y{A}^{opt}{\mathsf{\Psi }}_i^{\prime }(w,y)$ corresponds to the information sent from other nodes to node i via the network, and is considered as the network structure to be identified. As a result, the dynamics of the network are identified as

$$\begin{array}{cc}\hfill w^{+}=& {\mathit{F}}_{1}w+y\hfill \end{array}$$

(16a)

$$\begin{array}{cc}\hfill y^{+,id}=& {\mathrm{col}}_{i=1}^N\left(C_i{C}_y{A}^{opt}{\mathsf{\Psi }}_i(w_i,y_i)\right)+{\mathit{g}}^{id}(w,y),\hfill \end{array}$$

(16b)

where

$$\begin{array}{c}\hfill {\mathit{g}}^{id}(w,y)={\mathrm{col}}_{i=1}^N\left(C_i{C}_y{A}^{opt}{\mathsf{\Psi }}_i^{\prime }(w,y)\right)\end{array}$$

(17)

is the identified coupling function.

Remark 1.

Since $T{x}_i$ in (7b) is $n-m$ dimensional, theoretically only $n-m$ linearly independent variables are required to fully describe the dynamics. Without loss of generality, define ${\tilde{y}}_i$ to be a vector consisting of the first $n-m$ linearly independent entries in $y_i$ and define $\tilde{y}={\mathrm{col}}_{i=1}^N\left({\tilde{y}}_i\right)\in {\mathbb{R}}^{N(n-m)}$. Then, dynamics (9b) can be rewritten into

$$\begin{array}{c}\hfill y^{+}={\mathit{h}}^{\prime }(w,\tilde{y}),\end{array}$$

(18)

where ${\mathit{h}}^{\prime }:{\mathbb{R}}^{Nm}\times {\mathbb{R}}^{N(n-m)}\to {\mathbb{R}}^{Nm}$.

Next, we consider the case where $\dim \left(y_i\right)+m<n$. In such a case, with $y_i$ defined by $y_i=F_2{x}_i+C\tau \left(x_i\right)+CB{u}_i\left(x\right)$, as in (8), $\dim \left(\mathrm{col}(w_i,y_i)\right)<\dim \left(x_i\right)$, which means that additional variables are required for the dynamics of $x_i$ to be fully embedded into the space spanned by the new variables. Here, we make use of delay coordinates [32] to complement the dimension. Let r be the smallest integer such that $r·\dim \left(y_i\right)+m\ge n$, and rewrite the dynamics of the network (9) into

$$\begin{array}{cc}\hfill w^{+}=& {\mathit{F}}_{1}w+y,\hfill \end{array}$$

(19a)

$$\begin{array}{cc}\hfill y^{r+}=& \mathit{h}(w,y,\cdots ,y^{(r-1)+}),\hfill \end{array}$$

(19b)

where ${\mathit{F}}_1$ is defined the same as in (9). Further, define $z_i=y^{i+}\in {\mathbb{R}}^{Nm}$ for $i=1,\cdots ,r-1$ and define $z=\mathrm{col}(z_1,\cdots ,z_{r-1})$. Then, we have $\dim \left(\mathrm{col}(w,y,z)\right)=r·\dim \left(y_i\right)+m\ge n$ and the dynamics of x can be embedded into the space spanned by $w,y$ and z. The identification is then performed by finding an approximation $A^{opt}$ of the Koopman operator defined by

$$\begin{array}{cc}\hfill K{\psi }_i& (w,y,z_1,\cdots ,z_{r-1})={\psi }_i({\mathit{F}}_{1}w+y,z_1,z_2,\cdots ,\mathit{h}(w,y,z)),\hfill \end{array}$$

(20)

using data matrices defined by

$$\begin{array}{cc}\hfill X=& \left[\begin{array}{ccc}\mathsf{\Psi }\left(w\right[0],y[0],z[0\left]\right)& \cdots & \mathsf{\Psi }\left(w\right[M-1],y[M-1],z[M-1\left]\right)\end{array}\right],\hfill \end{array}$$

(21a)

$$\begin{array}{cc}\hfill Y=& \left[\begin{array}{ccc}\mathsf{\Psi }\left(w\right[1],y[1],z[1\left]\right)& \cdots & \mathsf{\Psi }\left(w\right[M],y[M],z[M\left]\right)\end{array}\right]\hfill \end{array}$$

(21b)

constructed with $M+r$ steps of measured data of w. The dynamics of the network are identified as

$$\begin{array}{cc}\hfill w^{+}=& {\mathit{F}}_{1}w+y,\hfill \\ \hfill y^{+}=& z_1,\hfill \\ \hfill z_1^{+}=& z_2,\hfill \\ \hfill & ⋮\hfill \\ \hfill z_{r-1}^{+}=& {\mathrm{col}}_{i=1}^N\left(C_i{C}_z{A}^{opt}{\mathsf{\Psi }}_i(w,y,z)\right)+{\mathit{g}}^{id}(w,y,z),\hfill \end{array}$$

where $C_z\in {\mathbb{R}}^{Nm\times q}$ is such that $z_{r-1}\equiv C_z\mathsf{\Psi }(w,y,z_1,\cdots ,z_{r-1})$, ${\mathsf{\Psi }}_i$ contains observables that solely depend on the states of node i, and

$$\begin{array}{c}\hfill {\mathit{g}}^{id}(w,y,z)={\mathrm{col}}_{i=1}^N\left(C_i{C}_z{A}^{opt}{\mathsf{\Psi }}_i^{\prime }(w,y,z)\right)\end{array}$$

(22)

is the identified coupling function, where ${\mathsf{\Psi }}_i^{\prime }=\mathsf{\Psi }-{\mathsf{\Psi }}_i$ as in (15). Note that the case where $\dim \left(y_i\right)+m\ge n$ can be considered as a special case where $r=1$ and z does not exist.

The proposed identification algorithm is summarized as Algorithm 1.

Algorithm 1 Proposed identification algorithm

Input: measured time series of the outputs of the nodes, $F{x}_i$ as an approximation of $f\left(x_i\right)$, C, and n Output:${\mathit{g}}^{id}(w,y)$ or ${\mathit{g}}^{id}(w,y,z)$    1. Initialization: find r as the minimum integer with which $r·\dim \left(y_i\right)+m\ge n$    2. Matrices construction:    if $r=1$ then       design an observable set $\mathsf{\Psi }(w,y)$ and construct data matrices $X,Y$ with (11)    else       design an observable set $\mathsf{\Psi }(w,y,z)$ and construct data matrices $X,Y$ with (21)    end if    3. Approximate the Koopman operator: calculate $A^{opt}$ with (12)    4. Obtain the coupling function:    if $r=1$ then       obtain ${\mathit{g}}^{id}(w,y)$ with (17)    else       obtain ${\mathit{g}}^{id}(w,y,z)$ with (22)    end if    5. Output:${\mathit{g}}^{id}(w,y)$ or ${\mathit{g}}^{id}(w,y,z)$

Next, we consider the relationship between the identified coupling function ${\mathit{g}}^{id}(w,y,z)$ and the original $\mathit{g}\left(x\right)$, and discuss the identification error in terms of the difference between the original and the identified dynamics of the measured output w.

Proposition 1.

If the amount of data is sufficiently large ($M\to \infty$) and the data are uniformly random, then for $i=1,\cdots ,N$ and $j=1,\cdots ,m$, the jth component of the identified coupling function for the ith node, i.e., ${\mathit{e}}_j^{\top }{C}_i{\mathit{g}}^{id}(w,y,z)$, is a projection of ${\mathit{e}}_j{(w_i^{+}-F_1{w}_i)}^{r+}$ onto $\mathrm{span}\left\{{\mathsf{\Psi }}_i\right\}$:

$$\begin{array}{cc}\hfill {\mathit{e}}_j^{\top }{C}_i{\mathit{g}}^{id}(w,y,z)=& {\mathbb{P}}_{\mathrm{span}\left\{{\mathsf{\Psi }}_i^{\prime }(w,y,z)\right\}}\left({\mathit{e}}_j^{\top }{(w_i^{+}-F_1{w}_i)}^{r+}\right)\hfill \end{array}$$

(23)

with respective to dynamics (19).

Proof. 

We first show the relationship between the theoretical and the identified dynamics of y, and then show the validity of Equation (23).

As shown in [25,35], the solution of optimization problem (12), i.e., $A^{opt}$, minimizes ${\parallel A\mathsf{\Psi }(w,y,z)-K\mathsf{\Psi }(w,y,z)\parallel }_{L_2}$ over the manifold where data are measured, so $A^{opt}$ is an approximation of the Koopman operator defined in (10), in the sense that for any complex-value scalar function $\phi (w,y,z)$ [35],

$$\begin{array}{c}\hfill {\mathbb{P}}_{\mathrm{span}\left\{\mathsf{\Psi }\right\}}\left(K\left({\mathbb{P}}_{\mathrm{span}\left\{\mathsf{\Psi }\right\}}\phi \right)\right)=c_{\phi }{A}^{opt}\mathsf{\Psi }(w,y,z),\end{array}$$

where $c_{\phi }={\mathrm{argmin}}_c{\parallel \phi -c\mathsf{\Psi }(w,y,z)\parallel }_{L_2}$. Since we can design $\mathsf{\Psi }$ to contain $w,y$ and z as observables, the evolution of the jth entry of $y_i$ is obtained as

$$\begin{array}{cc}\hfill {\mathit{e}}_j^{\top }{C}_i{y}^{r+,id}={\mathit{e}}_j^{\top }{C}_i{z}_{r-1}^{+,id}=& {\mathit{e}}_j^{\top }{C}_i{C}_z{A}^{opt}\mathsf{\Psi }(w,y,z)\hfill \\ \hfill =& {\mathbb{P}}_{\mathrm{span}\left\{\mathsf{\Psi }\right\}}\left({\mathit{e}}_j^{\top }{C}_i{z}_{r-1}^{+}\right)={\mathbb{P}}_{\mathrm{span}\left\{\mathsf{\Psi }\right\}}\left({\mathit{e}}_j^{\top }{C}_i{y}^{r+}\right),\hfill \end{array}$$

i.e., the identified evolution ${\mathit{e}}_j^{\top }{C}_i{y}^{r+,id}$ is a projection of the true evolution ${\mathit{e}}_j^{\top }{C}_i{y}^{r+}$ onto the space spanned by the observables in $\mathsf{\Psi }(w,y,z)$.

On the other hand, by the construction of ${\mathit{g}}^{id}(w,y,z)$ in (22), the coupling function of node i is obtained as a linear combination of the observables in ${\mathsf{\Psi }}_i^{\prime }(w,y,z)$, i.e.,

$$\begin{array}{cc}\hfill {\mathit{e}}_j^{\top }{C}_i{\mathit{g}}^{id}(w,y,z)=& {\mathbb{P}}_{\mathrm{span}\left\{{\mathsf{\Psi }}_i^{\prime }(w,y,z)\right\}}\left({\mathit{e}}_j^{\top }{C}_i{z}_{r-1}^{+,id}\right)\hfill \\ \hfill =& {\mathbb{P}}_{\mathrm{span}\left\{{\mathsf{\Psi }}_i^{\prime }(w,y,z)\right\}}{\mathbb{P}}_{\mathrm{span}\left\{\mathsf{\Psi }\right\}}\left({\mathit{e}}_j^{\top }{C}_i{y}^{r+}\right).\hfill \end{array}$$

Making use of dynamics (19a) that $w^{+}-{\mathit{F}}_{1}w=y$ and the fact that $\mathrm{span}\left\{{\mathsf{\Psi }}_i^{\prime }(w,y,z)\right\}\subset \mathrm{span}\left\{\mathsf{\Psi }(w,y,z)\right\}$, we have

$$\begin{array}{cc}\hfill {\mathit{e}}_j^{\top }{C}_i{\mathit{g}}^{id}(w,y,z)=& {\mathbb{P}}_{\mathrm{span}\left\{{\mathsf{\Psi }}_i^{\prime }(w,y,z)\right\}}\left({\mathit{e}}_j^{\top }{C}_i{y}^{r+}\right)\hfill \\ \hfill =& {\mathbb{P}}_{\mathrm{span}\left\{{\mathsf{\Psi }}_i^{\prime }(w,y,z)\right\}}\left({\mathit{e}}_j^{\top }{(w_i^{+}-F_1{w}_i)}^{r+}\right).\hfill \end{array}$$

where we substituted $C_{i}y=y_i=w_i^{+}-F_1{w}_i$. □

Proposition 1 means that the coupling function is obtained in terms of the r-step-future and the $(r+1)$-step-future values of w, which is estimated using the dynamics identified from measured data. On the other hand, the identification error of the proposed method depends on two factors, namely the design of the observable set $\mathsf{\Psi }(w,y,z)$ and the amount of measured data [25,31]. To reduce the identification errors, one could design the observable set sufficiently rich to obtain a close approximation of $\mathit{h}(w,y,z)$, and increase the amount of measurements.

Remark 2.

The Koopman mode decomposition theory guarantees that the evolution of any coupling function can be decomposed into a linear combination of the evolution of an infinite amount of eigenfunctions, i.e., $\phi ={\sum }_{j=1}^{\infty }K{\lambda }_j{\varphi }_j$, $\forall \phi \in \mathcal{F}$, and such decomposition holds globally in the space of state variables. In practical situations, since we can only handle a finite amount of variables, the dynamic-mode-composition-like numerical method we employed is only able to recover point spectra of the Koopman operator [36,37]. As a result, the proposed method gives an optimal coefficient matrix of the observable vector such that the corresponding linear combination approximates the coupling function over a certain set where data are measured.

Remark 3.

The observable set should be designed sufficiently rich to reach high accuracy, and the computational cost would blow up as the number of nodes or the complexity of the coupling function increase. Since there is no a priori knowledge about the coupling functions, we can only design the observable set to be as rich as possible to hope the spanned space contains the coupling function, i.e., using trigonometric basis or power series. Raising the amount of observables would also lead to higher computational costs, which reveals a trade-off between computation costs and identification accuracy of nonlinearity.

4. Numerical Examples

4.1. Identification without Dimension Complement

Consider a network of eight interconnected systems described by

$$\begin{array}{cc}\hfill x_{i1}^{+}=& x_{i1}+0.1\left(x_{i2}\right),\hfill \end{array}$$

(24a)

$$\begin{array}{cc}\hfill x_{i2}^{+}=& x_{i2}+0.1(-x_{i1}+x_{i2}-x_{i1}^2{x}_{i2}+x_{i3}),\hfill \end{array}$$

(24b)

$$\begin{array}{cc}\hfill x_{i3}^{+}=& x_{i3}+0.1(-x_{i3}+u_i),\hfill \\ \hfill u_i=& \sum _{j=1}^8{a}_{ij}(x_{2j}-x_{2i}),w_i={\left(\begin{array}{cc}{x}_{i1}& x_{i2}\end{array}\right)}^{\top },\hfill \end{array}$$

(24c)

for $i=1,\cdots ,8$, which are Van der Pol oscillators with damped inputs and discretized using the first order Euler method with 0.1-long time steps. Suppose that only linearized models of the oscillators are known:

$$\begin{array}{cc}\hfill w_{i1}^{+}=& w_{i1}+0.1w_{i2}+{\tau }_{i1}\left(x\right),\hfill \\ \hfill w_{i2}^{+}=& -0.1w_{i1}+1.1w_{i2}+{\tau }_{i2}\left(x\right),\hfill \\ \hfill x_{i3}^{+}=& 0.9x_{i3}+{\tau }_{i3}\left(x\right).\hfill \end{array}$$

Define $y_{i1}={\tau }_{i1}\left(x\right),y_{i2}={\tau }_{i2}\left(x\right)$ and consider the nodes described by $(w_i,y_i)$:

$$\begin{array}{cc}\hfill w_{i1}^{+}=& w_{i1}+0.1w_{i2}+y_{i1},\hfill \\ \hfill w_{i2}^{+}=& -0.1w_{i1}+1.1w_{i2}+y_{i2},\hfill \\ \hfill y_{i1}^{+}=& h_{i1}(w,y),\hfill \\ \hfill y_{i2}^{+}=& h_{i2}(w,y),\hfill \end{array}$$

where $w={\mathrm{col}}_{i=1}^8\left(w_i\right)$ and $y={\mathrm{col}}_{i=1}^8\left(y_i\right)$. Rewrite the dynamics of the network into

$$\begin{array}{cc}\hfill w^{+}=& \mathit{F}w+y,\hfill \\ \hfill y^{+}=& \mathit{h}(w,y),\hfill \end{array}$$

where $\mathit{F}=I_8\otimes \left[\begin{array}{cc}1& 0.1\\ -0.1& 1.1\end{array}\right]$.

Suppose that 5000 trajectories of three steps of the outputs, denoted by ${}^{j}w,{}^j{w}^{+},{}^j{w}^{2+}$, are measured from random initial points distributed uniformly in ${[-2,2]}^{16}$. Then, data for y and $y^{+}$ can be calculated as

$$\begin{array}{cc}\hfill {}^j{y}_{i1}=& {}^j{w}_{i1}^{+}-{}^j{w}_{i1}-0.1\left({}^j{w}_{i2}\right),\hfill \\ \hfill {}^j{y}_{i2}=& {}^j{w}_{i2}^{+}+0.1\left({}^j{w}_{i1}\right)-1.1\left({}^j{w}_{i2}\right),\hfill \\ \hfill {}^j{y}_{i1}^{+}=& {}^j{w}_{i1}^{2+}-{}^j{w}_{i1}^{+}-0.1\left({}^j{w}_{i2}^{+}\right),\hfill \\ \hfill {}^j{y}_{i2}^{+}=& {}^j{w}_{i2}^{2+}+0.1\left({}^j{w}_{i1}^{+}\right)-1.1\left({}^j{w}_{i2}^{+}\right),\hfill \end{array}$$

for $j=1,\cdots ,5000$. Define Koopman operator K by

$$\begin{array}{c}\hfill K\psi (w,y)=\psi (\mathit{F}w+y,\mathit{h}(w,y\left)\right),\end{array}$$

(25)

where $\psi :{\mathbb{R}}^{16}\times {\mathbb{R}}^{16}\to \mathbb{C}$. To obtain an approximation of K, define $\mathsf{\Psi }(w,y):{\mathbb{R}}^{16}\times {\mathbb{R}}^{16}\to {\mathbb{R}}^{321}$ as

$$\begin{array}{cc}\hfill \mathsf{\Psi }(w,y)=& \mathrm{col}(1,w,y,w_{i1}{w}_{i2},w_{i1}{y}_{i1},w_{i1}{y}_{i2},w_{i2}{y}_{i1},w_{i2}{y}_{i2},y_{i1}{y}_{i2},w_{i1}^2,w_{i2}^2,y_{i1}^2,y_{i2}^2,\hfill \\ \hfill & w_{i1}^2{w}_{i2},w_{i1}{w}_{i2}^2,w_{i1}^2{y}_{i1},w_{i1}{y}_{i1}^2,w_{i1}^2{y}_{i2},w_{i1}{y}_{i2}^2,w_{i2}^2{y}_{i1},w_{i2}{y}_{i1}^2,w_{i2}^2{y}_{i2},\hfill \\ \hfill & w_{i2}{y}_{i2}^2,y_{i1}^2{y}_{i2},y_{i1}{y}_{i2}^2,w_{i1}{w}_{i2}{y}_{i1},w_{i1}{w}_{i2}{y}_{i2},\hfill \\ \hfill & cos{w}_{i1},cos{w}_{i2},cos{y}_{i1},cos{y}_{i2},sin{w}_{i1},sin{w}_{i2},sin{y}_{i1},sin{y}_{i2},\hfill \\ \hfill & cos{w}_{i1}sin{w}_{i1},cos{w}_{i2}sin{w}_{i2},cos{y}_{i1}sin{y}_{i1},cos{y}_{i2}sin{y}_{i2}),\hfill \end{array}$$

(26)

where the variables with subscript i denote abbreviations of the corresponding states of all the nodes, i.e., $y_{i1}{w}_{i1}$ is an abbreviation of ${\mathrm{col}}_{i=1}^N\left(y_{i1}{w}_{i1}\right)$. Define data matrices $X,Y$ by

$$\begin{array}{cc}\hfill X=& \left[\begin{array}{ccc}\mathsf{\Psi }({}^{1}w,{}^{1}y)& \cdots & \mathsf{\Psi }({}^{5000}w,{}^{5000}y)\end{array}\right],\hfill \\ \hfill Y=& \left[\begin{array}{ccc}\mathsf{\Psi }({}^1{w}^{+},{}^1{y}^{+})& \cdots & \mathsf{\Psi }({}^{5000}{w}^{+},{}^{5000}{y}^{+})\end{array}\right].\hfill \end{array}$$

Then, a matrix approximation of K can be obtained as $A={\mathrm{argmin}}_H{\parallel HX-Y\parallel }_F$, and $\mathit{h}(w,y)$ can be obtained as

$$\begin{array}{c}\hfill {\mathit{h}}^{id}(w,y)=C_{y}A\mathsf{\Psi }(w,y),\end{array}$$

where $C_y=\left[\begin{array}{ccc}{\mathbf{0}}_{16\times 17}& I_{16}& {\mathbf{0}}_{16\times 288}\end{array}\right]$ is such that $C_y\mathsf{\Psi }(w,y)=y$. Entries of the obtained $C_{y}A$ is plotted in Figure 1, where the color at coordinate $(i,j)$ represents the value of entry ${\left[C_{y}A\right]}_{ij}$.

Next, the first node is taken as an illustrative example to show the process of obtaining the coupling function. The dynamics of $y_{11}$ and $y_{12}$ are identified as

$$\begin{array}{cc}\hfill y_{11}^{+,id}=& {\mathit{e}}_1^{\top }{\mathit{h}}^{id}=0,\hfill \\ \hfill y_{12}^{+,id}=& {\mathit{e}}_9^{\top }{\mathit{h}}^{id}=-0.084{\psi }_2-0.029{\psi }_{10}+0.010{\psi }_{15}+0.010{\psi }_{17}+0.899{\psi }_{26}-0.180{\psi }_{114}\hfill \\ \hfill & -0.022{\psi }_{122}-0.100{\psi }_{130}-0.001{\psi }_{162}-0.020{\psi }_{210}-0.093{\psi }_{258}+0.010{\psi }_{266}\hfill \\ \hfill & +0.009{\psi }_{290}-0.001{\psi }_{298}\hfill \\ \hfill =& -0.084w_{11}-0.029w_{12}+\underline{0.010w_{62}+0.010w_{82}}+0.899y_{12}-0.180w_{11}^2{w}_{21}\hfill \\ \hfill & -0.022w_{11}{w}_{21}^2-0.100w_{11}^2{y}_{12}-0.001w_{12}^2{y}_{12}-0.020w_{11}{w}_{12}{y}_{11}\hfill \\ \hfill & -0.093sin{w}_{11}+0.0102sin{w}_{12}+0.009cos{w}_{11}cos{w}_{11}-0.001cos{w}_{12}sin{w}_{12},\hfill \end{array}$$

where entries smaller than $\mathcal{O}(5\times {10}^{-4})$ are omitted. Here, only the terms $0.010{\psi }_{15}+0.010{\psi }_{17}$ contain states sent from other nodes, and are hence considered the coupling function. As a result, the dynamics of the first node are identified as

$$\begin{array}{cc}\hfill w_{11}^{+}=& w_{11}+0.1w_{12}+y_{11},\hfill \\ \hfill w_{12}^{+}=& -0.1w_{11}+1.1w_{12}+y_{12},\hfill \\ \hfill y_{11}^{+}=& 0,\hfill \\ \hfill y_{12}^{+}=& \sum _{i\in N_1}{\left[C_{y}A\right]}_{(9,i)}{\psi }_i+0.01w_{62}+0.01w_{82},\hfill \end{array}$$

where $N_1=\{2,10,26,114,122,130,162,210,258,266,290,298\}$. By performing the same procedures to all nodes, the topology of the network is then identified as shown in Figure 2. A comparison between a reconstructed system using the identified result and the original is also shown in Figure 3. As the figure shows, starting from the same initial position, the reconstructed system is able to track the original for the first 50 steps, and deviates due to identification errors.

Theoretically, complex-valued observables are required to ensure that the space spanned by the observables is invariant under the actions of Koopman operators. However, for the purpose of coupling function identification, instead of the full spectral properties, we are only interested in $K\mathrm{col}(w,y,z)$, i.e., the evolution of the states as observables. As shown in Proposition 1 and Section 4, [25], what the proposed method obtains is a projection of the coupling function onto the span of the observables, so we only have to make sure that the coupling function is contained in the span of the observables to reach high accuracy. As a result, in this section, real-valued observables are employed.

4.2. Identification with Dimension Complement

In this subsection, consider the case where the dimension of the output is so low that the dynamics of the nodes cannot be embedded into the space spanned by w and y, i.e., the case where $r>1$. Consider a network of 12 nodes described by

$$\begin{array}{cc}\hfill x_{i,1}^{+}=& 0.9x_{i,1}+x_{i,2}+x_{i,3},\hfill \end{array}$$

(27a)

$$\begin{array}{cc}\hfill x_{i,2}^{+}=& -0.9x_{i,2}+x_{i,3}+u_i,\hfill \end{array}$$

(27b)

$$\begin{array}{cc}\hfill x_{i,3}^{+}=& 0.01x_{i,3}+1.2(x_{i,1}+x_{i,2}+x_{i,3})(x_{i,1}+x_{i,2}+x_{i,3}-1),\hfill \\ \hfill u_i=& 0.1\sum _{j=1}^{12}{a}_{ij}(x_{i,2}-x_{j,2}),w_i=x_{i,1},\hfill \end{array}$$

(27c)

for $i=1,\cdots ,12$. The trajectory of node i described by (27) when $u_i=0$ is shown in Figure 4.

Suppose that only a linearized model in the space spanned by the output, which is also inaccurate, is known, i.e., $w_i^{+}=1.0w_i+{\tau }_i\left(x\right)$, where $1.0w_i$ is the inaccurate known part and ${\tau }_i\left(x\right)$ denotes the unknown dynamics. Reformulate the dynamics of the nodes into the following form

$$\begin{array}{cc}\hfill w_i^{+}=& w_i+y_i,\hfill \\ \hfill y_i^{+}=& z_i,\hfill \\ \hfill z_i^{+}=& h_i(w,y,z),\hfill \end{array}$$

and rewrite the dynamics of the network into

$$\begin{array}{cc}\hfill w^{+}=& w+y,\hfill \end{array}$$

(28a)

$$\begin{array}{cc}\hfill y^{+}=& z,\hfill \end{array}$$

(28b)

$$\begin{array}{cc}\hfill z^{+}=& \mathit{h}(w,y,z),\hfill \end{array}$$

(28c)

where $w={\mathrm{col}}_{i=1}^{12}\left(w_i\right)\in {\mathbb{R}}^{12}$, $y={\mathrm{col}}_{i=1}^{12}\left(y_i\right)\in {\mathbb{R}}^{12}$ and $z={\mathrm{col}}_{i=1}^{12}\left(z_i\right)\in {\mathbb{R}}^{12}$. Let $\psi (w,y,z):{\mathbb{R}}^{36}\to \mathbb{C}$ denote an observable and defined Koopman operator K by

$$\begin{array}{c}\hfill K\psi (w,y,z)=\psi (w+y,z,\mathit{h}(w,y,z\left)\right).\end{array}$$

Next, consider the problem of obtaining an approximation of K. Define a set of observable functions $\mathsf{\Psi }(w,y,z):{\mathbb{R}}^{36}\to {\mathbb{R}}^{109}$ by

$$\begin{array}{cc}\hfill \mathsf{\Psi }(w,y,z)=& \mathrm{col}(1,w,y,z,{\mathrm{col}}_{i=1}^{12}\left(w_i{y}_i\right),{\mathrm{col}}_{i=1}^{12}\left(w_i{z}_i\right),{\mathrm{col}}_{i=1}^{12}\left(y_i{z}_i\right),\hfill \\ \hfill & {\mathrm{col}}_{i=1}^{12}\left(w_i^2\right),{\mathrm{col}}_{i=1}^{12}\left(y_i^2\right),{\mathrm{col}}_{i=1}^{12}\left(z_i^2\right)),\hfill \end{array}$$

(29)

and suppose that a 203-step-long trajectory of the outputs of the coupled nodes in the network are measured, which is denoted by $w\left[k\right]\in {\mathbb{R}}^{12}$ for $k=1,\cdots ,203$. Then, data series of y and z are obtained as

$$\begin{array}{cc}\hfill y\left[k\right]=& w[k+1]-w\left[k\right],k=1,\cdots ,202,\hfill \\ \hfill z\left[k\right]=& y[k+1],k=1,\cdots ,201,\hfill \end{array}$$

and $\mathrm{col}\left(w\right[k],y[k],z[k\left]\right)$ for $k=1,\cdots ,201$ is a 201-step-long trajectory of system (28). Define data matrices $X,Y\in {\mathbb{R}}^{109\times 200}$ by

$$\begin{array}{cc}\hfill X=& \left[\begin{array}{ccc}\mathsf{\Psi }\left(w\right[1],y[1],z[1\left]\right)& \cdots & \mathsf{\Psi }\left(w\right[200],y[200],z[200\left]\right)\end{array}\right],\hfill \end{array}$$

(30a)

$$\begin{array}{cc}\hfill Y=& \left[\begin{array}{ccc}\mathsf{\Psi }\left(w\right[2],y[2],z[2\left]\right)& \cdots & \mathsf{\Psi }\left(w\right[201],y[201],z[201\left]\right)\end{array}\right],\hfill \end{array}$$

(30b)

and a matrix approximation A of Koopman K can be obtained as

$$\begin{array}{c}\hfill A=\underset{H}{\mathrm{argmin}}{\parallel HX-Y\parallel }_F.\end{array}$$

As the result of the identification, the obtained $CA$ matrix, where C is such that $C\mathsf{\Psi }(w,y,z)=\mathrm{col}(w,y,z)$, is shown in Figure 5, which corresponds to the identified dynamics of $w,y$ and z. The $\mathit{h}(w,y,z)$ function is identified as

$$\begin{array}{c}\hfill {\mathit{h}}^{id}(w,y,z)=C_{z}A\mathsf{\Psi }(w,y,z),\end{array}$$

where $C_z\in {\mathbb{R}}^{12\times 109}$ is such that $z\equiv C_z\mathsf{\Psi }(w,y,z)$, and is also the sub-matrix consisting of the 25th, $\cdots ,36$th rows in $CA$. As an illustrative example, the 26th row of $CA$, i.e., the second row of $C_{z}A$, which corresponds to the unknown dynamics of the second node, i.e., $h_2(w,y,z)$, reads

$$\begin{array}{cc}\hfill {\mathit{e}}_{26}^{\top }CA\mathsf{\Psi }(w,y,z)=& -3.8742{\psi }_3-0.1419{\psi }_5-3.6510{\psi }_{15}-0.1290{\psi }_{17}-2.0900{\psi }_{27}\hfill \\ & -0.1000{\psi }_{29}+7.6560{\psi }_{39}+0.2640{\psi }_{41}+2.6400{\psi }_{51}+2.6400{\psi }_{63}\hfill \\ & +4.0656{\psi }_{75}+0.1452{\psi }_{77}+3.6120{\psi }_{87}+0.1200{\psi }_{89}+1.2000{\psi }_{99}\hfill \\ \hfill =& -3.8742w_2-0.1419w_4-3.6510y_2-0.1290y_4-2.0900z_2\hfill \\ & -0.1000z_4+7.6560w_2{y}_2+0.2640w_4{y}_4+2.6400w_2{z}_2+2.6400y_2{z}_2\hfill \\ & +4.0656w_2^2+0.1452w_4^2+3.6120y_2^2+0.1200y_4^2+1.2000z_2^2,\hfill \end{array}$$

where readings smaller than $\mathcal{O}\left({10}^{-4}\right)$ are omitted. It can be seen that node 2 only receives transmission from node 4, which is explicitly identified as the terms in ${\mathit{e}}_{26}^{\top }CA\mathsf{\Psi }(w,y,z)$, i.e.,

$$\begin{array}{c}\hfill g_2^{id}=-0.1419w_4-0.1290y_4-0.1000z_4+0.2640w_4{y}_4+0.1452w_4^2+0.1200y_4^2.\end{array}$$

Figure 6 shows comparisons of trajectories of system (28) with the identified ${\mathit{h}}^{id}(w,y,z)$ function and the original system starting from the same initial values. Specifically, the new states $w,y,z$ and the corresponding true values $w^t,y^t,z^t$, calculated by

$$\begin{array}{cc}\hfill w_i^t=& x_{i,1},\hfill \\ \hfill y_i^t=& x_{i,2}+x_{i,3}-0.1x_{i,1},\hfill \\ \hfill z_i^t=& -0.09x_{i,1}-1.0x_{i,2}+0.91x_{i,3}+1.2(x_{i,1}+x_{i,2}+x_{i,3})(x_{i,1}+x_{i,2}+x_{i,3}-1.0)+u_i\left(x\right),\hfill \end{array}$$

respectively, are compared. As the figures show, the errors between the trajectories stay low for around 250 steps, and deviate due to small identification errors. The identified network topology is shown in Figure 7, and the coupling function is obtained from ${\mathit{h}}^{id}$ using (22). This example also indicates that incorrectness of the a priori linear model in the space spanned by the outputs would not disable the proposed identification method.

5. Conclusions

In this paper, we considered the identification problem of network structures using measured output data. We modeled the structures of networks as coupling functions that describe the data transmission in the networks, and proposed identification methods to identify the coupling functions from measured data. The identification was performed in a three-step manner, and we extracted the coupling function using the output and newly defined variables. The proposed method makes it possible to identify possibly nonlinear coupling function from measured output data of networks whose nodes have unknown dynamics. Numerical identification examples showed the usefulness and validity of the obtained results.