Numerically Stable form of Green’s Function for a Free-Free Uniform Timoshenko Beam

Abstract

Beam models are widely applied in civil engineering, transport, and industry because the beams are basic structural elements. When dealing with the high-order modes of beam in the context of applying the modal analysis method, the numerical instability issue affects the numeric simulation accuracy in many boundary conditions. There are two solutions in literature to overcome this shortcoming, namely refinement of the asymptotic form for the high order modes and reshaping the terms within the equation of the modes to eliminate the source of the numerical instability. In this paper, the numerical instability issue is signalled when the standard form of Green’s function, which includes hyperbolic functions, is applied to a free-free Timoshenko length-long beam. A new way is proposed based on new set of eigenfunctions, including an exponential function, to construct a new form of Green’s function. To this end, it starts from a new general form of Green’s function and the characteristic equation is obtained; then, based on the boundary condition, the Green’s function associated to the differential operator of the free-free Timoshenko beam is distilled. The numerical stability of the new form of the Green’s function is verified in a numerical application and the results are compared with those obtained by using the standard form of the Green’s function.

1. Introduction

Beams are structural elements characterized by the fact that the length is much higher than the cross-section dimensions and resist lateral loads. In addition to the cross-section shape and length, the beams are featured by the way they are supported at the ends, the equilibrium conditions, and the material from which they are made. Beams are extensively used in civil engineering, transport, and industry [1,2,3,4].

Several classical beam models are known that assume different mathematical forms depending on the working assumptions [5]. The Euler–Bernoulli model [6,7,8], the Rayleigh model [9,10], and the Timoshenko model [11,12] are mentioned. The Euler–Bernoulli model is the simplest because it considers only the bending deformation and the linear inertia. The Rayleigh model additionally introduces the rotation inertia and the Timoshenko model completes the beam model with the shear deformation. The Timoshenko model is a reliable model as it has been experimentally proven in many works, among which is ref. [13]. These models describe the propagation of bending waves through a beam with accuracy depending on the simplifications made. Thus, evanescent waves and propagating waves are highlighted. When the frequency of excitation is low, the wavelength of the propagating wave is much longer than the characteristic dimension of the cross-section of the beam, namely the radius of gyration, and the solutions given by the above models are convergent. For a high frequency of the excitation, the influence of the shear deformation and the inertia of the cross-section rotation becomes significant, and that is why the more accurate predictions are obtained using the Timoshenko model.

Moreover, also at high frequency, there are differences between the models in terms of the type of bending waves propagating along the beam. While the Euler–Bernoulli beam model shows the coexistence of evanescent and propagating waves regardless of the excitation frequency, the Timoshenko model predicts the transformation of evanescent waves into propagating waves if the frequency exceeds a certain value. The Timoshenko beam is said to have two spectra. The first spectrum is like that of the Euler–Bernoulli beam in the sense that evanescent and propagating waves coexist, and the second spectrum is characterized by the fact that two propagating waves with different wavelengths propagate through the beam.

The differential equations of motion of the beam models can be solved by several methods, including the following: the modal analysis method by which the response of the beam is the result of the superposition of its natural vibration modes [8,14,15]; the direct method where the input force is included in the boundary condition for the problem [6,16,17]; and the Green’s function method, which represents the frequency response to a unitary harmonic force (receptance), and the vibration is obtained by applying the convolution theorem [12,18,19,20].

The successful application of one or another of the methods for solving the differential equations of motion depends, among other things, on its numerical stability in the sense that the results must not be affected by substantial floating-point errors [21,22,23,24].

Numerical instability is related to the calculation in floating point when the small difference between two very large numbers is calculated. Numerical calculation in floating point is zero instead of a small, but significant number. Such situations were reported when numerical evaluation of the high-mode shapes of Euler–Bernoulli and Timoshenko uniform or stepped beams were performed to apply the modal analysis method [21,22,23,24,25,26,27].

The usual form of the mode shapes derived from the differential operators that describe the vibration of a beam depending on the boundary conditions is constructed using the pairs of trigonometric and hyperbolic functions: sine and cosine; and hyperbolic sine and hyperbolic cosine, respectively. The trigonometric functions describe the propagation of propagating waves, and the hyperbolic ones describe the propagation of evanescent waves.

The use of hyperbolic functions can lead to the numerically unstable shape

$$E(x)=\sinh k_{d}x-\cosh k_{d}x,$$

(1)

where k_d is the attenuation constant of the evanescent wave, and x, the coordinate of the beam. When the argument of the function E(x) is large enough, the result of the calculation in floating point is zero.

For instance, the modal shape of the n order of a free-free Euler–Bernoulli beam can be written as [28]

$$X_n(x)=\sin k_{n}x+\sinh k_{n}x-\frac{\sin k_{n}l-\sinh k_{n}l}{\cos k_{n}l-\cosh k_{n}l}\left(\cosh k_{n}x+\cos k_{n}x\right),$$

(2)

where l is the beam length and k_nl verifies the characteristic equation

$$\cos k_{n}l\cosh k_{n}l-1=0$$

(3)

It should be noted that for the Euler–Bernoulli beam model, the attenuation constant of the evanescent wave equals the wave number of the propagative wave and because of that, the trigonometric functions and the hyperbolic functions have the same arguments (k_nx or k_nl).

Figure 1 shows the modal shape for n = 10, 11, and 14, which has been calculated using the MATLAB environment of ordinary precision. It is observed that while the modal shape of the 11th order is affected at the beam end by the numerical instability, the modal shape of the 10th order is still calculated within an acceptable margin of error. When the order of the modal shape is higher, for instance, n = 14, the numerical calculation exhibits zero value because the modal shape is reduced to Equation (1) from a numerical viewpoint. A similar result has been reported in ref. [24]; however, this is for a clamped-clamped Euler–Bernoulli beam.

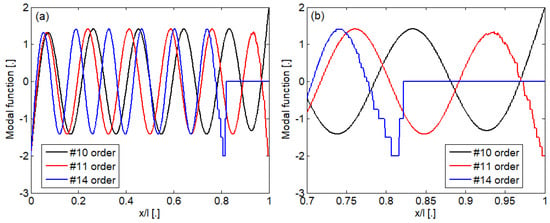
Figure 1. Illustrative for the numerically instability of the modal shape of a free-free Euler–Bernoulli beam: (a) full modal shape; (b) detail.

Two different solutions have been advanced: the construction of an asymptotic form for the high-order modes [25,27] and the restructuration of the equation of the modes to eliminate the source of the numerical instability [21,22,23,24,26].

In this paper, it is shown that the application of the Green’s function method can be affected by the problem of numerical instability, taking as an example the vibration of a free-free Timoshenko beam. The standard form of the Green’s function includes the hyperbolic sine and cosine functions, which model the evanescent waves whose existence is specific to the first spectrum; in addition, because of this, the calculated spectrum experiences distortions at medium frequencies in the case of long-length beams. It has been demonstrated that the numerical instability starts from the middle of the frequency range of the first spectrum and advances to both its ends as the beam length increases. To overcome this problem, a new approach is proposed which starts from a new basis in the solutions space of the differential operator of the Timoshenko beam, namely a new set of eigenfunctions including the exponential function of a positive and negative real argument to model the evanescent waves. By imposing the specific boundary conditions of the Timoshenko beam, a new form of the Green’s function is constructed, which proves to be numerically stable in the case of long-length beams.

2. Mechanical Model and Equations of Motion

Let us consider a uniform Timoshenko beam of length l under the action of a time-dependent transversal force (Figure 2). Parameters of the beam are as follows: Young’s modulus E, the shear modulus G, the density ρ, the mass per length unit m, the cross-section area S, the area moment of inertia I, and the shear coefficient κ.

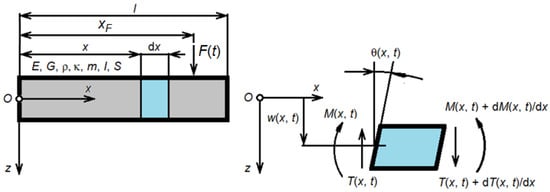
Figure 2. Mechanical model of the free-free Timoshenko beam.

Equations of motion describing the bending motion of the beam can be written as:

$$\begin{array}{l}GS\kappa \left[\frac{{\partial }^{2}w(x,t)}{\partial x^2}-\frac{\partial \mathsf{\theta }(x,t)}{\partial x}\right]-m\frac{{\partial }^{2}w(x,t)}{\partial t^2}=-F(t)\mathsf{\delta }\left(x-x_F\right)\\ EI\frac{{\partial }^2\mathsf{\theta }(x,t)}{\partial x^2}+GS\mathsf{\kappa }\left[\frac{\partial w\left(x,t\right)}{\partial x}-\mathsf{\theta }\left(x,t\right)\right]-\mathsf{\rho }I\frac{{\partial }^2\mathsf{\theta }\left(x,t\right)}{\partial t^2}=0,\end{array}$$

(4)

where w(x, t) and θ(x, t) are the displacement and rotation of the cross-section of the beam; F(t) is the transversal force, and x_F—the distance between the reference frame Oxz fixed at the left end of the beam and the active cross-section where the force is applied; t stands for the time and x stands for the coordinate along the beam; and, in the following, it defines the passive cross-section where the beam response is calculated.

Boundary conditions associated to the free-free beam refer to the shear force T(x, t) and the bending moment M(x, t):

$$T(x,t)=GS\mathsf{\kappa }\left[\frac{\partial w(x,t)}{\partial x}-\mathsf{\theta }(x,t)\right],\begin{array}{cc}& M(x,t)=\end{array}EI\frac{\partial \mathsf{\theta }(x,t)}{\partial x}$$

(5)

which must be zero at the beam ends

$$\begin{array}{l}\begin{array}{cc}\frac{\partial w(0,t)}{\partial x}-\mathsf{\theta }(0,t)=0,& \frac{\partial \mathsf{\theta }(0,t)}{\partial x}=0\end{array}\\ \begin{array}{cc}\frac{\partial w(l,t)}{\partial x}-\mathsf{\theta }(l,t)=0,& \frac{\partial \mathsf{\theta }(l,t)}{\partial x}=0\end{array}\end{array}$$

(6)

Considering the steady-state harmonic behaviour, the following complex variables can be introduced:

$$\begin{array}{ccc}\stackrel{-}{w}(x,t)=\stackrel{-}{w}(x)e^{i\mathsf{\omega }t},& \stackrel{-}{\mathsf{\theta }}(x,t)=\stackrel{-}{\mathsf{\theta }}(x)e^{i\mathsf{\omega }t},& \stackrel{-}{F}(t)=\stackrel{-}{F}{e}^{i\mathsf{\omega }t},\end{array}$$

(7)

where $\stackrel{-}{w}(x)$, $\stackrel{-}{\mathsf{\theta }}(x)$, and $\stackrel{-}{F}$ are the complex amplitudes; ω is the ungular frequency; and i² = −1. Appendix A presents the reason behind Equation (7).

Inserting the complex variables (7) in the equations of motion (4), it obtains

$$\begin{array}{l}GS\mathsf{\kappa }\left[\frac{{\mathrm{d}}^2\stackrel{-}{w}(x)}{\mathrm{d}{x}^2}-\frac{\mathrm{d}\stackrel{-}{\mathsf{\theta }}(x)}{\mathrm{d}x}\right]+{\mathsf{\omega }}^{2}m\stackrel{-}{w}(x)=-\stackrel{-}{F}\mathsf{\delta }\left(x-x_F\right),\\ EI\frac{{\mathrm{d}}^2\stackrel{-}{\mathsf{\theta }}(x)}{\mathrm{d}{x}^2}+GS\mathsf{\kappa }\left[\frac{\mathrm{d}\stackrel{-}{w}(x)}{\mathrm{d}x}-\stackrel{-}{\mathsf{\theta }}(x)\right]{+\mathsf{\omega }}^2\mathsf{\rho }I\stackrel{-}{\mathsf{\theta }}(x)=0.\end{array}$$

(8)

Boundary conditions (6) take the following form:

$$\begin{array}{l}\frac{\mathrm{d}\stackrel{-}{w}(0)}{\mathrm{d}x}-\stackrel{-}{\mathsf{\theta }}(0)=0,\begin{array}{cc}& \end{array}\frac{\mathrm{d}\stackrel{-}{\mathsf{\theta }}(0)}{\mathrm{d}x}=0\\ \frac{\mathrm{d}\stackrel{-}{w}(l)}{\mathrm{d}x}-\stackrel{-}{\mathsf{\theta }}(l)=0,\begin{array}{cc}& \end{array}\frac{\mathrm{d}\stackrel{-}{\mathsf{\theta }}(l)}{\mathrm{d}x}=0\end{array}$$

(9)

Eliminating the angle of rotation of the cross-section in (8), the following equation in the displacement of the beam results:

$$D_T\stackrel{-}{w}(x)=-\left(\frac{{\mathsf{\omega }}^2\mathsf{\rho }I}{GS\kappa }-1\right)\stackrel{-}{F}\mathsf{\delta }\left(x-x_F\right)-\frac{EI}{GS\kappa }\stackrel{-}{F} \mathsf{\delta } ″\left(x-x_F\right)$$

(10)

where D_T is the differential operator

$$D_T=EI\frac{{\mathrm{d}}^4}{\mathrm{d}{x}^4}+{\mathsf{\omega }}^2\mathsf{\rho }I\left(1+\frac{E}{G\mathsf{\kappa }}\right)\frac{{\mathrm{d}}^2}{\mathrm{d}{x}^2}+{\mathsf{\omega }}^{2}m\left(\frac{{\mathsf{\omega }}^2\mathsf{\rho }I}{GS\kappa }-1\right).$$

(11)

The corresponding boundary conditions associated to Equation (10), which are derived from Equation (9), are

$$\begin{array}{l}\begin{array}{cc}\frac{{\mathrm{d}}^2\stackrel{-}{w}(0)}{\mathrm{d}{x}^2}+k_s^2\stackrel{-}{w}(0)=0,& \frac{{\mathrm{d}}^3\stackrel{-}{w}(0)}{\mathrm{d}{x}^2}+\left(k_l^2+k_s^2\right)\frac{\mathrm{d}\stackrel{-}{w}(0)}{\mathrm{d}x}=0\end{array};\\ \begin{array}{cc}\frac{{\mathrm{d}}^2\stackrel{-}{w}(l)}{\mathrm{d}{x}^2}+k_s^2\stackrel{-}{w}(l)=0,& \frac{{\mathrm{d}}^3\stackrel{-}{w}(l)}{\mathrm{d}{x}^2}+\left(k_l^2+k_s^2\right)\frac{\mathrm{d}\stackrel{-}{w}(l)}{\mathrm{d}x}=0,\end{array}\end{array}$$

(12)

where

$$\begin{array}{cc}{k}_l^2=\frac{{\mathsf{\omega }}^2\mathsf{\rho }}{E},& k_s^2=\frac{{\mathsf{\omega }}^2\mathsf{\rho }}{G\mathsf{\kappa }}.\end{array}$$

(13)

In the next section, the solution to the differential equations (10) and the corresponding boundary conditions (12) is expressed in terms of Green’s functions associated to the D_T operator.

3. Green’s Functions Method

Green’s function of the D_T differential operator verifies the equation

$$D_{T}G(x,\mathsf{\xi })=\mathsf{\delta }(x-\mathsf{\xi })$$

(14)

and the boundary conditions derived from Equation (12)

$$\begin{array}{l}\begin{array}{cc}\frac{{\mathrm{d}}^{2}G(0,\mathsf{\xi })}{\mathrm{d}{x}^2}+k_s^{2}G(0,\mathsf{\xi })=0,& \frac{{\mathrm{d}}^{3}G(0,\mathsf{\xi })}{\mathrm{d}{x}^2}+\left(k_l^2+k_s^2\right)\frac{\mathrm{d}G(0,\mathsf{\xi })}{\mathrm{d}x}=0\end{array};\\ \begin{array}{cc}\frac{{\mathrm{d}}^{2}G(l,\mathsf{\xi })}{\mathrm{d}{x}^2}+k_s^{2}G(l,\mathsf{\xi })=0,& \frac{{\mathrm{d}}^{3}G(l,\mathsf{\xi })}{\mathrm{d}{x}^2}+\left(k_l^2+k_s^2\right)\frac{\mathrm{d}G(l,\mathsf{\xi })}{\mathrm{d}x}=0.\end{array}\end{array}$$

(15)

Green’s function is a linear combination of the eigenfunctions of that operator and to find these eigenfunctions, the starting point is the homogeneous equation derived from Equation (14)

$$D_{T}G(x,\mathsf{\xi })=0,$$

(16)

seeking the solutions of the following form

$$G(x,\mathsf{\xi })=A(\mathsf{\xi })e^{kx},$$

(17)

where A(ξ) is a function depending on the boundary conditions, and k is a complex parameter.

Inserting the form (17) in Equation (16), the characteristic equation of the D_T differential operator results:

$$k^4+\left(k_l^2+k_s^2\right)k^2+k_l^2{k}_s^2-k_{E-B}^4=0,$$

(18)

where

$$k_{E-B}=\sqrt[4]{\frac{{\mathsf{\omega }}^{2}m}{EI}}$$

(19)

is the wavenumber of the Euler–Bernoulli beam.

Solutions of the characteristic equation are the eigenvalues of the D_T differential operator, and their nature are depending on the angular frequency ω. Considering the first spectrum of the beam meaning

$${\mathsf{\omega }}_{\lim }<\sqrt{\frac{GS\mathsf{\kappa }}{\mathsf{\rho }I}},$$

(20)

the eigenvalues take the forms ±k_d and ±ik_p, where

$$k_{d,p}=\frac{\sqrt{2}}{2}\sqrt{\sqrt{{\left(k_l^2+k_s^2\right)}^2+4\left(k_{E-B}^4-k_l^2{k}_s^2\right)}\mp \left(k_l^2+k_s^2\right)}.$$

(21)

Appendix B gives the details of the calculation regarding Equation (21).

It should be mentioned that the eigenvalues are the propagation constants of the waves that travel in the Timoshenko beam, namely k_d is for the evanescent waves and ik_p is for the propagative waves. The minus sign indicates the progressive waves and the plus sign is associated to the regressive waves.

Figure 3 presents the propagation constant of the evanescent wave, k_d, and the imaginary part of the propagation constant of the propagative wave, k_p, versus the angular frequency within the frequency range of the first spectrum. While k_p increases monotonically from zero, the propagation constant k_d has an increasing–decreasing pattern with a maximum, max(k_d), at the angular frequency ω_o and a zero at ω_lim.

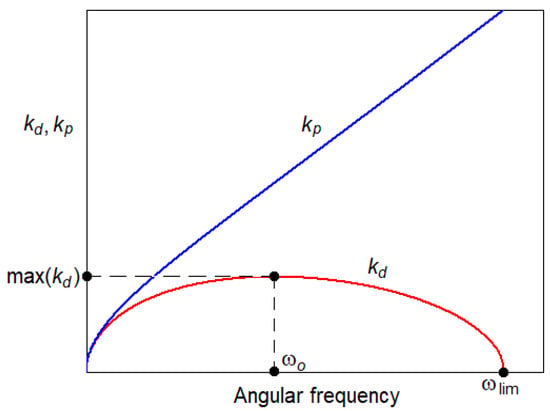
Figure 3. Propagation constants of the Timoshenko beam.

The angular frequency ω_o is obtained from the equation

$$\frac{\mathrm{d}{k}_d}{\mathrm{d}\mathsf{\omega }}=0.$$

(22)

After a few calculations detailed in Appendix C, the form is arrived at

$$\mathsf{\rho }{\left(\frac{1}{E}-\frac{1}{G\mathsf{\kappa }}\right)}^2{\mathsf{\omega }}^4+4\frac{S}{EI}{\mathsf{\omega }}^2-\frac{G{S}^2\mathsf{\kappa }}{E{I}^2\mathsf{\rho }}=0.$$

(23)

By searching for the positive solutions, the angular frequency corresponding to the maximum value of k_d is reached

$${\mathsf{\omega }}_o=\frac{G\mathsf{\kappa }}{E-G\mathsf{\kappa }}\sqrt{2\frac{ES}{\mathsf{\rho }I}\left(\sqrt{\frac{{\left(E-G\mathsf{\kappa }\right)}^2}{4EG\mathsf{\kappa }}+1}-1\right)},$$

(24)

which is close to the middle of the spectrum; E, G, and κ are constants of material and the denominator E − Gκ is positive.

Maximum value of k_d results:

$$\max \left(k_d\right)=\frac{\sqrt{2}}{2}\sqrt{\sqrt{{\left(k_{l_o}^2+k_{s_o}^2\right)}^2+4\left(k_{E-B_o}^4-k_{l_o}^2{k}_{s_o}^2\right)}-\left(k_{l_o}^2+k_{s_o}^2\right)},$$

(25)

where

$$\begin{array}{ccc}{k}_{l_o}^2=\frac{{\mathsf{\omega }}_o^2\mathsf{\rho }}{E},& k_{s_o}^2=\frac{{\mathsf{\omega }}_o^2\mathsf{\rho }}{G\mathsf{\kappa }},& k_{E-B_o}=\sqrt[4]{\frac{{\mathsf{\omega }}_o^{2}m}{EI}}.\end{array}$$

(26)

Corresponding to the above eigenvalues, the eigenfunctions usually used to construct Green’s functions are [29]:

$$\begin{array}{cccc}\sinh k_{d}x,& \cosh k_{d}x,& \sin k_{p}x,& \cos k_{p}x.\end{array}$$

(27)

Instead of the hyperbolic functions, the exponential functions are considered for Green’s function, which can be written as

$$G(x,\mathsf{\xi })=\{\begin{array}{cc}{G}^{-}(x,\mathsf{\xi })=A_1(\mathsf{\xi })e^{k_{d}x}+A_2(\mathsf{\xi })e^{-k_{d}x}+A_3(\mathsf{\xi })\sin k_{p}x+A_4(\mathsf{\xi })\cos k_{p}x& 0<x<\mathsf{\xi }\\ G^{+}(x,\mathsf{\xi })=B_1(\mathsf{\xi })e^{k_{d}x}+B_2(\mathsf{\xi })e^{-k_{d}x}+B_3(\mathsf{\xi })\sin k_{p}x+B_4(\mathsf{\xi })\cos k_{p}x& \mathsf{\xi }<x<l\end{array}$$

(28)

Green’s function and the first two derivatives are continuous functions for x = ξ, and the third derivative experiences a discontinuity of 1/(EI) magnitude

$$\begin{array}{cccc}{G}^{-}(\xi ,\xi )=G^{+}(\xi ,\xi ),& \frac{d{G}^{-}(\xi ,\xi )}{dx}=\frac{d{G}^{+}(\xi ,\xi )}{dx},& \frac{d^2{G}^{-}(\xi ,\xi )}{d{x}^2}=\frac{d^2{G}^{+}(\xi ,\xi )}{d{x}^2};& \frac{d^3{G}^{+}(\xi +0,\xi )}{d{x}^3}-\frac{d^3{G}^{-}(\xi -0,\xi )}{d{x}^3}\end{array}=\frac{1}{EI}$$

(29)

The above-mentioned conditions lead to the following matrix equation:

$$\left[\begin{array}{cccc}{e}^{k_d\mathsf{\xi }}& e^{-k_d\mathsf{\xi }}& \sin k_p\mathsf{\xi }& \cos k_p\mathsf{\xi }\\ k_d{e}^{k_d\mathsf{\xi }}& -k_d{e}^{-k_d\mathsf{\xi }}& k_p\cos k_p\mathsf{\xi }& -k_p\sin k_p\mathsf{\xi }\\ k_d^2{e}^{k_d\mathsf{\xi }}& k_d^2{e}^{-k_d\mathsf{\xi }}& -k_p^2\sin k_p\mathsf{\xi }& -k_p^2\cos k_p\mathsf{\xi }\\ k_d^3{e}^{k_d\mathsf{\xi }}& -k_d^3{e}^{-k_d\mathsf{\xi }}& -k_p^3\cos k_p\mathsf{\xi }& k_p^3\sin k_p\mathsf{\xi }\end{array}\right]\left[\begin{array}{c}{Y}_1\\ Y_2\\ Y_3\\ Y_4\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\\ \frac{1}{EI}\end{array}\right],$$

(30)

where

$$\begin{array}{cc}{Y}_i=B_i-A_i& i=1÷4.\end{array}$$

(31)

The solution to the matrix Equation (30) holds

$${\left[\begin{array}{cccc}{Y}_1& Y_2& Y_3& Y_4\end{array}\right]}^T=R{\left[\begin{array}{cccc}\frac{e^{-k_d\xi }}{2k_d}& -\frac{e^{k_d\xi }}{2k_d}& -\frac{\cos k_p\xi }{k_p}& \frac{\sin k_p\xi }{k_p}\end{array}\right]}^T,$$

(32)

where

$$R=\frac{1}{EI\left(k_d^2+k_p^2\right)}.$$

(33)

Using relations (28) and (32), Green’s function becomes

$$G(x,\mathsf{\xi })=A_1(\mathsf{\xi })e^{k_{d}x}+A_2(\mathsf{\xi })e^{-k_{d}x}+A_3(\mathsf{\xi })\sin k_{p}x+A_4(\mathsf{\xi })\cos k_{p}x+RH(x-\mathsf{\xi })\left[\frac{e^{k_d(x-\mathsf{\xi })}-e^{-k_d(x-\mathsf{\xi })}}{2k_d}-\frac{\sin k_p(x-\mathsf{\xi })}{k_p}\right]$$

(34)

where H(.) is the Heaviside step function.

Imposing that the Green’s function checks the boundary conditions (15), the functions A_i(ξ) can be calculated.

Inserting (34) in the boundary conditions for the beam displacement (15), it holds

$$\begin{array}{l}{A}_1(\mathsf{\xi })+A_2(\mathsf{\xi })+P{A}_4(\mathsf{\xi })=0\\ A_1(\mathsf{\xi })-A_2(\mathsf{\xi })+Q{A}_3(\mathsf{\xi })=0\\ e^{k_{d}l}{A}_1(\mathsf{\xi })+e^{-k_{d}l}{A}_2(\mathsf{\xi })+P\sin (k_{p}l)A_3(\mathsf{\xi })+P\cos (k_{p}l)A_4(\mathsf{\xi })=-R\left(\frac{e^{k_d(l-\mathsf{\xi })}-e^{-k_d(l-\mathsf{\xi })}}{2k_d}-P\frac{\sin k_p(l-\mathsf{\xi })}{k_p}\right)\\ e^{k_{d}l}{A}_1(\mathsf{\xi })-e^{-k_{d}l}{A}_2(\mathsf{\xi })+Q\cos (k_{p}l)A_3(\mathsf{\xi })-Q\sin (k_{p}l)A_4(\mathsf{\xi })=-R\left(\frac{e^{k_d(l-\mathsf{\xi })}+e^{-k_d(l-\mathsf{\xi })}}{2k_d}-Q\frac{\cos k_p(l-\mathsf{\xi })}{k_p}\right)\end{array}$$

(35)

where

$$\begin{array}{cc}P=\frac{k_s^2-k_p^2}{k_s^2+k_d^2},& Q=\frac{k_p\left(k_l^2+k_s^2-k_p^2\right)}{k_d\left(k_l^2+k_s^2+k_d^2\right)}.\end{array}$$

(36)

Solving the set of Equation (35), it results

$$\begin{array}{l}{A}_1(\mathsf{\xi })=\frac{R}{k_d\mathsf{\Delta }}{\mathsf{\Phi }}_1(\mathsf{\xi })\\ A_2(\mathsf{\xi })=-\frac{R}{k_d\mathsf{\Delta }}{\mathsf{\Phi }}_2(\mathsf{\xi })\\ A_3(\mathsf{\xi })=-\frac{R}{k_{d}Q\mathsf{\Delta }}\left({\mathsf{\Phi }}_1(\mathsf{\xi })+{\mathsf{\Phi }}_2(\mathsf{\xi })\right)\\ A_4(\mathsf{\xi })=-\frac{R}{k_{d}P\mathsf{\Delta }}\left({\mathsf{\Phi }}_1(\mathsf{\xi })-{\mathsf{\Phi }}_2(\mathsf{\xi })\right),\end{array}$$

(37)

where

$$\mathsf{\Delta }=2\left(1+e^{-2k_{d}l}\right)\cos k_{p}l-\left(\frac{P}{Q}-\frac{Q}{P}\right)\left(1-e^{-2k_{d}l}\right)\sin k_{p}l-4e^{-k_{d}l}$$

(38)

$$\begin{array}{l}{\mathsf{\Phi }}_1(\mathsf{\xi })=e^{-k_d(l+\mathsf{\xi })}-e^{-k_d\mathsf{\xi }}\cos k_{p}l+\left[e^{-k_d\mathsf{\xi }}\left(\frac{P}{Q}-\frac{Q}{P}\right)+e^{-k_d(2l-\mathsf{\xi })}\left(\frac{P}{Q}+\frac{Q}{P}\right)\right]\frac{\sin k_{p}l}{2}-\\ -\frac{k_d}{k_p}{e}^{-2k_{d}l}\left[P\sin k_p(l-\mathsf{\xi })+Q\cos k_p(l-\mathsf{\xi })\right]+\frac{k_d}{k_p}{e}^{-k_{d}l}\left(Q\cos k_p\mathsf{\xi }-P\sin k_p\mathsf{\xi }\right)\end{array}$$

(39)

$$\begin{array}{l}{\mathsf{\Phi }}_2(\mathsf{\xi })=e^{-k_d(l-\mathsf{\xi })}-e^{-k_d(2l-\mathsf{\xi })}\cos k_{p}l-\left[e^{-k_d\mathsf{\xi }}\left(\frac{P}{Q}+\frac{Q}{P}\right)+e^{-k_d(2l-\mathsf{\xi })}\left(\frac{P}{Q}-\frac{Q}{P}\right)\right]\frac{\sin k_{p}l}{2}+\\ +\frac{k_d}{k_p}\left[P\sin k_p(l-\mathsf{\xi })-Q\cos k_p(l-\mathsf{\xi })\right]+\frac{k_d}{k_p}{e}^{-k_{d}l}\left(Q\cos k_p\mathsf{\xi }+P\sin k_p\mathsf{\xi }\right).\end{array}$$

(40)

It should be outlined that the equation

$$\mathsf{\Delta }=2\left(1+e^{-2k_{d}l}\right)\cos k_{p}l-\left(\frac{P}{Q}-\frac{Q}{P}\right)\left(1-e^{-2k_{d}l}\right)\sin k_{p}l-4e^{-k_{d}l}=0$$

(41)

is the characteristic equation and gives the natural frequencies of the free-free Timoshenko beam. This form is termed as a numerically stable form of the characteristic equation.

Green’s function for the beam displacement is

$$\begin{array}{cc}\hfill G^w(x,\mathsf{\xi })& =\frac{R}{k_d\mathsf{\Delta }}\left({\mathsf{\Phi }}_1^{*}(\mathsf{\xi },x)-{\mathsf{\Phi }}_2(\mathsf{\xi })e^{-k_{d}x}-\frac{{\mathsf{\Phi }}_1(\mathsf{\xi })+{\mathsf{\Phi }}_2(\mathsf{\xi })}{Q}\sin k_{p}x-\frac{{\mathsf{\Phi }}_1(\mathsf{\xi })-{\mathsf{\Phi }}_2(\mathsf{\xi })}{P}\cos k_{p}x\right)+\hfill \\ & RH(x-\mathsf{\xi })\left[\frac{e^{k_d(x-\mathsf{\xi })}-e^{-k_d(x-\mathsf{\xi })}}{2k_d}-\frac{\sin k_p(x-\mathsf{\xi })}{k_p}\right]\hfill \end{array}$$

(42)

where

$$\begin{array}{c}{\mathsf{\Phi }}_1^{*}(\mathsf{\xi },x)={\mathsf{\Phi }}_1(\mathsf{\xi })e^{k_{d}x}=e^{-k_d(l+\mathsf{\xi }-x)}-e^{-k_d(\mathsf{\xi }-x)}\left[\cos k_{p}l-\left(\frac{P}{Q}-\frac{Q}{P}\right)\frac{\sin k_{p}l}{2}\right]+e^{-k_d(2l-\mathsf{\xi }-x)}\left(\frac{P}{Q}+\frac{Q}{P}\right)\frac{\sin k_{p}l}{2}-\\ -\frac{k_d}{k_p}{e}^{-k_d(2l-x)}\left[P\sin k_p(l-\mathsf{\xi })+Q\cos k_p(l-\mathsf{\xi })\right]+\frac{k_d}{k_p}{e}^{-k_d(l-x)}\left(Q\cos k_p\mathsf{\xi }-P\sin k_p\mathsf{\xi }\right).\end{array}$$

(43)

However, the Green’s function is symmetric due to the Maxwell-Betti theorem

$$G^w(x,\mathsf{\xi })=G^w(\mathsf{\xi },x)$$

(44)

and in virtue of this fact, the Green’s function can be calculated as

$$G^w(x,\mathsf{\xi })=\frac{R}{k_d\mathsf{\Delta }}\left({\mathsf{\Phi }}_1^{*}(\mathsf{\xi },x)-{\mathsf{\Phi }}_2(\mathsf{\xi })e^{-k_{d}x}-\frac{{\mathsf{\Phi }}_1(\mathsf{\xi })+{\mathsf{\Phi }}_2(\mathsf{\xi })}{Q}\sin k_{p}x-\frac{{\mathsf{\Phi }}_1(\mathsf{\xi })-{\mathsf{\Phi }}_2(\mathsf{\xi })}{P}\cos k_{p}x\right) \mathrm{for} 0 < x < \mathsf{\xi } < l.$$

(45)

In addition, for 0 < ξ < x < l, the Green’s function G^w(x, ξ) equals G^w(ξ, x) calculated with the above relation.

In the following lines, this function is termed as the numerically stable form of the Green’s function associated to the D_T differential operator and the F-F boundary conditions.

Indeed, examining the shape of functions Φ₁(ξ), Φ₂(ξ), and Φ*₁(ξ, x), corresponding to Equations (39), (40), and (43), respectively, which are included in the Equation (45) of Green’s function, no numerically unstable shape appears; and all the terms containing k_dl and k_d(ξ − x) are decreasing exponentials as l and (ξ − x) are increasing, assuring the numerical stability of Green’s function.

The solution to Equation (10) can be given in terms of the convolution theorem

$$\stackrel{-}{w}(x)={\displaystyle {\int }_0^l{G}^w(x,\mathsf{\xi })\left[\left(1-\frac{{\mathsf{\omega }}^2\mathsf{\rho }I}{GS\kappa }\right)\stackrel{-}{F}\mathsf{\delta }(\mathsf{\xi }-x_F)-\frac{EI}{GS\kappa }\stackrel{-}{F} \mathsf{\delta } ″(\mathsf{\xi }-x_F)\right]\mathrm{d}\mathsf{\xi }}=\stackrel{-}{F}{G}_F^w(x,x_F),$$

(46)

where $G_F^w(x,\mathsf{\xi })$ is Green’s function of the beam displacement to a transversal force, the so-called receptance

$$G_F^w(x,\mathsf{\xi })=\left(1-\frac{{\mathsf{\omega }}^2\mathsf{\rho }I}{GS\kappa }\right)G^w(x,\mathsf{\xi })-\frac{EI}{GS\kappa }\frac{{\partial }^2{G}^w(x,\mathsf{\xi })}{\partial {\mathsf{\xi }}^2}.$$

(47)

Starting from the eigenfunctions (27) and following the same way as above, the standard form of Green’s function of the D_T differential operator and F-F boundary conditions comes first

$$G_{st}^w(x,\mathsf{\xi })=\frac{R}{k_d{\mathsf{\Delta }}_{st}}\left({\mathsf{\Psi }}_1(\mathsf{\xi })\sinh k_{d}x+{\mathsf{\Psi }}_2(\mathsf{\xi })\cosh k_{d}x-\frac{1}{Q}{\mathsf{\Psi }}_1(\mathsf{\xi })\sin k_{p}x-\frac{1}{P}{\mathsf{\Psi }}_2(\mathsf{\xi })\cos k_{p}x\right),$$

(48)

where

$$\begin{array}{c}{\mathsf{\Psi }}_1(\mathsf{\xi })=Q^2\left(\cosh k_{d}l\cos k_p(l-\mathsf{\xi })-\cos k_p\mathsf{\xi }\right)-QP\sinh k_{d}l\sin k_p(l-\mathsf{\xi })-\\ \frac{Q}{P}\sinh k_d(l-\mathsf{\xi })\sin k_{p}l-\cosh k_d(l-\mathsf{\xi })\cos k_{p}l+\cosh k_d\mathsf{\xi }\end{array}$$

(49)

$$\begin{array}{c}{\mathsf{\Psi }}_2(\mathsf{\xi })=-Q^2\sinh k_{d}l\cos k_p(l-\mathsf{\xi })+QP\left(\sin k_p(l-\mathsf{\xi })\cosh k_{d}l+\sin k_p\mathsf{\xi }\right)+\\ \frac{P}{Q}\cosh k_d(l-\mathsf{\xi })\sin k_{p}l-\sinh k_d(l-\mathsf{\xi })\cos k_{p}l-\sinh k_d\mathsf{\xi }\end{array}$$

(50)

and

$${\mathsf{\Delta }}_{st}=2\left(\cosh k_{d}l\cos k_{p}l-1\right)+\left(\frac{Q}{P}-\frac{P}{Q}\right)\sinh k_{d}l\sin k_{p}l$$

(51)

gives the standard form of the characteristic equation

$${\mathsf{\Delta }}_{st}=2\left(\cosh k_{d}l\cos k_{p}l-1\right)+\left(\frac{Q}{P}-\frac{P}{Q}\right)\sinh k_{d}l\sin k_{p}l=0.$$

(52)

Then, Green’s function of the beam displacement due to a transversal force

$$G_{F,st}^w(x,\mathsf{\xi })=\left(1-\frac{{\mathsf{\omega }}^2\mathsf{\rho }I}{GS\kappa }\right)G_{st}^w(x,\mathsf{\xi })-\frac{EI}{GS\kappa }\frac{{\partial }^2{G}_{st}^w(x,\mathsf{\xi })}{\partial {\mathsf{\xi }}^2}.$$

(53)

holds in the standard form. Equation (51) is equivalent to Equation (20) from ref. [28] and Equation (53) is an alternative to Equation (15) from the same reference.

4. Numerical Application

In this section, the results from some numerical applications are presented to illustrate the effectivity of the numerically stable form of the frequency-domain Green’s function of the free-free uniform Timoshenko beam described in the above section. To this end, the following parameters of the Timoshenko beam are considered: E = 210 GPa, G = 8.08 GPa, κ = 0.4, ρ = 7850 kg/m³, S = 7.69∙10⁻³ m², and I = 30.55∙10⁻⁶ m⁴. These parameter values correspond to the UIC 60 rail type, extensively used in the modern railway tracks. The frequency range of interest is the first spectrum that is discretized by a step of 0.01 Hz. The limit frequency of the first spectrum is given by Equation (20) and for the numerical application, takes the value of 5123.6 Hz. All the calculations are performed using the MATLAB environment with regular precision.

Figure 4 shows the graphic of the Δ and Δ_st functions calculated with Equations (38) and (51); and considering the beam length of 1 m. The standard form Δ_st has a sharply modulated form; meanwhile, the numerically stable form Δ takes an almost harmonic shape. However, there is a perfect match between the zeros of these two forms. The natural frequencies of the beam are at: 956.3 Hz, 2022 Hz, 3144 Hz, 4147 Hz, and 5115 Hz.

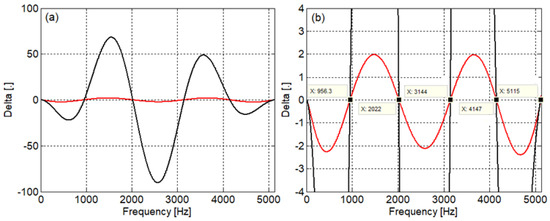
Figure 4. Determination of the natural frequencies of the free-free Timoshenko beam (l = 1 m): (a) graphic of Δ and Δ_st; (b) detail; ──, numerically stable form (Equation (38)); ──, standard form (Equation (51)).

Figure 5 represents the modulus of the beam receptance calculated using both numerically stable and standard forms at the middle (x = l/2) and at the first quarter (x = l/4) of the beam when the active cross-section is at middle (ξ = l/2) for the same beam length of 1 m; in addition, Figure 6 displays the modulus of the beam receptance at the middle and at the first third of the beam (x = l/3) when ξ = l/3. Generally speaking, the beam vibration is the result of the superposition of the symmetric and antisymmetric modes. When the active cross-section is at the beam middle, only the symmetric modes are excited, which explain why the beam receptance within the two diagrams exhibits peaks at three of the five resonance frequencies as can be seen in Figure 5. On the other hand, both symmetric and antisymmetric modes are excited when the active cross-section is situated in any other section excepting the one from the beam middle. This situation is illustrated in Figure 6, where the receptance at the first third has five peaks. However, at the beam middle, only the symmetric modes can be detected because this section is a node for any antisymmetric mode. Regarding the accuracy of the calculus, both forms give similar results as can be seen in the two figures.

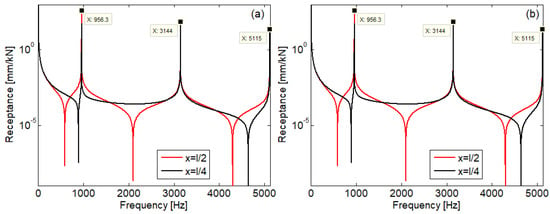
Figure 5. Beam receptance modulus when the active cross-section is at the beam middle (ξ = l/2): (a) numerically stable form; (b) standard form.

Figure 6. Beam receptance modulus when the active cross-section is at the first third (ξ = l/3): (a) numerically stable form; (b) standard form.

In spite of that, closer calculation shows the errors that appear between the results given by the two forms of Green’s function. Thus, Figure 7 and Figure 8 present the absolute values of the relative errors calculated in relation to the receptance obtained with the numerically stable form

$$\left|\mathsf{\epsilon }\right|=100\cdot \frac{\left|G_{F,st}^w(x,\mathsf{\xi })-G_F^w(x,\mathsf{\xi })\right|}{\left|G_F^w(x,\mathsf{\xi })\right|} [\%].$$

Figure 7. Errors between the results given by the two forms when the active cross-section is at the beam middle (ξ = l/2): (a) for receptance at the beam middle; (b) for receptance at the first quarter.

Figure 8. Errors between the receptances calculated by the two forms when the active cross-section is at the first third (ξ = l/3): (a) for receptance at the beam middle; (b) for receptance at the first third.

The errors are very low within the entire frequency range of the first spectrum. Relatively more high values can be observed around the resonance and anti-resonance frequencies; however, these are insignificant, being less than 8.2·10⁻⁸%.

As the beam length increases, the first spectrum becomes richer in harmonics components as can be seen in Figure 9, where the beam receptance was calculated following the same conditions as above (ξ = l/2, and x = l/2 and l/4; and ξ = l/3, and x = l/2 and l/3). Calculation was performed using the numerically stable form of Green’s function for a beam of 20 m length. Features like those highlighted in the case of the 1 m length beam can be outlined: only the symmetrical vibration modes of the beam are excited by the harmonic force applied at the beam middle (diagrams (a) and (b)); and the middle of the beam experiences only symmetrical vibration modes regardless of the section in which the excitation force acts (diagram (c)).

Figure 9. Beam receptance modulus of a 20 m length beam calculated using the numerically stable form of the Green’s function: (a) ξ = l/2 and x = l/2; (b) ξ = l/2 and x = l/4; (c) ξ = l/3 and x = l/2; (d) ξ = l/3 and x = l/3.

When the standard form of Green’s function is used to calculate the beam receptance, the results that are displayed in Figure 10 show numerical instability issues. Receptance calculation is affected by numerical instability mainly when the active cross-section and passive cross-section are identical, especially at the middle of the beam. Indeed, for a beam of a given length l that experiences numerical instability, the most affected component of the frequency response is the one for which k_dl = max(k_dl) = lmax(k_d) and whose angular frequency is ω_o, which is found near the middle of the domain of the first spectrum (see Figure 3). For the numerical application, f_o = ω_o/(2π) = 2304.9 Hz, which represents 89.97% of half of the limit frequency of 5123.6 Hz.

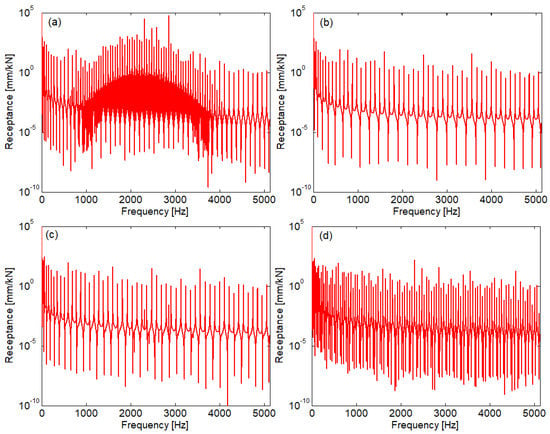
Figure 10. Beam receptance modulus of a 20 m length beam calculated using the standard form of Green’s function: (a) ξ = l/2 and x = l/2; (b) ξ = l/2 and x = l/4 ; (c) ξ = l/3 and x = l/2; (d) ξ = l/3 and x = l/3.

The magnitude of the errors induced by the numerical instability of the standard form of Green’s function can be evaluated following Figure 11. For all the cases examined, errors are very low at the ends of the spectrum; however, they take huge values at the middle frequency.

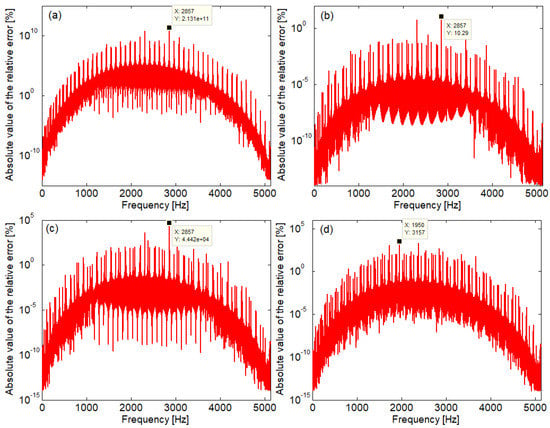
Figure 11. Relative errors between the results obtained with the two forms of Green’s function for a 20 m length beam: (a) ξ = l/2 and x = l/2; (b) ξ = l/2 and x = l/4; (c) ξ = l/3 and x = l/2; (d) ξ = l/3 and x = l/3.

5. Discussion

In this section, some aspects about the concerns regarding the numerical application of the new form of Green’s function of a long-length free-free Timoshenko beam are presented.

The critical parameter of Green’s function from a numerical calculation viewpoint is the beam length, l; and it has been shown what happens when the standard Green’s function is calculated for a long-length beam in the previous section.

Applying the new form of Green’s function, much attention must be paid to the partition step applied to the frequency domain of the first spectrum. If the step length is too large, then the accuracy of the calculation suffers, and the peaks of resonance and anti-resonance are missing. This aspect is illustrated in Figure 12, which shows the receptance modulus of a 100,000 m length beam calculated applying the numerically stable form of Green’s function (ξ = l/3, and x = l/2 and l/3). Figure 12a is obtained using the frequency partition step of 10 mHz, as used in the previous simulations. Figure 12b shows the receptance modulus of the beam when the step of the frequency partition is much finer, namely 10 μHz. The difference is very clear.

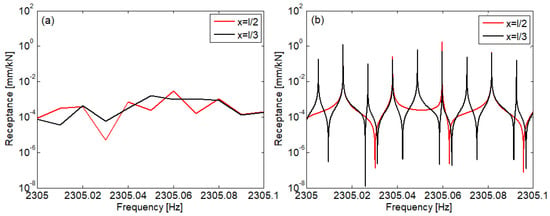
Figure 12. Beam receptance modulus of a 100,000 m length beam calculated using the numerically stable form of the Green’s function (ξ = l/3): (a) Δf = 10 mHz; (b) Δf = 10 μHz.

Obviously, the simulation time increases when the first spectrum of very long-length beams is investigated.

It has to be noticed that for such a long beam, the standard Green’s function does not work at all, and the result is NaN (not a number).

6. Conclusions

Studying beams dynamics is very important as the beams are basis components in mechanical structures. Several beam models are known; however, the most frequently used are the Euler–Bernoulli model and the Timoshenko model. The latter ensures the accuracy of theoretical predictions over an extended frequency range because the effect of the shear force on the rotation of the cross-sections and upon the rotary inertia is included. Among the methods of studying the dynamics of beams, the modal analysis method and Green’s function method can be listed. It is known that the application of modal analysis for higher modes of vibration presents difficulties caused by numerical instability.

In this paper, it was shown that the standard form of the Green’s function associated to the free-free Timoshenko beam built based on the hyperbolic sine and cosine functions presents the same difficulty related to the numerical instability when dealing with long-length beams. This is manifested primarily in the field of medium frequencies by the spectacular distortion of the beam’s frequency response, which spreads toward the spectrum ends as the length beam increases, but never reaching them. For this reason, it is not recommended to use the standard form of the Green’s function for the analysis of long-length beams. On the other hand, it was shown that this difficulty can be overcome if the Green’s function is built based on the exponential function. The new numerically stable form of Green’s function for the free-free Timoshenko beam model was deduced and its effectiveness was shown over the entire frequency range of the first spectrum.

Further research aims to determine the numerically stable form of the Green’s function for the usual end-resting cases.